The counterintuitive role of sexual selection in species maintenance and speciation

Significance

Sexual selection is generally considered to be an important force in the maintenance of species differentiation. Using population genetic models, we show that when isolated in its purest form of Fisherian sexual selection, sexual selection inhibits rather than assists species maintenance and speciation when isolated populations begin to exchange migrants. The stronger this type of sexual selection becomes, the more it erases any effects of local adaptation that drive trait divergence. Furthermore, if the strength of Fisherian sexual selection itself is allowed to evolve, sexual selection is lost. These results emphasize that additional complications have to be added to sexual selection scenarios for sexual selection to contribute to divergence; Fisherian sexual selection alone has the opposite effect.

Abstract

The pronounced and elaborate displays that often differ between closely related animal species have led to the common assumption that sexual selection is important in speciation, especially in geographically separated populations. We use population genetic models to examine the ability of Fisherian sexual selection to contribute to lasting species differentiation by isolating its effect after the onset of gene flow between allopatric populations. We show that when sexually selected traits are under ecologically divergent selection, the situation most favorable to speciation, mating preferences tend to introgress faster than trait alleles, causing sexual selection to counter the effects of local adaptation. As a consequence, the net amount of trait divergence often drops with stronger Fisherian sexual selection. Furthermore, alleles for progressively weaker preferences spread in this context until sexual selection is removed. The effects of pure Fisherian sexual selection on species maintenance are thus much more inhibitory than previously assumed.

The importance of premating isolation as the first barrier to gene flow between species (1, 2), coupled with showy differences between closely related species in sexually selected characters, has led researchers to postulate a causal relationship between sexual selection and speciation (3). This hypothesized relationship seems particularly logical in the case of allopatric speciation; sexual selection may cause mating preferences (usually in females) and trait phenotypes (usually in males) to diverge quickly from one another in isolated populations (4, 5). If this divergence removes the potential of populations to interbreed, separate species would result under the biological species concept (6). In fact, a prominent review of the topic states that “the most obvious way in which sexual selection could accelerate speciation … is via increased coevolution of male traits and female preferences in allopatric populations or if traits involved in mate recognition were under direct environmental selection” (ref. 7, pp. 85–86). Under the latter suggestion, speciation would be particularly favored because divergent environmental selection on traits would maintain trait variation and could guide sexual selection in opposite directions in incipient species (8). In fact, trait alleles that are both under ecologically divergent selection and a component of premating isolation have been termed “magic traits” because of this dual function, which allows speciation to occur unusually easily (8–10).

Whereas it is well established that sexual selection alone is unlikely to drive sympatric speciation (e.g., refs. 10 and 11), the quotation above demonstrates that it is still considered a driving force in speciation that is largely allopatric. We ask the question of whether Fisherian sexual selection per se can really play the role ascribed to sexual selection above, of promoting speciation and species maintenance in allopatry, if species boundaries are tested by the onset of gene flow. Specifically, we consider secondary contact of allopatric populations that have already diverged in preferences and traits and concentrate on the most favorable case for divergence, when sexually selected traits are also locally adapted.

By “Fisherian sexual selection” we are referring to sexual selection in what can be considered its most basic form, in which a genetically encoded female preference imposes differential mating success with regard to a male trait. This nonrandom mating generates linkage disequilibrium, so that evolution by sexual selection on the male trait leads to concomitant evolution of the preference itself (ref. 12, pp. 136–137). To isolate the role of Fisherian sexual selection in species maintenance we primarily consider selectively neutral female preferences. Neutrality of preferences follows the classic scenario considered in early and influential sexual selection models (4, 12, 13) and is viewed as a null model for sexual selection in its simplest form (14). In particular, this is the form of sexual selection used in the model by Lande (4) that arguably first popularized the idea of sexual selection promoting speciation and is still widely cited for this today.

The goal of this study is thus to understand the role that this simplest form of sexual selection plays in speciation and species maintenance; this forms an essential basis upon which to understand deviations from the Fisherian scenario in the form of more complicated (and more realistic) sexual selection assumptions. We touch upon the effects of some of these deviations from the Fisherian model (e.g., search costs, expression of the trait in both sexes, and a best-of-n model) in the process of exploring the robustness of our basic result.

Using population genetic modeling techniques, we find that if allopatric populations come into contact via the onset of gene flow, sexual selection, in its purest form, takes on an inhibitory role, drastically reducing trait differentiation due to divergent local adaptation. This is due to the fact that under this Fisherian model, preferences, which are not under direct selection, equilibrate with little population differentiation, even though trait frequencies may differ greatly due to local adaptation. This creates relatively greater mating opportunities for foreign, rare males in each population, directly countering the effects of local adaptation and reducing population differentiation at a trait locus. Importantly, stronger preferences exaggerate this effect. Fisherian sexual selection is thus a double-edged sword in the development of isolation under these conditions, potentially driving differentiation in allopatry but removing it if there is contact. Ultimately its role in allopatric speciation is tenuous, failing even if contact is initiated after substantive trait and preference divergence has occurred.

Model and Results

We consider a two-locus population genetic model with polygyny (Methods). Locus T has alleles T₁ and T₂, which control two sexually selected phenotypes in males. Locus P determines a female preference; P₁ females are 1 + α₁ times as likely to mate with a T₁ than a T₂ male upon encounter, whereas P₂ females similarly prefer T₂ males with preference strength 1 + α₂. Our basic model, in accordance with the Fisherian models of Lande (4) and Kirkpatrick (13), does not include costs to preferences (this assumption is varied below). Our models are haploid to facilitate analyses, but the key factors that lead to our qualitative results should be readily generalizable to diploids. We assume that two allopatric populations have diverged such that individuals in population 1 have primarily P₁ and T₁ alleles and those in population 2 have primarily P₂ and T₂ alleles. Secondary contact occurs between these populations by symmetric migration with rate m. The onset of migration leads to variation in preferences and traits within each population, and linkage disequilibrium between them becomes established due to nonrandom mating.

We focus on the most favorable situation for the maintenance of species differences, when the trait that is the object of sexual selection is also under ecologically divergent selection (7–10). Specifically, we assume the male trait T is locally adapted such that each trait allele is favored by viability selection (with selection coefficient s) in the population in which it became common in allopatry. The resulting models were analyzed by both numerical and analytical techniques (SI Text).

It is known that sexual selection has the potential to lead to the loss of variation in sexually selected traits across incipient species, eliminating reproductive isolation, and that this is more likely to occur if trait and preference frequencies are increasingly asymmetrical between the diverging types (15–19). Because our goal is to pinpoint the role of sexual selection in species maintenance when this maintenance occurs, we center our analyses on roughly symmetric starting conditions and focus (although not exclusively) on symmetric parameter values. These assumptions should bias our analysis against finding a negative role for sexual selection in maintaining differentiation.

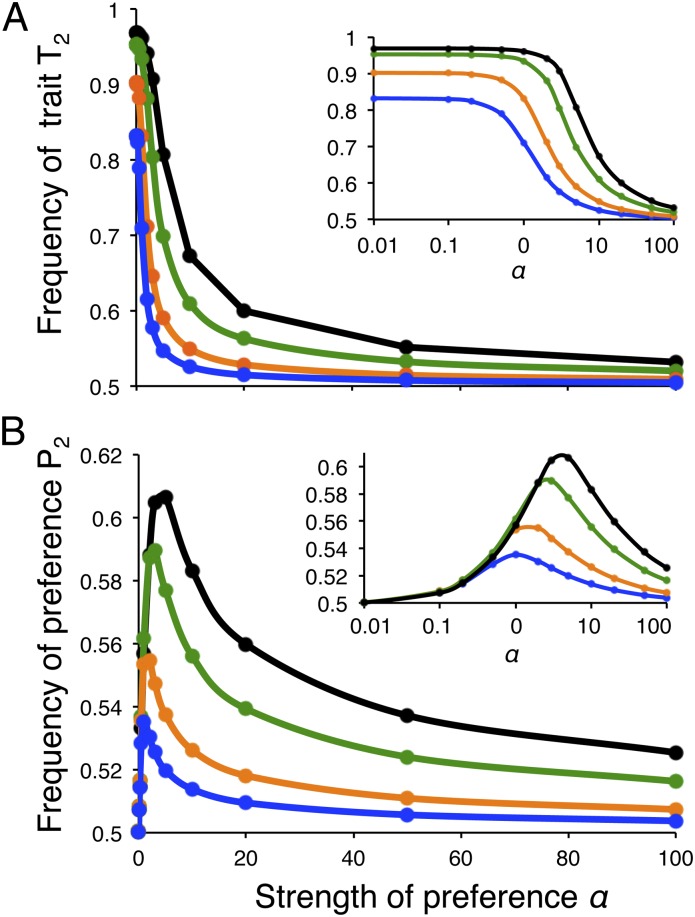
Contrary to intuition, we find that stronger Fisherian sexual selection reduces, rather than enhances, differences in the trait allele frequencies between populations. Although ecologically divergent selection often allows some divergence in trait frequencies to be maintained between populations, this divergence drops as preference strength increases (Fig. 1A). Qualitatively, this drop is very small when preference strengths are very weak, but can become quite notable when preferences rise to moderate strengths (e.g., α = 3 or 5), especially when local adaptation is not exceptionally strong (e.g., s = 0.2 or 0.1). Little divergence remains with very strong preferences. Furthermore, preference divergence is always relatively low. It peaks at moderate values of α and drops further with very strong preferences (discussed below and in Fig. 1B).

Fig. 1.

Male trait and female preference frequencies show a decrease in their differentiation between populations when sexual selection is strong. Shown are the frequencies in population 2 of (A) the trait T₂ and (B) the preference P₂ for a given strength of preference α₁ = α₂ = α from numerical simulations (SI Text). Insets show the same data with α on a Log scale. The frequencies of the T₁ and P₁ alleles in population 1 are seen to converge to the values shown here for population 2. Higher values thus represent more differentiation between the populations in trait and preference frequencies, whereas there is no differentiation at 0.5. In general, minor deviations from symmetry in parameter values did not alter our qualitative results, and the equilibrium values are independent of the starting conditions, although convergence may be very slow (SI Text). With strong asymmetry in s or α Fisherian sexual selection also does not allow for divergence, but the frequencies in both populations may converge to the same side of 0.5 (SI Text). Circles indicate simulation results and the lines connecting them are interpolations. Values of α are 0.01, 0.1, 0.2, 0.5, 1, 2, 3, 5, 10, 20, 50, and 100. The migration rate m = 0.01 and the selection coefficients for local adaptation are s = 0.9 (black), s = 0.5 (green), s = 0.2 (orange), and s = 0.1 (blue).

The inhibitory effect of Fisherian sexual selection on species maintenance can be understood by first noting differences in the magnitude of preference and trait divergence. Taking the perspective of population 2, the trait T₂ is maintained at a frequency t₂ greater than 0.5, indicating trait differentiation between the populations, due to a balance between migration (decreasing t₂) and a combination of viability and sexual selection (increasing t₂). The preference allele P₂ is likewise maintained at a frequency higher than 0.5 through a similar balance between migration and selection, but importantly, preference divergence is always relatively low.

Ultimately, low preference divergence is the result of the fact that viability and sexual selection are transmitted to the preference locus only via the presence of a genetic association, or linkage disequilibrium, between the preference and trait loci. In other words, under Fisherian sexual selection there is no direct selection acting on the preference locus, which has no effect on viability or the mating success of females; all selection on the preference acts indirectly through the trait (4, 13). Upon the onset of low levels of migration, linkage disequilibrium is weak (there is little genetic variation in each population), which causes only weak indirect selection favoring the preference allele P₂, so that migration is the stronger of the two effects. The preference thus tends to homogenize between the two populations and the equilibrium of P₂ in population 2 lies close to 0.5 (see also the results of approximations with weak selection and with strong preferences in SI Text and Fig. S1). We note that additionally, with strong preferences net selection on an initially divergent trait is often negative (below and Fig. S2), causing indirect selection on the preference allele to be also often negative; this reinforces the drop in preference frequencies observed from high initial levels of preference differentiation.

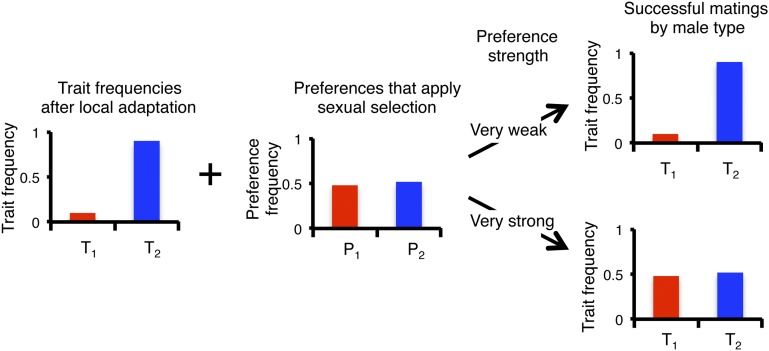
The relatively high frequency of P₁ individuals in population 2 that emerges from the effects above can have a striking effect on the trait frequencies and is responsible for the observed inhibitory effect of sexual selection. Local adaptation can lead to a high frequency t₂ in population 2 after viability selection. However, because close to half of the females in population 2 are P₁ females, T₁ males will have high mating success, relative to their frequency, in this population (Fig. 2). If preferences were very strong, close to half of the matings would go to T₁ males in this polygynous system, even if there were very few of them. Divergence due to local adaptation is thus countered, sometimes to the point of being erased, by strong Fisherian sexual selection. Furthermore, the interaction between preference and trait frequencies is akin to a feedback loop. With strong preferences the net forces of selection favoring T₂ are lower, leading to weaker indirect selection favoring P₂, which drives it even closer to a frequency of 0.5, in turn further reducing trait differentiation.

Fig. 2.

Mechanism whereby strong Fisherian sexual selection reduces divergence between populations. Consider trait frequencies in population 2. Under very weak sexual selection the trait frequencies among successfully mated males mirror the trait frequencies after local adaptation. With very strong sexual selection the frequencies of the trait alleles among successfully mated males instead mirror the frequencies of females that prefer each male type.

A version of the model in which traits are expressed in both sexes (departing from ref. 4) confirms a drop in local trait frequencies with stronger preferences when preference strength is low to moderate, but, interestingly, shows that this effect is reversed when preferences are already very high (α > ∼10; SI Text and Fig. S3). Stronger preferences increase the linkage disequilibrium between preference and trait loci. When preference strength and this disequilibrium are high enough, higher survival of females with the local trait allele can lead to a high frequency of females with local preferences at the time of mating, and this effect can increase if preferences are strengthened even further. A higher frequency of females with the local preference prevents or even reverses the erasure of local adaptation with stronger preferences that is described above.

A different perspective into the effects of natural and sexual selection on trait divergence in this Fisherian model can be gained by examining a decomposition of the recursion equations, using the notation of Barton and Turelli (20) and Kirkpatrick et al. (21) (here we return to the assumption that the trait is expressed only in males). Using this methodology, and exactly matching the equations developed in Methods, the recursion equations for T₂ and P₂ in population 2 can be written, respectively, as

$$\mathrm{\Delta }{t}_{2,2}=\frac{1}{2}{a}_{2_{0,T}}{t}_{2,2}^{\ast }\left(1-t_{2,2}^{\ast }\right)+m\left(t_{2,1}-t_{2,2}\right)$$ [1]

and

$$\mathrm{\Delta }{p}_{2,2}=\frac{1}{2}{a}_{2_{0,T}}{D}_2^{\ast }+m\left(p_{2,1}-p_{2,2}\right),$$ [2]

where t_2,i, p_2,i, and D_i indicate the frequencies of T₂, P₂, and the linkage disequilibrium between them in population i, respectively, and an asterisk indicates the values are after migration. The second terms in Eqs. 1 and 2 account for the change in the frequencies of the alleles due to migration (equation 29 in ref. 21). The first term in each equation accounts for the change in each allele frequency due to direct natural and sexual selection acting on the trait locus in Eq. 1 and indirect selection acting on the preference locus via linkage disequilibrium with the trait in Eq. 2. These changes occur only in males, leading to a coefficient of 1/2 for these terms.

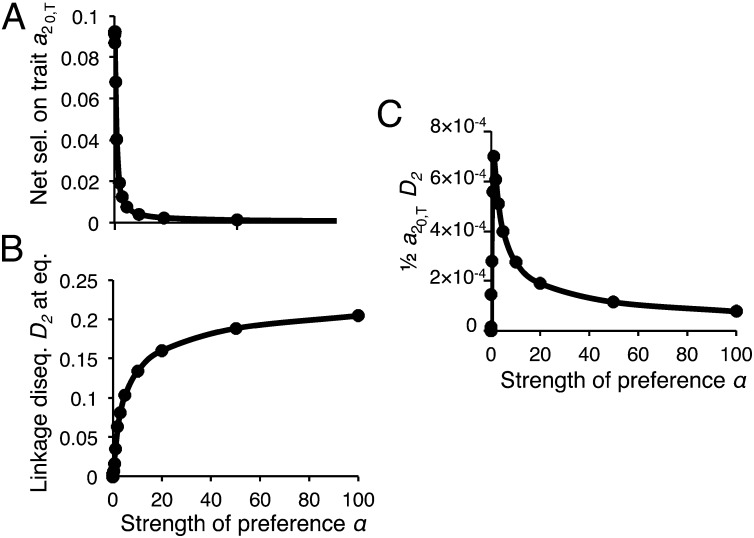
The coefficient $a_{2_{0.T}}$ is a measure of the net selection, from natural and sexual selection combined, on males at locus T in population 2 (20, 21) (the expression for $a_{2_{0.T}}$ is presented in SI Text). As can be seen from Eqs. 1 and 2, this term plays a critical role in determining evolution of both the preference and the trait. It is very often negative if the trait frequency t₂ is high and if α₁ is much larger than s (SI Text and Fig. S2), as would occur with strong Fisherian sexual selection.

Unlike trait differentiation, preference differentiation between populations shows a peak with increasing preference strength α (Fig. 1B). Ultimately, this peak occurs because when preferences are too weak, linkage disequilibrium between the preference and trait loci is too low to allow substantial preference divergence. It can be seen in Fig. 3 that the peaked shape results from an interaction, as α increases, between the decreasing forces of selection on the trait, $a_{2_{0.T}}$, and increasing linkage disequilibrium, D₂ (the effects of s on this peak are shown in Fig. S4). Preference differentiation is thus highest when preferences are strong enough to establish significant linkage disequilibrium, but not so strong to substantially diminish the net selection favoring the trait.

Fig. 3.

Peaks in preference divergence between populations are due to the counteracting effects of the strength of female preference on selection in males and on linkage disequilibrium (Eq. 2). The points were calculated using the equilibrium values for the preference and trait allele frequencies and the linkage disequilibrium between them (note that Eq. 2 employs these values after migration rather than the equilibrium values, but these values are very similar because the migration rate is very small). (A) The net force of selection acting on the trait T₂, $a_{2_{0.T}}$, for a set strength of preference α, using equilibrium values from numerical simulations of the exact recursion equations. (B) Equilibrium values for linkage disequilibrium between the preference and trait loci in population 2. (C) An approximation of the first term in Eq. 2, calculated as one-half of the product of the values plotted in A and B. For A–C the migration rate m = 0.01 and the selection coefficient for local adaptation s = 0.1.

We find that when local adaptation is absent, and traits are neutral with regard to viability selection, populations are unable to maintain any trait divergence after secondary contact, with any level of preference strength (22, 23). This result both was observed in numerical simulations and can be seen in the weak selection (quasi-linkage equilibrium) and strong preference approximations (SI Text).

The explanations presented above for the patterns of trait and preference frequencies strongly suggest that although our models are haploid to facilitate analyses, our qualitative results are likely to be readily generalizable to diploids, although this remains to be confirmed. The presence of only low amounts of preference differentiation (and subsequently the loss of trait differentiation) between populations relies on the fact that selection on preferences is indirect. This is a characteristic of Fisherian systems that does not depend on ploidy. Additionally, linkage disequilibrium between preferences and traits, which determines the strength of indirect selection on preferences, has been shown to have the same magnitude in haploid and diploid models (21).

Although the goal of this paper is to explore the effect of Fisherian sexual selection per se, we also considered a variant of the model with selection on the preference in the form of search costs (SI Text). Concerns about the effects of costs in sexual selection models stem from early findings that the lines of equilibria present in classic Fisherian models become reduced to a point if costs to preferences are present, so that costly preferences cannot be maintained (24). We note that a line of equilibria is not present in our model; in fact, the equilibria are isolated and nondegenerate. Therefore, such a structural instability is not expected. Costs, however, provide a source of direct selection on preferences, which may overwhelm indirect selection as the primary determinant of preference evolution (25). We find that our results are robust to the addition of weak search costs; with such costs evolution arrives at approximately the same equilibria as shown in Fig. 1, constituting weaker differentiation with stronger preferences. Higher costs can, however, lead either to the loss of variation across both trait and preference loci (and hence no differentiation) or in some cases to stronger differentiation with stronger preferences (SI Text and Table S1). The ability of search costs to promote species differentiation in some cases is consistent with the findings of previous models (26).

We additionally examined the results of a variant of our searching algorithm by exploring a best-of-n model (SI Text) (our original model is a “fixed relative preference” model in which all males are viewed, as assumed by refs. 4 and 13 and many subsequent papers). Best-of-n has been found in models of a single population to lead to very different results than does a fixed relative preference (27). We likewise find that best-of-n alters the results of our model (SI Text and Fig. S5), both when the sample of males n is small (in this case trait differentiation can either increase or decrease with stronger preferences, depending on the size of the sample and on preference strength) and when n is large (in this case preference variation or differentiation between populations is often lost, and when it is maintained trait differentiation decreases except at the very strongest preferences). We observed that with low n rare males have much lower mating success with rare females in the best-of-n model than with a fixed relative preference, which is consistent with the differences in the evolutionary effect of preference strength.

Our initial local adaptation model demonstrates that strong Fisherian sexual selection inhibits the maintenance of population differentiation between allopatric populations that come into contact, assuming preference strengths of a certain level. However, what if preference strength itself were to evolve? We addressed this possibility by adding a third locus that controls the value of the preference parameter α from the original model and allowed pairs of alleles at this locus to compete evolutionarily (Methods). Simulations of this model indicate that allelic variants for weaker and weaker preferences will successfully invade. Consistent with the results of the two-locus model above, these weaker preferences allow larger differences in the locally adapted traits to be maintained in each population. However, because preference strength evolves to zero, it is viability selection, not sexual selection that leads to these differences; traits no longer have a sexually selected function, only an ecological one.

Discussion

Speculation on the role of sexual selection in driving speciation and species maintenance traces back to the beginning of the explosion in sexual selection research seen in the past few decades (e.g., refs. 3, 4, 22, and 28). The more that this putative relationship is explored, however, the more tenuous it appears to be (e.g., refs. 10 and 11). Here we show that when sexual selection is isolated in a pure Fisherian form, it inhibits species maintenance in one of the situations in which its role seemed clearest, when the trait under sexual selection is also locally adapted. Furthermore, sexual selection is lost in this Fisherian system if preference strengths themselves are allowed to evolve.

What forces or scenarios may then explain the presence of sexually selected differences between species exchanging migrants? Our results suggest that researchers must look for more complicated scenarios than Fisherian sexual selection, even on a locally adapted trait, to explain an apparently divergent role of sexual selection between species with gene flow. Several candidates have been demonstrated or suggested to play such a role.

It has long been appreciated, for example, that preference differentiation, and consequently trait differentiation, may be maintained between populations when preferences themselves are under direct, divergent selection (9, 11, 29). This can occur when signal perception is affected by local environments that differ between sites (30). Search costs in the context of spatial structure may also cause direct selection on preferences that is divergent, as a result of positive frequency dependence (26); this effect can be seen in our model, in some cases, when costs are present and preferences are strong. We note, however, that the presence of search costs could exacerbate the loss of sexual selection through the evolution of weaker preference strengths if preferences are more costly when they are stronger (19, 31, 32). We expect that deviations from polygyny may also result in direct selection on preferences; it is plausible that these may be frequency dependent and could lead to divergence.

More complicated sexual selection scenarios than the Fisherian models considered above may lead to divergence without direct selection on preferences being involved. Condition dependence in which trait expression is dependent upon local adaptation, for example, has been shown to allow sexually selected differences to evolve and be maintained (33). Preference and/or trait differentiation may also be driven by the process of reinforcement, due to selection against hybrids or hybridization (34–36). We note that avoidance of hybridization, direct selection on preferences, or another mechanism may be necessary for divergence in the case when unique sets of preference and trait loci lead to sexually selected differences between species (37) (e.g., large size is preferred in one population and red color is preferred in another); without these forces it seems that nothing would stop both sets of preferences and traits from sweeping through both populations. On the simpler side, as presented above, when preferences are already high, stronger preferences can increase trait differentiation when traits are expressed in females as well as males. Finally, as discussed below, the preference function may be of great importance in determining divergence (22). These factors, and doubtless others as yet to be recognized, should be sought and identified in empirical systems.

In the model most similar to the one considered here, Lande (22) showed using a quantitative genetic framework that some preference functions can increase divergence along a cline. Specifically, Lande found that when a female’s preference for a male trait is an exponential function of the product of the preference and trait phenotypic values [a “psychophysical” mating preference (38)], differentiation of traits along a cline is exaggerated. Similar amplification along a cline can occur with a “relative” preference function, in which females prefer a male phenotype at a certain phenotypic distance from the mean phenotype in the population [as discussed above we also find increased divergence in some cases with a best-of-n model (27), in which the mating success of rare males with rare females is relatively low; see also ref. 23 for best-of-2 with density-dependent diffusion].

Although these results, in which sexual selection promotes diversification, form the primary message of his paper, Lande (22) also found that diversification is impeded when preferences are for specific male phenotypes (“absolute” mating preferences), provided that the covariance between preferences and traits is less than the genetic variance in the trait itself. Our model, which considers discrete instead of quantitative preferences and traits, matches the results of this final case, in which differentiation is inhibited. This suggests that discrete genetics of sexual selection best correspond to absolute preferences in a quantitative genetic model (and that, perhaps not surprisingly, covariances during Fisherian sexual selection are generally lower than trait variation). Lande (22) did not allow for the evolution of preference strength, so it is uncertain what effect this would have in the quantitative genetic framework.

Our models confirm (22, 23) that when local adaptation (viability selection) is absent, and Fisherian sexual selection alone drives divergence, population differentiation is lost after secondary contact regardless of the preference strength. This is entirely consistent with theory that finds that Fisherian sexual selection alone is also unable to drive de novo speciation with gene flow (10, 11); additional conditions are required (26, 33). Our result stresses that the rapid gain of premating isolation that may occur by pure Fisherian sexual selection alone in allopatry (4, 7) is very fragile indeed.

The finding of an inhibitory role for Fisherian sexual selection on species maintenance in our situation of geographically isolated populations exchanging migrants, although counterintuitive, falls in line with a growing body of literature that casts doubt upon the common perception of a positive contribution of sexual selection to speciation. Recent theoretical studies have found that sexual selection often impedes sympatric speciation by eroding trait variation or generating stabilizing selection on traits (11, 16–19, 39, 40). Sexual selection has also been found to be ineffective at driving continued divergence after secondary contact when females prefer males that match their own phenotype, rather than when there are separate female preference and male trait loci (41). Likewise, comparative studies of sexual selection and speciation, which generally include fully allopatric taxa in which the inhibitory effects described above cannot act, have yielded mixed results (42).

By adding support to the idea that premating isolation may often be readily reversible (43), the results presented here inform a long-standing controversy in the speciation literature: whether premating or postzygotic isolation is more important in speciation (44). The finding that sexual selection in its purest form will tend to erase divergence by local adaptation contrasts with the permanence of intrinsic postzygotic isolation. Speciation researchers should look past the most basic forms of Fisherian sexual selection to gain a better understanding of specific circumstances that might lead sexual selection to establish more permanent isolation and thus play a more substantial role in species maintenance.

Methods

Preference and Trait Divergence.

We model a deterministic system of two haploid populations exchanging migrants (a “two-island” model) with one locus for a preference, P, and one locus for a trait, T, each with two alleles. The frequencies of the four resulting genotypes P₁T₁, P₁T₂, P₂T₁, and P₂T₂ are designated x₁, x₂, x₃, and x₄, respectively.

The life cycle begins with symmetric migration of individuals between the populations at rate m, which describes the proportion of each population that consists of migrants right after the migration event (slight departures from symmetry in migration rates between the populations were not found to have qualitatively different effects on the results of the model). Thus, the frequency of genotype i in population k is

$$x_{i,k}^{\ast }=\left(1-m\right)x_{i,k}+m{x}_{i,l},$$ [3]

where l = 2 when k = 1 and l = 1 when k = 2.

Migration is followed by local adaptation of the characteristic trait allele to the environment of each population. Thus, in males allele T_k is favored in population k with relative fitness 1 + s_k. After this viability selection the genotypic frequencies in males (represented by subscript m) in population k are therefore

$$x_{i,k,m}^{\ast \ast }=\frac{\left(1+d{s}_k\right)x_{i,k}^{\ast }}{1+s_k{t}_k^{\ast }},$$ [4]

where d = 1 if genotype x_i has allele T_k and d = 0 otherwise ($t_k^{\ast }$ represents the frequency of allele T_k after migration). The selection coefficients were generally set so that s₁ = s₂ (such symmetric viability selection is a best-case scenario for population differentiation; simulation results indicate that slight departures from symmetry in local adaptation do not qualitatively alter the results). As described above, the model was also analyzed assuming no local adaptation (sexual selection alone), by setting s₁ = s₂ = 0. Viability selection does not occur in females in the main model, so $x_{j,k.f}^{\ast \ast }=x_{j,k}^{.\ast }$ (but see SI Text for a version of the model in which the trait is expressed and selected upon in both sexes).

Fisherian sexual selection follows viability selection. Specifically, across both populations, allele P_i causes a female to be 1 + α_i times as likely to mate with a T_i male than with a male with the other trait allele if she encounters one of each. The preference alleles thus have the same effect regardless of the population in which they are found. This female choice results in a 4 × 4 matrix M, the elements of which are the proportion of matings occurring between each pair of genotypes i in males and j in females, such that

$${\mathbf{M}}_{ij,k}=\frac{x_{i,k,m}^{\ast \ast }{x}_{j,k,f}^{\ast \ast }\left(1+b{\alpha }_1\right)\left(1+c{\alpha }_2\right)}{{\displaystyle {\sum }_i{x}_{i,k,m}^{\ast \ast }\left(1+b{\alpha }_1\right)\left(1+c{\alpha }_2\right)}},$$ [5]

where b = 1 if i is odd and j = 1 or 2 and b = 0 otherwise, and c = 1 if i is even and j = 3 or 4 and c = 0 otherwise. The normalization in the denominator ensures that every female has equal mating success. For most of the analysis of the system α₁ = α₂. Spot checks of weakly asymmetric cases (α₁ ≠ α₂) produce only weak deviations from the patterns with complete symmetry. Versions of this model that include costs to preferences incurred by lost mating opportunities (e.g., search costs) and that use a best-of-n searching algorithm are both described in SI Text.

Recombination and segregation follow mating, modeled using standard two-locus, two-allele equations for haploids, and leading to the production of zygotes in the next generation. Details of the numerical analysis of all model versions, which consisted of exact iterations of the recursion equations, are described in SI Text, as are details of approximations with weak and strong selection. All analyses were performed using Mathematica (45). Notebooks are archived in Dryad under 10.5061/dryad.mn643.

The Evolution of Preference Strength.

Here we add an additional locus, A, which controls the strength of mating preferences in the system. Specifically, when allele A₁ at this locus is fixed in a population, the model behaves according to the equations in the two-locus model described above. P₁ and P₂ females that carry the A₂ allele instead have preference strengths of 1 + α₃ and 1 + α₄, respectively. There is no restriction on the relative strength of the four α parameters, although for most of the analyses α₃ = α₄ (simulations yield qualitatively identical results with slight departures from symmetry).

In this three-locus system there are eight genotypes, ordered such that A₁P₁T₁, A₁P₁T₂, … A₂P₂T₂ are represented by the frequencies x₁, x₂, ... x₈, respectively. Eqs. 3 and 4 still hold. Mating now results in an 8 × 8 matrix M, where the proportion of matings occurring between genotypes i in males and j in females is

$${\mathbf{M}}_{ij,k}=\frac{x_{i,k,m}^{\ast \ast }{x}_{j,k,f}^{\ast \ast }\left(1+b{\alpha }_1\right)\left(1+c{\alpha }_2\right)\left(1+e{\alpha }_3\right)\left(1+g{\alpha }_4\right)}{{\displaystyle {\sum }_i{x}_{i,k,m}^{\ast \ast }\left(1+b{\alpha }_1\right)\left(1+c{\alpha }_2\right)\left(1+e{\alpha }_3\right)\left(1+g{\alpha }_4\right)}},$$ [6]

where b = 1 if i is odd and j = 1 or 2 and b = 0 otherwise, c = 1 if i is even and j = 3 or 4 and c = 0 otherwise, e = 1 if i is odd and j = 5 or 6 and e = 0 otherwise, and g = 1 if i is even and j = 7 or 8 and g = 0 otherwise. Again the normalization in the denominator ensures strict polygyny. Recursion equations for the genotype frequencies are generated using the standard equations for free recombination and segregation, assuming three loci with two alleles each in haploids.