Remnant of stripe order

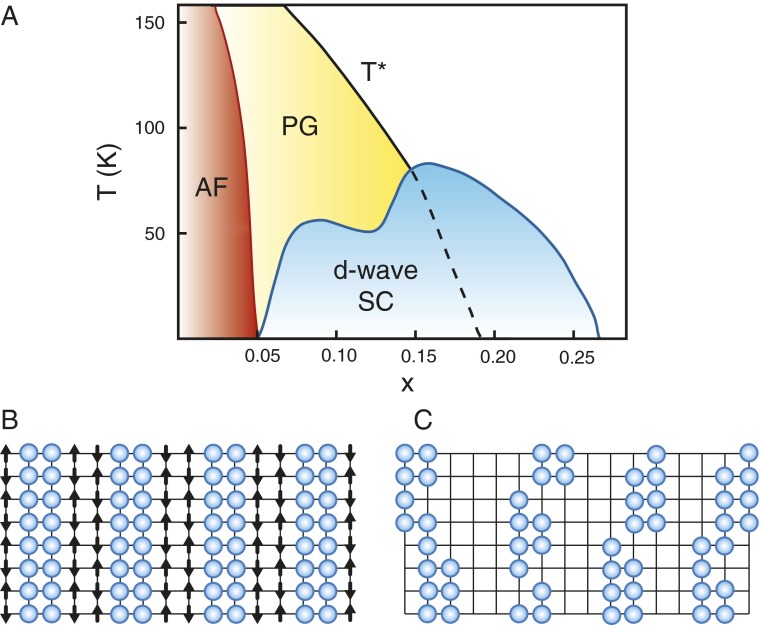
At a phenomenological level, the superconducting phase of the cuprate high T_c phase diagram shown in Fig. 1A can be characterized as a BCS (named for three theorists: Bardeen, Cooper, and Schrieffer) superconductor with a d-wave gap. However, a suitable phenomenological description of the so-called “pseudogap” region indicated by the yellow shaded region in Fig. 1A has been missing. This region is characterized by the absence of low-energy single-particle states with momenta near the part of the Fermi surface, where a maximum d-wave gap opens in the superconducting phase, leading to it being called the pseudogap region. A variety of experiments show evidence of short-range unidirectional charge and in some cases spin order in this region. However, there remained questions of whether the boundary shown as the black T* curve in Fig. 1A marks a cross-over or an actual phase transition, and if the latter, what characterizes the pseudogap phase. In PNAS, Nie et al. (1) discuss a phenomenological Landau–Ginzburg–Wilson theory of an incommensurate unidirectional charge density wave (stripes) in the presence of weak quenched disorder. The authors find that although long-range stripe order, schematically illustrated in Fig. 1B, is destroyed by the disorder, a remnant nematic order, shown in Fig. 1C, can survive. As Nie et al. discuss, this theory provides a framework for interpreting a number of experiments, as well as the basis for experimental protocols that can provide further tests for nematic order.

Fig. 1.

(A) A cuprate phase diagram of temperature versus hole-doping (holes/Cu) showing antiferromagnetism (AF), superconductivity (SC), and pseudogap (PG) regions. The T* line marks the upper boundary of the pseudogap region. (B) Schematic illustration showing the expectation value of the charge and spin density for a hole-doping of one-eighth, where the commensurability of the stripe structure with the lattice leads to pinning. The dip in the superconducting transition temperature T_c for a hole-doping of one-eighth is believed to be associated with this pinning. On a CuO₂ lattice, the doped holes would tend to have a higher density on the O sites, which in the present picture would correspond to a bond charge ordering rather than the site charge ordering shown here. (C) A snapshot of a typical electronic configuration of the holes in a nematic phase. Here for a hole-doping x ∼0.10 the long-range stripe order is absent and only the vertical or horizontal long range modulation remains as a remnant.

The authors note that although the spontaneous breaking of a continuous symmetry will not occur in the presence of random field disorder for dimensions less than or equal to four, the breaking of a discrete symmetry is possible for weak disorder in three dimensions. Specifically, Nie et al. (1) analyze a Landau–Ginzburg–Wilson model of a layered tetragonal lattice, which in the absence of disorder would have a unidirectional incommensurate striped phase, schematically illustrated in Fig. 1B. The authors explain that although this striped phase is destroyed by random quenched impurities, a remnant of it, associated with the x or y orientation of the stripes, remains provided there is coupling between the planes. This remnant of the striped phase appears as a nematic phase, schematically illustrated in Fig. 1C, which consists of stripe segments in which the long-range charge and spin order has melted, but the orientation of the segments along the x or y Cu-O-Cu bonds remains.

An important prediction of this theory is that there is a thermodynamic phase transition at the boundary of the pseudogap regime and a quantum critical point where T* goes to zero. However, as discussed by Nie et al. (1), the thermodynamic signal of the phase transition may be weak because the nematic order is not expected to open gaps on the Fermi surface. Nevertheless, ultrasonic measurements of the temperature dependence of the elastic moduli of YBa_2Cu_3O_{6+y} crystals have reported thermodynamic evidence that the pseudogap region is a distinct phase bounded by a line of phase transitions (2). Evidence that the pseudogap region is characterized by a phase with short-range charge order, consistent with nematic order, is seen in a variety of experimental NMR, scanning tunneling microscopy, and X-ray studies referred to by Nie et al. (1). For example, the symmetry-breaking that makes the Ox and Oy planar oxygen sites of the CuO₂ unit cell electronically inequivalent is seen directly in the atomically resolved tunneling response of BSCCO and Na-CCOC (3, 4). Furthermore the detailed intracell structure of the Ox and Oy charge distribution has been determined from these measurements. NMR measurements (5) of YBCO find a difference in the line broadening of the Ox and Oy planar oxygens. Although such a difference naturally arises from the orthorhombic structure of YBCO, the sudden increase of this difference below T* provides evidence of an electronic charge origin for this difference, which is consistent with the onset of nematic order. In their report, Nie et al. (1) discuss the structure factor S(Q), which determines the X-ray scattering cross-section. The authors also discuss the protocol for various possible measurements of the nematic phase, including the problem of the explicit symmetry-breaking associated with the orthorhombic nature of some of the materials.

The work by Nie et al. (1) raises further questions regarding the microscopic origin of the pseudogap and its relationship to superconductivity. If the pseudogap regime is characterized by nematic “melted stripe” correlations, are the stripes a secondary effect of other phenomena that occurs above the pseudogap transition? Various possibilities, such as Mott gap physics (6), Umklapp scattering processes (7), local d-wave pairing correlations (8), and an instability near the onset of spin density-wave order (9) have been suggested, but to sort this out it will be necessary to identify sharp experimental signatures that can be interpreted on the basis of controlled calculations.

If the pseudogap T* boundary ends at a quantum critical point, as indicated in Fig. 1,

The work by Nie et al. raises further questions regarding the microscopic origin of the pseudogap and its relationship to superconductivity.

what role do the critical nematic fluctuations play in the superconducting pairing mechanism? Recent magnetoresistance measurements of the electron effective mass find a quantum critical point for YBCO at a doping x ∼0.18, where T_c peaks provide evidence that quantum critical point fluctuations are important for obtaining high T_c (10). In addition, an analysis of angle-resolved photoemission data for Bi₂Sr₂CaCu₂O_{8+x}, which has a pseudogap, concludes that the spin-fluctuation pairing mechanism is not sufficient to account for the observed value of T_c (11). An insightful study of the Ising-nematic phase, which addresses a number of these issues, has recently appeared (12).

The paper by Nie et al. (1) is important because it provides a strong case that the pseudogap is a nematic phase, and focuses attention on the question of its microscopic origin and the role of nematic fluctuations in the high T_c pairing mechanism.