Hydrodynamic starvation in first-feeding larval fishes

Significance

A century ago, Johan Hjort described extreme mortality rates (>99%) of marine fish larvae within days of hatching and termed it the “critical period.” Although multiple hypotheses were raised to explain this mass mortality, the mechanisms behind it remained unresolved. Here, we show that first-feeding larvae experience “hydrodynamic starvation,” in which their hydrodynamic environment mechanistically limits their feeding performance. Our study offers an experimentally supported mechanism of starvation in larval fishes, focusing on the physics of suction feeding in low Reynolds numbers, rather than on prey concentrations and encounter. We believe our findings can help to better understand the early life history of marine fish and the selective forces they experience during the pelagic larval phase.

Abstract

Larval fishes suffer prodigious mortality rates, eliminating 99% of the brood within a few days after first feeding. Hjort (1914) famously attributed this “critical period” of low survival to the larvae’s inability to obtain sufficient food [Hjort (1914) Rapp P-v Réun Cons Int Explor Mer 20:1–228]. However, the cause of this poor feeding success remains to be identified. Here, we show that hydrodynamic constraints on the ubiquitous suction mechanism in first-feeding larvae limit their ability to capture prey, thereby reducing their feeding rates. Dynamic-scaling experiments revealed that larval size is the primary determinant of feeding rate, independent of other ontogenetic effects. We conclude that first-feeding larvae experience “hydrodynamic starvation,” in which low Reynolds numbers mechanistically limit their feeding performance even under high prey densities. Our results provide a hydrodynamic perspective on feeding of larval fishes that focuses on the physical properties of the larvae and prey, rather than on prey concentration and the rate of encounters.

Starvation is often considered a major cause of larval fish mortality (1–6). Therefore, the ability of larvae to find and capture food is critical for their survival. Newly hatched fish subsist on a limited supply of yolk and must encounter and successfully capture food before their energy resources become depleted (3, 7). In larval fishes, prey capture success is low at first feeding [occurring 2–4 d post hatching (DPH)] but increases rapidly during early development (3, 8). Correspondingly, larvae undergo a “critical period” of high mortality rates (of up to 99%) after which survival rates increase dramatically (2, 3, 7). The critical period commonly starts at first feeding and lasts 7–10 d, although the duration may vary among species and cohorts. Despite its impact on larval growth and survival, very little is known of the mechanism that underlies this mass mortality, especially during the critical period (1–6).

As a larval fish matures, the concomitant increases in its body length and swimming speed alter the outcome of the interaction between the larvae’s body and the fluid around it (9, 10). In general, at small body sizes and slow flow speeds organisms experience a hydrodynamic regime of low Reynolds numbers (Re), in which viscous forces (such as drag) dominate. Larger body size and faster flow facilitate a transition into a hydrodynamic regime of higher Re, where inertial forces dominate (see glossary in Table 1 for the Re equation; ref. 10). In larval fishes, this transition was shown to affect fundamental biological processes, such as respiration, metabolism, and swimming (11–14). Like many adult fishes, larval fish capture their prey using “suction feeding” (Fig. 1): they swim toward it and, when in close proximity, open their mouth while expanding the mouth cavity. The expansion of the mouth generates a strong inward flow of water. This flow exerts a force on the prey, drawing it into the predator’s mouth while at the same time countering possible escape responses (15–18). Because of the changes in Re throughout the various stages of larval ontogeny, the hydrodynamic interaction between a solid particle (the prey) and the unsteady suction flow produced by the predator is also expected to change. Indeed, high-speed filming of zebrafish larvae revealed that feeding kinematics depend strongly on Re (9). Numerical analysis of suction feeding under low Re conditions estimated that ∼40% of the energy invested in mouth opening is lost to frictional forces, rather than contributing to accelerating the fluid toward the mouth (19). However, it is not known whether low Re causes a reduction in feeding performance.

Table 1.

Glossary

Term	Definition
Reynolds number (Re)	A nondimensional parameter often used to characterize flow regimes. Re represents the ratio between inertial and viscous forces, and is often used to distinguish between laminar and turbulent flow. Re is defined as follows: $\mathrm{Re}=\left(\rho \cdot l\cdot u\right)/\mu$, where ρ is the density of the fluid (in kilograms per cubic meter), l is the characteristic length of the flow field (in meters), u is flow speed (in meters per second), and μ is dynamic viscosity (in newton⋅second per square meter). When Re is small (Re < 1), viscous forces dominate, and the flow is stable. As Re increases, inertial forces become more important. The flow becomes less stable and turbulence is likely to develop (usually at ∼Re > 105). Re is used for dimensional analysis and for dynamic scaling.
Dynamic scaling	When comparing two flow scenarios of a fully submerged body, the two regimes will be hydrodynamically identical if the nondimensional parameters (Re) are identical. It is possible to investigate the flow field generated by a small body size by using a large body size while simultaneously increasing the viscosity (or decreasing flow speed) and keeping the nondimensional parameters (Re) unchanged.
Dynamically scaled size	The equivalent length (l′) of a solid body in a dynamic-scaling experiment is obtained by keeping the Re constant. Dynamically scaled size is hereafter defined as follows: $l\prime =l\left(u_1{\mu }_2/u_2{\mu }_1\right)$, where l is the real length of the body, u1 and μ1 are flow speed and viscosity under nonmanipulated conditions, and u2 and μ2 are flow speed and viscosity under manipulated conditions. For example, under conditions of a twofold increase in fluid viscosity and constant flow speed, the dynamically scaled size of a 10-mm solid body decreases by twofold to 5 mm (Fig. 3).

Fig. 1.

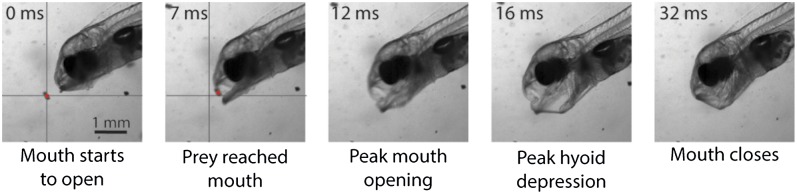
An image sequence (from Movie S3) of a 17 DPH S. aurata capturing a rotifer by suction feeding. By rapidly expanding the oral cavity and opening its mouth, the larva creates a negative pressure, causing water to rush into the mouth, drawing in the prey from a distance. The timing of each stage is denoted on the top of each image. The prey is marked by a red dot; the crosshair in the left panels represents location of the prey at t = 0 ms. Note that the camera was not moved; therefore, movement of the prey between t = 0 and t = 7 ms is solely due to the forces exerted by the suction flows. See also Movies S1 and S2 for failed attempts.

Our goal was to test the hypothesis that the hydrodynamic regime experienced by first-feeding larvae constrains their feeding performance. Using feeding experiments, dynamic-scaling experiments, high-speed video observations, and computer simulations, we set out to (i) test the effect of fish age on feeding rates and feeding success; (ii) determine the effect of size per se on feeding rates, relative to the effect of other traits that change during ontogeny; and (iii) test the effects of larval size on feeding dynamics and strike kinematics.

Results

Feeding Rate and Feeding Success as a Function of Larval Age.

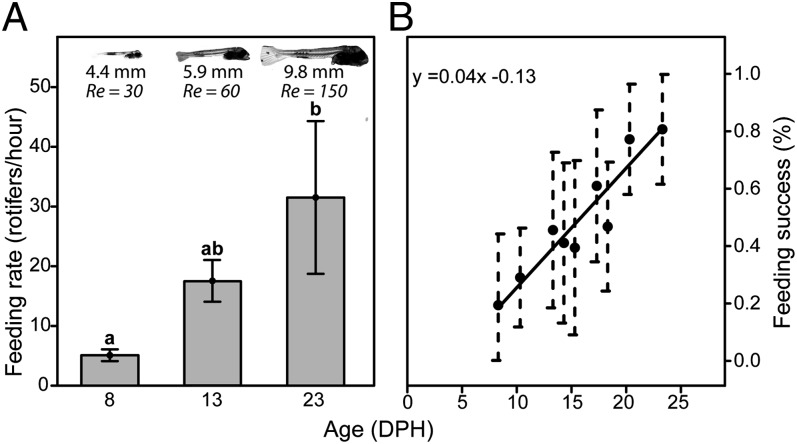
Feeding rates were measured for each larva by counting the number of prey items in the gut after a 30-min feeding session. Feeding rate increased significantly with larval age [Fig. 2A; ANOVA, F_(2,42) = 4.78, P = 0.013]. The twofold increase in body size that occurs from 8 to 23 DPH was reflected in an increase in Re from ∼30 to ∼150 (Fig. 2A). The increase in body size and Re was accompanied by a fivefold increase in feeding rate.

Fig. 2.

Feeding rates and capture efficiencies sharply increased as larvae grew. (A) Feeding rate for three age groups, 8, 13, and 23 DPH (corresponding to total lengths of 4.4, 5.9, and 9.8 mm, and Re of 30, 60, and 150, respectively). Letters above each bar represent post hoc test results (Tukey’s HSD, P < 0.01). (B) Capture success was age dependent (linear regression, R² = 0.88, P = 0.05). Capture success was defined as the percentage of strikes in which food remained in the mouth after mouth closing, divided by the total number of feeding attempts (n = 138, with a minimum of 10 attempts per group). Error bars are 95% binomial confidence intervals.

We used high-speed video to determine the outcome of prey capture attempts (SI Appendix and Movies S1–S3) and to quantify “feeding success,” hereafter defined as the proportion of successful feeding events out of the total number of feeding attempts. We found that, despite the multiple feeding attempts observed for 8 DPH larvae, feeding success for these larvae was meager (<20%). However, within the next 5 d, feeding efficiency doubled to >40%, and by 25 DPH, it had reached ∼80% (Fig. 2B).

Dynamic Scaling Experiments.

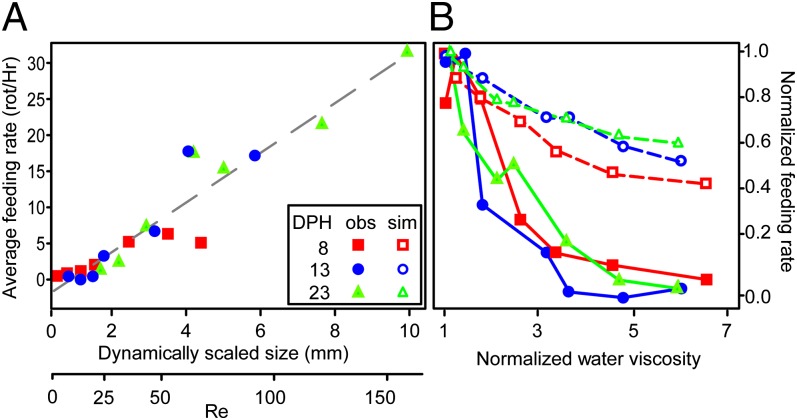
To separate the effects of age and size, we repeated the feeding experiments while manipulating water viscosities and quantifying feeding rates for larvae immersed in solutions that was up to sevenfold more viscous than seawater (Table 1 and Fig. 3). Gut content analysis for 8, 13, and 23 DPH indicated a strong effect of scaled size on feeding rates (Fig. 4A; for calculation of scaled size, see Fig. 3, Table 1, and SI Appendix, Table S3). Analysis of covariance (ANCOVA) indicated a strongly significant dependence of feeding rate on scaled size [continuous variable; F_(2,18) = 79.4, P < 0.0001, R² = 0.89]. However, larval age (factor) had no significant effect on feeding rate [F_(2,18) = 79.4, P > 0.40]. This result remained robust to alternative calculations of the scaled size and Re numbers (SI Appendix, Table S2). A similar correlation was observed between feeding rates and Re (R² = 0.83). Thus, in these experiments, the size-mediated hydrodynamic regime (as reflected in Re), rather than other ontogenetic factors, dictated larval feeding rates. This conclusion is further supported by an ANCOVA of normalized feeding rate, defined as feeding rate divided by the maximal feeding rate for a given age. This analysis indicated a significant effect of water viscosity on normalized feeding rate [F_(3,17) = 41.6, P < 0.0001] but a nonsignificant effect of age group [F_(3,17) = 41.6, P > 0.31; Fig. 4B].

Fig. 3.

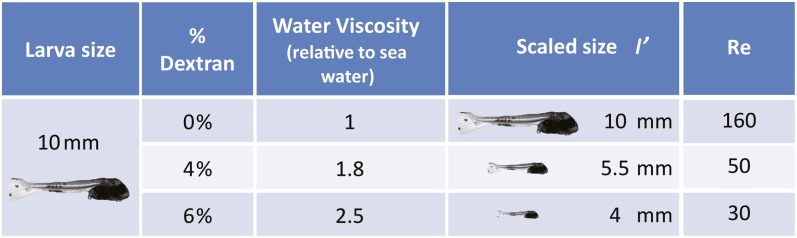
Example of dynamic scaling of larvae used to separate the effects of size from other ontogenetic effects. Larvae immersed in viscous solutions encountered an hydrodynamic regime equivalent to that encountered by smaller larvae in untreated water (Table 1). For example, water containing 4% dextran will be 1.8-fold more viscous than water alone, such that a 10-mm larva feeding in such solutions would experience a Re regime equivalent to that of a 5.3-mm larva in untreated water. The Re equation is in Table 1.

Fig. 4.

(A) The effect of dynamically scaled size on larval feeding rates. Feeding rate (rotifers consumed per hour) significantly increased with the dynamically scaled size of the larvae [F_(2,18) = 79.4, P < 0.0001], whereas no significant effect of age was observed [F_(2,18) = 79.4, P > 0.40]. (B) Feeding rates generated by an encounter rate model (dashed lines) were compared with measured feeding rates (solid lines) for all dextran treatments in the three larval age groups (8 DPH, red; 13 DPH, blue; 23 DPH, green). For all viscosity treatments, normalized feeding rates showed a significantly stronger decrease with increasing water viscosity [F_(5,36) = 75.6, P < 0.0001] than that expected based on the encounter rates alone [F_(5,36) = 75.6, P < 0.0001]. Slope comparisons revealed that viscosity-mediated effects on suction performance accounted for ∼75% of the decrease in feeding rates (major axis, R² = 0.74, P < 0.0001, slope = 2.52). Normalized feeding rates are defined as the feeding rate divided by the maximal rate.

Encounter Rate Model.

We constructed a computer simulation to test the effect of swimming speeds of predator and prey on encounter rates in the dynamic-scaling experiments. The decrease in feeding rate due to viscosity-mediated effects on swimming speeds of both predator and prey (SI Appendix, Table S1), as inferred from the encounter rate model, could not explain the marked decrease in feeding rates observed experimentally at high viscosities (Fig. 4B). The regression of observed and normalized feeding rates relative to those predicted from the encounter rate model revealed that slower swimming of the prey and predator could account for up to ∼25% of the experimentally assessed decrease in feeding rates (major axis, R² = 0.74, P < 0.0001, slope = 2.52). Thus, hydrodynamic effects on their ability to capture and handle prey had a major effect on the ability of larvae to feed.

Strike Kinematics and Viscosity.

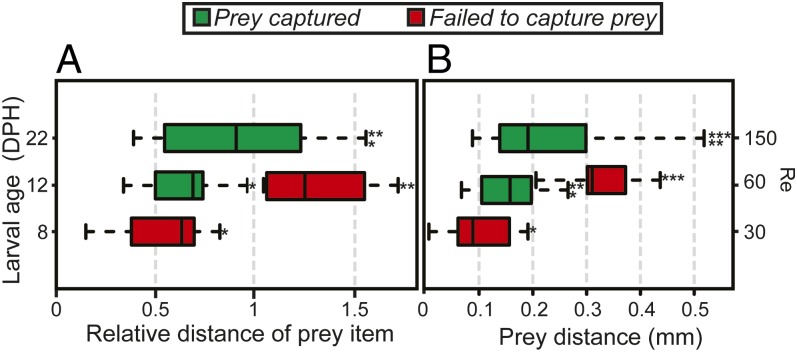
High-speed videos of feeding larvae [recorded at 1,000 frames per second (fps)] were analyzed to assess how larval age and size affect feeding kinematics. A comparison between unsuccessful and successful prey capture attempts (n = 5–21 per age group) revealed a significant effect of age on prey capture distance. We measured the distance of prey at the time of strike initiation for 8, 12, and 22 DPH larvae from high-speed videos and found that prey capture distance increased with larval age [ANOVA, F_(3,38) = 6.86, P < 0.0009; SI Appendix, Tables S7 and S8]. For instance, 8 DPH larvae operating at Re of ∼30 were unable to capture food even at a close distance (∼0.5 mouth diameters away from the mouth); whereas 4 d later, at Re of ∼60, successful strikes were recorded at these distances. The same pattern was repeated when comparing prey capture distances of 12–22 DPH larvae (Re of ∼60 and 150, respectively; Fig. 5).

Fig. 5.

Prey capture distance as a function of larval age. Relative distances (in maximal gape diameters; A) and absolute distances (in millimeters; B) of prey capture were measured for three larval age groups (8, 12, and 22 DPH, feeding under Re 30, 60, and 150, respectively). The red bars represent unsuccessful attempts, and the green bars represent successful attempts. Capture distance increased with larval age, with no significant difference noted between missed strikes of 8 DPH larvae and successful strikes of 12 DPH larvae. Similarly, no significant difference was observed between missed strikes of 12 DPH larvae and successful strikes of 22 DPH larvae (Tukey’s HSD, P < 0.002; SI Appendix, Tables S7 and S8).

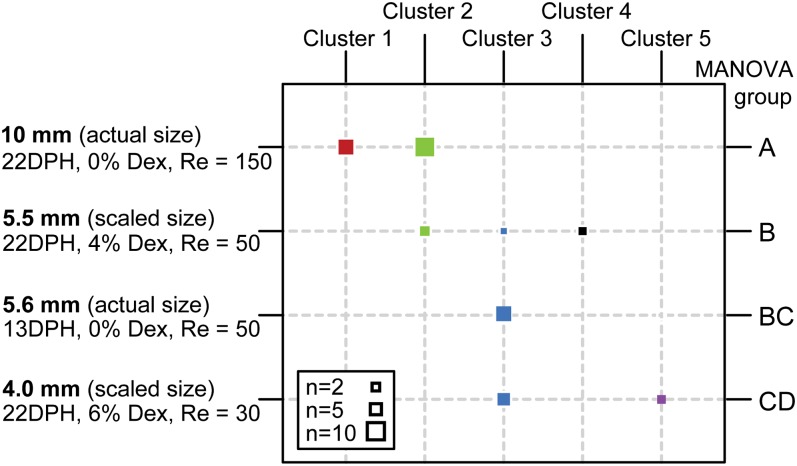
We further investigated whether strike kinematics of dynamically scaled larvae are representative of strikes made by younger (and thus smaller) individuals. We used discriminant analysis to explore the kinematic data for clusters of data points, generated based on the similarity of the data without an a priori hypothesis of predefined groups. We then compared the generated clusters to our predefined age and scaled size groups. This analysis revealed that the strike kinematics of dynamically scaled 22 DPH larvae at water viscosities of 2.5× clustered with those of young larvae (13 DPH) and were distinctly different from those of nonscaled 22 DPH larvae (Fig. 6). Multivariate analysis of variance (MANOVA) pairwise comparisons further revealed that the strike kinematics of larvae subjected to a 1.8× viscosity treatment were not statistically different from those of 13 DPH larvae in regular sea water (P > 0.29; Fig. 6 and SI Appendix, Table S6). Principal components analysis (PCA) of strike kinematics (with PC1-2 accounting for 76% of the total variation; SI Appendix, Table S5) indicated that successful strikes at lower Re were characteristically “high effort” strikes, featuring faster kinematics, greater excursions, and capture of prey from shorter distances.

Fig. 6.

Discriminant analysis of strike kinematics recorded for dynamically scaled and nonscaled 13 and 22 DPH larvae. Strikes clustered according to dynamically scaled size (and Re), rather than to age. Columns and similar colors represent clusters determined by the discriminant function, whereas the rows correspond to groups predefined by age and dextran (Dex) concentration (left axis). Square size represents group size. The results of MANOVA pairwise comparisons performed on a PCA of strike kinematics are summarized along the right axis.

Force Exerted on the Prey.

Why do small larvae fail to draw prey into their mouths, even from close range? To mechanistically answer this question, a model describing the force exerted on prey in the suction flow was used to quantitatively define the effect of mouth size on the ability to capture escaping prey (full description of model is provided in SI Appendix). This approach [hereafter referred to as suction-induced flow field (SIFF)] treats the aquatic predator–prey encounter as a hydrodynamic interaction between a solid particle, corresponding to the prey, and the unsteady suction flows around it (18). SIFF served to quantitatively assess feeding performance for each larval size, which we define as the maximal escape force that a prey can exert and still be captured by the striking larva. The maximal escape force of the prey was significantly correlated with the observed success rate [linear regression, R² = 0.88; F_(1,7) = 51.3, P < 0.0002; SI Appendix, Fig. S5]. SIFF indicates that first-feeding larvae are limited in the magnitude of force they can exert on swimming prey. As a result, prey capture distance and feeding success are compromised.

Discussion

First-feeding Sparus aurata larvae that fed at Re of ∼30 captured food at substantially lower rates compared with their older conspecifics that fed at Re of ∼150 (Fig. 2A). The observed increase in feeding rate with age could have been attributed to increasing demands for energy in the older larvae. However, high-speed videos of prey capture strikes showed that first-feeding larvae suffered lower prey capture success rates compared with their older conspecifics (Fig. 2B). This suggests that the low feeding rates are probably due to some sort of performance limitation imposed on younger larvae. During the critical period, larvae undergo multiple morphological and developmental changes that could improve their prey capture abilities. For example, the skeleton ossifies, muscle mass increases, the eyes grow, and coordination improves with age, all of which were hypothesized to impede feeding at a younger age, when less developed (3, 8, 9, 11–14, 20, 21). However, the Re that characterizes the larva’s suction flows suggests a shift in the hydrodynamic regime between first feeding larvae (feeding at Re < 60) and their older conspecifics that feed at Re of ∼150. Indeed, dynamic-scaling experiments revealed that feeding rates were determined, by and large, by the dynamically scaled size of the larvae. In these experiments, ontogenetic differences between age classes had no significant effect on feeding rates. The results indicate that the ability of larvae to capture their prey is dictated by the size-mediated hydrodynamic regime they experience.

The low Re regime experienced by first-feeding larvae could effect feeding rates via two mechanisms. First, larvae under low Re might swim more slowly, which could result in lower encounter rates with their prey, as has been previously hypothesized (12). Second, low Re could directly impede the suction-feeding mechanism. The encounter rate simulations indicate that the effect of swimming speed can explain only ∼25% of the observed decline in feeding rates with decreasing dynamically scaled size (Fig. 4B). Moreover, high-speed videos and SIFF modeling indicated that smaller larvae could capture only weakly escaping prey, and only from a very short distance (Fig. 5 and SI Appendix, Fig. S5). Taken together, these results reveal strong constraints on the ubiquitous suction-feeding mechanism of larval fishes under a low Re regime. We believe that these constraints may limit feeding rates and induce starvation even when prey encounter rates are high. Indeed, a critical period of larval mortality is commonly observed in mariculture facilities, with >70% mortality even under conditions of high food concentration (22). Moreover, DNA/RNA ratios in fed and starved larvae were indistinguishable during the first few days after feeding commenced (23), indicating that starvation in first-feeding larvae may occur regardless of feeding regime. Taken together, it appears that first-feeding larvae experience “hydrodynamic starvation,” attributed to the physical properties of the larva and prey, rather than to prey concentration and the rate of their encounter.

Hydrodynamic starvation during first feeding is attributed to the low Re regime in which the larvae feed. We therefore suggest that selection for successful feeding should favor larger larval size, realized through high growth rates and large initial size (i.e., at hatching). Indeed, egg size is strongly and negatively correlated with larval mortality rate between species (24). Paradoxically, although selection for larger initial larval size to overcome starvation during first feeding could have been expected, virtually all broadcasting fish species produce small eggs and larvae (25). This could imply that strong selection during an earlier life stage (i.e., in the egg or during mating) may in fact favor smaller egg size. The agents of such selection could include increased predation by visual predators, diffusion limitations on large propagules, environmental heterogeneity favoring more offspring at the cost of individual fitness, or fertilization constraints on large eggs (24).

We believe that our findings offer significant contribution to two fields: the study of larval ecology, and mariculture. In the context of larval ecology, our results suggest that estimating the natural food densities required for larval survival (26) is insufficient. To better predict larval survival rates, an integrative approach is warranted. In addition to prey concentrations, other factors appear to have critical consequences for the hydrodynamic interaction between prey and predator. These factors include the following: the size distribution of the prey and larvae (specifically their mouth size), prey escape response, and prey shape and density (mass/volume) (16, 18, 27). Our findings are also of relevance to the mariculture industry, where in addition to focusing on the food’s nutritional properties (28, 29) the physical properties of both food and larvae should also be considered. For example, selection for larger larvae, larvae with larger mouths, and the use of smaller prey should increase larval feeding rates, and perhaps reduce starvation-induced mortality.

Mortality during the critical period, identified by Hjort (1914) a century ago (1), was originally attributed to the inability of the larvae to find food in sufficient quantities, leading to larval starvation (1, 8, 30, 31). Although alternative hypotheses have been suggested to explain the variability seen in larval survival and recruitment, starvation is still widely considered a major agent of mortality in larval fishes (5, 30, 32). Here, we suggest a mechanistic explanation for the larva’s inability to obtain sufficient food. We conclude that first-feeding larvae experience hydrodynamic starvation, where low Reynolds numbers mechanistically limit their feeding performance even under high prey densities. Our study demonstrates how an understanding of the organism’s hydrodynamic environment promotes our understanding of basic ecological processes, and how large-scale ecological patterns can be governed by small-scale physics.

Materials and Methods

Model Organism.

We used gilthead seabream (Sparus aurata Linnaeus, 1758, Sparidae, Perciformes, Actinoperygii) larvae as our model for larval feeding. S. aurata is a typical pelagic spawner and is also of high commercial importance, commonly grown in fisheries. Larval size at hatching is ∼3.5 mm and first feeding initiates around 5 DPH at a body size of ∼4 mm. Larvae reach the stage of flexion at ∼21–24 DPH, at a size of ∼10 mm. Larvae for our experiments were provided by the Ardag commercial nursery and were kept in 19 °C aerated seawater at a salinity of 35 ppm.

Statistical Analysis.

All statistical analyses were performed using the software R statistics (33). Unless otherwise stated, ANOVA, ANCOVA, and regression were conducted with the lmPerm package (34), which calculated a P value based on a permutation procedure that is robust to nonhomogeneity of variance. Where appropriate, post hoc analyses were performed using Tukey’s honest significant difference (HSD).

Feeding Rate as a Function of Larval Age.

Throughout our experiments, we used rotifers (Brachionus rotundiformis) as our standard prey. Rotifers are universally used as food for first-feeding fish larvae in the mariculture industry. Rotifers swim ∼10-fold more slowly than S. aurata larvae (SI Appendix, Table S1) and cannot produce high-acceleration escape responses, unlike those of copepods. Rotifers have a distinct jaw-like structure termed mastex, made of chitin, which is not digested by the larvae. This allowed us to quantify the rotifers each larva consumed by counting the mastex in the larva’s gut (SI Appendix, Fig. S1) under a dissecting microscope. The duration of experiments was kept short (30 min) to ensure that mastex did not evacuate from the gut during the experiments.

We tested the effect of larval age on feeding rate for three age groups of S. aurata larvae: 8, 13, and 23 DPH. Age groups corresponded to mean lengths of 4.4, 5.9, and 9.8 mm, respectively. Twelve hours before the experiment, larvae were placed in filtered seawater (GF-F filter; nominal filtering capacity, 0.2 µm) to exclude food items. Before each feeding experiment, three larvae were sampled for gut content to ensure guts were empty. During the experiment, groups of three larvae were placed in a 100-mL transparent water container with rotifer density of ∼100 rotifers per mL for 30 min. Larvae were then killed and gut content of each larvae was determined. Overall, 12 larvae for each size group were examined (a total of 36 larval gut contents was analyzed). The number of prey in the gut was compared between different age groups using permutation-based ANOVA.

Feeding Success as a Function of Larval Age.

We developed an unbiased protocol to quantify feeding success of larvae throughout ontogeny. We defined feeding success as the proportion of successful feeding interactions out of the total number of feeding attempts. To document feeding interactions, we used a high-speed camera (1,920 × 1,440 pixels; Photron AS-6; 500 fps), equipped with a 60-mm macro Nikkor lens. During filming, six to eight larvae of each age group were placed in a small filming chamber (36 × 76 × 5 mm) with constant flow of chilled, aerated seawater with rotifers. We used backlight illumination from a light-emitting diode (LED) light placed behind the aquarium (SI Appendix, Fig. S2). The camera visualized a field of view of ∼40 × 30 mm and was set to trigger automatically when a larva entered a predefined field of view.

After filming, videos were reviewed and sorted into two categories: successful and unsuccessful feeding interactions. We defined feeding attempts as events in which a larva opened its mouth when a food item was observed at a distance of less than one-half a body length from the mouth. Successful feeding interactions were defined as those in which food entered and remained in the larva's mouth. Unsuccessful interactions were defined as those in which food was still outside the mouth when it closed. Overall, we analyzed 138 videos, with an average of 15 ± 2 videos per age group. We used least-square regression to describe feeding success as a function of larval age.

Dynamic-Scaling Experiments: Separating the Effect of Size on Feeding Rates.

Differences in feeding rates and feeding success of larvae could be attributed to the effect of size on the immediate hydrodynamic regime. However, these differences could also be attributed to ontogenetic changes in fin, mouth, bone, and/or eye morphologies, all of which bear functional implications regarding the ability to swim, detect prey, and maneuver (3, 8, 9, 11–14). We separated the relative contribution to size on feeding rates from other ontogenetic effects by conducting a series of dynamic-scaling experiments. In these experiments, we manipulated water viscosities to alter the hydrodynamic regime independently of larval age (35). For the dynamic-scaling experiments, we used three age groups (Fig. 3; 8, 13, and 23 DPH corresponding to lengths of 4.4, 5.9, and 9.8 mm). Fish from each age group were placed in containers filled with water of different viscosity levels (1–6.5× the viscosity of seawater; see SI Appendix, Table S3, for complete list of scaled sizes). Viscosity was manipulated using increasing concentrations (0–12% weight) of dextran (Sigma 31389; M_r, 40,000; Sigma). Water viscosity was determined for each experiment using a falling ball viscometer [Gilmont (36)]. Larvae were placed in 100-mL containers and the protocol from our feeding experiment (Feeding Rate as a Function of Larval Age) was followed for each viscosity level for each age group. We repeated the experiments until we had at least 10 larvae for each age group in each viscosity treatment (a total of 287 larvae).

To calculate the dynamically scaled size, we used the Reynolds (Re) equation (Table 1) to predict the equivalent larva size that should experience the same Re number given the increase in viscosity (Table 1). Reynolds numbers that characterize the suction flows were calculated using the diameter of the mouth as the typical length scale l (in meters) and the peak suction flow speed at the mouth center as the characteristic flow speed u (in meters per second). The diameter of the mouth was obtained from our high-speed videos (see below, Effects of Viscosity on Strike Kinematics). Because no direct measurements of suction flows in larval fish are available to date, we estimated u based on the slope of the scaling of flow speed with mouth size obtained from a computational fluid dynamics (CFD) model of the expanding larval mouth such that u = 1.81*log₁₀(l) + 0.51. For the dynamic-scaling experiments, we analyzed the results once with the above mentioned scaling, and again using the scaled size l′, such that u = 1.81*log₁₀(l′) + 0.51. The latter parameters apply to all of the Re calculations that appear throughout the text and figures. This is because viscous effects could reduce the allocation of energy to fluid acceleration (19). Both models nonetheless yielded similar results (SI Appendix, Table S2).

Re for swimming rotifers was calculated based on the rotifer’s measured length (0.2 mm), swimming speed (SI Appendix, Table S1), and water viscosity (SI Appendix, Table S1). Re for rotifers was estimated as ∼0.12 in untreated seawater and ∼0.013 in the highest viscosity treatment. Such a change in Re is not expected to affect the rotifer’s ability to evade the predator. Hence, we attribute changes in feeding rates due to increasing viscosity to the larva’s ability to capture the prey, rather than the prey’s ability to evade the larva.

Effects of Viscosity on Strike Kinematics.

Strike kinematics was analyzed for two age groups at three viscosity levels. The 22 DPH larvae were filmed in three viscosity treatments (1×, 1.8×, and 2.5× viscosity of seawater), and the 13 DPH larvae were filmed in normal (1×) viscosity of seawater. This distribution of groups represents larvae at a scaled size equivalent to 10 mm (22 DPH in seawater), 5.5 mm (22 DPH at viscosity of 1.8×), 4 mm (22 DPH at viscosity of 2.5×), and 5.6 mm (13 DPH in seawater). Filming was made using a high-speed video camera (Photron AS-6 set to 1,000 fps, 1,920 × 1,440 pixels), with a Nikkor 60-mm AF-D macro lens set to maximum magnification (providing a field of view of 16 × 12 mm). Larvae were placed in a narrow aquarium (26 × 76 × 5 mm), which was backlit using a LED light (SI Appendix, Fig. S2). Water and rotifers were circulated between the filming aquarium and a reservoir containing chilled oxygenated water using a peristaltic pump (SI Appendix, Fig. S2). We retained only videos in which the feeding fish was in the camera’s plane of focus, was facing sideways to the camera, and successfully captured its prey. Filming commenced until we had at least 10 successful feeding interactions for each group. For each video, we digitized the coordinates of four landmarks on the prey and larvae, including prey center of mass, larvae’s lower and upper jaw, and a point on its body. Tracking was made using DLTdv5 script in Matlab (37). From the digitization, we extracted the following kinematic parameters that characterize the predator: jaw opening speed, maximal gape size, time to peak gape, and the distance between prey and the larva's mouth at the onset of mouth opening. We also determined prey speed during the suction event and the timing of prey entrance into the mouth (SI Appendix, Table S4).

Discriminant Analysis of Strike Kinematics.

Discriminant analysis allowed us to explore the kinematic data for clusters of data points. These clusters are generated based on the similarity of the data and are unbiased by an a priori hypothesis of predefined groups. We used the Adegenet package (38) to find data clusters and compared them to our predefined age and scaled size groups. The input for the analysis was the 5 pc axes scores of a PCA analysis (SI Appendix, Table S5). Based on the rate of Bayesian information criterion score decrease (38), we allowed the algorithm to generate five clusters.

Effect of Age on Prey Capture Distance.

We used a high-speed high-resolution setup of the filming arena (Effects of Viscosity on Strike Kinematics) to determine strike initiation distance and maximal gape size through larval ontogeny. We filmed feeding strikes of 8, 12, and 22 DPH larvae (n = 5–21 per age group), and categorized them into successful and unsuccessful strikes. In this experimental setup, we obtained only unsuccessful strikes for 8 DPH larvae, whereas for 22 DPH larvae we obtained only successful strikes. From these videos, we measured the distance between the center of the larva's mouth and the prey at the time of strike initiation, and the maximal gape size for each strike. We also calculated the normalized strike initiation distance, defined as the absolute distance divided by peak gape diameter. We examined the effect of larval age and strike success on the absolute and normalized distance using a permutation-based one-way ANOVA.

Encounter Rate Model.

Larvae and prey that swim under low Re may swim more slowly than their physically larger counterparts (35). This effect could lead to a reduced encounter rate, which may then result in a reduced feeding rate. To quantify the effects of viscosity on the suction-feeding mechanism and on encounter rates, we ran a numerical simulation that models random encounters between a single larva and a single rotifer. We allowed the larva and the rotifer to move in a random manner inside a square arena measuring 60 × 60 pixels. An encounter was recorded when a larva was within a distance of 3 pixels from a rotifer. That reactive distance was determined such that arena size and encounter rate range were proportional to the size of the experimental aquarium and larvae, respectively. For each run of the simulation, time until encounter was determined and recorded. The only factor that determined encounter rate in our simulation was the swimming speeds of both rotifer and larva, which were adjusted to reflect the observed slowdown at higher viscosities. We first measured average swimming speeds of larvae and rotifers at different viscosity levels, and then converted all swimming speeds to relative speeds, with 1 being the highest average swimming speed measured (see SI Appendix, Table S1, for effect of viscosity on swimming speeds). Relative speeds of larvae and rotifers were input into the model as the probabilities to move one pixel within a given time step. Swimming speeds were obtained by filming larvae and rotifers in increasing water viscosities.

We ran the simulation 1,000 times for each larval size in each viscosity treatment. The time to prey capture was recorded for each run and averaged to yield the predicted encounter rate (encounters per unit time). We used the slope from a major axis regression [smatr package (39)] to calculate the ratio between simulated encounter rates vs. measured ones. A ratio lower than 1 implies that the decrease in feeding rate is mainly due to reduced encounter rate, whereas a ratio higher than 1 implies that feeding rate is reduced due to a mechanism other than the encounter rate (see SI Appendix for full model description and parameters).

Force Exerted on the Prey.

We used a one-dimensional model that solved the component forces exerted on a particle in an unsteady flow field, namely drag, acceleration reaction, and pressure gradient force. This model is described in detail elsewhere (16, 18) and in SI Appendix (SI Appendix, Figs. S3 and S4). In our calculations, the prey was considered captured if it crossed the orifice into the mouth. Forces were calculated for naturally buoyant spherical prey (0.1-mm diameter) initially located at a distance of one-half a mouth diameter on the centerline across from the orifice. We obtained mouth-opening kinematics from a successful feeding strike of 12 DPH larvae. The time to peak mouth opening did not scale with larval age. We obtained the scaling of mouth diameter with age by measuring peak mouth diameter from high-speed videos of 22 larvae between 8 and 23 DPH (two to three larvae per age group; typical filming interval, 2 d). Maximal flow speed at the location of the prey at each time step was obtained from detailed flow fields generated by a CFD model of suction-feeding larvae. The scaling of flow speed with larval length and the changes in spatial gradient in front of the mouth were also obtained from the above-mentioned CFD model. The prey was assigned a swimming force that operated to push it directly away from the mouth. Prey started swimming at the onset of the larva’s approach to it.

For each prey age group, we ran the model iteratively to determine the minimal force that the prey has to exert to evade the larva. This force was used as an indicator of feeding ability of the larva and was recorded for subsequent analysis. For the smallest larval size, we used a swimming force of 10⁻¹³ N and increased the force by 10% until prey was not captured. The initial value for the swimming force of each successive age group was 20% of that found for the youngest age group. The minimal force that the prey had to exert to evade the larvae ranged ∼10⁻⁸ N at 8 DPH to 7.85 × 10⁻⁷ N at 23 DPH.