Wireless power transfer to deep-tissue microimplants

Significance

Advances in miniaturization paved the way for tiny medical devices that circumvent conventional surgical implantation, but no suitable method for powering them deep in the body has been demonstrated. Existing methods for energy storage, harvesting, or transfer require large components that do not scale to millimeter dimensions. We report a wireless powering method that overcomes this challenge by inducing spatially focused and adaptive electromagnetic energy transport via propagating modes in tissue. We use the method to realize a tiny electrostimulator that is orders of magnitude smaller than conventional pacemakers. The demonstrated performance characteristics far exceed requirements for advanced electronic function and should enable new generations of miniaturized electronic implants.

Abstract

The ability to implant electronic systems in the human body has led to many medical advances. Progress in semiconductor technology paved the way for devices at the scale of a millimeter or less (“microimplants”), but the miniaturization of the power source remains challenging. Although wireless powering has been demonstrated, energy transfer beyond superficial depths in tissue has so far been limited by large coils (at least a centimeter in diameter) unsuitable for a microimplant. Here, we show that this limitation can be overcome by a method, termed midfield powering, to create a high-energy density region deep in tissue inside of which the power-harvesting structure can be made extremely small. Unlike conventional near-field (inductively coupled) coils, for which coupling is limited by exponential field decay, a patterned metal plate is used to induce spatially confined and adaptive energy transport through propagating modes in tissue. We use this method to power a microimplant (2 mm, 70 mg) capable of closed-chest wireless control of the heart that is orders of magnitude smaller than conventional pacemakers. With exposure levels below human safety thresholds, milliwatt levels of power can be transferred to a deep-tissue (>5 cm) microimplant for both complex electronic function and physiological stimulation. The approach developed here should enable new generations of implantable systems that can be integrated into the body at minimal cost and risk.

Progress in semiconductor technology has led to electronic devices that can augment or replace physiological functions; their ability to be implanted for direct interaction with organ systems relies on overall miniaturization of the device for simplified delivery (e.g., via catheter or hypodermic needle) and access to interstitial spaces. Advances over the past few decades enable most components in a biomedical device, including electrodes, oscillators, memory, and wireless communication systems, to be integrated on tiny silicon chips. However, the energy required for electronic function remains substantial and the consumption density has not been matched by existing powering technologies (1). As a result, the vast bulk of most implantable electronic devices consists of energy storage or harvesting components.

Although considerable progress has been made in energy storage technologies, batteries remain a major obstacle to miniaturization (2, 3) because their lifetimes are limited and highly constrained by the available volume, requiring periodic surgical replacement once the unit is depleted. Energy-harvesting strategies have been developed to eliminate batteries or to extend their function. Previous demonstrations include thermoelectric (4), piezoelectric (5–7), biopotential (8), or glucose (9, 10) power extraction. However, these methods are anatomically specific and, in their existing forms, yield power densities too low (<0.1 μW/mm²) for a microimplant.

Alternatively, energy can be transferred from an external source. Ideally, power transfer should be completely noninvasive and not specific to regions in the body. Most existing approaches for this type of transfer are based on electromagnetic coupling in the near field (11–20). Though well-suited for large devices and prostheses (21, 22), near-field methods do not address key challenges to powering a microimplant: weak coupling between extremely asymmetric source and receiver structures (23), dissipative and heterogeneous tissue (24), and regulatory power thresholds for general safety (25). These challenges, compounded by the intrinsic exponential decay of the near field, severely limit miniaturization beyond superficial depths (>1 cm), even if the battery can be removed.

Theory has indicated that these problems can be overcome in the electromagnetic midfield (23): energy transfer in this region, defined to be about a wavelength’s distance from the source, occurs through the coupling between evanescent fields in air and propagating modes in tissue. Using a patterned metal plate to control the near field, we demonstrate milliwatt levels of power transfer to a miniaturized coil deep in heterogeneous tissue (>5 cm), with exposure levels below safety thresholds for humans; this enables us to power a microimplant capable of delivering controlled electrical pulses to nearly anywhere in the body. The device consists of a multiturn coil structure, rectifying circuits for AC/DC power conversion, a silicon-on-insulator integrated circuit (IC) for pulse control, and electrodes, entirely assembled within a 2-mm diameter, 3.5-mm height device small enough to fit inside a catheter. We demonstrate wireless function by operating it in human-scale heart and brain environments, and by wirelessly regulating cardiac rhythm through a chest wall.

Theory

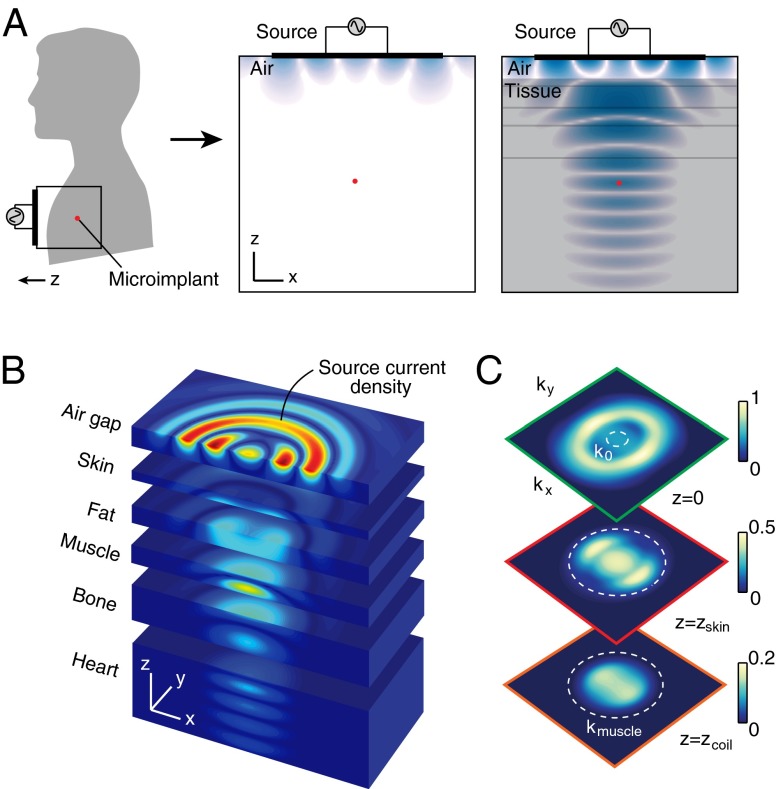
Since the first experiments in the 1960s (11), wireless powering for implantable electronics has primarily been based on coils coupled in the near field. Because quasi-static (nonradiative) magnetic fields mediate coupling, energy transfer through tissue is not substantially different from that in free space (20). Here, we describe a different approach in which a planar electromagnetic structure outside of the body generates a nonstationary evanescent field to induce energy transfer through the propagating modes of a tissue volume (Fig. 1A) (23). Using a patterned metal plate placed in close proximity to skin, the output field can be focused to dimensions much smaller than the vacuum wavelength, creating a high-energy density region within which the power-harvesting structure can be made extremely small.

Fig. 1.

Wireless energy transfer to a subwavelength coil. (A) Schematic for power transfer to a subwavelength coil mounted on the surface of the heart. Magnetic field (time snapshot $H_y$, logarithmic scale) (Right) in air and (Left) coupled into multilayered tissue. The source is solved using the optimization methodology for maximum power transfer through tissue multilayers at 1.6 GHz. The coil (red dot) is 5 cm from the source. (B) Expanded view of the magnetic field in tissue multilayers, revealing propagating waves that converge on the coil (linear scale). (C) Spatial frequency spectra at depth planes corresponding to the source (green box), the skin surface (red box, $z_{\text{skin}}=-1$ cm), and coil (orange box, $z_{\text{coil}}=-5$ cm). $k_0$, wavenumber in air; $k_{\text{muscle}}$, wavenumber in muscle tissue.

The physics underlying our powering method arises from an optimization methodology that bounds the performance achievable by any physical realization of the source (23). We begin by considering power transfer through the multilayer structure in Fig. 1B. The powering configuration consists of a source positioned a subwavelength distance above the skin layer and a small coil inserted in the cardiac tissue layer. Power transfer occurs when the source generates fields whose interaction with the coil results in work extraction by a load in the receiver circuit. For a subwavelength coil, only the lowest-order mode is important, and the power transfer mechanism can be described by electromagnetic induction characteristic of dynamic magnetic field interactions. The power transferred to the coil is given by

$$P_{SC}={\displaystyle \int d^{3}r{\mathbf{M}}_C\left(t\right)\cdot \frac{d{\mathbf{B}}_S\left(t\right)}{dt},}$$ [1]

where ${\mathbf{B}}_S$ is the magnetic field generated by the source and ${\mathbf{M}}_C$ the induced magnetization due to current in the coil. The electric and magnetic fields generated by a time-harmonic current density ${\mathbf{J}}_S$ on surface of the source conductor can be solved by decomposing the current density into its spatial frequency components, each of which obey the usual laws for refraction and reflection across planar interfaces (Materials and Methods). Using phasor notation with a time dependence of $\exp \left(-i\omega t\right)$, we define an efficiency

$$\eta =\frac{{\left|{\displaystyle \int d^{3}r {\mathbf{M}}_C^{\text{*}}\cdot {\mathbf{B}}_S}\right|}^2}{\left[{\displaystyle \int d^{3}r\mathrm{Im}\mathit{ϵ}\left(\omega \right){\left|{\mathbf{E}}_S\right|}^2}\right]\left[{\displaystyle \int d^{3}r\mathrm{Im}\mathit{ϵ}\left(\omega \right){\left|{\mathbf{E}}_C\right|}^2}\right]}.$$ [2]

Formally, η is the ratio of power available at the coil to the total absorbed power (23). Eq. 2 considers only dissipation in tissue; other losses, such as radiation and ohmic loss, arise in practice, but the amount of power that can be coupled into the body is essentially limited by electric field-induced heating. Efficiency as defined above is intrinsic to the fields in the tissue multilayer structure and gives an upper bound on the efficiency that can be obtained (SI Text).

The choice of source ${\mathbf{J}}_S$ that maximizes efficiency in Eq. 2 is key for efficient power transfer. The global optimum can be analytically solved for a specified powering configuration by defining an electric current with components tangential to a plane between the source structure and tissue. For every source, the electromagnetic equivalence theorem enables such a 2D current density to be chosen from the overall set $\mathcal{S}$ that is indistinguishable in the lower $z<0$ half-space from the physical source of the fields. Remarkably, the solution to the optimization problem, ${\text{maximize}}_{{\mathbf{J}}_S\in \mathcal{S}}\eta \left({\mathbf{J}}_S\right)$, can be found in closed form as a consequence of the vector space structure of $\mathcal{S}$ (23). In contrast to local optimization algorithms, this solution obtained is a rigorous bound on the performance that can be achieved by any physical realization of the wireless powering source.

By exploring such global solutions across a range of frequencies with appropriate dispersion models for biological materials (24), we were able to establish optimal power transfer for the chest wall structure. The solution yields a highly oscillatory electric current density that forces the output field to converge on the microimplant (Fig. 1B). Due to the high dielectric permittivity exhibited by biological materials at microwave frequencies, complete control of the propagating modes in tissue requires that the source “lens” affects evanescent wave components that lie outside of the light cone $k_x^2+k_y^2>k_0^2$ (Fig. 1C). Coherent interference of these modes confines the field at the focal plane to subwavelength dimensions, with a spot size subject to the diffraction limit in a high-index material. Unlike conventional near-field coupling, energy from the midfield source is primarily carried in propagating modes. As a result, the transport depth is limited by environmental losses rather than the intrinsic exponential decay of the near field. Theoretical studies have shown that energy transfer implemented with these characteristics can be 2–3 orders of magnitude more efficient than near-field systems (23, 26). Alternatively, for a given efficiency, the characteristic size of the coil can be made an order of magnitude smaller despite its depth in tissue (Fig. S1). The implementation of such a lensing source, however, requires electromagnetic structures more complex than conventional coil or dipole elements (27, 28).

Experimental Realization

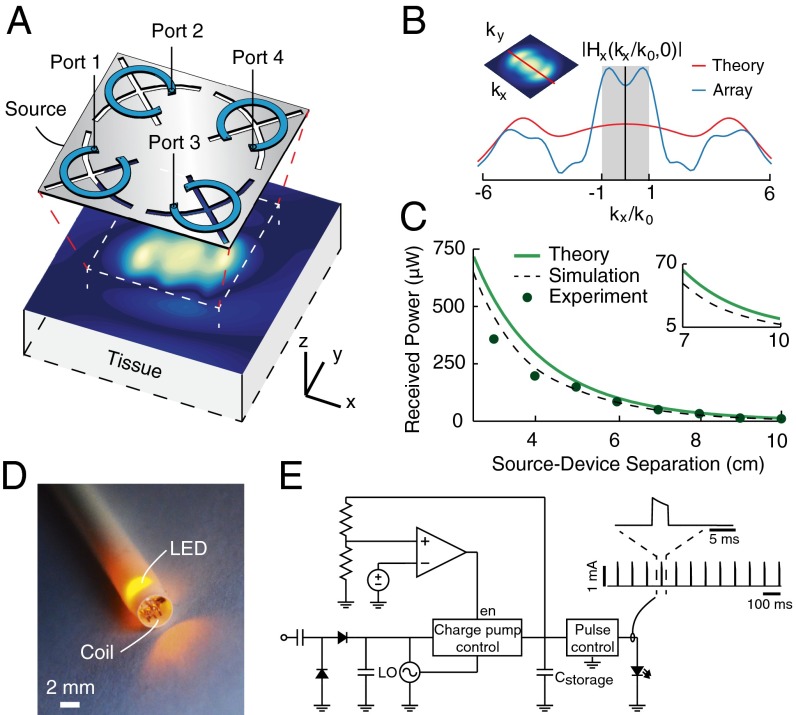
Our physical realization of midfield powering consists of a metal plate patterned with slot structures and excited by four independent radiofrequency ports (Fig. 2A and Materials and Methods). For appropriate phases between the port signals, the slot-array structure generates circular current paths that approximate the optimal current density (23). When positioned above tissue, the structure couples power from the external circuitry into the tissue volume with high efficiency (>90%), as evidenced by both low levels of backside radiation and a pronounced minimum in the scattering spectrum (Fig. S2B). Analysis of the fields on the surface of the skin shows that the evanescent spectrum approximates the theoretical optimum (Fig. 2B), although the contribution of the radiative modes is ∼2× greater owing to the inherent directionality of the planar structure. Regardless, when transferring power to a device submerged in a liquid solution with dielectric properties mimicking muscle tissue, experimental and numerical studies show that the design obtains efficiencies within 10% of the theoretical bound (Fig. 2C).

Fig. 2.

Midfield energy transfer with a patterned metal plate. (A) Schematic of the midfield source (dimensions 6 × 6 cm, operating frequency 1.6 GHz) and the magnetic field (time snapshot $H_y$) on the skin surface. (B) Corresponding spatial frequency spectrum along the $k_x$ axis compared with the theoretical optimum. (C) Theoretical, numerically simulated, and measured power received by a 2-mm diameter coil as a function of distance when coupling 500 mW into tissue. (D) Photograph of the device inserted in a 10 French (∼3.3 mm) catheter sheath for size comparison. The device is configured as a power detector, containing a 2-mm diameter coil, integrated circuits, and a LED for pulse visualization. (E) Circuit schematic of device with a representative sequence of stimulation pulses generated over 1 s. ${\text{C}}_{\text{storage}}$, charge storage capacitor; en, enable; LO, local oscillator.

At the scale of a microimplant, standard methods for electrical measurements are unsuitable because of coupling with conductive wire probes. We instead developed a custom integrated probe that separates the powering and measurement modalities by encoding the electrical power level into the frequency of optical pulses. The probe consists of a tiny power-harvesting coil (2 mm diameter) with terminals connecting to a circuit load configured with a rectifier, a microelectronic pulse control unit, and a light-emitting diode (LED; Fig. 2 D and E). A representative device with a yellow LED is shown in Fig. 2D inside a 10 French (∼3.3 mm) catheter sheath for size reference. An optical fiber guides light to a terminating photodiode at the measurement location. We were able to calculate the power transferred to the coil, calibrated for circuit-dependent inefficiencies, by recording the end-to-end power levels at multiple reference flash rates. From the nonlinear response of the circuit, a system of linear equations can be solved to yield the transfer efficiency (Fig. S3 and Materials and Methods).

Results

We evaluate the performance of our powering system in complex tissue geometries by designing two configurations that simulate power transfer to devices in the left ventricle of the heart and the cortex region of the brain. The source and device positions within a porcine tissue volume, shown in Fig. 3 A and B using MRI reconstructions, are separated by at least 5 cm. When coupling 500 mW into tissue (approximately the output power of cell phones), we measured the power transferred to the coil to be 195 μW for the heart and 200 μW for the brain configurations. These levels are far greater than requirements for advanced integrated circuits (Table S1); in comparison, cardiac pacemakers consume ∼8 μW (1, 29). The received power remains substantial (∼10 μW) even when the operating depth is increased to 10 cm. Provided that the fields can be refocused, computational studies show that the performance is insensitive to the fine structure and composition of the intermediate tissue (30).

Fig. 3.

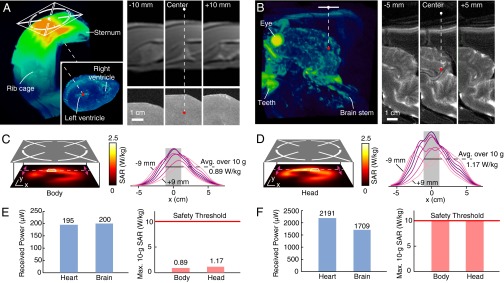
Received power and safety studies. (A) Configuration for power transfer across a porcine chest wall to the electrostimulation device on the heart surface reconstructed by MRI. The source center (white dot) and the coil (red dot) are 5 cm apart (1-cm air gap, 4-cm heterogeneous tissue). (B) Similar reconstruction when the device is inserted in the lower cortex region of a porcine brain. The source–receiver separation is 5.5 cm. (C and D) SAR distribution in a head/body-simulating liquid measured 1.2 cm from the metal plate when coupling 500 mW into tissue (Left). Distribution slices taken around the hotspot (Right; 1.5 mm spacing); the cubic averaging volume (10 g of tissue; ∼2.15 cm side length) is shaded. (E) Measurements of the power transferred to a device with a 2-mm diameter coil from the midfield source when coupling 500 mW into tissue for the configurations in A and B. Measurements of the maximum 10-g SAR and the exposure threshold. (F) Received power when the power coupled into tissue meets the maximum permitted level of exposure.

The excess energy dissipated over tissue poses potential safety concerns. Safety guidelines specify an exposure threshold of 10 W/kg averaged over 10 g of tissue in a controlled environment (25). To assess the exposure levels induced by power transfer, we operated our source over a simulated tissue volume defined by an anthropomorphic fiberglass shell. The spatial distribution of absorbed power was measured by scanning a robotic probe through dosimetric liquids mimicking the body and head (Fig. S4); standard procedures for demonstrating regulatory compliance were used (Materials and Methods). When coupling 500 mW of focused power into tissue, the maximum specific absorption rate (SAR) was found to be 0.89 W/kg for the body and 1.17 W/kg for the head, averaged over 10 g of tissue (Fig. 3 C and D). These levels are far below the exposure threshold for controlled environments (Fig. 3E). If the power coupled into tissue is allowed to meet the maximum permitted level of exposure, Fig. 3F shows that 2.2 mW and 1.7 mW can be transferred for the configurations shown in Fig. 3 A and B, respectively. The low body-averaged absorption (<0.04 W/kg for adult humans) and localized distribution suggest that the power transfer is unlikely to have a meaningful impact on core body temperatures (SI Text).

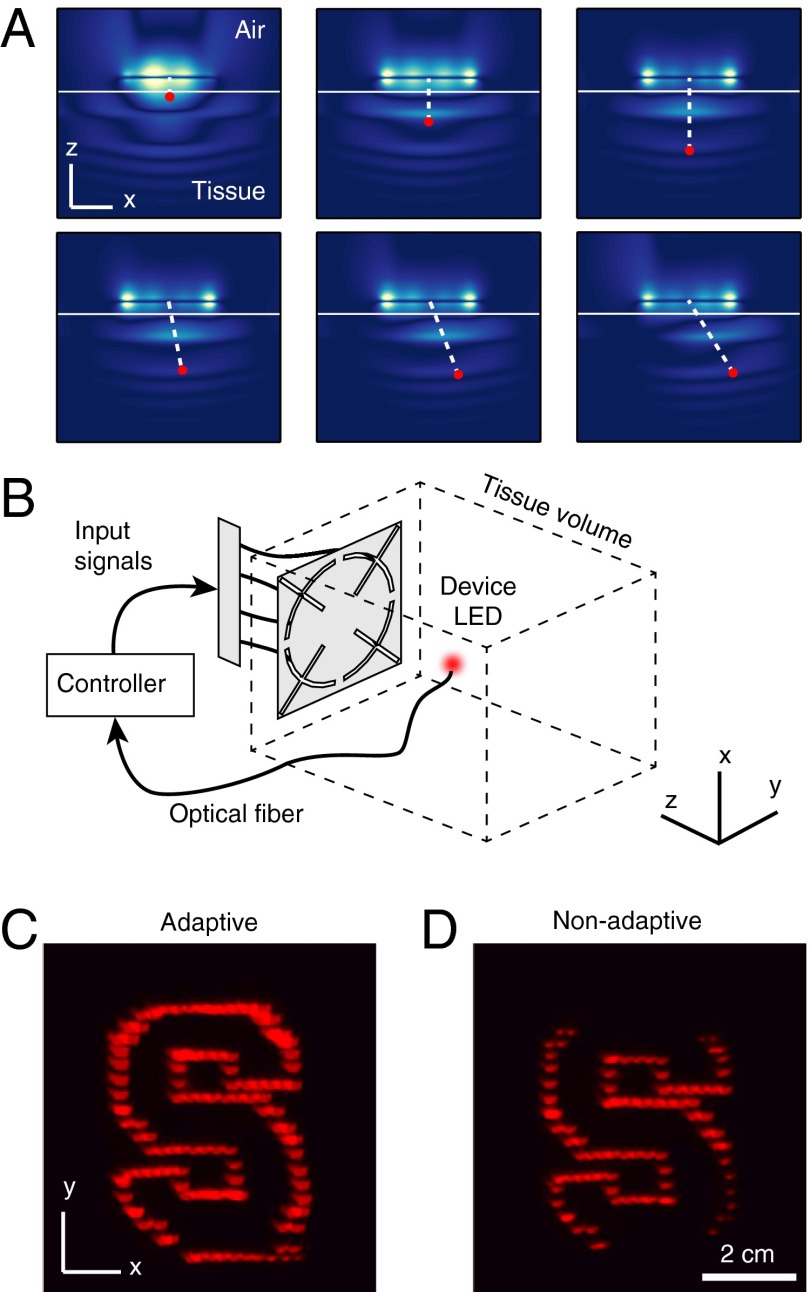
Clinical application may require that microimplants operate on organs in rhythmic motion (due to breathing or heartbeat) or move inside the body. The degrees of freedom provided by the phases of the input port signals enable various field patterns to be synthesized, including those with spatially shifted focal regions (Fig. 4A). Software control of these phases can refocus the fields without mechanical reconfiguration. We implemented a “greedy” phase search algorithm based on the closed-loop feedback relayed over an optical fiber (Fig. 4B) that obtains focusing-enhanced power transfer in real time. Over an S-shaped trajectory of motion, this adaptation eliminates dark regions that otherwise occur in the static case (Fig. 4 C and D), indicating a coverage area much wider than that intrinsic to the focal region (Fig. S5). Incorporating components for wireless communication in the device will enable an untethered realization of this and other related control algorithms.

Fig. 4.

Real-time dynamic focusing. (A) Field patterns with spatially shifted focal points designed by adjusting the relative phases between the port signals. (B) Experimental setup for measuring the transferred power to a moving device in a liquid solution whose properties mimic muscle tissue. (C) Strobed position of the LED as the wireless device moves in an S-shaped trajectory. A real-time control algorithm dynamically tracks for motion. (D) Same as C, but without dynamic focusing; the field pattern is static and focused at the center.

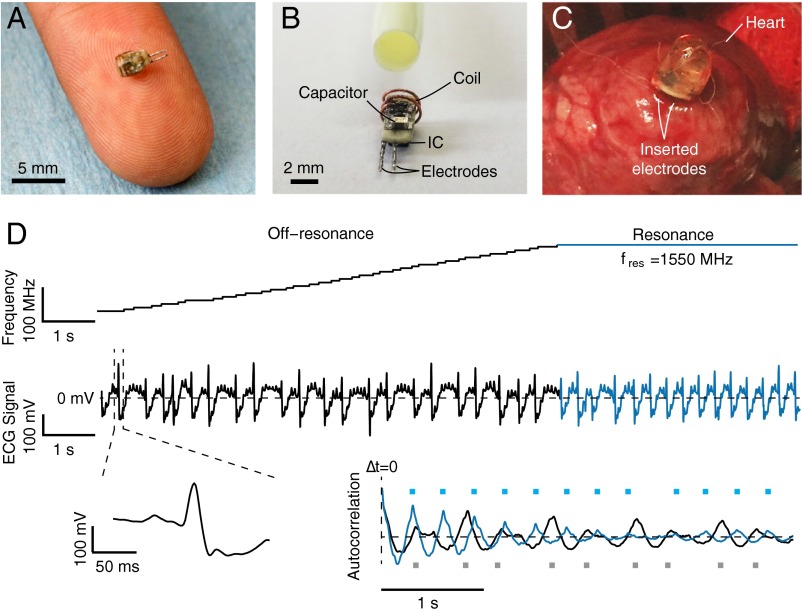
As a demonstration of stimulation capabilities in vivo, we inserted the wireless electrostimulator into the lower epicardium of a rabbit. The heart rate of the rabbit was monitored by ECG. The electrostimulator device shown in Fig. 5 A–C is 2 mm in diameter, weighs 70 mg, and is capable of generating 2.4-μJ pulses at rates dependent on the extracted power; its characteristic dimension is at least an order of magnitude smaller than existing commercial pacemakers (29) due to the absence of a battery (Fig. S6B). A portable, handheld source placed ∼4.5 cm above the device after closing the chest, was used to couple 1 W of power into the chest. Cardiac rhythm can be controlled in a fully wireless manner by adjusting the operating frequency—when coincident with the resonant frequency of the circuit, the pulse amplitudes are sufficient to pace the heart, as indicated by the increased rate and regularity of the ECG signal (Fig. 5D). Systems based on similar concepts can be applied for any other optical or electrical stimulation task in the body, including neurons or muscle cells; they can also potentially be generalized to networks of individually addressable probes for coordinated mapping and stimulation.

Fig. 5.

Wireless cardiac pacing. (A) Photograph of the wireless electrostimulator on a human finger. The device is 2 mm in diameter. (B) Same device before epoxy encapsulation next to a 10-French (∼3.3 mm) catheter sheath for size comparison. (C) Photograph of the electrostimulator inserted in the lower epicardium of a rabbit via open-chest surgery. After implantation, the chest was closed and a portable, battery-powered source was positioned ∼4.5 cm (1-cm air gap, ∼3.5-cm chest wall) above the device. (D) The operating frequency of the source (Top) adjusted to the estimated resonant frequency of the circuit and maintained for several seconds. Cardiac activity of the rabbit monitored by ECG (Middle), magnified view of a single heartbeat (Bottom Left), and autocorrelation function (Bottom Right) of both the off-resonance (black) and resonant (blue) sections of the ECG signal. Peaks in the autocorrelation function are marked with squares.

Conclusion

We have demonstrated a wireless powering method that can power microimplants at nearly any location in the body. Because the performance characteristics shown here far exceed requirements for integrated technologies (optoelectronics, microelectromechanical systems sensors, and logic units), there are considerable possibilities for new generations of microimplants: the size, for example, can be further reduced to micrometer scales (23) or more sophisticated functions implemented, such as real-time monitoring of chronic disease states or closed-loop neural sensing and control. Future systems may also incorporate a small rechargeable battery to enable continuous operation without an externally worn power source. These capabilities should substantially increase the viability of implanting electronics in living systems.

Materials and Methods

Numerical Methods.

The fields shown in Fig. 1 A and B were calculated from the spectral components of an in-plane source current density ${\mathbf{J}}_S\left(k_x,k_y\right)$ using the dyadic Green’s function method. This method reduced to a simple transfer function because the plane-wave components are eigenfunctions of propagation in the multilayer structure. At each depth z, for example, we apply a dyad ${\mathbf{G}}_H\left(k_x,k_y,z\right)$ to calculate the magnetic field $\mathbf{H}\left(k_x,k_y,z\right)={\mathbf{G}}_H\left(k_x,k_y,z\right){\mathbf{J}}_C\left(k_x,k_y\right)$. An inverse Fourier transform yields the fields at each depth. The fields in Fig. 4A were calculated using a commercial electromagnetic simulator (CST Studio Suite; Computer Simulation Technology). The patterned metal plate was placed above a tissue multilayer (1-cm air gap, 4-mm skin, 8-mm fat, 8-mm muscle, 16-mm bone, 144-mm heart) and the fields calculated by a time-domain solver. A similar simulation setup—with tissue layers simplified to a slab with the dielectric properties of the liquid solution (0.5% saline)—was used to obtain the simulation curve in Fig. 2C. The port phases were reconfigured at each depth to maximize power transfer.

Electromagnetic Region of Operation.

To select the frequency of operation, theoretical efficiency vs. frequency curves were generated by solving for the optimal η in a multilayer model of tissue (1-cm air gap, 4-mm skin, 8-mm fat, 8-mm muscle, 1-mm bone, ∞ heart) across a wide search range (10 MHz to 4 GHz) for coils oriented in the x and z directions (23). Fig. 1A shows the magnetic field component $H_x$ at 1.6 GHz. The upper frequency bound is selected to be about the self-resonance frequency of the coil. The coil losses were taken into account using an analytical model for a loop of wire embedded in uniform tissue, as well as impedance matching by imposing the constraint $Q<10$, where Q is the quality factor (30). Using the Debye dispersion model for each tissue type (24), the peak efficiency was found to occur at 1.6 GHz. Because each efficiency is the maximum that can be obtained by any implementation of the source, we concluded that 1.6 GHz is the optimal frequency for this configuration.

Source Design.

The midfield source realization consists of a patterned metal structure excited at four ports with rf signals of controlled phases (Fig. S2A). The plate was fabricated on a 1.6-mm FR4 substrate with feed and patterned copper layers. Semirigid coaxial cables were used to connect each excitation port to the control board. An rf signal at 1.6 GHz was brought from the signal generator to the control board and then separated to four lines using a Wilkinson power divider. Following power division, the signals were connected to parallel stages for variable attenuation, phase shifting (analog 400°, +3.5/−2.0° error), and amplification (gain 14 dB). The phase shifters are voltage controlled and adjusted using a National Instruments 9264 CompactDAQ module via LabVIEW.

Probe Design.

The probe consists of a receiving coil, rectifier, charge pump, flash control integrated circuit, and an LED (Fig. 2D). The coil was wound with an inner diameter of 2 mm using copper wire (200 μm diameter), with variable number of turns (between 1 and 15) depending on the design frequency. For the rectifier circuit, two Schottky diodes (Skyworks SMS7630 series) and two 10-nF capacitors were arranged in a charge pump configuration. At low frequencies, an additional capacitor was used to match the impedance of the coil and the rectifier. A charge pump and flash control integrated circuit was placed after the rectifier for upconverting the rectified voltage to the 2.0 V necessary to drive the LED. Charge was stored on a discrete 4.7-μF capacitor, and discharged through the LED (ROHM PICOLED) when a specified threshold voltage was reached. The entire probe was encapsulated in epoxy, connected to an optical fiber for power information readout. The minimum power to operate the device is ∼10 μW. All components were bonded to a printed circuit board of Rogers 4350 substrate.

Efficiency Calibration.

The efficiency of power transfer was experimentally measured with the probe in Fig. 2E. To calibrate for the circuit losses, which are substantial (> 50%) in the design, the nonlinear behavior of the circuitry was exploited to form a set of linearly independent equations from which unknown coil parameters can be solved. This system of equations was obtained by considering the circuit in Fig. S3A where the coil is represented by an inductance $\left(L_C\right)$, in series with a resistance $\left(R_C\right)$ and a voltage source $\left(V_C\right)$, where the latter two parameters are unknown. The nonlinear circuit was characterized at two reference pulse rates, $r_1$ and $r_2$, by finding the corresponding pseudoimpedances $Z_{R,n}:=V_{R,n}/I_{R,n}$ when the circuit is at resonance. The corresponding amplitudes $I_{R,n}$ and $V_{R,n}$ were found using harmonic balance analysis with commercial circuit design tools (Advanced Design Systems; Agilent). From the reduced circuit in Fig. S3B, we obtained the following equations by a straightforward application of Kirchhoff’s voltage law: $V_{C,n}=\left(R_C+Z_{R,n}\right)I_{C,n}$ for $n=1,2$. The two equations are linearly independent if the reference rates correspond to operation in a nonlinear region of the circuit. For each powering configuration, an additional equation was obtained by adjusting the power level at the source until the observed pulse rate equals $r_1$ and $r_2$. Recording the two reference power levels $P_{S,1}$ and $P_{S,2}$, an additional equation $V_{C,2}/V_{C,1}=\sqrt{P_{S,2}/P_{S,1}}$ was obtained, permitting the unknown parameters $V_{C,n}$ and $R_C$ to be solved. The efficiency was then found by directly calculating $\eta ={\left|V_{C,n}\right|}^2/8R_C{P}_{S,n}$. When including intermediate circuit losses, the efficiency in Fig. 3 A and B was reduced by a factor of ∼2, depending on environmental loading effects. The power flowing through the pulse control units was measured to be 90 μW and 82.5 μW for the body and head configurations, respectively.

Tissue Imaging.

MRI of porcine tissue in Fig. 3 A and B was performed at the Stanford Magnetic Resonance Systems Research Lab. A T2-weighted spin-echo pulse sequence was used for the heart and chest; T2-weighted fast spin-echo was used for the head. Reconstruction was performed with the OsiriX software package.

Specific Absorption Rate Measurement.

Radiofrequency exposure levels were characterized in a SAR measurement laboratory (Bay Area Compliance Laboratories). The midfield source was placed under a tank (Twin Specific Anthropomorphic Mannequin, shell thickness 0.2 cm) filled with a tissue-simulating solution (head and body) and configured to couple 500 mW of focused power into the tank (Fig. S4). A robotic arm (Staubli Robot TX90XL) scanned a three-axis electric field probe (dosimetric ET3DV6) along the tank surface directly above the source; control and processing were performed in real time (DASY4 system). Interpolation routines in DASY4 software enables the maximum field locations to be pinpointed even on relatively coarse grids. High-resolution scans were then performed over cube-shaped 1-g and 10-g volumes of tissue centered at the detected hotspot with parameters chosen in accordance with guidelines. The field amplitudes measured by the probe were processed through commercial software (DASY4 PRO). Data visualization was performed on SEMCAD and MATLAB without further processing. Before all measurements, the output power level was verified with a power meter and a test verification scan was performed with a calibrated dipole source. All testing procedures and equipment are the same or equivalent to those used to demonstrate safety compliance to international standards for consumer electronics, including cell phones and other wireless equipment.

Probe Trajectory Visualization.

A power measurement device was attached to the end of a fiber optic cable and submerged in a liquid solution (0.5% saline). A custom-built 3D positioner (LEGO Mindstorms) moved the device in an S-shaped trajectory. A photo sequence was obtained in a dark room with 1/2-s exposure every 5 s while the device was in motion. The entire S-shaped path was completed in 20 min. The composite image was created by thresholding the brightness of each image and superimposing the result.

Cardiac Pacing.

Adult New Zealand white rabbits (3–4 kg; Charles River Laboratories) were used for the cardiac pacing study. All animals were housed in individual cages at animal facilities and monitored routinely by veterinary staff. Animals were allowed to acclimatize to the holding facilities for 5–7 d before the procedures. Each animal was given access to food pellets, hay, and water ad libitum and maintained on a 12-h light/dark cycle throughout the experiment. Before the surgical procedure, each animal received a dose of i.v. antibiotics (cefazolin 20–30 mg/kg) and the surgical site was shaved using clippers followed by a surgical scrub using Betadine. During the surgical procedure, rabbits were anesthetized (ketamine 35 mg/kg, xylazine 5 mg/kg, i.m. injection) followed by endotracheal intubation and inhalation of isoflurane (0.8–4.0%). Once confirmed that the animal was completely sedated, a vertical midline incision was made and sternotomy was performed using aseptic conditions. The pericardium was excised to expose the heart. Following heart exposure, the 2-mm pacemaker device was implanted into the apex of the heart and the chest was closed using 6-0 Prolene sutures for the pacing experiment. All procedures were approved and followed the rules set by the Animal Care Committee of Stanford University.