Quenched disorder and vestigial nematicity in the pseudogap regime of the cuprates

Significance

Recent experiments show that a tendency toward charge density wave (CDW) order, long documented in certain structurally special members of the cuprate family, is a ubiquitous feature of the pseudogap regime in these high-temperature superconductors. We show that quenched disorder plays a key role in this problem, inevitably limiting the growth of CDW correlations even in the most perfect existing crystals and rounding the associated phase transitions. However, weak disorder operating on a unidirectional CDW leaves behind a sharply defined vestigial point-group symmetry breaking and an associated phase transition. We suggest that such electron-nematic order is an essential feature of the pseudogap phase and that the associated quantum critical point may play an essential role in the physics of high-temperature superconductivity.

Abstract

The cuprate high-temperature superconductors have been the focus of unprecedentedly intense and sustained study not only because of their high superconducting transition temperatures, but also because they represent the most exquisitely investigated examples of highly correlated electronic materials. In particular, the pseudogap regime of the phase diagram exhibits a variety of mysterious emergent behaviors. In the last few years, evidence from NMR and scanning tunneling microscopy (STM) studies, as well as from a new generation of X-ray scattering experiments, has accumulated, indicating that a general tendency to short-range–correlated incommensurate charge density wave (CDW) order is “intertwined” with the superconductivity in this regime. Additionally, transport, STM, neutron-scattering, and optical experiments have produced evidence—not yet entirely understood—of the existence of an associated pattern of long-range–ordered point-group symmetry breaking with an electron-nematic character. We have carried out a theoretical analysis of the Landau–Ginzburg–Wilson effective field theory of a classical incommensurate CDW in the presence of weak quenched disorder. Although the possibilities of a sharp phase transition and long-range CDW order are precluded in such systems, we show that any discrete symmetry-breaking aspect of the charge order—nematicity in the case of the unidirectional (stripe) CDW we consider explicitly—generically survives up to a nonzero critical disorder strength. Such “vestigial order,” which is subject to unambiguous macroscopic detection, can serve as an avatar of what would be CDW order in the ideal, zero disorder limit. Various recent experiments in the pseudogap regime of the hole-doped cuprates are readily interpreted in light of these results.

Because the spontaneous breaking of a continuous symmetry is forbidden (1) in the presence of “random-field” disorder in dimension $d\le 4$, effects of disorder are significant for the physics of incommensurate charge density wave (CDW) ordering, even in crystalline materials, such as the high-temperature superconductor YBCO, which can in other respects be considered extremely well ordered. However, because $d=2$ is the lower critical dimension for breaking a discrete symmetry, as in the random-field Ising model (1–3), if a putative CDW ground state breaks a discrete symmetry (e.g., a point-group symmetry), a finite temperature transition at which this symmetry is broken will persist in the presence of weak disorder in $d=3$.

Here, with the case of the cuprates in mind, we study a model of a layered system with tetragonal symmetry that in the absence of disorder undergoes a transition to a unidirectional incommensurate CDW (stripe-ordered) phase. We thus express the density at position $\overrightarrow{r}$ in plane m as

$$\rho \left(\overrightarrow{r},m\right)=\overline{\rho }+\left[{\psi }_x\left(\overrightarrow{r},m\right)e^{iQx}+{\psi }_y\left(\overrightarrow{r},m\right)e^{iQy}+\mathrm{C}.\mathrm{C}.\right]+\dots ,$$ [1]

where Q is the magnitude of the CDW ordering vector, ${\psi }_{\alpha }$ (with $\alpha =x,y$) are the two components of a slowly varying complex vector field, and the ellipsis refers to higher harmonics. Broken symmetries are defined, as usual, by taking the asymptotic long-distance limit of the appropriate thermal $\left(\langle \rangle \right)$ and configuration averaged $\left(\overline{;}\right)$ two-point correlation function, ${\lim }_{\left|\overrightarrow{R}\right|\to \infty }\overline{\langle O^{†}\left(\overrightarrow{r}+\overrightarrow{R},m\right)O\left(\overrightarrow{r},m\right)\rangle }\equiv \overline{\langle {\left|O\left(m\right)\right|}^2\rangle }$: In a stripe-ordered state, $\overline{\langle {\psi }_x\rangle }\ne 0$ and $\overline{\langle {\psi }_y\rangle }=0$ (or vice versa) and $\mathcal{N}\equiv \overline{\langle {\left|{\psi }_x\right|}^2\rangle }-\overline{\langle {\left|{\psi }_y\right|}^2\rangle }\ne 0$; in a checkerboard state $\overline{\langle {\psi }_x\rangle }=\overline{\langle {\psi }_y\rangle }\ne 0$, and $\mathcal{N}=0$, whereas in an “Ising nematic” phase, $\overline{\langle {\psi }_x\rangle }=0$, $\overline{\langle {\psi }_y\rangle }=0$, and $\mathcal{N}\ne 0$. For each of these states, the pattern of broken symmetry could, depending on details of the interactions between neighboring planes, propagate from plane to plane in different ways, thus breaking the point-group symmetries as well as translation symmetry in the z ($\perp$ to the plane) direction in different ways.

In Eq. 6, below, we introduce an effective Landau–Ginzburg–Wilson field theory expressed in terms of the above fields. For simplicity, we assume that the interplane couplings (of magnitude $V_z$) are weak compared with the in-plane interactions and favor identical ordering in neighboring planes; however, it is straightforward to generalize this to cases in which more complex patterns of interplane ordering are favored. The stripe state breaks a continuous $\left(U\left(1\right)=O\left(2\right)\right)$ symmetry (translations) and a discrete $Z_2$ symmetry associated with the choice of whether the stripes are modulated in the x or y direction. In the nematic phase, translational symmetry is preserved but the point-group ($Z_2$) symmetry is still broken. We obtain explicit results for the phase diagram and various correlation functions of this model, using a saddle-point (mean-field) approximation and the replica trick. This approximation becomes exact in an $N\to \infty$ limit of this in which ${\psi }_{\alpha }$ is taken to be an N-component field, and the $O\left(2\right)\times O\left(2\right)\times Z_2$ symmetry of the original model is generalized to $SO\left(N\right)\times SO\left(N\right)\times Z_2$. We also outline a procedure (explored in more detail in SI Text) to establish an explicit correspondence between the effective field theory for the nematic order parameter and a random-field Ising model (RFIM).

Principal Results

Because the general behavior of the system can be motivated largely from symmetry considerations starting directly from the assumption of a stripe-ordered state, we begin by presenting our key results on the basis of qualitative arguments and then discuss how these results follow from the systematic analysis of the effective field theory.

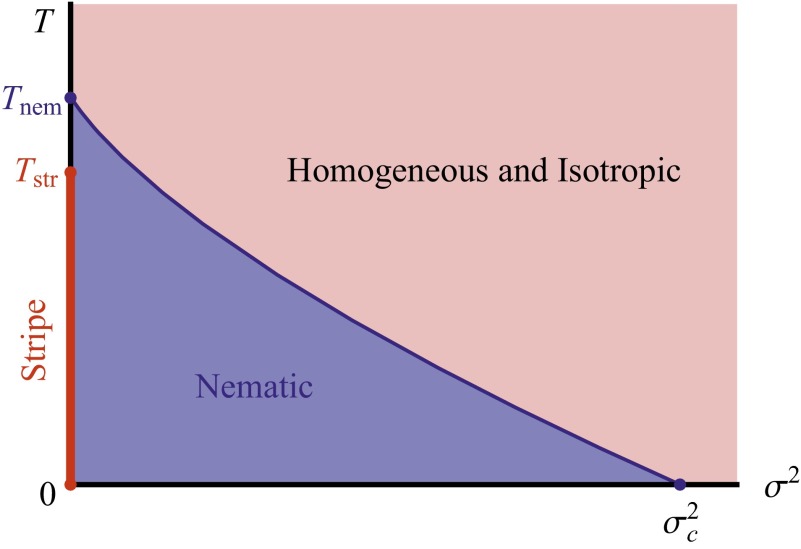
The structure of the phase diagram in the temperature (T) and disorder (σ) plane is shown in Fig. 1. In the absence of disorder, stripe order necessarily survives up to a nonzero critical temperature, $T_{ \mathrm{str}}$. Here, it is possible that there is a single transition to a fully symmetric state, or it is possible, as displayed in Fig. 1, for the symmetry to be restored in a sequence of two transitions, resulting in the existence of an intermediate nematic phase for $T_{ \mathrm{str}}\le T<T_{ \mathrm{nem}}$. (Both scenarios occur in the model defined in Eq. 6, depending on the value of $V_z$; the situation shown in Fig. 1 pertains to the case $V_z<0.37J$, whereas for larger $V_z$, there is apparently a single first-order transition without an intermediate nematic phase.) Assuming the transitions to be continuous, the transitions at $T_{ \mathrm{str}}$ and $T_{ \mathrm{nem}}$ are in the 3D-XY and 3D-Ising universality classes, respectively. (Note that both $T_{\mathrm{str}}$ and $T_{\mathrm{nem}}$ remain nonvanishing in the limit $V_z\to 0$, although for $V_z=0$, the stripe state would have only quasi–long-range order.

Fig. 1.

Schematic phase diagram of a highly anisotropic (quasi-2D) tetragonal system as a function of the mean-squared disorder, ${\sigma }^2$. The phase diagram is computed from the solution of the self-consistency equations for the lattice version of the model (Eq. 6) defined in SI Text with $V_z=0.01{\kappa }_{\parallel },{\kappa }_{\perp }=0.98{\kappa }_{\parallel },$ and $\mathrm{\Delta }=0.25{\kappa }_{\parallel }$. ${\sigma }_c$ is the critical disorder strength beyond which there is no nematic transition.

Nonzero disorder precludes the existence of long-range stripe order; under some circumstances, for weak enough disorder, the stripe order could give way to quasi–long-range stripe-glass order (4–6), but this is not generic (7) and is not seen in our effective field theory, at least at the level of the approximate solution we have obtained. However, the nematic phase has Ising symmetry so it survives as long as the disorder is less than a critical strength, ${\sigma }_c$. This is an example of a more general phenomenon, which we have named “vestigial order”; although the tendency toward stripe order is the essential piece of microscopic physics, the nematic phase is more robust as a phase of matter and can serve as an avatar of stripe order that can be detected in macroscopic measurements (8). Although ${\sigma }_c$ necessarily vanishes as $V_z\to 0$, it does so (9) only as ${\sigma }_c\sim {\left[\log \left|T_{\mathrm{nem}}/V_z\right|\right]}^{-1/2}$, so it is typically not very small even in highly anisotropic (quasi-2D) systems.

To obtain explicit expressions for measurable quantities requires making approximations. One important quantity is the structure factor, $S\left(\overrightarrow{q}\right)$, which determines the X-ray scattering cross section. For $T>T_{ \mathrm{str}}$, invoking the fluctuation dissipation theorem and linear response analysis, it is straightforward to obtain expressions for S in terms of the susceptibility, G, of the ideal (disorder-free) system to second order in σ. Specifically, near the fundamental ordering vectors $\left(k_x^2+k_y^2\ll Q^2\right)$,

$$\begin{array}{c}S\left(Q+k_x,k_y,k_z\right)=TG\left(k_x,k_y,k_z;\mu +\mathcal{N}\right)\\ +{\sigma }^2{\left[G\left(k_x,k_y,k_z;\mu +\mathcal{N}\right)\right]}^2,\\ S\left(k_x,Q+k_y,k_z\right)=TG\left(k_y,k_x,k_z;\mu -\mathcal{N}\right)\\ +{\sigma }^2{\left[G\left(k_y,k_x,k_z;\mu -\mathcal{N}\right)\right]}^2\end{array}$$ [2]

(see below for the definition of μ). Even in the limit of weak disorder, this expression is invalid for $T<T_{ \mathrm{str}}$, reflecting the nonperturbative destruction of long-range CDW order by quenched randomness. However, in the Gaussian approximation we define below, which is exact in the previously mentioned large N limit, an expression of precisely this same form is obtained that is valid for all σ and T; however, with G replaced by an effective susceptibility,

$$G\left(\overrightarrow{k};\mu \right)={\left[{\kappa }_{\parallel }{k}_x^2+{\kappa }_{\perp }{k}_y^2+V_z{\mathit{ϵ}}_z\left(k_z\right)+\mu \right]}^{-1}.$$ [3]

Here ${\mathit{ϵ}}_z\left(k_z\right)$ is the z-direction dispersion that depends on the details of the interplane interactions, and $\mathcal{N}$ and μ are effective couplings that are implicit functions of T and σ determined by the self-consistency Eqs. 9 and 10, below. In the isotropic phase $\mathcal{N}=0$, whereas in the nematic phase or in the presence of explicit orthorhombic symmetry breaking by the lattice, $\mathcal{N}\ne 0$.

Because there is an actual thermodynamic phase transition involved, direct probes of the nematic phase should, in principle, be possible and unambiguous. There are, however, two aspects of the problem that make this less straightforward than it at first seems. In the first place, the number of degrees of freedom per unit cell involved in a nematic transition may be relatively small. For instance, nematic order does not generically open gaps anywhere on the Fermi surface, leading to a relatively weak signature in the specific heat (10), even when the nematic transition occurs at low T; when the transition occurs at relatively high T, where multiple contributions to the specific heat are large, the smallness of the thermodynamic signal is still more of an issue. More importantly, because the transition is in the universality class of the RFIM, the intrinsic slow dynamics (3) imply that, starting at a cooling-rate–dependent temperature strictly larger than $T_{ \mathrm{nem}}$, the nematic ordering can no longer equilibrate and hence all thermodynamic signatures will be dynamically rounded. This is further exacerbated by the fact that any uniaxial strain will couple linearly to the nematic order parameter, so uniaxial strain (or any weak orthorhombicity of the host crystal) will round the transition and random strains will broaden it.

There are, however, clear ways to detect nematic order. Although this has been undertaken in various ways in the context of the cuprates (11–21), the most successful strategy has been developed in the context of studies of the Fe-based high-temperature superconductors (22). Several general observations underlie these strategies:

• i) Any quantity that is odd under $C_4$ rotations (or the corresponding element of the point-group symmetry that is broken in the nematic phase) vanishes in the isotropic phase and grows linearly in proportion to $\mathcal{N}$ for small $\mathcal{N}$ and can thus be used as a proxy for the nematic order parameter. Examples include the resistivity anisotropy (14, 23, 24), ${\rho }_{xx}-{\rho }_{yy}$, any local density that is odd under $C_4$ rotation, or a structural (e.g., orthorhombic) distortion (25). Consider, for instance, the bond-charge density on x-directed and y-directed bonds from site $\overrightarrow{R}$, ${\rho }_x\left(\overrightarrow{R}\right)$ and ${\rho }_y\left(\overrightarrow{R}\right)$, which for the cuprates (11) also corresponds to the charge density on the corresponding in-plane O sites. A direct measure of nematicity is $Q_{\mathcal{N}}\equiv \overline{\langle {\rho }_x\left(\overrightarrow{R}\right)\rangle }-\overline{\langle {\rho }_y\left(\overrightarrow{R}\right)\rangle }\propto \mathcal{N}$. A different measure, which is directly related to local CDW order, is ${\tilde{Q}}_{\mathcal{N}}\equiv \overline{\langle {\left|\delta {\rho }_x\left(\overrightarrow{R}\right)\right|}^2\rangle }-\overline{\langle {\left|\delta {\rho }_y\left(\overrightarrow{R}\right)\right|}^2\rangle }$, where

$$\begin{array}{c}\delta {\rho }_{\alpha }\equiv {\rho }_{\alpha }-\overline{\langle {\rho }_{\alpha }\rangle },\\ \overline{\langle {\left|\delta {\rho }_x\left(\overrightarrow{R}\right)\right|}^2\rangle }={\sigma }^2{A}_2\left(\mu +\mathcal{N}\right),\\ \overline{\langle {\left|\delta {\rho }_y\left(\overrightarrow{R}\right)\right|}^2\rangle }={\sigma }^2{A}_2\left(\mu -\mathcal{N}\right),\end{array}$$ [4]

• and

$$A_p\left(\mu \right)\equiv {\displaystyle \int \frac{d\overrightarrow{k}}{{\left(2\pi \right)}^3}{\left[G\left(\overrightarrow{k},\mu \right)\right]}^p}=-\left(\frac{1}{p-1}\right)\frac{\partial A_{p-1}}{\partial \mu }$$ [5]

• with $G\left(\overrightarrow{k};\mu \right)$ given in Eq. 3. A quantity similar to $Q_{\mathcal{N}}$, referred to in ref. 17 as “intra-unit-cell-nematic” order, has been investigated in scanning tunneling microscopy (STM) studies of cuprate high-temperature superconductors with suitable surfaces. As has been shown in ref. 11 (and discussed below), bulk NMR measurements on cuprates can be performed to obtain $Q_{\mathcal{N}}$ and ${\tilde{Q}}_{\mathcal{N}}$.

• ii) The uniaxial volume preserving strain, $b^{ \mathrm{eff}}\equiv {\mathit{ϵ}}_{xx}-{\mathit{ϵ}}_{yy}$, acts as a symmetry-breaking field (Eq. 11) conjugate to $\mathcal{N}$. Thus, from the strain dependence of any of the electronic proxies for $\mathcal{N}$, it is possible to infer the differential susceptibility, $\chi \equiv \partial \mathcal{N}/\partial b^{\mathrm{eff}}$. Less obviously, but equally importantly, the ability to apply a symmetry-breaking field can, under appropriate circumstances, permit at least two real-world complications to be circumvented: (a) In an orthorhombic crystal, there is an explicit symmetry-breaking field that rounds the nematic transition and implies the existence of a nonzero $\mathcal{N}$ even for $T>T_{\mathrm{nem}}$; however, if the orthorhombicity is sufficiently weak, it is possible (22) to measure χ at nonzero $b^{\mathrm{eff}}$ and to extrapolate the result to $b^{\mathrm{eff}}=0$, thus correcting for the presence of orthorhombicity. (b) Where macroscopic detection of symmetry breaking is precluded due to domain formation, cooling in the presence of a symmetry-breaking field can orient the order parameter macroscopically, permitting macroscopic measurements to detect its presence.

Explicit Model

To make the present considerations concrete, we consider the simplest classical effective field theory (26–28) of an incommensurate CDW in a tetragonal crystal, with effective Hamiltonian

$$\begin{array}{c}\mathrm{\mathscr{H}}=\frac{{\kappa }_{\parallel }}{2}{\left|{\partial }_{\alpha }{\psi }_{\alpha }\right|}^2+\frac{{\kappa }_{\perp }}{2}{\left|{\partial }_{\overline{\alpha }}{\psi }_{\alpha }\right|}^2-\frac{\mathrm{\Delta }}{2N}{\left[{\left|{\psi }_x\right|}^2-{\left|{\psi }_y\right|}^2\right]}^2\\ +\frac{U}{2N}{\left[{\left|{\psi }_x\right|}^2+{\left|{\psi }_y\right|}^2-\mathrm{\Lambda }N\right]}^2\\ -V_z\left[{\psi }_{\alpha }^{†}\left(\overrightarrow{r},m\right){\psi }_{\alpha }\left(\overrightarrow{r},m+1\right)+\mathrm{C}.\mathrm{C}.\right]\\ -\left[h_{\alpha }^{†}\left(\overrightarrow{r},m\right){\psi }_{\alpha }\left(\overrightarrow{r},m\right)+\mathrm{C}.\mathrm{C}.\right]-\left[b_{\alpha }^{†}{\psi }_{\alpha }+\mathrm{C}.\mathrm{C}.\right]+\dots \end{array}$$ [6]

Here $\alpha =x$, y is a spatial index for which the Einstein summation convention is adopted, $\overline{\alpha }$ signifies the complement of α, and each ${\psi }_{\alpha }$ is a $SO\left(N\right)$ vector, where in the case of the CDW, $N=2$ with the two components corresponding to the real and imaginary parts of the amplitude—the generalization to arbitrary N permits a controlled solution in the large N limit. In the following analysis, we assume that $\mathrm{\Delta }>0$, which is to say that stripe order is favored over checkerboard. In the absence of disorder and significant thermal fluctuations, one might focus on temperatures in the neighborhood of the mean-field CDW transition temperature, $T_{MF}$, where $\mathrm{\Lambda }=0$ for $T>T_{MF}$ and $\mathrm{\Lambda }>0$ for $T<T_{MF}$. Here, we focus on the range of temperatures for which $\mathrm{\Lambda }>0$, where there is a well-developed local amplitude of the CDW order parameter, but in which the effects of weak random fields spoil the long-range CDW ordering at long distances. We further assume that all of the remaining coupling constants are positive. Finally, h is a Gaussian random field,

$$\begin{array}{c}\overline{h_{\alpha i}\left(\overrightarrow{r},m\right)}=0,\\ \overline{h_{\alpha i}\left(\overrightarrow{r},m\right)h_{\beta j}\left({\overrightarrow{r}}^{\prime },m^{\prime }\right)}={\sigma }^2{\delta }_{\alpha \beta }{\delta }_{ij}{\delta }_{m,m^{\prime }}\delta \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right),\end{array}$$ [7]

with $i,j=1,\dots ,N$, and b is an explicit symmetry-breaking field, which is assumed to vanish unless otherwise stated. The ellipsis represents higher-order terms in the usual Landau–Ginzburg expansion.

It is convenient to introduce two scalar Hubbard–Stratonovich fields, $\zeta \left(\overrightarrow{r},m\right)$ and $\varphi \left(\overrightarrow{r},m\right)$ in place of the quartic terms in $\mathrm{\mathscr{H}}$,

$$\begin{array}{l}\frac{U}{2N}{\left[{\left|\psi \right|}^2-N\mathrm{\Lambda }\right]}^2-\frac{\mathrm{\Delta }}{N}{\left({\left|{\psi }_x\right|}^2-{\left|{\psi }_y\right|}^2\right)}^2\\ \hspace{1em}\to \frac{{\zeta }^2}{2U}+\frac{{\varphi }^2}{2\mathrm{\Delta }}+\frac{1}{\sqrt{N}}\left[i\zeta \left({\left|\psi \right|}^2-\mathrm{\Lambda }N\right)+\varphi \left({\left|{\psi }_x\right|}^2-{\left|{\psi }_y\right|}^2\right)\right],\end{array}$$ [8]

where ${\left|\psi \right|}^2={\left|{\psi }_x\right|}^2+{\left|{\psi }_y\right|}^2$. In the “hard-spin limit,” $U\to \infty$, ζ simply enforces the constraint ${\left|\psi \right|}^2=\mathrm{\Lambda }N$, whereas ϕ is conjugate to the nematic order parameter, $\mathcal{N}=2\langle \varphi \rangle /\sqrt{N}$.

Approximate Solution

There are a number of approximate ways to analyze this effective field theory. First, to carry out the configuration averages over realizations of the random fields, we introduce n replicas of each field. The replicated field theory can then be used directly to generate the cumulant expansion (7) or, in the conventional manner, by taking the $n\to 0$ limit when computing physical properties.

Because the CDW never orders, it is also reasonable to treat the fluctuations of ψ in a self-consistent Gaussian approximation—this approximation becomes exact (at least in the loose sense commonly used in the field) in the limit $N\to \infty$. The fluctuations of ζ do not involve any broken symmetries, and so to the same level of approximation, these can be treated in a saddle-point approximation, yielding the self-consistency equation in terms of $\mu \equiv 2i\zeta /\sqrt{N}$, which in the hard-spin limit $\left(U\to \infty \right)$ becomes

$$\mathrm{\Lambda }=T\left[A_1\left(\mu +\mathcal{N}\right)+A_1\left(\mu -\mathcal{N}\right)\right]+{\sigma }^2\left[A_2\left(\mu +\mathcal{N}\right)+A_2\left(\mu -\mathcal{N}\right)\right],$$ [9]

with $A_p$ given in Eq. 5. Note that this constraint imposes a physically appropriate sum rule on the integrated scattering intensity, ${\displaystyle \int d\overrightarrow{k}S\left({\widehat{e}}_{x}Q+\overrightarrow{k}\right)}+{\displaystyle \int d\overrightarrow{k}S\left({\widehat{e}}_{y}Q+\overrightarrow{k}\right)}={\left(2\pi \right)}^3\mathrm{\Lambda }$.

Although not necessary (see below), we can similarly evaluate the nematic order parameter approximately directly from the saddle-point equation for ϕ in the limit $n\to 0$:

$$\frac{\mathcal{N}}{\left(2\mathrm{\Delta }\right)}=T\left[A_1\left(\mu -\mathcal{N}\right)-A_1\left(\mu +\mathcal{N}\right)\right]+{\sigma }^2\left[A_2\left(\mu -\mathcal{N}\right)-A_2\left(\mu +\mathcal{N}\right)\right].$$ [10]

This relates the nematicity to the difference in the integrated scattering intensities, $\mathcal{N}{\left(2\pi \right)}^3=2\mathrm{\Delta }\left[{\displaystyle \int d\overrightarrow{k}S\left({\widehat{e}}_{y}Q+\overrightarrow{k}\right)}-{\displaystyle \int d\overrightarrow{k}S\left({\widehat{e}}_{x}Q+\overrightarrow{k}\right)}\right]$.

Fig. 1 was obtained by numerically solving the self-consistency equations for a lattice version of the same model with $V_z=0.01{\kappa }_{\parallel },{\kappa }_{\perp }=0.98{\kappa }_{\parallel }$. In the presence of stronger interplane couplings, $V_z>0.37{\kappa }_{\parallel }$, the phase diagram has a different topology; in the $\sigma =0$ limit there is a single first-order transition from a stripe-ordered phase to the disordered phase with no intermediate nematic phase, and whereas for nonzero σ the stripe phase is again replaced by a nematic phase, for weak enough disorder the nematic transition is now first order. As long as $V_z\ne 0$, the solution obtained in this way is qualitatively reasonable; however, whereas for nonzero σ, $\mu -\left|\mathcal{N}\right|>0$, which rightly implies that there is no stripe-ordered phase, we obtain a solution with nonzero $\mathcal{N}$ for low enough T, even in the 2D limit $V_z\to 0$ where such a state is forbidden on general grounds. This is an artifact of the mean-field, saddle-point approximation for the nematic field. In SI Text, we treat the effective field theory for ϕ more accurately. Specifically, we show that upon integrating out the CDW fluctuations, the replicated field theory for ϕ is of the same form as the replicated field theory of the RFIM. At $T=0$ and in the limit of weak disorder, we can similarly map a correspondence between the two models by identifying the domain-wall energies and the mean-square disorder strength. These two exercises make explicit what is apparent by symmetry—that the problem of nematic ordering is equivalent to the ordering of the RFIM. The two qualitatively interesting aspects of this correspondence are that

$$b^{\mathrm{eff}}\sim {\left|b_x\right|}^2-{\left|b_y\right|}^2\hspace{1em}\mathrm{and}\hspace{1em}{\sigma }^{\mathrm{eff}}\sim {\sigma }^2\sqrt{A_4\left(\mu \right)},$$ [11]

where $b^{\mathrm{eff}}$ and ${\sigma }^{\mathrm{eff}}$ are, respectively, the uniform component and the root mean-squared variations of the effective magnetic fields that appear in the RFIM. Importantly, this means that if the disorder is weak (σ is small), the effective disorder felt by the nematic component of the order parameter is parametrically smaller still. The mapping between the two models permits one to connect problems of vestigial nematic ordering to the rich and well-studied phenomenology of the RFIM (3).

Some Implications for Experiments in the Cuprates

Clear evidence of the growth of short-range correlated CDW order in the pseudogap regime of the phase diagram has been found in a large number of experiments in multiple families of hole-doped cuprates. (For reviews see refs. 16 and 20; for an update, see ref. 29.) Spectacular new evidence has come from NMR (11, 30), STM (12, 13, 31, 32), and a new generation of X-ray scattering experiments (33–37) concerning ubiquitous CDW order and from transport (14, 15), STM (16, 17), neutron-scattering (18), and optical (8, 38–42) experiments indicating the existence of an associated pattern of long-range–ordered point-group symmetry breaking with an electron-nematic character. To interpret their significance, one would extrapolate the results to an “ideal hole-doped cuprate,” one without quenched disorder and without structural peculiarities that lower the symmetry of the problem. At least the existing observations make clear that there is a ubiquitous tendency to charge order with a well-defined period λ that is a few times the lattice constant. λ depends on the doping concentration and certain structural details, presumably indicating that the electron–phonon coupling plays a role in determining some aspects of the CDW order. The preferred orientation of the CDW is always along the Cu-O bond (x and y) directions. [In LSCO, the density wave-ordering vector is rotated slightly from the x and y directions, but this is an unimportant detail for the present purposes, which is a necessary corollary (27) of the particular orthorhombic structure of that material.]

However, there is no consensus about whether, in the absence of quenched randomness, the CDW order within each plane would be dominantly striped $\left(\mathrm{\Delta }>0\right)$ or checkerboard $\left(\mathrm{\Delta }<0\right)$; whether the CDW order would be static (long-range ordered, $\mathrm{\Lambda }>0$) or fluctuating (short-range correlated, $\mathrm{\Lambda }=0$); and indeed whether the CDW phenomena seen in different cuprates are siblings or distant cousins. As discussed previously in refs. 27 and 28 in the context of STM studies of the cuprates, in the presence of substantial disorder (σ not small) the structure factor itself typically does not differ greatly between a “failed” stripe phase (i.e., with $\mathrm{\Lambda }>0$ and $\mathrm{\Delta }>0$) and a failed checkerboard phase (i.e., with $\mathrm{\Lambda }>0$ and $\mathrm{\Delta }<0$) nor show whether the disorder is pinning what would otherwise be fluctuating order $\left(\mathrm{\Lambda }=0\right)$ or breaking up into domains what would otherwise be long-range CDW order $\left(\mathrm{\Lambda }>0\right)$. To see this, consider the expression for the structure factor in Eq. 2; it has no explicit dependence on either Λ or Δ, but rather depends on them only implicitly through the self-consistency equations for μ and $\mathcal{N}$. Because quenched disorder absolutely precludes long-range CDW order, $\mu >\left|\mathcal{N}\right|$ independent of $\Lambda$; only by approaching the limit of vanishing disorder would it be possible to distinguish unambiguously whether the correlation length, $1/\xi =\sqrt{\kappa \left(\mu -\left|\mathcal{N}\right|\right)}$ $\left({\kappa }_{\perp }={\kappa }_{\parallel }\equiv \kappa \right)$, is finite because of disorder or because of thermal or quantum fluctuations. Moreover, even in the presence of orthorhombicity $\left(\left|b^{\mathrm{eff}}\right|>0\right)$ or spontaneous nematic symmetry breaking (both of which result in $\mathcal{N}\ne 0$), as long as ξ is not too long (or, more precisely, as long as $\mu \gg \left|\mathcal{N}\right|$), the structure factor breaks $C_4$ symmetry only weakly.

It has been suggested that stripe and checkerboard order can be distinguished by studying the structure factor at harmonics of the ordering vector; for example, whereas either a stripe- or a checkerboard-ordered system with multiple macroscopic domains would exhibit second harmonic peaks at $2Q\widehat{x}$ and $2Q\widehat{y}$, only the checkerboard state would exhibit a second harmonic peak at ${\overrightarrow{Q}}_{xy}=Q\left(\widehat{x}+\widehat{y}\right)$. This distinction does not pertain to an uncondensed CDW: Peaks in $S\left(\overrightarrow{q}\right)$ at harmonics of the fundamental ordering vector arise as composites of the fundamental fields. The leading contribution near the second-harmonic ${\overrightarrow{Q}}_{xy}=Q\left(\widehat{x}+\widehat{y}\right)$ is given by

$$S\left({\overrightarrow{Q}}_{xy}+\overrightarrow{k}\right)\sim {\displaystyle \int \frac{d\overrightarrow{q}}{{\left(2\pi \right)}^3}S\left(Q\widehat{x}+\overrightarrow{q}\right)S\left(Q\widehat{y}+\overrightarrow{k}-\overrightarrow{q}\right)}.$$ [12]

This does not distinguish between the two cases any better than do the fundamentals.

Thus, even though CDW formation is probably the fundamental ordering phenomenon involved, the nature of the “ideal phase diagram” may be more directly inferred by studying the vestigial order. If, within the Cu-O planes, evidence can be adduced for the existence of long-range nematic order, this likely implies that the ideal system would have long-range stripe order ($\mathrm{\Delta }>0$ and $\mathrm{\Lambda }>0$), both because nematic order is a natural consequence of the existence of a striped ground state and because, even in the absence of quenched randomness, $T_{\mathrm{nem}}$ is never much above $T_{\mathrm{str}}$. If, considering the effects of interplane interactions, the striped ground state is gyrotropic (8) (analogous to a cholesteric liquid crystal), for instance if the stripe orientation defines a handed spiral from plane to plane, then experiments that detect vestigial gyrotropic order can likewise be interpreted as evidence of a stripe-ordered ground state in the ideal limit.

Compelling evidence of nematic order within the Cu-O plane in BSCCO has been obtained from STM studies in refs. 13, 17, and 19. (For a contrary opinion, see ref. 43.) In YBCO (in which the native orthorhombicity of the lattice complicates the analysis), evidence of nematic order has been inferred from transport anisotropy (14, 15), from a strongly T-dependent growth in the anisotropy of the magnetic structure factor measured in neutron scattering (18) (although in a regime of doping below that in which X-ray evidence of CDW correlations has been found), and, for doping concentrations with the Ortho II structure, directly from anisotropy in the charge structure factor itself (35, 36, 44). In LBCO (45, 46), because the LTT crystal structure produces a strong, explicit $C_4$ symmetry breaking in each plane, it is possible to unambiguously identify the charge order as consisting of stripes that rotate by $\pi /2$ from plane to plane (46). Moreover, in all three of these materials, as well as in Hg-1201, the onset of a spontaneous Kerr signal (38–41) occurs below an onset temperature that correlates with the onset of other measures of the growth of local CDW correlations.

There are several sorts of experimental protocol that could more unambiguously test for nematic order. As was done in the case of the Fe-based superconductors in ref. 22, the ideal experiments would involve measuring an electronic property that is odd under $C_4$ rotation (and hence proportional to $\mathcal{N}$) as a function of uniaxial strain to look for evidence of a divergent differential nematic susceptibility. Particularly interesting would be NMR measurements of the quadrupolar broadening of the in-plane O lines, following along the lines undertaken (in orthorhombic YBCO in the absence of applied strain) in ref. 11 (where a T-dependent difference $\overline{\langle {\left|\delta {\rho }_x\right|}^2-{\left|\delta {\rho }_y\right|}^2\rangle }$ was already noted in ref. 11 as possible but inconclusive evidence of nematicity).

There are also numerous dynamical implications of the correspondence between the nematic order parameter and the RFIM. Characteristic features of the expected hysteresis and noise implied by this correspondence (47, 48) have been reported in mesoscale samples of YBCO (49). Repeating this same sort of experiment, but with controlled manipulation of a uniaxial strain, will likely open up other routes to study vestigial nematic order.

It is worth noting that the effect of quenched disorder differs qualitatively if instead of being incommensurate, the CDW is commensurate: Here, the ordered phase breaks translation symmetry discretely, so long-range CDW order survives up to a critical disorder strength, ${\sigma }_c$, although naturally ${\sigma }_c$ decreases rapidly with the order of the commensurability. This observation may be relevant in the context of recent high-magnetic-field studies of YBCO (50, 51) that have detected a field-driven phase transition to a charge-ordered state that has been identified (50) as a commensurate CDW. Although no direct (diffraction) evidence of commensurate CDW order has been reported in any of the cuprates, the very fact that a sharp transition to a commensurate CDW phase is possible makes this an attractive identification of the high-field phase.

In light of the clear evidence of ubiquitous CDW correlations with significant short-range order (i.e., a moderately large ξ) and the growing evidence of nematic order, it is reasonable to suppose that, absent quenched randomness, a state with long-range stripe order would be found below a transition temperature, T_str, which is in the neighborhood of that at which X-rays see an onset of short-range CDW order in the actual materials. There is also significant evidence supporting the notion that important fluctuation effects in the cuprates are associated with the existence of a quantum critical point (of a still to be agreed upon nature) under the superconducting dome; a corollary of the above analysis is that, given that disorder is always relevant, this quantum critical point cannot be associated with the onset of a putative translation symmetry-breaking transition, but could still be related to the onset of nematic order.