A Subspace Approach to High-Resolution Spectroscopic Imaging

Abstract

Purpose

To accelerate spectroscopic imaging using sparse sampling of (k, t)-space and subspace (or low-rank) modeling to enable high-resolution metabolic imaging with good signal-to-noise ratio (SNR).

Methods

The proposed method, called SPICE (SPectroscopic Imaging by exploiting spatiospectral CorrElation), exploits a unique property known as partial separability of spectroscopic signals. This property indicates that high-dimensional spectroscopic signals reside in a very low-dimensional subspace and enables special data acquisition and image reconstruction strategies to be used to obtain high-resolution spatiospectral distributions with good SNR. More specifically, a hybrid CSI/EPSI pulse sequence is proposed for sparse sampling of (k, t)-space, and a low-rank model-based algorithm is proposed for subspace estimation and image reconstruction from sparse data with the capability to incorporate prior information and field inhomogeneity correction.

Results

The performance of SPICE has been evaluated using both computer simulations and phantom studies, which produced very encouraging results. For 2D spectroscopic imaging experiments on a metabolite phantom, a factor of 10 acceleration was achieved with a minimal loss in SNR compared to the long CSI experiments and with a significant gain in SNR compared to the accelerated EPSI experiments.

Conclusion

SPICE is able to significantly accelerate spectroscopic imaging experiments, making high-resolution metabolic imaging possible.

INTRODUCTION

MR spectroscopic imaging (MRSI or spatially-resolved MR spectroscopy) has been recognized as a powerful tool for non-invasive metabolic studies (1–4), but clinical and research applications of this technology have been developing more slowly than was expected. One reason for this situation is the problems of long data acquisition time, poor spatial resolution, and low signal-to-noise (SNR) that have limited the use of the existing spectroscopic imaging techniques for in vivo applications.

Over the past few decades, significant efforts have been made to address the above problems, resulting in a large number of new data acquisition and reconstruction methods for spectroscopic imaging. For fast data acquisition, one key approach is to incorporate echo-planar-type of data acquisition schemes with spectroscopic imaging. Many methods (and pulse sequences) have been proposed to implement this data acquisition strategy (see (5) for a comprehensive review; also see (6–14) for a more detailed discussion of some of the EPSI methods). Although EPSI methods can significantly reduce the data acquisition time for spatiospectral encoding, it is at the expense of SNR, which is a significant limitation for in vivo spectroscopic imaging experiments. Another more recent approach to accelerated spectroscopic imaging is to use parallel imaging (15, 16). It is expected that parallel data acquisition using phased array coils will be an integral part of any method to accelerate spectroscopic imaging experiments.

Advanced image reconstruction for MRSI has been focusing on using prior information to compensate for the lack of sufficient measurements or SNR. To this end, a number of reconstruction models have also been proposed (17–25), but reconstruction methods alone have failed to provide the level of improvements in spatial resolution, data acquisition speed, and SNR needed to have a major impact on in vivo spectroscopic imaging.

In this paper, we propose a new approach to both data acquisition and image reconstruction to accelerate spectroscopic imaging. The proposed approach, called SPICE (SPectroscopic Imaging by exploiting spatiospectral CorrElation), exploits a unique property known as partial separability (PS) of spectroscopic signals (26,27). This property indicates that high-dimensional spectroscopic signals reside in a very low-dimensional subspace and enables special data acquisition and image reconstruction strategies to be used to obtain high-resolution spatiospectral distributions with good SNR. More specifically, a hybrid CSI/EPSI pulse sequence is proposed for rapid and sparse sampling of (k, t)-space (or spatiospectral encoding), and a PS/low-rank model-based algorithm is proposed for subspace estimation and image reconstruction from sparse data with the capability to incorporate prior information and field inhomogeneity correction. The performance of SPICE has been evaluated using both computer simulations and phantom studies. For 2D spectroscopic imaging experiments on a brain metabolite phantom, SPICE achieved effectively 100×100 spatial encodings in 6 minutes. The SNR of the resulting SPICE reconstructions is significantly better than that of the EPSI reconstructions with the same spatiospectral resolution and data acquisition time, and is comparable to that of the CSI reconstructions from 60 ×60 spatial encodings acquired in one hour. The proposed method and some representative results are described in the subsequent sections.

THEORY

Subspace Modeling

In spectroscopic imaging, the measured data can be expressed as

$$\begin{array}{l}s(\mathbf{k},t)=\underset{V}{\int }\underset{{\mathrm{\Omega }}_f}{\int }\rho (\mathbf{r},f)e^{-i2\pi ft}{e}^{-i\gamma \mathrm{\Delta }B(\mathbf{r})t}{e}^{-i2\pi \mathbf{kr}}\mathit{dfdr}+\xi (\mathbf{k},t)\\ =\underset{V}{\int }\stackrel{\sim }{\rho }(\mathbf{r},t)e^{-i\gamma \mathrm{\Delta }B(\mathbf{r})t}{e}^{-i2\pi \mathbf{kr}}d\mathbf{r}+\xi (\mathbf{k},t),\end{array}$$ [1]

where ρ(r, f) is the desired spatiospectral function, V the excited volume of interest, Ω_f the desired spectral bandwidth, γ the gyromagnetic ratio, ΔB (r) the B₀ field inhomogeneity map and ξ (k, t) the measurement noise (often assumed to be white Gaussian).

SPICE exploits an important property of ρ̃(r, t), known as spatiotemporal partial separability (PS) (26). More specifically, we express ρ̃ (r, t) as (26, 27)

$$\stackrel{\sim }{\rho }(\mathbf{r},t)=\sum _{l=1}^L{c}_l(\mathbf{r}){\varphi }_l(t),$$ [2]

where ${\{{\varphi }_l(t)\}}_{l=1}^L$ can be viewed as a set of temporal basis functions, ${\{c_l(\mathbf{r})\}}_{l=1}^L$ are the corresponding spatial coefficients (can also be viewed as spatial basis), and L is the model order (also called the order of separability (26)). In spectroscopic imaging, the PS model can be justified by the fact that the object imaged has only a finite (L) number of tissue types, each of which has a distinct spectral structure, or that ρ (r, f) has a finite number (L) of spectral components. It has been shown that partial separability implies low-rankness (26). More specifically, the Casorati matrix formed from ρ̃ (r, t) over any point set ${\{({\mathbf{r}}_p,t_q)\}}_{p,q=1}^{P,Q}$

$$\mathcal{C}\left({\{\stackrel{\sim }{\rho }({\mathbf{r}}_p,t_q)\}}_{p,q=1}^{P,Q}\right)=\left[\begin{array}{cccc}\stackrel{\sim }{\rho }({\mathbf{r}}_1,t_1)& \stackrel{\sim }{\rho }({\mathbf{r}}_1,t_2)& \cdots & \stackrel{\sim }{\rho }({\mathbf{r}}_1,t_Q)\\ \stackrel{\sim }{\rho }({\mathbf{r}}_2,t_1)& \stackrel{\sim }{\rho }({\mathbf{r}}_2,t_2)& \cdots & \stackrel{\sim }{\rho }({\mathbf{r}}_2,t_Q)\\ ⋮& ⋮& \ddots & ⋮\\ \stackrel{\sim }{\rho }({\mathbf{r}}_P,t_1)& \stackrel{\sim }{\rho }({\mathbf{r}}_P,t_2)& \cdots & \stackrel{\sim }{\rho }({\mathbf{r}}_P,t_Q)\end{array}\right]$$

has a rank upper-bounded by L. This implies that ρ̃ (r, t) resides in a low-dimensional space (or has a small number of degrees of freedom). More specifically, assume that ρ̃ (r, t) can be represented by ${\{\stackrel{\sim }{\rho }({\mathbf{r}}_m,t_n)\}}_{m,n=1}^{M,N}$ in the conventional pixel representation. Then, when viewed as a vector (formed from ρ̃ (r_m, t_n)), it resides in a M N-dimensional space. However, the PS property implies that ${\{\stackrel{\sim }{\rho }({\mathbf{r}}_m,t_n)\}}_{m,n=1}^{M,N}$ actually resides in a very low-dimensional subspace (spanned by ${\{{\varphi }_l(t)\}}_{l=1}^L$, for example). This property enables special data acquisition and image reconstruction strategies to be used to obtain high-resolution spatiospectral distributions with good SNR, which are described next.

Data Acquisition: Extended (k, t) Coverage with Sparse Sampling

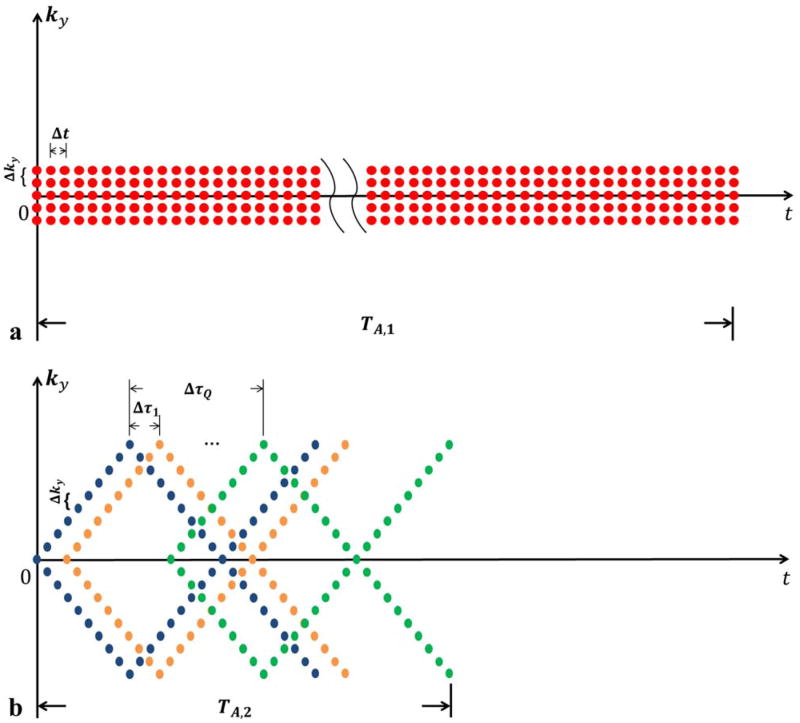
To exploit the PS property for high-resolution spectroscopic imaging, SPICE uses a special data acquisition (or spatiospectral encoding) strategy to achieve extended (k, t) coverage with sparse sampling. The data acquisition scheme (illustrated in Fig. 1) has two key features: (a) acquisition of a data set, 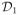(with limited k-space coverage but in high temporal resolution), for determination of the temporal basis (in high temporal resolution), and (b) acquisition of a data set, (with extended k-space coverage but limited temporal sampling), for determination of the spatial coefficients (in high spatial resolution). This data acquisition scheme can be implemented using a hybrid CSI/EPSI pulse sequence, an example of which is shown in Fig. 2. The CSI component is used to generate (with good SNR) while the EPSI component is used to generate (with high data acquisition speed). With the PS model, SPICE offers a range of flexibility for implementing the EPSI component to collect . For example, in the sequence in Fig. 2, SPICE encodes two spatial dimensions in the FID signals (in contrast to traditional EPSI sequences that usually encodes one spatial dimension) and uses echo shifting (of different excitations) for spectral encoding. As a result, the SPICE sequence samples (k, t)-space only sparsely. This sparse sampling scheme is enabled by the PS model with temporal basis (capturing the full spectral information). It improves the efficiency of spatiospectral encoding, thus reducing data acquisition time. More alternative data acquisition strategies for collecting are discussed in the Discussion section.

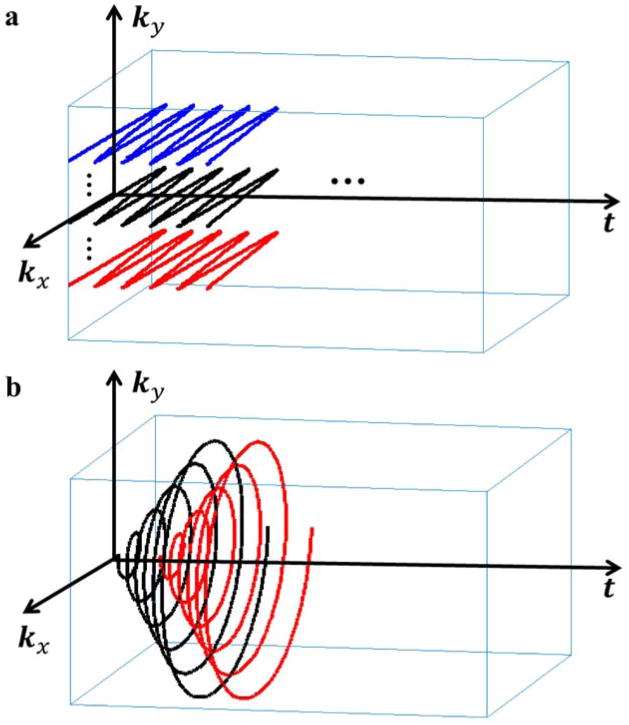
Figure 1.

An example of SPICE (k, t)-space sampling for 2D spectroscopic imaging (with k_x pointing into the page): (a) (k, t)-space sampling for data in for subspace estimation. 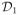covers only a limited region of central k-space (based on SNR consideration), and sample the free precession period (T_A;1) fully (to capture the spectral information); (b) (k, t)-space sampling for data in for determination of the spatial coefficients. Note that a set of FIDs with different echo shifts (Δt₁, Δt₂, … Δt_q) is collected, each of which traverses entire k-space (also see Fig. 2) but with limited spectral encoding (T_A;2 < T_A;1).

Figure 2.

A prototypical hybrid CSI/EPSI sequence for SPICE: (a) the CSI component used to collect the data in 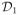with limited k-space coverage but full spectral encoding, and (b) an EPSI-like component used to acquire the data in with extended k-space coverage but limited spectral encoding. Note that there is only one k_y reversal in each TR due to SNR consideration, although more k_y reversals can be included in principle. Note also that the proposed EPSI component supports bipolar acquisition but requires additional correction if data acquired on both positive and negative Gx are used.

Reconstruction from Sparse Data

For notation convenience, we assume that ${\mathcal{D}}_1={\{s_1({\mathbf{k}}_m,t_n)\}}_{m,n=1}^{M_1,N_1}$ and ${\mathcal{D}}_2={\{s_1({\widehat{\mathbf{k}}}_m,{\widehat{t}}_n)\}}_{m,n=1}^{M_2,N_2}$. It is understood that: (a) ${\{t_n\}}_{n=1}^{N_1}$ sample the time interval of interest in high resolution while ${\{{\widehat{t}}_n\}}_{n=1}^{N_2}$ sample the interval sparsely, and (b) ${\{{\mathbf{k}}_m\}}_{m=1}^{M_1}$ cover limited k-space locations while ${\{{\widehat{\mathbf{k}}}_m\}}_{m=1}^{M_2}$ cover the entire desired region of k-space (to provide the necessary spatial resolution). SPICE reconstructs ρ̃ (r, t) from the data in 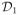and using a two-step procedure: (a) determination of the temporal basis, and (b) determination of the spatial coefficients.

Determination of the temporal basis (or temporal subspace), ${\{{\varphi }_l(t_n)\}}_{l=1}^L$ for n = 1, 2, … , N₁, from 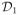is fairly easy if the effect of field inhomogeneity ΔB(r) on s₁(k_m, t_n) is negligible. In practice, ΔB(r) can be significant, and we need to first remove/reduce its effect on s₁(k_m, t_n). Assuming that ΔB(r) is available (which can be acquired during the MRSI experiment), field inhomogeneity correction on limited k-space spectroscopic data can be done using the method in (28), although more advanced methods can also be developed and used for solving this problem. The corrected data, denoted as s̃₁(k_m, t_n), is then used to form an M₁ × N₁ Casorati matrix $\mathcal{C}\left({\{{\widehat{s}}_1({\mathbf{k}}_m,t_n)\}}_{m,n=1}^{M_1,N_1}\right)$. The SVD is then applied to this Casorati matrix and its L principal right singular vectors are chosen as ${\{{\varphi }_l(t_n)\}}_{l=1}^L$.

After {ϕ_l (t_n)} are determined, the spatial coefficients, ${\{c_l({\mathbf{r}}_m)\}}_{l=1}^L$, can be determined from the sparse data in by solving a least-squares problem. For notation convenience, we rewrite ${\{\stackrel{\sim }{\rho }({\mathbf{r}}_m,t_n)\}}_{m,n=1}^{M,N}={\{{\sum }_{l=1}^L{c}_l({\mathbf{r}}_m){\varphi }_l(t_n)\}}_{m,n=1}^{M,N}$ as CΦ (27, 29) (with C ∈ 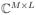and Φ 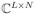such that C_ml = c_l(r_m) and Φ_ln = ϕ_l(t_n), where M = M₂ and N = N₁ for the proposed data acquisition scheme), and use s₂ ∈ 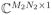to denote the vector containing all the data in , 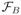to represent the Fourier transform operator including the B₀ field inhomogeneity effect described in Eq. (1), and ⊓ to represent the (k, t)-space sampling operation used for collecting the data in . Then, the spatial coefficients can be determined as

$$\widehat{\mathbf{C}}=arg\underset{\mathbf{C}}{min}{\Vert {\mathbf{s}}_2-\sqcap {\mathcal{F}}_B\{\mathbf{C}\mathrm{\Phi }\}\Vert }_2^2+\lambda \mathrm{\Psi }(\mathbf{C},\mathbf{\Phi }),$$ [3]

where the ${\Vert ·\Vert }_2^2$ term measures the data consistency of a reconstruction, and Ψ (·) is a regularization function with regularization parameter λ. There are many choices for Ψ (·) to incorporate prior information about ρ̃ (r, t) or ρ (r, f) (including both quadratic and sparsity-promoting penalties (20–22,25)). In this paper, we focus on demonstrating the concept and potential of SPICE and use $\mathrm{\Psi }(\mathbf{C},\mathbf{\Phi })={\Vert \mathbf{WDC}\mathbf{\Phi }\Vert }_F^2$, where D is a finite difference operator and W contains edge weights derived from a high-resolution anatomical image (20). Note that if {ϕ_l(t_n)} are orthonormal basis, ${\Vert \mathbf{WDC}\mathbf{\Phi }\Vert }_F^2={\Vert \mathbf{WDC}\Vert }_F^2$ and an additional diagonal weighting matrix can be included as ${\Vert \mathbf{WDC}\mathbf{\Lambda }\Vert }_F^2$ to penalize noisy basis. The weightings in 3 can be determined from the singular value distribution of the Casorati matrix. Integrating this regularization function into Eq. [3] yields a weighted-ℓ₂ regularized least-squares problem that can be solved efficiently (20).

METHODS

We have evaluated SPICE using computer simulations and experimental studies on phantoms.

Simulation Study

We used the high-resolution spatiospectral numerical phantom described in (30) for our simulation study. The phantom has 128 × 128 matrix size and 512 time points sampled at a bandwidth of 1200 Hz, and contains spatial distributions of commonly observed ¹H metabolites (see (30) for a more detailed description). We generated (k, t)-space measurements from this phantom with or without field inhomogeneity effects introduced through a coregistered in vivo ΔB₀ map according to Eq. [1]. A simulated full data set without the field inhomogeneity effects was used as the gold standard to compare three acceleration methods: (i) SPICE, (ii) low-resolution CSI, and (iii) EPSI (7). The effect of field inhomogeneity was included for all three schemes, which were set up to have the same acquisition time. Additional noise was added into the simulated EPSI data to account for the SNR difference due to different readout bandwidths. The field inhomogeneity corrected conjugate phase (CP) algorithm (31) was used to obtain the CSI and EPSI reconstructions, which are compared with the corresponding SPICE reconstructions.

Phantom Study

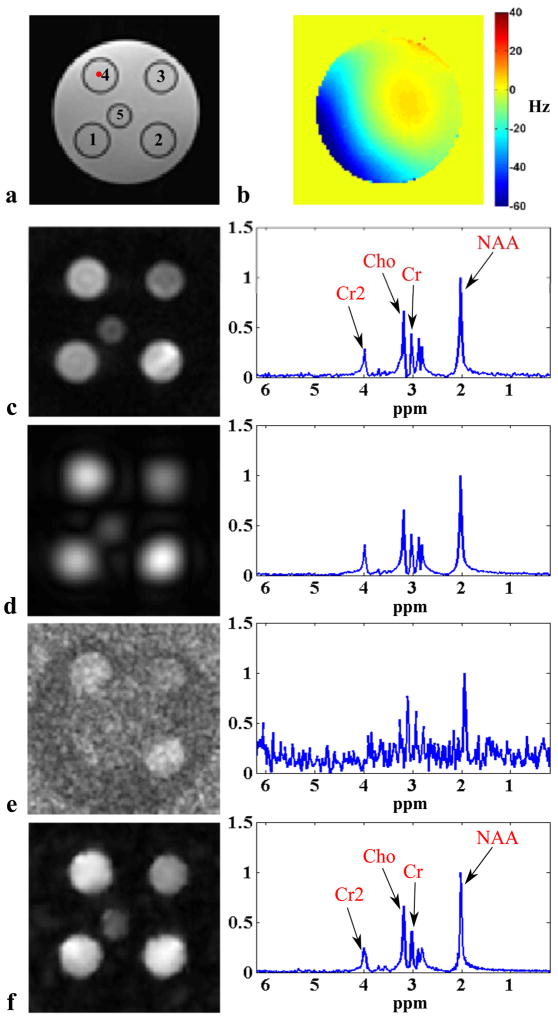
Two phantoms were constructed for our study: a water-oil phantom and a metabolite phantom. The water-oil phantom is a cylindrical jar containing NaCl-doped water and three rows of vials filled with vegetable oil, corn coil and peanut oil, respectively. The metabolite phantom is a cylindrical jar containing NaCl-doped water and five vials with different sizes (Fig. 5a), which were filled with metabolite solutions of physiologically relevant concentrations. More specifically, vial 1 contains 20 mmol/L NAA, 15 mmol/L creatine (Cr) and 10 mmol/L choline-chloride (Cho); Vial 2 contains 20 mmol/L NAA, 10 mmol/L Cr and 5 mmol/L Cho; Vial 3 contains NAA, Cr, Cho and myo-inositol (mI) all at 10 mmol/L; Vial 4 contains 15 mmol/L NAA, 8 mmol/L Cr and 5 mmol/L Cho; and Vial 5 contains the same solution as vial 3.

Figure 5.

Experimental results from a metabolite phantom shown in (a) with spectroscopic imaging data acquired in the presence of B₀ inhomogeneity shown in (b): (c) CSI reconstruction from 60 × 60 spatial encodings, (d) CSI reconstruction from 19 × 19 spatial encodings, (e) EPSI reconstruction from 100 × 100 spatial encodings with two averages, and (f) SPICE reconstruction with 12 × 12 CSI encodings in 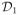, 45 echo shifts in with five averages, and L = 12. The left column shows the spatial distributions of NAA and the right column shows the spectra from the voxel identified by the red dot in (a). Field inhomogeneity correction was included for all the cases as described in the text. The results in (d)–(f) correspond to a factor of 10 reduction in data acquisition time (6 min) compared to the high-resolution CSI acquisition in (c).

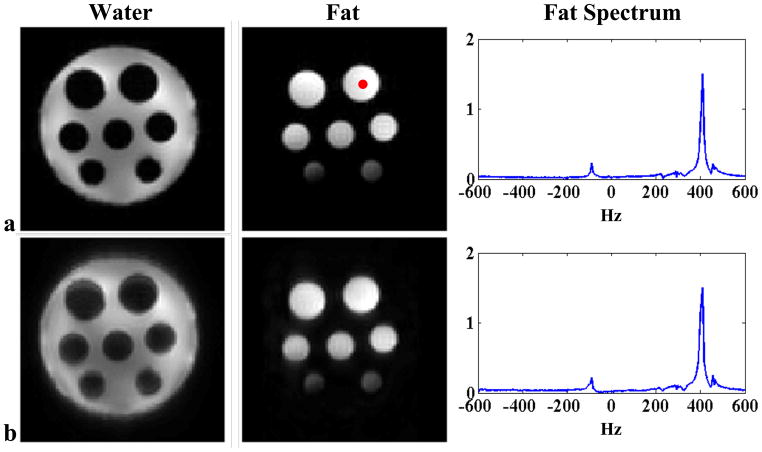
Experiments on the phantoms were conducted on a 3T Siemens Trio scanner (Siemens Health-care USA) equipped with a 12-channel receiver headcoil. The experiments on the water-oil phantom were focused on evaluating the feasibility of SPICE under practical conditions. So the proposed (k, t)-space sparse sampling scheme and the corresponding reconstruction algorithm were implemented as described. A set of experimental results is shown in Fig. 4, with the following imaging parameters: TR/TE= 1000/30 ms, 220 ×220 mm² FOV, 5 mm slice thickness, 128 ×128 matrix size and 167 kHz readout bandwidth (i.e., 6 μs dwell time). A total of 64 excitations without water suppression was used for acquiring the SPICE data set (16 for 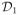with eight spatial encodings and two temporal interleaves and 48 for each with 128 × 128 spatial encodings). The SPICE reconstruction was performed coil by coil with L = 16 and followed by SVD-based coil combination (32). For comparison, an EPSI data set (with the same k-space coverage and 256 echoes) was also acquired using 256 excitations. The total acquisition time for the SPICE experiment is 1/4 of that for the EPSI experiment. In addition, a T₁-weighted anatomical image was acquired using a gradient-echo sequence for defining W, and a ΔB₀ map was acquired using a double gradient-echo field mapping sequence for field inhomogeneity correction.

Figure 4.

Experimental results from a water-oil phantom: (a) field inhomogeneity corrected CP reconstruction from an EPSI data with 128 × 128 spatial encodings, and (b) SPICE reconstruction with eight conventional EPSI encodings in 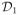(two temporal interleaves), 48 echo shifts in (a total of 64 excitations) and L = 16. Note that the reconstructions are almost comparable but the data acquisition time for the SPICE experiment is only 1/4 of that for the EPSI experiment.

For the experiments on the metabolite phantom, water suppression is necessary to reveal the spatiospectral distributions of the metabolites. Therefore, water-suppressed CSI data were acquired using a modified version of the commercial CSI sequence with: TR/TE = 1000/30 ms, FOV = 250 × 250 mm², slice thickness = 10 mm, matrix size = 60 × 60, FID length = 512, and spectral bandwidth = 2000 Hz. The total data acquisition time was one hour. Water-suppressed EPSI data were acquired using a customized 2D EPSI sequence that encodes chemical shifts plus one spatial dimension for each FID using oscillating gradients. The other spatial dimension was phase encoded. The data acquisition parameters for the EPSI experiment were: TR/TE = 1000/30 ms, FOV = 250×250 mm², slice thickness = 10 mm, matrix size = 100×100, number of echoes = 256, readout bandwidth = 167 kHz and echo spacing = 830 μs. The total data acquisition time for two temporal interleaves and five averages was 16.7 minutes. For both the CSI and EPSI sequences, the WET pulses were used for water suppression (33). The HSVD algorithm was also used to further remove any residual water signals in both the CSI and EPSI data (34). As in the water-oil phantom experiments, a T₁-weighted image (Fig. 5a) and a ΔB₀ map (Fig. 5b) were also acquired.

Similarly to the simulation study, we used a field inhomogeneity corrected reconstruction obtained from the 60 × 60 CSI data as a reference to compare three acceleration methods: (i) SPICE, (ii) low-resolution CSI, and (iii) EPSI, with the same data acquisition time (6 minutes). The SPICE data set contains 12 × 12 CSI encodings (for 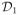) and 45 echo shifts each with 100 × 100 spatial encodings averaged five times (for ). Note in this experiment, was retrospectively sampled from the full EPSI data to avoid potential water removal issues with sparse data and only data acquired on the positive gradients were used to avoid echo inconsistency in bipolar acquisition. With the same data acquisition time (6 minutes), the CSI acquisition generated 19 × 19 spatial encodings while the EPSI acquisition generated 100 × 100 spatial encodings averaged twice. The SPICE reconstruction was performed coil by coil with L = 12 before coil combination. The field inhomogeneity corrected CP algorithm was used for both the CSI and EPSI reconstructions.

RESULTS

Figure 3 shows one set of representative simulation results. The SPICE reconstruction was obtained with 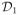containing 8 × 8 CSI encodings each with 512 FID samples, containing 48 echo shifts each with 128 × 128 spatial encodings (averaged four times) and L = 8. The CSI reconstruction was obtained from 16 × 16 spatial encodings while the EPSI reconstruction was obtained from 128 × 128 spatial encodings (averaged twice) both with 512 FID samples (under the assumption that the SPICE, CSI, and EPSI have the same acquisition time). As can be seen, the CSI reconstruction shows significant blurring and ringing artifacts, which were reduced in the EPSI reconstruction but at the expense of a significant loss of SNR, as expected. The SPICE reconstruction shows very good resolution and SNR.

Figure 3.

Simulation results: (a) the gold standard, (b) CSI reconstruction from 16 × 16 spatial encodings, (c) EPSI reconstruction from 128 × 128 spatial encodings averaged twice, and (d) SPICE reconstruction from 8 × 8 CSI encodings in 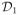, 48 echo-shifts in averaged four times and L = 8. The left column shows the spatial distributions of a frequency component at 345 Hz and the right column shows the spectra corresponding to the voxel identified by the red dot for each case.

Figure 4 presents one set of representative experimental results from the water-oil phantom, which demonstrates that SPICE works with its data acquisition and reconstruction scheme under practical spectroscopic imaging conditions. In this experiment, SPICE offers a factor of four acceleration over the EPSI experiment with comparable results.

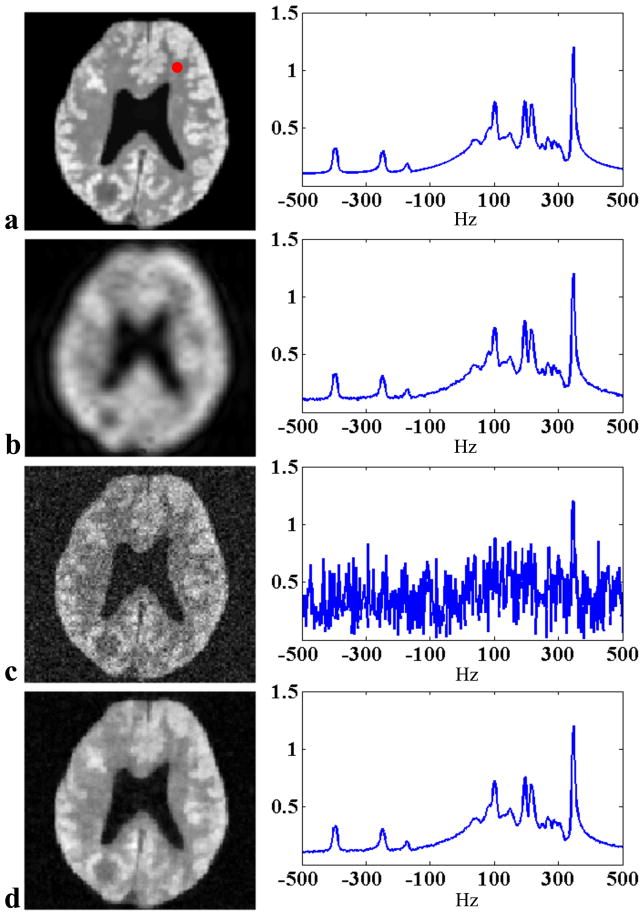
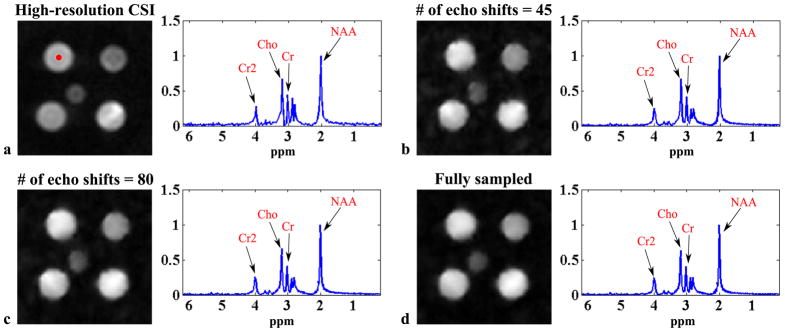
Figure 5 shows a set of experimental results from the metabolite phantom. As can be seen, the low-resolution CSI reconstruction has high SNR but suffers from serious truncation artifacts. The EPSI reconstruction has high spatial resolution but very low SNR due to the small voxel size and the high readout bandwidth. SPICE achieves both high spatial resolution and reasonable SNR with the same acquisition time. Note also that the SPICE reconstruction has almost comparable SNR to the high-resolution CSI reconstruction (see the spectra in the right column of Fig. 5), but with a factor of 10 acceleration in data acquisition. Figure 6 compares SPICE reconstructions with different amounts of data. As expected, the reconstructions improve as the number of echo shifts used increases. Note that if a full (instead of sparsely sampled) (k, t)-space EPSI data set is used for determination of the spatial coefficients, SPICE is equivalent to subspace denoising (30) but with a “known” subspace structure determined from a complementary high SNR data set ( 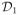). The subspace constraint makes the denoising more effective especially for data of very low SNRs.

Figure 6.

Experimental results from the metabolite phantom in Fig. 5a: (a) the high-resolution CSI reconstruction in Fig. 5c and SPICE reconstructions with 12 × 12 CSI encodings in 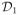, L = 12 and different numbers of echo shifts in : (b) 45 echo shifts, (c) 80 echo shifts, and (d) the entire EPSI data set.

DISCUSSION

We have demonstrated the feasibility of SPICE to achieve high-resolution spectroscopic imaging with good SNR. Both data acquisition and image reconstruction can be further optimized for practical applications.

First, SPICE data acquisition involves selecting several key parameters including M₁ (the number of encodings in 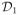) and N₂ (the number of echo shifts in ). Theoretically, M₁ and N₂ need to be not smaller than L, which is easy to satisfy since L is typically a small number. In practice, however, larger M₁ and N₂ are needed to ensure accurate estimation of the temporal basis in the presence of field inhomogeneity and stable solution of the spatial coefficients from Eq. [3]. Based on our experience, M₁ ≥ 10 × 10 for 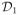and N₂ ≥ 3L for work reasonably well. Nevertheless, M₁ and N₂ should be optimized for a specific MRSI experiment under the experimental time constraints. In addition, SPICE offers a lot of flexibility in sampling (k, t)-space for collecting 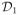and . In our current implementation, 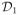is collected using a CSI sequence, which can be replaced by a traditional EPSI scheme if further improvement in data acquisition speed is desired. is collected using a modified EPSI sequence with extended k-space coverage and using echo-shifting for spectral encoding. SPICE can also collect in traditional EPSI trajectories (Fig. 7a) or spiral EPSI trajectories (Fig. 7b). The advantages and disadvantages of these data acquisition schemes should be further studied for a specific MRSI application.

Figure 7.

Two alternative (k, t)-space sampling trajectories that can be used to generate : (a) EPSI trajectories, and (b) spiral EPSI trajectories. Note that in (a), the echo spacing is not constrained by the spectral Nyquist criterion as in traditional EPSI schemes. In both cases, different colors represent trajectories for different excitations.

Second, SPICE image reconstruction requires specifying L (the PS model order) and λ (regularization parameter). In principle, L is upper-bounded by the number of spectral components and the number of distinct tissue types in ρ (r, f) (26, 30). The choice of L can be further modified by examining the singular value distribution of the Casorati matrix formed from the data in (as is done in this paper), or based on some rank selection criteria (e.g., (30, 35, 36)). In practice, it is desirable to use an L larger than needed or estimated to avoid any potential model truncation errors. This would not create a problem associated with using noisy temporal basis because of the weightings (Λ) on the corresponding spatial coefficients. The regularization parameter, λ, was chosen based on the discrepancy principle (37) in this work. More advanced schemes can also be used (37). Furthermore, SPICE allows for the use of advanced regularization schemes. The current weighted-ℓ₂ regularization is advantageous in terms of computational efficiency and performance characterization. Additional constraints along the spectral dimension can be included. Non-quadratic or sparsity-promoting penalties (21, 25) can also be used to further improve reconstruction quality.

Several other factors should also be considered in optimizing SPICE for practical MRSI applications, including correction of B₀ inhomogeneity, suppression/removal of water and fat signals for ¹H MRSI experiments, and parallel data acquisition. When the field inhomogeneity map is not accurate, the residual field inhomogeneity can increase the PS model order and broaden the spectral lineshape. Based on our experience, with a proper choice of L (discussed above), SPICE is rather tolerant to residual field inhomogeneity. But this issue should be further investigated. For ¹H spectroscopic imaging, suppression/removal of water and fat signals is necessary, which has been well studied for CSI and EPSI acquisitions. SPICE samples (k, t)-space sparsely for efficient spatiospectral encoding, thus specialized water and fat suppression/removel methods need to be developed. This issue is under investigation and will be addressed in a subsequent paper. Integrating parallel imaging with SPICE can further accelerate high-resolution spectroscopic imaging experiments, especially for 3D experiments. In the current paper, the parallel imaging capability was not fully exploited and SPICE reconstructions were performed coil by coil and then combined together. Further investigation is necessary to optimize both data acquisition and image reconstruction for parallel SPICE spectroscopic imaging experiments.

It is also worth noting that partial separability, which SPICE is based on, is a general property that exists in various kinds of high-dimensional imaging data. The PS model has been successfully used in several imaging applications, including cardiac imaging (38), dynamic speech imaging (39), parameter mapping (40) and diffusion imaging (41). It has also been utilized for processing CSI data sets (25,30), although SPICE is the first attempt to use the subspace model to dictate both data acquisition and image reconstruction for high-resolution spectroscopic imaging.

CONCLUSIONS

We have presented a new approach called SPICE to accelerate spectroscopic imaging through subspace modeling and sparse sampling of (k, t)-space. Very encouraging results have been obtained from computer simulations and phantom studies, which demonstrate an unprecedented capability of SPICE for high-resolution spectroscopic imaging. With further development to optimize SPICE data acquisition and image reconstruction, SPICE may provide a powerful tool for high-resolution metabolic imaging with many potential applications.