Abstract
Randomized trials remain the most accepted design for estimating the effects of interventions, but they do not necessarily answer a question of primary interest: Will the program be effective in a target population in which it may be implemented? In other words, are the results generalizable? There has been very little statistical research on how to assess the generalizability, or “external validity,” of randomized trials. We propose the use of propensity-score-based metrics to quantify the similarity of the participants in a randomized trial and a target population. In this setting the propensity score model predicts participation in the randomized trial, given a set of covariates. The resulting propensity scores are used first to quantify the difference between the trial participants and the target population, and then to match, subclassify, or weight the control group outcomes to the population, assessing how well the propensity score-adjusted outcomes track the outcomes actually observed in the population. These metrics can serve as a first step in assessing the generalizability of results from randomized trials to target populations. This paper lays out these ideas, discusses the assumptions underlying the approach, and illustrates the metrics using data on the evaluation of a schoolwide prevention program called Positive Behavioral Interventions and Supports.
Keywords: Causal inference, External validity, Positive Behavioral Interventions and Supports, Research synthesis
1 Introduction
Randomized trials remain the most accepted design for estimating the effects of interventions, and they serve as the basis for the recommendations being made for prevention and treatment programs by the U.S. Department of Education (What Works Clearinghouse), the Substance Abuse and Mental Health Services Administration (National Registry of Evidence-based Programs and Practices), the Agency for Healthcare Research and Quality (Evidence-based Practice Centers), and researchers (the Cochrane Collaboration). While crucial for assessing efficacy, randomized trials do not necessarily answer a question of primary policy interest: Will the program be effective in a target population in which it may be implemented? In other words, are the results generalizable? Efficacy trials assess whether an intervention works under ideal circumstances, often including a rather homogeneous set of participants (Flay, 1986). As defined by Campbell (1957), p. 297, “The second criterion is that of external validity, representativeness, or generalizability: to what populations, settings, and variables can this effect be generalized?” Effectiveness trials are a step in the direction of generalizability, in that they assess whether the intervention works in real-world conditions, with a broader set of participants (Flay, 1986). However, even effectiveness trials rarely are done using participants that are representative of the target populations in which the interventions being evaluated may eventually be implemented (Rothwell, 2005a). Statistical methods to assess the generalizability of results from effectiveness trials to target populations are needed (National Institute of Mental Health, 1999; Institute of Medicine, 2006).
This paper focuses on the aspect of generalizability related to differences in the characteristics of participants in an effectiveness trial and in a target population. Participants in effectiveness trials are rarely representative of the target population of interest and effects often vary for different types of people and in different contexts. This combination means that the results seen in a randomized trial may not reflect the effects that would be seen if the intervention were implemented in a different target population (Flay et al., 2005). As an example, one explanation for discrepancies regarding the effects of hormone replacement therapy for post-menopausal women in the Women’s Health Initiative randomized trial and the Nurse’s Health Study observational study is differences in the types of women in the two studies (Grodstein et al., 2003), although other possible explanations have also been provided (Hernan et al., 2008). Another example relates to recommendations concerning breast conservation vs. mastectomy for women with breast cancer; the General Accountability Office was concerned that the results obtained from randomized trials may not carry over to women in general medical practice, and so also used observational data methods to estimate the effects for a broader group of women (Rubin, 2008). This issue is similar to that of the representativeness of results from web-based surveys where respondents opt-in for participation; some recent work has investigated implications for survey research, but without a focus on studies estimating causal effects (Couper and Miller, 2008).
The work in this paper is related to proposals to use weighting-based approaches to estimate effects for a target population using data from a randomized trial (e.g., Shadish et al., 2002; Cole and Stuart, 2010; Haneuse et al., 2009; Pan and Schaubel, 2009). These proposals use ideas similar to Horvitz-Thompson estimation for sample surveys and inverse probability of treatment weighting (IPTW) for non-experimental studies (Lunceford and Davidian, 2004), but where the trial sample is weighted to represent the population. In this paper we take a step back to develop diagnostics to help researchers determine when such generalizations may be possible and reliable, and also investigate other propensity score approaches in addition to weighting. Almost no metrics for this purpose are currently available. Glasgow et al. (2006) discusses the need for considering and measuring the “reach” of an intervention in terms of patient participation and representativeness, but discuss only very simple metrics. The state of the art currently is to simply compare the covariates one by one and make qualitative statements regarding the similarity of subjects in a trial and some target population, but it can be difficult to summarize across many covariates. The work described here aims to provide summary measures of representativeness with respect to observed pre-treatment characteristics. In particular, we investigate the use of propensity scores to measure and quantify differences between the participants in a randomized trial and a target population and use results from the propensity score literature on how to quantify differences between two groups and determine how large a difference is too much for reliable comparison, applying those results to a new area.
The proposed methods are illustrated using a randomized trial of a schoolwide behavior improvement program, Positive Behavioral Interventions and Supports (PBIS; Sugai and Horner, 2006). The trial involved the random assignment of 37 public elementary schools from five Maryland school districts to PBIS or a control condition (Bradshaw et al., 2009). Primary outcomes of interest include behavior and academic performance, as measured by student discipline problems, school climate, and student test scores. We also take advantage of school-level data available for all elementary schools across the state of Maryland. The question of interest is how similar the schools in the trial are to those across the state, and whether the results from the trial might hold across the state of Maryland; this is the policy question of interest to policymakers deciding whether or not PBIS should be recommended or implemented statewide. This paper focuses on the statistical ideas and concepts; future work will discuss more of the substantive issues associated with the PBIS intervention itself and generalizing its effects.
This paper outlines the main idea behind using propensity scores to measure similarity of participants in and out of a randomized trial and illustrates it using the PBIS data. In particular, Section 2 describes previous work in methods to assess or enable generalizability. Section 3 then proposes two diagnostic measures that use propensity scores to help quantify how similar the subjects in a trial are to the target population. Section 4 applies those measures to the motivating example of the PBIS program, and Section 5 concludes.
2 Previous work assessing generalizability
To this point, research emphasis has generally been on internal validity–obtaining unbiased effect estimates for the participants in a trial. Less attention has been paid to external validity–addressing whether those participants are representative of the population and whether the effects are generalizable (Imai et al., 2008). The following two sections describe the methods that have been used to assess generalizability, first in terms of study design strategies and then in terms of data analysis techniques.
2.1 Study design
To provide a framework for thinking about these issues, Imai et al. (2008) decompose the estimation error in the estimate of a population treatment effect (Δ) into components due to sample selection and to treatment assignment:
where S refers to bias due to sample selection and T refers to bias due to treatment selection. The subscript X refers to observed variables and U to unobserved. Different study designs focus on different quantities. For example, randomized experiments have ΔTX = ΔTU = 0, but may have larger ΔSX and ΔSU than do observational studies. Observational study methods such as propensity score matching (Stuart, 2010) focus on reducing ΔTX, and sensitivity methods such as in Rosenbaum (2002) assess the potential impact of ΔTU on study conclusions.
Relatively less attention has been paid to the size of ΔSX and ΔSU in randomized experiments. Standard methods that make qualitative arguments regarding the generalizability of results assume that the results from the trial directly carry over to the population: that ΔSX = ΔSU = 0. In this paper we focus on methods to assess the amount of sample selection bias due to observed covariates, ΔSX. While there may still be bias due to ΔSU, the methods discussed here at least provide a way to reduce bias in Δ due to ΔSX .
One of the most straightforward ways of ensuring the generalizability of results from randomized trials is to enroll in the trial a representative sample from the target population. However, only a handful of studies have used random assignment of a fully representative (e.g., random) sample from a population to estimate program effects (Cook, 2007). Examples include the national evaluations of Upward Bound (U.S. Department of Education, 2009) and Head Start (U.S. Department of Health and Human Services, 2005), although even that Head Start evaluation excluded certain centers, such as those that were under-enrolled and those serving Native American populations. There has been increasing attention given to practical clinical trials, which aim to enroll a very large and diverse sample of patients, from a range of settings (Peto et al., 1995; Insel, 2006). However, those trials require large amounts of time and money and are not always feasible. There has also been some discussion of purposively sampling units that are either heterogeneous (to reflect the range of units that are in the target population) or that are typical of that population (Shadish et al., 2002), but those ideas seem to have been rarely used in practice, at least in a formal way.
2.2 Study analysis
Another strategy is to use existing data to assess the generalizability of existing studies, which is the approach we take here. Other methods in this area include meta-analysis (Hedges and Olkin, 1985; Sutton and Higgins, 2008), cross-design synthesis (Prevost et al., 2000), and the confidence profile method (Eddy et al., 1992). Many of these approaches aim to model treatment effects as a function of study parameters, such as randomized vs. non-randomized, and the explicit inclusion/exclusion criteria, and they generally rely on having a relatively large set of studies to include in the analysis. Unfortunately there is often only one or two studies from which conclusions can be drawn. In addition, little attention is usually paid to the types of participants enrolled in the various studies included, and how variation in their characteristics may affect the results.
Perhaps the most common way of generalizing results to a target population is through post-stratification, which re-weights the effects based on population distributions. As a simple example, imagine a target population with 50% males and 50% females, but a randomized trial that had 20% males and 80% females. A simple post-stratification would estimate effects separately by gender and then average the male and female effects using the population proportions (50/50). Post-stratification can be very effective when there are only a small number of variables to control for, but is infeasible when there are many (or continuous) variables, leading to a very large number of post-stratification cells. Frangakis (2009) discusses a more complex scenario for post-stratification, where generalizability also depends on post-treatment variables. Post-stratification is closely related to methods that model treatment by covariate interactions to investigate whether effects vary across individuals (e.g., Rothwell, 2005b; Wang et al., 2007). In fact investigation of subgroup effects and effect heterogeneity is a crucial step in determining what covariates are crucial to control for in the methods we propose, as discussed further below.
Weisberg et al. (2009) posit a simple model to account for differences between a trial sample and a population due to inclusion or exclusion criteria, for a setting with a binary outcome. They provide formulas for the amount of bias that may be created and show that depending on whether high-risk patients are particularly included or excluded, the estimated effect may change considerably, or even reverse sign. In work that is probably most similar to that presented here, Greenhouse et al. (2008) provide a case study of assessing generalizability, comparing the characteristics of pediatric participants in randomized trials of antidepressants to the general population of children and adolescents. That work represented an important advance in raising this issue, in the context of an important policy question regarding antidepressants and suicidality.
3 Using propensity scores to assess generalizability
3.1 Formal setting
We consider a setting where a randomized trial has been conducted to estimate the effect of a program, P, relative to a control condition, C, on a sample of participants, Ψ, of size n. By “program” we mean any intervention of interest, whether preventive or a treatment for a particular disorder or disease. The participants in Ψ may be individuals or they may be at a higher level, such as communities or schools, as in the case of PBIS. In the trial the program P has been randomly assigned to participants in Ψ, forming a program group and a control group that are only randomly different from each other on all background characteristics. Interest is in determining the effectiveness of the program P in a target population, represented by Ω, where Ψ is a subset of Ω. We refer to Ψ as the “sample” and Ω as the “population.” In the PBIS example, Ψ consists of the 37 schools in the effectiveness trial; Ω consists of all public elementary schools in the state not in the trial and not implementing PBIS. We assume that for all participants in Ω (or a representative sample of them) we observe a set of background characteristics X, which describe both the participants themselves and their broader contexts. In the PBIS study, X consists of characteristics such as test scores, enrollment, and demographics.
For subject i we denote membership in the randomized trial sample by Si, Ti indicates membership in the treatment vs. control group (only defined for those with Si = 1), and Yi(1) and Yi(0) are the potential outcomes under treatment and control, respectively (Rubin, 1977). Following the notation in Imai et al. (2008), the treatment effect for individual i is the difference in potential outcomes, Yi(1) − Yi(0), although results could be extended to other functions of the potential outcomes, such as their ratio. The standard intent to treat estimates from a randomized trial, such as a difference in means of the outcome in the treated and control groups, yields an unbiased estimate of the sample average treatment effect (SATE):
However our estimand of interest is the population average treatment effect (PATE):
When the treatment effect is constant PATE=SATE, but that will generally not be the case. While the PATE is a clearly defined measure of impact in a given population, in many research settings the target population changes over time or space. In such cases, there may be more than one PATE that is of interest. For a simple setting with one effect modifier, Cole and Stuart (2010) give an equation for the bias, which depends on 1) the proportion of the population not sampled, 2) the heterogeneity in the treatment effects, 3) the prevalence of the effect modifier in the population, and 4) the strength of the association between the effect modifier and sample selection.
3.2 Key assumptions
We make three primary assumptions. Assumption 1 is that, given X, all subjects in the population have some probability of being selected for the trial:
Assumption 2 is that there are no unmeasured variables that are related to both sample selection and the treatment effect (E(ΔSU) = 0), which we term “unconfounded sample selection” (see also Cole and Stuart, 2010). This assumption is similar to the assumption of ignorable treatment assignment in observational studies (Rosenbaum and Rubin, 1983b) or the “missing at random” assumption with respect to missing data (Rubin, 1976). Formally, this assumption says that sample selection is independent of the potential outcomes, given the observed covariates:
Assumption 3 is that treatment assignment is randomly assigned (hence independent of the potential outcomes) and independent of sample selection, given the observed covariates:
The combination of Assumptions 1 and 3 also implies that each subject has a positive probability of receiving the treatment, comparable to the assumption of “strongly ignorable treatment assignment” in Rosenbaum and Rubin (1983b).
The validity of Assumption 1 depends on the definition of the target population. In settings where some individuals in the initial target population would never receive the treatment of interest (e.g., a targeted intervention that is only given to at-risk students who have already exhibited some problem behaviors), the target population should be redefined to include only those individuals to whom the treatment may be given. Assumption 3 is met in randomized trials where the random assignment is done after the sample selection, and where treatment assignment depends only on observed characteristics X. It thus arguably is not an assumption per se; we include it here for completeness. Assumption 2 is arguably the hardest to meet, and relies on having all potential moderators of the treatment effect measured. This assumption is discussed further below.
Given these three assumptions we discuss two diagnostics for generalizability, both based on the propensity score. First, the average propensity score difference between the sample and the population, and second, the use of propensity score methods to compare observed and predicted outcomes under control for the population.
3.3 Propensity score distance as a measure of similarity
The first diagnostic tool we propose is the propensity score distance between the participants in the trial and the target population, as a way to summarize their similarity. Here, the propensity scores model the probability of being in the randomized trial; using inverse propensity score weights will allow the trial participants to weight up to the target population (Cole and Hernan, 2008; Cole and Stuart, 2010). The propensity score is typically defined as the probability of receiving some program (or “treatment”) versus a comparison condition, given a set of observed baseline characteristics (Rosenbaum and Rubin, 1983b). Propensity score matching, subclassification, or weighting can help ensure that the program and comparison subjects being compared in a non-randomized study are as similar as possible. This is done by comparing groups of subjects with similar propensity scores, who, by virtue of the properties of the propensity score, will also have similar distributions of the observed background covariates. In this way, propensity scores attempt to replicate a randomized experiment in the sense of comparing subjects who did and did not receive the treatment who have no systematic differences on the observed covariates (Ho et al., 2007; Stuart, 2010).
Here, to summarize differences between the trial sample and the target population, the propensity score will model membership in the randomized trial sample, rather than receipt of the treatment. In particular, we use a logistic regression model of the probability of being in the randomized trial (S) with the covariates (X) as predictors: , where pi = P(Si = 1|Xi). We use to denote the estimated probability of sample selection for subject i. In a connection to the discriminant function, these propensity scores serve as the scalar summary of the covariates that distinguishes the most between the trial participants and the target population (Rubin and Thomas, 1992). They thus can provide a summary measure of the similarity (or dissimilarity) of the trial participants and the population: just as propensity scores can be used to identify when treatment and control groups are too far apart for reliable causal inference (Rubin, 2001), they can be used to also identify when a sample is too different from a population of interest to yield reliable generalizations.
We define the propensity score difference between the trial sample and population (Δp) as the difference in average propensity scores between those in the trial and those not in the trial:
If the sample is actually a (very large) random sample from the population, then we would expect essentially no difference in the mean propensity scores between those sampled and not sampled. In that case, E(pi|Si = 1) = E(pi|Si = 0) and E(Δp) = 0. As we will see later in the PBIS example, in finite samples, there is likely to be a small, positive value for Δp, reflecting small chance differences between the trial participants and the population. When there are systematic differences between the trial sample and population we will expect that these means will be quite different. In the standard propensity score context of observational studies, simulation studies and theoretical approximations originally developed in the context of matching within propensity score calipers (Cochran and Rubin, 1973; Rubin, 1973) have indicated that propensity score means that differ by more than 0.25 standard deviations indicate a large amount of extrapolation and heavy reliance on the models being used for estimation (Ho et al., 2007; Stuart, 2010), although this is by no means a set criterion, and in fact some researchers recommend a more stringent criterion of 0.1 (Mamdani et al., 2005).
3.4 Using propensity score methods to match the control group to the population and compare predicted and observed outcomes
A second way in which we can use the propensity scores to assess generalizability is by using propensity score methods to make the control group look like the target population and compare the predicted outcomes under control to the outcomes actually observed in the population. We discuss three methods here: inverse probability of treatment weighting (IPTW), full matching, and subclassification. All three of these methods can be thought of as weighting the control group to the population; the methods vary in the coarseness of the weights, with subclassification the coarsest and IPTW the finest. In fact, IPTW can be thought of as an extreme where the number of individuals and subclasses goes to infinity (Rubin, 2001).
IPTW methods give each individual their own weight, calculated as the inverse propensity scores, i.e., in our setting, the inverse probability of being in the sample: . These are conceptually similar to the weights used in in non-response adjustments in survey sampling (Kalton and Flores-Cervantes, 2003). This weighting forms a pseudo-population with characteristics similar to those of the target population. If no one in the population was receiving the intervention of interest, then, if the weights are effective, the weighted control group outcomes should be similar to the outcomes observed in the target population. Mathematically, we can extend results in Horvitz and Thompson (1952) and Lunceford and Davidian (2004), where the expectations are taken over the target population:
In this expression e(X) reflects the probability of treatment assignment, e(X) = P(T = 1|X), which is known in a randomized experiment. The above equations show that the probability of treatment assignment and trial participation-weighted control group mean will be an unbiased estimate of the population potential outcome under control, given the assumptions detailed above. In this way we can use the similarity of the weighted control group means to the population means as a diagnostic for how well the generalization is likely to work.
However, a concern about IPTW methods is that the results can be somewhat unstable, especially if there are extreme weights, and the method is more sensitive to the specification of the propensity score model than are other propensity score approaches (Kang and Schafer, 2007). We thus also consider two other methods of re-weighting the control group to resemble the population, which use coarser weights. At the other extreme, subclassification methods form a relatively small (e.g., 5-10) number of subclasses and group individuals with similar propensity score values (e.g., by the quintiles of the propensity score distribution). However, subclassification approaches can suffer from having too few subclasses and thus insufficient bias reduction (Lunceford and Davidian, 2004; Stuart, 2010).
We thus also consider a third approach, full matching (Hansen, 2004; Stuart and Green, 2008), which can be thought of as a compromise between IPTW and subclassification (Stuart, 2010). Full matching forms a relatively large number of subclasses, where in our use each subclass will have at least one member of the sample and at least one member of the target population, but the ratio of sample to population members in each subclass can vary. The subclasses reflect the fact that some areas of the propensity score space will have relatively few sample members and many population members, while other areas will have relatively few population members and many sample members. Full matching has been shown to be optimal in terms of reducing propensity score differences within subclasses (Rosenbaum, 1991).
For both subclassification and full matching the control group members in the trial are given weights proportional to the number of population members in their subclass. For example, sample members in a subclass with 2 sample members and 10 population members would receive weights proportional to 5 (10/2), while sample members in a subclass with 10 sample members and 2 population members would receive weights proportional to 0.2 (2/10). For details on the construction of the weights following full matching see Stuart and Green (2008).
4 Applying methods to PBIS study
We now apply the diagnostic tools described above to the group-randomized trial of Positive Behavioral Interventions and Supports (PBIS). PBIS is a schoolwide prevention program that aims to improve school climate by creating improved systems and procedures that promote positive change in staff and student behaviors (Sugai and Horner, 2006). It is being widely disseminated by the U.S. Department of Education and many state governments. By 2010, over 10,000 schools across the United States, representing approximately 10% of all U.S. public schools, were implementing PBIS (Technical Assistance Center on Positive Behavioral Interventions and Supports, 2010). Because the intervention operates at the school level, the unit of analysis is the school.
We combine information from two datasets to illustrate the use of propensity scores for assessing generalizability. First, the randomized effectiveness trial of the universal system of school-wide PBIS, called “Project Target,” began in 2002 among a sample of 37 Maryland public elementary schools that volunteered for the study (Bradshaw et al., 2009). Those 37 schools were randomized to treatment and control in two years (2002, 2003); for our illustrative purposes here we pool the two years together. Second, we have longitudinal data on all public elementary schools across Maryland, from 1993 through 2007. This provides the population data necessary to estimate the probabilities of participation in the trial and compare the schools in the trial to schools across the state.
State-level coordinated training is required to implement the PBIS intervention. The state of Maryland has a mechanism for training schools in PBIS, which was used to train both the PBIS schools in the trial and non-trial schools that chose to implement PBIS (Barrett et al., 2008). Because some elementary schools were implementing PBIS outside of the trial, as the target population we consider the 717 elementary schools in the state that had not implemented PBIS by 2006 and that were not participating in the Project Target trial; subsequent use of the term “state population” refers to this subsample of the full state population. Excluding the schools participating in the trial from the state population of interest increases clarity and precision.
We consider variables measured in 2002 as pre-trial covariates and examine outcomes measured in 2003 and later. Observed characteristics of the schools (both in the trial and statewide) include characteristics of the students (e.g., percent of students classified as special-education, percent who qualify for free or reduced price meals, average math and reading test scores), as well as of the schools themselves (e.g., enrollment). Schools in the PBIS trial are somewhat different from the population of elementary schools across Maryland on these observed characteristics (Table 1). In 2002, the schools enrolled in the trial had somewhat lower test scores, more students eligible for Title 1 (a measure of poverty), and higher suspension rates than other schools across the state.
Table 1.
Baseline characteristics of schools in Project Target (PT) trial and schools across the state of Maryland. All variables measured in 2002. Test score variables reflect the percentage of students scoring in the “Advanced” or “Proficient” ranges on the Maryland state standardized test. Trend shows change from 2000 to 2002. p-values shown from t-tests or chi-square tests, as appropriate.
| Characteristic (2002) |
PT schools | non-PT schools | p-value of difference |
||
|---|---|---|---|---|---|
| Mean | SD | Mean | SD | ||
| Total enrollment | 485 | 150 | 480 | 177 | 0.85 |
| Attendance rate | 95.3 | 0.7 | 95.4 | 1.5 | 0.80 |
| % students Caucasian | 60.3 | 31.7 | 53.8 | 34.0 | 0.23 |
| % students eligible for free or reduced meals |
39.7 | 20.0 | 36.2 | 27.5 | 0.31 |
| % students eligible for Title 1 |
47.3 | 49.6 | 26.3 | 41.4 | 0.02 |
| % students in special ed | 13.8 | 5.6 | 15.2 | 15.4 | 0.21 |
| 3rd grade math test | 27.4 | 15.2 | 32.1 | 20.5 | 0.08 |
| 3rd grade reading test | 32.9 | 16.4 | 34.5 | 20.4 | 0.57 |
| 5th grade math test | 44.6 | 18.6 | 51.3 | 29.9 | 0.05 |
| 5th grade reading test | 54.2 | 17.9 | 53.2 | 26.0 | 0.75 |
| Trend in 3rd grade math scores | −19.2 | 18.9 | −15.9 | 16.6 | 0.31 |
| Trend in 3rd grade reading scores | −12.3 | 18.6 | −11.9 | 14.6 | 0.90 |
| Trend in 5th grade math scores | −13.4 | 20.9 | −11.9 | 18.4 | 0.66 |
| Trend in 5th grade reading scores | 1.3 | 19.1 | −1.9 | 16.8 | 0.33 |
| % of students suspended | 6.3 | 4.5 | 4.5 | 5.1 | 0.03 |
|
| |||||
| Sample size | 37 | 680 | |||
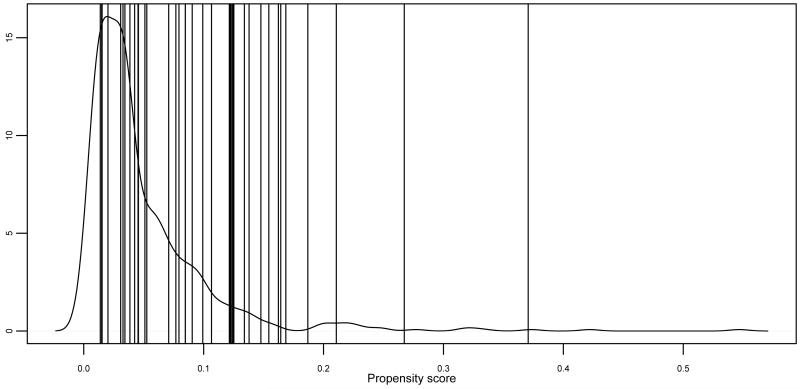
To summarize these differences, a propensity score (logistic regression) model was fit predicting membership in the Project Target trial given the set of characteristics in Table 1. Figure 1 shows the distribution of propensity scores among schools across the state and for the schools in the Project Target trial. In general there is overlap of the propensity scores, with many of the trial schools in the range of propensity scores with high density among the schools across the state, but also with a number of the trial schools with relatively large propensity scores. We can also quantify this, in that the difference in average propensity scores between the schools in the trial and those across the state (Δp) is 0.055. The standardized difference (standardized by the standard deviation of the propensity score) is 0.73, a substantial difference, and a size indicated by Rubin (2001) to lead to unreliability of standard regression modeling because of the resulting extrapolation.
Figure 1.
Distribution of propensity scores among the schools across the state (density plot) and schools in Project Target trial (vertical lines). State population consists of all elementary schools across the state of Maryland not implementing PBIS and not enrolled in the trial.
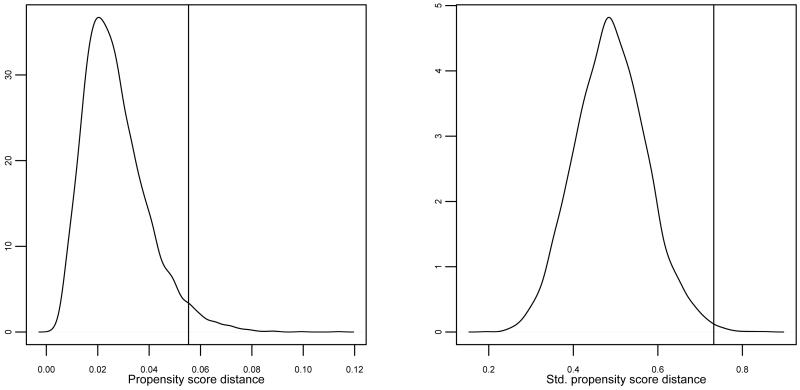
We can also compare these differences with what would be expected in repeated random draws of the same size. This allows us to determine what size propensity score difference we would expect if the schools in the trial were in fact selected randomly from the population. Figure 2 shows the distribution of the difference in mean propensity scores between sampled and unsampled schools, given repeated samples of size 37 drawn from the population of Maryland public elementary schools that had not implemented PBIS by 2006. Because the propensity score is defined relative to a particular sample, the propensity scores themselves are re-calculated within each random sample. While a propensity score distance of approximately 0.02 would be expected, our observed difference of 0.055 would happen in only 24 of 1000 samples randomly drawn from the population. Similarly, while a standardized difference of size 0.5 would be expected, only 3 of the 1000 samples that we drew had a standardized difference as large as our observed value of 0.73.
Figure 2.
Distribution of propensity score distances between sampled and unsampled schools, where samples of size 37 repeatedly drawn from population of elementary schools in Maryland. Left-hand plot shows simple differences (sampled minus unsampled); right-hand side shows standardized difference, standardized by standard deviation of propensity scores. Vertical line in each shows the value observed for the Project Target trial schools.
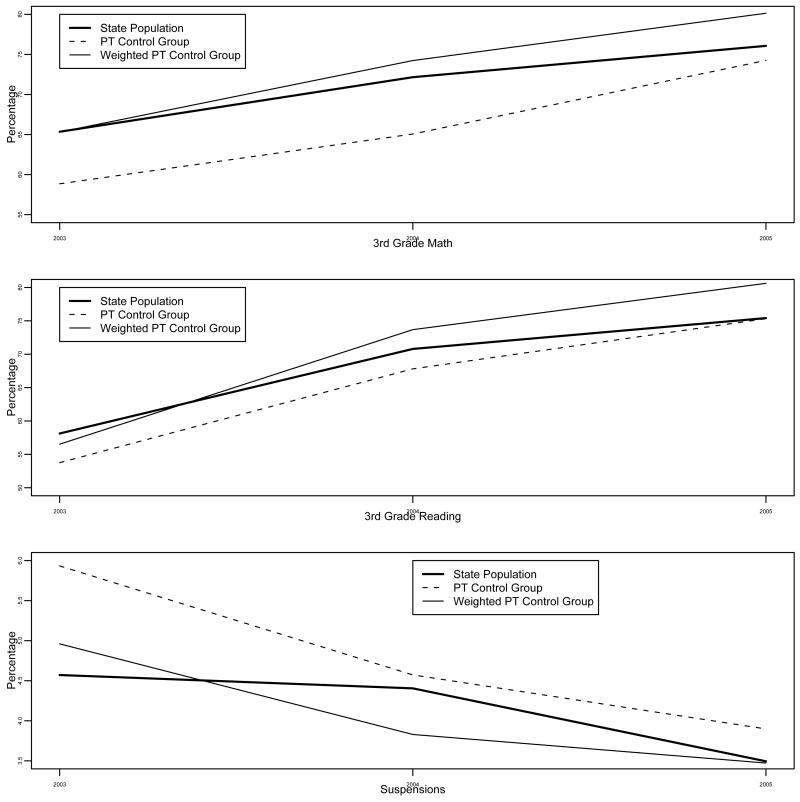
We then used the three propensity score adjustment methods described above (IPTW, full matching, and subclassification) to match the control group in the PT trial to the state population. The results were broadly similar for the three approaches and thus we show only the results for full matching, which can be considered the intermediate approach. Figure 3 thus illustrates the second diagnostic tool, which is to examine the comparability of the weighted control group means to the values observed in the population. Despite the differences seen between the trial and non-trial schools above, it appears that the control schools in the trial reflect what was happening across the state as a whole, when weighted up to represent the population. We used three outcomes for this illustration: the percentage of 3rd grade students scoring proficient or higher on the yearly statewide reading and mathematics exams, and the percentage of students suspended during the school year. The thick solid line shows the average value for each outcome, averaged across all schools in the state that were not implementing PBIS and not in the trial, over the time period from 2003 to 2005. The dashed line shows the same average, but calculated using the control schools in the trial. The large distance between the dashed line and the thick solid line illustrates the overall difference between the schools in the trial and those in the state: on average, the schools in the trial had lower test scores and higher suspension rates than those across the state. The thin solid line shows the average for the control schools in the trial, but weighted using weights calculated from propensity score full matching. For all three outcomes, and especially the test scores, the trial control schools’ weighted average tracks the true state mean quite closely, seen by the similarity of the two solid lines in each panel of Figure 3. This is particularly true for outcomes in 2003 to 2004, which is expected given that the propensity scores were estimated using variables measured in 2002 and before. Interestingly, using IPTW seemed to track the population outcomes slightly better than full matching, while subclassification tracked the population outcomes slightly less well. Future work should further compare these approaches and their use in generalizing trial results. These results indicate that, despite the apparently large differences on the pre-treatment covariates, when weighted appropriately, the schools in the trial may help us learn about population effects across the state of PBIS on 3rd grade math and reading tests and suspension rates.
Figure 3.
Observed and predicted outcome values for schools across the state of Maryland. For math and reading scores, numbers shown are percent of children scoring “Proficient” or “Advanced” on the standardized test. Numbers shown for suspensions are the percentage of students suspended in a school year. Black thick line shows observed state averages, where the state population refers to schools across the state not implementing PBIS and not enrolled in the trial. Thin dashed line shows average for control schools in Project Target trial; thin solid line shows weighted average for control schools in trial, with weights calculated from full matching. For all three outcomes, the weighted average tracks the state mean much more closely than the observed average among control schools in the trial.
5 Discussion
Propensity scores offer a promising way to assess the similarity between a trial sample and a target population of interest. However, there is still much work remaining in this area. The methods presented here assume that individual-level data is available for the population, or at least for a representative sample from that population. This type of data is becoming more readily available, through nationally representative datasets or through administrative datasets such as Medicare claims, Veteran’s administration records files, or health system administrative data sources. Similarly, the No Child Left Behind Act requires states to collect and keep school records data on academic performance and discipline for reporting purposes. However, in cases where individual- (or school-) level population data may not be available, Cole and Stuart (2010) present an alternative approach that uses only summary statistics on the population of interest.
An important question for this work regards variable selection and model estimation. These issues may be informed by similar work in the broader propensity score literature (e.g., Brookhart et al., 2006), however it will be important to consider whether the implications are different in this setting. For example, it will likely be especially important to include strong predictors of the outcome, and particularly moderators of the treatment effects, in the propensity score model. Because of this, it is also important for current trials to investigate effect heterogeneity and which covariates are effect modifiers. A related issue is how to weight the characteristics that are observed. By default, propensity scores effectively weight each characteristic by how predictive it is of membership in the trial sample. However, researchers are likely to have prior information on which characteristics moderate the treatment effects, and thus are particularly important to control for. Future work will develop methods that prioritize these key characteristics by giving them more emphasis in the summary measure. One possible approach is to combine propensity scores with another multivariate distance (such as the Mahalanobis distance) calculated using those key characteristics (Rubin and Thomas, 2000). A second possible approach is to combine propensity scores with the prognosis score methods recently developed by Hansen (2008). Prognosis scores effectively weight each characteristic by how predictive it is of the outcome under control, Y(0).
In many settings it is likely that both individual- and contextual-level factors moderate the effects of interventions. For example, the effects of school-based smoking prevention programs may be moderated by both individual characteristics such as gender and race, but also by the characteristics of the school and community. In the current study we have dealt with this by incorporating both individual-level measures as well as characteristics of the schools. In other cases, where individual-level data is available, a more direct way of doing so would be to use a multilevel/hierarchical framework, in which the relationship between participation in the trial and the individual and context level characteristics are modeled at separate levels: one for individuals and one for the context. This is discussed in the context of randomized experiments in Brown et al. (2008) and Hong and Raudenbush (2006).
The methods described in this paper assume that all the effect moderators are observed (unconfounded sample selection). This is a crucial assumption, and it is important to assess the validity of it. In the case of PBIS, there has been very little research into the effectiveness of PBIS (Bradshaw et al., 2010), and in fact the Maryland trial was only the second randomized trial of PBIS done in the country (the other is described in Horner et al., 2009). Therefore, relatively little is known about potential school-level moderators of the effects of PBIS. The theory of the PBIS intervention, and of school-based interventions in general, leads us to believe that we likely observe most of the major variables that may affect the effectiveness of the PBIS intervention (e.g., academic achievement, school size). However, some important variables, such as the schools’ organizational capacity to implement the program (Bradshaw et al., 2009), the principals’ support for PBIS (Kam et al., 2003), or the reasons why the principals volunteered the school to participate in the trial are missing from these analyses. Although some of this data is available for the schools in the trial, unfortunately none are available state-wide. A potential consequence of these possible unobserved confounders is that the methods described in this paper may be more appropriate for some outcomes than for others. For example, we repeated the analyses for 5th grade test scores and found that there were still substantial differences between the weighted control schools’ outcomes and the average outcomes across the state. One potential explanation for this varied performance across grades is possible unobserved differences in discipline problems between the schools in the trial and those across the state. Schools that volunteered to participate in the trial may have done so in part because of relatively high disciplinary problems, which tend to manifest themselves more in the later elementary school years (Koth et al., 2009); the principals of the participating schools may have felt more of a need to participate in the trial to have the possibility of getting the PBIS intervention. Thus, even when weighted using the characteristics in Table 1, the 5th graders in the trial schools may have been more different from those across the state, especially as compared to 3rd graders. This would be an example of an unmeasured characteristic that differs between the sample and population, which in particular may impact 5th grade scores more than 3rd grade scores. This may in part also be why the results for suspensions look somewhat worse than for 3rd grade test scores (Figure 3). The diagnostics presented here can help determine when the weights are sufficient for generalization, or when unobserved variables are likely to cause a problem, as seen for the 5th grade test scores. Future work will also investigate methods to assess the sensitivity of effect estimates to an unobserved moderator, along the lines of Rosenbaum and Rubin (1983a).
As more and more high-quality effectiveness trials are carried out, the clear next research questions will involve external validity and generalizing the results from those trials. Some recent work has started investigating weighting methods to generalize results to target populations, but diagnostics are first needed to help determine when such generalization is reasonable. The methods propose here provide a first step towards assessing the similarity of participants in a trial to those in a population, allowing researchers to begin to examine the extent to which the results seen in trials may generalize more broadly. Assuming that these diagnostics indicate it is safe to proceed, future work should expand these approaches to actually generate effect estimates for target populations of interest.
Acknowledgments
This research was supported by the National Institute of Mental Health (K25 MH083846, PI Stuart; 1 R01 MH67948-1A1, PI Leaf), the Centers for Disease Control (R49/CCR318627, PI Leaf), and the Institute of Education Sciences (R305A090307, PI Bradshaw).
References
- Barrett S, Bradshaw C, Lewis-Palmer T. Maryland state-wide PBIS initiative: Systems, evaluation, and next steps. Journal of Positive Behavior Interventions. 2008;10:105–114. [Google Scholar]
- Bradshaw C, Mitchell M, Leaf P. Examining the effects of Schoolwide Positive Behavioral Interventions and Supports on student outcomes: Results from a randomized controlled effectiveness trial in elementary schools. Journal of Positive Behavior Interventions. 2010;12(3):133–148. [Google Scholar]
- Bradshaw CP, Koth CW, Thornton LA, Leaf PJ. Altering school climate through school-wise Positive Behavioral Interventions and Supports: Findings from a group-randomized effectiveness trial. Prevention Science. 2009;10:100–115. doi: 10.1007/s11121-008-0114-9. [DOI] [PubMed] [Google Scholar]
- Brookhart MA, Schneeweiss S, Rothman KJ, Glynn RJ, Avorn J, Sturmer T. Variable selection for propensity score models. American Journal of Epidemiology. 2006;163(12):1149–1156. doi: 10.1093/aje/kwj149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown CH, Wang W, Kellam SG, Muthen B, Petras H, Toyinbo P, Poduska J, Ialongo N, Wyman PA, Chamberlain P, Sloboda Z, MacKinnon DP, Windham A, The Prevention Science Methodology Group Methods for testing theory and evaluating impact in randomized field trials: Intent-to-treat analyses for integrating the perspectives of person, place, and time. Drug and Alcohol Dependence. 2008;95:S74–S104. doi: 10.1016/j.drugalcdep.2007.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell DT. Factors relevant to the validity of experiments in social settings. Psychological Bulletin. 1957;54(4):297–312. doi: 10.1037/h0040950. [DOI] [PubMed] [Google Scholar]
- Cochran WG, Rubin DB. Controlling bias in observational studies: A review. Sankhya: The Indian Journal of Statistics, Series A. 1973;35:417–446. [Google Scholar]
- Cole SR, Hernan MA. Constructing inverse probability weights for marginal structural models. American Journal of Epidemiology. 2008;168(6):656–664. doi: 10.1093/aje/kwn164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole SR, Stuart EA. Generalizing evidence from randomized clinical trials to target populations: the ACTG-320 trial. American Journal of Epidemiology. 2010;172:107–115. doi: 10.1093/aje/kwq084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook TD. Evidence-based practice: Where do we stand?; The Gwen Iding Brogden Distinguished Lecture, The 20th Annual Research Conference-A System of Care for Children’s Mental Health: Expanding the Research Base; 2007; Available at http://rtckids.fmhi.usf.edu/rtcconference/20thconference/iding.cfm. [Google Scholar]
- Couper MP, Miller PV. Web survey methods: Introduction. Public Opinion Quarterly. 2008;72(5):831–835. [Google Scholar]
- Eddy D, Hasselblad V, Shachter R. Meta-analysis by the confidence profile method: The statistical synthesis of evidence. Academic Press, Inc.; New York: 1992. [Google Scholar]
- Flay BR. Efficacy and effectiveness trials (and other phases of research) in the development of health promotion programs. Preventive Medicine. 1986;15:451–474. doi: 10.1016/0091-7435(86)90024-1. [DOI] [PubMed] [Google Scholar]
- Flay BR, Biglan A, Boruch RF, Castro FG, Gottfredson D, Kellam S, Moscicki EK, Schinke S, Valentine J. Standards of evidence: Criteria for efficacy, effectiveness and dissemination. Prevention Science. 2005;6:151–175. doi: 10.1007/s11121-005-5553-y. [DOI] [PubMed] [Google Scholar]
- Frangakis CE. The calibration of treatment effects from clinical trials to target populations. Clinical Trials. 2009;6:136–140. doi: 10.1177/1740774509103868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasgow RE, Nelson CC, Strycker LA, King DE. Using RE-AIM metrics to evaulate diabetes self-management support interventions. American Journal of Preventive Medicine. 2006;30(1):67–73. doi: 10.1016/j.amepre.2005.08.037. [DOI] [PubMed] [Google Scholar]
- Greenhouse JB, Kaizar EE, Kelleher K, Seltman H, Gardner W. Generalizing from clinical trial data: A case study of the risk of suicidality among pediatric antidepressant users. Statistics in Medicine. 2008;27:1801–1813. doi: 10.1002/sim.3218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grodstein F, Clarkson T, Manson J. Understanding the divergent data on postmenopausal hormone therapy. New England Journal of Medicine. 2003;348:645–650. doi: 10.1056/NEJMsb022365. [DOI] [PubMed] [Google Scholar]
- Haneuse S, Schildcrout J, Crane P, Sonnen J, Breitner J, Larson E. Adjustment for selection bias in observational studies with application to the analysis of autopsy data. Neuroepidemiology. 2009;32:229–239. doi: 10.1159/000197389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen BB. Full matching in an observational study of coaching for the SAT. Journal of the American Statistical Association. 2004;99(467):609–618. [Google Scholar]
- Hansen BB. The prognostic analogue of the propensity score. Biometrika. 2008;95(2):481–488. [Google Scholar]
- Hedges LV, Olkin I. Statistical methods for meta-analysis. Academic Press; Burlington, MA: 1985. [Google Scholar]
- Hernan M, Alonso A, Logan R, Grodstein F, Michels K, Willett W, Manson J, Robins J. Observational studies analyzed like randomized experiments: An application to postmenopausal hormone therapy and coronary heart disease (with discussion) Epidemiology. 2008;19:766–779. doi: 10.1097/EDE.0b013e3181875e61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho DE, Imai K, King G, Stuart EA. Matching as nonparametric preprocessing for reducing model dependence in parametric causal inference. Political Analysis. 2007;15(3):199–236. [Google Scholar]
- Hong G, Raudenbush SW. Evaluating kindergarten retention policy: A case study of causal inference for multilevel observational data. Journal of the American Statistical Association. 2006;101(475):901–910. [Google Scholar]
- Horner R, Sugai G, Smolkowski K, Eber L, Nakasato J, Todd A, Esperanza J. A randomized, wait-list controlled effectiveness trial assessing school-wide Positive Behavior Support in elementary schools. Journal of Positive Behavior Interventions. 2009;11(3):133–144. [Google Scholar]
- Horvitz D, Thompson D. A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association. 1952;47:663–685. [Google Scholar]
- Imai K, King G, Stuart EA. Misunderstandings among experimentalists and observationalists in causal inference. Journal of the Royal Statistical Society Series A. 2008;171(2):481–502. [Google Scholar]
- Insel TR. Beyond efficacy: The STAR*D trial. The American Journal of Psychiatry. 2006;163:5–7. doi: 10.1176/appi.ajp.163.1.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Institute of Medicine . Improving the quality of health care for mental and substance-use conditions. The National Academies Press; Washington, D.C.: 2006. Quality Chasm Series. [PubMed] [Google Scholar]
- Kalton G, Flores-Cervantes I. Weighting methods. Journal of Official Statistics. 2003;19:81–97. [Google Scholar]
- Kam C, Greenberg M, Walls C. Examining the role of implementation quality in school-based prevention using the PATHS curriculum. Prevention Science. 2003;1:55–63. doi: 10.1023/a:1021786811186. [DOI] [PubMed] [Google Scholar]
- Kang JD, Schafer JL. Demystifying double robustness: A comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science. 2007;22(4):523–539. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koth C, Bradshaw C, Leaf P. Teacher Observation of Classroom Adaptation-Checklist (TOCA-C): Development and factor structure. Measurement and evaluation in counseling and development. 2009;42:15–30. [Google Scholar]
- Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Statistics in Medicine. 2004;23:2937–2960. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
- Mamdani MM, Sykora K, Li P, Normand S-LT, Streiner DL, Austin PC, Rochon PA, Anderson GM. Reader’s guide to critical appraisal of cohort studies: 2. assessing potential for confounding. British Medical Journal. 2005;330:960–962. doi: 10.1136/bmj.330.7497.960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Institute of Mental Health . Tech. rep. National Institute of Mental Health; Bethesda, MD: 1999. Bridging science and service: A report by the NIMH Council’s clinical treatment and services research workgroup. Available at http://www.nimh.nih.gov/publicat/nimhbridge.pdf. [Google Scholar]
- Pan Q, Schaubel DE. Evaluating bias correction in weighted proportional hazards regression. Lifetime data analysis. 2009;15:120–146. doi: 10.1007/s10985-008-9102-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peto R, Collins R, Gray R. Large-scale randomized evidence: Large, simple trials and overviews of trials. Journal of Clinical Epidemiology. 1995;48(1):23–40. doi: 10.1016/0895-4356(94)00150-o. [DOI] [PubMed] [Google Scholar]
- Prevost TC, Abrams KR, Jones DR. Hierarchical models in generalized synthesis of evidence: An example based on studies of breast cancer screening. Statistics in Medicine. 2000;19:3359–3376. doi: 10.1002/1097-0258(20001230)19:24<3359::aid-sim710>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- Rosenbaum PR. A characterization of optimal designs for observational studies. Journal of the Royal Statistical Society, Series B (Methodological) 1991;53(3):597–610. [Google Scholar]
- Rosenbaum PR. Observational Studies. 2nd Edition Springer Verlag; New York, NY: 2002. [Google Scholar]
- Rosenbaum PR, Rubin DB. Assessing sensitivity to an unobserved binary covariate in an observational study with binary outcome. Journal of the Royal Statistical Society Series B. 1983a;45(2):212–218. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983b;70:41–55. [Google Scholar]
- Rothwell PM. External validity of randomised controlled trials: “To whom do the results of this trial apply?”. The Lancet. 2005a;365(9453):82–93. doi: 10.1016/S0140-6736(04)17670-8. [DOI] [PubMed] [Google Scholar]
- Rothwell PM. Subgroup analysis in randomised controlled trials: importance, indications, and interpretation. The Lancet. 2005b;365(9454):176–186. doi: 10.1016/S0140-6736(05)17709-5. [DOI] [PubMed] [Google Scholar]
- Rubin DB. The use of matched sampling and regression adjustment to remove bias in observational studies. Biometrics. 1973;29:185–203. [Google Scholar]
- Rubin DB. Inference and missing data (with discussion) Biometrika. 1976;63:581–592. [Google Scholar]
- Rubin DB. Assignment to treatment group on the basis of a covariate. Journal of Educational Statistics. 1977;2:1–26. [Google Scholar]
- Rubin DB. Using propensity scores to help design observational studies: application to the tobacco litigation. Health Services & Outcomes Research Methodology. 2001;2:169–188. [Google Scholar]
- Rubin DB. For objective causal inference, design trumps analysis. Annals of Applied Statistics. 2008;2(3):808–840. [Google Scholar]
- Rubin DB, Thomas N. Characterizing the effect of matching using linear propensity score methods with normal distributions. Biometrika. 1992;79:797–809. [Google Scholar]
- Rubin DB, Thomas N. Combining propensity score matching with additional adjustments for prognostic covariates. Journal of the American Statistical Association. 2000;95:573–585. [Google Scholar]
- Shadish WR, Cook TD, Campbell DT. Experimental and quasi-experimental designs for generalized causal inference. Houghton Mifflin Company; Boston, MA: 2002. [Google Scholar]
- Stuart EA. Matching methods for causal inference: A review and a look forward. Forthcoming in Statistical Science. 2010 doi: 10.1214/09-STS313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart EA, Green KM. Using full matching to estimate causal effects in non-experimental studies: Examining the relationship between adolescent marijuana use and adult outcomes. Developmental Psychology. 2008;44(2):395–406. doi: 10.1037/0012-1649.44.2.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugai G, Horner R. A promising approach for expanding and sustaining school-wide positive behavior support. School Psychology Review. 2006;35:245–259. [Google Scholar]
- Sutton AJ, Higgins JP. Recent developments in meta-analysis. Statistics in Medicine. 2008;27(5):625–650. doi: 10.1002/sim.2934. [DOI] [PubMed] [Google Scholar]
- Technical Assistance Center on Positive Behavioral Interventions and Supports [accessed on July 23, 2010];PBIS School Count/Homepage. 2010 http://www.pbis.org/
- U.S. Department of Education . Tech. rep. Office of Planning, Evaluation, and Policy Development, Policy and Program Studies Service; Washington, D.C.: 2009. The impacts of regular Upward Bound on postsecondary outcomes seven to nine years after scheduled high school graduation. [Google Scholar]
- U.S. Department of Health and Human Services . Tech. rep. Administration for Children and Families; Washington, D.C.: 2005. Head start impact study: First year findings. [Google Scholar]
- Wang R, Lagakos SW, Ware JH, Hunter DJ, Drazen JM. Statistics in medicine - reporting of subgroup analyses in clinical trials. The New England Journal of Medicine. 2007;357(21):2189–2194. doi: 10.1056/NEJMsr077003. [DOI] [PubMed] [Google Scholar]
- Weisberg H, Hayden V, Pontes V. Selection criteria and generalizability within the counterfactual framework: explaining the paradox of antidepressant-induced suicidality? Clinical Trials. 2009;6:109–118. doi: 10.1177/1740774509102563. [DOI] [PubMed] [Google Scholar]