Scale-Invariant Sparse PCA on High Dimensional Meta-elliptical Data

Abstract

We propose a semiparametric method for conducting scale-invariant sparse principal component analysis (PCA) on high dimensional non-Gaussian data. Compared with sparse PCA, our method has weaker modeling assumption and is more robust to possible data contamination. Theoretically, the proposed method achieves a parametric rate of convergence in estimating the parameter of interests under a flexible semiparametric distribution family; Computationally, the proposed method exploits a rank-based procedure and is as efficient as sparse PCA; Empirically, our method outperforms most competing methods on both synthetic and real-world datasets.

1 Introduction

Principal component analysis (PCA) is a powerful tool for dimension reduction and feature selection. Let ${\mathit{x}}_1,\dots ,{\mathit{x}}_n\in {ℝ}^d$ be n observations of a d-dimensional random vector X with covariance matrix Σ. PCA aims at estimating the leading eigenvectors u₁, …, u_m of Σ.

When the dimension d is small compared with the sample size n, u₁, …, u_m can be consistently estimated by the leading eigenvectors ${\widehat{\mathit{u}}}_1,\dots ,{\widehat{\mathit{u}}}_m$ of the sample covariance matrix (Anderson, 1958). However, when d increases at the same order or even faster than n, this approach can lead to poor estimates. In particular, Johnstone and Lu (2009) showed that the angle between ${\widehat{\mathit{u}}}_1$ and u₁ may not converge to 0 if d/n → c for some constant c > 0. To handle this challenge, one popular assumption is to impose sparsity constraint on the leading eigenvectors. For example, when estimating the leading eigen-vector u₁ := (u₁₁, …, u_1d)^T, we may assume that s := card({j : u_1j ≠ = 0}) < n. Under this assumption, different variants of sparse PCA have been developed, more details can be found in d’Aspremont et al. (2004), Zou et al. (2006), Shen and Huang (2008), Witten et al. (2009), Journée et al. (2010), and Zhang and El Ghaoui (2011). The theoretical properties of sparse PCA in feature selection and parameter estimation have been investigated by Amini and Wainwright (2009), Ma (2013), Paul and Johnstone (2012), Vu and Lei (2012), and Berthet and Rigollet (2012).

There are several drawbacks of the classical PCA and sparse PCA: (i) It is not scale-invariant, i.e., changing the measurement scale of variables makes the estimates different (Chatfield and Collins, 1980); (ii) It is not robust to possible data contamination or outliers (Puri and Sen, 1971); (iii) The theory of sparse PCA relies heavily on the Gaussian or sub-Gaussian assumption, which may not be realistic for many real-world applications.

In the low dimensional settings, remedies for the drawbacks (ii) and (iii) include generalizing the Gaussian distribution to elliptical distribution (Fang et al., 1990), and considering some robust estimators (Huber and Ronchetti, 2009). One research line is to develop various PCA estimators for the elliptical data (Möttönen and Oja, 1995; Choi and Marden, 1998; Marden, 1999; Visuri et al., 2000; Croux et al., 2002; Jackson and Chen, 2004). The theoretical properties of these elliptical distribution based PCA estimators have been established under the classical asymptotic framework (i.e., the dimension d is fixed) by Hallin et al. (2010), Oja (2010), and Croux and Dehon (2010). Along another research line, multiple robust PCA estimators have been proposed to address the outlier and heavy tailed issues via replacing the sample covariance matrix by a robust scatter matrix. Such robust scatter matrix estimators include M-estimator (Maronna, 1976), S-estimator (Davies, 1987), median absolute deviation (MAD) proposed by Hampel (1974), and S_n and Q_n estimators (Rousseeuw and Croux, 1993). These robust scatter matrix estimators have been exploited to conduct robust (sparse) principal component analysis (Gnanadesikan and Kettenring, 1972; Maronna and Zamar, 2002; Hubert et al., 2002; Croux and Ruiz-Gazen, 2005; Croux et al., 2013). The theoretical performances of PCA based on these robust estimators in low dimensions were further analyzed in Croux and Haesbroeck (2000).

In this article we propose a new method for conducting sparse principal component analysis on non-Gaussian data. Our method can be viewed as a scale-invariant version of sparse PCA but is applicable to a wide range of distributions belonging to the meta-elliptical family (Fang et al., 2002). The meta-elliptical family extends the elliptical family. In particular, a continuous random vector $\mathit{X}≔{(X_1,\dots ,X_d)}^T\in {ℝ}^d$ follows a meta-elliptical distribution if there exists a set of univariate strictly increasing functions $f≔{\left\{f_j\right\}}_{j=1}^d$ such that f(X) := (f₁(X₁), …, f_d(X_d))^T follows an elliptical distribution with location parameter 0 and scale parameter Σ⁰, whose diagonal values are all 1. We call Σ⁰ the latent generalized correlation matrix. By treating ${\left\{f_j\right\}}_{j=1}^d$ as nuisance parameters, our method estimates the leading eigenvector θ₁ of Σ⁰ by exploiting a rank-based estimating procedure and can be viewed as a scale-invariant PCA conducted on f(X). Theoretically we show that when s is fixed, it achieves a parametric rate of convergence in estimating the leading eigenvector. Computationally, it is as efficient as sparse PCA. Empirically, we show that the proposed method outperforms the classical sparse PCA and two robust alternatives on both synthetic and real-world datasets.

The rest of this paper is organized as follows. In the next section, we review the elliptical distribution family and introduce the meta-elliptical distribution. In Section 3, we present the statistical model, introduce the rank-based estimators, and provide computational algorithm for parameter estimation. In Section 4, we provide theoretical analysis. In Section 5, we provide empirical studies on both synthetic and real-world datasets. More discussion and comparison with related methods are put in the last section.

2 Elliptical and Meta-elliptical Distributions

In this section, we briefly review the elliptical distribution and introduce the meta-elliptical distribution family. We start by first introducing the notation: Let $\mathbf{M}=\left[{\mathbf{M}}_{jk}\right]\in {ℝ}^{d\times d}$ and $\mathit{v}={(v_1,\dots ,v_d)}^T\in {ℝ}^d$ be a d-dimensional matrix and a d-dimensional vector. We denote v_I to be the subvector of v whose entries are indexed by a set I. We also denote M_I,J to be the submatrix of M whose rows are indexed by I and columns are indexed by J. Let M_I* and M_*J be the submatrix of M with rows in I, and the submatrix of M with columns in J. Let supp(v) := {j : v_j ≠ = 0}. For 0 < q < ∞, we define the ℓ₀, ℓ_q and ℓ_∞ vector norms as ||v||₀ := card(supp(v)), ${\mid \mid \mathit{v}\mid \mid }_q≔{\left({\Sigma }_{i=1}^d{\mid v_i\mid }^q\right)}^{1∕q}$ and ${\mid \mid \mathit{v}\mid \mid }_{\infty }≔{\max }_{1\le i\le d}\mid v_i\mid$. We define the matrix ℓ_max norm as the elementwise maximum value: ||M||_max := max{|M_ij|}. Let Λ_j(M) be the j-th largest eigenvalue of M. In particular, we denote Λ_min(M) := Λ_d(M) and Λ_max(M) := Λ₁(M) to be the smallest and largest eigenvalues of M. Let ||M||₂ be the spectral norm of M. We define $\left(\mathbf{M}\right)≔{({\mathbf{M}}_{\ast 1}^T,\dots ,{\mathbf{M}}_{\ast d}^T)}^T$ and ${𝕊}^{d-1}≔\{\mathit{v}\in {ℝ}^d:{\mid \mid \mathit{v}\mid \mid }_2=1\}$ be the d-dimensional unit sphere. For any two vectors $\mathit{a},\mathit{b}\in {ℝ}^d$ and any two squared matrices $\mathbf{A},\mathbf{B}\in {ℝ}^{d\times d}$, we denote the inner product of a and b, A and B by 〈a, b〉 := a^Tb and 〈A, B〉:= Tr(A^TB). For any matrix $\mathbf{M}\in {ℝ}^{d\times d}$, we denote diag(M) to be the diagonal matrix with the same diagonal entries as M. For any univariate function f, we denote f(M) = [f(M_jk)] to be a d × d matrix with f applied on each entry of M. Let I_d be the identity matrix in ${ℝ}^{d\times d}$. For two random vectors X and Y, we denote $\mathit{X}\stackrel{d}{=}\mathit{Y}$ if they are identically distributed.

2.1 Elliptical Distribution

We briefly overview the elliptical distribution. In the sequel, we say a random vector X = (X₁, …, X_d)^T is continuous if the marginal distribution are all continuous. X possesses density if it is absolutely continuous with respect to the Lebesgue measure.

Definition 2.1 (Elliptical distribution). A random vector Z = (Z₁, …, Z_d)^T follows an elliptical distribution if and only if Z has a stochastic representation: $\mathit{Z}\stackrel{d}{=}\mu +\xi \mathbf{A}\mathit{U}$. Here $\mu \in {ℝ}^d$, q := rank(A), $\mathbf{A}\in {ℝ}^{d\times q}$, ξ ≥ 0 is a random variable independent of U, $\mathit{U}\in {𝕊}^{q-1}$ is uniformly distributed on the unit sphere in ${ℝ}^q$. Letting Σ := AA^T, we denote Z ~ EC_d(μ, Σ, ξ). We call Σ the scatter matrix.

In Definition 2.1, there can be multiple A’s corresponding to the same Σ, i.e., there exist ${\mathbf{A}}_1\ne {\mathbf{A}}_2\in {ℝ}^{d\times q}$ such that ${\mathbf{A}}_1{\mathbf{A}}_1^T={\mathbf{A}}_2{\mathbf{A}}_2^T=\Sigma$. To make the representation unique, we always parameterize an elliptical distribution by the scatter matrix Σ instead of A.

The model family in Definition 2.1 is not identifiable. For example, Σ is unique only up to a constant scaling, i.e., for some constant c > 0, if we define ξ* = ξ/c and A* = cA, then $\xi \mathbf{A}\mathit{U}\stackrel{d}{=}{\xi }^{\ast }{\mathbf{A}}^{\ast }\mathit{U}$. To make the model identifiable, we require the condition that max_1≤i≤dΣ_ii=1. We define Σ⁰ := diag(Σ)^−1/2 · Σ · diag(Σ)^−1/2 to be the generalized correlation matrix.

2.2 Meta-elliptical Distribution

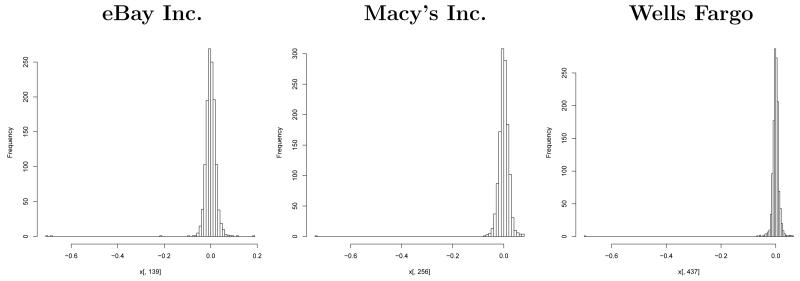
Real world data are usually nonGaussian and asymmetric. To illustrate the nonGaussianity and asymmetry issues, we consider the stock log return data in S&P 500 index, collected from Yahoo! Finance (finance.yahoo.com) from January 1, 2003 to January 1, 2008, including 452 stocks and 1,257 data points. Table 1 illustrates the nonGaussianity issue of the stock log-return data. Here we conduct the three marginal normality tests as in Table 1 at the significant level of 0.05. It is clear that at most 24 out of 452 stocks would pass any of three normality test. Even with Bonferroni correction there are still over half stocks that fail to pass any normality tests. Figure 1 plots the histograms of three typical stocks, “eBay Inc.”, “Macy’s Inc.”, and “Wells Fargo”, in the sectors of information technology, consumer discretionary, and financials separately. We see that the log-return values are skewed to the left.

Table 1.

Normality test of the stock log-return data. This table illustrates the number of 452 stocks rejecting the null hypothesis of normality at the significance level 0.05.

Significance level	Kolmogorov-Smirnov	Shapiro-Wilk	Lilliefors
0.05	428	449	449
0.05/452	269	448	426

Figure 1.

Illustration of the asymmetry issue of the log-return stock data.

Though the elliptical distribution family has been widely used to model heavy-tail data (Oja, 2010), it assumes that the distribution contours to exhibit ellipsoidal structure. To relax this assumption, Fang et al. (2002) introduced the concept of meta-elliptical distribution under a copula framework. In this section we introduce the concept of meta-elliptical using a different approach, which extends the family defined in Fang et al. (2002).

First, we define two sets of symmetric matrices:

$$\begin{array}{cc}\hfill {\mathcal{R}}_d^{+}& =\{\Sigma \in {ℝ}^{d\times d}:{\Sigma }^T=\Sigma ,\mathrm{diag}(\Sigma )={\mathbf{I}}_d,\Sigma \succ 0\},\hfill \\ \hfill {\mathcal{R}}_d& =\{\Sigma \in {ℝ}^{d\times d}:{\Sigma }^T=\Sigma ,\mathrm{diag}(\Sigma )={\mathbf{I}}_d,\Sigma \underset{¯}{\succ }0\}.\hfill \end{array}$$

The meta-elliptical distribution family is defined as follows:

Definition 2.2 (Meta-elliptical distribution). A continuous random vector X = (X₁, …, X_d)^T follows a meta-elliptical distribution, denoted by X ~ ME_d(Σ⁰, ξ; f₁, …, f_d), if there exist univariate strictly increasing functions f₁, …, f_d such that

$${\left(f_1\right(X_1),\dots ,f_d(X_d\left)\right)}^T\sim E{C}_d(0,{\Sigma }^0,\xi ),\text{where}{\Sigma }^0\in {\mathcal{R}}_d.$$ (2.1)

Here, Σ⁰ is called the latent generalized correlation matrix. When

$${\left(f_1\right(X_1),\dots ,f_d(X_d\left)\right)}^T\sim N_d(0,{\Sigma }^0),$$

we say that X follows a nonparanormal distribution, denoted by X ~ NPN_d(Σ⁰; f₁, …, f_d).

The meta-elliptical is a strict extension to the nonparanormal defined in Liu et al. (2012). They both assume that after unspecified marginal transformations the data follow certain distributions. However, the nonparanormal exploits a Gaussian base distribution while the meta-elliptical exploits an elliptical base distribution.

On the other hand, we would like to point out that Definition 2.2 extends the family originally defined in Fang et al. (2002) in three aspects: (i) The generating variable ξ does not have to be absolutely continuous; (ii) The parameter Σ⁰ is strictly enlarged from ${\mathcal{R}}_d^{+}$ to ${\mathcal{R}}_d$; (iii) X does not necessarily possess density. Moreover, even if these two definitions are the same confined in the distribution set with density existing, we define the meta-elliptical in fundamentally different ways by characterizing the transformation functions instead of characterizing the density functions. By exploiting this new definition, we find that several results provided in the later sections can be easier to understand.

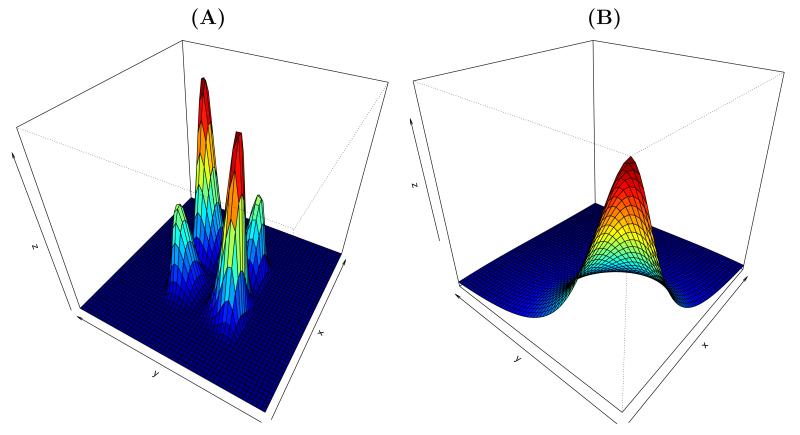
The meta-elliptical family is rich and contains many useful distributions, including multivariate Gaussian, rank-deficient Gaussian, multivariate t, logistic, Kotz, symmetric Pearson type-II and type-VII, the nonparanormal, and various other asymmetric distributions such as multivariate asymmetric t distribution (Fang et al., 2002). To illustrate the modeling flexibility of the meta-elliptical family, Figure 2 visualizes the density functions of two meta-elliptical distributions.

Figure 2.

Densities of two 2-dimensional meta-elliptical distributions. (A) The component functions have the form f₁(x) = sign(x)|x|² and f₂(x) = x³, and after transformation follows a Gaussian distribution. (B) The component functions have the form f₁(x) = f₂(x) = log(x), and after transformation follows a Cauchy distribution. In both cases the latent generalized correlation matrix has all off-diagonal values to be 0.5.

3 Methodology

We propose a new scale-invariant sparse PCA method based on the meta-elliptical distribution family. More specifically, under a meta-elliptical model X ~ ME_d(Σ⁰, ξ; f₁, …, f_d), the proposed method aims at estimating the leading eigenvector of Σ⁰. Since the diagonal entries of Σ⁰ are all 1, the proposed method is scale-invariant. From Definition 2.2, the proposed method is equivalent to conducting scale-invariant sparse PCA on the transformed data (f₁(X₁), …, f_d(X_d))^T which follow an elliptical distribution.

3.1 Statistical Model

The statistical model of our proposed method is defined as follows:

Definition 3.1. We consider the following model, denoted by ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$, which is defined to be the set of distributions:

$${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)≔\{\mathit{X}:\mathit{X}\sim M{E}_d({\Sigma }^0,\xi ;f_1,\dots ,f_d)suchthat{\theta }_1,theleadingeigenvectorof{\Sigma }^0,satisfies{\mid \mid {\theta }_1\mid \mid }_0=s.\}.$$ (3.1)

This model allows asymmetric and heavy tail distributions with nontrivial tail dependency. It can be used as a powerful tool for modeling real-world data.

3.2 Method

We now provide the proposed method that exploits the model (3.1). One of the key components of the proposed rank based method is the Kendall’s tau correlation matrix estimator, which will be explained in the next section.

3.2.1 Kendall’s tau based Correlation Matrix Estimator

The Kendall’s tau statistic was introduced by Kendall (1948) for estimating pairwise correlation and has been used for principal component analysis in low dimensions (Croux et al., 2002; Gibbons and Chakraborti, 2003). More specifically, let X := (X₁, …, X_d)^T be a d-dimensional random vector and let $\tilde{\mathit{X}}≔{({\tilde{X}}_1,\dots ,{\tilde{X}}_d)}^T$ be an independent copy of X. The Kendall’s tau correlation coefficient between X_j and X_k is defined as

$$\tau (X_j,X_k)≔\mathbb{P}\left(\right(X_j-{\tilde{X}}_j\left)\right(X_k-{\tilde{X}}_k)>0)-\mathbb{P}\left(\right(X_j-{\tilde{X}}_j\left)\right(X_k-{\tilde{X}}_k)<0).$$

The next proposition shows that for meta-elliptical distribution family, we have a one-to-one map between ${\Sigma }_{jk}^0$ and τ(X_j, X_k).

Theorem 3.2. Given X ~ ME_d (Σ⁰, ξ; f₁, …, f_d) meta-elliptically distributed, we have

$${\Sigma }_{jk}^0=\sin \left(\frac{\pi }{2}\tau (X_j,X_k)\right).$$ (3.2)

Proof. It is obvious that the Kendall’s tau statistic is invariant under strictly increasing transformations to the marginal variables. Moreover, Lindskog et al. (2003) show that the Kendall’s tau statistic is invariant to different generating variables ξ’s. Combining these two results and Equation (6.6) of Kruskal (1958), we obtain the desired result.

Let ${\mathit{x}}_1,\dots ,{\mathit{x}}_n\in {ℝ}^d$ with x := (x_i1, …, x_id)^T be n data points of X. The sample version Kendall’s tau statistic is defined as:

$${\widehat{\tau }}_{jk}≔\frac{2}{n(n-1)}\sum _{1\le i<i^{\prime }\le n}\mathrm{sign}(x_{ij}-x_{i^{\prime }j})\mathrm{sign}(x_{ik}-x_{i^{\prime }k}).$$

It is easy to see that ${\widehat{\tau }}_{jk}$ is an unbiased estimator of τ(X_j, X_k). Using ${\widehat{\tau }}_{jk}$, we define the Kendall’s tau correlation matrix as follows:

Definition 3.3 (Kendall’s tau correlation matrix). We define the Kendall’s tau correlation matrix $\widehat{\mathbf{R}}=\left[{\widehat{\mathbf{R}}}_{jk}\right]$ to be a d by d matrix with element entry to be

$${\widehat{\mathbf{R}}}_{jk}=\sin \left(\frac{\pi }{2}{\widehat{\tau }}_{jk}\right).$$ (3.3)

3.2.2 Rank-based Estimators

Given the model ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$, Theorem 3.2 provides a natural way to estimate θ₁. In particular, we solve the following optimization problem:

$${\widehat{\theta }}_{1,k}^{\ast }≔\underset{v\in {ℝ}^d}{\arg \max }{\mathit{v}}^T\widehat{\mathbf{R}}\mathit{v},\text{subject to}\mathit{v}\in {𝕊}^{d-1}\cap {𝔹}_0\left(k\right),$$ (3.4)

where ${𝔹}_0\left(k\right)≔\{\mathit{v}\in {ℝ}^d:{\mid \mid \mathit{v}\mid \mid }_0\le k\}$, k is a sufficiently large tuning parameter, and $\widehat{\mathbf{R}}$ is the Kendall’s tau correlation matrix. Equation (3.4) is a combinatorial optimization problem and hard to compute. The corresponding global optimum is denoted by ${\widehat{\theta }}_{1,k}^{\ast }$.

Because the estimator ${\widehat{\theta }}_{1,k}^{\ast }$ is very hard to compute, we consider an alternative way to estimate θ₁ using the truncated power algorithm proposed by Yuan and Zhang (2013). This algorithm yields an estimator ${\tilde{\theta }}_{1,k}$.. Here $k≔{\mid \mid {\tilde{\theta }}_{1,k}\mid \mid }_0$ is a hypothesized value for s (the number of nonzero elements of θ₁) and can be treated as a tuning parameter.

More specifically, we apply the classical power method, but within each iteration t we project the intermediate vector x_t to the intersection of the d-dimension sphere ${𝕊}^{d-1}$ and the ℓ₀ ball with radius k > 0. In detail, we sort the absolute values of the elements of x_t from the highest to the lowest, find the highest k absolute values, truncate all the others to zero, and then normalize the truncated vector such that it lies in ${𝕊}^{d-1}\cap {𝔹}_0\left(k\right)$. To provide the detailed algorithm, we first introduce some additional notation. For any vector $\mathit{v}\in {ℝ}^d$ and an index set J ˄ {1, …, d}, we define the truncation function TRC(·,·) to be

$$\mathrm{TRC}(\mathit{v},J)≔{(v_1\cdot I(1\in J),\dots ,v_d\cdot I(d\in J\left)\right)}^T,$$ (3.5)

where I(·) is the indicator function. The truncated power algorithm is presented in Algorithm 1.

The formulation of the truncated power algorithm is nonconvex and the performance of the estimator relies on the selection of the initial vector v⁽⁰⁾. In practice, we use the estimate obtained from the SPCA algorithm (Zou et al., 2006) as the initial vector. We set the termination criteria to be ||v^(t)−v^(t−1)||₂≤ 10⁻⁴.

In Section 4, we show that, by appropriately setting the initial vector v⁽⁰⁾, the algorithm converges and the corresponding estimator ${\tilde{\theta }}_{1,k}$ is a consistent estimator of θ₁. In practice, we find that this algorithm always converges on all the synthetic and real-world data.

Algorithm 1.

Truncated Power Method

3.3 Estimating the Top m Leading Eigenvectors

We exploit the iterative deflation method to estimate the top m leading eigenvectors θ₁, …, θ_m of Σ⁰. This method is proposed by Mackey (2009) and its empirical performance is further evaluated in Yuan and Zhang (2013). In detail, for any positive semidefinite matrix $\Gamma \in {ℝ}^{d\times d}$, its deflation with respect to the vector $\mathit{v}\in {ℝ}^d$ is defined as:

$$\mathbf{D}(\Gamma ,\mathit{v})≔({\mathbf{I}}_d-{\mathit{vv}}^T)\Gamma ({\mathbf{I}}_d-{\mathit{vv}}^T).$$

In this way, D(Γ, v) is positive semidefinite, left and right orthogonal to v, and symmetric. To estimate θ₁, …, θ_m, we exploit the following approach: (i) The estimate ${\widehat{\theta }}_1$ (can be either ${\widehat{\theta }}_{1,k}^{\ast }$ or ${\tilde{\theta }}_{1,k}$) of θ₁ is calculated using Equation (3.4) or the truncated power method; (ii) Given ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_j$, we estimate ${\widehat{\theta }}_{j+1}$ by plugging ${\Gamma }^{(j+1)}≔\mathbf{D}({\Gamma }^{\left(j\right)},{\widehat{\theta }}_j)$ into Equation (3.4) or the truncated power method (Γ⁽¹⁾ := Σ⁰).

4 Theoretical Properties

In this section we provide the theoretical properties of the estimators ${\widehat{\theta }}_{1,k}^{\ast }$ and ${\tilde{\theta }}_{1,k}$. In the analysis, we adopt the double asymptotic framework in which the dimension d increases with the sample size n. This framework more realistically reflects the challenges of many high dimensional applications (Bühlmann and van de Geer, 2011).

4.1 Latent Generalized Correlation Matrix Estimation

In this section we focus on estimating the latent generalized correlation matrix Σ⁰. In the next theorem we prove the rate of convergence $O_P\left(\sqrt{\log d∕n}\right)$ for $\mid {\widehat{\mathbf{R}}}_{jk}-{\Sigma }_{jk}^0\mid$ uniformly over all indices j, k. This is an important result, which indicates that the Gaussian parametric rate in estimating the correlation matrix obtained by Bickel and Levina (2008) can be extended to the meta-elliptical distribution family using the Kendall’s tau statistic.

Theorem 4.1. Let x₁, …, x_n be n observations of X ~ ME_d(Σ⁰,ξ; f₁, …, f_d) and let $\widehat{\mathbf{R}}$ be defined as in Equation (3.3). We have, with probability at least 1 − d^−5/2,

$${\mid \mid \widehat{\mathbf{R}}-{\Sigma }^0\mid \mid }_{\max }\le 3\pi \sqrt{\frac{\log d}{n}}.$$ (4.1)

Proof. The result follows from Theorem 4.2 in Liu et al. (2012) but with a slightly different probability bound. A detailed proof is provided in Appendix A.2 for self-completeness.

4.2 Leading Eigenvector Estimation

We analyze the estimation errors of the global optimum ${\widehat{\theta }}_{1,k}^{\ast }$ and the estimator ${\tilde{\theta }}_{1,k}$ obtained from the truncated algorithm. We say that the model ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$ holds if the data are drawn from one probability distribution in ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$. The next theorem provides an upper bound on the angle between ${\widehat{\theta }}_{1,k}^{\ast }$ and θ₁.

Theorem 4.2. Let ${\widehat{\theta }}_{1,k}^{\ast }$ be the global optimum to Equation (3.4), the model ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$ hold, and k ≥ s. For any two vectors ${\mathit{v}}_1\in {𝕊}^{d-1}$ and ${\mathit{v}}_2\in {𝕊}^{d-1}$, let $\mid \sin \angle ({\mathit{v}}_1,{\mathit{v}}_2)\mid ≔\sqrt{1-{\left({\mathit{v}}_1^T{\mathit{v}}_2\right)}^2}$. Then we have, with probability at least 1 − d^−5/2,

$$\mid \sin \angle ({\widehat{\theta }}_{1,k}^{\ast },{\theta }_1)\mid \le \frac{6\pi }{{\lambda }_1-{\lambda }_2}\cdot k\sqrt{\frac{\log d}{n}},$$ (4.2)

when λ_j := Λ_j(Σ⁰) for j = 1,2.

Proof. The key idea of the proof is to exploit the results in Theorem 4.1 in bounding the estimation error. Detailed proofs are presented in Appendix A.3.

Remark 4.3. When s, λ₁, λ₂ do not scale with (n, d) and k ≥ s is a fixed constant, the rate of convergence in parameter estimation is $O_P\left(\sqrt{\log d∕n}\right)$, which is the minimax optimal parametric rate shown in Vu and Lei (2012) under certain model class.

In the next corollary, we provide a feature selection result for the proposed method. Given that the selected tuning parameter k is large enough, we show that the support set of θ₁ can be consistently recovered in a fast rate by imposing a constraint on the minimum absolute value of the signal part of θ₁.

Corollary 4.4 (Feature selection). Let ${\widehat{\theta }}_{1,k}^{\ast }$ be the global optimum to Equation (3.4), the model ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$ hold, and k ≥ s. Let Τ:= supp(θ₁), and ${\widehat{ϴ}}_k^{\ast }≔supp\left({\widehat{\theta }}_{1,k}^{\ast }\right)$. If we further have $mi{n}_{j\in ϴ}\mid {\theta }_{1j}\mid \ge \frac{6\sqrt{2\pi }}{{\lambda }_1-{\lambda }_2}\cdot k\sqrt{\frac{\log d}{n}}$, then $\mathbb{P}(ϴ\subset {\widehat{ϴ}}_k^{\ast })\ge 1-d^{-5∕2}$.

Proof. The key of the proof is to construct a contradiction given Theorem 4.2 and the condition on the minimum value of ${\{\mid {\theta }_{1j}\mid \}}_{j=1}^d$. Detailed proof is shown in Appendix A.4

In the next theorem, we provide a result on the convergence rate of the estimator ${\tilde{\theta }}_{1,k}$ obtained by exploiting the truncated power algorithm. This theorem, coming from Yuan and Zhang (2013), indicates that under sufficient conditions ${\tilde{\theta }}_{1,k}$ converges to θ₁ in a $s\sqrt{\log d∕n}$ rate.

Theorem 4.5. If the model ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$ holds, the conditions in Theorem 1 in Yuan and Zhang (2013) hold, and k ≥ s, we have, with probability at least 1 − d^−5/2,

$$\mid \sin \angle ({\tilde{\theta }}_{1,k},{\theta }_1)\mid \le C\cdot (s+2k)\sqrt{\frac{\log d}{n}},$$

for some generic constant C not scaling with (n; d; s).

The result in Theorem 4.5 is a direct consequence of Theorem 1 in Yuan and Zhang (2013) and therefore the proof is omitted. Here we note that, similar as Corollary 4.4, it can be shown that under certain conditions, $\mathrm{supp}\left({\theta }_1\right)\subset \mathrm{supp}\left({\tilde{\theta }}_{1,k}\right)$ with high probability.

4.3 Principal Component Estimation

In this section, we consider estimating the latent principal components of the meta-elliptically distributed data. To estimate the latent principal components instead of the eigenvectors of the latent generalized correlation matrix, one needs to obtain good estimates of the unknown transformation functions f₁, …, f_d.

Let X ~ ME_d(Σ⁰, ξ; f₁, …, f_d) follow a meta-elliptical distribution and x₁, …, x_n be n observations of X with x_i := (x_i1, …, x_id)^T. Let Z := (f₁(X₁), …, f_d(X_d))^T be the transformed random vector. By definition, Z ~ EC_d(0, Σ⁰, ξ) is elliptically distributed. Let Q_g be the marginal distribution function of Z (From Proposition A.2, we know all the elements of Z share the same marginal distribution functions). If Q_g is known, we can estimate f₁, …, f_d as follows. For j = 1, …, d, let ${\widehat{F}}_j(t;{\delta }_n)$ be defined as

$${\widehat{F}}_j(t;{\delta }_n)≔\{\begin{array}{cc}{\delta }_n,\hfill & \text{if}t<{\delta }_n\hfill \\ \frac{1}{n}{\Sigma }_{i=1}^{n}I(x_{ij}\le t),\hfill & \text{if}{\delta }_n\le t\le 1-{\delta }_n\hfill \\ 1-{\delta }_n,\hfill & \text{if}x>1-{\delta }_n\hfill \end{array}\phantom{\}}.$$

We define

$${\widehat{f}}_j(t;{\delta }_n)≔Q_g^{-1}\left({\widehat{F}}_j\right(t;{\delta }_n\left)\right)$$ (4.3)

to be an estimator of f_j. When Q_g(·) = Φ(·), where Φ(·) is the distribution function of the standard Gaussian, we have the following theorem, showing that ${\widehat{f}}_j(\cdot ;{\delta }_n)$ converges to f_j(·) uniformly over an expanding interval with high probability.

Theorem 4.6 (Han et al. (2013)). Suppose that X ~ NPN_d(Σ⁰; f₁, …, f_d) and for j = 1, …, d, let $g_j≔f_j^{-1}$ be the inverse function of f_j. For any 0 < γ 1, we define

$$I_n≔\left[g_j\left(-\sqrt{2(1-\gamma )\log n}\right),g_j\left(\sqrt{2(1-\gamma )\log n}\right)\right],$$

then $\underset{t\in I_n}{\sup }\mid {\widehat{f}}_j(t;{\left(2n\right)}^{-1})-f_j\left(t\right)\mid =O_P\left(\sqrt{\frac{\log \log n}{n^{\gamma }}}\right)$. Here ${\widehat{f}}_j(t;{\delta }_n)≔{\Phi }^{-1}\left({\widehat{F}}_j\right(t;{\delta }_n\left)\right)$.

Using Theorem 4.6, we have the following theorem, which shows that, under appropriate conditions, we can recover the first principal component of any data point x.

Theorem 4.7. For any observation x := (x₁, …, x_d)^T of X ~ NPN_d(Σ; f₁, …, f_d), under the conditions of Theorem 4.2, letting

$$\widehat{f}\left(\mathit{x}\right)≔{\left({\widehat{f}}_1(x_1;{\left(2n\right)}^{-1}),\dots ,{\widehat{f}}_d(x_d;{\left(2n\right)}^{-1})\right)}^T\text{and}f\left(\mathit{x}\right)≔{\left(f_1\right(x_1),\dots ,f_d(x_d\left)\right)}^T,$$

and b be any positive constant such that (s + k)n^−b/2 = o(1),we have

$$\mid \widehat{f}{\left(\mathit{x}\right)}^T{\widehat{\theta }}_{1,k}^{\ast }-f{\left(\mathit{x}\right)}^T{\theta }_1^{\ast }\mid =O_P\left(\sqrt{(s+k)\cdot \frac{\log \log n}{n^{1-b∕2}}}+\frac{k}{\lambda 1-{\lambda }_2}\sqrt{\frac{(s+k)\log d\log n}{n}}\right),$$

where ${\theta }_1^{\ast }≔sign\left({\theta }_1^T{\widehat{\theta }}_{1,k}^{\ast }\right)\cdot {\theta }_1$.

Proof. Theorem 4.7 is proved by combining the results in Theorems 4.2 and 4.6. More details are presented in Appendix A.5.

5 Experiments

In this section we evaluate the empirical performance of the proposed method on both synthetic and real-world datasets and compare its performance with the classical sparse PCA and two additional robust sparse PCA procedures. We use the truncated power method proposed by Yuan and Zhang (2013) for parameter estimation. The following four methods are considered:

• Pearson: the classical high dimensional scale-invariant PCA using the Pearson’s sample correlation matrix as the input;

• S_n: The sparse PCA using the robust S_n correlation matrix estimator (Rousseeuw and Croux, 1993; Maronna and Zamar, 2002) as the input;

• Q_n: The sparse PCA using the robust Q_n correlation matrix estimator (Rousseeuw and Croux, 1993; Maronna and Zamar, 2002) as the input;

• Kendall: The proposed method using the Kendall’s tau correlation matrix as the input.

Here the robust Q_n and S_n correlation matrix estimates are calculated by the R package robustbase (Rousseeuw et al., 2009). We also tried the sparse robust PCA procedure proposed in Croux, Filzmoser, and Fritz. (2013), implemented in the R package pcaPP. However, we found that the grid algorithm, which is used in their paper to estimate sparse eigenvectors, has convergence problem when the dimension is high, which makes the obtained estimator perform very bad. Therefore, we did not include this procedure in the draft for comparison.

5.1 Numerical Simulations

In the simulation study we sample n data points from a given meta-elliptical distribution. Here we set d = 100. We first construct Σ⁰ using a similar idea as in Yuan and Zhang (2013): First a covariance matrix is synthesized through the eigenvalue decomposition, where the first two eigenvalues are given and the corresponding eigenvectors are pre-specified to be sparse. More specifically, let

$$\Sigma ≔\sum _{j=1}^2({\omega }_j-1){\mu }_j{\mu }_j^T+{\mathbf{I}}_d,\text{where}{\omega }_1=6,{\omega }_2=3.$$

We set u₁ and u₂ as follows:

$$u_{1j}=\{\begin{array}{cc}\frac{1}{\sqrt{10}}\hfill & 1\le j\le 10\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\text{and}{u}_{2j}=\{\begin{array}{cc}\frac{1}{\sqrt{10}}\hfill & 11\le j\le 20\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$

The latent generalized correlation matrix Σ⁰ is Σ⁰ = diagΣ()^−1/2 · Σ · diag(Σ)^−1/2. We then consider six different schemes to generate the data matrix $\mathbf{X}≔{({\mathit{x}}_1,\dots ,{\mathit{x}}_n)}^T\in {ℝ}^{n\times d}$:

Scheme 1: Let x₁, …, x_n be n observations of X ~ N_d(0, Σ⁰).

Scheme 2: Let x₁, …, x_n be n observations of X ~ N_d(0, Σ⁰), but with 5% entries in each x_i randomly picked up and replaced by −5 or 5.

Scheme 3: Let x₁, …, x_n be n observations of X ~ NPN_d(Σ⁰; f₁, …, f₁) with f₁(x) = x³.

Scheme 4: Let x₁, …, x_n be n observations of X ~ ME_d(Σ⁰, ξ₁; f₀, …, f₀) with f₀(x) = x and ${\xi }_1\stackrel{d}{=}\sqrt{\kappa }{\xi }_1^{\ast }∕{\xi }_2^{\ast }$. Here ${\xi }_1^{\ast }\stackrel{d}{=}{\chi }_d$ and ${\xi }_2^{\ast }\stackrel{d}{=}{\chi }_{\kappa }$ with $\kappa \in {\mathbb{Z}}^{+}$. In this setting, X follows a multivariate t distribution with degree of freedom κ (Fang et al., 1990). Here we set κ = 3.

Scheme 5: Let x₁, …, x_n be n observations of X ~ ME_d(Σ⁰, ξ₂; f₀, …, f₀) with ξ₂ ~ F (d, 1), i.e., ξ₂ follows an F-distribution with degree of freedom d and 1.

Scheme 6: Let x₁, …, x_n be n observations of X ~ ME_d(Σ⁰, ξ₃; f₀, …, f₀) with ξ₃ follows an exponential distribution with the rate parameter 1.

Here Schemes 1 to 3 represent three different versions of the Gaussian data: (i) The perfect Gaussian data; (ii) The Gaussian data contaminated by outliers; (iii) The Gaussian data contaminated by marginal transformations. Schemes 4-6 represent three different elliptical distributions, which are all heavy-tailed and belong to the meta-elliptical family.

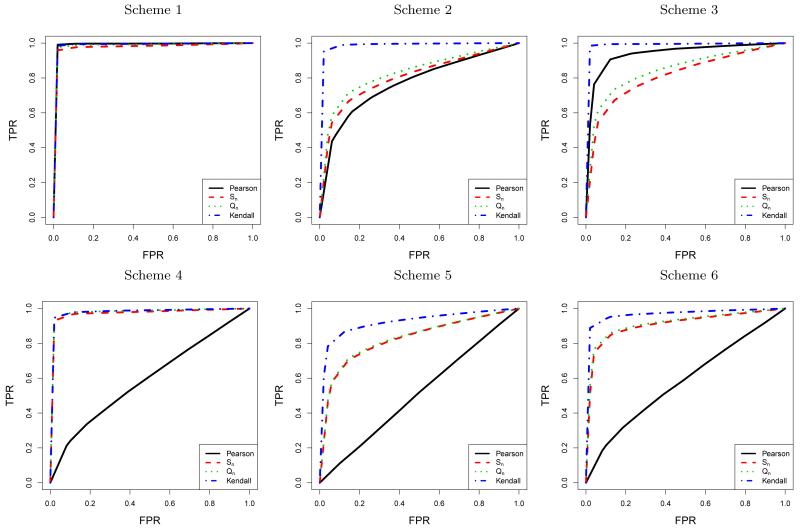
For n = 50, 100, 200, we repeatedly generate the data matrix X according to Schemes 1 to 6 for 1,000 times. To show the feature selection results for estimating the support set of the leading eigenvector θ₁, Figure 3 plots the false positive rates against the true positive rates for the four different estimators under different schemes.

Figure 3.

ROC curves under Scheme 1 to Scheme 6. Here n = 100 and d = 100.

To illustrate the parameter estimation performance, we conduct a quantitative comparison of the estimation accuracy of the four competing method. For all methods, we fix the tuning parameter (i.e., the cardinality of the estimate’s support set) to be 10. Table 2 shows the averaged distances between the estimated leading eigenvector and θ₁, with standard deviations presented in the parentheses. Here the distance between two vectors ${\mathit{v}}_1,{\mathit{v}}_2\in {𝕊}^{d-1}$ is defined as $\mid \sin \angle ({\mathit{v}}_1,{\mathit{v}}_2)\mid$.

Table 2.

Quantitative comparison on the datasets under the six generating schemes. The averaged distances with standard deviations in parentheses are presented. Here n is changing from 50 to 200 and d is fixed to be 100.

Scheme	n	Pearson	Sn	Qn	Kendall
Scheme 1	50	0.422(0.555)	0.607(0.473)	0.555(0.259)	0.473(0.266)
	100	0.121(0.158)	0.188(0.140)	0.158(0.110)	0.140(0.201)
	200	0.068(0.071)	0.072(0.072)	0.071(0.018)	0.072(0.024)
Scheme 2	50	0.911(0.878)	0.882(0.631)	0.878(0.105)	0.631(0.131)
	100	0.806(0.715)	0.737(0.264)	0.715(0.169)	0.264(0.213)
	200	0.484(0.354)	0.381(0.093)	0.354(0.222)	0.093(0.246)
Scheme 3	50	0.822(0.907)	0.921(0.473)	0.907(0.154)	0.473(0.101)
	100	0.562(0.700)	0.737(0.140)	0.700(0.214)	0.140(0.202)
	200	0.228(0.356)	0.410(0.072)	0.356(0.156)	0.072(0.255)
Scheme 4	50	0.947(0.679)	0.704(0.678)	0.679(0.095)	0.668(0.227)
	100	0.910(0.247)	0.269(0.248)	0.247(0.157)	0.238(0.239)
	200	0.873(0.079)	0.084(0.084)	0.079(0.232)	0.074(0.063)
Scheme 5	50	0.977(0.911)	0.910(0.854)	0.911(0.028)	0.854(0.102)
	100	0.976(0.718)	0.722(0.532)	0.718(0.028)	0.532(0.214)
	200	0.978(0.297)	0.305(0.147)	0.297(0.029)	0.147(0.244)
Scheme 6	50	0.959(0.848)	0.862(0.771)	0.848(0.060)	0.771(0.143)
	100	0.931(0.548)	0.569(0.373)	0.548(0.108)	0.373(0.250)
	200	0.840(0.156)	0.165(0.103)	0.156(0.223)	0.103(0.170)

Both Figure 3 and Table 2 show that when the data are non-Gaussian but follow a meta-elliptical distribution, Kendall constantly outperforms Pearson in terms of feature selection and parameter estimation. Moreover, when the data are indeed Gaussian distributed, there is no obvious difference between Kendall and Pearson, indicating that our proposed rank-based method is a good alternative to the classical scale-invariant sparse PCA under the meta-elliptical model.

We then compare Kendall with S_n and Q_n. In Scheme 1, for the Gaussian data, Kendall slightly outperforms S_n and Q_n. For the data with outliers, S_n and Q_n performs better than the classical sparse PCA estimates, but are not as robust as Kendall. For different elliptical distributions explored in Schemes 4 to 6, Kendall has the best overall performance compared to S_n and Q_n. The results for the non-elliptically distributed data, as explored in Scheme 3, shows a significant difference between our proposed method and the other two robust sparse PCA approaches. In this case we are interested in, instead of the correlation matrix of the meta-elliptically distributed data, the latent generalized correlation matrix, which S_n and Q_n fail to recover.

5.2 Equity Data Analysis

In this section we investigate the performance of the four competing methods on the equity data explored in Section 2.2. The data come from Yahoo! Finance (finance.yahoo.com). We collect the daily closing prices for J = 452 stocks that are consistently in the S&P 500 index from January 1, 2003 to January 1, 2008. This gives us altogether T = 1, 257 data points, each data point corresponds to the vector of closing prices on a trading day. Let St = [St_t,j] denote the closing price of stock j on day t. We are interested in the log-return data X = [X_tj] with X_tj := log(St_t,j/St_t−1,j).

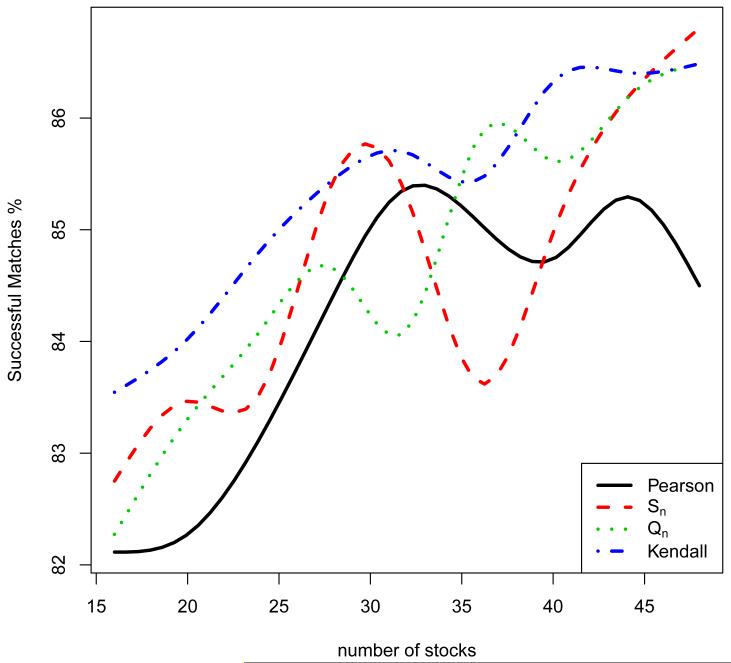
We evaluate the ability of using only a small number of stocks to represent the trend of the whole stock market. To this end, we run the four competing methods on the log-return data X and obtain the top four leading eigenvectors. Here the iterative deflation method discussed in Section 3.3 is exploited with the same tuning parameter k in each deflation step. Let A_k be the support set of the estimated leading eigenvectors by one of the four methods. We define $T_t^W$ and $T_t^{A_k}$ as

$$T_t^W≔I\left(\sum _{j}S{t}_{t,j}-\sum _{j}S{t}_{t-1,j}>0\right),T_t^{A_k}≔I\left(\sum _{j\in A_k}S{t}_{t,j}-\sum _{j\in A_k}S{t}_{t-1,j}>0\right),$$

where I(·) is the indicator function. In this way, we can calculate the proportion of successful matches of the market trend using the stocks in A_k as:

$${\rho }_{A_k}≔\frac{1}{T-1}\sum _{t=2}^{T}I(T_t^W=T_t^{A_k}).$$

We visualize the result by plotting (card(A_k), ρ_Ak) in Figure 4, which shows that Kendall summarizes the trend of the whole stock market better than the other three methods.

Figure 4.

Successful matches of the market trend proportions only using the stocks in the support sets of the estimated loading vectors. The horizontal-axis represents the cardinalities of the estimates’ support sets; the vertical-axis represents the percentage of successful matches.

Moreover, we examine the stocks selected by the four competing methods. The 452 stocks are categorized into 10 Global Industry Classification Standard (GICS) sectors, including Consumer Discretionary (70 stocks), Consumer Staples (35 stocks), Energy (37 stocks), Financials (74 stocks), Health Care (46 stocks), Industrials (59 stocks), Information Technology (64 stocks), Telecommunications Services (6 stocks), Materials (29 stocks), and Utilities (32 stocks). Table 3 provides a more detailed description of these ten categories with their numbers and abbreviations provided.

Table 3.

The ten categories of the stocks with their numbers and abbreviations provided.

Name	Number	Abbreviation
Consumer Discretionary	70	CD
Consumer Staples	35	CS
Energy	37	E
Financials	74	F
Health Care	46	HC
Industrial	59	I
Information Technology	64	IT
Telecommunications Services	6	TS
Materials	29	M
Utilities	32	U

We estimate the top four leading eigenvectors using the four competing methods with the same k = 30 in each deflation step. The obtained non-zero features’ categories are presented in Table 4. We see that, in general, Kendall has the best ability in grouping the stocks of the same category together. Therefore, Kendall provides a more interpretable result.

Table 4.

The categories of the nonzero terms in the top four leading eigenvectors calculated by the four competing methods. The abbreviations are listed in Table 3. (Note: 30F means 30 stocks are from the Financials category.)

Method	PC1	PC2	PC3	PC4
Pearson	29F,1I	6CD,5F,8I,1IT,10M	8F,2E,3M,17U	8CD,1F,1I,20IT
Sn	29F,1I	2CD,2F,12I,14M	3I,27IT	3F,27U
Qn	29F,1I	2CD,2F,12I,1IT,13M	2I,28IT	3F,27U
Kendall	30F	15I, 15M	10CD, 10F,10I	3I, 27IT

6 Discussion

We propose a new scale-invariant sparse principal component analysis method for high dimensional meta-elliptical data. Our estimator is semiparametric but achieves a fast rate of convergence in parameter estimation, and is robust to both modeling assumption and data contamination. Therefore, the new estimator can be a good alternative to the classical sparse PCA method.

Although the rank-based Kendall’s tau statistic has been exploited for principal component analysis in low dimensions (see, for example, Croux et al. (2002)), our work is fundamentally different from the existing literature. The main difference can be elaborated in the following three aspects: (i) We generalize the Kendall’s tau statistic to high dimensions, while the current literature only focuses on the low dimension settings; (ii) Our theoretical analysis are fundamentally different from the previous low dimensional analysis, which exploits classical semiparametric theory under which the dimension d is usually fixed; (iii) Most existing methods and theories are built upon the Gaussian or elliptical model, while we consider the meta-elliptical model.

There is another trend in exploiting robust (sparse) PCA (see, for example, Maronna and Zamar (2002) and Croux et al. (2013)). The empirical comparisons conducted in this paper indicate that, confined in the meta-elliptical family, the proposed rank-based method can be more efficient in parameter estimation and feature selection than these additional robust procedures. Moreover, our proposed method achieves the nearly parametric rate of convergence in parameter estimation, while to the best of our knowledge the performance of these robust sparse PCA procedures in high dimensions is mostly unknown.

Vu and Lei (2012) and Ma (2013) considered sparse principal component analysis and studied the rates of convergence under various modeling and sparsity assumptions. Our method is different from theirs in two aspects: (i) Their analysis relies heavily on the Gaussian or sub-Gaussian assumption, which no longer holds under the meta-elliptical model; (ii) They exploit the Pearson’s sample covariance or correlation matrix as the algorithm input, while we advocate the usage of the Kendall’s tau correlation matrix in the meta-elliptical model.

Liu et al. (2012) and Xue and Zou (2012) proposed a procedure called the nonparanormal SKEPTIC, which exploits the nonparanormal family for graph estimation. The non-paranormal SKEPTIC also adopts rank-based methods in high dimensions. Our method is different from theirs in three aspects: (i) We advocate the use of meta-elliptical family, of which the nonparanormal is a subset; (ii) We advocate the use of the Kendall’s tau, which is adaptive over the whole meta-elliptical family but instead of the Spearman’s rho statistic; (iii) Their focus is on graph estimation, in contrast, this paper focuses on principal component analysis. In a preliminary version of this work (Han and Liu, 2012), they mainly focused on estimating the first leading eigenvector of the latent generalized correlation matrix by directly solving Equation (3.4), which is practically intractable. In contrast, we exploit a computationally feasible procedure (truncated power method) for scale-invariant sparse PCA, and provide theoretical guarantee of convergence for this algorithm. Moreover, our method estimates the latent principal components, which are crucial in practical applications, and we provide the theoretical analysis of convergence for the corresponding estimators.

For the principal component estimation algorithm in Section 4.3, when Q_g is unknown, we could estimate f₁, …, f_d using the following method:

1. Test whether the original data is elliptically distributed by using some existing techniques (Li et al., 1997; Huffer and Park, 2007; Sakhanenko, 2008). If yes, we set ${\widehat{f}}_j\left(t\right)=(t-{\widehat{\mu }}_j)∕{\widehat{\sigma }}_j$. Here ${\widehat{\mu }}_j$ and ${\widehat{\sigma }}_j$ are the marginal sample mean and standard deviation for the j-th entry.

2. If not, we construct a set of marginal distribution functions:

   $$\Pi ≔\{Q_g:Q_g\text{is a well defined marginal distribution function}\}.$$

3. For any Q_g ∈ Π, we calculate $\widehat{f}=\{{\widehat{f}}_1,\dots ,{\widehat{f}}_d\}$ using Equation (4.3).

4. We transform the data using $\widehat{f}$.

5. We test whether the transformed data is elliptically distributed by using the techniques exploited in step 1.

We iterate steps 3-5 until we cannot reject the null hypothesis in step 5 for some Q_g. This is a heuristic method whose theoretical justification is left for future investigation. Other future directions include analyzing the robustness property of the method to more noisy and dependent data.

A Appendix

A.1 Properties of the Elliptical Distribution

The next proposition provides two alternative ways to characterize an elliptical distribution and their proofs can be found in Fang et al. (1990).

Proposition A.1 (Fang et al. (1990)). A random vector Z = (Z₁, …, Z_d)^T satisfies that Z ~ EC_d(μ,Σ,ξ) if and only if Z has the characteristic function exp(it′μ)φ(t′Σt), where $i:\sqrt{-1}$ and φ is a properly-defined characteristic function. We denote Z ~ EC_d(μ,Σ,φ) in this setting. If ξ is absolutely continuous and Σ is non-singular, then the density of Z exists and is of the form:

$$p_Z\left(z\right)={\mid \Sigma \mid }^{-1∕2}g\left({(z-\mu )}^T{\Sigma }^{-1}\right(z-\mu \left)\right),$$

where g : [0, ∞) → [0,∞). We denote Z ~ EC_d(μ,Σ, g). Here ξ, φ and g uniquely determine one of the other.

The next proposition provides three important properties of the elliptical distribution.

Proposition A.2. If a random vector Z is elliptically distributed, we have:

• For any $q\in \mathbb{N}$,$\mathit{v}\in {ℝ}^q$, and any matrix $\mathbf{B}\in {ℝ}^{d\times q}$, v + B^TZ is elliptically distributed. In particular, if Z ~ EC_d(μ,Σ,ξ), then v + B^TZ ~ EC_q(v + B^Tμ, B^TΣB,ξ).

• Let Z ~ EC_d(μ,Σ,ξ) and Σ⁰ be the generalized correlation matrix of Z. If rank(Σ) = q and $𝔼{\xi }^2<\infty$, then $𝔼\left(\mathit{Z}\right)=\mu$, $\mathrm{Cov}\left(\mathit{Z}\right)=\frac{𝔼\left({\xi }^2\right)}{q}\Sigma$, and Cor(Z) = Σ⁰.

• If Z ~ EC_d(0,Σ,φ) with diag(Σ) = I_d, then the marginal distributions of Z are the same.

Proof. The proof of the first two assertions can be found in Fang et al. (1990). To prove the third assertion, we use Proposition A.1 to obtain the characteristic function of Z_j for any $1\le j\le d:𝔼\exp \left(it{Z}_j\right)=𝔼\exp \left(it{e}_j^T\mathit{Z}\right)=\psi \left(t^2{\mathit{e}}_j^T\Sigma {\mathit{e}}_j\right)=\psi \left(t^2\right)$, where $t\in ℝ$ and e_j is the j-th canonical basis in ${ℝ}^d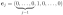$, i.e., for 1 ≤ j ≤ d. The result follows from the one-to-one map between the characteristic functions and the random variables.

A.2 Proof of Theorem 4.1

Proof. Realizing that ${\widehat{\tau }}_{jk}$ is a 2nd order U-statistic and sign (x_ij − x_i′k) (x_ik − x_i′k) is bounded in [−1; 1], using Equation (5.7) in Hoeffding (1963), we have

$$\mathbb{P}(\mid {\widehat{\tau }}_{jk}-\tau (X_j,X_k)\mid >t)=\mathbb{P}(\mid {\widehat{\tau }}_{jk}-𝔼({\widehat{\tau }}_{jk})\mid >t)\le 2\exp \left(-\frac{n{t}^2}{8}\right).$$

Therefore, we have

$$\begin{array}{cc}\hfill \mathbb{P}(\mid {\widehat{\mathrm{R}}}_{jk}-{\Sigma }_{jk}^0\mid >t)& =\mathbb{P}\left(\mid \sin \left(\frac{\pi }{2}{\widehat{\tau }}_{jk}\right)-\sin \left(\frac{\pi }{2}\tau (X_j,X_k)\right)\mid >t\right)\hfill \\ \hfill & \le \mathbb{P}\left(\mid {\widehat{\tau }}_{jk}-\tau (X_j,X_k)\mid >\frac{2}{\pi }t\right)\hfill \\ \hfill & \le 2\exp \left(-\frac{n{t}^2}{2{\pi }^2}\right).\hfill \end{array}$$

Taking the union bound, we have

$$\mathbb{P}({\mid \mid \widehat{\mathrm{R}}-{\Sigma }^0\mid \mid }_{\max }>t)\le d^2\exp \left(-\frac{n{t}^2}{2{\pi }^2}\right).$$

This completes the proof.

A.3 Proof of Theorem 4.2

Proof. Under the model ${\mathcal{M}}_d({\Sigma }^0,\xi ,f;{\theta }_1,s)$, we define λ_j := Λ_j(Σ⁰) and θ_j to be the corresponding eigenvector for j = 1, …, d. We then define ${\Psi }_0:{\Sigma }_{j=2}^d{\lambda }_j{\theta }_j{\theta }_j^T$ and let

$$\epsilon ≔\mid \sin \angle ({\theta }_1,{\widehat{\theta }}_{1,k}^{\ast })\mid \text{and}{\Sigma }^0={\lambda }_1{\theta }_1{\theta }_1^T+{\Psi }_0.$$

For all $\theta \in {𝕊}^{d-1}$, we have

$$\begin{array}{cc}\hfill \langle {\Sigma }^0,{\theta }_1{\theta }_1^T-{\theta \theta }^T\rangle & =\langle {\Sigma }^0,{\theta }_1{\theta }_1^T\rangle -\langle {\lambda }_1{\theta }_1{\theta }_1^T+{\Psi }_0,{\theta \theta }^T\rangle \hfill \\ \hfill & ={\lambda }_1-{\lambda }_1{\langle {\theta }_1,\theta \rangle }^2-\langle {\Psi }_0,{\theta \theta }^T\rangle ,\hfill \end{array}$$ (A.1)

and

$$\begin{array}{cc}\hfill \langle {\Psi }_0,{\theta \theta }^T\rangle & ={\theta }^T{\Psi }_0\theta ={\theta }^T({\mathbf{I}}_d-{\theta }_1{\theta }_1^T){\Sigma }^0({\mathbf{I}}_d-{\theta }_1{\theta }_1^T)\theta \hfill \\ \hfill & \le {\lambda }_2{\mid \mid ({\mathbf{I}}_d-{\theta }_1{\theta }_1^T)\theta \mid \mid }_2^2={\lambda }_2-{\lambda }_2{\langle {\theta }_1,\theta \rangle }^2.\hfill \end{array}$$

Moreover, by definition,

$${\sin }^2\angle ({\theta }_1,\theta )=1-{\left({\theta }_1^T\theta \right)}^2=1-{\langle {\theta }_1,\theta \rangle }^2.$$ (A.2)

Combining Equation (A.1) with Equation (A.2), we have

$$\langle {\Sigma }^0,{\theta }_1{\theta }_1^T-{\theta \theta }^T\rangle \ge ({\lambda }_1-{\lambda }_2)(1-{\langle {\theta }_1,\theta \rangle }^2)=({\lambda }_1-{\lambda }_2){\sin }^2\angle ({\theta }_1,\theta ).$$

Therefore, letting ${\widehat{\theta }}_{1,k}^{\ast }$ be the global optimum to Equation (3.4), we have

$$\begin{array}{cc}\hfill {\epsilon }^2& \le \frac{1}{{\lambda }_1-{\lambda }_2}\langle {\Sigma }^0,{\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\rangle \hfill \\ \hfill & \le \frac{1}{{\lambda }_1-{\lambda }_2}\left(\langle {\Sigma }^0-\widehat{\mathbf{R}},{\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\rangle +\langle \widehat{\mathbf{R}},{\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\rangle \right)\hfill \\ \hfill & \le \frac{1}{{\lambda }_1-{\lambda }_2}\langle {\Sigma }^0-\widehat{\mathbf{R}},{\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\rangle .\hfill \end{array}$$ (A.3)

The last inequality holds because θ₁ is feasible in the optimization constraint in (3.4), implying that

$$\langle \widehat{\mathbf{R}},{\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\rangle =\mathrm{Tr}\left(\widehat{\mathbf{R}}{\theta }_1{\theta }_1^T\right)-\mathrm{Tr}\left(\widehat{\mathbf{R}}{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\right)={\theta }_1^T\widehat{\mathbf{R}}{\theta }_1-{\widehat{\theta }}_{1,k}^{\ast T}\widehat{\mathbf{R}}{\widehat{\theta }}_{1,k}^{\ast }\le 0.$$

Therefore, using Equation (A.3),

$$\begin{array}{cc}\hfill {\epsilon }^2& \le \frac{1}{{\lambda }_1-{\lambda }_2}\langle {\Sigma }^0,-\widehat{\mathbf{R}},{\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\rangle \hfill \\ \hfill & =\frac{1}{{\lambda }_1-{\lambda }_2}\langle \mathrm{vec}({\Sigma }^0-\widehat{\mathbf{R}}),\mathrm{vec}({\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T})\rangle \hfill \\ \hfill & \le \frac{1}{{\lambda }_1-{\lambda }_2}{\mid \mid \mathrm{vec}(\widehat{\mathbf{R}}-{\Sigma }^0)\mid \mid }_{\infty }\cdot {\mid \mid \mathrm{vec}({\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T})\mid \mid }_1,\hfill \end{array}$$ (A.4)

where the last inequality is by the Hölder inequality. Letting $\vartheta =\mathrm{vec}({\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}$, we have

$$\begin{array}{cc}\hfill {\mid \mid \vartheta \mid \mid }_2^2& ={\mid \mid {\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T}\mid \mid }_F^2=\mathrm{Tr}\left(({\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T})({\theta }_1{\theta }_1^T-{\widehat{\theta }}_{1,k}^{\ast }{\widehat{\theta }}_{1,k}^{\ast T})\right)\hfill \\ \hfill & =2(1-{\left({\theta }_1^T{\widehat{\theta }}_{1,k}^{\ast }\right)}^2)=2{\epsilon }^2,\hfill \end{array}$$

implying that

$${\mid \mid \vartheta \mid \mid }_1\le \sqrt{{\mid \mid \vartheta \mid \mid }_0}{\mid \mid \vartheta \mid \mid }_2\le \sqrt{2k^2}\cdot \sqrt{2{\epsilon }^2}=2k\epsilon .$$ (A.5)

Therefore, combining Equation (A.4) with Equation (A.5), we get

$${\epsilon }^2\le \frac{{\mid \mid \mathrm{vec}(\widehat{\mathbf{R}}-{\Sigma }^0)\mid \mid }_{\infty }}{{\lambda }_1-{\lambda }_2}.2k\epsilon ,$$

which is equivalent to saying that

$$\epsilon \le \frac{2k{\mid \mid \mathrm{vec}(\widehat{\mathbf{R}}-{\Sigma }^0)\mid \mid }_{\infty }}{{\lambda }_1-{\lambda }_2}.$$

Using Theorem 4.1, we have, with probability at least 1 − d^−5/2,

$$∊\le \frac{2k{\mid \mid \mathrm{vec}(\widehat{\mathbf{R}}-{\Sigma }^0)\mid \mid }_{\infty }}{{\lambda }_1-{\lambda }_2}\le \frac{6\pi }{{\lambda }_1-{\lambda }_2}\cdot k\sqrt{\frac{\log d}{n}}.$$

This completes the proof.

A.4 Proof of Corollary 4.4

Proof. Without loss of generality, we may assume that ${\theta }_1^T{\widehat{\theta }}_{1,k}^{\ast }\ge 0$ because otherwise we can simply conduct appropriate sign changes in the proof. We first note that card $\left({\widehat{ϴ}}_k^{\ast }\right)=k\ge \text{card}\left(ϴ\right)$. if $ϴ\not\subset {\widehat{ϴ}}_k^{\ast }$, then $ϴ∕{\widehat{ϴ}}_k^{\ast }\ne 0$. This implies that,

$${\mid \mid {\widehat{\theta }}_{1,k}^{\ast }-{\theta }_1\mid \mid }_2\ge {\mid \mid {({\widehat{\theta }}_{1,k}^{\ast }-{\theta }_1)}_{ϴ∕{\widehat{ϴ}}_k^{\ast }}\mid \mid }_2\ge \underset{j\in ϴ}{\min }\mid {\theta }_{1_j}\mid \ge \frac{6\sqrt{2\pi }}{{\lambda }_1-{\lambda }_2}\cdot k\sqrt{\frac{\log d}{n}}.$$

We then have

$${\sin }^2\angle ({\widehat{\theta }}_{1,k}^{\ast },{\theta }_1)=1-{\left({\theta }_1^T{\widehat{\theta }}_{1,k}^{\ast }\right)}^2\ge 1-{\theta }_1^T{\widehat{\theta }}_{1,k}^{\ast }=\frac{{\mid \mid {\theta }_1-{\widehat{\theta }}_{1,k}^{\ast }\mid \mid }_2^2}{2},$$

implying that

$$\mid \sin \angle ({\widehat{\theta }}_{1,k}^{\ast },{\theta }_1)\mid \ge \frac{{\mid \mid {\widehat{\theta }}_{1,k}^{\ast }-{\theta }_1\mid \mid }_2}{\sqrt{2}}\ge \frac{{\min }_{j\in ϴ}\mid {\theta }_{1_j}\mid }{\sqrt{2}}=\frac{6\pi }{{\lambda }_1-{\lambda }_2}\cdot k\sqrt{\frac{\log d}{n}}.$$ (A.6)

Therefore, applying Theorem 4.2, we get

$$\mathbb{P}(ϴ\not\subset {\widehat{ϴ}}_k^{\ast })\le \mathbb{P}\left(\mid \sin \angle ({\widehat{\theta }}_{1,k}^{\ast },{\theta }_1)\mid \ge \frac{6\pi }{{\lambda }_1-{\lambda }_2}\cdot k\sqrt{\frac{\log d}{n}}\le d^{-5∕2}\right).$$ (A.7)

This completes the proof.

A.5 Proof of Theorem 4.7

Proof. Without loss of generality, we assume that ${\theta }_1^T{\widehat{\theta }}_{1,k}^{\ast }\ge 0$. We define $\mathcal{S}=\{j_1,\dots ,j_v\}=\mathrm{supp}\left({\theta }_1\right)\cup \mathrm{supp}\left({\widehat{\theta }}_{1,k}^{\ast }\right)$, where $v=\text{card}\left(\mathcal{S}\right)\le s+k$. we further define

$$T_n=\left[g_{j_1}(-\sqrt{b\log n}),g_{j_1}(\sqrt{b\log n}\right]\times \dots \times \left[g_{j_v}(-\sqrt{b\log n)},g_{j_v}(\sqrt{b\log n)}\right],$$

for some 0 < b < 1. Moreover, we define the event M_n as

$$M_n≔\{\mathit{v}\in {ℝ}^d:{\mathit{v}}_{\mathcal{S}}\in T_n\}.$$

Thus, conditioning on M_n, using Theorem 4.6, we have

$$\mid \widehat{f}{\left(\mathit{x}\right)}^T{\widehat{\theta }}_{1,k}^{\ast }-f{\left(\mathit{x}\right)}^T{\theta }_1^{\ast }\mid \le \mid {\left(\widehat{f}\right(\mathit{x})-f(\mathit{x}\left)\right)}^T{\widehat{\theta }}_{1,k}^{\ast }\mid +\mid f{\left(\mathit{x}\right)}^T({\widehat{\theta }}_{1,.k}^{\ast }-{\theta }_1^{\ast })\mid \le {\mid \mid {\left(\widehat{f}\right(x)-f(x\left)\right)}_{\mathcal{S}}\mid \mid }_2+{\mid \mid {\left(f\right(x\left)\right)}_{\mathcal{S}}\mid \mid }_2{\mid \mid {\widehat{\theta }}_{1,k}^{\ast }-{\theta }_1^{\ast }\mid \mid }_2{O}_P\left(\sqrt{(s+k)\cdot \frac{\log \log n}{n^{1-b∕2}}}\right)+O_P\left(\frac{k}{{\lambda }_1-{\lambda }_2}\sqrt{\frac{\log d}{n}}\right)\cdot {\mid \mid {\left(f\right(\mathit{x}\left)\right)}_{\mathcal{S}}\mid \mid }_2.$$ (A.8)

Since f_j(x_j) ~ N_d(0, 1), using Mill’s inequality, we have

$$\mid f_j\left(x_j\right)\mid =O_P(\sqrt{\log n}\Rightarrow {\mid \mid {\left(f\right(\mathit{x}\left)\right)}_{\mathcal{S}}\mid \mid }_2=O_P(\sqrt{(s+k)\log n}).$$ (A.9)

Finally, using Mill’s inequality again, we have

$$\mathbb{P}=\left(f_j\right(x_j)\ge \sqrt{n\log n})=O\left(n^{-b∕2}\right)\Rightarrow \mathbb{P}(\mathit{x}\in M_n^c)=O\left(\right(s+k\left)n^{-b∕2}\right)=o\left(1\right).$$ (A.10)

Combining Equations (A.8), (A.9), and (A.10), we have the desired result.