Learning Redundant Motor Tasks with and without Overlapping Dimensions: Facilitation and Interference Effects

Abstract

Prior learning of a motor skill creates motor memories that can facilitate or interfere with learning of new, but related, motor skills. One hypothesis of motor learning posits that for a sensorimotor task with redundant degrees of freedom, the nervous system learns the geometric structure of the task and improves performance by selectively operating within that task space. We tested this hypothesis by examining if transfer of learning between two tasks depends on shared dimensionality between their respective task spaces. Human participants wore a data glove and learned to manipulate a computer cursor by moving their fingers. Separate groups of participants learned two tasks: a prior task that was unique to each group and a criterion task that was common to all groups. We manipulated the mapping between finger motions and cursor positions in the prior task to define task spaces that either shared or did not share the task space dimensions (x-y axes) of the criterion task. We found that if the prior task shared task dimensions with the criterion task, there was an initial facilitation in criterion task performance. However, if the prior task did not share task dimensions with the criterion task, there was prolonged interference in learning the criterion task due to participants finding inefficient task solutions. These results show that the nervous system learns the task space through practice, and that the degree of shared task space dimensionality influences the extent to which prior experience transfers to subsequent learning of related motor skills.

Introduction

Skill is the ability to bring about some end result with maximum certainty and minimum outlay of time and energy (Guthrie, 1952). In acquiring skill, previously learned tasks can profoundly influence the learning of new tasks and this transfer of skill between tasks can be positive (resulting in facilitation of learning the new task) or negative (resulting in interference). Although traditional accounts of skill transfer depend on notions of task similarity that cover a wide range of tasks, e.g., theory of identical elements (Woodworth and Thorndike, 1901) or stimulus-response compatibility (Osgood, 1949), a critical issue is to understand what specific task characteristics need to be “similar” or “dissimilar” for positive or negative transfer to occur between motor tasks.

The structural learning hypothesis (Braun et al., 2009, 2010) proposes that when learning a motor task, the brain gradually learns the structure of the task by identifying the subset of available motor control variables that influence task performance and by restricting exploration to stay within this subspace of control. We refer to this subspace as the task space. The structural learning hypothesis also predicts that the motor system should avoid control variable changes that do not affect performance. We refer to this second subspace as the task's null space. Structural learning is supported by experimental observations from diverse tasks including goal-directed reaching (Braun et al., 2009), acquisition of sensorimotor associations (Braun et al., 2010), and learning of novel finger coordination patterns (Mosier et al., 2005).

Another prediction of this hypothesis is that the amount of positive or negative transfer between two tasks should depend on whether the structures in the two tasks are similar or dissimilar (Braun et al., 2009; Kobak and Mehring, 2012). This prediction appears to be supported by studies of goal-directed reaching that require hand path compensations for visual feedback distortions (e.g., learning a visuomotor rotation after exposure to similar rotations or dissimilar shear distortions). However, given that the measure of similarity in such tasks remains unclear, we tested if the similarity could be captured by the degree to which the two task spaces share dimensions.

We sought to clarify conditions under which people exhibit skill transfer in a novel experiment wherein the task space (i.e., the coordination patterns that influence task performance) could be manipulated carefully. Participants wore a data glove and learned to control a virtual object (a cursor) by finger motions (Mosier et al., 2005). Participants learned two tasks: a prior task and a criterion task. We manipulated the mapping between finger and cursor motions so that the task space of the prior task either shared or did not share the task space dimensions (x-y axes) of the criterion task. We observed positive transfer when the two tasks shared task space dimensions and negative transfer when they did not. The results show that similarity in task space dimensions between two tasks is a critical variable that influences skill transfer and that this transfer is caused by preferential exploration along previously learned task spaces.

Materials and Methods

Fifty healthy adults (aged 18–35, 22 female) participated in this study, which was comprised of three experimental sessions conducted on separate days within a 7 d period (44/50 participants came to the lab on 3 consecutive days and the remaining six participants visited the lab three times within a period spanning 4–6 d). All participants were right-handed. Participants provided written, informed consent to procedures approved by the Institutional Review Board at Marquette University. Participants were randomly assigned to one of five groups (n = 10/group), which differed in the task practiced on day 1 (the prior task). All subjects performed the same task on days 2 and 3 (the criterion task).

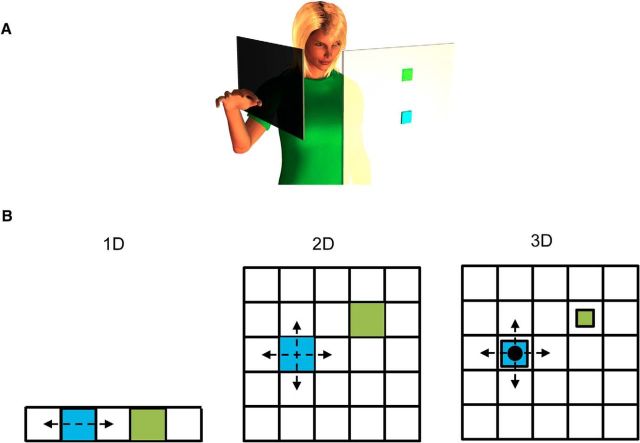
Participants were seated 100 cm in front of a 22 inch (55.8 cm) monitor. Vision of the participants' arm and hand was obscured using a plastic barrier (Fig. 1A). Participants wore a data glove on their right hand (CyberGlove; Immersion Technologies). We recorded signals from 19 bend sensors from the fingers and thumb at a rate of 60 samples per second and used these signals to control the position of a “virtual point” on a computer screen. The participants' task was to coordinate finger motions so as to move the point between targets comprising a 5 × 5 grid (Fig. 1B). The point was “virtual” in that it determined the position of a visual cursor (which was displayed by highlighting the grid cell that the point was in) during movement in training trials (described below) but was invisible otherwise.

Figure 1.

Experimental setup. A, Participants wore a data glove and performed a virtual reaching task wherein hand posture was mapped onto cursor position on a screen. Participants moved the cursor to capture targets on the screen. B, Variations of tasks for different groups. In 1D tasks, the cursor (highlighted in blue) only moved in one dimension and participants had to capture targets (shown in green) arranged in a single row. In 2D tasks, the cursor could move in two dimensions and participants had to capture targets arranged in a square grid. In the 3D task, the cursor could move in two dimensions and also change size. Participants had to match both the target location and size.

We sought to quantify the extent to which prior practice of a virtual reaching task influences the subsequent learning and performance of a second criterion task that either shared or did not share the task space dimensions with the first task. For example, we defined a 2D task space by mapping the 19-dimensional vector h representing the hand posture onto the 2D (x,y) position p of a virtual point through homogeneous transformation matrix A (Eq. 1) having 2 rows and 20 columns (cf. Mosier et al., 2005; Liu and Scheidt, 2008):

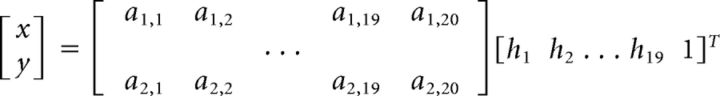and

Values for the elements of matrix A were determined from an initial calibration procedure described below. A 1D task such as the mapping of hand postures onto the x coordinate of the point requires A to have a single row of 20 elements. Similarly, a 3D task requires A to have 3 rows and 20 columns. In this case, hand postures could be mapped onto the x,y,z position of the point (with the z-dimension representing size). We exploited the possibility of embedding the 1D and 2D tasks into a more complex 3D task using judicious definitions of the A matrices to assess the extent to which the brain capitalizes on recently acquired knowledge of task space structure to facilitate learning of novel tasks. Throughout this manuscript, vectors are represented by lower-case bold typeface characters whereas matrices are represented by characters in upper-case bold typeface.

Procedure

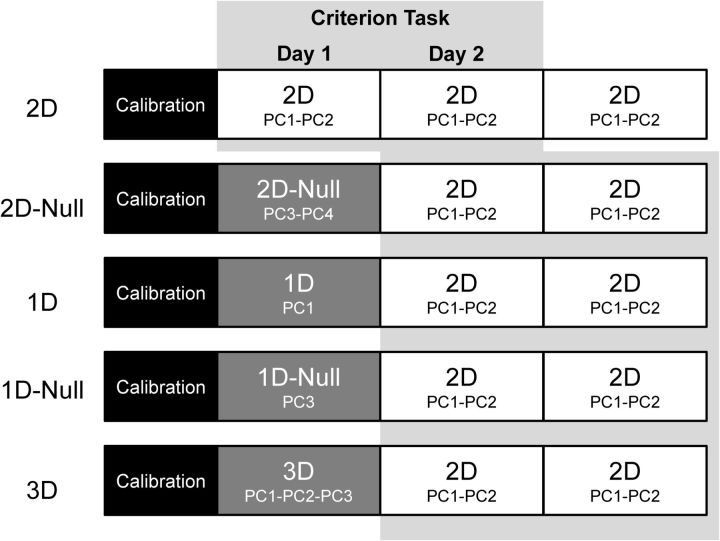
Figure 2 depicts the sequence of experimental testing conditions examined over the three testing sessions. Day 1 testing included a calibration phase, which yielded data that we used to establish the hand-to-screen mappings during experimental testing (i.e., matrix A).

Figure 2.

Practice schedule. Participants were divided into five groups. On day 1, all participants performed an initial calibration and a prior task that differed between groups. On days 2 and 3, all participants performed a common criterion task (the 2D task using PC1-PC2). For the 2D group, the prior task was the same as the criterion task and served as a control group. All comparisons between groups were made during the first 2 d of practice at the criterion task; i.e., days 1 and 2 for the 2D group and days 2 and 3 for the remaining groups (indicated by the gray shading in the background).

Calibration.

Each participant generated a calibration dataset by replicating each of the 24 hand postures corresponding to the static characters of the American Manual Alphabet (i.e., all but J and Z, which require hand motion; cf. Liu and Scheidt, 2008). Subjects were provided photographic images of the desired hand postures on the computer screen. Gesture formation was coached by the investigator who ensured minimal difference between desired and realized hand shapes at the moment of data sampling. The sequence of calibration postures was recorded three times and the average of the three was used to establish subject-specific hand-to-screen mappings using principal component analysis (PCA; cf. Liu and Scheidt, 2008). For the purposes of this study, we were most interested in the first four principal components, which accounted for an average of 71% (range 63–85%) of the hand-shape variance within the calibration datasets. For each subject on testing days 2 and 3, the A matrix was constructed by appending their first two principal components as row vectors. Each row of the matrix was then scaled so that all targets in the workspace were reachable. The last column of the A matrix implemented a translation that shifted the hand's mean posture during calibration to the center of the visual display.

Participant groups.

All groups performed two tasks: a prior task and a criterion task. The participant's goal in both tasks was to make hand gestures that would move the visual cursor between target locations on the screen (a virtual reaching task). The five participant groups differed in the prior task that they practiced during the experimental testing phase of day 1 (Fig. 2). The different tasks were obtained by manipulating both the number of principal components embedded in the A matrix (i.e., whether the task was 1D, 2D, or 3D) and also which principal components were used; i.e., whether A contained the task space components of the criterion task (PC1 or PC2) or the null space components of the criterion task (PC3 or PC4). The 2D group, which served as the control group, practiced the 2D task using PC1 and PC2 on all 3 d. For this group, the prior task was the same as the criterion task. The remaining four test groups practiced a different prior task on day 1. The 1D group practiced a 1D task using PC1. The 1D-Null group practiced a 1D task using PC3. The 2D-Null group practiced a 2D task using PC3-PC4. Finally, the 3D group practiced a 3D task using PC1-PC2-PC3. On days 2 and 3, the four test groups all switched to the criterion 2D task wherein PC1 and PC2 were embedded in the A matrix.

Training.

Each day's testing session lasted between 1.5 and 2 h and each included three blocks of 125 target-capture trials. In each block, 100 training trials were performed with full, ongoing visual cursor feedback and 25 blind trials were performed without cursor feedback. The sequence of trials was pseudorandomized such that blind trials sampled the entire target set at a rate of one target per every five trials. Two blind trials were never performed consecutively.

For the 2D tasks (Fig. 1B, middle), participants saw a square grid of 25 targets. During training trials, feedback of cursor position was provided by highlighting in blue the square that contained the cursor location p (Eq. 1). Participants were instructed to reach to the target (highlighted green) as quickly and accurately as possible, using all available information. Trials ended in one of two ways: (1) if the participant successfully moved the cursor to the target, the target turned yellow for 1 s and a pleasant auditory tone was provided and (2) if the participant failed to capture the target square when they stopped moving their hand, the target turned black and a different auditory tone was provided. For blind trials, the target was presented but no cursor feedback was provided during movement. However, after hand motion ceased, the square containing the cursor was highlighted for 1 s as in training trials.

For the 1D tasks, participants saw a single row of five targets and cursor motion was constrained to the horizontal screen axis (i.e., there was no y-axis motion of the cursor). For the 3D task, we imposed an additional size constraint on the cursor and on the 25 targets from the 2D task (i.e., both the target and cursor could be one of five different sizes corresponding to a tiling of the z-axis identical to the tilting of the x- and y-axes). The third row in the A matrix mapped hand gestures onto the size of the cursor. Participants were instructed to match the size of the target as well as its location (Fig. 1B, right).

Data analysis.

In the text that follows, we considered each target square on the screen to be one unit in size. We then defined three measures of kinematic performance. Movement time was computed as the time between movement initiation (i.e., when the virtual point's displacement first exceeded a threshold of 0.3 units for at least 9 of 12 consecutive samples) to the time when the trial ended (i.e., when the target was acquired or the participant stopped moving their hand). Stopping was defined as the when the Euclidean distance between successive glove data samples fell below a threshold of 2 sensor bit values (∼1°) for at least 9 of 12 samples). Because participants had no information about how close the cursor was to the center of the highlighted square during training or with knowledge of results (KR) feedback, we computed Endpoint Error as the number of squares between the target and the cursor when the trial ended (i.e., the chessboard distance). If the participant reached the target, endpoint error was 0; if the participant landed on a square adjacent to the target, endpoint error had a value of 1, etc. Endpoint error was computed separately for training trials and blind trials. Because we allowed participants unlimited time to reach a target, our primary metric for assessing motor skill learning and transfer during training trials was the movement time. To examine trajectory straightness, we defined Normalized Path Length as the distance traveled between the starting and final position divided by the straight line distance between the starting and final point. For a straight-line cursor trajectory, the normalized path length would be 1.

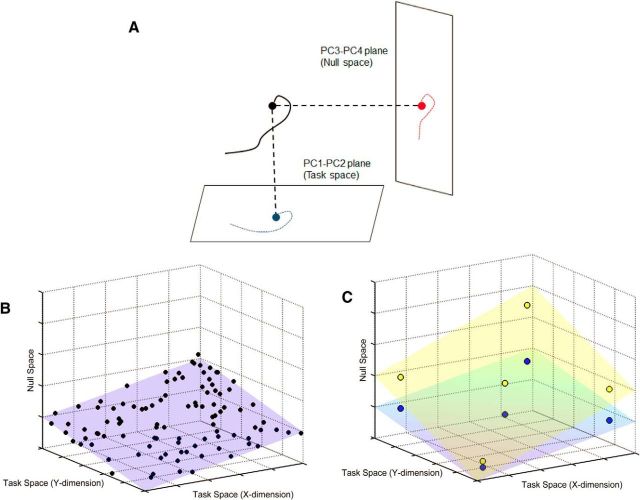
In addition to these task performance metrics in the space of visual cursor motion, we also computed three performance metrics in the hand posture space to quantify the strategies used by the participant. First, we evaluated an Exploration index by computing the ratio of the path length in the primary null space plane (PC3-PC4 of the calibration data) to the path length in the task space plane (PC1-PC2 of the calibration data). In this metric, the hand posture was projected to the two planes and the path length was computed separately in each plane (Fig. 3A). Before projecting, all principal components were made unit length so that there was no difference due to different scaling factors. A smaller value of the exploration index indicated that participants were exploring more selectively along the task space.

Figure 3.

Representation of computation of exploration index, planarity, and null space dispersion. A, For the exploration index, the hand posture was projected on to two planes: the task space (indicated in blue), and the null space (indicated in red). The path length was calculated separately in each plane and the exploration index was computed as ratio of the null space path length to the task space path length. B, C, The schematic represents a simplified version with a 2D task space (i.e., the floor of the graph) and a 1D null space (the height dimension). B, For planarity, we used all the hand postures in the corresponding block (shown by the black circles) and computed the VAF by the first two PCs (i.e., represented by the best fitting plane in blue). C, For the null space dispersion, we used only the hand postures during target capture (five targets are shown for simplicity) and we computed the ratio of the variance along the null space to the variance along the task space. Two possible strategies for achieving the same five targets in the task plane are shown in blue and yellow. In this scenario, the null space dispersion would be higher for a strategy represented by the yellow plane compared with the strategy represented by the blue plane.

Second, because the 2D task can be solved most efficiently if finger motions are limited only to a plane, we computed hand posture planarity by examining how much of hand posture variance during training was captured by the first two PCs obtained by applying PCA to the training trial data (not the calibration data). These new PCs generally were distinct from the PC1 and PC2 obtained using the calibration data. Perfectly planar exploration would result in a planarity value of 100% (Fig. 3B). Finally, we evaluated the extent to which training trial hand postures upon target capture were aligned to the task space by computing the null space dispersion. This performance measure was computed as the ratio of hand posture variance accounted for (VAF) within the task's null space (here evaluated within the plane spanned by calibration dataset PC3 and PC4) to the hand posture variance accounted for by the task space (i.e., the plane spanned by calibration dataset PC1 and PC2). Low values of null space dispersion indicate that hand postures at target capture are aligned primarily along the task space of the criterion task (Fig. 3C). It is important to note that the null space dispersion and exploration index give related but complementary information since the null space dispersion was computed only when participants reached a target (i.e., it did not take into account the path that the participants used), whereas the exploration index was computed based on the path length.

Statistical analysis.

We used these six performance measures to examine whether prior practice in each of the five training conditions would influence learning and performance of a novel 2D target capture task (i.e., the criterion task). To do so, we compared the first 2 d of practice on the criterion task (i.e., the 2D task) for each of the five groups (i.e., days 1 and 2 for the 2D group, and days 2 and 3 for the remaining groups). These 2 d are referred to as the day 1 and day 2 of practice in the criterion task. The third day of practice in the 2D group and the first day of practice (i.e., the prior task) in the remaining groups were not used for statistical analysis.

All dependent variables during the criterion task were analyzed using a Practice block (4) × Group (5) mixed model repeated-measures ANOVA. Practice block had four levels and was comprised of the first and last block of each of the first two exposure days. For the planarity and null space dispersion measures, we analyzed the first and last 100 training trials on each day to obtain more robust variance estimates. For training trial performance on the remaining measures, we analyzed the average performance in first and last 20 training trials of each day. In evaluating blind trial performance, we analyzed the first and last five blind trials each day.

To minimize the number of pairwise comparisons, post hoc comparisons for practice block were restricted to comparing the first block of the first day and the last block of the second day. For investigating the effect of group, we made the following planned comparisons: (1) each group was compared individually to the 2D group (which served as the control group) to determine how prior practice influenced learning the 2D task when compared with naive learning (i.e., to determine the amount of transfer) and (2) the 1D group was compared with the 3D group to examine the effect of practicing reduced versus augmented dimensionality tasks on subsequent learning of the criterion task. Where applicable, violations of sphericity were corrected using the Greenhouse–Geisser correction (denoted by ε).

Results

We excluded from analysis those training trials in the criterion task where participants “gave up” and landed further than one square from the target (i.e., where endpoint error >1 unit). We also excluded the occasional training trial where by happenstance, the distance traveled between targets was <0.1 units (since normalized path length was divided by this distance, spurious results could be obtained if this distance were too small). One participant in the 3D group was excluded from further analysis because of an uncharacteristically large number of such trials during the criterion task training (20 of 600 trials). For the remaining participants, the average number of training trials excluded was 2 of 600 trials (0.33%). No blind trials were excluded from analysis. Also, none of the trials were excluded from the prior training because applying this criterion would result in a significant portion of trials being excluded in the 3D task, which was extremely difficult.

Movement time in training trials

Twenty sample trajectories from one participant in the 2D group at the beginning and end of 2 d of practice in the criterion task reveal a dramatic reduction in searching behavior as the participant learned the task (Fig. 4).

Figure 4.

Sample trajectories from a typical participant in the 2D group: early in practice (i.e., first 20 training trials of day 1) and after 2 d of practice (last 20 training trials of day 2). The filled circles represent the points where participants stopped moving their hand. Notice that cursor trajectories become straighter with practice even though visual feedback of cursor motion was limited to highlighting of individual tiles in the 5 × 5 grid.

Performance in the prior task

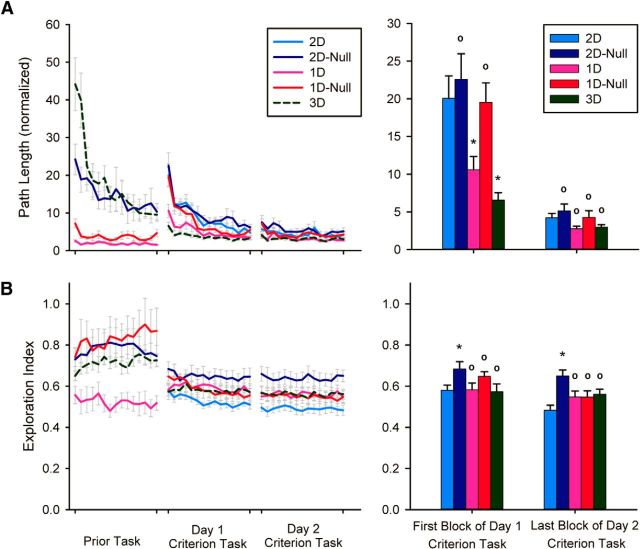
Performance in the prior tasks for all groups except the 2D group (which did not have a prior task) is shown in Figures 4–6. The biggest effect that was evident was that the task difficulty correlated with the dimensionality of the task (i.e., the 1D tasks were the easiest to perform, the 2D task was of intermediate difficulty, and the 3D task was the most difficult). This pattern was reflected in the movement time, endpoint error, and path length. In terms of the exploration index, the results indicated that participants were exploring the appropriate spaces as defined by the prior task. Thus, the 1D group explored the null space the least whereas the 1D-Null and 2D-Null groups explored it the most. Planarity was also lower in the 3D task (since the task cannot be achieved by simply moving along a plane) and highest in the 1D tasks. The null space dispersion showed a tendency for the 1D-Null and 3D groups to have solutions that were more distributed along the null space than the 2D-Null and 1D groups. The performance in the prior tasks was not used for statistical analyses.

Figure 5.

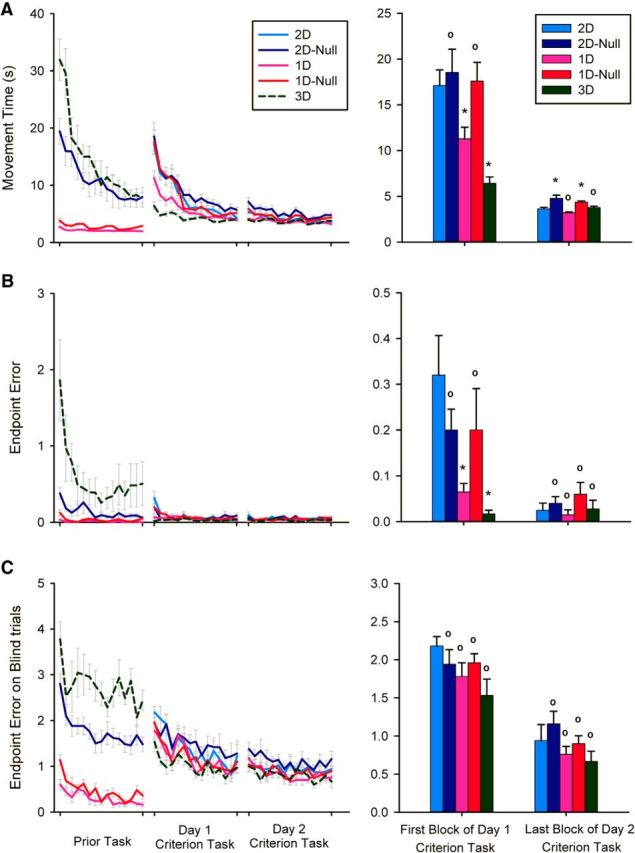
A, Mean movement time, and (B) endpoint error in training trials of all groups during the prior task and the first 2 d of practice at the criterion task. C, Endpoint error in blind trials of all groups during the prior task and the first 2 d of practice at the criterion task. A–C, The bar graph on the right shows the comparison of all groups on the 2D criterion task at first exposure and after 2 d of practice. Error bars represent 1 SE (between-participant). * indicates significantly different from 2D group (p < 0.05), ° indicates not significantly different from 2D group.

Figure 6.

A, Path length and (B) exploration index of all groups during prior practice and the first 2 d of practice at the criterion task. A, B, The bar graph on the right shows the comparison of all groups on the 2D criterion task at first exposure and after 2 d of practice. Error bars represent 1 SE (between-participant). * indicates significantly different from 2D group (p < 0.05), ° indicates not significantly different from 2D group.

Performance in the criterion task

All five participant groups reduced movement time with practice and we found significant differences between groups both early and late in training (Fig. 5A). Figure 5B reveals a main effect of practice block (F_(3,132) = 146.00, p < 0.001, ε = 0.386) and of group (F_(4,44) = 10.28, p < 0.001) as well as a significant block × group interaction (F_(12,132) = 6.32, p < 0.001, ε = 0.386). Post hoc analysis of this interaction revealed that at the beginning of criterion task, movement times from the 1D and 3D groups were smaller than those from the 2D group (p < 0.05 in both cases), which demonstrates a clear performance benefit from prior training with shared dimensionality (both reduced and augmented) with the criterion task. In contrast, initial performances in the criterion task in the 1D-Null and 2D-Null groups (that did not share task dimensions with the criterion task) were not significantly different from initial exposure performance in the 2D group suggesting that the performance benefits of reduced and augmented practice were specific to the type of information provided during training and not merely due to exposure to the target capture task. At the end of practice, movement times in the 3D and 1D groups were not significantly different from those in the 2D group, whereas movement times in the 2D-Null and 1-D Null groups were significantly greater than the 2D group (p < 0.05 in both cases). This finding demonstrates the potential for long-lasting interference between null space and task space training. Also, the difference between the 1D and the 1D-Null groups was statistically significant both early and late in practice, indicating that the transfer effects were not simply due to task familiarity. For the comparison of reduced versus augmented dimensionality, although initial movement times in the 3D group tended to be less than those in the 1D group, the difference did not quite reach statistical significance (p = 0.059).

Endpoint error in training trials

All groups reduced training trial endpoint errors over 2 d of criterion task exposure (Fig. 5B, right). We found significant differences between groups early in practice such that groups with longer movement times also had larger endpoint errors. This eliminated the possibility that participants in certain groups had longer movement times simply because they were trading off speed for accuracy. There was a main effect of practice block (F_(3,132) = 14.32, p < 0.001, ε = 0.547), a main effect of group (F_(4,44) = 4.63, p = 0.003), and a significant interaction between these factors (F_(12,132) = 2.72, p = 0.016, ε = 0.547). Analysis of this interaction revealed that at the beginning of practice, the 1D and 3D groups had smaller endpoint errors than did the 2D group (p < 0.05 in both cases). At the end of practice, however, there were no differences between groups. We also found no significant differences between endpoint errors made by the 1D and 3D groups at any time during the criterion task practice.

Endpoint error and movement time in blind trials

Endpoint errors in criterion task blind trials also decreased significantly with practice in all groups (Fig. 6). Thus, concurrent visual feedback was not necessary to perform the task and all groups were able to form task-appropriate feedforward movement commands. There was a main effect of practice block (F_(3,132) = 53.40, p < 0.001) but no effect of group (F_(4,44) = 1.59, p = 0.19) nor block × group interaction (F_(12,132) = 0.68, p = 0.77). We also found no significant differences between the normalized path lengths made by the 1D and 3D groups at any time during criterion task exposure.

Movement time in the blind trials reflected a task familiarity effect wherein initial movement times in the 2D group were significantly higher from the rest of the groups (2D group: 10.3 ± 4.7 s; other groups combined: 4.7 ± 1.2 s). By the end of practice, however, none of the groups had movement times significantly different from the others (2D group: 3.7 ± 1.6 s; other groups combined: 3.5 ± 1.2 s).

Normalized path length in training trials

The pattern of results for normalized path length was similar to that for endpoint error. While participants took straighter and shorter paths to the target with practice, there were significant differences between groups on initial exposure to the criterion task but not at the end of 2 d of practice (Fig. 5C). Specifically, we found a main effect of practice block (F_(3,132) = 100.27, p < 0.001, ε = 0.449), a main effect of group (F_(4,44) = 6.75, p < 0.001), and a significant block × group interaction (F_(12,132) = 5.09, p < 0.001, ε = 0.449). Analysis of the interaction revealed that normalized path lengths were shorter in the 3D and 1D groups compared with the 2D group at the beginning of practice (p < 0.05 in both cases). However, at the end of practice, none of the test groups made movements that were systematically longer or shorter than those made by the 2D group. We also found no significant differences between the normalized path lengths made by the 1D and 3D groups at any time during criterion task exposure.

Exploration of task space in training trials

Across groups, the exploration index of the task space decreased with learning, showing that participants reorganized their finger motions so as to move preferentially along the task space. However, there was a significant difference between groups in this regard. We observed a main effect of practice block (F_(3,132) = 13.02, p < 0.001), and a main effect of group (F_(4,44) = 3.81, p = 0.01). Post hoc comparisons of the group effect indicated that the 2D-Null group had a higher exploration index than the 2D group both initially in practice and after 2 d of practice. In contrast, all other groups decreased null space exploration with learning.

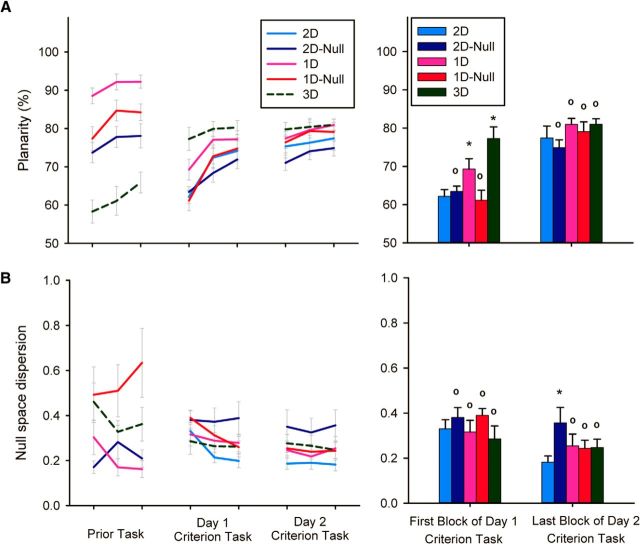
Planarity of hand postures in training trials

Across groups, the variance accounted by the first 2 PCs increased with practice in the criterion task, indicating that participants increasingly aligned their finger movements along the task space. However, task space VAF differed across groups early in practice (Fig. 7A). We found a main effect of practice block (F_(3,132) = 60.92, p < 0.001, ε = 0.75) and a main effect of group (F_(4,44) = 3.23, p = 0.021) as well as a significant block × group interaction (F_(12,132) = 2.69, p = 0.008, ε = 0.75). Analysis of the interaction revealed that, early in practice, the 1D and 3D groups had higher VAF than did the 2D group (p < 0.05 in both cases), whereas VAFs in the 2D-Null and 1D-Null groups did not differ significantly from that in the 2D group. By the end of practice, however, none of the groups differed significantly from the 2D group. We also found no significant differences between the 1D and 3D groups.

Figure 7.

A, Planarity and (B) null space dispersion of all groups during prior practice and the first 2 d of practice at the criterion task. Right, The bar graph shows the comparison of all groups on the 2D criterion task at first exposure and after 2 d of practice. Error bars represent 1 SE (between-participant). * indicates significantly different from 2D group (p < 0.05), ° indicates not significantly different from 2D group.

Null space dispersion in training trials

Across groups, the null space dispersion decreased with practice in the criterion task, further supporting the idea that participants increasingly aligned their finger motions along the task space with practice. Here, however, we observed significant differences between groups late in practice (Fig. 7B). In particular, we observed a main effect of practice block (F_(3,132) = 15.09, p < 0.001, ε = 0.719) as well as a significant block × group interaction (F_(12,132) = 2.067, p = 0.042, ε = 0.719). Whereas analysis of the interaction showed that none of the groups were significantly different from the 2D group at the beginning of criterion task practice, the null space dispersion was significantly higher in the 2D-Null group compared with the 2D group by the end of practice. We found no significant differences between the 1D and 3D groups.

Discussion

The aim of the study was to examine how transfer of skill between two motor tasks might depend on the degree of similarity between their task spaces. By careful specification of task space dimensions (defined by the matrix A in Eq. 1), we manipulated the extent to which task dimensions of the prior task were “shared” or “not shared” with the criterion task. The results showed that there was positive transfer (i.e., facilitation) when the task spaces had shared dimensions, whereas we found evidence of negative transfer (i.e., interference) when the task spaces did not share dimensions. Participants in the 1D and 3D groups (who had a map that was either a subset or a superset of the map in the criterion task) showed shorter movement times and path lengths compared with the naive performance when initially exposed to the criterion task, indicating that they were able to transfer the skill learned in the prior task to facilitate performance. In contrast, the initial performance of the 1D-Null and 2D-Null groups, whose prior task was in the null space of the 2D task, was not significantly different from naive performance.

Moreover, in terms of movement time, we also found evidence for sustained interference even after extensive practice on the criterion task (600 trials spread over 2 d; Fig. 3A). While all groups increased planarity of hand postures with practice (indicative of learning the criterion task space), the exploration index and the null space dispersion metrics showed that the 2D-Null group in particular continued to explore the null space and settled on movement solutions that were dispersed more along the null space of the criterion task than the 2D group (suggesting that representation of the prior task space persisted over days despite extensive practice on the criterion task). Thus, prior practice in the null space of the criterion task created a motor memory that constrained exploration to this space and eventually biased the movement solutions used when learning the criterion task. Our use of the term “motor memory” does not imply that the same movement kinematics were repeated, but rather that the exploration space in the criterion task was constrained by learning the prior task. Also, it is important to note that while the primary metric of movement time showed long-lasting effects, other parameters such as the normalized path length, endpoint error on blind trials, and planarity did not show any significant group differences by the end of 2 d of practice. These suggest that prior practice in the null space of the task did not directly impair learning or generalization per se, but instead created conditions for learning suboptimal solutions (as shown by the longer movement times required to achieve the task).

In addition, when comparing the 1D and 3D groups that shared task space dimensions with the criterion task, we found no evidence to suggest any long-term benefit to reduced-dimensional (i.e., the 1D group) or augmented-dimensional practice (i.e., the 3D group) compared with practicing the criterion task itself. We also found that the transfer effects due to the prior task were not simply due to a general facilitation due to task familiarity because groups differed systematically depending on prior practice (e.g., 1D vs 1D-Null).Together, our results demonstrate how task space dimensions learned while practicing one task can subsequently bias exploration, performance, and skill in subsequent tasks having either similar or dissimilar task space dimensions.

Structural learning

The finding that the 1D and 3D participant groups extracted a low-dimensional structure in the prior task that constrained exploration when solving the 2D criterion task is consistent with the idea of structural learning described previously (Braun et al., 2009; Kobak and Mehring, 2012). Previous tests of structural learning have also shown that a prior learned structure influences transfer to novel perturbations (Braun et al., 2009; Kobak and Mehring, 2012), but these have focused primarily on short-term adaptations (over a few tens of trials). In contrast, by using a novel task that was also redundant (i.e., having multiple solutions), we found that a prior learned structure influenced the movement solutions adopted for the criterion task, which resulted in performance differences that lasted several hundred trials. These results support the idea that the structure representations are flexible and can be influenced by prior experience (Yousif and Diedrichsen, 2012; Berger et al., 2013).

The idea that exploration favors the task space over the null space when coordinating multiple degrees of freedom is also consistent with models that emphasize the minimization of both task error and movement effort (Todorov and Jordan, 2002; Todorov, 2004). In this view, any exploration along the null space could effectively be considered “wasted effort” because it does not contribute to cursor motion. It is important to note, however, that this finding is not at odds with studies demonstrating preferential exploration along the null space (i.e., variance in the null space is typically larger than the task space; Scholz and Schöner, 1999; Latash et al., 2002; Nazarpour et al., 2012). If the task goal is to explore different parts of the workspace (e.g., acquiring different spatial targets as in the present study or different force levels as in Park et al., 2010), then the motor system needs to be able to restrict its exploration to the task space to produce different movement outcomes. However, when the goal is to maintain stability (i.e., maintain a posture or force level in the presence of perturbations, or achieve a consistent outcome over repeated trial attempts), then selectively exploring the null space may become a more important consideration since the goal is to avoid any changes in the movement outcome. In other words, whether the motor system explores the task space or the null space depends on the stability requirements of the task, and recent studies have found evidence that both phenomena can occur concurrently in the same task (Park et al., 2010; Ranganathan et al., 2013).

Influence of prior learned coordination patterns on motor learning

Transfer paradigms have been used extensively to explore motor memory and consolidation in tasks where movement patterns to be generated are already well learned and the amount of interference between tasks depends primarily on the extent to which the learned movement patterns conflict with those required to perform the novel task in the same experimental context. Examples include learning to compensate a reversal in the relation between the motion of a control interface and the motion of a visual display (Lewis et al., 1951), learning to compensate a reversal in the direction of an external force field (Brashers-Krug et al., 1996), compensation for opposing visuomotor rotations (Krakauer et al., 1999), and the learning of nonoverlapping sequences (Walker et al., 2003). In these cases, interference between motor tasks is typically observed as a performance decrement in the learning of the second task. Here, by using a task that had considerable motor redundancy, we showed that learning a prior task not only influenced performance of the second task, but also that the movement solutions used to solve the second task were contingent upon those learned in first task (as indicated by the null space dispersion). The results support the hypothesis that learning rarely occurs on a blank slate (Zanone and Kelso, 1992; Kelso, 1995) and that learning can be influenced by previously learned (or intrinsic) patterns of coordination (Ranganathan and Newell, 2009; Ganesh et al., 2010; Liu et al., 2011; de Rugy et al., 2012), and may include even compensatory coordination patterns such as those seen after stroke (Raghavan et al., 2010). These results further suggest that models of motor learning and skill transfer need to account for the influence of existing repertoire of coordination patterns in addition to more common considerations of optimality (e.g., the minimization of effort or kinematic errors).

Summary and conclusions

We found that the transfer between two tasks requiring the coordination of multiple degrees of freedom was related to the similarity in task space dimensions of the two tasks. Moreover, we found evidence that the movement solutions used to solve a given motor task were contingent on the task space dimensions of previously learned tasks. These results are consistent with the idea that the nervous system uses learned task structure to constrain motor exploration to low-dimensional task spaces and that preferential exploration along previously learned structures can lead to positive as well as negative biases in the learning and long-term performance of related tasks.