Platelet Dynamics in Three-Dimensional Simulation of Whole Blood

Abstract

A high-fidelity computational model using a 3D immersed boundary method is used to study platelet dynamics in whole blood. We focus on the 3D effects of the platelet-red blood cell (RBC) interaction on platelet margination and near-wall dynamics in a shear flow. We find that the RBC distribution in whole blood becomes naturally anisotropic and creates local clusters and cavities. A platelet can enter a cavity and use it as an express lane for a fast margination toward the wall. Once near the wall, the 3D nature of the platelet-RBC interaction results in a significant platelet movement in the transverse (vorticity) direction and leads to anisotropic platelet diffusion within the RBC-depleted zone or cell-free layer (CFL). We find that the anisotropy in platelet motion further leads to the formation of platelet clusters, even in the absence of any platelet-platelet adhesion. The transverse motion, and the size and number of the platelet clusters are observed to increase with decreasing CFL thickness. The 3D nature of the platelet-RBC collision also induces fluctuations in off-shear plane orientation and, hence, a rotational diffusion of the platelets. Although most marginated platelets are observed to tumble just outside the RBC-rich zone, platelets further inside the CFL are observed to flow with an intermittent dynamics that alters between sliding and tumbling, as a result of the off-shear plane rotational diffusion, bringing them even closer to the wall. To our knowledge, these new findings are based on the fundamentally 3D nature of the platelet-RBC interaction, and they underscore the importance of using cellular-scale 3D models of whole blood to understand platelet margination and near-wall platelet dynamics.

Introduction

Platelets or thrombocytes constitute an essential component of human blood due to their role in the formation of hemostatic plug and thrombus (1–3). These phenomena require that the platelets come within close proximity to the vessel wall, initiating platelet-wall contact followed by adhesion. Experiments with flowing blood showed an elevated platelet concentration near the wall (4–7). It has long been known that the red blood cells (RBCs) play a critical role in platelet margination and near-wall excess (8–11). Normal, healthy RBCs are extremely deformable (12,13) In a shear flow, the RBCs experience a wall-normal force that arises due to their deformation and propels them away from the wall. By volume exclusion, the platelets marginate toward the wall (8–11,13–16). The migration also causes a nonuniform RBC concentration in the wall-normal direction and, hence, a spatially varying RBC-platelet collision rate resulting in collision-induced platelet margination (14–18). Once marginated, the dynamics of the platelets within the near-wall RBC-depleted region (hereafter termed the cell-free layer (CFL)) can also be affected by the flowing RBCs at the edge of the CFL. The dynamics of the marginated platelets inside the CFL in turn determines the probability of platelet-wall contact. The importance of RBC-platelet interaction is aptly emphasized in a recent theoretical work in which platelet adhesion was shown to be controlled by the RBC-platelet pairwise collision and the finite size of the platelets (17,18).

Experimental quantification of RBC-platelet interactions and their connection to macroscale platelet transport in whole blood on the cellular scale is a difficult task. High-fidelity computer simulations that model blood as a suspension of finite-sized cellular components provide an alternative approach. Several 2D models (see, e.g., Chandran and colleagues (19,20), Crowl and Fogelson (21,22), Skorczewski et al. (23), and Shi et al. (24)) have emerged over the past years using this approach. In addition to reproducing many experimental observations, these studies have provided new insights into RBC-platelet interactions. For example, AlMomani et al. (19) showed that fluctuations in hydrodynamic stresses imparted by the RBCs also resulted in platelet margination. Crowl and Fogelson (21,22) found that platelet diffusivity was spatially varied, which, along with the volume exclusion, could partly explain platelet margination. Moreover, they proposed an additional spatially varying drift that enhanced the RBC-induced margination and also prevented the platelets from reentering the RBC-rich zone, thereby acting as a barrier. More recently, Skorczewski et al. (23) considered platelet dynamics near a thrombus, and observed that platelet tumbling near the vessel wall was strongly influenced by nearby RBCs, and that the thickness of the CFL was greatly reduced near the thrombus.

Although the aforementioned 2D models have provided a wealth of information on platelet-RBC interaction, a major shortcoming of such models is their inability to shed light on platelet movement in the transverse direction, i.e., along the direction of the vorticity of shear flow. The RBC-platelet collision is fundamentally three-dimensional in nature. Prior 3D model studies of pairwise collision of deformable particles in shear flow showed that a significant displacement of the particles could occur in the transverse direction (25). In the case of platelets, such movements can collectively lead to diffusion in the transverse direction. Therefore, the motion of platelets in the vorticity direction can greatly influence their near-wall dynamics and adhesion. The first 3D simulation of RBC-platelet suspension was reported by Zhao and colleagues (26,27), who observed that margination was irreversible and that platelet diffusivity was inhomogeneous in the wall-normal direction. In addition, their 3D model supported the notion of the additional drift proposed by Fogelson and co-workers based on their 2D model (21,22). However, as noted by Zhao and colleagues (26,27), the 2D model overpredicted platelet diffusivity.

Evidently, there is a need for 3D simulations to advance our understanding of platelet dynamics in whole blood. In addition to the translational diffusion in the third dimension, the 3D nature of the RBC-platelet collision can result in a rotational diffusion about the flow direction, leading to a variation in the off-shear plane orientation of the platelets. Quantification of such off-shear plane rotation and its influence on platelet dynamics has not been reported in the literature. Furthermore, in a shear flow, deformable particles such as RBCs often form clusters, leading to a local anisotropy in RBC concentration (28). It is not known how such anisotropic RBC concentration affects platelet margination or how anisotropic platelet diffusion affects near-wall platelet dynamics. To that end, in this article, we present a high-fidelity cellular-scale 3D computational model of platelet dynamics in whole blood. The dynamics and the large deformation of the RBCs are resolved with high accuracy in our model. The simulation results show that the RBC distribution in whole blood becomes naturally anisotropic and results in a fast and discontinuous platelet margination. Platelet translational diffusion inside the CFL is observed to be anisotropic, which leads to platelet cluster formation, increasing the likelihood of clot formation. This study demonstrates the ability of cellular-scale 3D models of whole blood to enhance our understanding of platelet margination and near-wall platelet dynamics.

Methods

Margination of platelets and their near-wall dynamics are simulated in whole blood in 3D using a front-tracking/immersed boundary method (29,30). Description of the numerical method is given elsewhere (31–34). The whole blood is represented as a suspension of many RBCs and platelets. We consider a linear shear flow of $\mathbf{u}=\left\{\dot{\gamma }y,0,0\right\}$ bounded between two walls mimicking a parallel-plate Couette flow chamber. Here, $\dot{\gamma }$ is the shear rate, x is the flow direction, y represents the velocity gradient direction, and z is the vorticity direction (Fig. 1). RBCs are modeled as liquid-filled elastic capsules of biconcave resting shape with end-to-end distance 7.8 μm, surface area 134.1 μm², and volume of 94.1 μm³ (35). The RBC membrane is assumed to be resistant to shear deformation, area dilatation, and bending. The resistance to shear deformation and area dilatation are modeled using the strain energy function developed by Skalak et al. (36). A finite-element method is used to obtain the membrane tension resulting from shear deformation and area dilatation (31). The bending resistance of the membrane is modeled according to Helfrich’s formulation (37). The platelets are modeled as nearly rigid oblate capsules with an end-to-end distance of 3.6 μm and a thickness of 1.1 μm (35). The fluid motion is governed by the continuity and Navier-Stokes equations, which are solved by a projection method (31). The flow domain is a rectangular box that is periodic in the x and z directions, but wall-bounded in the y direction. The no-slip condition is applied on the top and bottom walls. The domain is discretized using a fixed (Eulerian) rectangular grid. The surface of each RBC is discretized using 20,480 triangular elements (or 10,242 Lagrangian nodes) and that of each platelet is discretized using 1280 triangular elements (or 642 nodes). We use the radius of the equivalent sphere, $a_o={\left(3V/4\pi \right)}^{1/3}$, as the length scale, where V is the RBC volume, and the inverse shear rate, ${\dot{\gamma }}^{-1}$, as the timescale. The RBC and platelet membrane shear moduli are 2.5 × 10⁻⁶ N/m and 1.7 × 10⁻⁴ N/m, respectively. Dimensionless time is denoted by $t^{\ast }=t\dot{\gamma }$. The effect of inertia is small, as the Reynolds number, Re, is $\rho a_o^2\dot{\gamma }/{\mu }_o\lesssim {10}^{-2}$, where ${\mu }_o$ is the plasma viscosity.

Figure 1.

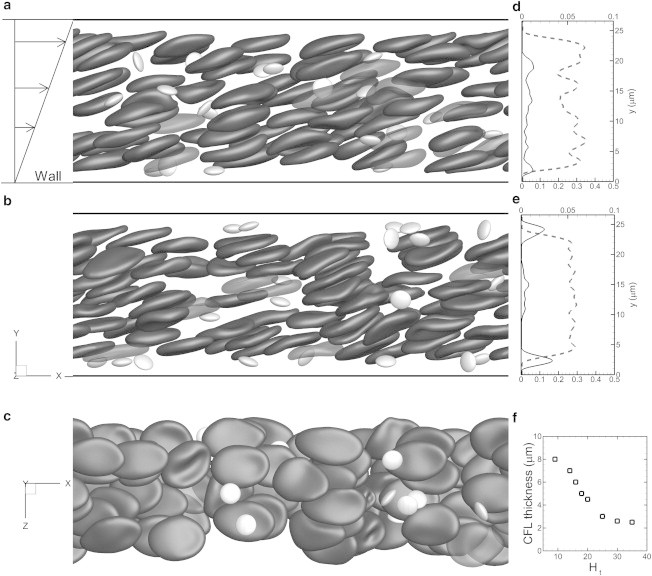
Representative snapshots showing instantaneous cell distribution from our whole-blood simulation in shear flow at hematocrit H_t = 23% in a channel of 71 μm length and 27 μm height. (a–c) Views along the vorticity (z) direction (a and b) at dimensionless time t^∗ = 20 (a) and 450 (b), and from the bottom of the channel at t^∗ = 450 (c). (d and e) Average RBC (dashed line, lower axis) and platelet (solid line, upper axis) concentration distributions across the channel height at times t^∗ = 20 and 450. (f) Average thickness of the RBC-depleted region (CFL) near the wall as a function of H_t.

Results

Platelet margination and role of RBC suspension microstructure

We performed a total of 18 simulations of whole-blood suspension at a constant shear rate of ∼1000 s⁻¹, and with hematocrit, H_t, ranging from 9% to 36%. The channel lengths considered are 36, 54, and 71 μm, with heights of 27 and 54 μm. One limitation of the simulations is the relatively smaller computational domain compared to an actual blood vessel and the use of a periodic boundary condition, which are needed to make the 3D calculations tractable for very long simulations. The Eulerian resolution is ∼9 mesh points/μm in the y direction and 6.8 mesh points/μm in the x and z directions. There are at least 53 Eulerian points across one RBC diameter, which is sufficient to resolve the cell dynamics based on our prior studies (see the Supporting Material for accuracy and grid independence of the model). The number of RBCs in the computational box ranges from 32 to 90 and that of platelets from 4 to 20. For normal blood, the RBC/platelet ratio is $\sim$ 16–20:1 (35). We considered a higher platelet count that could occur locally in a blood vessel under pathological and nonphysiological conditions. Fig. 1 shows three snapshots of platelet margination through flowing RBCs in whole-blood suspension. The RBCs and platelets are distributed randomly at the beginning of the simulation. The snapshots in Fig. 1, a and b, show the cell distribution at t^∗ ≈ 20 and 450, respectively. Accumulation of platelets near the walls is observed in Fig. 1 b. Evolution of the cell distribution at intermediate times is given in the Supporting Material. The RBCs are deformed significantly; the resting biconcave shape is no longer visible and the cells assume a more elongated disklike shape. Due to interaction between neighboring cells, the motion of each cell is quite irregular, which results in further deformation. Fig. 1 b reveals that the RBCs often flow in clusters, in which they are stacked vertically. Note that there is no adhesion potential used in the model presented here. Although adhesion potential is important if red blood cell aggregation and platelet coagulation are being considered, it is not the focus of this study. Since cell aggregation is not considered in our model, these clusters are formed naturally due to cellular motion driven by hydrodynamic forces. Furthermore, since the RBCs are deformable, the lubrication force between adjacent cells prevents them from physical contact. Thus, as long as there is sufficient Eulerian resolution ($\gtrsim 4$ points) between adjacent membranes, simulations are stable. Also visible in Fig. 1 b are cavities that are plasma-rich regions formed between adjacent clusters. These clusters and cavities form the microstructures in the suspension, making the instantaneous and local RBC distribution highly anisotropic. Prior studies of sheared suspension flows have shown microstructure formation and resulting anisotropy (28). As will be shown later, the RBC microstructure in whole blood has a significant role in platelet margination. Fig. 1, d and e, shows the RBC and platelet concentration distributions. Formation of an RBC-depleted region (a CFL) and increased platelet concentration near the walls are evident. The average CFL thickness obtained from the simulations (Fig. 1 f) ranges from 2.5 to 8 μm for H_t = 36–9%, respectively.

Sample trajectories of marginating platelets are shown in Fig. 2 a. Two different types of trajectory can be identified. In type A, a continuous but slow diffusive motion of a platelet toward the wall occurs through the entire margination process. This is the well-known shear-induced diffusion that is a result of the interaction between a platelet and a single RBC (8–10,13,14). It is a slow process because the platelets undergoing such motion are rarely observed to reach the wall even after 500 dimensionless time in the simulation. In type B, the margination appears to be a discontinuous process consisting of three phases: a slow lateral diffusive motion when the platelets are still within the RBC-rich region (Fig. 2 a, phase I). During this motion, the platelets mostly drift longitudinally along the flow direction, with only small lateral drift. This is followed by a fast lateral movement, which brings the platelets abruptly out of the RBC-rich layer and into the CFL (Fig. 2 a, phase II). Once within the CFL (Fig. 2 a, phase III), the platelet trajectories are nearly parallel to the vessel wall, with fluctuations caused by their collision with RBCs. Fig. 2 b shows the RBC and platelet concentrations near the CFL. Marginated platelets mostly accumulate just outside the RBC-rich zone, and their concentration decreases as the wall is approached. As a result, marginated platelets are subjected to continuous collisions with the RBCs flowing at the CFL edge. As will be shown later, such collisions dictate the platelet dynamics inside the CFL.

Figure 2.

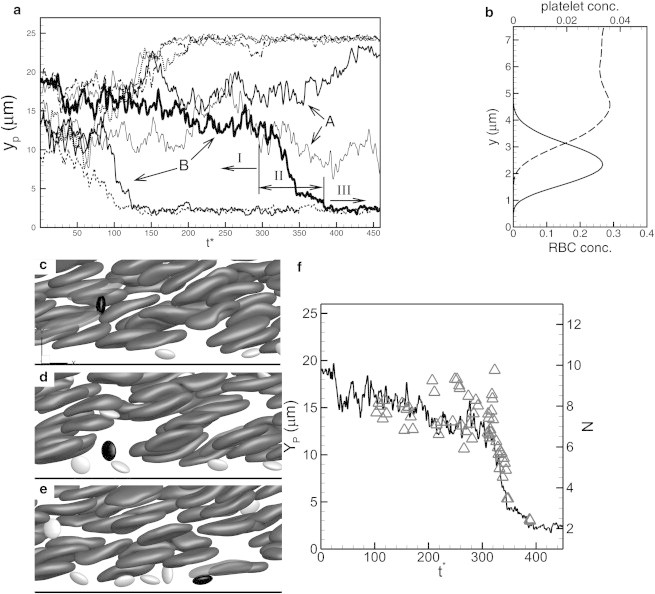
(a) Sample platelet trajectories from simulations in channels of 27 μm height, showing platelets with a continuous and slow diffusive motion (A), and those with a discontinuous and fast motion (B). For the latter type (B), the margination consists of a slow diffusive motion (phase I), an abrupt and large change in platelet lateral position (phase II), and a nearly wall-parallel motion inside the CFL (phase III). (b) RBC (dashed line, lower axis) and platelet (solid line, upper axis) concentration distributions near the CFL. Marginated platelets mostly concentrate just outside the RBC-rich zone. (c–e) Time-resolved snapshots showing that phase II in the type B trajectory is a result of a platelet getting pushed by an RBC cluster (a), then entering into a cavity (b), and finally marginating to the CFL (c). (f) Trajectory of the platelet (line, left axis) identified in c–e shown along with the number of RBCs, N (triangles, right axis), found instantaneously in a spherical volume of radius $3a_0$ surrounding the platelet.

The discontinuous margination was noted recently by Lee et al. (38) in their experimental study of submicron particle dispersion in mouse microvasculature. Platelet trajectories presented in Zhao et al. (27) also suggest the occurence of rapid margination. Our simulations suggest that the discontinuous margination is due to the microstructures formed by the RBCs. If a platelet is first hit by a cluster and then enters into a cavity, a large and sudden change in its lateral position can occur. If the cavity extends from near the wall into the RBC-rich region, such an interaction can abruptly bring the platelet out of the RBC-rich layer and into the CFL. Thus, the platelet can use the cavity as an express lane for fast margination toward the wall. Fig. 2, c–e, shows time-lapse snapshots illustrating the discontinuous margination process. In Fig. 2 c, a platelet interacts with RBC clusters (phase I), following which it enters into a cavity in Fig. 2 d (phase II). A significant drop in its lateral position occurs during this phase. The platelet then enters into the CFL (phase III). To further elaborate on the roles of microstructure, we compute the local RBC count by considering a spherical volume of radius $3a_0$ surrounding the platelet (Fig. 2 f). The RBC count becomes higher before the onset of the abrupt drop in platelet lateral position, implying an encounter with one or more RBC clusters. Thereafter, both the RBC count and the platelet position drop rapidly implying a fast lateral movement of the platelet through a cavity. We did not find any correlation between rapid platelet margination and hydrodynamic pressure or stress field. The cavity-assisted margination is likely due to a volume-exclusion effect.

Platelet diffusion in the RBC-rich region and in the CFL

The platelet trajectories in Fig. 2 a show that the marginated platelets do not reenter the RBC-rich region. Thus, the margination process is irreversible, as noted earlier (21,22,26,27). The observation also supports the notion that the RBCs flowing near the edge of the CFL provide a barrier against the platelets (21,22). Furthermore, the trajectory inside the CFL suggests that the lateral (y) movement of the platelets is significantly hindered due to the confinement effect from the wall and the RBCs flowing at the CFL edge. As a result, the platelet motion inside the CFL is not purely diffusive. Fig. 3 a compares platelet diffusion in the RBC-rich region to that in the CFL by means of the mean-squared displacement (MSD) of the platelet in the y direction. Inside the RBC-rich region, the MSD is linear after the initial transience, suggesting a diffusive transport. Platelet diffusivity in the lateral direction inside the RBC-rich region was measured as $\sim 3\times {10}^{-7}$ cm²/s at shear rates of ∼1000 s⁻¹, in agreement with previously reported values (16,26), and it is two to three orders of magnitude higher than the Brownian diffusivity, suggesting RBC-augmented diffusion. In contrast, the MSD in the CFL does not grow with time after the initial transience, suggesting that lateral motion of the marginated platelets is not diffusive because they are confined by the RBCs and the wall.

Figure 3.

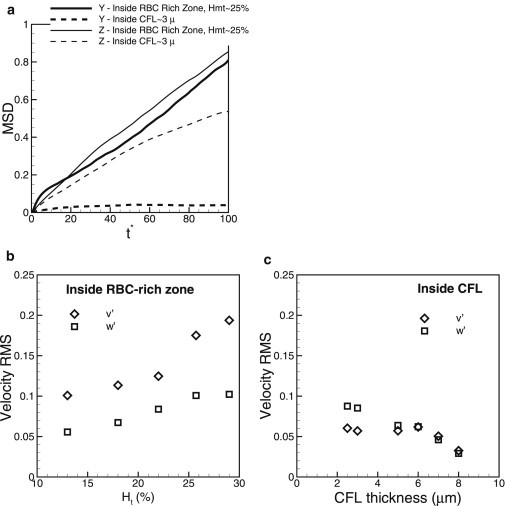
(a) Mean-squared displacement (y′²) for lateral (wall-normal) motion of platelets inside the RBC-rich zone (thick solid line) and the CFL (thick dashed line), and (z′²) inside the RBC-rich zone (thin solid line) and inside the CFL (thin dashed line). (b and c) RMS velocity fluctuation of platelets inside the RBC-rich zone and the CFL, respectively, in the wall-normal direction (v′, open diamonds) and transverse direction (w′, open squares).

As a further quantification of the platelet diffusive motion, root mean-squared (RMS) velocity fluctuations for the wall-normal direction $\left(v^{\prime }\right)$ and the vorticity direction $\left(w^{\prime }\right)$ were computed. Note that in our 3D model, platelets can move in the z direction due to platelet-RBC interaction although there is no mean flow in z. Fig. 3 b shows the RMS fluctuations inside the RBC-rich zone as functions of hematocrit. Both $v^{\prime }$ and $w^{\prime }$ increase with increasing hematocrit due to increasing platelet-RBC collisions. Interestingly, although $w^{\prime }$ values are smaller than $v^{\prime }$ values, they are comparable, suggesting a significant diffusion in the transverse direction. By considering separate simulations of an RBC interacting with a platelet in a shear flow, we verified that such interaction can often result in a significant platelet displacement in the z-direction, although there is no mean flow in z. A similar observation has been obtained previously for pairwise interactions of deformable particles in 3D in shear flow (25). Thus, our 3D simulations show that in whole blood, platelet diffusion in the transverse direction is comparable to that in the wall-normal direction.

Fig. 3 c compares $v^{\prime }$ and $w^{\prime }$ inside the CFL. Here, $v^{\prime }$ is significantly less than in the RBC-rich zone due to the hindered lateral motion of the platelets. $w^{\prime }$ is also less in the CFL than in the RBC-rich zone, but it is higher than $v^{\prime }$, and it increases with decreasing CFL thickness. This is because reducing the CFL thickness results in more frequent RBC-platelet collision; although the platelets cannot move in the wall-normal direction due to confinement, they can easily move in the transverse direction. This result implies that platelet diffusion inside the CFL is anisotropic; diffusion is hindered in the wall-normal direction, but could be higher in the transverse direction.

Formation of platelet clusters

As a result of the transverse motion, marginated platelets come close to each other and form clusters (Fig. 4 a). Such cluster formation could be a precursor to clot formation if the platelets are activated. We observe clusters varying in size and number. Fig. 4 b shows the size and number of clusters over time in a simulation with H_t = 17% and a CFL thickness of 6 μm. A cluster is identified when the surface-to-surface distance between adjacent platelets is <∼750 nm. Using this criterion, we determine the cluster size, i.e., the number of platelets in a given cluster, and also track the number of clusters in the simulations. Fig. 4 b shows that the size and number of clusters are highly dynamic, varying from 0 to 5 and from 0 to 4, respectively, over time for the specific simulation considered. Note that the platelets are randomly drawn to each other, and cluster formation is entirely due to RBC-platelet interaction and platelet diffusion, as our model does not consider platelet activation. Furthermore, since our model does not consider platelet aggregation, these clusters exist for a short time.

Figure 4.

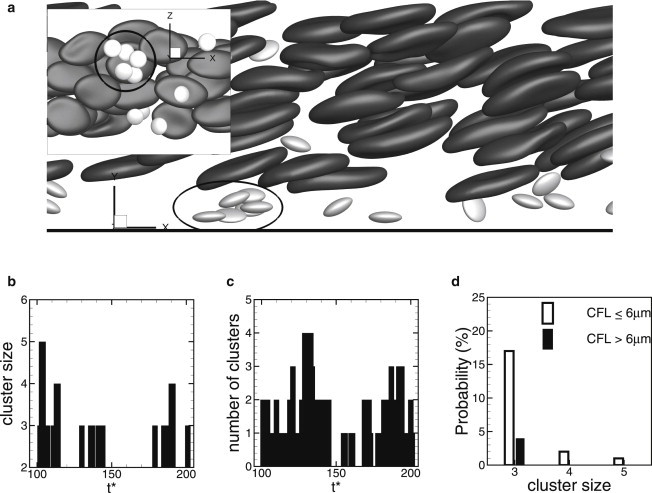
(a) Formation of a platelet cluster inside the CFL. (Inset) View from the bottom of the channel. (b and c) Size (b) and number (c) of clusters over time in a simulation at H_t = 17% (CFL thickness 6 μm). (d) Probability of finding a cluster of size 3–5 for CFL thickness ≤6 μm (open bars), and >6 μm (solid bars).

We find that the size and probability of formation of the platelet clusters are highly dependent on CFL thickness. Fig. 4 d shows the probability of finding a cluster of size 3–5 in two different groups, one based on CFL thickness ≤6 μm and the other on CFL thickness >6 μm. A thinner CFL significantly increases the probability by increasing both the size and number of clusters. For CFL thickness >6 μm, the largest cluster observed consists of three platelets, whereas for CFL thickness ≤6 μm, the largest cluster contains five platelets. The probability of finding a cluster of three platelets is ∼4% for CFL thickness >6 μm and 17% for CFL thickness ≤6 μm. The probability decreases significantly with increasing cluster size. Thus, the large clusters form only occasionally and are short-lived.

Comparison of platelet dynamics in the RBC-rich zone and the CFL

In absence of the RBCs, an isolated platelet flowing near a wall executes either a tumbling or a sliding motion (39,40). The tumbling is characterized by a rotational (flipping) motion like a rigid ellipsoid. Far from a bounding wall, the tumbling dynamics is described by the theory proposed in Jeffery (41). Near a wall, the period of tumbling increases due to an additional drag induced by the wall. Very close to the wall, a full tumbling is no longer possible; instead, a sliding motion occurs. During sliding, the long axis of the platelet remains nearly parallel to the wall and oscillates slowly with small amplitude. If an isolated platelet is released into the flow with its axis of revolution normal to the wall, our simulation predicts that the sliding motion occurs when the distance between the platelet center and the wall is $y_p\lesssim 1.5$ –1.7 μm, and tumbling occurs at greater values of y_p.

Fig. 5 shows how platelet dynamics is affected in the presence of RBCs in 3D whole-blood simulation. Apart from the lateral location of the platelet center $\left(y_p\right)$, platelet dynamics are described by two angles, the tumbling angle (θ) between the major axis of the platelet contour in the shear plane and the flow direction (x), and the off-shear plane angle (ϕ) between the major axis of the platelet contour in the yz plane and the z axis. When $\varphi =0$, the axis of revolution is in the shear plane, so that the platelet is oriented parallel to the wall. When $\varphi \ne 0$, the axis of revolution tilts out of the shear plane. Thus, ϕ quantifies platelet rotation about the flow direction, which cannot be achieved using a 2D model. For tumbling, θ varies between +π/2 and −π/2, and for sliding, both θ and ϕ are ≈0. Fig. 5 shows that platelet dynamics in the presence of RBCs is very irregular, unlike the periodic motion of an isolated platelet. In the RBC-rich zone, tumbling dynamics occurs but in an irregular manner (Fig. 5 a). In the CFL, both tumbling and sliding are observed, depending on the distance between the platelet center and the wall. In addition, an intermittent dynamics is observed in which the tumbling is converted to sliding and vice versa. Fig. 5 c shows a sliding-to-tumbling transition and Fig. 5 d shows a tumbling-to-sliding transition. Fig. 5 e shows a transition from tumbling to sliding and then back to tumbling. We find that such transitions are a result of the collisions of the marginated platelets with the RBCs flowing at the edge of the CFL. In 3D, such collisions result in a large off-shear plane angle, ϕ. Both our own and prior 3D modeling show that for an isolated platelet, sliding can change to tumbling if the platelet is released with a large ϕ (39). Therefore, in whole blood, the 3D nature of platelet-RBC interaction results in platelet rotation out of the shear plane, which in turn converts sliding to tumbling. As noted earlier in Fig. 2 b, the concentration of marginated platelets peaks just at the CFL edge, resulting in frequent collisions with the RBCs. Furthermore, the marginated platelets often accumulate in the plasma-rich cavities near the CFL, and they tumble due to reduced confinement.

Figure 5.

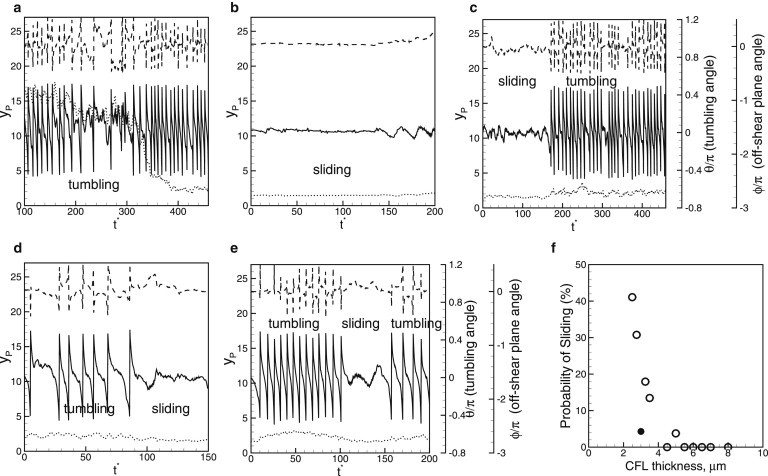
(a–e) Platelet dynamics in 3D whole-blood simulation. Shown here are the lateral location of the platelet center (y_p, dotted line, left axis), tumbling angle (θ, solid line, first right axis), and off-shear plane angle (ϕ, dashed line, second right axis). (f) Probability of platelet sliding motion as a function of CFL thickness for platelets distributed within the entire CFL (open circles), and for platelets located just outside the RBC-rich zone (solid circles).

To quantify the role of CFL thickness on platelet dynamics, we computed the probability of sliding (Fig. 5 f). The results are grouped in two sets, one containing platelets distributed throughout the CFL and the other containing marginated platelets flowing near the edge of the CFL. Fig. 5 f shows that for the first set, sliding motion occurs when the CFL thickness becomes comparable to the platelet size (∼3.5 μm). Note that this CFL thickness corresponds to a distance from the platelet center to the wall of ∼1.75 μm, which is close to the length scale below which an isolated platelet exhibits sliding motion, as explained above. The probability of sliding increases with decreasing CFL thickness, as platelet tumbling is increasingly impeded due to confinement. However, the collision effect seems to be dominant; even for a CFL thickness as small as 2.5 μm (H_t = 36%), only ∼40% of platelets are observed to slide. For the second set, for which CFL thickness is ∼3μm, <5% of platelets are observed to slide. Thus, the RBC-platelet collision significantly reduces the probability of sliding, even when the CFL thickness is small.

To quantify platelet orientation in 3D, we plot the probability distribution of the off-shear plane angle, ϕ, and the tumbling angle, θ for three sets of platelets (Fig. 6), those inside the RBC-rich zone, and marginated platelets inside CFLs of thickness 3 μm and 6–8 μm. Inside the RBC-rich zone, the distribution of ϕ is relatively uniform, although it is higher as ϕ → 0. The distribution becomes more biased toward $\varphi =0$ when marginated platelets are considered. For the CFL thickness of 6–8 μm, RBC-platelet collision is less frequent, and hence, a significantly higher probability of $\varphi =0$ is observed. For the CFL thickness of 3 μm, increased collision with the RBCs results in the platelet axis tilting out of the shear plane, reducing the probability of $\varphi \approx 0$. The probability distribution of the tumbling angle, θ, is shown in Fig. 6 b for the same three sets, as well as for an isolated platelet, based on Jeffery’s theory (41). The probability at $\theta \approx 0$ is higher for the marginated platelets than for those in the RBC-rich zone, and increases with decreasing CFL thickness due to the increasing number of sliding platelets.

Figure 6.

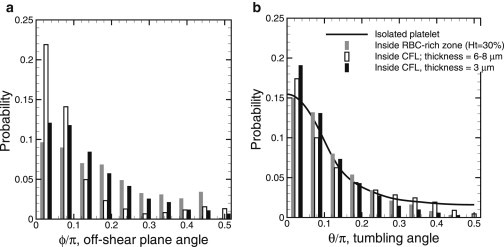
Platelet orientation in 3D: Probability distribution of the off-shear plane angle ϕ (a) and tumbling angle θ (b) for platelets inside the RBC-rich zone (gray bars), for 6- to 8-μm-thick platelets inside the CFL (open bars), for 3-μm-thick platelets inside thte CFL (solid bars), and for an isolated platelet far from a wall (line).

The platelet tumbling frequency in whole blood is shown in Fig. 7 a as a function of the distance from the wall for $H_t=$ 25%. Also shown is the tumbling frequency of a platelet in the absence of RBCs, which approaches Jeffery’s theory (41) at distances far from the wall, but decreases rapidly as the wall is approached due to a wall-induced drag. This qualitative picture is significantly affected in whole blood. Fig. 7 a shows that the average tumbling frequency is significantly less for a platelet in the RBC-rich zone than for an isolated platelet. This reduced frequency is likely due to geometrical confinement imparted by the surrounding RBCs. As the CFL is approached, the frequency increases due to a reduction in the local RBC concentration. Inside the CFL, the wall effect becomes more important, and the frequency decreases with distance from the wall in a manner qualitatively similar to that observed for an isolated platelet. Thus, in whole blood, the highest tumbling frequency occurs for platelets flowing near the edge of the CFL.

Figure 7.

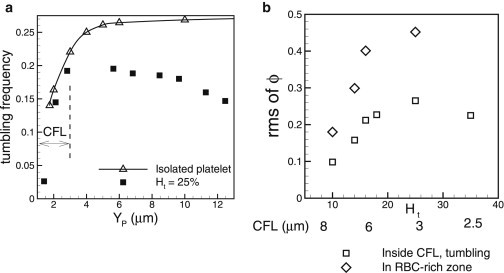
(a) Platelet tumbling frequency in dimensionless form as $2\pi /\dot{\gamma }T$ as a function of distance from the wall in whole blood (solid squares) at H_t = 25%, and for an isolated platelet (open triangles). The CFL thickness is 3 μm, as shown. (b) RMS of off-shear plane angle ϕ as a function of hematocrit. Shown here are the data for platelets flowing inside the RBC-rich zone (open diamonds), and for tumbling platelets flowing inside the CFL (open squares). The thickness of the CFL is shown below the lower axis.

Angular fluctuation and rotational diffusion

To further quantify the 3D nature of platelet-RBC interaction, we obtain the RMS of the fluctuations of the off-shear plane angle, ϕ (Fig. 7 b). In the RBC-rich zone, the RMS increases with increasing hematocrit due to increasing platelet-RBC collisions. Fluctuations are significant, and the RMS is as high as 0.45 rad. For $H_t\gtrsim 25$%, the RMS appears to reach a plateau due to increased RBC confinement. In the CFL, the RMS is reduced compared to that inside the RBC-rich zone, and it shows a nonmonotonic trend with respect to the CFL thickness. The RMS first increases with decreasing CFL thickness due to more platelet-RBC collisions, but it then decreases as a result of increasing confinement as the CFL thickness becomes very small. We compute the mean-squared angular displacement $\langle \Delta {\varphi }^{\prime 2}\rangle$ and obtain the platelet rotational diffusivity, $D_{\varphi }=\langle \Delta {\varphi }^{\prime 2}\rangle /2t\approx 1$ –4 s⁻¹ for a shear rate of ∼1000 s⁻¹, which is nearly one to two orders of magnitude higher than the rotational Brownian diffusion (42).

Implication in platelet-wall adhesion

As a measure of the likelihood of platelet-wall adhesion, the minimum distance between a platelet surface and the wall, Y_min, over time is shown for a marginated platelet (Fig. 8 a). The time history shows that Y_min varies significantly over time. In general, our results show that in the presence of RBCs, $Y_{min}$ is reduced more when a platelet is tumbling than when it is sliding. This result is consistent with earlier studies on isolated platelets, which found that a tumbling-like dynamics termed pole vaulting brings the platelets closest to the wall (39). However, we found here that in whole blood, large fluctuations in the off-shear plane angle, ϕ, can also bring a sliding platelet very close to the wall (Fig. 8 a). To quantify how tumbling and sliding dynamics affect the wall-platelet proximity, we obtained the average of Y_min over time and number of platelets (∼50), as well as the lowest value of Y_min, from simulations with H_t = 25–35%. We obtain averages of Y_min ≈ 1060 nm for the tumbling platelets and Y_min ≈ 860 nm for the sliding platelets. In contrast, the lowest $Y_{min}$ values found are ≈420 nm for tumbling platelets and 625 nm for sliding platelets (Fig. 8 b). Platelet-wall adhesion is mediated via von Willebrand factor molecules (1,2,23). Our results imply that the initial contact between a platelet and the wall may occur during the tumbling phase by the ultralarge von Willebrand factor molecules with a length scale of 250–750 nm. However, these bonds can easily break due to large wall-normal and transverse velocity fluctuations, and due to higher tumbling frequency, as noted previously in Fig. 7 a. Sliding platelets are more likely to form stable adhesion with the wall.

Figure 8.

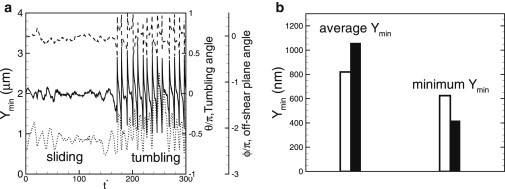
Minimum distance, Y_min (dotted line, left axis), over time between a platelet surface and the wall for a marginated platelet. Also shown are the tumbling angle, θ (solid line), and the off-shear plane angle, ϕ (dashed line). (b) Average and lowest values of Y_min for tumbling (solid bars) and sliding (open bars) platelets.

Discussion and Conclusion

We presented a 3D modeling study of platelet dynamics in whole blood using a high-fidelity numerical methodology that accurately resolves the dynamics and large deformation of every single cell, and successfully predicts the formation of the RBC-depleted zone (the CFL) and the near-wall excess of platelets. We focus on the platelet dynamics close to and in the CFL, and show that this region plays a critical role in clot formation by affecting the near-wall platelet motion and platelet-wall contact. We found that the cellular microstructures formed by RBCs in a shear flow play a critical role in platelet margination. These microstructures are formed by RBCs stacked along the wall-normal direction making instantaneous RBC distribution highly anisotropic. The anisotropy occurs naturally by hydrodynamic forces and creates local cavities in RBC distribution. A platelet can enter a cavity and use it as an express lane for fast margination toward the wall. Although it is known that platelets experience augmented diffusion due to their interaction with RBCs (8–11), this finding suggests that further augmentation occurs as a result of the local anisotropy in the RBC distribution.

Inside the CFL, platelet motion in the wall-normal direction is severely hindered due to greater confinement of the platelets between the wall and the RBCs flowing at the edge of the CFL. As a result, the wall-normal motion of the platelets is not purely diffusive inside the CFL. In contrast, inside the RBC-rich zone, platelet diffusivity in the wall-normal direction is found to be two to three orders of magnitude higher than the Brownian diffusion.

An important outcome of our 3D simulation is the quantification of platelet motion in the transverse (vorticity) direction. The 3D nature of the platelet-RBC interaction results in significant platelet movement in the transverse direction. This observation is consistent with the results from prior 3D model studies of pairwise collision of deformable particles in shear flow, which showed significant displacement of the particles in the vorticity direction (25). In whole blood, such movements collectively lead to platelet diffusion in the transverse direction, which cannot be predicted in a 2D simulation. We find that inside the RBC-rich zone, platelet velocity fluctuations in the transverse direction are comparable to that in the wall-normal direction. Relating the RMS of the velocity fluctuations to the diffusivity $\left(D\approx v^{\prime 2}\tau \right)$, we infer that in the RBC-rich zone, platelet diffusivity in the transverse direction is slightly smaller but comparable to diffusivity in the wall-normal direction. In the CFL, the results are completely different: platelet movement is severely hindered in the wall-normal direction, but not in the transverse direction. As a result, the RMS fluctuation is significantly higher in the transverse direction than in the wall-normal direction. Therefore, our 3D model shows that not only is platelet diffusion in whole blood inhomogeneous in the wall-normal direction, but it is also anisotropic, particularly inside the CFL. The anisotropy increases with decreasing CFL thickness as the latter causes an increase in the platelet-RBC collision rate and at the same time an increased confinement. The anisotropy is likely to play an important role in platelet motion near a thrombus, where the thickness of the CFL is greatly reduced (23).

We find that the strong anisotropy in platelet motion inside the CFL leads to platelet cluster formation even in the absence of any platelet-platelet aggregation. Although short-lived, such hydrodynamically driven clusters may serve as the precursor to the formation of a hemostatic plug and thrombus. The cluster size and number are found to increase with decreasing CFL thickness in a way qualitatively similar to that of the transverse velocity fluctuation increases. The increasing platelet diffusion in the transverse direction with decreasing CFL thickness leads to higher probability of platelet cluster formation. Such a mechanism of cluster formation is absent in a 2D model.

Our model further shows that due to the 3D nature of the RBC-platelet collisions, the platelet axis of revolution continually moves out of the shear plane, leading to a strong rotational diffusion that increases with increasing hematocrit. The rotational diffusivity is estimated to be one to two orders of magnitude higher than the Brownian rotational diffusivity. Our simulations show that the platelet dynamics in whole blood differs significantly from that of an isolated platelet. In the RBC-rich zone, the platelet tumbling frequency is well below that of an isolated platelet. The highest frequency is attained just outside the RBC-rich zone. The tumbling motion is highly irregular due to RBC-platelet collision. In the CFL, the platelet dynamics is determined by two competing effects, namely, the confinement by the wall and the RBCs at the edge of the CFL, and collisions with RBCs. Whereas the former effect induces a sliding motion of the marginated platelets, the latter induces tumbling. Although most marginated platelets are observed to tumble just outside the RBC-rich zone, we found that the platelets further inside the CFL flow with an intermittent dynamics that alternates between sliding and tumbling. The transition from sliding to tumbling and vice versa is a result of the off-shear plane rotational diffusion and hence is less likely to happen in a 2D simulation. As a result of the transition, we find that platelet sliding occurs less frequently than tumbling. A platelet in tumbling motion instantaneously comes closer to the wall than a sliding platelet, but the average distance from the wall to the platelet surface is found to be higher in tumbling than in sliding.

In conclusion, the high-fidelity 3D simulations of whole blood presented here demonstrate the importance of finite cell size, anisotropy, and three-dimensionality in platelet-RBC interaction, platelet margination, and platelet-wall adhesion. The overall picture that arises from this study is that the local anisotropy in RBC distribution in whole blood results in fast and discontinuous platelet margination. The anisotropic nature of the platelet translational diffusion in the CFL leads to platelet cluster formation and increases the likelihood of clot formation. The rotational diffusion of platelets with respect to their off-shear plane orientation converts the motion of the marginated platelets from sliding to tumbling and brings them closer to the wall, increasing the likelihood of platelet-wall contact. This study underscores the significance of platelet motion in the transverse direction and warrants further experimentation in which platelet motion in whole blood can be tracked over time and simultaneously in all three dimensions.