Dynein Regulation: Going into Circles Can Set Things Straight

It has long been known that eukaryotic cilia and flagella are autonomous oscillators capable of generating a beat cycle independent of regulation by the parent cell (1). In cilia and flagella, the mechanism that regulates the dynein motor activity to generate the beat cycle has been a matter of speculation and controversy. As of this writing, there are three rather distinct hypotheses, each with fairly good experimental support.

• 1.Central-pair spoke hypothesis: There is a body of evidence showing that doublets slide when activated by control elements in the central pair and spoke apparatus. This has given rise to the idea that the beat cycle can only be explained by cyclical activation of dyneins on specific doublets (2) through regulatory elements in the central pair, spoke, and nexin/dynein regulatory complex.
• 2.Resistive-load hypothesis: The second class of regulatory schemes has a long and rather varied history, and contends that the dynein motor itself has an oscillatory character. The latest and most extensively elaborated incarnation of this idea was developed by Camalet et al. (3) and Jülicher and Prost (4). It posits that when ordered assemblages of dynein are harnessed to a resistive mechanical load they reach a threshold of force that terminates their action. This leads to coordinated episodes of synchronized pulling and release. In this view, the assemblage size and resistive properties acting on the group determine the coordinated cycling of motor activity.
• 3.Geometric-clutch hypothesis: It is hypothesized that dynein activity is regulated by transverse stress that develops in the axoneme when it is distorted by bending. In this view, the dyneins themselves are free running motors that pull whenever they can form an engagement with the adjacent doublet. However, their ability to engage and pull is controlled by the spacing between the doublets, which in turn is modified by the transverse force (t-force) acting on the doublet pair (5).

The idea that curvature is crucial to regulating dynein activity was first proposed and modeled by Brokaw (6). The geometric-clutch hypothesis also has an element of curvature control, because t-force depends on curvature, but rather than acting as a direct action of curvature, it is the resulting t-force that pulls the doublets apart or pushes them together to terminate, or activate, episodes of motor activity.

In 1986, Kamiya and Okagaki (7) carried out a classic experiment which showed that a cycle of bending, separation, and reattachment could be observed between pairs of individual doublets of frayed Chlamydomonas axonemes. This seemed to be strong experimental support that the rudiments of a beat cycle could be established with just two isolated doublets. If viewed as representing the minimal essential components for the underlying mechanism that generates the beat in intact flagella, then clearly the higher-order regulatory elements of the spokes and central pair are not necessary to the fundamental mechanism of the beat cycle.

The two-doublet experiment could not discriminate between the resistive-load and the geometric-clutch hypotheses because either one can account for the observed experimental result. A more detailed analysis of two-doublet interactions by Aoyama and Kamiya (8) was initially interpreted as ruling out curvature and t-force as the switching principle, because some of the doublet pairs executed oscillations with minimal change in curvature. In 2009, Brokaw (9) computer-modeled the experimental results obtained from that study. He showed that buckling of the doublet that is under compression could potentially generate sufficient t-force to disengage the dyneins by a t-force-dependent mechanism, without a significant visible change in overall curvature of the pair. This again left the issue unresolved, because both the geometric-clutch hypothesis and the resistive-force hypothesis are potentially compatible with observation.

In this issue of Biophysical Journal, a clever set of experiments and physical analyses, carried out by Mukundan et al. (10), provide what is believed to be new evidence to discriminate among the hypotheses. They utilize the two-doublet experimental methodology, but they modify the working conditions to slow things down, and induce a quasi-equilibrium state that is more amenable to straight-forward physical analysis. When the two-doublet experiment is done with low (10 μM) ATP, the doublets slide more slowly, stay attached to each other longer, and undergo a pause just before separation. During that pause, there is a Newtonian balance between active bending torque and torque that arises from elastic resistance to bending the doublets. This balance can be analyzed with considerable accuracy.

If dyneins along the entire doublet pair are pulling, the bending torque should be greatest at the basal end of the pair and decrease progressively to the tip. They did not observe this result. Instead, they observed a circular curvature everywhere except near the tip. This shows that just before complete dissociation, all of the bending torque is being generated in a short segment of dyneins near the tip, and indicates that the dyneins more proximally located along the doublet are turning off when a threshold of curvature and/or resultant t-force is reached. Fig. 1 provides a schematic of the likely status of the dynein under this condition. In the final quasi-equilibrium state, before doublet separation, only the dyneins at the tip are still pulling. The authors show analytically that this result is only compatible with curvature control and/or t-force control of dynein deactivation. Consequently, it is the occurrence of the circular arc that sets matters straight.

Figure 1.

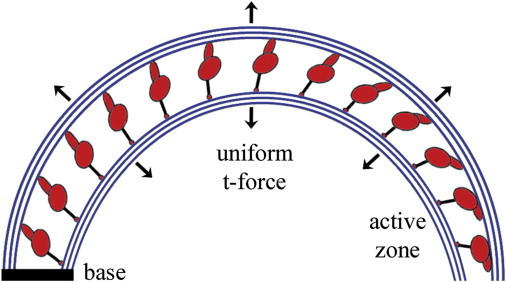
Dynein inactivation without doublet dissociation. In the two-doublet experiment of Mukundan et al. (10), the only dynein contributing force for bending is localized at the tip of the doublets. The remaining dyneins still resist dissociation, but are ineffective at contributing bending torque, possibly due to undocking of the dynein head.

Their careful analysis also derives values for the force per dynein head (5 pN) and the t-force/micron of length (0.2 nN/μm). The values they report are in agreement with the values predicted for operation of the geometric-clutch mechanism, and also match the force per dynein reported from stalling force measurements on reactivated bull sperm (11).

The pause that is present just before the doublets separate is obvious in their two Supporting Movies. It is this pause that allows the final balance of active moment and elastic resistance to be analyzed rigorously without complicating effects from viscous drag. This pause also raises a separate issue that may be quite important and requires further consideration. The circular curvature means that the dyneins along most of the doublet length have stopped pulling, but the pause before separation means they have not yet let go of their binding sites on the adjacent doublet. They do eventually let go; that is why the doublets separate, yet unlike the earlier two-doublet results, the substantial pause at low ATP separates the two events. This is telling us something quite important. Curvature and/or t-force can terminate active force generation without pulling the dyneins off of their binding sites, at least not immediately. Furthermore, the dyneins themselves are capable of acting as passive linkages to form and maintain a bend, because these doublets no longer have permanent interdoublet connections.

In 2002, Alan Hunt and I (12) wrote a short overview article in which we speculated that because dynein has a rather flaccid stem, it may need a third anchor-point to effectively transmit force between the doublets. Such anchoring is also suggested by the beautiful freeze-etch images of Goodenough and Heuser (13,14), who showed how dynein in rigor appears to have the head of the molecule tightly nested on the A-tubule of the doublet, whereas in relaxed axonemes the globular heads are in an undocked condition suspended between the doublets. The tighter association of the globular head when the axoneme is in the rigorlike state may also be necessary to the power stroke.

If it is indeed the case that the dynein head needs to be anchored for effective longitudinal force transmission, it may be that deactivation of the dynein has two stages: first, the undocking of the globular head; and second, complete release. Low ATP may facilitate the resolution of the two stages, because high ATP has long been known to decrease the microtubule binding affinity of dynein (15). The new observation also raises the possibility that undocking of the dynein head may be sufficient to terminate longitudinal force transmission during the normal beat cycle in intact flagella, and that complete release of the stalk from the B-subtubule may not be necessary. This might explain why it has been so difficult to observe dissociation of the dynein stalk from the B-subtubule in transmission electron microscopy and freeze-etch replicas of the axoneme. This is a very interesting and possibly essential detail of understanding how things work in the intact axoneme of cilia and flagella, and requires further exploration to completely straighten out the issue.