Ultimate Use of Two-Photon Fluorescence Microscopy to Map Orientational Behavior of Fluorophores

Abstract

The orientational distribution of fluorophores is an important reporter of the structure and function of their molecular environment. Although this distribution affects the fluorescence signal under polarized-light excitation, its retrieval is limited to a small number of parameters. Because of this limitation, the need for a geometrical model (cone, Gaussian, etc.) to effect such retrieval is often invoked. In this work, using a symmetry decomposition of the distribution function of the fluorescent molecules, we show that polarized two-photon fluorescence based on tunable linear dichroism allows for the retrieval of this distribution with reasonable fidelity and without invoking either an a priori knowledge of the system to be investigated or a geometrical model. We establish the optimal level of detail to which any distribution can be retrieved using this technique. As applied to artificial lipid vesicles and cell membranes, the ability of this method to identify and quantify specific structural properties that complement the more traditional molecular-order information is demonstrated. In particular, we analyze situations that give access to the sharpness of the angular constraint, and to the evidence of an isotropic population of fluorophores within the focal volume encompassing the membrane. Moreover, this technique has the potential to address complex situations such as the distribution of a tethered membrane protein label in an ordered environment.

Introduction

Fluorescence microscopy is able to explore complex cellular processes in isolated cells and tissues, with a high potential to image dynamical processes at a nanoscale spatial resolution. The complementary use of light polarization in fluorescence imaging, introduced decades ago to measure molecular orientational behaviors (1), is an evolving field, mostly due to its apparent complexity in terms of technical implementation as well as data analysis and interpretation.

Technically, polarized microscopy schemes were initially proposed based on the use of two states of polarization, either on the excitation path (linear dichroism) (2,3), on the detection path (fluorescence anisotropy) (1,4,5), or on both excitation and detection paths (6–8). These schemes are, however, limited in their imaging capability; indeed, two directions of excitation polarization impose a geometry that does not give access to all possible orientations in an ordered sample, whereas analyzing the fluorescence light polarization along a given direction is very sensitive to depolarization mechanisms such as energy transfer (9) or scattering of the emitted light in turbid media (10). One way to overcome these limitations that is compatible with microscopy imaging is to vary the excitation polarization state in a tunable linear dichroism scheme, with no analyzer in the detection path. However, implementation of such a technique necessitates ensuring a fine control of the polarization at the focal spot of the objective lens (11–13), which is possible only if polarization distortions are characterized and compensated for (14,15). This scheme shows the possibility of imaging molecular order based on one-photon, two-photon, and three-photon fluorescence processes in molecular assemblies such as lipid probes in living cells (12), receptor proteins in cell membranes (16,17), protein aggregates in amyloid fibrils (18), and protein crystals (19).

In addition to this technical specificity, the interpretation of polarized fluorescence signals requires modeling the associated physical process, including molecular orientational behaviors. Polarized excitation implies coupling between excitation dipoles that fluctuate in orientation (Fig. 1 a) and a tunable incident polarization. Although this process is dynamic in time and is spatially distributed, the result of the measurement is an average over the integration time and the spatial scale of the focal volume, leading to a steady-state-like observation. Individual orientations and positions thus cannot be resolved in ensemble measurements, and the measured quantity is rather an angular distribution, f(θ,φ), representing the statistical occurrence of molecules at given orientation angles, as illustrated in Fig. 1 b. To date, interpreting polarized fluorescence data has been based primarily on a priori known models of this angular distribution, invoking quite simple molecular-disorder mechanisms. For instance, lipid probes in cell membranes have been supposed to follow a Gaussian or Cone-like angular constraint, both of which encompass interactions with their local environment (11,12,20–22) as well as sub-resolution-scale membrane morphological features (12) (Fig. 1, b and c). In this context, the ability of polarized fluorescence microscopy to probe changes in lipid membrane composition (as induced, for example, by cholesterol depletion (12,20)), cytoskeleton degradation, and modification of the membrane tension (12) has been demonstrated. Although quantitative results can be depicted, the models invoked here are based on a priori knowledge about molecular statistical disorder behavior. Lipid probe orientations can be addressed by quite simple models, but the case of labeled proteins in cell membranes, where the angular constraint is governed by the orientational freedom of the link between the label and the protein, possible protein conformational changes, orientational constraints undergone by the protein inside the membrane, and the orientational disorder imposed by the membrane local morphology, is a more complex issue. Fig. 1, d–f, displays an example of such a case, where it is clear that there are more unknown parameters compared to the lipid-probe case depicted in Fig. 1, a–c. Until now, such a situation has been treated using both excitation/detection polarization paths as mentioned above (7) or pure linear dichroism, which provides only qualitative information (3).

Figure 1.

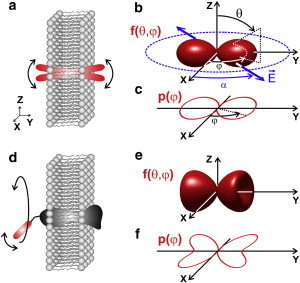
(a) Orientational freedom of a single fluorescent probe in a membrane. (b) Space- and time-averaging in an ensemble of probes are described by a 3D distribution, f(θ,φ), of single dipoles oriented with angles (θ,φ), as probed by the electric field. (c) Corresponding 2D effective angular distribution, p(φ), given by Eq. 4. (d) A single fluorescent dipole linked to a membrane protein with a given angular constraint in the membrane. (e) Corresponding ensemble averaging orientation in a 3D distribution. (f) 2D effective distribution. To see this figure in color, go online.

It becomes clear from these examples that a precise investigation of biomolecular organization using the orientation of fluorophores as a reporter requires that the orientational constraint model reproduce a realistic situation with the highest fidelity. However, investigating complex systems such as that represented in Fig. 1 d necessitates the introduction of an increasing number of unknown parameters and an increasing level of angular detail, not all of which is accessible using polarized fluorescence techniques. Mathematically, a high level of detail corresponds to high angular frequencies and therefore to high orders of symmetry in the angular description of the distribution function f(θ,φ). In distributions that exhibit cylindrical symmetry, only the θ-dependence is relevant, and it is generally represented by Legendre-polynomial-averaged quantities (6,7,23–25). It is known that compared to linear optical processes, high-order nonlinear excitation processes, which benefit from more refined angular photoselections (26,27), give access to a higher order of symmetry (27–29). The use of polarized two-photon (11,20,28,30) or three-photon excitation fluorescence (19) has benefited from this approach. However, it has not yet been possible to take full advantage of the interpretation of high symmetry orders in fluorescence imaging, because such interpretation is restricted to simple angular distribution models (11,20,22). In addition, the few existing works that have aimed at exploiting this information to provide a finer degree of analysis of the orientational behavior of fluorophores have been performed at the scale of the sample (cuvette or membrane) (6,7,23–25,28), a scale at which it is not possible to investigate complex samples. Nevertheless, these analyses have contributed to the discovery of the coexistence of two orientational populations (parallel and perpendicular to the membrane) of the 1,6-diphenyl-1,3,5-hexatriene (DPH) fluorescent probe in lipid vesicles (24,25).

The aim of this work is to provide high-order symmetry information in fluorescence imaging, where all locations of a sample can be explored at a diffraction-limited scale. We develop a theoretical framework of polarized two-photon fluorescence based on tunable linear dichroism, using a symmetry decomposition of the distribution function of the fluorescent probes that relies on circular angular functions. This decomposition makes it possible to avoid assumptions based on a priori knowledge about the molecular disorder distribution, particularly distributions that are not of cylindrical symmetry. Using this approach, it is also possible to establish the optimal level of detail at which any angular distribution can be retrieved using two-photon tunable linear dichroism. We show mathematically that a minimum of five polarization measurements is needed to reach this optimal level. We propose a data-processing method that provides an accurate picture of the orientational distribution up to the fourth-order symmetry at each pixel of the image. We show that the obtained symmetry parameters can be related to physical properties of molecular angular distribution functions, such as angular width (disorder), steepness (sharpness of the angular constraint potential), and shape (hollow versus filled angular spread). This method can be easily implemented on any two-photon microscope system and is based on simple arithmetic operations.

Materials and Methods

Sample preparation

Multilamellar vesicles (MLVs) were made from 1,2-dipalmitoyl-sn-glycero-3-phosphocholine lipid (DPPC) (31) mixed with a 1 mM solution of di-8-ANEPPQ in absolute ethanol to obtain a 1% w/w of di-8-ANEPPQ. Thin films were hydrated in phosphate-buffered saline (PBS, pH 7.4) for 1 h above the main phase-transition temperature (45°C), leading to formation of 1- to 30-μm MLVs. The sample was placed between two spaced coverslips.

Experiments in cells were carried out on fibroblastlike COS-7 cells (CRL-1657, American Type Culture Collection (ATCC), Manassas, VA). COS-7 cells were grown in an incubator at 37°C in Lab-Tek chambers (Nunc, Rochester, NY) in Dulbecco’s modified Eagle’s medium (Gibco, Saint Aubin, France) completed by 10% fetal bovine serum and 1% sodium pyruvate. Cells were washed and kept in Hanks buffered salt solution containing 10 mM HEPES (HBSS/HEPES), pH 7.4, at 37°C, for the duration of the imaging process. They were labeled with di-8-ANEPPQ directly before measurements. For labeling, cells were washed and incubated in insertion buffer (130 mM NaCl, 5 mM KCl, 10 mM CaCl₂, 5 mM glucose, and 10 mM HEPES) with 1 μM di-8-ANEPPQ for 2 min at room temperature. After incubation, cells were washed again and kept in HBSS/HEPES at 37°C throughout the imaging process.

Two-photon microscope

The polarization-resolved two-photon tunable linear dichroism setup is based on an inverted two-photon excitation fluorescence microscope. A Ti:Sapphire laser beam (wavelength 900 nm, pulse duration 150 fs, repetition rate 80 MHz, Coherent, Inc., Santa Clara, CA) is reflected on a dichroic mirror (650DCXP, Chroma, Rockingham, VT) and focused onto the sample by a high-NA objective lens (CFI Apo Lambda S LWD, 40×, NA 1.15, water immersion, Nikon, Tochigi, Japan), reaching a lateral optical resolution of ∼300 nm with an average power of ∼5 mW. Fluorescence images are obtained by scanning the focused beam in the sample plane using galvanometric mirrors (6200H, Cambridge Technology, Lexington, MA), with a typical dwell time of 100 μs/pixel. The fluorescence light is collected in the backward direction by the same objective lens, spectrally filtered (HQ540/80M-2P, Chroma, Bellows Falls, VT), and recorded by a photon-counting module (MP-973, PerkinElmer Optoelectronics, Santa Clara, CA). For polarization-resolved measurements, the linear incident polarization is rotated in the sample plane using a half-wave plate (AHWPM05M-980, Thorlabs, Newton, NJ) mounted in a rotation stage (PR50CC, Newport, Irvine, CA) placed just before the objective lens. Images are recorded for each linear incident polarization angle, α, scanned in regular steps between 0° and 180° relative to the horizontal sample direction, x. The linearity of the incident polarization state, as well as the polarization distortions occurring in the detection path, are ascertained by a control measurement according to a methodology developed by Kress, Wang, and colleagues (12,13). Since the rotating half-wave plate is placed after the reflection dichroic mirror, negligible distortion is measured in the excitation path. Since detection is unpolarized, the only parameter relevant here, diattenuation, is negligible in the detection path.

Data processing and display

Raw data, consisting of image stacks of photon counts (where the third dimension corresponds to the angle α), were processed using a program written in Matlab. Background signal, although very weak, was systematically measured in a dark area of the image and subtracted from the data set. In the case of weak signals, photon counts were summed up with the eight-neighbor pixels. Then, numerical values of parameters S₂, φ₂, $S_4^{\left(\text{s}\right)}$, and $S_4^{\left(\text{a}\right)}$ (see definitions in the Theory section) were directly computed at every pixel of interest by applying Eqs. 10–16. Data points were subsequently filtered, following the same approach as described in Kress et al. (12). In the results presented here, the criteria were 1), a total number of photons, $I_0={\sum }_{i=1}^{N}I\left({\alpha }_i\right)$, larger than 5000, to ensure a reasonable precision on the retrieved parameters (12); 2), a normalized χ-square value <3, a value that was found to discard data affected by signal instabilities such as sample drift, photobleaching, etc. For selected points, displayed filtered-out distribution, $\tilde{p}\left(\phi \right)$, was calculated as $\tilde{p}\left(\phi \right)=1+S_2\text{cos}\left[2\left(\phi -{\phi }_2\right)\right]+S_4^{\left(\text{s}\right)}\text{cos}\left[4\left(\phi -{\phi }_2\right)\right]+S_4^{\left(\text{a}\right)}\text{sin}\left[4\left(\phi -{\phi }_2\right)\right]$. Maps of the total intensity, I₀, the symmetry order parameters, and the χ-square values are provided in the Supporting Material for all investigated samples.

Numerical simulations

The numerical data set (see Results) was generated using a cone model of aperture ψ for the effective distribution function (see definition in the Theory section), defined as

$$p\left(\phi \right)=\{\begin{array}{ll}1,\hfill & \text{if}\left|\phi \right|\le \psi /2\hfill \\ 0,\hfill & \text{else},\hfill \end{array}$$ (1)

where −π < φ < π, and φ = 0 corresponds to the direction locally perpendicular to the membrane. The fluorescence intensity I(α) was calculated at every pixel of the membrane by means of Eq. 3, scaled in agreement with the desired value of I₀, and an artificial photon-counting noise was added using a Poisson random number generator.

Theory

Fluorescence response from an ensemble of dipoles under polarized excitation

In the model, the excitation light, $\overrightarrow{E}$, is assumed to be linearly polarized in the sample plane, oriented by an angle α with respect to the horizontal x axis, as illustrated in Fig. 1 c. The polarization dependence of the collected two-photon fluorescence intensity in a steady-state regime can be written as (11)

$$I\left(\alpha \right)\propto {\int }_0^{\pi }\text{d}\theta \text{sin}\theta {\int }_0^{2\pi }\text{d}\phi {\left|\overrightarrow{\mu }\left(\theta ,\phi \right)\cdot \overrightarrow{E}\left(\alpha \right)\right|}^{4}f\left(\theta ,\phi \right)J\left(\theta \right),$$ (2)

where the ∝ sign encompasses intensity factors and collection efficiency. f(θ,φ) is the averaged orientational distribution function of fluorophores, defined by their 3D orientation (θ,φ) in the macroscopic sample frame. $\overrightarrow{\mu }=\mu \left(\text{sin}\theta \text{cos}\phi ,\text{sin}\theta \text{sin}\phi ,\text{cos}\theta \right)$ is the absorption dipole vector of the fluorophores, θ is their angle with respect to the z axis perpendicular to the sample plane, and φ is the angle of their (x,y) sample-plane projection with respect to the x axis. The factor J(θ) is the detection probability of fluorescence that takes into account the out-of-plane orientation, θ, of the dipole and the numerical aperture of the objective lens, as introduced in Axelrod (1) and further adapted in Kress et al. (12) for unpolarized detection. We assume here that the incident polarization lies in the sample plane with $\overrightarrow{E}=\left(\text{cos}\alpha ,\text{sin}\alpha ,0\right)$. Note that a high-NA focusing does not maintain linear polarization over the entire focal volume, with a contribution of longitudinal polarization of ∼40% relative to the in-plane component appearing in its border (32). This contribution is, however, negligible here, since the excitation-field amplitude is brought to the fourth power in Eq. 2.

Due to the in-plane nature of the excitation field, only in-plane components of the $\overrightarrow{\mu }$ vector will contribute to Eq. 2, leading to a separation of the variables θ and φ in the dot product. We therefore define an effective 2D distribution function, p(φ), so that Eq. 2 can be written as

$$\begin{array}{l}I\left(\alpha \right)\propto {\int }_0^{2\pi }{\left|{\overrightarrow{\mu }}^{2D}\left(\phi \right)\cdot \overrightarrow{E}\left(\alpha \right)\right|}^{4}p\left(\phi \right)\text{d}\phi \\ \propto {\int }_0^{2\pi }{\text{cos}}^4\left(\phi -\alpha \right)p\left(\phi \right)\text{d}\phi ,\end{array}$$ (3)

with ${\overrightarrow{\mu }}^{2D}\left(\phi \right)=\mu \left(\text{cos}\phi ,\text{sin}\phi ,0\right)$ and

$$p\left(\phi \right)={\int }_0^{\pi }f\left(\theta ,\phi \right){\text{sin}}^5\left(\theta \right)J\left(\theta \right)\text{d}\theta .$$ (4)

The effective distribution function p(φ) is not a sample-plane projection of the 3D function f(θ,φ), nor of its 2D section. As is apparent in Eq. 4, it is an integrated function over all out-of-plane contributions, weighted by the photoexcitation effect, and it strongly emphasizes responses from fluorophores lying in the sample plane, as illustrated in Fig. 1, c and f. For functions with a cylindrical symmetry axis lying in that plane, the shape of p(φ) describes well the angular constraint behavior undergone by the fluorophores, making it a valuable reporter of molecular order.

Symmetry decomposition of the effective distribution function

The angular distribution function p(φ) is intrinsically periodic with a period of 2π. Without loss of generality, it can therefore be expanded as an infinite circular decomposition resembling an infinite Fourier series,

$$p\left(\phi \right)=p_0\left[1+\sum _{n=1}^{+\infty }{S}_n\text{cos}\left[n\left(\phi -{\phi }_n\right)\right]\right],$$ (5)

that is characterized by an infinite set of parameters S_n and φ_n. The parameter S_n, which denotes a molecular order parameter of nth symmetry or nth symmetry order, characterizes the amplitude of this symmetry order in the effective distribution function. The angle φ_n refers to its orientation in the sample plane.

Inserting Eq. 5 into Eq. 3, using orthogonality properties of cosine functions, allows us to write I(α) as

$$I\left(\alpha \right)\propto 1+\frac{2S_2}{3}\text{cos}\left[2\left(\alpha -{\phi }_2\right)\right]+\frac{S_4}{6}\text{cos}\left[4\left(\alpha -{\phi }_4\right)\right].$$ (6)

This equation establishes that the two-photon fluorescence intensity is exclusively sensitive to the second and fourth symmetry orders of the effective distribution, p(φ). To illustrate how these parameters are related to p(φ), Fig. 2 shows various cases of arbitrary distributions p(φ) together with the angular features carried by the second and fourth symmetry orders. It appears clearly that the second symmetry order carries mainly information about the directionality of the distribution, quantified by the value of S₂ and its overall orientation angle, φ₂. The fourth symmetry order, quantified by S₄, because of its fourfold symmetry, oriented along the direction φ₄, reveals an additional level of detail about the shape of the distribution, either the peaked nature of the distribution (Fig. 2 B), its abrupt variations (Fig. 2, C and E), or its asymmetry (Fig. 2, F and G). The right column in Fig. 2 shows how these distributions are filtered out by two-photon fluorescence, by plotting the filtered-out distribution $\tilde{p}\left(\phi \right)$, obtained from p(φ) by limiting the sum of Eq. 5 to the terms n = 2 and n = 4 only. In most of the cases, $\tilde{p}\left(\phi \right)$ reproduces the main features of p(φ) with high fidelity, meaning that limiting the distribution function to its second and fourth symmetry orders brings already a high level of information about its shape. This decomposition of the distribution function allows us in particular to manipulate characteristic parameters (symmetry orders and orientations) without needing to invoke a priori known shapes of molecular angular constraint.

Figure 2.

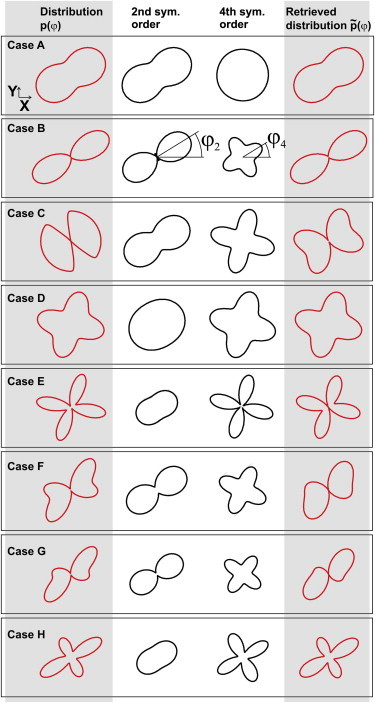
Several examples of effective orientation distributions, p(φ) (first column), angular features carried by the second and fourth symmetry orders (second and third columns, respectively), and filtered-out angular distribution, $\tilde{p}\left(\phi \right)$, as seen by two-photon fluorescence (fourth column). To see this figure in color, go online.

Note that one-photon fluorescence, governed by a photoexcitation term, ${\left|\overrightarrow{\mu }\left(\theta ,\phi \right)\cdot \overrightarrow{E}\left(\alpha \right)\right|}^2$ in Eq. 2, is only sensitive to the second symmetry order (n = 2), so that angular distributions are only seen through this single symmetry order. As illustrated in the second column of Fig. 2, the second symmetry order provides a limited level of information, which can lead to strong ambiguities between possible retrieved distributions, for example, in Fig. 2, A versus C, F versus G, or D versus E.

Retrieval of symmetry order parameters

According to Eq. 6, retrieving orientational distribution information by means of two-photon fluorescence can be reduced to the determination of four parameters, namely, S₂, φ₂, S₄, and φ₄. Fourier algebra provides an elegant way to solve this problem without invoking complex fitting procedures. Using the periodicity of I(α), we write it as a Fourier series,

$$I\left(\alpha \right)\propto 1+\sum _{k=1}^{+\infty }\left[A_k\text{cos}\left(k\alpha \right)+B_k\text{sin}\left(k\alpha \right)\right],$$ (7)

where nonzero terms are only for k = 2 and k = 4, in agreement with Eq. 6. If the measurement is performed at N discrete angles regularly spaced, α₁ = 0, …, α_i = (i−1)π/N, …, α_N = (N−1)π/N (in radians), the Fourier coefficients of the measured signal are given by

$$A_k=\frac{2}{I_0}\sum _{i=1}^{N}I\left({\alpha }_i\right)\text{cos}\left(k{\alpha }_i\right)$$ (8)

$$B_k=\frac{2}{I_0}\sum _{i=1}^{N}I\left({\alpha }_i\right)\text{sin}\left(k{\alpha }_i\right),$$ (9)

where $I_0={\sum }_{i=1}^{N}I\left({\alpha }_i\right)$, so that the distribution parameters are directly obtained using

$$S_2=\frac{3}{2}\sqrt{A_2^2+B_2^2},$$ (10)

$$S_4=6\sqrt{A_4^2+B_4^2},$$ (11)

$${\phi }_2=\frac{1}{2}\text{arctan}\left(B_2,A_2\right),$$ (12)

$${\phi }_4=\frac{1}{4}\text{arctan}\left(B_4,A_4\right),$$ (13)

where arctan denotes here the four-quadrant inverse tangent function. One can show mathematically that Eqs. 8 and 9, which use a discrete sum to compute Fourier coefficients instead of continuous integrals, are valid for N ≥ 5 in our specific case, where we only consider k = 2 and k = 4.

Equations 10–13 show that the order parameters S₂, S₄, φ₂, and φ₄ can be independently obtained from the measured intensity, I(α_i). They play distinct roles in the description of the angular distribution, as discussed above. In particular, the second order governs the directionality of this function. This can be emphasized by writing Eq. 6 so that all angular dependences are written relative to φ₂,

$$I\left(\alpha \right)\propto 1+\frac{2}{3}{S}_2\text{cos}\left[2\left(\alpha -{\phi }_2\right)\right]+\frac{1}{6}{S}_4^{\left(\text{s}\right)}\text{cos}\left[4\left(\alpha -{\phi }_2\right)\right]+\frac{1}{6}{S}_4^{\left(\text{a}\right)}\text{sin}\left[4\left(\alpha -{\phi }_2\right)\right],$$ (14)

with

$$S_4^{\left(\text{s}\right)}=S_4\text{cos}\left[4\left({\phi }_4-{\phi }_2\right)\right],$$ (15)

$$S_4^{\left(\text{a}\right)}=S_4\text{sin}\left[4\left({\phi }_4-{\phi }_2\right)\right].$$ (16)

It is clear in Eq. 14 that 1), the angle φ₂, which reports on the main orientation of the distribution, introduces an angular shift of the response; and 2), the three remaining parameters, S₂, $S_4^{\left(\text{s}\right)}$ (where superscript s denotes symmetric), and $S_4^{\left(\text{a}\right)}$ (where superscript a denotes antisymmetric) describe the shape of the distribution independent of its orientation φ₂ in the sample plane. Fig. 3 depicts the values of these parameters, plotted for each case of Fig. 2, showing their distinct roles. $S_4^{\left(\text{a}\right)}$ is nonvanishing only for asymmetric distributions (e.g., Fig. 2, cases F and G). In the case of a symmetric distribution, (φ₄ − φ₂) is indeed either 0 or 45°, leading to $S_4^{\left(\text{a}\right)}=0$. In contrast to previously used decompositions based on Legendre polynomials, the circular decomposition of the effective distribution function therefore provides information on the magnitude of its symmetry orders (S₂, $S_4^{\left(\text{s}\right)}$), on its global orientation, φ₂, but also on its departure from cylindrical symmetry (magnitude of $S_4^{\left(\text{a}\right)}$), which is useful information in the case of strongly distorted orientational mechanisms. In the examples given in Fig. 2, only cases F and G exhibit this property, with a more pronounced departure to symmetry for G, as emphasized by its stronger $S_4^{\left(\text{a}\right)}$ component.

Figure 3.

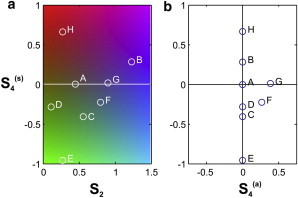
Plot of the values of S₂, $S_4^{\left(\text{s}\right)}$, and $S_4^{\left(\text{a}\right)}$ for each distribution case in Fig. 2. (a) Plot projected in the $\left(S_2,S_4^{\left(\text{s}\right)}\right)$ plane. (b) Plot projected in the $\left(S_4^{\left(\text{a}\right)},S_4^{\left(\text{s}\right)}\right)$ plane. To see this figure in color, go online.

Results

Numerical simulations

To quantify its precision, the method proposed here was tested on a simulated data set, mimicking a spherical membrane, in which a fluorescent probe was inserted along the lipid direction. The effective distribution function of the probe in the membrane was modeled using a cone of angular aperture ψ = 100° (see Materials and Methods) pointing in a direction perpendicular to the membrane, with a total intensity of I₀ = 5000 photons on the membrane, values that are consistent with experimental results reported here.

The results are depicted in Figs. 4 and S1. In Fig. 4 a, processed pixels are displayed using the same colorscale as in Fig. 4 b, where there is a unique color associated with every set of values $\left(S_2,S_4^{\left(\text{s}\right)}\right)$. Predictably, it shows values distributed homogeneously over the contour of the membrane. Polar plots of the corresponding filtered-out distributions $\tilde{p}\left(\phi \right)$ are superimposed as illustrations for a few points. In agreement with the model that was chosen, they show a clear directionality perpendicular to the membrane contour.

Figure 4.

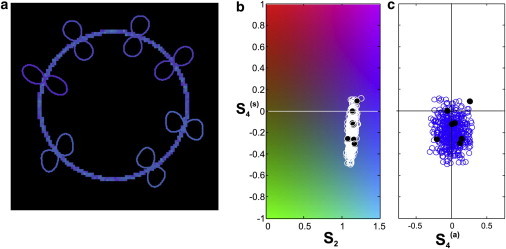
(a) Results on simulated data. The color at each pixel indicates the value of S₂ and $S_4^{\left(\text{s}\right)}$, based on the same colorscale as in b. The retrieved, $\tilde{p}\left(\phi \right)$, is shown for a few selected points. (b) Distribution of $\left(S_2,S_4^{\left(\text{s}\right)}\right)$ values. (c) Distribution of $\left(S_4^{\left(\text{a}\right)},S_4^{\left(\text{s}\right)}\right)$ values. To see this figure in color, go online.

The distributions of the obtained values of S₂, $S_4^{\left(\text{s}\right)}$, and $S_4^{\left(\text{a}\right)}$ are summarized in Fig. 4, b and c. The mean values were found to be $\langle S_2\rangle =1.13$, $\langle S_4^{\left(\text{s}\right)}\rangle =-0.20$, and $\langle S_4^{\left(\text{a}\right)}\rangle =0$. The spread of the values, which shows the ultimate uncertainty of the method, was quantified through their standard deviation. It was found that SD(S₂) = 0.03, $\text{SD}\left(S_4^{\left(\text{s}\right)}\right)=0.12$, and $\text{SD}\left(S_4^{\left(\text{a}\right)}\right)=0.12$. Additional simulations, which are not displayed here, show that these standard deviation values 1), are the same irrespective of the effective distribution, p(φ), that was chosen to generate the data set; and 2), only depend on the total intensity, I₀, and scale according to $1/\sqrt{I_0}$.

One can see that the uncertainty for $S_4^{\left(\text{s}\right)}$ and $S_4^{\left(\text{a}\right)}$ is systematically four times larger than that on S₂, which is a direct consequence of the factors in Eqs. 10 and 11. Nevertheless, the overall level of precision accessible by the method under a reasonable number of photon counts make it sensitive enough to identify specific responses on physical samples, as demonstrated in the next sections.

Molecular order in lipid membranes

Measured values of S₂, $S_4^{\left(\text{s}\right)}$, and $S_4^{\left(\text{a}\right)}$ for the case of the di-8-ANEPPQ lipid probe embedded in artificial multilamellar DPPC vesicles (MLVs) and COS 7 cell membranes are depicted in Fig. 5, using the same format as in Fig. 4. Raw data are supplied in the Supporting Material. Measurements were performed in the equatorial plane of the membrane 3D contour, where the distribution is expected to lie in the sample plane. In all cases, the asymmetric contribution was found to be negligible, with $\langle S_4^{\left(\text{a}\right)}\rangle \sim 0$, clear evidence for symmetric distributions, as expected from the membrane geometry.

Figure 5.

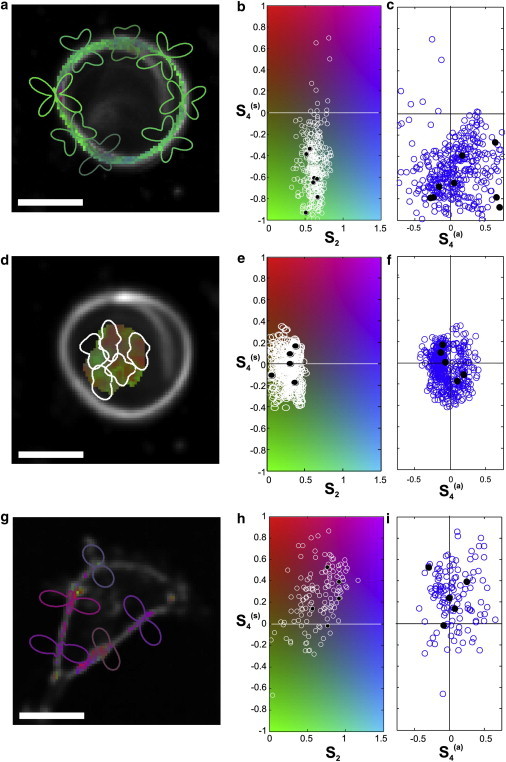
(a) Results on the outer part of an MLV made of DPPC doped with the di-8-ANEPPQ lipid probe. The color at each pixel indicates the values of S₂ and $S_4^{\left(\text{s}\right)}$, based on the same colorscale as in b. The retrieved distribution, $\tilde{p}\left(\phi \right)$, is shown for a few selected points. (b) Distribution of $\left(S_2,S_4^{\left(\text{s}\right)}\right)$ values. (c) Distribution of $\left(S_4^{\left(\text{a}\right)},S_4^{\left(\text{s}\right)}\right)$ values. (d–f) Same analysis as described in c–e in the central area of the MLV. (g–i) Same analysis as in c–e on a COS 7 cell doped with di-8-ANEPPQ. Scale bars, 10 μm. To see this figure in color, go online.

In the case of artificial membranes made of MLVs, very similar observations could be made from one MLV to the other. The distribution of the lipid probe fluorophores on the outer part of the multilayer structure (Fig. 5, a–c, and S2) is shown to exhibit a high degree of order (〈S₂〉 = 0.62) together with a relatively high fourth-order contribution ($\langle S_4^{\left(\text{s}\right)}\rangle =-0.52$). The resulting filtered-out effective distribution is depicted for several points along the membrane contour (Fig. 5 a). The filtered-out distribution function, $\tilde{p}\left(\phi \right)$, represented for several points of the membrane shows typical representations of a hollow distribution that narrows in its central part, similar to Fig. 2, case C. Possible geometric models compatible with these features will be discussed in the next section. The inner part of the multilayer assembly (Figs. 5, d and e, and S3) exhibits an unambiguously different order, with the symmetry order parameters (〈S₂〉 = 0.28 and $\langle S_4^{\left(\text{s}\right)}\rangle \sim 0$) showing a weaker directionality and a loss of orientational order, as expected from the higher degree of orientational averaging due to the high diversity of membrane curvatures encountered in the center of the MLV.

Interestingly, the values measured on the cell membranes show dramatically different features (Figs. 5, g–i, and S4). Although the second order parameter (〈S₂〉 = 0.64) exhibits values quite similar to those in the outer part of the MLV membrane, the fourth order parameter differs strongly, with a positive value ($\langle S_4^{\left(\text{s}\right)}\rangle =0.26$). The corresponding distribution function, $\tilde{p}\left(\phi \right)$, shows a strong directionality perpendicular to the membrane contour. The observation reported in Fig. 5, g–i, is representative of all observed cells, with some slight variations due to visible cell-to-cell heterogeneities.

Note that the depicted information is obtained here for all pixels of the image; therefore, no particular care must be taken with respect to the membrane direction or shape, in contrast to methods based on linear dichroism or anisotropy. In addition, each pixel contains a set of four different parameters that can provide refined information on the angular distribution function undergone by the fluorescent molecules. This set of parameters contains all accessible information and makes it possible to avoid oversimplification of the model or erroneous distributions.

Discussion

Even though the method described here does not require the use of any model of angular distribution, three commonly applied geometrical models are investigated to provide a comprehensive geometrical picture and a basis of comparison with previous studies. Since we consider only symmetric distributions, $S_4^{\left(\text{a}\right)}=0$. Three models are considered, all characterized by their angular aperture, ψ: 1), a cone model, as defined by Eq. 1; 2), a Gaussian model, defined by

$$p\left(\phi \right)=\text{exp}\left(-2{\phi }^2\text{/}{\psi }^2\right);$$ (17)

and 3), a double Gaussian model (two Gaussian lobes of width σ, angularly distant from ψ) defined by

$$p\left(\phi \right)=\text{exp}\left[-2{\left(\phi -\psi /2\right)}^2/{\sigma }^2\right]+\text{exp}\left[-2{\left(\phi +\psi /2\right)}^2/{\sigma }^2\right],$$ (18)

where −π < φ < π. The first two cases are more representative of molecules embedded in a disordered medium, such as lipid probes in a membrane, whereas the third case would be more suited for a membrane protein label, for instance (Fig. 1 d). For all cases, we computed the values of S₂ and $S_4^{\left(\text{s}\right)}$ using, in agreement with Eqs. 5 and 15 (where φ₂ was set to 0),

$$\begin{array}{l}{S}_2=\frac{2}{p_0}{\int }_{-\pi }^{\pi }p\left(\phi \right)\text{cos}\left(2\phi \right)d\phi ,\\ S_4^{\left(\text{s}\right)}=\frac{2}{p_0}{\int }_{-\pi }^{\pi }p\left(\phi \right)\text{cos}\left(4\phi \right)d\phi ,\end{array}$$

with $p_0={\int }_{-\pi }^{\pi }p\left(\phi \right)\text{d}\phi$.

The values of S₂ and $S_4^{\left(\text{s}\right)}$ obtained for different angular apertures ψ are plotted for the cone and Gaussian models in Fig. 6 a, and for the double Gaussian model, for two different values of σ, in Fig. 6 b. As expected, for all models, when the angular aperture, ψ, increases, the value of S₂ decreases, consistent with loss of directionality and angular constraint. Of more interest, the value of $S_4^{\left(\text{s}\right)}$ clearly exhibits different behavior depending on the model used. Starting from high positive values for all models when ψ = 0, $S_4^{\left(\text{s}\right)}$ decreases regularly down to zero for the Gaussian model when ψ increases (Fig. 6 a, red). For the cone model, $S_4^{\left(\text{s}\right)}$ changes its sign, becoming negative for ψ > 90°, with an extreme negative value of $S_4^{\left(\text{s}\right)}=-0.43$ for ψ = 130°, and then tends back toward 0 for higher ψ (Fig. 6 a, black). This analysis shows that closed distributions within a given angular aperture (from the sharp cone to the smoother Gaussian function) will be confined within a given range for $S_4^{\left(\text{s}\right)}$ which cannot be <−0.43. The way to increase this range is to create a higher degree of fourth-order symmetry in the distribution, which is provided in hollow angular shapes exhibiting two peaks, such as in the double Gaussian function (Fig. 6 b). For the two double Gaussian models, which are more sophisticated, involving two parameters, ψ and σ, one can still observe a clear trend: when ψ increases, $S_4^{\left(\text{s}\right)}$ decreases regularly down to negative values, reaching its lower extreme at an aperture of ψ = 90°, corresponding to distributions having a pure fourfold symmetry, without directionality (S₂ = 0). It appears that the value of σ determines the amplitude with which $S_4^{\left(\text{s}\right)}$ varies as a function of ψ. Although only two cases of σ are plotted here, other values would produce similar curves, vertically shifted according to the value of σ.

Figure 6.

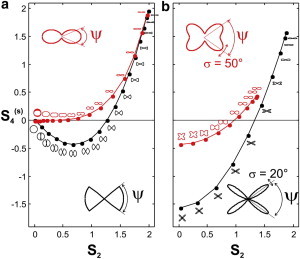
Values of S₂ and $S_4^{\left(\text{s}\right)}$ for different geometrical models of angular distributions, for different values of the angular aperture ψ. The corresponding distribution, p(φ), is plotted for information near each data point. (Insets) Shapes of the geometrical models showing the angles. (a) Cone (black) and Gaussian (red) models. ψ varies from 0° to 180° in steps of 10°. (b) Double Gaussian, for σ = 20° (black) and σ = 50° (red). ψ varies from 0° to 90° in steps of 10°. To see this figure in color, go online.

This confirms the major role played by fourth-order symmetry information, and its ability, together with the second order, to waive ambiguities of the inferred geometric models for the angular distribution function. For instance, due to their clear negative value, the experimental values of $S_4^{\left(\text{s}\right)}$ measured on the external membrane of the MLV make it unrealistic to invoke a Gaussian model to describe the distribution function. What is required instead is a steeper model, such as a cone with ψ ∼ 140° or a double Gaussian with ψ ∼ 65° and σ ∼ 40°, the two models that exhibit quite similar polar plots for the distribution function. Similar to these observations, strong and negative fourth-order values have been observed in DPPC lipid membrane vesicles doped with the lipid probe 1-(4-(trimethylamino)phenyl)-6-phenylhexa-1,3,5-triene (TMA-DPH) (24). The observations in that study are consistent with the fact that both di-8-ANEPPQ and TMA-DPH possess the ability to interact strongly with their nearby lipids present, most probably in the outer membrane leaflet, thus leading to quite strong interactions that differ from a pure harmonic force potential. Note that this observation encompasses both local molecular-scale interaction and mesoscopic-scale behaviors, where the local membrane morphology perturbation, at the subdiffraction scale, might lead to a higher disorder. This is illustrated in the central part of the MLV where the morphology disorder within the excitation focal volume surpasses the molecular-scale constraint, thus leading to a much higher disorder.

In contrast to the observations in artificial lipid membranes, the results obtained on cell membranes indicate a strong directionality of the distribution. Although the angular aperture of the distribution function is very similar in both cases, the fourth-order symmetry observed in cells is positive and of smaller amplitude. This value can be explained neither by a close distribution function of cone/Gaussian shape nor by a hollow function. One possible explanation for this high positive value is the presence of an isotropic population in the excitation focal volume that shifts the $\left(S_2>0,S_4^{\left(\text{s}\right)}>0\right)$ region of Fig. 6 toward lower, still positive values. Such a population can occur if some of the fluorophores do not insert properly into the membrane, or are embedded in completely disordered parts of the membrane (occurring, for example, by vesiculation, endocytosis, etc.). This population would still contribute to the fluorescence signal by an isotropic response. Although the method described here does not in principle allow isolation of such an isotropic contribution, we derive below a basic expression showing that its effect on the retrieved parameters S₂, $S_4^{\left(\text{s}\right)}$, and $S_4^{\left(\text{a}\right)}$ makes it possible to quantify the presence of an isotropic population in some cases. For an oriented species that coexists, in a fraction η, with an isotropic species, in a fraction (1 − η), the angular distribution of Eq. 5 must be generalized as

$$p^{\text{mix}}\left(\phi \right)=p_0\left[\eta \left[1+\sum _{n=1}^{+\infty }{S}_n\text{cos}\left[n\left(\phi -{\phi }_n\right)\right]\right]+\left(1-\eta \right)\right],$$ (19)

where symmetry order parameters S_n and φ_n refer to the pure oriented species. Eq. 19 can be easily simplified as

$$p^{\text{mix}}\left(\phi \right)=p_0\left[1+\sum _{n=1}^{+\infty }{S}_n^{\text{mix}}\text{cos}\left[n\left(\phi -{\phi }_n\right)\right]\right],$$ (20)

where the parameters $S_n^{\text{mix}}$, defined by $S_n^{\text{mix}}=\eta S_n$ refer now to the mixture. The distribution p(φ) can be replaced by p^mix(φ) in all mathematical derivations, so that the method will return $S_2^{\text{mix}}$, $S_4^{\left(\text{s}\right),\text{mix}}$, and $S_4^{\left(\text{a}\right),\text{mix}}$, which are the parameters of the purely oriented system scaled by a factor η. Therefore, if the fraction η has been quantified by another means, the method still allows access to the parameters of the purely oriented system. Alternatively, in the case of a known oriented species, the method allows quantification of the fraction η. In the case of COS 7 cell membranes, presented here, the measured value suggests for instance, that the observed distribution contains a Gaussian (or cone) distribution, together with an isotropic distribution, in fraction 50:50. Removing this population would lead to angular apertures of ∼80°. This is much smaller than the ∼140° aperture that a measurement of only S₂ would give, invoking Gaussian or cone models, as previously reported (12,20). However, this value is compatible with measurements of molecular order, S₂, in membranes under tension, obtained by one-photon fluorescence (12). The apparent high disorder values generally measured in cell membranes using pure second-order information is therefore most likely attributable to additional disordered populations hampering a clear view of the real distribution function, as expected from the complex membrane morphology, dynamics, and heterogeneity that take place at a subdiffraction scale.

Conclusion

It has been shown here that a polarized fluorescence method based on tunable linear dichroism and symmetry decomposition of the angular distribution function of fluorophores can report on refined orientational mechanisms taking place in membranes. Analysis of the accessible second- and fourth-order information, demonstrated for two-photon microscopy, provides a more sophisticated and precise approach. This complements traditional methods, which rely either on the use of a distribution model or on the measurement of pure angular disorder. This method can be applied to any sample containing molecular orientation specificity that can be related to a biological function, such as complex systems related to protein conformational changes in cell membranes of complex shape.