Vertex Models of Epithelial Morphogenesis

Abstract

The dynamic behavior of epithelial cell sheets plays a central role during numerous developmental processes. Genetic and imaging studies of epithelial morphogenesis in a wide range of organisms have led to increasingly detailed mechanisms of cell sheet dynamics. Computational models offer a useful means by which to investigate and test these mechanisms, and have played a key role in the study of cell-cell interactions. A variety of modeling approaches can be used to simulate the balance of forces within an epithelial sheet. Vertex models are a class of such models that consider cells as individual objects, approximated by two-dimensional polygons representing cellular interfaces, in which each vertex moves in response to forces due to growth, interfacial tension, and pressure within each cell. Vertex models are used to study cellular processes within epithelia, including cell motility, adhesion, mitosis, and delamination. This review summarizes how vertex models have been used to provide insight into developmental processes and highlights current challenges in this area, including progressing these models from two to three dimensions and developing new tools for model validation.

Introduction

The generation of shape, or morphogenesis, in biological structures is frequently driven, at least in part, by the deformation of epithelial tissues. In simple epithelial sheets, the cells are all polarized such that their apical sides form one surface of the sheet, while their basal sides form the opposite surface. The cells form tight lateral attachments to each other via surfaces that are oriented perpendicular to the apicobasal axis (Fig. 1 a). Intracellular protein filaments cross the cytoplasm of each cell and attach to specialized cell junctions, typically beltlike structures located on the lateral surfaces of cells that are formed by membrane-bound adhesion molecules. These junctions are localized closer to the apical than basal sides of the cells (Fig. 1 b). One of the types of junction, the adherens junction, acts to tie the surfaces of adjacent cells to each other, and is involved in the transmission of force from cell to cell. The other type of apically localized junction provides a barrier function by inhibiting the movement of water, solutes, and cells from one body compartment to another; this type of junction, exemplified by tight junctions in vertebrates and septate junctions in Drosophila, is less evolutionarily conserved between different types of animals.

Figure 1.

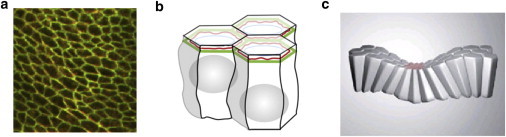
Epithelial sheet morphology and organization. (a) Confocal microscope image of part of the follicular epithelium in Drosophila, with cell membranes visualized using an E-cadherin antibody, illustrating a typical polygonal cell packing geometry. (b) Schematic representation of the organization of neighboring cells in an epithelial sheet, connected via adhesion molecules (green) and cytoskeletal components (red) nearer their apical surface. (c) Schematic representation of epithelial bending associated with apical constriction. Images reproduced from Farhadifar et al. (24) and Lecuit et al. (2).

The highly organized nature of epithelial sheets means that they can achieve complex morphogenetic processes through the coordinated movement and rearrangement of individual cells (Fig. 1 c). Such processes mediate a wide range of important developmental events, such as extensive bending and folding of epithelia, for example during gastrulation (1), or tissue elongation by convergent extension, a process in which cells systematically move and change neighbors (2). Epithelial sculpting can also generate tubular structures, in which the apicobasal polarity defines the inside and outside of the tube and the tight attachments between cells allow for the control of material transfer into and out of the tube. A key example of such tube morphogenesis is the formation of the neural tube in vertebrates (3,4).

Mechanics plays a key role in driving epithelial morphogenesis (2). Cytoskeletal mechanics and cell-cell adhesion both affect individual cell geometry and morphology (5), as well as tissue-level dynamics (6,7). Mechanotransduction or other forms of mechanical feedback may also play a role in regulating or fine-tuning growth during development (8). Recent advances in understanding how mechanical changes in cells orchestrate tissue morphogenesis and remodeling have been facilitated by new imaging tools and fluorescent probes to measure tissue deformation (9) and the dynamics of key proteins within cells and tissues (1,10).

The past decade has witnessed remarkable progress in experimental studies of epithelial dynamics, largely due to increased molecular understanding of epithelial cell biology and advances in live-imaging techniques. Computational modeling offers a complementary tool with which to study the roles of mechanics and cellular signaling in morphogenetic processes. Models can be used to develop abstract representations of biological systems, test competing hypotheses, and generate new predictions that can then be validated experimentally. To this end, a variety of different cell-based modeling approaches have been developed for studying how processes at the level of a single cell affect collective dynamics in epithelial sheets (11,12).

In cell-based models, each cell is characterized by a state vector, which includes information on the cell’s mechanical state (for example, position and velocity) as well as its internal biological state (for example, the cell’s progress through the cell cycle). Such models provide natural candidates for modeling the behavior of multicellular systems. A number of discrete approaches have been developed for modeling cell populations. These vary in type, from fixed-lattice cellular automata and the cellular Potts model, to off-lattice models that allow continuous cell movements.

In this review, we focus on a class of off-lattice models termed “vertex models”, in which each cell is approximated geometrically by a polygon that represents the cell’s membrane. Within vertex models, rules are set up to define how each vertex moves, based on location and connection between vertices and on geometrical features, such as surface area or volume of neighboring cells. The precise rules and methods of implementation and simulation differ between models and may be adapted to a particular biological problem.

Vertex models have been used extensively to investigate the cellular mechanisms and physical mechanics of autonomous epithelial monolayer deformations, which are of considerable importance in development. Key benefits of vertex models over other approaches include their ability to explicitly incorporate cell neighbor rearrangements within an epithelial sheet and the ease with which results may be interpreted biologically. The origins of these models may be traced to the study of inorganic structures such as soap bubbles (13), foams (14), and grain boundaries (15); in all of these systems, surface tension and pressure drive dynamics. Honda and Eguchi (16) were the first to use these models to study epithelial sheet deformations. A comprehensive review of vertex models for biological systems developed up to 2004, and their relation to lattice-based and cell-center models, can be found in Brodland (17). In addition, Hardin and Walston (18) have reviewed studies of the mechanisms and mechanics underlying cell rearrangements of epithelial sheets in comparison to those of nonepithelial deep cells.

In the next section, we provide a thorough description of vertex models, summarizing the underlying equations and most established methods of computational implementation. We then go on to illustrate the utility of these models through recent studies in which adaptations of vertex models were used to address a variety of biological questions. We conclude by discussing future computational challenges in this area.

Vertex Model Approaches

In vertex models, each cell is represented as a polygon, with vertices and edges shared between adjacent cells. Most vertex models represent either a cross-section of an epithelial sheet, or just the apical surface of an epithelial sheet. These simplifications allow one to treat the cells as two-dimensional, reducing computational complexity. The locations of the vertices and the connections among them together provide complete information about the prevailing state of the model cell sheet. On top of this framework of vertices and connecting edges, vertex models include equations of motion that govern how vertices move, given the current configuration of vertices. Additionally, many vertex models incorporate rules that govern changes in connection among vertices, and therefore allow for changes in cell neighbor relationships. These approximations are suitable in the case of tightly packed cell sheets, where the intercellular space is negligible, and is based on experimental observations that cells in epithelial tissues are often arranged in polygonal or polyhedral structures (19) and can move around relative to other cells (20).

Below, we review some common forms of the equations of motion, along with established methods of computational implementation, and typical rules for rearrangements of vertex connectivity.

Equations of motion

In vertex models, changes in cell shape and position over time are largely due to motion of the vertices. Vertices typically obey deterministic equations of motion, under the assumption that in closely-packed cell aggregates the stochastic motion of cells is mitigated by the strong interactions between cells, although it is straightforward to relax this assumption (21). It is standard to make the following two simplifying approximations: first, that motion may be described by considering each vertex to be embedded in a viscous medium that applies a drag force on it with mobility coefficient η; and second, that inertia is vanishing. This leads to first-order dynamics, with the evolution of the position x_i of vertex i determined by

$$\eta \frac{\text{d}{\mathbf{x}}_i}{\text{d}t}={\mathbf{F}}_i,$$ (1)

where F_i(t) denotes the total force acting on vertex i at time t. The mobility coefficient η determines the timescale over which mechanical relaxation occurs.

One difference among vertex models in the literature lies in the definition of the force F_i in Eq. 1. The choice of form for the function F_i reflects which forces are thought to dominate epithelial mechanics for the system being studied. Some commonly modeled forces include tension or elastic forces due to the combined action of a cell’s actomyosin cortex and adherens junctions, or pressure, due to hydrostatic pressure in some cases or some type of membrane conservation in others. Note that the forces acting on each vertex may either be given explicitly (22,23), or else an energy function may be specified, whose gradient is assumed to exert a force on each vertex (16,24). To illustrate this, one example of each type follows. For consistency of notation, in each case we suppose that at time t, each vertex i is associated with a set of cells S_i(t) and there are N(t) cells in the population. We let l_ij(t) denote the length of the cell edge (or bond) i, j shared by vertices i and j, and we denote the apical surface area and perimeter of each cell α by A_α(t) and P_α(t), respectively.

The model of Weliky and Oster (22) and Weliky et al. (25) employs an explicit force-based approach. In this particular model, three components are assumed to contribute to the force on each vertex from each cell containing that vertex. The first two terms describe the tensions in the cell membrane, which act in the direction of the cell membrane and are proportional to the perimeter of the interface. The third term describes the cortical pressure, which is the difference between the osmotic pressure tending to expand the cytoplasm and the restraining elastic pressure generated by the actin polymer fibers. For simplicity the authors assume the cortical pressure to be inversely proportional to the total area of the cell, and directed such that it bisects the internal angle at the vertex. Using the notation we defined earlier, the total force acting on vertex i is thus given by the sum

$${\mathbf{F}}_i=\sum _{\alpha \in S_i}\left({\kappa }_{\alpha }{P}_{\alpha }\left({\hat{\mathbf{u}}}_i^{\alpha }+{\hat{\mathbf{v}}}_i^{\alpha }\right)+\frac{{\beta }_{\alpha }}{A_{\alpha }}{\hat{\mathbf{p}}}_i^{\alpha }\right),$$ (2)

where ${\hat{\mathbf{u}}}_i^{\mathit{\alpha }}$ and ${\hat{\mathbf{v}}}_i^{\mathit{\alpha }}$ are unit vectors parallel to the edge associated with cell α connecting vertex i with its clockwise and counterclockwise neighbors, and ${\hat{\mathbf{p}}}_i^{\mathit{\alpha }}$ is a unit vector outwards from cell α, bisecting the angle between adjacent edges. The parameters κ_α and β_α determine the relative force contributions from the membrane tension and elasticity of the cell, and their values must be specified. The directions of the force vectors in Eq. 2 are illustrated for a single cell in Fig. 2 a. This model was used by Weliky and Oster to demonstrate that force considerations alone could explain the key features of epiboly, a coordinated cell movement during gastrulation in the teleost fish Fundulus heterclitus (22). This model was also applied to the African frog Xenopus laevis, where it was shown that cell motility rules such as contact inhibition and polarized protrusive activity were required to recapitulate normal notochord development (25). These examples reflect a common use of vertex models: examining how altering parameter values or cellular behaviors is likely to affect tissue-level dynamics, which is typically impossible to do in vivo.

Figure 2.

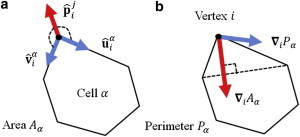
Illustration of key parameters in the explicit force- and energy-based models of vertex mechanics. (a) Forces acting on a given vertex i due to a given cell α associated with it, according to the explicit-force based model given by Eq. 2. (b) Forces acting on the vertex due to the cell according to Eq. 4, derived from the energy-based model given by Eq. 3.

A variation on the above approach is employed in the models of Brodland and co-workers (26–33), where the only forces acting at each vertex are directed along cell edges. This corresponds to the parameter β_α taking the value zero in Eq. 2. In addition, the authors use a finite element-based formulation, in which additional vertices are placed at each cell’s centroid and a triangular mesh is formed. This more detailed description allows the incorporation of mechanical effects of cytoskeletal components on strain fields within the cell. However, it requires the introduction of orthogonal systems of dashpots (viscous truss elements) to avoid cell edges from becoming progressively stiffer as they shorten, an artifact that would prevent cell intercalation (33). These models have been used extensively by these authors in studying the biophysics of cell sorting and engulfment during embryogenesis.

In some cases, rather than explicitly identifying forces, it may be preferable to consider forces arising as a result of energy minimization. For instance, whereas the above description encodes the responses to cell compression and stretching in pressure and tension terms respectively, an alternative, and in some cases more suitable, approach would be to evaluate the stored energy in both the cell body and cell membrane, and sum this over all cells. This total stored energy, U, is a function of cell vertex positions that corresponds to the work required to deform the junctional network of cells.

Some of the earliest studies using an energy-based approach were conducted by Honda and co-workers (16,20,34–36), who investigated how epithelial cells undergoing mechanical relaxation and neighbor exchange processes might minimize their surface area while retaining a constant volume. For our concrete example, however, we will consider an energy function by Farhadifar et al. (24), which has recently seen extensive use in modeling wing disk epithelia. This energy function encodes constraints associated with the limited ability of each cell to undergo elastic deformations, volumetric changes, and other movements due to adhesion to other cells. Using our notation defined earlier, the energy function is defined by

$$U=\sum _{\alpha =1}^N\left(\frac{K_{\alpha }}{2}{\left(A_{\alpha }-A_{\alpha }^{\left(0\right)}\right)}^2+\frac{{\text{Γ}}_{\alpha }}{2}{P}_{\alpha }^2\right)+\sum _{i,j}{\text{Λ}}_{ij}{l}_{ij}.$$ (3)

The area elastic modulus K_α, bond tension parameter Λ_ij, perimeter coefficient Γ_α, and preferred cell area A_α⁽⁰⁾ are all model parameters whose values must be specified. In vertex models using this energy function, the choice of preferred cell area A_α⁽⁰⁾ depends on how cell growth is incorporated into the model. The remaining mechanical parameters are typically assumed to be the same for all cells for simplicity, except in cases where data on variability in cell mechanical behavior are available, or where the model is being used to explore the consequences of nonuniform mechanical properties. For example, in a model of cell sorting at the Drosophila anteroposterior compartment boundary (37), a larger value for Λ_ij was assigned along the compartment boundary to reflect a hypothesized increase in myosin-based tension. Considering the active force arising from this energy function for a given cell, the first summation in the above expression gives rise to an outward force due to limited cell compressibility and an opposing line tension resulting from myosin-dependent cortical contractility, whereas the other summation gives rise to a force associated with cell-cell adhesion. Note that the bond tension parameters Λ_ij may take positive or negative values, according to whether surface tension or adhesion dominates the behavior of cell boundaries.

For a given energy function U, the force on each vertex is determined by the negative derivative of the energy with respect to the coordinates of that vertex, F_i = −∇_iU, where ∇_i denotes the gradient operator evaluated at x_i. Computing the gradient of Eq. 3 and exploiting the fact that the movement of vertex i affects only the energy of the cells associated with it, the force F_i may be written explicitly as

$${\mathbf{F}}_i=\sum _{\alpha \in S_i}\left(-K_{\alpha }\left(A_{\alpha }-A_{\alpha }^{\left(0\right)}\right){\nabla }_i{A}_{\alpha }-{\text{Γ}}_{\alpha }{P}_{\alpha }{\nabla }_i{P}_{\alpha }\right)-\sum _j{\text{Λ}}_{ij}{\nabla }_i{l}_{ij},$$ (4)

where now the first sum runs over cells associated with vertex i and the second sum runs over vertices sharing an edge with it. The directions of the force vectors in Eq. 4 are illustrated for a single cell in Fig. 2 b. Note that while K_α and Γ_α in Eq. 4 serve an analogous purpose to β_α and κ_α in Eq. 2, the effect of varying these parameters is different in the two force expressions. The directions of the force vectors also differ, as highlighted in Fig. 2. Conceptually, force-based approaches may seem more appropriate for dynamic tissues far from mechanical equilibrium or those for which forces are well characterized, whereas an energy-based approach is more intuitive when studying a system relaxing toward equilibrium or one in which nonlocal effects are thought to play a role. However, we emphasize that these two approaches are equivalent when simulated using Eq. 1.

Whereas some simulations using energy-based models (38) derive forces and solve an equation of motion for each vertex as given by Eq. 1, other studies assume that the tissue evolves quasistatically, so that the minimum energy of the system is obtained instantaneously between cell rearrangement events (24). If stochastic effects are thought to be significant, then an alternative method of simulation is to use a Metropolis algorithm, in an analogous manner to the cellular Potts model (39). In this approach (40), at each time step a cell is chosen to make a trial displacement, which is tested to see if it decreases the total energy of the system and is accepted with Boltzmann-weighted probability. For a single realization, this simulation method is more efficient than numerical integration of equations of motion. However, it suffers from the lack of an intuitive meaning or physical correlate for the temperature parameter that weights the probability of accepting a trial displacement causing an energy gain. Furthermore, this method, developed for finding equilibrium states, lacks a well-defined timescale, because the progression of the simulation through energy states in an attempt to locate an energy minimum does not necessarily correspond to the progression of states taken by a developing system.

Junctional rearrangements

Many of the earliest vertex models dealt with cross-sections of epithelial sheets, and so did not need to permit cell neighbor rearrangement. Later vertex models instead represented the epithelial sheet within its plane (that is, en face), and so to faithfully describe cell behavior, had to allow cell neighbor rearrangements (that is, changes in connectivity among the vertices in the model). To accurately describe epithelial dynamics, cells must be allowed to form and break bonds, and be prevented from (self) intersecting. This is implemented through simple operations, such as cell neighbor exchange (also called a T1 transition) and, in certain circumstances, vertex/edge merging (a T3 transition). The evolution of the system is thus a combination of relaxation to mechanical equilibrium and changes in tissue connectivity according to the prescribed cell rearrangement processes.

Cell neighbor exchange occurs when the distance between two connected vertices becomes less than a minimum threshold distance, generally much smaller than a typical edge length. The vertices are moved and placed a specified distance apart and the local tissue connectivity is altered, as illustrated in Fig. 3 a. If the two neighboring vertices are only associated with a single cell, for example on the boundary of a tissue, then the two vertices are instead merged. Similar types of cell neighbor exchanges, or intercalations, occur commonly in real epithelial tissues. They may occur passively as the tissue undergoes global deformation, for example during germband extension (41), or may be an active process as cells dynamically change their shape.

Figure 3.

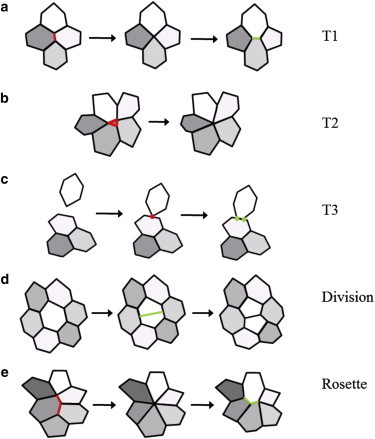
Schematic diagram of junctional rearrangements, cell division, and cell removal in vertex models. (a) A T1 transition, in which two vertices sharing a short edge merge into a single vertex, which then decomposes into two new vertices such that the local network topology is changed. (b) A T2 transition, in which a cell shrinks to zero area and is removed, corresponding to delamination and/or apoptosis. (c) Example of a T3 transition, in a vertex/edge intersection is avoided by replacing the approaching vertex with two new vertices that are associated with the element. (d) Cell division, in which a parent cell is divided (in this case through its short axis) through the addition of two new vertices, resulting in two daughter cells. (e) Formation and resolution of multicellular rosettes, a generalization of T1 transitions involving a larger number of cells. (a–e) Edges or vertices that are removed (red); edges or vertices that are created (green).

Vertex/edge merging may be implemented to allow the simulation of epithelial sheets with voids (for example, to study the closure of wounds in tissues) and moving boundaries, and occurs when a vertex is about to intersect the edge of another cell (38). In this case the vertex is incorporated into the element. An example of such an operation is illustrated in Fig. 3 c.

Computational details

As previously discussed, the most common method of simulating vertex models is to solve equations of motion for each vertex. In practice, time is discretized and at each time step the following steps are performed:

• 1.The internal state of each cell (for example, its progress through the cell cycle) is updated;
• 2.Any required junctional rearrangements, cell divisions, or cell death/delaminations are implemented; and
• 3.Equation 1 is solved numerically for each vertex in parallel, for example using a forward Euler discretization, and the position of each vertex is updated.

The time taken to perform Steps 1 and 3 is expected to scale approximately linearly with the number of cells. The main computational burden in such simulations lies in recognizing and performing junctional rearrangements. Although searching for T1 and T2 transitions may be performed efficiently, T3 transitions are more computationally costly to search for and implement. Further computational details on the implementation of vertex models are provided in Fletcher et al. (42).

Uses and Extensions of the Vertex Model

Vertex models have been used to describe a variety of biological phenomena. We present a summary of applications of vertex models to epithelial morphogenesis in Table 1, that highlights the key strengths of each of these models. In many cases, this has necessitated modifying or extending previously developed vertex models. A summary of some of these adaptations is included below.

Table 1.

Summary of applications to date of vertex models to epithelial morphogenesis

Process	System	Reference(s)	Key strength
Size regulation in wing disk	Drosophila	(8,24,51,53–55)	Addresses combined effect of mechanics and morphogen signaling on tissue size.
Regulation of dorsoventral compartment boundary	Drosophila	(57)	Addresses dynamics of cell bond tension along boundary.
Regulation of anteroposterior compartment boundary	Drosophila	(37,56)	Provides quantitative estimates for tensions required for boundary formation.
Germband extension	Drosophila	(67)	Compares hypothesis mechanisms for active cell intercalation.
Ventral furrow formation	Drosophila	(80)	Addresses emergence of ventral band of constricted cells.
Cell division and tissue elongation in wing disk	Drosophila	(21,67,72,81)	Assesses effect of polarized tension on cell and tissue orientation.
Dorsal appendage formation	Drosophila	(63)	Assesses effect of patterned tension on three-dimensional tissue deformation and cell rearrangements.
Cell geometric order in eye	Drosophila	(82)	Allows direct comparison with observed cell shape changes.
Convergent extension and cell sorting	Multiple	(17,27,28,83–86)	Allows comparison of cell-level hypotheses.
Neurulation	Multiple	(29,32)	Assesses three-dimensional morphogenetic movements.
Rosettes in visceral endoderm	Mouse	(23)	Compares scenarios with(out) rosette formation.
Polarity in blastocyst	Mouse	(65)	Assesses mechanisms underlying stable three-dimensional cell packing.
Notochord morphogenesis	Xenopus	(25)	Compares hypothesized cell motility rules.
Epiboly	Fundulus	(22)	Allows direct comparison with observed cell rearrangements and shape changes.
Cone photoreceptor organization	Zebrafish	(43)	Addresses interplay between mechanical factors and planar cell polarity signaling.

Patterning of mechanical properties

The pioneering work of Odell et al. (40,49) first demonstrated the use of vertex models to study how spatial patterning in either active forces or passive mechanical properties may lead to tissue deformation. In these studies, a cross section of an embryo was modeled as a ring of cells; for each cell, the four defining vertices were interconnected and subject to a viscoelastic force. The apical edges, located on the outer side of the ring, were assigned the additional hypothesized property of actively contracting in response to stretch. Small initial asymmetries were shown to lead to changes in the overall shape of the tissue. Depending on details included in the model, such as the compressibility of the embryo interior, different patterns of deformation could emerge, leading to simulations that qualitatively resembled events such as sea urchin gastrulation or Drosophila ventral furrow formation.

Subsequent studies by several groups have examined a variety of alternative patterns of force and material properties that can give rise to similar tissue deformations. In Drosophila ventral furrow formation, for example, models have suggested a potential role for pushing by cells adjacent to the furrow, or buckling due to uniform changes in apical tension throughout the tissue; such modeling studies have been influential in guiding experimental work in this intensely studied system (45). Similar approaches have also been used to examine the mechanics underlying tissue deformation in other systems, including a newly proposed mechanism driving invagination of the optic cup in vertebrates, where, in contrast to the above examples, invagination is apically convex (46,47).

Cell growth, division, and death

Recent vertex models dealing with the behavior of cells within the plane of the epithelial sheet have borrowed many elements from models of foams; however, one feature that is not generally found in foams but is very important to the structure of biological tissues is the ability of cells to grow, divide, and die. Operations representing cell division and death both modify tissue connectivity and add significant computational complexity, but in many cases are essential components of the biological process being studied. Below, we describe how some models have implemented these processes, and some of the biological insights gained from such models.

Usually, it is assumed that when a cell undergoes division, it splits into two cells of equal area (48). This can be accomplished by placing two new vertices where a dividing line that passes through the cell’s centroid intersects the cell perimeter, thereby creating two daughter cells from a single parent cell (Fig. 3 d). Initially, however, a specific dividing line or angle of mitosis must be chosen. This may be drawn from a uniform distribution for isotropic cell division, or in the direction of the shortest axis through the cell’s centroid (35,48), or biased in a certain direction if directed proliferation and cell polarity are considered (87). It has been shown that the choice of division plane orientation can have a significant effect on the resulting epithelial sheet topology, and in particular on the frequency of hexagonal cells within the tissue (50).

Many vertex models that include cell proliferation assume that cell divisions occur stochastically rather than including a detailed description of the cell cycle. Such models may neglect cell growth between mitotic events and assign to each cell a random time to the next division (24), for example, or stochastically increase each cell’s volume at each time step and select mitotic cells as those whose volume exceeds some threshold (23,87). In some cases, however, it may be important that the regulation of cell growth and division may be more explicitly modeled. One recent example is a model of wing imaginal disk size regulation developed by Aegerter-Wilmsen et al. (51), in which growth and progress of each cell through the cell cycle was modulated by the concentrations of key proteins associated with mechanotransduction and morphogen signaling. This model, discussed further in the next section, supports the hypothesis that wing disk growth is regulated by both growth factors and compression, and shows the utility of vertex models in studying the poorly understood topic of size control.

In models that incorporate apoptosis or delamination, the removal of cells with small areas is also allowed through what is termed a T2 transition (Fig. 3 b). In this case, cell death occurs if the area of a cell drops below some threshold, often after becoming triangular through a series of T1 transitions as it shrinks in size. In some models, the removal of small elements is an artifact of the mechanical model itself (24). In other models, however, cell death or delamination is modeled explicitly, as for example in a recent study of crowding-induced cell delamination in the fly notum (88), which used a vertex model in combination with live imaging to establish a mechanical component to cell competition (89) in this system.

One biological question that has been addressed using vertex models that incorporate cell death and division is the control of packing geometries in an epithelial sheet. Using the Drosophila wing disk as a model system, Farhadifar et al. (24) characterized the distribution of polygon number, or sidedness, among the cells, as well as the relationship between sidedness and cell area. They then showed that these characteristics could be simulated using a vertex model including an energy function with cell elasticity and junctional forces, randomized cell division, and T1 and T2 type network rearrangement. The range of parameters for the energy function that produced such results was relatively wide, but could be refined by comparing experimental and simulated ablation of individual cell boundaries (24).

In addition to presenting an analysis of the differential contributions of cell mechanics and cell proliferation, this study also provided a realistic model for wing disk epithelia that has been utilized in much subsequent work, including a demonstration of a role for tissue deformation in regulating planar polarity (52), investigations into possible roles for morphogen gradients or physical forces in regulating cell division (24,51,53–55), and studies of the role of patterned tension in forming straight compartment boundaries (37,56,57). We discuss efforts made to analyze vertex model behavior in more detail later, but for now highlight the need for further work to gain a systematic understanding of how the chosen implementation of cell growth, division, and death affect the resulting equilibrium and dynamic behavior of a simulated epithelial sheet.

Incorporating patterning and feedback

Some cases of epithelial morphogenesis can be modeled reasonably well by assuming specified patterns of cellular mechanical properties, but without explicitly modeling the processes leading to this patterning. In many cases, however, the mechanical patterning and the tissue-shape changes due to this patterning may happen concurrently and can affect or feed-back into each other. Vertex models can be easily modified to incorporate mechanical or chemical feedback, and in fact, one of the earliest vertex models included a simple type of feedback in assuming the cellular property of stretch-activated contraction (40,49). Recent models have expanded the types and complexity of patterning or feedback considered, as described in the examples below, and this remains a promising area for future development.

Some recent investigations have incorporated a computational model describing morphogen transport within a tissue coupled to a vertex model describing cell behavior (56,58). These include the theoretical study by Smith et al. (58), who showed how an arbitrary Lagrangian-Eulerian formulation and the finite-element method may be used to numerically solve reaction-diffusion equations governing morphogen transport within a tissue. In this work the rate of growth of each cell was considered to increase linearly with the local concentration of a generic morphogen. An alternative method was adopted by Schilling et al. (56), who modeled the production, diffusion, and local sensing of the signaling molecule Hedgehog (Hh) in the context of cell sorting at the anterior/posterior boundary in the Drosophila wing primordium. Here the authors applied the finite-volume method, a numerical discretization that is common in computational fluid dynamics, to solve the reaction-diffusion equations governing Hh signaling. The authors’ model of cell mechanics, built on the energy-based model of Farhadifar et al. (24) described in Eq. 3, included a modified bond tension parameter Λ_ij, which depended on the ratio of the concentrations within the cells sharing vertices i and j of a putative target gene of Hh signaling. This modification allowed the intracellular response to the Hh pathway to influence cell mechanical behavior. As more detailed biological information becomes available, it will become important to develop accurate methods of solution for such transport models when coupled to vertex models on growing or deforming surfaces.

Other recent investigations have examined interactions between mechanical properties and signaling at a cellular level (43,51). One recent example is a model for the highly ordered packing of cells in the zebrafish retina (43). This model includes a phenomenological description of planar cell polarity (PCP) in addition to a vertex model describing the shapes and locations of cells. The localization of PCP proteins affects the mechanical model through terms representing edge tension, and thus affects tissue geometry. The tissue geometry, in turn, constrains the interactions that can occur between PCP proteins within a cell or between neighboring cells; these interactions shape the subsequent localization of PCP proteins. Simulation results suggested that the highly ordered cell packing in the adult retina requires the interactions of an externally applied force, representing intraocular pressure, and progressive growth and division of cells exhibiting PCP.

This hypothesis was supported by observations of a polarized distribution of Crumbs2a protein, which is important in maintaining the apical-basal polarity thought to mediate cell-cell adhesion in this system. Further model predictions of cone mosaic defects arising from mechanical perturbations were matched by observations of the cone mosaic in bugeye mutant fish, whose phenotype includes elevated intraocular pressure. This combination of modeling and experiment sheds light on the complex and bidirectional nature of the relationship between PCP and cell mechanics, and could in future be extended to investigate how the global PCP orientation is preserved in tissues exhibiting large-scale cell movements (43).

Another recent model incorporating complex feedback describes the integration of several proposed mechanisms for regulating Drosophila wing disk size (51). This model has two components: a coupled set of differential algebraic equations that describes the interactions of proteins associated with morphogen and cell-cell signaling (including Notch, Dpp, and Wg) within a regulatory network; and a vertex model that describes cell growth and division, and changes in cell shape. These components interact in complex ways. For example, mechanical compression, which is approximated using the weighted average of the area of a cell and its surroundings as described in the vertex model, modulates the activity of multiple proteins in the regulatory network. The regulatory network, in turn, affects the rate at which cells progress through the cell cycle and biases the randomly chosen direction of cell division (51). The model is able to recapitulate a number of experimental observations, including spatially uniform growth in the face of a Dpp gradient and a significant increase in cell cycle time during disk growth, as well as spatially nonuniform growth patterns in disks with artificially induced uniform Dpp. This model constitutes a useful computational framework within which competing hypotheses for the regulation of growth by morphogen signaling and the mechanical environment could be compared in silico. Further iterative development of this model, incorporating systematic parameter analysis and assessment of which experimentally observed features can or cannot be reproduced in each model iteration, may help us gain insight into those factors to which the model are most sensitive or toward which future experimental investigations should be directed.

Rosettes

Until fairly recently, exactly three cells were thought to meet at any vertex within the plane of typical epithelial tissue, although four cells briefly meet as an intermediate state during a T1 transition. Similarly, in most models, cell neighbor exchanges ensure that every interior vertex is always associated with exactly three cells and every boundary vertex is associated with one or two cells, given an initial configuration of this form. However, in some developmental processes a prominent event is the formation of multicellular rosettes, where four or more cells share a common vertex. This observation was first made in Drosophila germ-band extension (90), and has since been made in a variety of epithelial tissues. Although genetic evidence supports the idea that intercalation through multicellular rosettes is more efficient in promoting germ-band extension than intercalation through T1 transitions alone (46), the difficulty in selectively interfering with rosette formation means that the biological importance of these structures is still largely unknown.

In this context, Trichas et al. (23) implemented rosette formation in a vertex model and used their model to test the functional importance of rosettes in migration of the mouse anterior visceral endoderm (AVE). The AVE consists of a small group of specialized cells within the mouse visceral endoderm (VE), a simple epithelium that covers the epiblast and extraembryonic ectoderm (ExE) of the egg-cylinder stage mouse embryo (Fig. 4 a). The AVE is responsible for specifying anterior patterning in the epiblast, the tissue from which the fetus is chiefly derived. To accomplish this, the AVE must migrate proximally from its initial position at the distal tip of the VE to the part that overlies the boundary between epiblast and extraembryonic ectoderm. The AVE then induces anterior pattern in the underlying epiblast by restricting expression of posterior markers to the opposite side of the epiblast cup. Mutations that prevent AVE migration result in severe gastrulation defects.

Figure 4.

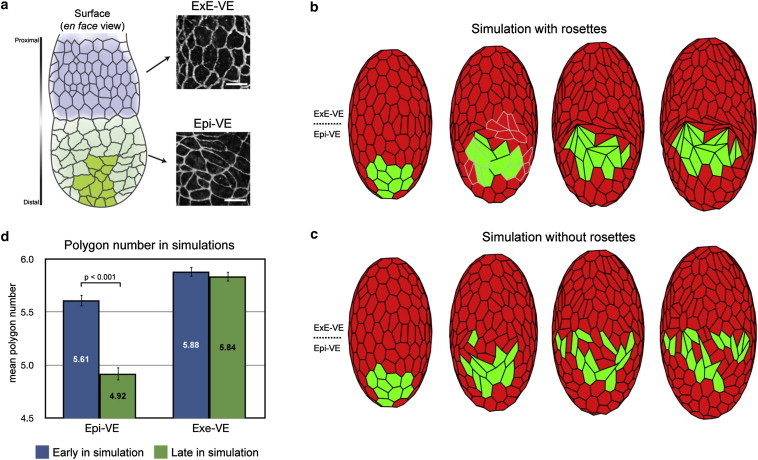
Simulation of AVE cell migration in the mouse VE with and without rosettes. (a) Schematic diagram of the visceral endoderm (VE) of a mouse egg-cylinder. The portions of the VE that cover the extraembryonic ectoderm (ExE-VE, blue) and that cover the epiblast (Epi-VE, green) as well as the proximally migrating AVE cells (dark green) are indicated. Differences in cell shapes are illustrated by high magnification views of the VE of an egg-cylinder stage mouse embryo stained with the tight junction marker ZO-1. (b) Snapshots of vertex model simulations of the mouse VE where rosettes are allowed to form (highlighted in gray), showing AVE cells (green) migrating in a single group. (c) As in panel b, but where rosettes are not allowed to form, showing AVE cells dispersing. (d) Comparison of mean polygon number in the ExE-VE and Epi-VE early and late in model simulations (corresponding to before and during AVE migration), recapitulating the experimentally observed reduction in mean polygon number in the Epi-VE. Images reproduced from Trichas et al. (23).

During AVE migration, the VE maintains integrity as an epithelial monolayer, and the portion of the VE through which the AVE migrates undergoes significant levels of cell movement and intercalation (61,62). Furthermore, this portion of the VE undergoes a dynamic change in cell packing, including the formation of multicellular rosettes comprised of four, five, or more cells (23).

To investigate the significance of this observation, Trichas et al. (23) developed a vertex model to explore how varying rosette numbers might affect AVE migration, independent of other processes. This model employed a force-based approach similar to the models of Weliky and Oster (22) and Weliky et al. (25), incorporating experimentally observed cell growth and division. To account for the curved tissue geometry, the apical surface of each VE cell was approximated by a polygon lying on the surface of an ellipsoid representing the epiblast and extraembryonic ectoderm; this ellipsoid grew linearly over time to simulate tissue growth. At each discrete time step, forces were assumed to act tangentially to the surface at each vertex, and vertices were then projected back onto the ellipsoid; with sufficiently small time steps, this procedure should be equivalent to introducing explicit forces simulating adhesion between VE cells and the underlying tissue. A subset of cells at the distal tip of the ellipsoid was specified as the AVE, and migration was executed by increasing the pressure force at one or more of the proximal-most vertices of each AVE cell.

To allow for rosette formation in addition to simple T1 transitions, cell neighbor exchange was replaced by a vertex/vertex merge operation (Fig. 3 e) if any cell edge length fell below a specified threshold. By varying this threshold, the authors were able to control the ability for rosettes to form, and thus investigate the effect of rosettes on AVE migration. For a threshold for merging that resulted in a similar density of rosettes to that observed experimentally, model simulations reproduced experimentally observed AVE migratory behavior in a qualitative sense (Fig. 4 b). For a threshold of zero, no rosettes formed, and model simulations showed abnormally disordered and dispersed AVE cells (Fig. 4 c), closely recapitulating experimental observations in mutant embryos where planar cell polarity (PCP) signaling was disrupted. These results indicate that rosettes may play an important role in the ordered nature of AVE migration. In a more quantitative test, the authors considered the polygon numbers of cells early and late in AVE migration, and found that the correlation between rosette formation and change in overall polygon number agreed well between experimental and simulation results.

Taken together, the theoretical and experimental observations generated by Trichas et al. (23) suggest that rosettes play an important role in organizing the collective motion of migrating AVE cells by coordinating cell intercalation events. While not directly addressed in this study, an interesting future direction would be to investigate the effect of tissue curvature on the importance and role of multicellular rosettes, in this and other systems.

Three-dimensional models

Although the two-dimensional approximation common in vertex models is suitable in some cases, many morphogenetic processes are three-dimensional in nature. Certainly, some of these processes can be understood by considering a two-dimensional cross section of the tissue, as in models describing ventral furrow formation. In systems without such simple geometry, however, such an approach may not be possible.

In one recent approach to modeling three-dimensional morphogenetic events, the vertex model established for the Drosophila wing disk (24) was adapted and modified by allowing the essentially two-dimensional sheet of cells to move freely in three dimensions (63). Computationally, this adaptation primarily consisted of reformulating the calculations of length and area needed for implementing the equations of motion. Because this model retained two-dimensional network connectivity, cell neighbor exchanges could still be implemented as simple T1 transitions. This model was developed for studying the formation of the dorsal appendages of Drosophila eggshells, and was used to test the proposed hypothesis that formation of the dorsal appendage tubes could be driven strictly by patterns of tension within the apical surface of the follicular epithelium. Patterns of tension based on the experimentally observed localization were implemented in this model, and found to be sufficient to induce both bending of the cell sheet through a buckling instability and ordered cell intercalation. These simulation results were qualitatively very similar to the morphological changes observed experimentally (Fig. 5).

Figure 5.

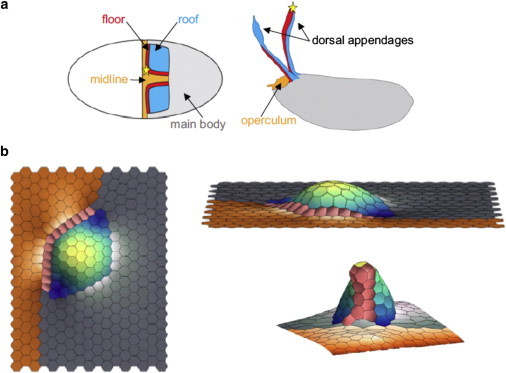
Simulation of three-dimensional epithelial morphogenesis in the developing Drosophila egg. (a) Schematic showing the locations of populations of different cell types within the follicular epithelium. (Left panel) Initial locations of the roof cells (blue), floor cells (red), midline cells (orange), and nonspecialized main body cells (gray). (Right panel) Final locations of these cell types relative to the completely formed eggshell. (b) (Clockwise from left) Top and side view of a vertex model simulation of out-of-plane tissue deformation, and final configuration showing a single completely formed appendage. Images reproduced from Osterfield et al. (63).

It will be interesting to see if a similar approach could be used to examine the forces that may direct morphogenesis of other three-dimensional structures. Possible systems that may be amenable to this approach include those in which apical patterns of myosin appear to control morphogenesis, and where tissue morphogenesis may be significantly understood through consideration of just the apical surface; for example, trachea formation in Drosophila (47). Other systems to which this approach may apply include those where the length scale of the patterned tension is much greater than the thickness of the cell sheet; for example, wing disk eversion (64). In these cases, the two-dimensional model sheet may represent the entire thickness of the epithelial sheet.

A more comprehensive approach to modeling three-dimensional morphogenesis would involve representing cells as three-dimensional prisms, rather than as two-dimensional polygons. Such an approach has been successful in simulating the behavior of cell aggregates, including modeling the emergence of geometric asymmetry in the mouse blastocyst (65,66). Additionally, this approach has been used to model epithelial-like cells, such as in comparing potential mechanisms underlying intercalation of cells in a spherical shell (67). The effects of varying model assumptions, including rules for network rearrangements and cell division, and parameters for the driving energy function, have begun to be explored in these types of models (59,68,69). However, at this point, any comparison of these models to three-dimensional tissues remains highly qualitative. An important future direction will be to collect informative experimental measurements, possibly including characterization of statistical properties of cells or direct measurements of mechanical properties, to allow for more quantitative comparisons, and the identification of appropriate model assumptions.

The computationally efficient simulation of both three-dimensional vertex models and two-dimensional approximations on curved surfaces remains a challenge. Future work should reveal to what extent vertex models will be suited to addressing three-dimensional morphogenetic processes, and to what extent alternative three-dimensional representations, such as the subcellular element model (70), may be required to account for details such as the mechanical contributions of cell-matrix adhesion (71) or centripetal cytoplasmic contractile activity (72).

Analysis of vertex model behavior and experimental validation

To date, to our knowledge, there has been little systematic study of the physical properties of vertex models or of the effect of varying constitutive assumptions. A notable exception is the work of Farhadifar et al. (24), who studied the role of cell mechanics and cell division in determining network packing geometry and morphology. They were the first to estimate the values of key model parameters characterizing the effects of contractility and adhesion in the proliferating wing disk epithelium of Drosophila. This was achieved by analyzing movements of the junctional network after laser ablation of individual cell boundaries and comparing them to the corresponding behaviors in the vertex model. This comparison of experiment and theory allowed the authors to restrict the range of possible parameter values to a small region for which the vertex model accounts for the observed vertex movements induced by laser ablation, epithelial packing geometries, and area variations.

Building on this work, Staple et al. (55) undertook a systematic analysis of the ground states of this vertex model, which correspond to the absolute minima of the energy function for a given number of cells. The authors obtained the phase diagram for this model, thus determining for which regions in parameter space different types of ground states exist. In other work, Li et al. (50) used a force-based vertex model to study the general mechanisms of regulating cell topology in animal epithelial cells. The authors showed that different schemes of division plane orientation could account for observed differences in topological distributions in natural proliferating epithelia. Their simulation results also suggested that mechanical forces play important roles in regulating cell topology of animal proliferating epithelia: adopting a particular division scheme may reduce the stress exerted on cell edges, whereas increased tension on the boundary between proliferating cells and quiescent cells induced by differential proliferation can significantly affect local cell topology.

Although computational models are still used primarily to gain qualitative insight into the behavior of epithelial dynamics, an increasing number of integrative studies have tried to place such models on a quantitative footing through validation against experimental measurements of forces within tissues. The most successful approach so far involves ablating individual junctions with a laser and inferring the tension from the initial speed of vertex recoil (37,73,74). Because this method is invasive and samples only a small number of junctions, alternative noninvasive approaches are needed.

Recently, several studies have developed inverse problem frameworks that allows for estimation of key model parameters based on the output of noninvasive experimental protocols (75–77). Chiou et al. (75) and Ishihara and Sugimara (76) considered an explicit force-based approach similar to Weliky and Oster (22) and assumed that an epithelial tissue is in instantaneous mechanical equilibrium. From static images, the authors inferred the effective tension along each intercellular interface and internal pressure within each cell in the tissue. Chiou et al. (75) employed a mechanical inverse method based on the fact that, because they appear linearly within the resulting force balance equations for an observed tissue configuration, point estimates for these parameters may be found via a pseudo-inverse method once additional constraints (such as minimal variation of tensions and pressures across the tissue) are imposed. In contrast, Ishihara and Sugimara (76) adopted a Bayesian approach, inferring a posterior distribution for each mechanical parameter given an observed tissue configuration and prior distribution encoding known constraints on these values. Parameter estimates were found to be consistent with other force readouts, for example from experiments involving laser-cutting of cortical actin cables. In other work, Brodland et al. (77) allowed for tissues to be out of mechanical equilibrium, and used time-lapse data to estimate vertex velocities and hence infer the active forces driving cell movement.

While the above work enables the inference of key mechanical parameters in vertex models, there is still a lack of established methods for semiautomated tracking of cell division and delamination events in time-lapse data, which limits our ability to obtain sufficient data for parameterization when these processes are incorporated into vertex models.

Future Directions in Computational Modeling of Epithelial Sheets

As demonstrated in the examples summarized above, cell-based vertex models have played an increasingly important role in the study of morphogenesis, particularly in epithelial tissues. An important challenge is posed by the computational cost associated with analyzing these models, because they are increasingly complicated by the incorporation of stochastic behavior or the mathematical descriptions of the physical and biochemical mechanisms underlying cellular behavior. Systematic and rational model reduction is therefore a critically important tool to avoid intractability. One possible resolution of this problem is to develop a coarse-grained model that captures, at least the qualitatively, the key features of the original model but is more amenable to efficient simulation or mathematical analysis. In the context of vertex models, Brodland et al. (26) have derived a continuum biomechanical model whose material properties are equivalent to their individual cell-based description, including cell neighbor rearrangements. In other work, Fozard et al. (78) used homogenization theory to derive a continuum description of a one-dimensional vertex model in the absence of proliferation.

We conclude by highlighting a major barrier to the wider use of individual cell-based models as a computational tool by the scientific community: the lack of standards or benchmarks. It is still the case that previously developed models and methods are often not reused effectively, because they are typically not available as rigorously tested, open-source simulation software. It is therefore difficult to guarantee the reproducibility of computational results. This problem is beginning to addressed, for example by the CHASTE project (79), which provides an open-source C++ implementation of vertex models of epithelial tissues (42). Nevertheless, a more systematic and comprehensive description of specific vertex models in the literature remains a challenge.