Pore Dynamics and Conductance of RyR1 Transmembrane Domain

Abstract

Ryanodine receptors (RyR) are calcium release channels, playing a major role in the regulation of muscular contraction. Mutations in skeletal muscle RyR (RyR1) are associated with congenital diseases such as malignant hyperthermia and central core disease (CCD). The absence of high-resolution structures of RyR1 has limited our understanding of channel function and disease mechanisms at the molecular level. Previously, we have reported a hypothetical structure of the RyR1 pore-forming region, obtained by homology modeling and supported by mutational scans, electrophysiological measurements, and cryo-electron microscopy. Here, we utilize the expanded model encompassing six transmembrane helices to calculate the RyR1 pore region conductance, to analyze its structural stability, and to hypothesize the mechanism of the Ile4897 CCD-associated mutation. The calculated conductance of the wild-type RyR1 suggests that the proposed pore structure can sustain ion currents measured in single-channel experiments. We observe a stable pore structure on timescales of 0.2 μs, with multiple cations occupying the selectivity filter and cytosolic vestibule, but not the inner chamber. We further suggest that stability of the selectivity filter critically depends on the interactions between the I4897 residue and several hydrophobic residues of the neighboring subunit. Loss of these interactions in the case of polar substitution I4897T results in destabilization of the selectivity filter, a possible cause of the CCD-specific reduced Ca²⁺ conductance.

Introduction

Transport of Ca²⁺ ions is an important component of cellular signaling and physiology. Various ion channels regulate Ca²⁺ storage and release (1). The ryanodine receptor (RyR) is a sarcoplasmic reticular channel, responsible for rapid release of Ca²⁺ ions from intracellular storage. RyR channels are symmetric tetramers, with a monomer mass of 565 kDa (2,3). The structure of full-length channels remains unknown. Biophysical studies and genetic analysis have provided a tentative map of protein domains, including the transmembrane domain (TMD) of ∼400 residues, and ∼4600 residues of extrareticular region, featuring multiple binding and regulation sites (1–4). Hypothetical structure of the RyR1 TMD compatible with cryo-EM reconstruction (4) has been proposed recently (5,6) (Fig. 1), based on single-channel data and homology modeling using a potassium voltage-gated channel structure. This model has been successfully applied to interpret results of RyR1 mutagenesis experiments, using a static estimate of the amino-acid substitution free energy change (ΔΔG). Here, we use the RyR1 structural model to investigate conductance and other dynamic properties of the RyR1 six-helix TMD using all-atom explicit solvent molecular dynamics (MD) simulations.

Figure 1.

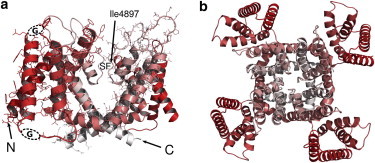
RyR1 transmembrane domain model. (Red-to-white transition) N-to-C direction. (a) Side view, front and rear monomers removed for clarity. One of the monomers is shown with side chains to better visualize the topology. (Arrows) Location of N- and C-terminals of this monomer; (dashed ovals) glycine linkers. (SF) Location of the selectivity filter. (b) Top view on the tetramer. To see this figure in color, go online.

We employ atomistic MD simulation using the classical force field, to analyze stability and conductance of ion channels embedded into lipid membranes. Previously, similar methods have been applied to high-resolution (experimentally obtained) structures of ion channels (7–12). Computational estimates of channel conductance usually result in significant underestimation of ionic currents (11). Suggested reasons are finite size effects (11), the low dielectric constant of the lipid bilayer (11), and errors in hydrogen-bond strength (13), resulting from neglected electronic polarizability. However, despite the deficiencies of conventional nonpolarizable force fields, their application in numerous computational studies has increased our understanding of internal functioning of ion channels (8,12,14). Although absolute values of channel conductance cannot be reproduced in simulations, certain phenomena, such as the effect of amino-acid substitution on conductance, can be predicted based on known structural models. Structural models obtained by indirect methods pose an additional challenge to dynamical simulations. Here, we demonstrate the direct correspondence between behavior of our model and in vitro observations, which allows us to develop a hypothesis on a possible mechanism of a central core disease (CCD)-causing mutation.

Methodology

Structural model

We perform model simulations of the open state of the rabbit RyR1 (UniProtKB accession No. P11716) transmembrane domain, which includes six membrane-spanning helices (S1–S6) (5,6), lumenal loops, pore helix, selectivity filter, and connecting polyglycine loops. Specifically, these included regions consist of residues: 4561–4580, 4638–4662, 4784–4948. Segments are connected using eight-residue polyglycine loops, which are not submerged into the membrane.

System setup

We have utilized the CHARMM27 force field (15–17), modified to include protein-lipid interactions (18) and the TIP3P water model. All simulations were conducted in a cubic box with three-dimensional periodic boundaries, at 300°K and a constant pressure of 1 bar. The MD time step was set at 3 fs, and the van der Waals and Coulomb cutoff radii were 1.2 nm. In all simulations, systems were neutral and KCl was present at 0.27 M average concentration. In simulations with Ca²⁺, CaCl₂ was added at 0.16 M average concentration.

To prepare the simulated system, we first constructed a solvated lipid bilayer by combining nine preequilibrated tiles of the POPC bilayer (19), with additional equilibration performed at constant pressure for 30 ns. Next, we immersed the RyR1 tetramer into the membrane, removing all overlapping lipid molecules. Bilayer orientation was normal to the Z-coordinate axis. Protein atoms were initially restrained to initial positions with a harmonic potential of 8 kJ/nm²/mole. Restraints were gradually released by halving the potential in the series of seven equilibration runs of 20 ns. Production runs were performed for 210 ns, while collecting full system snapshots every 60 ps, and compact snapshots (only protein and ions) every 3 ps. Umbrella sampling has been done using single K⁺ probe ion and umbrella potential of 960 kJ/mole/nm² (∼400 k_BT/nm²). Samples were collected in 1.5-ns simulations at 70 sampling points spaced 0.1 nm apart. This sample density allows sufficient histogram overlapping (see Fig. S1 in the Supporting Material) for quick convergence of the WHAM solver (http://www.gromacs.org/Documentation/Gromacs_Utilities/g_wham).

Channel conductance strongly depends on conformation of pore-forming segments, therefore it is important to reduce the influence of systematic conformational changes that occur during protein relaxation. The most noticeable changes are the stretching of S5 and S6 helices and the increase of helical contents at and near the selectivity filter. These adjustments might reflect transition to the native state of the RyR TMD model, or be caused by force-field artifacts. The helical bend between S5 helix and S4-S5 linker is a characteristic feature of several cation channels, and evidence exists that it may be part of a voltage-driven channel activation machinery (20). However, it was shown that, in a similar setup, CHARMM22/27 force fields have a tendency to overstabilize α-helical conformations (21). Therefore, we chose to preserve the bend between the S5 helix and S4-S5 linker by imposing point restraints between the backbone atoms. Similarly, we preserved the bent structure of the S6 helix near G4934 (a characteristic element of many ion channels) and the extended conformation of the selectivity filter. The rest of the RyR model structure is primarily helical and did not indicate any tendency to change the secondary structure during MD simulations. To stabilize bending sites, we apply distance restraints to O and N atoms of residues separated by three positions along the chain (1–4 type potential, detailed parameter files are provided in the Supporting Material). These restraints are local in nature and do not affect the relative position of monomers, or their tertiary structure. This approach is different from positional restraints applied to the entire model, which may be necessary when using coarse-grained force fields or in the case of extremely long simulations (14). Hence, we refer to our model as “unrestrained”, meaning the absence of positional restraints and tertiary structure-stabilizing restraints.

The pore profile was measured using the program HOLE (22), with an algorithm based on fitting the sphere of largest possible radius while scanning along the pore axis. This program measures pore radius and detects pores, including cases when the pore axis is aligned with the vertical axis. Pore cutoff radius was set to 0.7 nm. This cutoff defines points of entrance into the pore (i.e., when the test sphere can be expanded to this radius without clashing with pore walls, the test sphere is assumed to be outside of the pore). The pore profile has been calculated for every stored snapshot of the simulated trajectory. Per-snapshot profiles have been used to evaluate pore average and minimum and maximum radii, and to monitor pore-profile changes with time.

Preparation of wild-type (WT) and mutant channels

We constructed rabbit RyR1 cDNA, as explained in Ramachandran et al. (5) and Gao et al. (23) and confirmed mutations by sequencing. We expressed the channel cDNAs transiently in HEK 293 cells (24) and prepared crude membrane fractions and proteoliposomes containing purified recombinant channels, as described in Gao et al. (23) and Lee et al. (25).

[³H]Ryanodine binding

Binding of this highly specific alkaloid is a good indicator of RyR1 channel stability and activity (26). We determine the channel binding capacity B_max as described in Ramachandran et al. (5).

Single-channel recordings

Single-channel currents were measured as described earlier in Ramachandran et al. (5). Briefly, K⁺ currents were measured in symmetrical 250 mM of KCl. Permeability ratio was determined in additional presence of 10 mM of Ca²⁺ on the trans side (corresponding to SR luminal side) and using a modified form of the Goldman-Hodgkin-Katz equation (5).

Results

Stability of the model structure

Structural integrity of the model is an important indication of residue assignment accuracy. Defects in residue assignment lead to formation of energetically unfavorable contacts and quick deterioration of structure in the course of equilibration. We have tested stability of unconstrained structure in dynamic simulations to obtain an indication that modeled structure does not have essential defects or large deviations from the protein native state.

The structural stability test is subject to the limitations of simulation force fields. Typically, available structures of crystallized proteins do not represent the ground-state structures for the commonly used force-field types. The mismatch is in part due to the inaccuracies in structure determination or homology model construction, and in part due to certain atomic properties (e.g., electronic polarization (13)) not accounted for in the force fields. As a result, channel proteins undergo fast (<1 ns) adjustments at the start of a simulation and slowly reach a new stable state in ∼100 ns (9). Stability of the protein model can be estimated by the root-mean-square deviation (RMSD) from the initial structure. The relaxed state retains a similarity that depends on protein size, and for our system size, we expect an RMSD of ∼0.5 nm (9,10) (Fig. 2 a). In the course of 100 ns simulations of RyR1 TMD, the protein undergoes rapid (<1 ns) expansion (RMSD ∼ 0.25 nm) followed by slow structure adjustments, reaching RMSD ∼ 0.5 nm (Fig. 2 a) for the tetramer and RMSD ∼ 0.4 nm for monomers.

Figure 2.

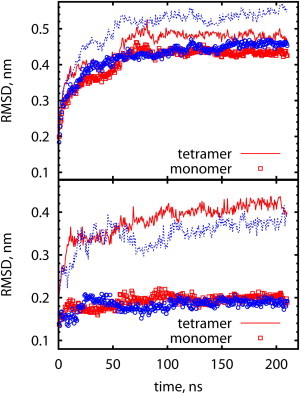
Structural stability of (a) RyR1 TMD, and (b) selectivity filter; for two trajectories indicated by color, each trajectory is 210 ns long. (Lines) RMSD for the tetramer; (symbols) average RMSD for monomers. To see this figure in color, go online.

Stability of the pore vestibule, including the selectivity filter (SF), is critical for measuring channel conductance. This is because permeation of a solvated ion into the pore depends on precise interplay between SF residues and an ion, which is required for ion desolvation. In our model, SF has been assigned residues 4894-GGGIGD-4899 (5,6). Deviation from starting structure of SF segments of an RyR1 monomer (Fig. 2 b) rapidly saturates at RMSD ∼ 0.2 nm. For the tetramer, SF deviations reach larger RMSD ∼0.4 nm mainly due to the overall expansion trend of the channel during equilibration. The magnitude of fluctuations of the SF structure is large compared to sizes of atoms and ions, but is similar to the resolution of experimentally determined structures of ion channels.

During the last 50 ns, random fluctuations of RMSD of both the SF and the entire TMD are comparable or exceed the directed RMSD drift. Small drift may suggest that the system is trapped in the metastable state, but a rigorous test of system stability would require analysis of a significantly larger number of trajectories.

To analyze the internal structure of the channel pore we have computed the pore profile, represented by the radius of the pore cross-section along the pore axis. The profile of the central pore (Fig. 3 a) exhibits features similar to other cation channels (27,28). The lumenal-side ion reservoir (left side) is followed by a selectivity filter, a hydrophobic chamber, and a cytosolic side gate and ion reservoir. The constriction site at Z = 5.5 nm (Fig. 3 a) corresponds to the inner site of the selectivity filter formed by G4894. Average pore diameter at this site is ∼0.25 nm. Potassium ion diameter in the CHARMM force field is 0.304 nm, therefore it would not be able to penetrate the channel unless permitted by thermal fluctuations (29,30) of the pore walls (Fig. 3 a). Moreover, due to the fluctuations, the pore at the SF may sporadically widen to a diameter of ∼0.5 nm, which is consistent with the observation that organic cations such as tetramethyl ammonium may be able to penetrate into the pore from the lumenal side (31).

Figure 3.

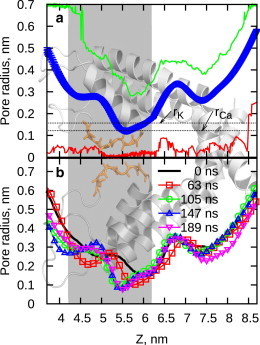
Dynamics of the pore profile. Background image shows structure of pore helixes of the two opposing subunits for visual reference. (a) Average pore profile. (Green line, maximum observed radius; red line, minimum observed radius; blue symbols, average pore radius.) (b) Time evolution of the pore profile. (Lines) Average profile computed over an interval of 21 ns, starting at the time indicated on the legend. (Gray box) Position of the selectivity filter. To see this figure in color, go online.

During the simulation, the pore profile undergoes mild rearrangement, and the inner side of the selectivity filter shifts outwards by ∼0.5 nm, stabilizing after 100 ns (Fig. 3 b). The constriction site of the selectivity filter also becomes narrower, possibly reflecting the channel preference for the smaller Ca²⁺ ions.

Conductance

Ionic conductance in channels is a complex process, involving ion adsorption and desorption near and within the channel pore, conformational changes of pore-lining residues, pore-shape fluctuations, and collective ion transport, each occurring at different timescales. At the moment, timescales achievable in atomistic MD simulations are not sufficient for observing a sufficient number of ion transmission events.

To explicitly calculate channel conductance, it is necessary to measure the ion transmission rate. However, the characteristic timescale of ion passage through channels is typically of ∼1 μs, currently accessible only to a few dedicated supercomputers and for systems of limited size (12,20). An indirect approach to obtain an estimate of conductance is based on a Kramer’s-type theory developed for the complex energy landscape of ion channels by Roux and Karplus (32). In this approach, the potential of mean force (PMF) and transverse diffusion coefficients are calculated and used to compute conductance under the assumption of a diffusion-limited ion transport regime. We calculate the PMF by umbrella sampling using one of the cations to probe the potential field. We place probe sites at 0.1 nm separation along the coordinate axis normal to the bilayer and restrict them by harmonic potential relative to the protein center of mass.

We perform simulations of each system with a probe ion in place for 1.5 ns, save the probe position every 0.3 ps, and use distributions of probes’ positions to compute PMF using the Gromacs WHAM solver. The simulation duration 1.5 ns is chosen from an estimate based on the bulk diffusion coefficient to allow the probe ion to sample an area (∼3 nm²) larger than the pore cross-section (∼0.5 nm², near the entrance). This simulation time also allows other cations to populate the SF and cytosolic gate regions, as we observed by comparing ion densities with 100-ns-long simulations (data not shown). The presence of other ions is particularly important in the SF region, because there is evidence (33) that selectivity filter structure may be stabilized by cations. We utilize the trajectories obtained in these PMF simulations to determine local diffusion coefficients, as discussed in the next section. Despite the presence of many ions in the pore, conductance that is estimated from PMF implies translocation of ions one by one, without taking into account collective effects of ionic conductance, and therefore it will always underestimate channel conductance. However, estimated conductance can still be useful in the analysis of effects due to sequence modifications, when these modifications do not affect collective effects in ion transmission.

The calculated PMF (Fig. 4 a) exhibits a characteristic binding site, corresponding to negatively charged region at the lumenal vestibule. The binding site is followed (Fig. 4 a, left-to-right) by the abrupt increase in PMF on the 1-nm-long segment (4.9 nm < Z < 5.9 nm) corresponding to the selectivity filter region between G4894 and G4898. The next dip at position 6.2 nm corresponds to the hydrophobic chamber, which is followed by the narrow hydrophobic pore (6.5 nm < Z < 8 nm) forming the second transmission rate-limiting barrier peaked at positions of Q4933 and I4937.

Figure 4.

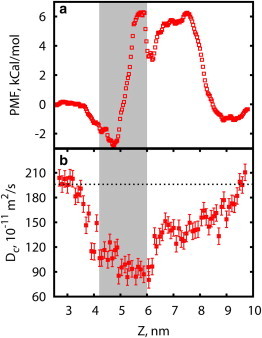
(a) One-dimensional potential of mean force of a single potassium ion along the pore axis. (b) Diffusion coefficient profile. Every point is obtained in an independent simulation with a probe ion restrained at the specified position along the pore axis. (Dashed line) Experimental value of K⁺ bulk diffusion coefficient D_c = 1.96 × 10⁻⁹ m²/s from Hille and Stuart (36). (Gray box) Position of the selectivity filter. To see this figure in color, go online.

Diffusion

Bulk ion diffusion coefficients obtained for the TIP3P water model and CHARMM27 force field are significantly close to experimental values. Diffusion in the pore remains a somewhat controversial subject. Computational studies assume a significant (<10% of bulk) (34) or a lesser (>50% of bulk) (27) slowdown of ion diffusion in the pore. Direct measurements on diffusion rates in the channel pore are not available at the moment, however electrophysiological measurements suggest that ion translocation may occur at nearly bulk diffusion rates (35).

We have computed probe ion diffusion coefficients (Fig. 4 b) using trajectories obtained in umbrella sampling procedure. At short timescales, ion displacement is small compared to the potential width and umbrella restraint can be neglected. We have computed ion mean-square displacement (MSD) along the pore axis. We then fitted it by a linear function in the range where RMSD does not exceed 0.01 nm, which is small, compared to thermally induced root-mean-square (RMS) fluctuations in umbrella potential of 0.07 nm, but is comparable to an atom size. By fitting ion MSD to the Einstein equation MSD = 2D(z)t we have obtained the transverse diffusion coefficient D(z) required to estimate channel conductance. At such a small MSD, ion motion is not significantly affected by the umbrella potential, while ion is still able to dissipate energy via its environment, including atoms with which it is currently in contact. Diffusion coefficient of potassium ions (Fig. 4 b) outside the pore is in agreement with experimental data (D_c = 1.96 × 10⁻⁹ m²/s) (36). Inside the pore we observe slowdown of ion diffusion, which lowers at potential barriers to ∼55 and 30%, respectively, of the bulk value (Fig. 4 b), consistent with prior observations (27).

Conductance

The maximum conductance can be estimated using a simple equation based on the single-ion nonpolarizable environment approximation as described by Allen et al. (11),

$${\gamma }_{\text{max}}=\frac{e^2}{k_{\text{B}}T{L}^2}{\langle D{\left(z\right)}^{-1}{e}^{W\left(z\right)/k_{\text{B}}T}\rangle }^{-1}{\langle e^{-W\left(z\right)/k_{\text{B}}T}\rangle }^{-1},$$ (1)

where L is channel pore length, W(z) is the PMF, and D(z) is one-dimensional diffusion coefficient. Using this equation and computing averages over the segment of length L = 7.1 nm (2.8 nm < Z < 9.9 nm), we obtain maximum conductance of K⁺ ions γ_K = 203 ± 8 pS. The estimated conductance of the model channel is smaller than the experimental conductance, γ_K ∼ 801 pS (37), and follows the trend previously observed in potassium-channel models based on crystal structures. Due to the approximate nature of Eq. 1, the limited agreement between simulated and experimental conductance is reasonable. The discrepancy can also attributed to known simulation limitations, such as electronic polarization not supported by a force field, using single-ion PMF approximation and limited sampling (11).

Ion selectivity

RyR1 is capable of transmitting both monovalent and divalent cations. Strong selectivity is observed in divalent cations (37), with a measured permeability ratio of P_Ca/P_K ∼ 6 (38). There is also evidence of RyR conductance preference for certain alkali ions (34). The selectivity mechanism of cation channels has been attributed to a difference in ionic radii, carboxylic interactions, or adsorption strength (39,40). Similar to potassium channels, selectivity in RyR1 likely results from the stronger adsorption and higher local concentration near the pore lumenal entrance. The effect of charged residues on selective occupation of lumenal vestibule is well pronounced (Fig. 5 a). Concentration of divalent cations in both lumenal and cytosolic vestibules is higher than that of monovalent cations, despite the lower bulk concentration. This difference in ion binding affinity may be viewed as a component of the selectivity mechanism, in agreement with the charge/space competition principle (41,42). In contrast to the SF area, the inner chamber appears to be unoccupied by cations in the course of the 200-ns simulations (Fig. 5 a). The gap in ion density is almost 2-nm long and signifies presence of high potential barriers, which prevent formation of a continuous ion file. Another preferential Ca²⁺ binding site is clearly visible at the cytosolic side (Fig. 5 a), likely formed by the charged residues of D4938, E4942, and D4945 (43). Under physiological conditions, the cytosolic side of the RyR pore is capped by the large regulatory region, modulating interactions of the TMD vestibule with Ca²⁺. In addition, Ca²⁺-specific interactions with the cytosolic vestibule observed in the simulations may also play a role in the calcium-regulated Ca²⁺ release.

Figure 5.

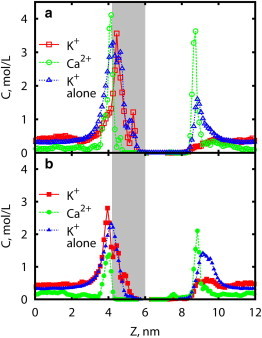
Ion density profile for mixture of monovalent and divalent ions. The Z axis is normal to the membrane. (a) WT RyR1; (b) D4899Q mutant. (Squares and circles) K⁺ and Ca²⁺ ion densities, respectively, when both ions are present in solution. (Triangles) K⁺ density when no other cations are present. To see this figure in color, go online.

Neutralizing negatively charged mutations

Extensive negative charges at the lumenal entrance are a distinctive feature of the RyR1 channel, compared to other structurally similar cation channels (6). Neutralizing mutations of D4899 and E4900 result in a reduction of RyR1 conductance and selectivity (44).

In Fig. 6, we substituted aspartic acid at position 4899 with asparagine and glutamine to reduce charge while preserving hydrogen-bond-forming ability, which may be necessary for structural stability. In simulations, we observe loss of selective binding of Ca²⁺ ions at the lumenal vestibule (Fig. 5 b), and ion density in this region now correlates with the average ion concentration. Conductance reduction is also observed in simulations, resulting from the significantly higher potential barrier (Fig. 6), as compared to the WT channel. As a result, the PMF has lost the characteristic dip at Z ∼ 4.5 nm and indicates a higher barrier for ion transmission. The calculated maximum conductance γ_K is reduced to 36 ± 5 pS for G4899Q and 25 ± 4 pS for G4899N, in accord with an increased barrier by a proportion comparable to experimentally observed conductance (γ_K of G4899Q = 164 pS = 1/5 of γ_K of WT RyR1 and γ_K of G4899N ∼90 pS = 1/9 of γ_K of WT RyR1 (44)).

Figure 6.

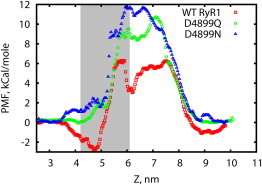
One-dimensional single ion K⁺ PMF for the D4899Q and D4899N mutants. Neutralization mutations result in weaker adsorption in the lumenal vestibule and higher entrance barrier compared to WT. To see this figure in color, go online.

CCD mutation mechanism

Central core disease, linked to the number of substitutions in RyR1 in the TMD regions of R4860H, G4890R, R4892W, I4897T, G4898R, and G4898E, has been described (45–47). These mutations reduce Ca²⁺ release rates and single-channel conductances in proportion to the number of mutant subunits (47,48), which can be attributed to the increased size of the side chain of the pore-lining amino acid and partial blockade of the ion diffusion path. However, the steric hindrance argument does not directly apply to the case of the I4897T mutant, because the threonine side chain is one atom shorter than that of isoleucine. Therefore, we hypothesized that Ca²⁺ flux-reducing effects of I4897T may be of a dynamic nature.

To analyze change in dynamics due to amino-acid substitution, we have simulated the RyR1 TMD at a lowered temperature of 250°K and compared the RMS fluctuations of the selectivity filter region. We have computed fluctuations of the side-chain atoms of residue 4897 over 10 trajectories of 10 ns (Fig. 7). Despite the averaging over 10 trajectories, the residual noise makes it difficult to draw a definitive conclusion about residue stability. However, results of these simulations (Fig.7) suggest that, during significant time intervals, the I4897T mutant exhibits larger fluctuations at the mutation site compared to the WT protein. Based on this apparent increase of the side-chain fluctuations, we hypothesize that destabilization of the residue at position 4897 may be caused by an impairment of the hydrophobic interactions between the residue and the hydrophobic groove where it rests in the WT tetramer (Fig. 8).

Figure 7.

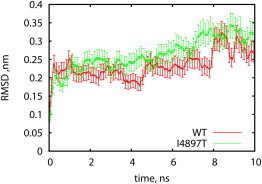
RMS fluctuations of the side-chain atoms of residue 4897 (isoleucine in WT RyR1, threonine in I4897T mutant) relative to the backbone stretch between G4894 and G48998. Analysis begins after an initial relaxation period of 1 ns. For visual improvement, curves were smoothed using a running average over a window of 0.12 ns. Fluctuations of the threonine side chain remain higher during the course of almost the entire simulation. To see this figure in color, go online.

Figure 8.

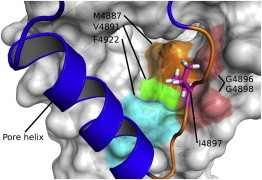
Hydrophobic interactions made by I4897 to the surface of the neighbor subunit. (Colored patches) Surface of residues in contact with I4897; (orange) selectivity filter; (red sticks) I4897. Indicated glycine residues are part of the selectivity filter on the neighbor subunit, which may be stabilized by interactions with I4897. To see this figure in color, go online.

To further validate the hypothesis of stabilization of the SF region by hydrophobic interface of I4897, we studied stability and conductance of several RyR1 mutants, where residues at positions of M4887 and V4891 were substituted by other hydrophobic residues. We have also attempted I4897Y substitution to mimic the SF stabilizing role of SF tyrosine in potassium channels. Properties of mutant channels that we were able to characterize are summarized in the Table 1. We observe that all hydrophobic mutations produce stable and functional channels. A noticeable degradation of ligand binding in the case of the V4891A mutant does not actually affect its conductance and selectivity. In the case of the K⁺-mimicking mutant I4897Y, the substitution has dramatic consequences, destabilizing the channel with near-complete loss of ryanodine-binding ability. The filter tyrosine in K⁺ channels typically forms polar bonds with polar residues of the neighbor subunit (W68 and T72 in KcsA (49), W114 and T118 in MthK (50), Y55 and S70 in NAK2K (51), T107 in KirBac1.1 (52)), and their interaction with SF tyrosine supports the SF structure, which appears to be necessary for ion selectivity (51). In our RyR1, the model interface between the I4897 and the neighbor subunit has no polar residues capable of forming a stabilizing hydrogen bond to the Y4897, which is a probable cause of the destabilization and low yield of I4897Y RyR1 mutant.

Table 1.

Properties of wild-type (WT) and mutant RyR1 in single-channel experiments

	Cells with caffeine responsea	Bmax of [3H] RyR bindingb	Po (2 μM Ca)c	Po (0.1 μM Ca)c	γK+d	PK/PCae	γK+ (WT)/γK+ (mut)
	(%WT)	(%WT)			(pS)
WT	100	100	0.24 ± 0.04(16)	0.01 ± 0.01(8)	801 ± 7(17)	6.7 ± 0.2(12)	1.0
			0.11 ± 0.04(6)	0.02 ± 0.01(4)	751 ± 16(5)	6.8 ± 0.1(5)	0.94
M4887G	96.6,66.3(2)	47.3 ± 18.8 (3)	0.21,0.39(2)	0.01(2)	788,782(2)	6.7(1)	0.98,0.98
			0.15 ± 0.03(6)	0.01 ± 0.01(4)	774 ± 12(5)	7.0 ± 0.3(3)	0.97
M4887A	104.7 ± 12.6(4)	96.7 ± 23.1(3)	0.37 ± 0.06(6)	0.01 ± 0.01(4)	782 ± 2(6)	7.1 ± 0.2(4)	0.98
M4887V	87.5 ± 19.8(4)	62.2 ± 15.1(3)	0.44 ± 0.11(9)	0.01 ± 0.01(4)	785 ± 8(9)	6.7 ± 0.3(4)	0.98
V4891A	38.7 ± 18.6(4)	63.7 ± 3.2(3)	0.37 ± 0.06(9)	0.01 ± 0.01(4)	809 ± 4(9)	6.5 ± 0.4(4)	1.01
I4897Y	46.0 ± 8.3(4)	3 ± 3(3)	ND	ND	ND	ND	ND

The values denote the mean ± SE. ND, not determined. Bold text indicates recordings with membrane fractions.

^aPopulation of cells exhibiting Ca²⁺ release in response to caffeine.

^bMaximum binding capacity.

^cOpen channel probability.

^dK⁺ conductance.

^eSelectivity of Ca²⁺ over K⁺.

Discussion

We studied dynamic properties of the ryanodine receptor pore model to complement the prior structural data with an analysis of pore dynamics. Pore dynamics is an essential element of the ion translocation process, because fluctuations of the pore profile can attenuate the kinetic barriers and increase the conductance.

Static models can reproduce conductance using averaged pore profiles, tuned to recapitulate experimental observations for specific mutants or changes in system composition. A study of the rigid model of the RyR1 channel (34), based on a cylindrical selectivity filter flanked by conical atria, was shown to capture essential components of the ion permeation and selectivity processes, such as channel geometry and atrial charge distribution. This model assumed fixed diameter of SF inner opening of 0.4 nm in radius. This estimate was based on experimental measurements using blockage by large organic cations (31,53,54), and therefore corresponds to the upper estimate of the fluctuating pore size. To quantitatively recapitulate experimental ion currents, this rigid model requires that ion diffusion coefficients in the pore to be set at ∼1–4% of their bulk values. This reduction of diffusion coefficient is stronger than is observed in MD simulations at the selectivity filter, 10–50% of bulk values (27,55), and is likely a result of pore geometry that is less constrictive than that of the atomistic models.

A study of RyR2 (56), which bears a high degree (93%) of sequence identity at the pore region, is in agreement with our analysis of structural properties of RyR1 pore region. We observe the major potential barriers at the cytosolic side entrance near residue G4941 (G4873 in RyR2) and at the inner opening of the selectivity filter near residue G4895 (G4827 in RyR2). However, there are significant differences between the ion transport properties of these channels’ pores, as observed in MD simulations.

The 10-ps duration of simulation runs of the RyR2 model (56) is sufficient to relax amino-acid side chains, while essentially preserving backbone structure. Consistent with short simulation runs, modeling of the ion passage has required the use of unphysically fast ions, traversing the pore at supersonic speeds. This effectively rigid backbone structure results in the complex system of five kinetic barriers that were observed in the RyR2 pore simulations (56). In our flexible fluctuating pore model, we observe only two significant energetic barriers—one at the SF inner opening and another at the cytosolic side. The difference between the two models should be attributed to the difference of simulation timescales, because in the thermodynamic limit barrier, the structure is invariant to the method of analysis. Because the energetic landscape is the major factor influencing ion transport, analysis of channel conductance should involve sampling of pore profile on timescales required for ion passage.

We have generated two trajectories of 200 ns, and >100 of shorter trajectories in the range 12–30 ns, but no ion passage event has been registered. Absence of ion passage events is expected given the low transmembrane ion diffusion rate and low ion occupancy of the pore between the SF and cytosolic gate barriers. The average weighted diffusion rate (32) of D_eff = 0.11 nm²/ns for WT RyR1 estimated from the PMF analysis corresponds to translocation time of >150 ns for a 4-nm-long pore. Another reason for the low transmission rate may be the ∼2-nm-long gap in the channel pore, which appears to be unoccupied (almost never visited) by the cations (Fig. 5) in all of our simulations. This gap is larger than the gap of ∼0.5 nm observed in simulations of the potassium channel (20). While the low ionic occupancy of the inner pore cavity is in agreement with a single-ion channel model (57), it may also indicate the deficiencies of the model pore structure and the need for its further refinement.

A common motif in potassium channels is the selectivity filter that includes a tyrosine residue (KcsA Y78 (49), MthK Y62 (50), KvAP Y199 (58), NAK2K Y66 (51), KirBac1.1 Y113 (52)), which rests in the hydrophobic groove of the neighbor subunit, and is believed to stabilize the proper filter structure to allow ion transmission (49,59). In our model of the RyR TMD, a similar role is assumed by the isoleucine I4897, which forms hydrophobic contacts (51) with M4887, V4891, F4922, G4896, and G4898 of the neighbor subunit (Fig. 8). Because the two glycine residues are part of the selectivity filter, stability of the filter may be supported by the contacts made with I4897, in agreement with the previously stated hypothesis on the role of this residue (60). In this case, the effect of the disease mutation I4897T can be explained by the loss of the hydrophobic interactions due to replacement of the hydrophobic isoleucine with the polar threonine, which results in destabilization of the selectivity filter and reduction of conductance.

Conclusions

Although structure of RyR1 still remains to be characterized, we have used the previously proposed RyR1 TMD structure to characterize pore stability and estimate the ion conductance. In MD simulations, RyR1 model behaves similarly to models based on crystallized K⁺ channels. The channel remains stable for at least 210 ns, and maintains a pore capable of ion transfer. In agreement with a recent study (61), in absence of its large cytoplasmic component, the RyR1 transmembrane domain in MD simulations can be stable on its own. The selectivity filter remains stable, and exposes, into the pore, the oxygen atoms required to substitute the ion solvation shell.

We have estimated the maximum channel conductance from the potential of mean force and one-dimensional diffusion coefficient. The estimated conductance is one-fourth of that of experimental currents, but within the expected range for this type of simulation. The discrepancy in analogous studies has been attributed to the lack of electronic polarization effects in classical force fields and the use of single-ion approximation. Charged residues at the lumenal entrance result in a preferable accumulation of divalent Ca²⁺ ions compared to monovalent K⁺. The disparity of ion distribution near the lumenal vestibule may be playing a role in channel selectivity. Difference in the ion concentration between WT RyR1 and the neutralizing mutant results in reduced selectivity and conductance.

Simulations of the CCD-related RyR1 mutant I4897T provide initial data in support of the hypothesis of the dynamic nature of this mutation’s effect, which manifests itself in destabilization of the selectivity-filter structure. Increased fluctuations of SF residues destroy the fine-tuned interactions between the diffusing ions and the SF backbone oxygen atoms, which aid ion desolvation and passage into the pore. A possible method of SF structure stabilization and rescue of channel function may employ a ligand, potentially identified by virtual screening against the proposed TMD structure.