Abstract
Quantitative magnetization transfer (qMT) imaging can provide indices describing the interactions between free water protons and immobile macromolecular protons. These indices include the macromolecular proton fraction (MPF), which has been shown to correlate with myelin content in white matter. Because of the long scan times required for high-resolution spinal cord imaging, qMT studies of the human spinal cord have not found wide-spread application. Herein, we investigated whether these limitations could be overcome by utilizing only a single MT-weighted acquisition and a reference measurement, as was recently proposed in the brain. High-resolution, in vivo qMT data were obtained at 3.0 tesla in the spinal cords of healthy volunteers and patients with relapsing remitting multiple sclerosis (MS). Low- and high-resolution acquisitions (low/high resolution = 1×1×5 mm3/0.65×0.65×5 mm3) with clinically acceptable scan times (12 min/7 min) were evaluated. We also evaluated the reliability over time and the sensitivity of the model to the assumptions made in the single-point method, both in disease and healthy tissue. Our findings suggest that the single point qMT technique can provide maps of the MPF in the spinal cord in vivo with excellent grey/white matter contrast, can be reliably obtained within reasonable scan times, and are sensitive to MS pathology. Consistent with previous qMT studies in the brain, the observed MPF values were higher in healthy white matter (0.16±0.01) than in grey matter (0.13±0.01) and in MS lesions (0.09±0.01). The single point qMT technique applied at high resolution provides an improved method for obtaining qMT in the human spinal cord and may offer a reliable outcome measure for evaluating spinal cord disease.
Keywords: Multiple Sclerosis, Quantitative Magnetization Transfer, Spinal Cord, High-Resolution
Introduction
The spinal cord is responsible for mediating neurological function between the brain and the peripheral nervous system and is somatotopically organized — sensory information is conveyed through the dorsal columns, while the lateral columns convey a significant fraction of motor function. The integrity of these organized columns is vital to preserving specific neurological function; therefore, even small spinal cord lesions (e.g multiple sclerosis (MS)) can result in severe neurological impairment. While the absolute mechanism of the pathophysiology of MS and nervous system tissue deterioration remains challenging to unravel, there is a body of evidence that suggests that axonal loss resulting in spinal cord atrophy may relate to clinical impairment (Cohen et al., 2012; Rocca et al., 2011). Conventional MRI (i.e. spin-density, T1- and T2-weighted) can be used to measure atrophy or determine the location of inflammatory lesions in the spinal cord, but the relationship between conventional MRI indices (e.g. atrophy, lesion burden) and nervous system function and disease progression over time tends to be poor (Stankiewicz et al., 2009).
More quantitative MRI measurements, such as magnetization transfer (MT) and diffusion tensor imaging (DTI) metrics have been applied to the cervical spinal cord to investigate the relationship between neurological function and spinal cord microstructure (Cohen-Adad et al., 2011; Ellingson et al., 2008; Filippi and Agosta, 2010; Freund et al., 2010; Nair et al., 2010; Naismith et al., 2013; Oh et al., 2013; Poloni et al., 2011; Smith et al., 2009; Zackowski et al., 2009). Importantly, as these measurements report on microstructural changes that may precede atrophy, they potentially offer greater prediction of spinal cord function than conventional methods. While quantitative MRI methods have shown promise for characterizing spinal cord damage in diseases such as MS (Stroman et al., 2014; Wheeler-Kingshott et al., 2014), widespread adoption has been challenged by the low signal to noise ratio (SNR), long acquisition times, and sensitivity to motion.
The focus of this work is on magnetization transfer (MT) imaging. Briefly, in addition to free water protons observed with conventional MRI, there are protons residing on immobile macromolecules in tissue (Wolff and Balaban, 1989). Conventional MRI cannot image these protons directly because their T2 relaxation times are too short (≈10 μs) to be captured by typical readout schemes. However, these macromolecular protons communicate with the surrounding water and, thus, can be indirectly imaged by exploiting this exchange, which is referred to as the MT effect. Importantly, MT imaging can serve as a surrogate marker for white matter myelin density in nervous system tissue (Koenig, 1991; Kucharczyk et al., 1994; Schmierer et al., 2007) and, therefore, may be a more specific biomarker of disease evolution. Despite this promise, MT imaging has faced significant challenges in the spinal cord.
The contrast in an MT experiment is generated via application of a radiofrequency (RF) irradiation pulse at an offset frequency with respect to water (Δω) to selectively saturate the spectrally broad macromolecular protons. This saturation is then transferred to the free water pool via MT, resulting in an observed signal attenuation. The MT effect is often semi-quantitatively characterized via the MTR, which has been shown to correlate with myelin content (Schmierer et al., 2007). Unfortunately MTR is also sensitive to pulse sequence design, B1 and B0 inhomogeneity (Berry et al., 1999), as well as by tissue relaxation times and other non-MT-specific NMR parameters (Henkelman et al., 1993; Stanisz et al., 2005). This limits the ability of researchers and clinicians to create a standard MTR metric to define pathology. To overcome some of these limitations and to derive indices that are directly reflective of MT phenomena, quantitative MT (qMT) has been developed and implemented in the brain, but rarely in the spinal cord (Levesque et al., 2010b; Samson et al., 2013; Sled and Pike, 2001; Smith et al., 2009; Stanisz et al., 2005). qMT typically requires images to be acquired at multiple RF irradiation powers and/or offsets, generating a so-called MT z-spectrum for each voxel (Hinton and Bryant, 1996). The resulting z-spectrum can then be fit to a two (or more)-pool model to estimate quantitative indices, such as the macromolecular proton fraction (MPF), defined as the macromolecular pool size divided by the sum of the macromolecular and free pool sizes, or f, as reported by Yarnykh (2012), the MT exchange rate from the macromolecular pool to the free pool (kmf), and the transverse and longitudinal relaxation times for each pool (Stanisz et al., 2005). Often, the focus is on the MPF as it has been shown to correlate well with white matter myelin density (Odrobina et al., 2005; Ou et al., 2009; Schmierer et al., 2007; Underhill et al., 2011), and may offer a biomarker of demyelination and axonal loss in white matter pathologies.
While qMT offers indices reflective of tissue physiology, translation of this methodology into the spinal cord within a clinically feasible scan time has proven to be a challenge. Even in the brain, collection of multi-power, multi-offset, high SNR, voxel-wise MT z-spectra can result in scan times as long as 30-45 minutes for whole-brain coverage at low resolution (Yarnykh, 2012). As the cord is small (only 1.5 cm in diameter at the cervical levels), with its component white and grey matter groups on the order of millimeters, even higher resolution is necessary, exacerbating the scan time problem. Additionally, at these high-resolutions, transverse spinal cord motion resulting from cardiac and respiratory cycles, as well as cerebrospinal fluid pulsation, can lead to substantial artifacts. Lastly, the spinal cord is surrounded by large bones that create spatially varying susceptibility gradients. Importantly for qMT, these susceptibility gradients can alter the effective B1 and B0 fields, leading to spatially dependent RF powers and offset frequencies. Fortunately, when performing qMT in the spinal cord, the model incorporates both B1 and B0 corrections, which can minimize the impact of spatially varying B1 and B0 errors in the estimated MPF value.
A new method to perform a qMT analysis using only a single MT-weighted acquisition and a reference measurement (no RF saturation) has been recently proposed for the brain (Yarnykh, 2012). This method imposes constraints on the two-pool model in order to derive quantitative maps of the MPF in tissue from a single offset measurement (n.b., additional T1, B1, and B0 measurements are also performed). Using this model, improved resolution or reduced sensitivity to motion can potentially be realized in clinically relevant scan times, making it a viable approach for the spinal cord. Thus, the goal of this study was to determine the feasibility of translating this single-point approach to the cervical spinal cord as a means of performing high resolution, rapid qMT imaging. Toward this end, we performed in vivo qMT in the cervical spinal cord of healthy controls and MS patients using (i) a low-resolution, multi-offset and power MT acquisition with a full model fit (the gold-standard); and (ii) high-resolution, single-point fits using the optimal offset and power from numerical simulations (c.f. Methods). We evaluated the robustness of the single-point methods and sensitivity for disease in patients with MS. Additional numerical studies were performed to assess the affect of the constraints on the single-point qMT parameters. Lastly, the reproducibility of the acquisition and analysis methods was experimentally studied.
Materials and Methods
Data Acquisition
The local Institutional Review Board approved this study, and signed informed consent was obtained prior to the examination. Data were obtained from ten healthy volunteers (5 male, age range 23 – 28 years, mean age 25.6±1.7 years) and two female relapsing-remitting MS (RRMS) patients (31 and 25 years) on a 3.0 tesla Philips Achieva scanner (Philips Healthcare, Best, The Netherlands). A quadrature body coil was used for excitation and a 16-channel neurovascular coil was used for signal reception. A second acquisition was acquired on five of the volunteers after a minimum of two weeks to address reproducibility. The field-of-view (FOV) was centered between the C3 and C4 vertebral bodies, and spanned, at minimum, the C2 to C5 vertebral levels in all subjects. Parallel imaging with sensitivity encoding (SENSE) and second-order shimming was used to minimize image artifacts arising from susceptibility differences between bone and tissue.
Two MT protocols were performed: 1) a low spatial resolution acquisition (1 × 1mm2) at 8 offsets (Δω) and 2 powers (αMT) with a “full-fit” analysis (Yarnykh, 2002; Yarnykh and Yuan, 2004) and 2) a high-resolution acquisition (0.65 × 0.65 mm2) at 1 offset and power with a “single-point” analysis (Yarnykh, 2012). For the full-fit qMT experiment, MT-weighted images were acquired using a 3D MT-prepared spoiled gradient echo sequence (Sled and Pike, 2001) with a GRE readout, TR/TE/α = 50 ms/2.3 ms/6°, and SENSE acceleration factor = 2. Nominal resolution was 1 × 1 mm2 in-plane (reconstructed to 0.6 × 0.6mm2) over 12 slices (5 mm reconstructed slice thickness). Other parameters were: FOV = 150 × 150 mm2, and 2 signal averages. MT weighting was achieved using a 20-ms, single-lobed sinc pulse with Gaussian apodization, αMT = 360° and 820°, and offset frequencies (Δω) = 1, 1.5, 2, 2.5, 8, 16, 32, 100 kHz (chosen to approximately logarithmically sample the expected MT z-spectra (Yarnykh, 2012)). The total scan time for the low-resolution, full-fit acquisition was 12 minutes, 15 seconds. High-resolution, single-point MT-data were acquired using the same parameters, except: nominal in-plane resolution = 0.65 × 0.65 mm2, and six signal averages. It should be noted that six signal averages for the single-point scan were chosen to approximate the SNR of the full-fit acquisition while also minimizing blurring due to intra-scan motion. MT weighting was achieved using the same pulse as the full-fit experiment but at Δω = 2.5 and 100 kHz, and an αMT of 820°. The single point RF irradiation offset was chosen based on numerical simulations to minimize bias in the MPF estimate (c.f. Results). The total scan time for the high-resolution, single-point acquisition was 7 minutes.
To correct for B1 and B0 inhomogeneities across the spinal cord, B1 and B0 maps were acquired using fast 3D techniques — B0: dual-TE GRE with TR/TE1/TE2 = 50/4.6/6.9 ms and α = 60°; B1: dual-TR actual flip angle (AFI) GRE method (Yarnykh, 2007) with TR1/TR2/TE = 30/130/2.8 ms and α = 60°. T1 mapping was performed using a multiple flip angle (MFA) acquisition with TR/TE = 20/4.6 ms and α = 5, 10, 15, 20, 25, 30°. A high-resolution multi-echo gradient echo (mFFE) scan was also performed and all echoes were averaged to generate a high contrast reference image for registration (Held et al., 2003). The mFFE was obtained with TR/TE/ΔTE = 700/7.2/8.8 ms and α = 28°. Nominal in-plane resolution was 0.65 × 0.65 mm2. Acquisition times were 45 seconds for the B0 map, 1 minute 12 seconds for the B1 map, 1 minute 30 seconds for the T1 map, and 5 minutes 30 seconds for the mFFE, resulting in a total acquisition time of ≈32 minutes.
Image Processing
All data analyses were performed in MATLAB R2013a (Mathworks, Natick, MA). Prior to data fitting, all images were cropped to an area immediately around the spinal cord and co-registered to the mFFE volume using the FLIRT package from FSL v5.0.2.1 (FMRIB, Oxford, UK) (Jenkinson et al., 2002; Jenkinson and Smith, 2001). The co-registration was limited to translation and rotation (±5°) in-plane only (i.e. translation in x and y, and rotation about the z-axis). Following co-registration, qMT parameter maps were generated for each volunteer and patient using the full-fit qMT model described in Yarnykh (2002) & Yarnykh and Yuan (2004). This model contains six independent parameters: R1m, R1f, T2m, T2f, MPF = M0m/(M0f + M0m), and kmf = kfm*(1-MPF)/MPF. It has been shown that the signal dependence on R1m is weak (Henkelman et al., 1993; Morrison and Henkelman, 1995); therefore, it was set to 1 s−1 for fitting purposes. R1obs (1/T1obs) maps were reconstructed by regressing MFA data to the spoiled gradient echo signal equation in the steady-state (Fram et al., 1987). The resulting maps were then used to determine the parameter R1f, as described by Yarnykh (2002) & Yarnykh and Yuan (2004). The remaining parameters were estimated for each voxel by fitting the full-fit qMT data to the two-pool MT model (Yarnykh, 2002; Yarnykh and Yuan, 2004). For all fitting, the nominal offset frequency and RF amplitudes were corrected in each voxel using B0 and B1 maps, respectively.
It has been shown that T2m, kmf, and the product T2fR1f can all be fixed during the fitting process because they all exhibit relatively constant values across tissues (Yarnykh and Yuan, 2004). Note that T2f can be determined from the constrained T2fR1f value and an R1f estimate from the MFA data, while kfm can be determined using the first-order mass action kinetics (Underhill et al., 2011). Thus, these constraints result in a model where MPF is the only free parameter.
To estimate reasonable fixed parameter values for the single-point qMT analysis, histograms of T2fR1f, kmf, and T2m were created over the spinal cord for all slices and healthy volunteers from the full-fit analysis, and the median value of each histogram was chosen to enter into the single-point qMT analysis. Then, using the median values of the constraints and the optimal offset and power (determined from the numerical analysis below), the high-resolution, single-point data were analyzed to generate high-resolution MPF maps.
To numerically evaluate the error from only using a single offset to calculate MPF, Monte Carlo simulations were performed. For the simulations, we chose to study white matter, but also considered the case where the MPF and T1 may be altered to model changes that may be experienced in pathologic conditions such as MS (so-called “lesion” in the Results). We do note, however, that modeling a lesion in this manner underestimates the complexity of the disease process, but nevertheless provides an estimate of the bias in the MPF that may be encountered in vivo in patient populations. All data were numerically generated from the equations provided in Portnoy and Stanisz (2007). Gaussian noise was added to the data (SNR = 70 at thermal equilibrium to match experimental studies), and a single-point analysis was performed over 10,000 noise realizations for each of the following: (i) at each sampled offset and power to numerically evaluate the optimal sampling parameters for the single-point analysis, and (ii) over a range for fixed values for kmf, T2fR1f, and T2m to evaluate the potential bias generated by the incorrect assumptions about these values. For the first set of simulations, the relative root mean square (RMS) error (, where MPFact and MPFest are the actual and estimated MPF values, respectively) was calculated in order to assess the combined effect of noise and bias for each combination of offset and power. For the second set of simulations, only the bias () resulting from the constrained parameters was assessed.
Statistical Analysis
Mean MPF values for the single-point and the full-fit scans were calculated in the following regions of interest (ROI) for each slice: dorsal column, left lateral column, right lateral column, and grey matter, as shown in Fig. 1b. ROIs were placed manually using MIPAV (NIH, Bethesda, MD) for each slice of each subject. In subjects with MS lesions, lesion ROIs were placed fully circumscribing lesions identified on the mFFE, while white matter and grey matter ROIs were placed in normal appearing regions in a similar fashion as the healthy volunteers. Statistical comparisons were performed on the mean MPF values from each ROI i) between the left and right lateral columns, ii) between the lateral and the dorsal columns, iii) between white matter and grey matter, iv) across slices and across subjects, and v) across time. Non-parametric Wilcoxon rank-sum tests were performed for the difference tests and the Kruskal-Wallis (non-parametric ANOVA) test was performed to evaluate differences across slices and volunteers. To avoid confounds of multiple-comparisons, we chose the significance threshold to be p < 0.01. Reproducibility and variability across time was assessed using Bland-Altman analysis (Bland and Altman, 1986). For each time point, each volunteer contributed a single MPF value for white matter (WM) and grey matter (GM), which were averaged over the entire cord. As part of this analysis, the normalized Bland-Altman difference (DBA), 95% confidence interval for the difference, and the limits of agreement (1.96*SD of the difference across scans) were calculated.
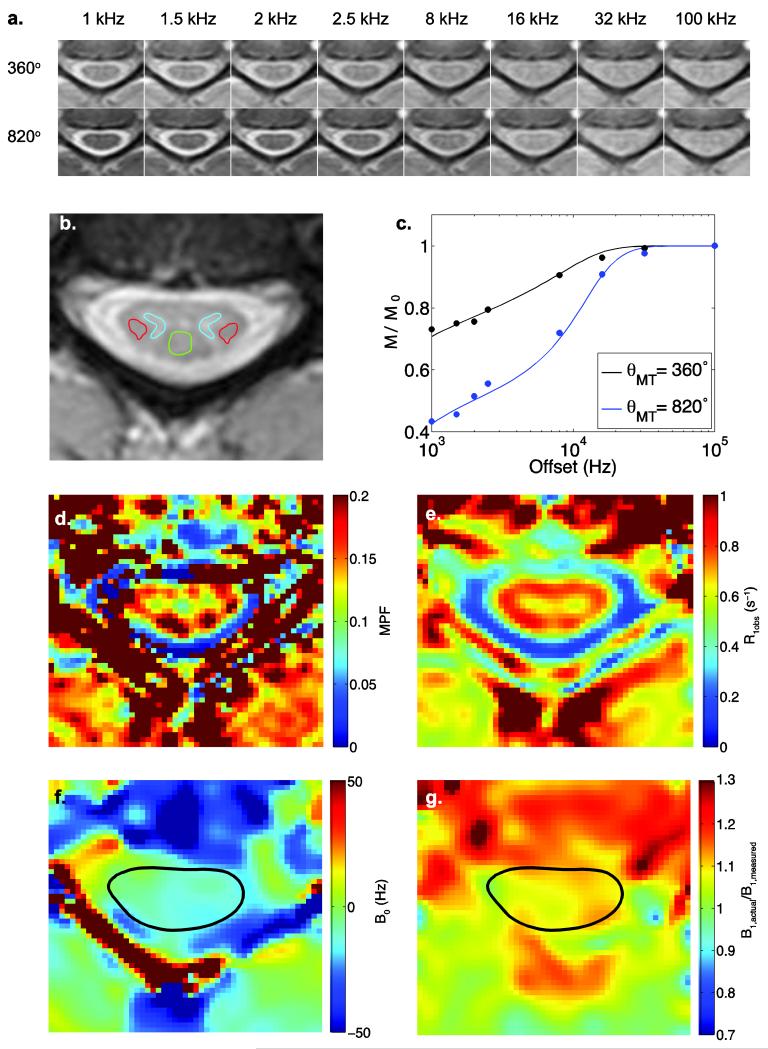
Figure 1.
Full fit qMT data for a representative subject at C3/C4. (a.) Raw qMT data cropped to be centered around the spinal cord. (b.) The high-resolution anatomical image used to co-register the images, with ROIs drawn indicating the left and right lateral columns (red), the dorsal column (green) and the grey matter (blue). (c.) Z-spectra fit to experimental data taken from the dorsal column between C3 and C4. (d.) Representative full fit MPF map determined from the qMT data shown in (a.). (e.) Example R1obs map of the spinal cord. (f. & g.) Example B0 and B1 maps of the spinal cord, respectively.
Results
Data Acquisition
Representative MT-weighted images in a healthy volunteer at the level of C3/4 are shown in Fig. 1a, and corresponding high-resolution mFFE data are given in Fig. 1b. Note that the cropped images shown in Fig. 1a and Fig. 1d-g are derived from the registration process (c.f. Methods). Figure 1c shows mean ROI data (circles) placed in the lateral column white matter of a healthy volunteer at powers = 360° (black) and 820° (blue). The solid lines denote the full-fit qMT analysis, which agrees well with the experimental data (χ2 = 0.005, p < 0.001). Figure 1d shows the derived MPF map at the same level. Note that in the MPF (and R1obs) map, the grey matter is clearly delineated from the surrounding white matter as indicated by lower MPF (and R1obs) values in general. Note also the poor quality of the fitting near tissue interfaces (such as the spinal cord bordering the CSF), which may be related to a poor estimation of kmf in these regions due to partial volume effects with CSF, and may be further exacerbated by the choice of motion correction strategies, spatial interpolation and within scan motion. For comparison, R1obs, B0, and B1 maps are shown in Fig. 1e, f, and g respectively. The average T1,obs values for the lateral columns, dorsal column, and grey matter were found to be 1.24±0.20, 1.24±0.23, and 1.33±0.19 seconds, respectively.
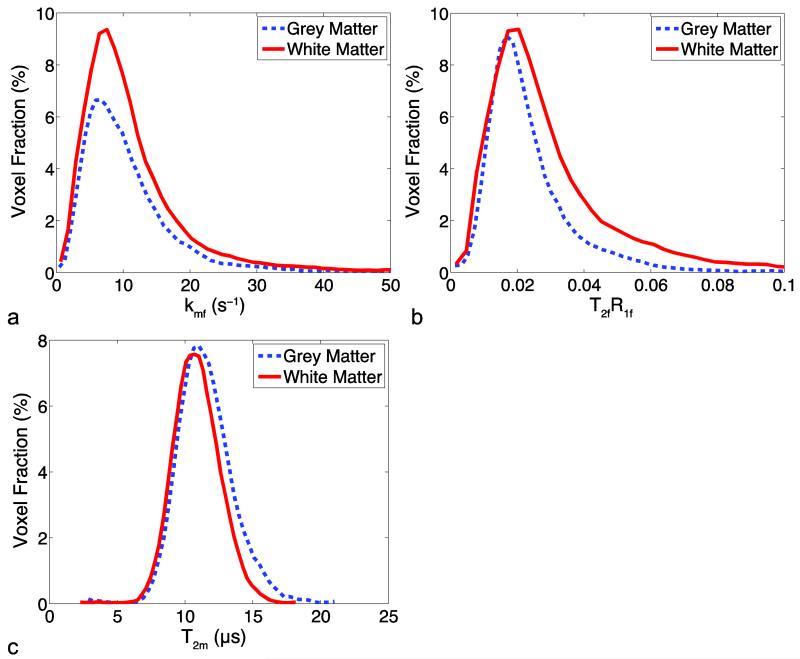
Figure 2 shows whole cord histograms for each single-point constrained parameter (kmf, T2fR1f, T2m) derived from the full-fit analysis approach over all healthy volunteers for white matter and grey matter. All histograms have a single peak for each tissue type, although kmf and T2fR1f are left-skewed with long tails at high values, and each histogram has similar peaks across tissue types. The median values of each parameter used for single-point fitting constraints were: kmf = 8.95 s−1, T2fR1f = 0.0232, T2m = 10.8 μs.
Figure 2.
Histograms of the full fit model parameters for the control group subjects for (a) the exchange rate constant kmf, (b) T2fR1f, and (c) T2m, normalized to the total number of voxels and computed with the bin sizes 0.78 s−1, 0.0031, and 0.37 μs for kmf, T2fR1f, and T2m, respectively.
Numerical Error Analysis
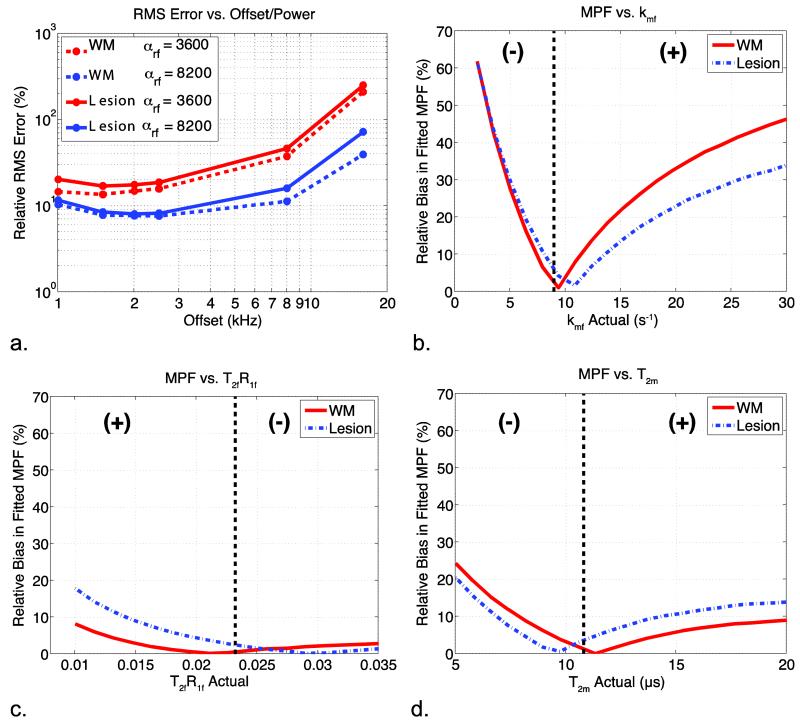
Figure 3 shows the numerical analysis of errors comparing full-fit qMT estimates of the MPF to the single-point methods. The MPF relative RMS error as a function of RF offset and power is shown in Fig. 3a for simulated healthy white matter (dashed) and lesion data (solid). For healthy white matter, a minimum RMS error is seen for MT offsets between 1.5 and 3 kHz for both αMT values. The lesion has a slightly greater RMS error over all offsets and powers, but tracks with the healthy (dashed) values at intermediate offset values. In fact, lesion and white matter RMS error were statistically indistinguishable at offsets = 1.5 to 3 kHz at αMT = 820°.
Figure 3.
Analysis of the errors associated with the single-point analysis of MPF. (a) The RMS error associated with each offset and power for white matter and a lesion. (b, c, & d) The relative bias associated with inaccurate fixed values for kmf, T2fR1f, and T2m, respectively. The dotted line represents median value for each parameter over all healthy subjects, which was the fixed value for all analyses, and the (+) and (−) represent the sign of the bias on either side of the inflection point for each plot. When not varied, parameters were set to: Δω = 2.5 kHz, RF power = 820°, T2m = 10.8 μs, T2fR1f = 0.0232, and kmf = 8.95 s−1.
The bias in the estimated MPF value associated with incorrect parameter choices for kmf, T2fR1f, and T2m are shown in Fig. 3b, c, and d, respectively. Note that T2fR1f and T2m stay below 20% for all constrained parameter values and tissue types indicating that incorrect assumptions for T2fR1f and T2m values do not introduce a significant source of bias in the MPF estimate. Incorrect assumptions about kmf can result in a significant level of MPF bias in some cases, however, a 50% increase/decrease in kmf will result in a 20% bias in the observed MPF, or an over-/underestimation of only 0.02 for an MPF of 0.1. While the kmf chosen for this analysis is chosen via histogram analysis derived from healthy control data, simulations predict that the slightly elevated kmf in lesions biases estimates of the MPF by less than 10%. The estimates for the other median MT parameters values in the MS patients are similar to the healthy controls (kmf = 8.54 s−1, T2fR1f = 0.0311, and T2m = 10.3 μs); therefore, we do not expect assumptions regarding these parameters to be a significant source of bias in lesions.
Comparison to MS
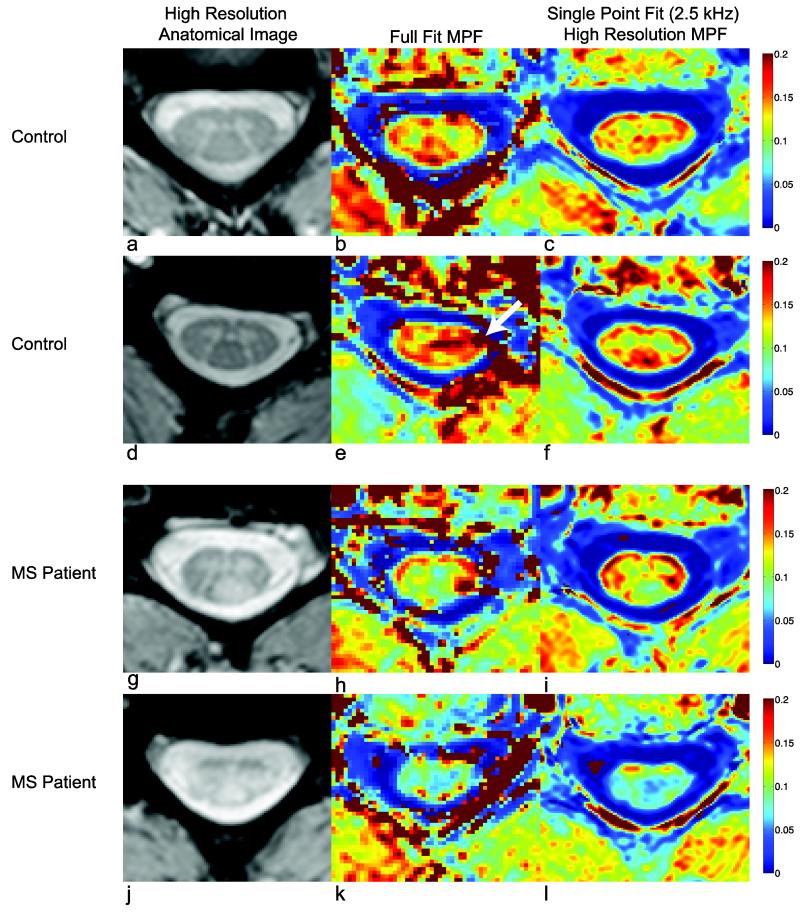
Anatomical mFFE and MPF maps are displayed in Fig. 4. Figures 4a-c and Fig. 4d-f illustrate results in two different healthy volunteers at the level of C3/4 with full-fit and high-resolution single-point maps taken at Δω = 2.5 kHz and αMT = 820°. Note that the contrast is such that dense white matter regions (lateral, dorsal, and ventral columns) have a higher MPF value (red) compared to the grey matter (green), while the CSF exhibits little to no MT effect (blue). The single-point maps show contrast between white and grey matter more clearly than the full-fit MPF maps, and agreed with the size and location of the anatomical definition shown in the mFFE. Additionally, the single-point MPF shows more consistent values in the CSF and at the boundary between the spinal cord and CSF. Note the artifact in Fig. 4e (arrow), which is not seen in the single-point method. Since the constraints are applied rather than calculated for each slice, aberrant data points (due to motion, or pulsation) may have a smaller impact on the overall quality of the fit. Additionally, the application of median values also reduces the artifacts that arise due to poor fitting at tissue interfaces. Lastly, at higher resolution, the detail of the grey matter butterfly can be appreciated in Fig. 4f. Figure 4g shows an mFFE at the level of C3/4 in a patient with relapsing-remitting MS who presented with sensory deficits localized to lesions in the dorsal column (Fig. 4g). The high-resolution, single-point MPF map (Fig. 4i) shows a reduced MPF value (0.09±0.01) in the lesion compared to the lateral and ventral columns (red, 0.17±0.02) and compared to healthy control white matter (0.16±0.01). Importantly, the single-point MPF maps show similar MPF values to the full-fit maps even when pathology is present. While simulations (Fig. 3) predict an underestimation of the MPF of approximately 5% due to the decrease in kmf of approximately 0.5 s−1, this does not solely explain the large decrease in MPF observed in the lesion. For example, if the normal white matter MPF = 0.16, this underestimation would change this MPF estimate to 0.15, which is still within one standard deviation of the normal white matter MPF. This is also the case when looking at the MPF maps for the second MS patient (Fig. 4j-l). This patient presented with difficulty walking, sensory and motor impairment; examination of the mFFE reveals lesions in both lateral columns, and fasciculus gracilis of the dorsal column, but the ventral columns appear intact. The MPF (Fig. 4k,l) corroborates the location of tissue damage and the high-resolution single-point MPF map more clearly delineates intact ventral columns (0.14±0.01) even though the majority of the cord shows a substantially lowered MPF (0.07±0.01) compared to healthy volunteers.
Figure 4.
Comparison of full-fit and high-resolution single-point MPF maps for two controls (a-f) and high-resolution single-point MPF maps for two MS subjects (g-j).
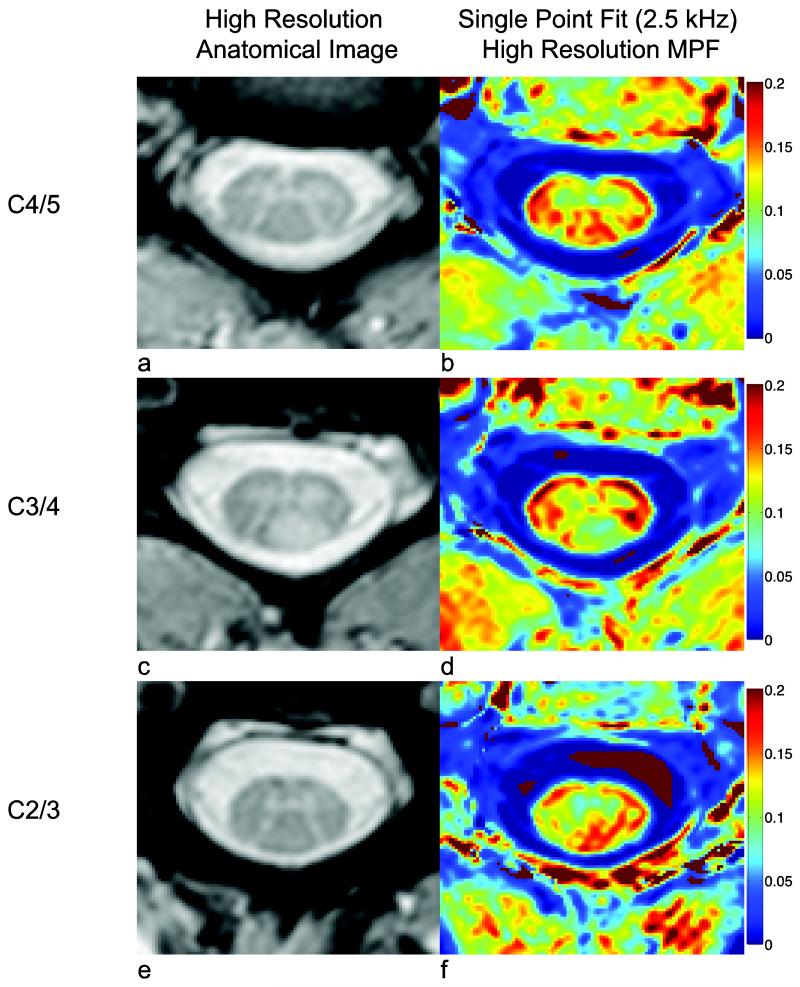
Figure 5 shows images of the MPF and the mFFE at spinal cord levels caudal to (Fig. 5a, b), at the level of (Fig. 5c, d), and rostral to the dorsal column lesion (Fig. 5 e, f) in the first MS patient. The MPF of the dorsal column lesion seen in Fig. 5d appears to not be well visualized at more rostral and caudal levels. At the level of C2/3 (rostral to the dorsal column lesion), the right lateral column appears to be normal on the mFFE, and this is confirmed by the MPF values (C2/3:0.16±0.01, C3/4:0.09±0.01, C4/5:0.15±0.01), which indicates the white matter MPF returns to normal values rostral and caudal to the lesion.
Figure 5.
MPF maps caudal (a-b) and rostral (e-f) to the lesion (c-d) shown for the first MS patient (shown in Fig. 4g-i).
Statistical Analysis
Table 1 shows mean column wise MPF (±SD) values over healthy controls and the p-value for the Wilcoxon rank-sum comparison between the full-fit and single-point derived MPF. Importantly, there is no significant difference between the MPF estimates from each method for white matter (p > 0.5), but a trend is noted for grey matter (p = 0.06), which is likely due to the quality of the full-fit near tissue boundaries and especially in the small grey matter structures.
Table 1.
Mean MPF and Wilcoxon rank-sum tests for the difference between the full-fit and the high-resolution single-point fit for the dorsal column (DC), lateral columns (LC), and grey matter (GM).
| Mean MPF | Wilcoxon Rank-Sum | ||
|---|---|---|---|
|
|
|||
| Full Fit | Single Point | p-value | |
|
|
|||
| DC | 0.16±0.01 | 0.15±0.01 | 0.79 |
| LC | 0.16±0.02 | 0.16±0.01 | 0.57 |
| GM | 0.14±0.01 | 0.13±0.01 | 0.06 |
Table 2 shows the p-values for Wilcoxon Rank-Sum comparisons across columns (Left vs. Right Lateral Column, Dorsal Column vs. Lateral Column, and white matter vs. grey matter) and Kruskal-Wallis comparisons across volunteers. There were no statistical differences between left and right lateral columns (p = 0.39, p = 0.57) or between lateral and dorsal columns (p = 0.43, p = 0.52) for either the single-point method or the full-fit analysis, respectively. However, the MPF was significantly different between white and grey matter for both the full-fit (p = 0.001) and the single-point fit (p < 0.001). When comparing across volunteers and slices, there were no significant differences across slices and volunteers in both the full-fit and single-point fit for all tissue types, indicating the ability for both single- and full-fit analyses to robustly generate similar MPF values throughout the cervical spinal cord. It should be pointed out that the Kruskal-Wallis test shows a trend towards significance when comparing across volunteers with the single-point method.
Table 2.
P-values for the Wilcoxon rank-sum test and the Kruskal-Wallis test for full-fit and high-resolution single-point MPF maps. Tests were performed to evaluate the lateral column left vs right column differences (Left/Right), dorsal column vs lateral column differences (DC/LC), and white matter (lateral column and dorsal column) vs grey matter (WM/GM) differences.
| Wilcoxon Rank-Sum | Kruskal-Wallis | ||||
|---|---|---|---|---|---|
|
| |||||
| Full Fit | Single Point | Full Fit | Single Point | ||
|
|
|
||||
| Left/Right | 0.57 | 0.39 | WM | 0.15 | 0.04 |
| DC/LC | 0.52 | 0.43 | GM | 0.75 | 0.05 |
| WM/GM | 0.001 | <0.001 | |||
Table 3 shows the Bland-Altman analysis of reproducibility of the MPF values for white and grey matter. The confidence intervals for white and grey matter overlap zero for both the full-fit and the single-point MPF and, thus, are not significantly different from time point one to time point two. Interestingly, in white and grey matter, the single-point, high-resolution images have approximately 2-fold smaller limits of agreement and 95% confidence intervals, and also display lower DBA values, indicating that the MPF derived from single-point methods are less variable across time compared to the lower resolution scans.
Table 3.
The 95% confidence intervals, and limits of agreement for the Bland-Altman test for the full-fit and high-resolution single-point fit in white matter and grey matter in 5 volunteers. The table also displays the p-values for the paired t-test.
| White Matter | Grey Matter | |||
|---|---|---|---|---|
|
|
||||
| Full Fit | Single Point | Full Fit | Single Point | |
|
|
||||
| Mean Difference | −0.02±0.03 | −0.008±0.016 | −0.005±0.018 | −0.001±0.008 |
| 95% Confidence Intervals | (−0.06,0.02) | (−0.03,0.01) | (−0.03,0.02) | (−0.01,0.008) |
| Limits of Agreement | (−0.08,0.05) | (−0.04,0.02) | (−0.04,0.03) | (−0.02,0.01) |
| p-value | 0.29 | 0.34 | 0.56 | 0.76 |
| DBA (%) | 10.26 | 5.33 | 3.84 | 0.90 |
Discussion
The goal of this study was to demonstrate the feasibility of high-resolution MPF mapping of the human spinal cord in vivo. We compared the MPF across volunteers, between left and right lateral columns, between lateral and dorsal columns, between white and grey matter, and evaluated the slice-wise variability as well as the test-retest reliability for white and grey matter in the cervical spinal cord. We show that the MPF can be consistently obtained in healthy volunteers, and that the MPF is significantly decreased in the lesions of patients with MS. The ability to generate MPF maps from only a single qMT measurement may increase the clinical applicability of spinal cord qMT imaging because of the opportunity to obtain either high-resolution quantitative mapping, or rapid estimation (46 seconds/offset at 1×1×5 mm3) of the MPF at lower resolution.
Currently, qMT of the spinal cord at 3.0 tesla has been limited (Dortch et al., 2010), although several semi-quantitative measurements using the MTR (Berry et al., 1999) and MTCSF (Smith et al., 2005) have been reported (Cohen-Adad et al., 2011; Filippi and Rocca, 2007; Grossman et al., 2000; Hickman et al., 2004; Rovaris et al., 2008). One challenge facing the MTR and MTCSF is that they are sequence and scanner dependent (Berry et al., 1999; Henkelman et al., 1993; Stanisz et al., 2005) and, therefore, cannot readily be used to quantitatively study tissue changes in the spinal cord across sites. In contrast, qMT-derived MPF values have been shown to be scanner independent and correlated with myelin content (Odrobina et al., 2005; Ou et al., 2009; Schmierer et al., 2007; Underhill et al., 2011), but typically suffer from long acquisition times. Utilizing a single-point qMT measurement (with appropriate constraints) estimates of the MPF can be obtained in less time and at higher resolution. As can be seen from Fig. 4, the higher resolution gained from only utilizing one off-resonance measurement provides benefits in characterizing the MPF at tissue interfaces in the spinal cord. The increased resolution also provides more accurate delineation of white and grey matter in healthy tissue, and additionally allows for straightforward lesion detection in demyelinating diseases such as MS. It should be pointed out that other novel methods have been presented to obviate the long acquisition times and derive MT indices that quantitatively reflective the magnitude of the MT effect (Samson et al., 2013). They differ from the method proposed in this manuscript by employing a fit to the signal equation for an MT-prepared FLASH sequence rather than imposing constraints on the two-pool model for MT.
It is important to note, that while MPF mapping of the human spinal cord in vivo has also been limited (Dortch et al., 2010), MPF measurements of spinal cord white matter in this study agree well with previously published MPF data in the brain (Yarnykh, 2012) for the single-point methodology as well as the multi-point acquisitions (Levesque et al., 2010a). The lack of significant differences between the lateral and dorsal columns could be related to the fact that in the healthy cord, there are only subtle differences between the myelin density of the dorsal and lateral column. The qMT-derived MPF values for grey matter are also in good agreement with literature reports of grey matter in the brain.
Interestingly, when comparing the single-point and full-fit estimates of the MPF, a trend towards significance is seen from the former when evaluating the MPF across healthy volunteers. The complete analysis is shown in Table 2, which displays the results of the Kruskal-Wallis (non-parametric ANOVA) test. When examining controls across slices and across subjects, the full-fit displayed no significant variation across subjects (p > 0.1), whereas the single-point MPF trended towards significance at the p = 0.01 level (p = 0.04 and p = 0.05, respectively). This is intriguing because it offers the possibility that the single-point method may be sensitive to subtle differences between volunteers; or it may be that an improvement in the resolution minimized sensitivity to tissue interfaces.
The test-retest values of the model also did not demonstrate significant bias, indicating the model may be able to allow one to follow the MPF over time. Furthermore, as can be seen from the Bland-Altman analysis shown in Table 3, the single-point analysis displayed less variability over time than the full-fit analysis. This suggests that the temporal variability in the single-point method is less susceptible to day-to-day variations in the scanner as well as patient motion, potentially due to the constraints that are applied to generate the MPF index. We should point out, however, that differences in resolution, SNR, and CNR play a role in test-retest reliability, making it difficult to compare across protocols. Another confound is that for high-resolution scans, the within scan motion can be greater and is challenging to correct post-hoc, especially in the cord. Nevertheless, both the full-fit and single-point methods provide relatively robust test-retest reliability, which may have important implications for tracking pathology.
When choosing constraints for the one-point analysis, care must be taken when choosing the value for kmf, as substantially erroneous estimates of kmf can lead to large variations in the MPF estimates (Fig. 3). The median kmf in the MS patients (kmf = 8.54) was slightly different from that observed in the controls (kmf = 8.95), which may have lead to some of the observed differences in the MPF when lesions are present. According to Figure 3, this kmf error would lead to an inflation of the estimated MPF of < 5% in patients. This is also seen experimentally in Fig. 4h, j, k, and l, where, although there are minor differences between the full-fit and single-point MPF maps, the overall spatial correspondence of the lesion and magnitude of the estimated MPF are similar. When comparing the single-point MPF map of the patients to the anatomical images, the single-point, high-resolution MPF image more accurately depicts the pathology seen in the anatomical image, indicating that any small inaccuracies in the MPF do not change the impression of decreased MPF in lesions and are tolerable when considering trade-offs with respect to motion artifacts, etc. This is also the case when examining the areas around the lesion, where the MPF does not show appreciable partial volume effects.
The current clinical gold standard for visualizing white matter pathology is the MTR, however, it has been shown to be sensitive to B1 and B0 effects, pulse sequence design, hardware limitations, and scanner field strength (Berry et al., 1999; Henkelman et al., 1993; Stanisz et al., 2005). Nevertheless, it is important to cast the findings of our single-point method in light of the conventional MTR. To compare the single-point qMT-derived MPF to the MTR, we calculated the MTR using the high-resolution single-point MT data (αMT = 820°, Δω = 2.5kHz) which is defined as: MTR = 1-S(Δω)/S0, where S(Δω) and S0 are the signals obtained with and without RF irradiation, respectively. Similar to the MPF, the MTR in healthy controls shows no differences between dorsal (0.45±0.02) and lateral (0.45±0.02) columns (p=0.68), but significant differences between white (0.45±0.02) and grey (0.42±0.02) matter (p = 0.009) are noted and expected. However, the MTR across slices and volunteers shows significant differences (Kruskal-Wallis, p < 0.001). While it is difficult to assume that either the MPF or MTR should (or should not) be different across volunteers, it has been shown that over a small segment of the spinal cord, tissue relaxation and myelin density should not vary significantly. Thus, we hypothesize that a measure sensitive to these phenomena should also not be different. Since the MTR varies over slices for healthy volunteers whereas the MPF does not, we postulate that the B1, B0, and T1 correction applied to generate the MPF minimizes the impact of slice-wise, periodic fluctuations that can directly impact the accuracy of the estimate of MT-derived indices.
When considering reproducibility, the MTR shows no significant differences over time for both white (p = 0.63) and grey (p = 0.21) matter. However, Bland-Altman analysis shows that the MTR has a larger LOA and 95% confidence interval span (MTR LOA white matter = (−0.06,0.07), gray matter = (−0.03,0.06); 95% CI white matter = (−0.03,0.05), gray matter = (−0.01,0.05)), which underscores the importance of correcting both B1 and B0 in the MPF calculation.
In the two patients studied, we found that the MPF and MTR show different sensitivities. For the first patient (Fig. 4 g-i), the MPF in the lesion shows approximately a 50% reduction in the MPF value (0.09±0.01) compared to the lateral and ventral columns (0.17±0.02), and compared to healthy control white matter (0.16±0.01). The MTR, however, shows a 7% reduction (0.41±0.02) in the lesion compared to the lateral and ventral columns (0.44±0.06). For the second patient (Fig. 4j-l), the MPF in the ventral columns (0.14±0.01) is slightly reduced (by 9%) yet it is still similar to the healthy control average in the ventral columns; the majority of the cord, however, is substantially lower (0.07±0.01). The MTR for this patient in the same regions shows a larger reduction (0.31±0.02) over the bulk of the cord compared to the ventral columns (0.44±0.01), and compared to healthy volunteers but still a smaller relative change than the MPF. We hypothesize that the change in T1 between lesion types may play a role in the observed sensitivity of the MTR to different lesions, which are removed in the single-point MPF calculation. In summary, the MPF in well-delineated (Fig. 4 g-i) and diffuse (Fig. 4 j-l) lesions show a greater relative signal reduction than the MTR, yet neither the MPF nor the MTR reveals rostral-caudal reductions at vertebral levels above and below the lesion (MTR C2/3:0.44±0.02, C3/4:0.41±0.02, C4/5: 0.43±0.03).
It should be pointed out that for both the single-point and full-fit MPF calculations, motion correction is important in determining the fidelity of the derived indices. In this work, we chose to use a standard motion correction package, FLIRT (FSL, FMRIB, Oxford UK), and the resulting images were transformed using linear interpolation. While visually this resulted in excellent spatial agreement between the target and the MT-weighted scans, alternative methods for spatial interpolation could be considered. Indeed, the interpolation choice may have an impact on the magnitude of partial volume effects at the cord boundary. A future study could examine the impact of motion correction on the derived maps. Additionally, motion within the scan cannot be overlooked. For high-resolution scans, the spinal cord will move more rapidly than the time it takes to sample the full k-space for our 3D acquisition and may result in blurring at the interfaces. Ideally cardiac and/or respiratory triggering could be used, but the dynamic change in the TR with each trigger may influence the assumption of a steady state magnetization. The findings herein suggest that while this motion may result in blurring, the constraints of the single-point model minimize the impact of motion on the estimated MPF values, especially at tissue interfaces.
While the scan times were within the clinical domain, this study did not pursue fast imaging methods such as segmented EPI to further accelerate scan times. These methods could be utilized to further decrease scan times, although additional considerations (e.g., susceptibility effects) need to me made when employing EPI readouts. This study also did not optimize the excitation flip angle in the qMT sequence. While the small flip angle was chosen to reduce T1 effects that may be present at larger flip angles, a larger flip angle would provide more signal and, therefore, may be necessary in order to provide balance between scan time and SNR.
Conclusions
The results of this study demonstrate the feasibility of performing qMT imaging in human spinal cord in vivo. The development of this technique allows for a higher resolution quantitative scan of the spinal cord in less time than is needed for a conventional full-fit qMT acquisition. In healthy subjects, intra-subject reliability (i.e. test-retest) and through cord similarities were demonstrated for both full-fit and single-point acquisitions. This method was also performed on patients with multiple sclerosis with well-described spinal cord lesions, providing preliminary evidence that this method can be utilized to illustrate pathology in vivo. Future work includes further investigating the effects of pathology on the kmf, and high field applications of this methodology.
Acknowledgements
We would like to thank Ms. Donna Butler, Ms. Leslie McIntosh, Ms. Kristen George-Durrett, Ms. Clair Kurtenbach, and Mr. David Pennell, who provided invaluable assistance with data collection. This work was supported by NIH/NIBIB K01 EB009120 (SAS), NIH/NIBIB K25 EB013659 (RDD), and NIH/NCI R25 CA136440 (AKS).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Berry I, Barker GJ, Barkhof F, Campi A, Dousset V, Franconi JM, Gass A, Schreiber W, Miller DH, Tofts PS. A multicenter measurement of magnetization transfer ratio in normal white matter. J Magn Reson Imaging. 1999;9:441–446. doi: 10.1002/(sici)1522-2586(199903)9:3<441::aid-jmri12>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- Cohen AB, Neema M, Arora A, Dell’oglio E, Benedict RH, Tauhid S, Goldberg-Zimring D, Chavarro-Nieto C, Ceccarelli A, Klein JP, Stankiewicz JM, Houtchens MK, Buckle GJ, Alsop DC, Guttmann CR, Bakshi R. The relationships among MRI-defined spinal cord involvement, brain involvement, and disability in multiple sclerosis. J Neuroimaging. 2012;22:122–128. doi: 10.1111/j.1552-6569.2011.00589.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen-Adad J, El Mendili MM, Lehericy S, Pradat PF, Blancho S, Rossignol S, Benali H. Demyelination and degeneration in the injured human spinal cord detected with diffusion and magnetization transfer MRI. Neuroimage. 2011;55:1024–1033. doi: 10.1016/j.neuroimage.2010.11.089. [DOI] [PubMed] [Google Scholar]
- Dortch RD, Welch EB, Gore JC, Smith SA. Quantitative Magnetization Transfer Imaging of Human Cervical Spinal Cord at 3T; ISMRM Annual Meeting; Hawaii. 2010. [Google Scholar]
- Ellingson BM, Ulmer JL, Kurpad SN, Schmit BD. Diffusion tensor MR imaging in chronic spinal cord injury. AJNR Am J Neuroradiol. 2008;29:1976–1982. doi: 10.3174/ajnr.A1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filippi M, Agosta F. Imaging biomarkers in multiple sclerosis. J Magn Reson Imaging. 2010;31:770–788. doi: 10.1002/jmri.22102. [DOI] [PubMed] [Google Scholar]
- Filippi M, Rocca MA. Magnetization transfer magnetic resonance imaging of the brain, spinal cord, and optic nerve. Neurotherapeutics. 2007;4:401–413. doi: 10.1016/j.nurt.2007.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fram EK, Herfkens RJ, Johnson GA, Glover GH, Karis JP, Shimakawa A, Perkins TG, Pelc NJ. Rapid calculation of T1 using variable flip angle gradient refocused imaging. Magn Reson Imaging. 1987;5:201–208. doi: 10.1016/0730-725x(87)90021-x. [DOI] [PubMed] [Google Scholar]
- Freund P, Wheeler-Kingshott C, Jackson J, Miller D, Thompson A, Ciccarelli O. Recovery after spinal cord relapse in multiple sclerosis is predicted by radial diffusivity. Mult Scler. 2010;16:1193–1202. doi: 10.1177/1352458510376180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossman RI, Barkhof F, Filippi M. Assessment of spinal cord damage in MS using MRI. J Neurol Sci. 2000;172:S36–S39. doi: 10.1016/s0022-510x(99)00276-2. [DOI] [PubMed] [Google Scholar]
- Held P, Dorenbeck U, Seitz J, Frund R, Albrich H. MRI of the abnormal cervical spinal cord using 2D spoiled gradient echo multiecho sequence (MEDIC) with magnetization transfer saturation pulse. A T2* weighted feasibility study. J Neuroradiol. 2003;30:83–90. [PubMed] [Google Scholar]
- Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29:759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- Hickman SJ, Hadjiprocopis A, Coulon O, Miller DH, Barker GJ. Cervical spinal cord MTR histogram analysis in multiple sclerosis using a 3D acquisition and a B-spline active surface segmentation technique. Magn Reson Imaging. 2004;22:891–895. doi: 10.1016/j.mri.2004.01.056. [DOI] [PubMed] [Google Scholar]
- Hinton DP, Bryant RG. 1H magnetic cross-relaxation between multiple solvent components and rotationally immobilized protein. Magn Reson Med. 1996;35:497–505. doi: 10.1002/mrm.1910350408. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Koenig SH. Cholesterol of myelin is the determinant of gray-white contrast in MRI of brain. Magn Reson Med. 1991;20:285–291. doi: 10.1002/mrm.1910200210. [DOI] [PubMed] [Google Scholar]
- Kucharczyk W, Macdonald PM, Stanisz GJ, Henkelman RM. Relaxivity and magnetization transfer of white matter lipids at MR imaging: importance of cerebrosides and pH. Radiology. 1994;192:521–529. doi: 10.1148/radiology.192.2.8029426. [DOI] [PubMed] [Google Scholar]
- Levesque IR, Giacomini PS, Narayanan S, Ribeiro LT, Sled JG, Arnold DL, Pike GB. Quantitative magnetization transfer and myelin water imaging of the evolution of acute multiple sclerosis lesions. Magn Reson Med. 2010a;63:633–640. doi: 10.1002/mrm.22244. [DOI] [PubMed] [Google Scholar]
- Levesque IR, Sled JG, Narayanan S, Giacomini PS, Ribeiro LT, Arnold DL, Pike GB. Reproducibility of quantitative magnetization-transfer imaging parameters from repeated measurements. Magn Reson Med. 2010b;64:391–400. doi: 10.1002/mrm.22350. [DOI] [PubMed] [Google Scholar]
- Morrison C, Henkelman RM. A model for magnetization transfer in tissues. Magn Reson Med. 1995;33:475–482. doi: 10.1002/mrm.1910330404. [DOI] [PubMed] [Google Scholar]
- Nair G, Carew JD, Usher S, Lu D, Hu XP, Benatar M. Diffusion tensor imaging reveals regional differences in the cervical spinal cord in amyotrophic lateral sclerosis. Neuroimage. 2010;53:576–583. doi: 10.1016/j.neuroimage.2010.06.060. [DOI] [PubMed] [Google Scholar]
- Naismith RT, Xu J, Klawiter EC, Lancia S, Tutlam NT, Wagner JM, Qian P, Trinkaus K, Song SK, Cross AH. Spinal cord tract diffusion tensor imaging reveals disability substrate in demyelinating disease. Neurology. 2013;80:2201–2209. doi: 10.1212/WNL.0b013e318296e8f1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odrobina EE, Lam TY, Pun T, Midha R, Stanisz GJ. MR properties of excised neural tissue following experimentally induced demyelination. NMR Biomed. 2005;18:277–284. doi: 10.1002/nbm.951. [DOI] [PubMed] [Google Scholar]
- Oh J, Saidha S, Chen M, Smith SA, Prince J, Jones C, Diener-West M, van Zijl PC, Reich DS, Calabresi PA. Spinal cord quantitative MRI discriminates between disability levels in multiple sclerosis. Neurology. 2013;80:540–547. doi: 10.1212/WNL.0b013e31828154c5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou X, Sun SW, Liang HF, Song SK, Gochberg DF. The MT pool size ratio and the DTI radial diffusivity may reflect the myelination in shiverer and control mice. NMR Biomed. 2009;22:480–487. doi: 10.1002/nbm.1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poloni G, Minagar A, Haacke EM, Zivadinov R. Recent developments in imaging of multiple sclerosis. Neurologist. 2011;17:185–204. doi: 10.1097/NRL.0b013e31821a2643. [DOI] [PubMed] [Google Scholar]
- Portnoy S, Stanisz GJ. Modeling pulsed magnetization transfer. Magn Reson Med. 2007;58:144–155. doi: 10.1002/mrm.21244. [DOI] [PubMed] [Google Scholar]
- Rocca MA, Horsfield MA, Sala S, Copetti M, Valsasina P, Mesaros S, Martinelli V, Caputo D, Stosic-Opincal T, Drulovic J, Comi G, Filippi M. A multicenter assessment of cervical cord atrophy among MS clinical phenotypes. Neurology. 2011;76:2096–2102. doi: 10.1212/WNL.0b013e31821f46b8. [DOI] [PubMed] [Google Scholar]
- Rovaris M, Judica E, Ceccarelli A, Ghezzi A, Martinelli V, Comi G, Filippi M. Absence of diffuse cervical cord tissue damage in early, non-disabling relapsing-remitting MS: a preliminary study. Mult Scler. 2008;14:853–856. doi: 10.1177/1352458507088103. [DOI] [PubMed] [Google Scholar]
- Samson RS, Ciccarelli O, Kachramanoglou C, Brightman L, Lutti A, Thomas DL, Weiskopf N, Wheeler-Kingshott CA. Tissue- and column-specific measurements from multi-parameter mapping of the human cervical spinal cord at 3 T. NMR Biomed. 2013;26:1823–1830. doi: 10.1002/nbm.3022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmierer K, Tozer DJ, Scaravilli F, Altmann DR, Barker GJ, Tofts PS, Miller DH. Quantitative magnetization transfer imaging in postmortem multiple sclerosis brain. J Magn Reson Imaging. 2007;26:41–51. doi: 10.1002/jmri.20984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled JG, Pike GB. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn Reson Med. 2001;46:923–931. doi: 10.1002/mrm.1278. [DOI] [PubMed] [Google Scholar]
- Smith SA, Golay X, Fatemi A, Jones CK, Raymond GV, Moser HW, van Zijl PC. Magnetization transfer weighted imaging in the upper cervical spinal cord using cerebrospinal fluid as intersubject normalization reference (MTCSF imaging) Magn Reson Med. 2005;54:201–206. doi: 10.1002/mrm.20553. [DOI] [PubMed] [Google Scholar]
- Smith SA, Golay X, Fatemi A, Mahmood A, Raymond GV, Moser HW, van Zijl PC, Stanisz GJ. Quantitative magnetization transfer characteristics of the human cervical spinal cord in vivo: application to adrenomyeloneuropathy. Magn Reson Med. 2009;61:22–27. doi: 10.1002/mrm.21827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med. 2005;54:507–512. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- Stankiewicz JM, Neema M, Alsop DC, Healy BC, Arora A, Buckle GJ, Chitnis T, Guttmann CR, Hackney D, Bakshi R. Spinal cord lesions and clinical status in multiple sclerosis: A 1.5 T and 3 T MRI study. J Neurol Sci. 2009;279:99–105. doi: 10.1016/j.jns.2008.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stroman PW, Wheeler-Kingshott C, Bacon M, Schwab JM, Bosma R, Brooks J, Cadotte D, Carlstedt T, Ciccarelli O, Cohen-Adad J, Curt A, Evangelou N, Fehlings MG, Filippi M, Kelley BJ, Kollias S, Mackay A, Porro CA, Smith S, Strittmatter SM, Summers P, Tracey I. The current state-of-the-art of spinal cord imaging: Methods. Neuroimage. 2014;84:1070–1081. doi: 10.1016/j.neuroimage.2013.04.124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Underhill HR, Rostomily RC, Mikheev AM, Yuan C, Yarnykh VL. Fast bound pool fraction imaging of the in vivo rat brain: association with myelin content and validation in the C6 glioma model. Neuroimage. 2011;54:2052–2065. doi: 10.1016/j.neuroimage.2010.10.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler-Kingshott CA, Stroman PW, Schwab JM, Bacon M, Bosma R, Brooks J, Cadotte DW, Carlstedt T, Ciccarelli O, Cohen-Adad J, Curt A, Evangelou N, Fehlings MG, Filippi M, Kelley BJ, Kollias S, Mackay A, Porro CA, Smith S, Strittmatter SM, Summers P, Thompson AJ, Tracey I. The current state-of-the-art of spinal cord imaging: Applications. Neuroimage. 2014;84:1082–1093. doi: 10.1016/j.neuroimage.2013.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolff SD, Balaban RS. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn Reson Med. 1989;10:135–144. doi: 10.1002/mrm.1910100113. [DOI] [PubMed] [Google Scholar]
- Yarnykh VL. Pulsed Z-spectroscopic imaging of cross-relaxation parameters in tissues for human MRI: theory and clinical applications. Magn Reson Med. 2002;47:929–939. doi: 10.1002/mrm.10120. [DOI] [PubMed] [Google Scholar]
- Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007;57:192–200. doi: 10.1002/mrm.21120. [DOI] [PubMed] [Google Scholar]
- Yarnykh VL. Fast macromolecular proton fraction mapping from a single off-resonance magnetization transfer measurement. Magn Reson Med. 2012;68:166–178. doi: 10.1002/mrm.23224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarnykh VL, Yuan C. Cross-relaxation imaging reveals detailed anatomy of white matter fiber tracts in the human brain. Neuroimage. 2004;23:409–424. doi: 10.1016/j.neuroimage.2004.04.029. [DOI] [PubMed] [Google Scholar]
- Zackowski KM, Smith SA, Reich DS, Gordon-Lipkin E, Chodkowski BA, Sambandan DR, Shteyman M, Bastian AJ, van Zijl PC, Calabresi PA. Sensorimotor dysfunction in multiple sclerosis and column-specific magnetization transfer-imaging abnormalities in the spinal cord. Brain. 2009;132:1200–1209. doi: 10.1093/brain/awp032. [DOI] [PMC free article] [PubMed] [Google Scholar]