7 Å resolution in protein two-dimensional-crystal X-ray diffraction at Linac Coherent Light Source

Abstract

Membrane proteins arranged as two-dimensional crystals in the lipid environment provide close-to-physiological structural information, which is essential for understanding the molecular mechanisms of protein function. Previously, X-ray diffraction from individual two-dimensional crystals did not represent a suitable investigational tool because of radiation damage. The recent availability of ultrashort pulses from X-ray free-electron lasers (XFELs) has now provided a means to outrun the damage. Here, we report on measurements performed at the Linac Coherent Light Source XFEL on bacteriorhodopsin two-dimensional crystals mounted on a solid support and kept at room temperature. By merging data from about a dozen single crystal diffraction images, we unambiguously identified the diffraction peaks to a resolution of 7 Å, thus improving the observable resolution with respect to that achievable from a single pattern alone. This indicates that a larger dataset will allow for reliable quantification of peak intensities, and in turn a corresponding increase in the resolution. The presented results pave the way for further XFEL studies on two-dimensional crystals, which may include pump–probe experiments at subpicosecond time resolution.

1. Introduction

Knowledge of the atomic structure of membrane proteins, especially the structural changes triggered by external stimuli [1,2], is of keen interest. A two-dimensional protein crystal is a two-dimensional periodic array of the same motif, forming a single layer of molecules. This is a favourable arrangement for membrane proteins, because the lipidic component between the proteins closely mimics the natural environment in the cell membrane [3]. Moreover, it can be assumed that the structure in the two-dimensional crystal environment is almost the same as in the natural state, and that potential structural changes are not as restricted as may happen in three-dimensional crystals [4].

Since the 1970s, electron microscopy (EM) has exploited the signal enhancement brought about by the two-dimensional periodic structure and provided a few dozen unique structures with resolution less than 1 nm [5–7]. The key of that success is that, unlike in diffraction-type experiments, both amplitude and phase of the Bragg reflections are experimentally accessible [8]. Continuous methodological improvements [9–11] that include, in particular, cryo-cooling of the sample [12] have led to structures at atomic resolution [13]. However, a real breakthrough in terms of high-throughput has always been hampered by radiation damage.

The situation is even more critical with X-rays, for which the ratio between useful diffraction and damaging absorption events is far worse [14]. Until the advent of X-ray free-electron lasers (XFELs) [15,16], the experiments were limited to powder diffraction in transmission from pelleted bacteriorhodopsin (bR) two-dimensional crystals [17], and to grazing-incidence diffraction from bR two-dimensional crystals floating at the water–air interface [18]. While X-ray diffraction from a single two-dimensional crystal would offer remarkable advantages, synchrotron sources are limiting, in that radiation damage destroys the sample faster than the accumulation of sufficient signal in the Bragg peaks. At XFELs, the situation is radically different: diffract-before-destroy experiments in the framework of serial femtosecond crystallography [19] on submicrometre-sized three-dimensional crystals have recently proved that the femtosecond XFEL pulses outrun the damage, and that they are of sufficient intensity to generate meaningful Bragg peak signals. The above results prompted us to extend the application of the diffract-before-destroy concept to two-dimensional protein crystals under close-to-physiological conditions of hydration and temperature, thus avoiding the deleterious effects of cryogenic cooling. Further considerations in support of this approach were related to the stronger penetration power of X-rays, which possibly allows the acquisition of diffraction data at larger tilt angles than feasible with cryo-EM, as well as to the perspective of exploiting the finite size of the two-dimensional crystal in the direction perpendicular to the crystal plane for direct phase retrieval [20], not possible in standard three-dimensional crystallography.

Even though the single-layer arrangement strongly reduces the scattering power of two-dimensional crystals, the feasibility of diffract-before-destroy experiments was demonstrated during a Linac Coherent Light Source (LCLS) beamtime at the coherent diffraction imaging (CXI) station in May 2012, where we captured subnanometre Bragg diffraction from individual two-dimensional crystals [21]. The submicrometre-sized X-ray focus available at CXI enhanced the probability of simultaneously illuminating only a small number of two-dimensional crystals. However, during this initial beamtime, the single-crystal hit rate was so low that averaging data for a complete sampling of all Bragg peaks was impossible. Thus, the attainable resolution remained signal-to-noise limited, which affected the overall interpretability of the achieved results.

Here, we describe a larger dataset acquired in May 2013, and show that a key point is to merge data from different crystals to enhance the signal-to-noise ratio of the measurable Bragg reflections. Although limited by the small number of analysable diffraction images, our approach led us to conclude that the prepared sample diffracts to at least 7 Å, and indicates that reliable determination of the reflection intensities just requires more diffraction patterns.

2. Methods

(a). X-ray diffraction measurements

The measurements were performed at the 0.1 μm focus environment of the CXI experimental station of the LCLS XFEL [22], at an X-ray wavelength of 8.8 keV (1.4 Å) and with nominal pulse energies of about 2 mJ.

The sample was supported by a solid silicon wafer, shaped with an extended array of 100 × 100 μm² thin windows consisting of a 5 nm carbon film with a 40 nm poly(methyl methacrylate) layer. About 2.2 μg bR two-dimensional crystals, with a typical size of 0.5–1.0 μm, were suspended in 15 μl of 0.5% w/v glucose solution. This was painted on the backside part of the wafer, so that it could adhere to the carbon face of the windows. After drying, the remaining layer of glucose acted as protection against dehydration in the vacuum chamber.

The XFEL was run in ‘burst mode’, and the wafer was moved transversely to the beam, so that every X-ray pulse hit a new, undamaged window. In this way, the effective rate of diffraction image acquisition was about 1 Hz.

(b). Diffraction image analysis

For a two-dimensional crystal, the X-ray cross section is markedly different from zero only around the Bragg rods. These are lines perpendicular to the two-dimensional crystal plane. Their projection onto this plane corresponds to the reciprocal lattice of the two-dimensional crystal lattice. Each rod is therefore labelled by indices (h, k) corresponding to the two reciprocal unit cell vectors (a_*, b_*). Peaks in two-dimensional crystal diffraction images originate from the intersection of the Ewald sphere with the Bragg rods, and thus they are labelled with the same pair of indices. In the simplest approach, we considered only the images which exhibited a clear diffraction pattern from a single two-dimensional crystal, with the crystal plane almost perpendicular to the incoming beam. Such images were tagged because of the characteristic diffraction peak positions (‘peak lattice’). In an individual image, only the most prominent peaks are visible. To evaluate the potential completeness of the measurable peaks, we enhanced the signal-to-noise ratio by averaging the intensities of small sectors of diffraction images, with the sectors centred at the position of equivalent peaks. This allowed us in particular to merge data from different images. To do that, however, we needed (i) to determine precisely the orientation of each peak lattice, which was possible based on the positions of the most prominent peaks, and (ii) to index each lattice, which required the intensities of those prominent peaks as input, and which includes, among various aspects, the assessment of the face of the two-dimensional crystal exposed to the beam. The details of the protocol will be presented in a future publication.

3. Results and discussion

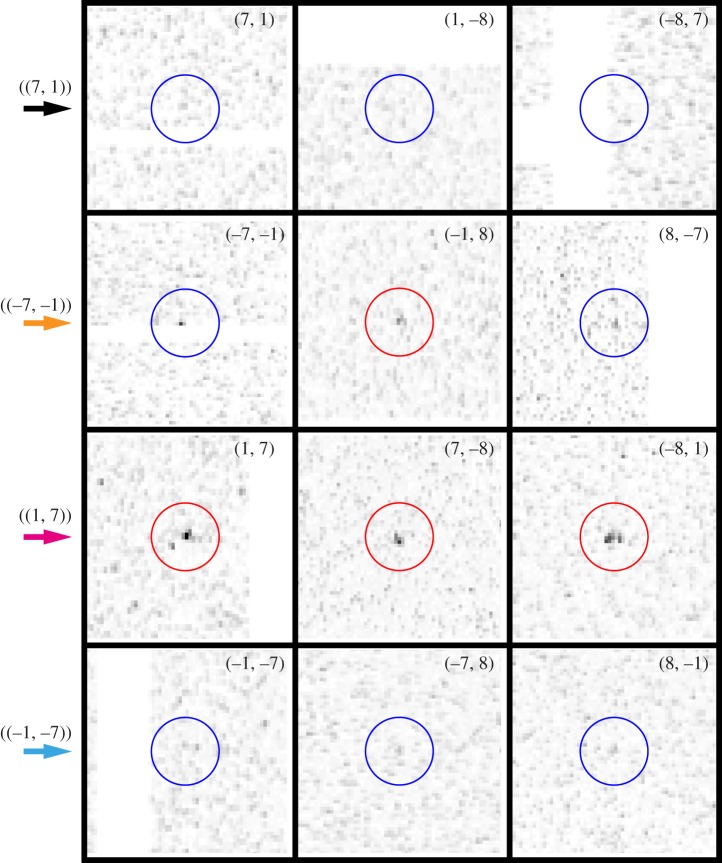
The considered dataset consisted of 324 diffraction images, acquired within about 6 min of beamtime. Among these, 15 exhibited clear diffraction patterns originating from a single bR two-dimensional crystal, out of which 11 were unambiguously indexed. Figure 1 shows a typical example. The peaks are indeed positioned on an easily recognizable sixfold symmetric pattern, originating from the two reciprocal unit cell vectors (a_*, b_*) shown in green, which in the case of the particular bR sample used are known to have equal length 2π/62.45 Å and to form an angle of 60° [5,10]. The red circles mark the positions of prominent peaks that were used to find the exact orientation of the peak lattice with respect to the beam axis, perpendicular to the figure.

Figure 1.

Example of a diffraction image from a single bR two-dimensional crystal. The dashed ring corresponds to 10 Å resolution. The circles mark the positions of expected diffraction peaks at lower than 7 Å resolution. The precise orientation of the peak lattice was derived from the positions of the prominent, easily identifiable peaks encircled in red. The basis vectors (a_*, b_*) of the two-dimensional reciprocal space lattice are shown as green arrows. The small arrows mark the position of peaks in the classes ((7, 1)) (black), ((1, 7)) (magenta), ((−7, −1)) (orange) and ((−1, −7)) (cyan), each class consisting of three equivalent peaks.

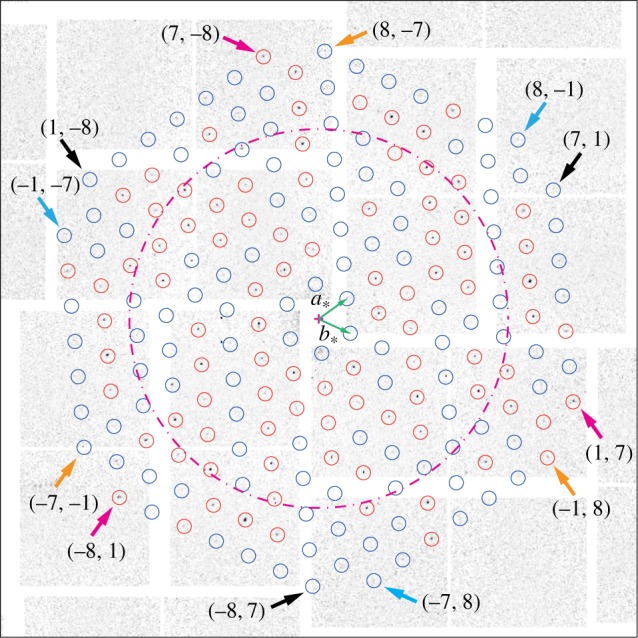
Because of Friedel's law, for perpendicular incidence, the p₃-symmetry of the two-dimensional crystal would result in a sixfold symmetric diffraction intensity for short incoming X-ray wavelength. This limit is not achieved within the actual experimental set-up. Owing to the curvature of the Ewald sphere, the (h, k) and (−h, −k) peaks are no longer Friedel pairs, which is manifest in that the symmetry of the observed peak intensities is clearly reduced from six- to threefold. Crystallographically equivalent peaks are related only by a 120° rotation, meaning that peaks (h, k), (−h−k, h) and (k, −h−k) belong to the same equivalence class, which we label by ((h, k)). Figure 2 displays the peaks observed for classes ((7, 1)), ((−7, −1)), ((1, 7)) and ((−1, −7)), all at 7.2 Å resolution, as magnifications of the diffraction image of figure 1 around the concerned peak positions. The peak intensity variations within a class are in part recognizable by eye, and can be explained as the joint effect of Poisson statistics with small tilts of the individual two-dimensional crystals. Indeed, tilts of less than 25° can hardly be assessed from the peak positions alone [23].

Figure 2.

Magnifications of the diffraction image of figure 1 around peak positions in classes ((7, 1)), ((−7, −1)), ((1, 7)) and ((−1, −7)). The colour coding given by the arrows on the left is the same as in figure 1.

The 11 indexable images were further used for enhancing the peak signals. Figure 3 displays image sector sums for the equivalence classes of figure 2. Each plot arises from the intensity sum of at least 20 image sectors. In this way, almost all peaks up to a resolution of about 7 Å became observable. Peaks in the class ((1, 7)) are clearly visible in most of the individual patterns, and therefore also emerge as prominent features in the image sector sum. By contrast, the ((−7, −1)) and ((−1, −7)) reflections represent typical peaks that can hardly be identified in a single diffraction image (figure 2), yet appear as a clear peaks in the sum. Finally, ((7, 1)) exemplifies the few reflections being so weak that they do not emerge from noise even after the summing procedure, although one can guess that a peak-like feature is present.

Figure 3.

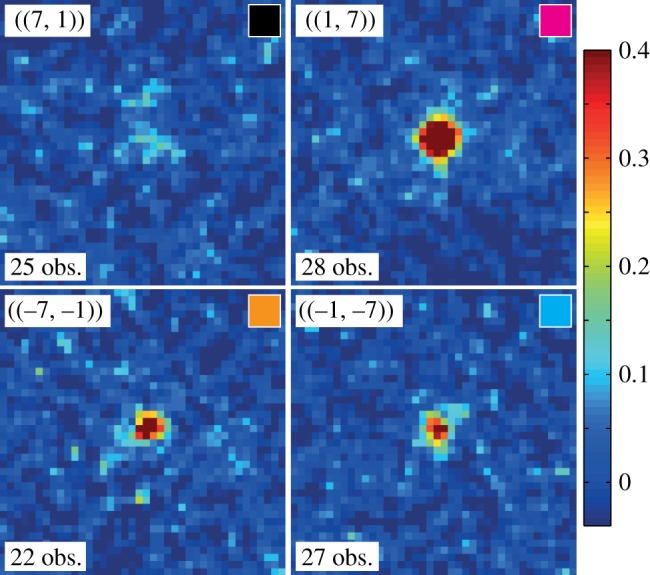
Examples of ‘image sector sums’ (see text) for the four peak classes ((7, 1)), ((−7, −1)), ((1, 7)) and ((−1, −7)), all at 7.2 Å resolution. For each peak, the number of observations is indicated, and the colour in the small box at the top right of each panel corresponds to that of the arrows in figure 1. The intensity colour scale is the same for all four panels. Maximum intensity is about 40 times the background noise, calculated as the average on all image sector sums of the local noise level measured away from the central peak region.

At this point, we note that two overall indexing ambiguities are intrinsic and can be fixed arbitrarily. They correspond to an arbitrary choice of the reference orientation of the two-dimensional crystal. First, exchanging ((h, k)) and ((k, h)) results in reversing the face of the two-dimensional crystal exposed to the positive out-of-plane direction. We fixed this freedom in order to be consistent with the conventions used in reference [24]. Second, swapping ((h, k)) with ((−h, −k)) corresponds to a 180° rotation (equivalent to a 60° rotation) of the crystal.

From the described results, we conclude that the prepared two-dimensional crystals diffract to at least 7 Å. A proper, complete measurement of the peak intensities will benefit from merging data from a larger diffraction image set. We are working towards using images arising from the illumination of a few two-dimensional crystalline domains, where diffraction spots still remain well separated and therefore indexable; indeed, about 30% of the 324 images in the dataset discussed in this paper belonged to this category. From the sample preparation point of view, the aim is to increase the percentage of indexable images, and especially to avoid powder-like rings, by tuning the protein concentration in the solution to be painted on the wafer. We also plan to optimize the shape of the X-ray focus by cutting tails in the transverse direction that weakly illuminate neighbouring two-dimensional crystals, giving rise to a spotty, ring-like background. Finally, we expect to increase the image acquisition rate by reducing the translational motion of the stage between two subsequent image acquisitions. This may be possible by using wafers with either smaller and closer windows, or with rectangular windows with an extended dimension, to be scanned at the full repetition rate of the FEL. In summary, we believe that simple and straightforward modifications will drastically improve the output, potentially providing valuable scientific returns to the ongoing efforts on two-dimensional crystal snapshot diffraction at XFELs.

4. Conclusion

Acquisition of diffraction data from single two-dimensional crystals of proteins mounted on a solid support was previously shown to be feasible at XFELs in diffract-before-destroy mode. Here, we demonstrated that exploiting the currently available X-ray pulse energies of about 2 mJ and merging data from multiple images makes it possible unambiguously to identify diffraction peaks to a resolution of at least 7 Å. Multiple sampling of the same diffraction peak enhances the signal-to-noise ratio, which leads to enhanced resolution compared with the processing of single diffraction patterns. The above results relied on a limited number of single-crystal diffraction images, which leaves ample space for progress. The experiments were performed at room temperature, offering an obvious advantage with respect to techniques that need cryo-cooling to reduce radiation damage to the sample. The set-up can be extended to pump–probe experiments, paving the way for structural dynamics studies of membrane proteins.

Funding statement

C.J.T., X.D.L. and G.F.X.S. acknowledge the Femtosecond and Attosecond Science and Technology (ETH-FAST) Initiative in Switzerland. Part of the work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under contract no. DE-AC52-07NA27344 and Pacific Northwest National Laboratory (operated by Battelle Memorial Institute) under contract no. DE-AC05–76RL01830. Support was provided by the UCOP Lab Fee Programme (award no. 118036), NIH grant numbers 5RC1GM091755 and GM095583, NSF award MCB-1021557 and NSF STC award 1231306, LLNL Lab-Directed Research and Development Project 012-ERD-031 and the PNNL Chemical Imaging Initiative. Part of the work was also supported by the Center for Biophotonics Science and Technology, a designated NSF Science and Technology Center managed by the University of California, Davis, CA under Cooperative agreement no. PHY0120999.