Registration of adaptive optics corrected retinal nerve fiber layer (RNFL) images

Abstract

Glaucoma is the leading cause of preventable blindness in the western world. Investigation of high-resolution retinal nerve fiber layer (RNFL) images in patients may lead to new indicators of its onset. Adaptive optics (AO) can provide diffraction-limited images of the retina, providing new opportunities for earlier detection of neuroretinal pathologies. However, precise processing is required to correct for three effects in sequences of AO-assisted, flood-illumination images: uneven illumination, residual image motion and image rotation. This processing can be challenging for images of the RNFL due to their low contrast and lack of clearly noticeable features. Here we develop specific processing techniques and show that their application leads to improved image quality on the nerve fiber bundles. This in turn improves the reliability of measures of fiber texture such as the correlation of Gray-Level Co-occurrence Matrix (GLCM).

1. Introduction

Retinal imaging provides vital information for the study, diagnosis and treatment of retinal pathologies. This information can be obtained non-invasively using ophthalmoscopes. In recent years, ophthalmic devices have been integrated with adaptive optics (AO) technology to provide high resolution retinal images that reveal retinal microstructures. Highly accurate and reliable image processing techniques are necessary for the development of automated diagnostic tools that will facilitate the use of AO retinal imaging technology in regular clinical practice [1, 2].

The RNFL is formed by retinal ganglion cell axons and represents the innermost layer of the retina. The ganglion cell axons are spread out as a thin layer with striations (nerve fiber bundles). Retinal Nerve Fiber Layer Defects (RNFLD) can be used to diagnose glaucoma, which is the leading cause of preventable blindness across the western world [3–5]. A recent clinical review of glaucoma refers to it as a group of pathological eye conditions with several causes that, usually associated with ocular hypertension, result in damage to the optic nerve head (ONH) and loss of visual field (VF) [6]. The World Health Organization estimated that in 2010 glaucoma accounted for 2% of visual impairment and 8% of global blindness [7]. Loss of axonal tissue in the RNFL has been reported to be one of the earliest detectable glaucomatous changes, which can proceed to morphological changes in the ONH and VF loss [8, 9]. For this reason, many studies have focused on thinning of the RNFL and RNFLD using various imaging technologies [10, 11]. It is therefore essential to obtain high quality RNFL images for early and accurate diagnosis.

Adding AO to imaging systems such as flood-illuminated ophthalmoscopes, Scanning Laser Ophthalmoscopes (SLO) and OCT devices has recently allowed researchers to identify individual nerve fiber bundles, providing high-resolution images of both the RNFL and ONH [1, 2, 9, 12–15]. In this work, sequences of RNFL images are obtained using a commercial AO-assisted flood illumination device. The original RNFL images are often corrupted by intensity variations referred to as shading or intensity inhomogeneity. This is due to inherent imperfections of the image formation process such as non-uniform illumination, uneven spatial sensitivity of the sensor or camera imperfections [16]. It affects automatic image processing, such as segmentation, registration and characterization of retinal features [17]. We have previously described a novel wavelet based method of pre-processing for the correction of uneven illumination in AO flood retinal images [18]. Nevertheless, the final image quality is also limited by motions of the eye that occur on short time scales. These motions can lead to blurring and distortion of the retinal images. More complex warping is considered in the registration of SLO images due to the fact that the image is acquired point-by-point while the eye is moving [19, 20], and is not expected to apply to the snap-shot fundus imaging carried out here. In the case of flood illumination systems, rigid transformations to correct for global translation and rotation will be applicable. In medical image processing, cross-correlation techniques are usually used to measure displacements between images. These use image intensities for direct matching, without the need to detect image features. Cross-correlation has been used already to register images obtained using various AO assisted flood illumination retinal cameras [21–23]. Although the cross-correlation approach can work well, its performance can be severely compromised by factors such as changes in the image intensity, noise, and reduced overlap area when there is large image motion [24]. In this work, we show that the phase correlation technique is more robust than cross-correlation for the estimation of translational motion [25]. However, both correlation methods fail when there are changes in scale or rotation. Various methods have been described in the literature for the estimation of rotational motion. These include bilateral matching between local features of Harris-corner points detected in both input and reference images to measure rotation [26], and the Radon transform [27, 28]. The combination of Fourier based techniques and log-polar transformations has also been applied to measure rotation, translation and scaling [29–32]. Although many techniques claim to accurately measure rotational motion, we have encountered two main issues: (i) most commonly a reference image is matched against a rotated version of itself and (ii) they are intended to measure large angles of rotation (typically >1-2°) with relatively low accuracy. These techniques fail when estimating small rotation angles and/or the image quality or content is changing. In an earlier study, we found that the maximum value of rotation in the retinal images does not exceed 1°, which for an image size of 1k pixels, corresponds to 8-9 pixels at the edge of the image [33].

Our earlier work with AO retinal images focused on the cone photoreceptor layer using a peak tracking approach to correct for rotation [18], which demonstrated the improvement in image quality resulting from correcting rotation for angles less than 1°. On the other hand, the RNFL image sequence does not have clearly noticeable cone photoreceptors and the retinal vessels have natural movement or pulsing. Hence methods based on local features, control points or peak tracking are not optimal to estimate the rotation. In this work, we applied and compared approaches to register and de-rotate the RNFL image sequences, which included the Radon transform, log-polar transform and an exhaustive search. The effectiveness of the registration approaches was evaluated using the gray level co-occurrence matrix (GLCM). This technique provided a useful measure of the structural contrast of the nerve fiber layers and has the potential to be useful as an imaging bio-marker for glaucoma.

2. Methods

The sequences of images used here were obtained using a commercial AO-assisted fundus imager (rtx1, Imagine Eyes, Orsay, France). The deformable mirror of the rtx1 was used to select the appropriate plane of focus. The focal plane was adjusted to acquire images of the RFNL close to the ONH. Each sequence consisted of a series of 40 frames. Each frame had an exposure time of 9 ms and there was an interval of 105 ms between each frame in the series. This work was part of study protocol on the clinical application of AO retinal imaging approved by the local ethical committee (ASL RMA, Rome, Italy). All research procedures adhered to the tenets of the Declaration of Helsinki. Images of the RFNL were acquired from healthy volunteers older than 18 years old. For the purpose of this work, intended to disclose an effective method of registration of AO flood RFNL images, the results are shown only for one case.

Uneven illumination of the RFNL image was corrected before registration. A wavelet based approach was used to remove the variations in the uniformity of the illumination of the retina. The result of the wavelet based approach was compared with homomorphic filtering and spatial filtering methods, as described in previous work [18]. The quality of each image was analyzed in order to select the sharpest image in the sequence, which was used as a reference image during registration of the images. The sharpness metric, described by Fienup & Miller [34], was used as a quality metric to measure the image sharpness.

In this study, translational motion has been measured using cross-correlation (CC) and phase correlation (PC) techniques while rotational motion has been determined using Radon, log-polar and exhaustive search approaches. The cross-correlation approach has been described in many publications [35]; it is used to find the translation (or more complex transformation) which maximizes the cross-correlation between a template image and the images to be registered. In this work, we used the image with the highest sharpness value as the template. In phase correlation, the inverse Fourier transform of the cross-power spectrum of the template image and the image to be registered gives a delta function at a position corresponding to the required translation [31]. An advantage of this approach is that filtering in the Fourier domain can be effectively implemented to reduce the effect of noise.

2.1 Radon transform

For an arbitrary function f(x,y) the Radon transform is defined by [36],

$$\widehat{f}=Rf={\displaystyle \underset{L_{r,\theta }}{\int }f(x,y)}ds$$ (1)

where L_r,θ is a line making an angle θ with the y axis at a distance r from the origin. If an image f(x,y) is rotated through an angle ψ then the Radon transform of the rotated image is given by:

$$R{f}_{\psi }(r,\theta )=Rf(r,\theta -\psi )$$ (2)

This means that rotation of an image corresponds to translation on the angular variable (θ) of the Radon transform. This translation is estimated using cross-correlation. The Radon transform of the input images is carried out using the Matlab Radon function.

2.2 Log-polar transform

The log-polar transformation is a nonlinear and non-uniform sampling of Cartesian co-ordinates to log-polar co-ordinates. In the log-polar transformation, radial lines in Cartesian space are mapped into horizontal lines, while arcs are mapped to vertical lines in the polar coordinate space. The pixels in a log-polar sampled image can be characterized by the ring number R(where$R\in \{0,\mathrm{...},n_r-1\}$) and the wedge or angular number W(where $W\in \{0,\mathrm{...},n_w-1\}$) given by [37]:

$$R=\frac{(n_r-1)\log \left(\frac{r}{r_{\min }}\right)}{\log \left(\frac{r_{\max }}{r_{\min }}\right)}$$ (3)

$$W=\frac{n_w\theta }{2\pi }$$ (4)

where r is the radial distance from the centre (x_c,y_c) and θ is the angle, n_r is the number of rings, n_w is the number of wedges or sectors, r_min is the radius of the smallest ring in the log-polar samples and r_max is the radius of the largest ring in the log-polar samples. In general, the choice of values for the parameters of the log-polar transform is not obvious. In this work, Young’s method [37] was used to decide the parameters of the log-polar grid. In order to measure rotational motion between two log-polar converted images (i.e., reference and input), cross-correlation or phase correlation was applied. We refer to the first approach as rotation angle calculated using cross-correlation on the log-polar transformed image (LPNCC). The combination of log-polar representation with phase correlation for images which are translated and/or rotated is called the Fourier-Mellin (FM) transform [29].

2.3 Exhaustive search

We have implemented another approach to finding the rotation between the reference and the input images, which we refer to as exhaustive search (ES). In this work, we used ES only to measure rotation because translation has already been estimated and scale changes were found to be negligible. The input image, I₂, which is to be aligned with reference image I₁ is rotated over a range of angles, from −1° to + 1°. For each angle, the phase correlation between the input and reference images is obtained, and the angle θ_coarse corresponding to the highest peak value is obtained. The angular step size is now reduced (typically by a factor of 10) and a new search carried out about θ_coarse. The procedure is repeated until convergence or until a minimum step size (typically 0.01°) is reached. The accuracy of the method improves as the step size is reduced, but the array size and computation time increase. We refer to this method as exhaustive search phase correlation (ESPC).

2.4 Texture analysis

In order to investigate the effectiveness of the registration approaches, we performed texture analysis on the final RNFL images with translation correction alone and with translation correction and de-rotation using ESPC. We used the GLCM for this purpose [38]. The co-occurrence matrix of an image is defined as the distribution of co-occurring values at a given offset and angle. The co-occurrence matrix C for an n × m image I, parameterized by an offset (Δx, Δy), is defined as:

$$C_{\Delta x,\Delta y}(i,j)={\displaystyle \sum _{p=1}^m{\displaystyle \sum _{q=1}^n\left\{\begin{array}{l}1,ifI(p,q)=iandI(p+\Delta x,q+\Delta y)=j\\ 0,otherwise\end{array}\right\}}}$$ (5)

where i and j are the image intensity values of the image, p and q are the spatial positions in the image I and the offset (Δx,Δy) depends on the direction θ used and the distance d at which the matrix is computed. The (Δx, Δy) parameterization makes the co-occurrence matrix sensitive to rotation. Choosing an offset vector, such that the rotation of the image is not equal to 180°, will result in a different co-occurrence matrix for the same (rotated) image. This can be avoided by forming the co-occurrence matrix using a set of offsets sweeping through 180° (i.e., 0, 45, 90, and 135 degrees) at the same distance to achieve a degree of rotational invariance. For images comprising repetitive texture patterns, the correlation of GLCM measured at four directions exhibits periodic behavior with a period equal to the spacing between adjacent texture primitives. When the texture is coarse, the correlation function drops off slowly, whereas for fine textures it drops off rapidly. The correlation of GLCM is used as a measure of periodicity of texture as well as a measure of the scale of the texture primitives [39]. The GLCM has been calculated using the Matlab graycomatrix function.

3. Results

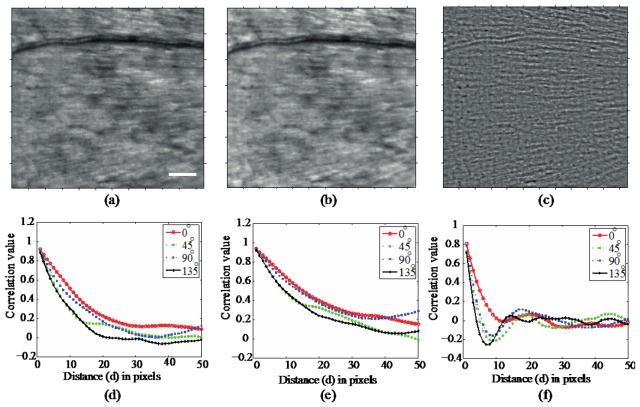
In order to understand the effectiveness of different methods of uneven illumination correction, the average images obtained after correcting the translation (using PC) and rotational motion (using ESPC) and the corresponding correlation of GLCM have been calculated, as shown in Fig. 1 . The correlation curves of GLCM for the mean-subtraction and homomorphic methods of uneven illumination correction (Fig. 1(d), and 1(e)) show a slow fall-off and do not have periodic ripples corresponding to the nerve fiber bundles. It indicates that these two methods are not suitable for RNFL images when-analyzing the nerve fiber bundles. On the contrary, the Daubechies wavelets at decomposition level 3-4 provided the best illumination correction while maintaining the image information. The average registered image using wavelet based uneven illumination correction and its correlation of GLCM are shown in Fig. 1(c) and 1(f) respectively. The correlation curves clearly show the repeated pattern and contain deep fall-off at 135° orientation.

Fig. 1.

Average images obtained after correcting the translation (using PC) and rotational motion (using ESPC) using different techniques to correct for uneven illumination: (a) subtracting the average filtered image; (b) homomorphic filtering and (c) wavelet approach. In (d-f) the corresponding correlation of GLCMs respectively. The length of the scale bar is 100µm.

We have then carried out the image registration in two stages: (i) estimation of translation and (ii) estimation of rotation. In order to estimate the translation, (i) the sharpest image of the sequence has been used as the reference image and (ii) both cross-correlation and phase correlation with parabolic interpolation were used for sub-pixel measurement. The result of correlation techniques for measuring horizontal and vertical translational displacements is shown in Fig. 2 .

Fig. 2.

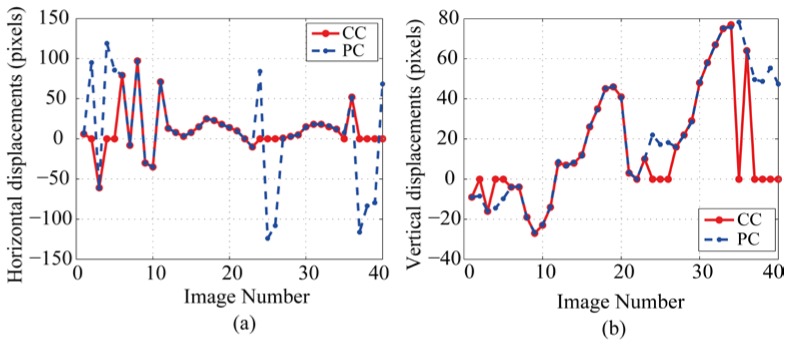
(a) Horizontal and (b) vertical displacement measured using cross-correlation (CC) and phase correlation (PC).

Visual examination of the registered sequence of images confirmed that the discrepancies between the two techniques occur when cross-correlation fails to correctly measure displacements (in this case for 11 of the 40 frames, 27.5%). We have also found that the translations measured using cross-correlation are sensitive to the size of the window used and the method of background correction. The best results were obtained when a window of side length approximately 75% of the total image side and wavelet background correction were used. We observed visually that the result of translation correction using phase correlation was better than cross-correlation in terms of clear visibility of RNFL structures, as shown in Fig. 3(a) and 3(b) respectively.

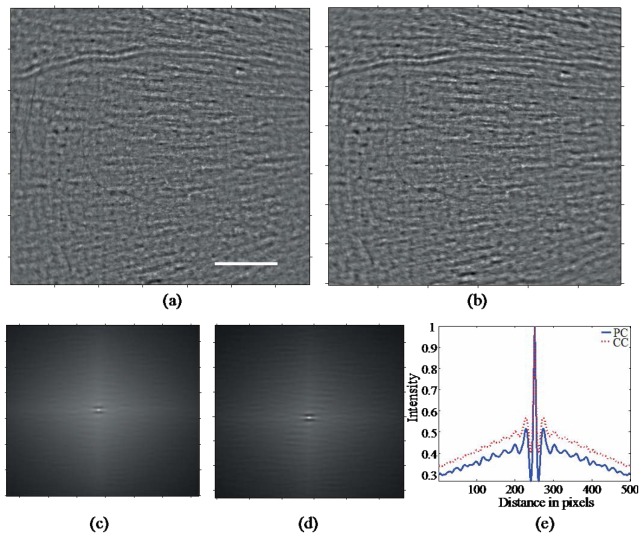
Fig. 3.

Image sequence corrected for translation using (a) cross-correlation and (b) phase correlation, (c-d) autocorrelation function (ACF) of the images shown in Fig. 3(a)-3(b) respectively and (e) intensity line profiles taken from ACF shown in Fig. 3(c)-3(d) respectively. The scale bar is 100µm.

Although the integrated result of both methods looks visually similar (Fig. 3(a)-3(b)), the auto-correlation function (ACF) of each of the average images shown in Fig. 3(c)-3(d) indicates that the ACF from registration using phase correlation has very clear structure compared with using cross-correlation. An intensity line profile taken from the ACF of both images shows that the image striations, corresponding to the retinal nerve fiber bundles, are clearer when phase correlation is used for registration (Fig. 3(e)). In the case of cross-correlation, most of the images corresponding to incorrect residual motion have been identified as having poor quality, as shown in Fig. 4 . However, the phase correlation method measured the displacements for them too, which demonstrates its robustness.

Fig. 4.

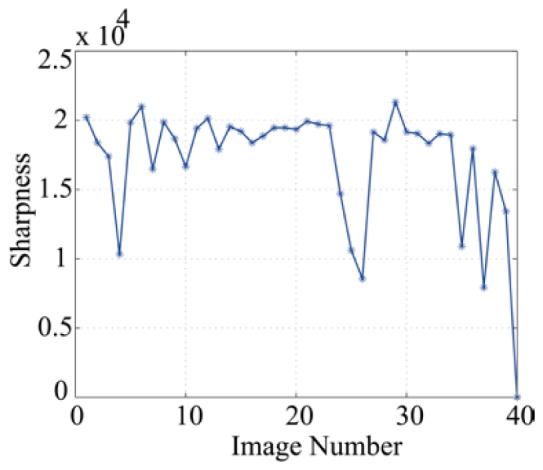
Temporal variation of sharpness of the RNFL image sequence (from Fig. 3) measured using the Fienup metric. Most of the images of poor quality are in the last 10 frames.

In the case of rotation, we compared four approaches: (a) Radon transform (b) log-polar transform, (c) Fourier-Mellin and (d) exhaustive search. We firstly tested these methods for a single retinal frame rotated by a set of known values (test image) and then applied them to a full retinal image sequence with unknown rotations.

For the test image sequence, all of the techniques performed well down to an angular step size of 0.1°. In the case of a real retinal image sequence, the results of each approach are shown in Fig. 5 . The angle measured using the Radon transform is shown in Fig. 5(a). The rotation angles were applied to de-rotate the image sequence. However, residual rotation (even >1°) is visually evident, indicating that the measurement is not correct. We have also applied the measured angle of rotation from ESPC to de-rotate the image sequence and found that the residual rotation appears negligible. We therefore consider the ESPC approach as a standard while evaluating registration accuracy. The LPNCC and FM approaches have been compared with the ESPC method, as shown in Fig. 5(b). The rotation angle calculated using LPNCC and ESPC are very similar; while the FM approach seems to be significantly different (≥0.9°) for several frames. Typically, LPNCC only fails for a few poor quality frames. The RMS difference between the rotation angles measured using ESPC and LPNCC was 0.007° whereas it was 0.09° between ESPC and FM. The resultant average image after translation correction using PC plus rotation correction using ESPC is shown in Fig. 6(a) .

Fig. 5.

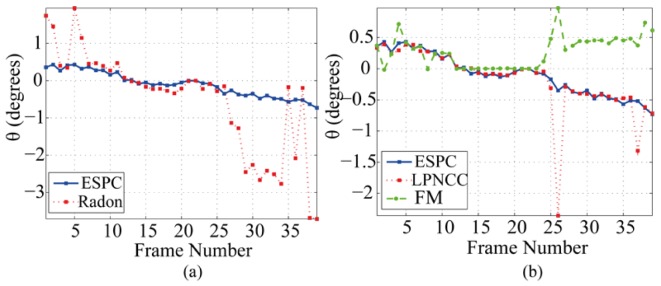
Angle of rotation measured using (a) Radon and ESPC and (b) LPNCC, FM and ESPC.

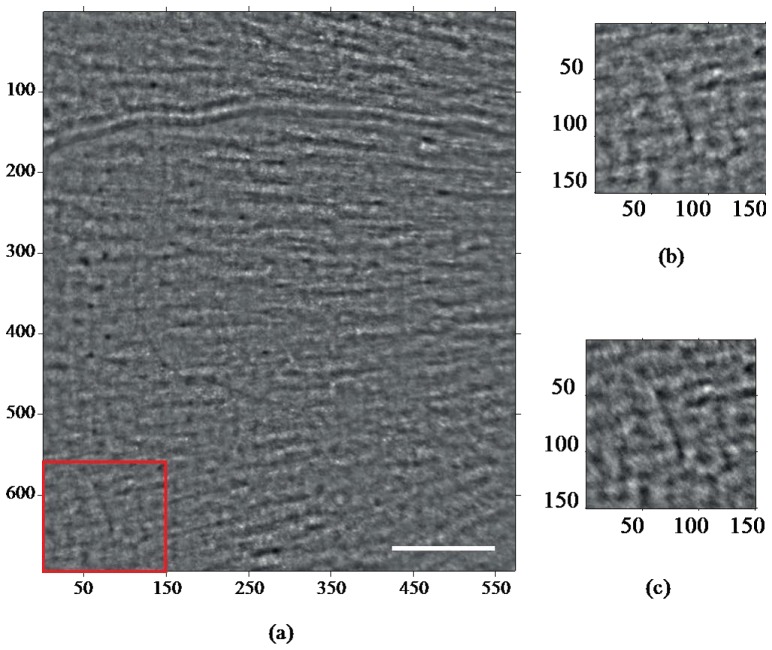
Fig. 6.

(a) Average of translation corrected and de-rotated image using PC and ESPC respectively (b) zoom of a 150x150 pixel window highlighted in (a); (c) zoom of the same window from average registered image (translation corrected only). The scale bar is 100µm.

In order to assess the improvement in correcting rotation, a section of the translation corrected and de-rotated images of size 150 x 150 pixels was taken at the bottom left corner of the image, as shown in Fig. 6(b) and Fig. 6(c) respectively. These sampling windows have retinal nerve fiber bundles which visually appear oriented between 0° and 45°. In analyzing the fiber texture, we have used the GLCM as described in section 2.

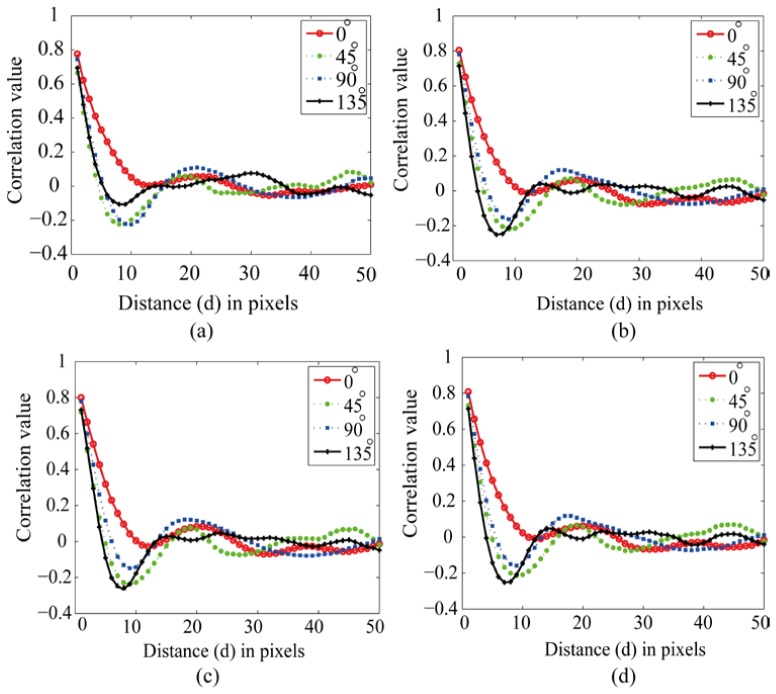
Figure 7 shows the correlation of the GLCM at four directions (0°, 45°, 90° and 135°) corresponding to the final images obtained with translation correction alone and with translation correction and de-rotation using ESPC. Since the nerve fiber bundles are oriented along approximately 45°, we expect the correlation to fall off quickly at 135°. The comparison of results shows a deeper fall-off at 135° for the de-rotated sample area than for the translation corrected window. On the other hand, the GLCM of the translation-only corrected section (Fig. 7(a)) shows similar falloffs for orientations of 45° and 135°. The GLCM correlation was then obtained using different de-rotation methods: the Radon, log-polar and exhaustive search approaches have been compared and shown in Fig. 8 . The correlation of GLCM for the Radon transform approach (Fig. 7(a)) does not have the clear fall-off at 135° and does not exhibit the ripples which correspond to the retinal nerve fiber bundles. This is due to the incorrect measurement of the angle of rotation, as shown in Fig. 5(a). In contrast, the correlation curve of GLCM for an average image obtained using the LPNCC approach (Fig. 8(b)) shows a deep fall-off at 135° and ripples. This curve is very similar to the correlation curve for GLCM using the ESPC approach (Fig. 8(d)). Finally, the correlation of the GLCM for an average image obtained using FM is very similar to the ESPC result with a slightly less deep fall-off; the ripples, however, are not as clearly indicated as with the ESPC method.

Fig. 7.

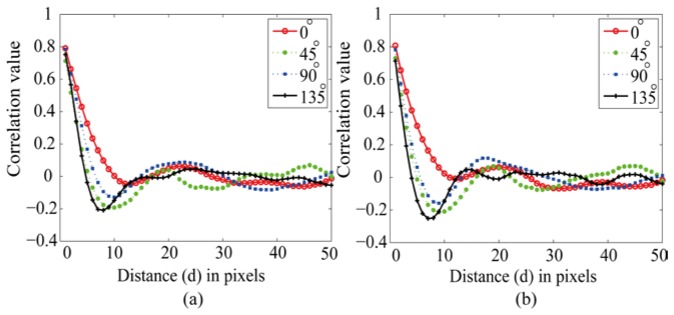
Correlation of the GLCM of sampling areas shown in Fig. 6: (a) translation corrected and (b) translation and rotation corrected. The ripples represent the presence of a repeating pattern in the image, corresponding to the nerve fiber striae. The curve corresponding to 135° indicates that the nerve fiber structure is clearer in the de-rotated data.

Fig. 8.

Correlation of GLCM for de-rotated average images using (a) Radon (b) LPNCC (c) FM and (d) ESPC.

4. Conclusion

The aim of this work was to identify the best approach for image registration of AO-flood illuminated RNFL images. We found that phase correlation is more robust than cross-correlation irrespective of the method of uneven illumination correction or size of the image while estimating the translational motion. The rotational motion has been measured using four different approaches: the Radon transform, LPNCC, FM and ESPC. We found that the result of measuring rotation using the ESPC approach is more accurate and robust irrespective of the method of uneven illumination correction or translation correction approach. The result of the ESPC approach has therefore been used as a standard to verify the registration accuracy and compared with the other methods of estimating rotation, as shown in Fig. 5. The result of LPNCC in measuring the angle of rotation is very close to ESPC.

In conclusion, the registration of RNFL images is best when the uneven illumination correction using the wavelet approach is combined with phase correlation for correcting translation and ESPC for correcting rotational motion. This is of particular interest, as the improvement obtained through rotational motion correction will be significant in the case of mosaicing images used to form a larger field of view, which aids improvement in diagnostic tools. Recently, a method using the Harris-Stephen interest point detector for AO flood-illuminated assisted images has been described [40]. The authors applied cross-correlation between small windows of detected feature-points followed by an affine model to minimize a least-square criterion between reference and input image in order to estimate translation, rotation and scale. In our study, the registration approach did not rely on retinal features as these may or may not be detectable in RNFL images. We found that LPNCC could be an effective approach for registering the RNFL images, which is computationally efficient. It fails only in the case of very poor quality frames. Currently, it takes approximately 3-4 minutes and 1-2 minutes on an 8-core PC for the best possible processing using the ESPC and LPNCC methods respectively, which could be considered a barrier for clinical implementation. However, the code has not been optimized for speed, and carrying this out, together with advances in computer hardware would certainly solve this problem.

We have proposed the correlation of GLCM to compare the effectiveness of the different processing techniques. The correlation of GLCM showed a sharp fall-off followed by periodic ripples that were clearest after the best processing (wavelet based uneven illumination correction + PC + ESPC) was carried out. Texture analysis based on correlation of GLCM was further shown to be potentially useful as a measure of the nerve fiber structure. The method retains information on spatial structures and for images comprising repetitive texture patterns, such as RNFL images, the correlation of GLCM measured at four directions show periodic behavior with the period equal to the spacing between adjacent texture primitives. The next stage of our work will involve applying this processing to RNFL images acquired from patients. AO imaging could potentially help to recognize early glaucomatous damage and to identify patients who could benefit from more intensive observation and management.