Genome scan for cognitive trait loci of dyslexia: rapid naming and rapid switching of letters, numbers, and colors

Abstract

Dyslexia, or specific reading disability, is a common developmental disorder that affects 5–12% of school-aged children. Dyslexia and its component phenotypes, assessed categorically or quantitatively, have complex genetic bases. The ability to rapidly name letters, numbers, and colors from rows presented visually correlates strongly with reading in multiple languages and is a valid predictor of reading and spelling impairment. Performance on measures of rapid naming and switching, RAN and RAS, is stable throughout elementary school years, with slowed performance persisting in adults who still manifest dyslexia. Targeted analyses of dyslexia candidate regions have included RAN measures, but only one other genome-wide linkage study has been reported. As part of a broad effort to identify genetic contributors to dyslexia, we performed combined oligogenic segregation and linkage analyses of measures of RAN and RAS in a family-based cohort ascertained through probands with dyslexia. We obtained strong evidence for linkage of RAN letters to the DYX3 locus on chromosome 2p and RAN colors to chromosome 10q, but were unable to confirm the chromosome 6p21 linkage detected for a composite measure of RAN colors and objects in the previous genome-wide study.

Introduction

Dyslexia is a complex trait that affects 5–12% of school-aged children (Katusic et al. 2001; Shaywitz et al. 1990). It is characterized by difficulty in learning to read and spell that is not otherwise attributable to cognitive or sensory impairments, psychiatric disorders, or neurological disorders. In children, the disorder is characterized by difficulties learning to name letters and associate sounds with letters, followed by difficulties in oral reading. Presentation changes with age as affected individuals adjust to these difficulties (Berninger et al. 2001; Bruck 1993), but deficits in reading fluency (rate), spelling, and written expression may persist into adulthood (Schulte-Korne et al. 2007).

Dyslexia involves deficits in different working memory components (Berninger et al. 2006). These include orthographic coding of letters in written words, phonological coding of sounds in spoken words, phonological loop for integrating naming codes and visual or orthographic codes as measured by rapid automatized naming (RAN), and supervisory switching attention, an executive function as measured by rapid automatic switching (RAS). One view is that rapid naming of visual stimuli including letters, numbers, colors, and objects primarily assesses phonological processes (Vaessen et al. 2009). Another view is that RAN and RAS assess the cross-code integration of phonological codes (names) and orthographic (letters or numerals) or visual codes. Whether a language has one-to-one or many-to-one mapping of graphemes (letter units) and phonemes (sound units), phonology coding (especially phoneme analysis) is linked to reading development (Cronin 2013; Lervag and Hulme 2009) and the integration of phonological coding and orthographic coding is frequently impaired in individuals with dyslexia (Raskind et al. 2012; Wolf and Bowers 1999). For instance, children with dyslexia were slower and less accurate than children without dyslexia in RAN for pictures (Catts 1986; Denckla and Rudel 1976a; Wolf and Bowers 1999). Whether mapping is one-to-one or many-to-one between letters and phonemes, RAN, which assesses the visual/orthographic-phonological integration and thus the phonological loop of working memory (Berninger and Richards 2010), outperforms phonological awareness as a single predictor of reading competency throughout elementary school grades (Cronin 2013; de Jong and van der Leij 2002; Landerl and Wimmer 2008; Lervag and Hulme 2009). RAN for colors or objects is even predictive of future reading problems in pre-reading children as young as 3.5 years (Compton 2003; Lepola et al. 2005; Lervag and Hulme 2009; Puolakanaho et al. 2007). Furthermore, RAN scores are quite stable throughout elementary school years (Cronin 2013) and RAN deficits persist through college in students who still manifest reading impairment (Cirino et al. 2005; Vukovic et al. 2004).

RAS differs from RAN in that on RAN the stimulus category stays the same (consistently letters or numbers or colors) but on RAS the stimulus categories constantly change (letter then number then letter then number, etc., or letter then number then color, etc.) (Wolf 1986). Because performance on RAS tests requires shifting focus between different classes of stimuli, it involves an executive function in working memory for switching attention (Altemeier et al. 2008; Wolf and Bowers 1999). In one study, RAS was the most consistently unique working memory predictor of various literacy outcomes for children with or without dyslexia during early and middle childhood (Altemeier et al. 2008).

There is abundant evidence that dyslexia has a complex genetic basis. Heritability estimates range from 40–60% (Raskind et al. 2012). Twin studies (DeFries et al. 1991; Pennington et al. 1991; Willcutt et al. 2000) and family studies (Chapman et al. 2003; Gilger et al. 1994; Igo et al. 2006a; Konig et al. 2011; Naples et al. 2009; Raskind et al. 2005; Rubenstein et al. 2011; Schulte-Korne et al. 2007; Wijsman et al. 2000; Wolff and Melngailis 1994; Ziegler et al. 2005) provide strong evidence for a genetic component to either a discrete diagnosis of dyslexia or one of its component phenotypes. A recent review of reported findings demonstrates that a number of different loci have been implicated, suggesting that there is likely to be genetic heterogeneity underlying dyslexia (Raskind et al. 2012).

Only a few of these studies focused on RAN and RAS measures. König et al. (Konig et al. 2011) conducted a genome scan of a number of component traits of dyslexia, including RAN letters, RAN numbers, and a composite score of RAN colors and RAN objects. They used a single proband sib pair design, with probands selected from a German population based upon deficits in spelling, and between one and three siblings of the proband collected regardless of affectation status. By variance component linkage analysis, they found a locus on chromosome 6p21 with strong evidence for linkage to the RAN colors/objects composite score (LOD score = 5.87, empirical p-value = 1.00×10⁻⁷). None of the RAN letters or RAN numbers genome scans had a linkage signal that reached the level of genome-wide significance.

Some targeted analyses that include the RAN measures have also been conducted to confirm regions previously identified using other component phenotypes of dyslexia. Grigorenko et al. (Grigorenko et al. 2001) found evidence of linkage to the DYX8 region on chromosome 1p34-p36 using a RAN colors and RAN objects composite score. Tzenova et al. (Tzenova et al. 2004) looked at this same region using an age adjusted RAN numbers score, but did not find evidence for linkage. de Kovel et al. (de Kovel et al. 2008) used a composite measure of five RAN scores to look at regions of 12 different chromosomes previously implicated in dyslexia. None of their strongest results included evidence for linkage with this phenotype, but they did find weak evidence for linkage to regions corresponding to DYX3 on chromosome 2p15-p16 and DYX8.

Here we report a genome scan for several measures of RAN and RAS phenotypes in families ascertained through a proband with reading difficulties. We focus on these phenotypes because they are stable predictors of dyslexia across a wide age range. In addition, they are correlated with other measures of reading in our sample. We wish to determine whether there is evidence for a pattern of inheritance for the RAN or RAS measures, and if so, to identify regions of the genome with evidence for linkage to these measures. Another goal of our study is to see if we can replicate the RAN colors/objects evidence found by König et al. (Konig et al. 2011) using a separate sample of multigenerational families and the RAN colors scores only.

Methods

Sample

The sample used in this study has been described in detail elsewhere (Berninger et al. 2006; Raskind et al. 2000). Briefly, individuals between ages 6 and 15 years were ascertained by low reading performance relative to Verbal Comprehension Factor Score (VIQ), with performance below the population mean. Subjects who were impaired on any of 10 specific measures of reading were selected as probands, though most were impaired on several measures (mean 6.7 measures per proband). Probands were further limited to those with a VIQ of at least 90, and were also excluded if they had other comorbid conditions related to learning disabilities, with the exception of ADHD.

Family members of each proband who agreed to participate were added to the study using a sequential sampling strategy (Cannings et al. 1978). This study obtained informed consent from all participants and was approved by the University of Washington institutional review board. For the current analysis based on available data, 1789 of the individuals were included in covariate adjustments. The joint segregation-linkage analysis included 1956 individuals in 260 families of sizes 4 to 23 in 2 to 4 generations, with omissions due to lack of phenotype information, lack of genotype information, or uninformative pedigree structure.

Phenotypes

Language processing was assessed using prepublication versions of the rapid automatized naming of letters (RANLET), numbers (RANNUM) and colors (RANCOL) measures (Denckla and Rudel 1976b; Wolf 1986). These tasks involve naming each letter (number or color) from a list of letters (numbers or colors). Two of the Rapid Alternating Stimulus naming measures (Wolf 1986) were also administered. These involve naming aloud alternating letters and numbers (RASLN), and naming aloud alternating colors, letters, and numbers (RASCLN). Each of these scores is measured as time to completion in seconds. We also created two new measures, RANLNavg, defined to be the average of RANLET and RANNUM, and RASavg, defined to be the average of RASLN and RASCLN. These averages were created because these pairs of scores measure similar traits on the same scale, and are similar to composite scores used in previous studies (Konig et al. 2011; Meyer et al. 1998a; Meyer et al. 1998b). We may also gain precision in the measurements by averaging the scores together, which is further supported by high correlations of these traits in this sample (r(RANLET, RANNUM) = 0.903, r(RASCLN, RASLN) = 0.919).

A second set of scores that were standardized by grade according to external information was also available. We will refer to the grade-normed scores as RANCOLZ, RANLETZ, RANNUMZ, RASCLNZ, and RASLNZ, respectively. These were obtained by using pre-publication grade-specific means and standard deviations to standardize the scores. For any individuals above grade 9, the grade 9 means and standard deviations were used. As for the raw scores, we computed RANLNavgZ by averaging RANLETZ and RANNUMZ, and RASavgZ by averaging RASCLNZ and RASLNZ.

Genotypes

The marker data used are identical to those used in a previous analysis of different endophenotypes. Details on genotyping and map selection are described elsewhere (Brkanac et al. 2007; Chapman et al. 2004; Igo et al. 2006a; Rubenstein et al. 2011). In brief, the analysis was based on a genome scan of 477 short tandem repeat (STR) markers obtained from the Marshfield Genotyping service in two batches. Because the batches were obtained at two different times, both Marshfield panels 10 and 13 were used. Families were chosen for genotyping based on a rank order determined by power analyses of phenotypes used for sample ascertainment. Within each family, marker data were obtained on as many relatives as were available and agreed to a blood sample. A total of 1128 subjects in families of sizes 4 to 23 were genotyped, with an average of 372 markers typed for each subject. An additional 96 subjects had a small number of markers (3–30) genotyped for other targeted analyses in this data set. Details on the family structure of genotyped individuals were previously provided (Brkanac et al. 2007). For the current paper, all references to map positions are based on the Haldane map function (Haldane 1919). Marker positions in the sequence are based on Rutgers map build 36 (Matise et al. 2007) or the NCBI human genome reference assembly GRCh37 aligned to the Rutgers map in both analysis of our sample and in alignment of previously published results to our results (http://www.ncbi.nlm.nih.gov/projects/genome/guide/human/index.shtml). The position given is that of the base pair corresponding to the 3' start site of the STR.

Data Cleaning

Eliminating errors in the data improves the power to detect linkage and reduces the number of false signals. Details of previous pedigree and marker data cleaning procedures are described elsewhere (Chapman et al. 2004; Igo et al. 2006a; Raskind et al. 2005). Briefly, this process included correcting or eliminating relationship inconsistencies, Mendelian inconsistencies, unlikely genotypes, and markers with excessive errors. In this study, we omitted seven children who were assessed using kindergarten norms. For the remaining individuals, discrepancies between the raw scores and grade-normed scores were detected in 1.7% of the pairs of scores. Further investigation identified errors in the grade-normed scores as the source of most of the discrepancies. We therefore recomputed the grade-normed scores to match the given raw scores.

Covariate Adjustments

It is important to adjust for covariates to eliminate as many non-genetic factors that may affect our analyses as possible, reduce within-genotype variance, and increase power to detect genetic effects (Wijsman and Amos 1997). Therefore, a predictive linear model for each of the RAN and RAS measures was constructed to account for non-genetic factors that appeared to be important in our sample. Furthermore, our model assumes that the residuals from the joint segregation-linkage analysis are normally distributed. Because the RAN and RAS scores have a strongly right skewed distribution, we used a logarithmic transformation for the raw scores. A square root transformation was used for the grade-normed scores, because the grade adjustment led to a less extreme right skew in the distribution of these scores. To ensure that the transformed scores could be computed, a constant was added to the grade-normed scores so that they were all nonnegative.

We investigated several different adjustment models without explicitly accounting for relationships in the sample. Covariates considered included grade, age, cohort (a variable defined to be 1 if the individual is at least 216 months old, or 0 if the individual is less than 216 months old), sex, interactions between age and cohort, and up to a three-way interaction between age, cohort and sex. Grade is commonly considered when using the RAN or RAS scores for diagnostic purposes. Age was investigated in addition to grade due to evidence of differences across ages in scores that had been grade-normed in this and other studies (Hsu et al. 2002). We evaluated age as a linear term, a quadratic term, and as a linear or quadratic spline. The knot in the spline was placed at age 18 (216 months), resulting in two connected curves modeling the differences in the RAN or RAS score across ages separately in youths (< 216 months) and adults (≥ 216 months). A cohort effect was also considered to allow for additional differences in scores between youths and adults. Sex (with males serving as the baseline) was included for three reasons: (1) previous observations in this sample (Hsu et al. 2002), (2) male bias in the probands in this sample (Raskind et al. 2000), and (3) the observation of gender differences in many (Berninger et al. 2008; Flannery et al. 2000; Hsu et al. 2002; Katusic et al. 2001; Rutter et al. 2004; Wadsworth et al. 1992), although not all (Shaywitz et al. 1990; Wadsworth et al. 1992), studies of learning disabilities. The two-way interaction between age and cohort allows for possible differences in the effects of age in youths and adults. The three-way interaction between age, cohort, and sex allows for possible differences in age effects between female youths, female adults, male youths, and male adults. The best fitting model was determined by including a covariate if its coefficient was significant at the 0.05 level for a majority of the phenotypes studied. Though this may result in overfitting in the few models for which a covariate is not significant, inclusion of a few extra covariates is not expected to substantially affect the values of the adjusted phenotypes.

Joint linkage-segregation analysis

Using the residuals from the covariate adjusted models, joint linkage and segregation analysis was conducted to estimate the number of diallelic quantitative trait loci (QTLs) needed to explain the data as well as their positions in the genome. Residuals that were more than 4 standard deviations from the mean were winsorized to help prevent spurious QTLs from appearing in the joint segregation-linkage analyses (Igo et al. 2006b). Winsorizations affected between 0 and 6 individuals in each measure. A total of 9 individuals had at least one raw score winsorized, and a total of 12 individuals had at least one grade-normed score winsorized.

It was not clear a priori how the incorporation of outside information into the grade-norms would affect the results of the joint linkage-segregation analysis. Due to the possibility that information external to the sample may add noise or bias to the results, we used the residuals from the models with the raw score outcomes in the main analyses. We also conducted secondary analyses using the residuals from the models with grade-normed score outcomes.

The genetic models of each of the QTLs, including their effect sizes, dominance structures, and other parameters, were also determined. This analysis was conducted using Loki 2.4.7 and provides estimates of the posterior distributions of model parameters using a Bayesian reversible-jump MCMC approach (Heath 1997). Analysis is carried out conditional on the pedigree data, phenotype data, marker data, and user-specified prior distributions on the QTL parameters. Reversible-jump MCMC allows the number of parameters in the model to vary, so that we can estimate the number of QTLs in addition to their parameter values, and thus a multilocus trait model can be addressed without need to pre-specify the number of QTLs and their parameter values.

We used the adjusted RAN and RAS scores for input to the analysis, with the prior distribution on the number of QTLs in the model a truncated Poisson distribution with mean 2, a maximum of 17 QTLs in the model, and a value for the variance of the genotype effects, τ_β, that was four times the adjusted phenotypic variance. Values of τ_β ranged from 0.15 to 0.24 for the raw score residuals, and 0.30 to 0.55 for the grade-normed score residuals. Details about the number of QTLs assumed in the prior distribution are relatively unimportant, as long as they allow a sufficient range of values for the MCMC sampler in evaluating the model space (Wijsman and Yu 2004). Use of τ_β in this range is generally a good choice of parameter value (Wijsman and Yu 2004). The number of iterations used was 500,000, with a burn in of 1000 iterations, and a thinning interval of 5. We used the genome-scan markers and map described above, with allele frequencies estimated from the data, based on a uniform prior distribution.

Statistical inference was based on the posterior distribution of model parameters, summarized through marginal distributions of the modal classes of models. Individual QTLs were further summarized as follows. The alleles for each diallelic QTL were labeled as `A' and `a' for the allele contributing to high and low scores, respectively, with p_A referring to the allele frequency of the A allele. The AA (or homozygote) genotype effect was defined as the difference between the mean genotype values of the AA and aa genotypes, or μ_AA − μ_aa. The Aa (heterozygote) effect was similarly defined as the difference between the mean genotype values of the Aa and aa genotypes, or μ_Aa − μ_aa.

For posterior QTL model distributions, we summarized all QTLs with localization to a chromosome and strong evidence for linkage. We used Bayes Factors (Kass and Raftery 1995) to evaluate the strength of evidence for linkage, where the Bayes Factor for linkage is the ratio of the posterior to prior odds that a QTL is located in a particular interval, with the prior odds based on the prior distributions used for analysis. For computation of Bayes Factors, we accumulated the information in 2 cM non-overlapping bins across the genome. For the strongest linkage signals, we also obtained estimated p-values by simulating 1000 replicates of marker genotypes in a 40 cM region around the strongest signals under the null hypothesis of no linkage, followed by re-analysis with the real phenotype data (Igo and Wijsman 2008). Simulations used the same conditions as the analysis, but with 100,000 iterations. In addition, analyses of all chromosomes where we found a Bayes Factor greater than 10 were re-run under the same conditions, but with 10,000,000 iterations to reduce Monte Carlo error.

Results

Phenotypes

Summaries of the raw and grade-normed scores are given in Tables I and II. Mean raw scores range from 23–35 seconds to complete each task. Mean grade-normed scores range from 0.3–1.5. Although these scores are normed to have a mean of 0 in the general population, we expect to see higher mean values due to the sample ascertainment. In our sample, females complete the tasks ~3 seconds faster than males, and adults complete the tests ~15.5 seconds faster than youths, on average.

Table I.

Means and standard deviations of the unadjusted phenotypes.

Phenotype	Number of observations	Raw score		Grade-normed score
		Mean	SD	Mean	SD
RANCOL	1766	34.94	12.48	0.32	1.35
RANNUM	1776	23.66	10.72	0.65	1.55
RANLET	1779	24.35	11.03	0.94	1.58
RANLNavg	1780	24.02	10.64	0.80	1.47
RASCLN	1765	33.85	16.66	1.22	1.86
RASLN	1778	29.53	15.73	1.48	2.00
RASavg	1778	31.71	16.21	1.36	1.87

Table II.

Summary statistics averaged over all 7 phenotypes, by subject group.

Group	Number in group	Raw score		Grade-normed score
		Mean	SD	Mean	SD
Females	871	27.24	12.64	0.75	1.59
Males	910	30.41	15.59	1.18	1.83
Youths	725	38.07	17.32	1.51	2.00
Adults	1056	22.54	6.44	0.60	1.40
Probands	287	42.02	16.81	2.06	2.08
Non-probands	1494	26.34	12.27	0.76	1.57
All	1781	28.86	14.31	0.97	1.73

Covariate Adjustments

Age and sex were significant predictors (p < 0.05) for each of the phenotypes. When using the raw scores as the outcome, the best fitting predictive model is of the form:

$$\log \left(\text{raw score}\right)={\beta }_0+{\beta }_1(\text{age}-216)+{\beta }_2\left(\text{sex}\right)+{\beta }_3(\text{age}-216)\left(\text{cohort}\right)+{\beta }_4\left(\right(\text{age}-216\left)^2\right)+{\beta }_5\left(\right(\text{age}-216\left)^2\right)\left(\text{cohort}\right).$$

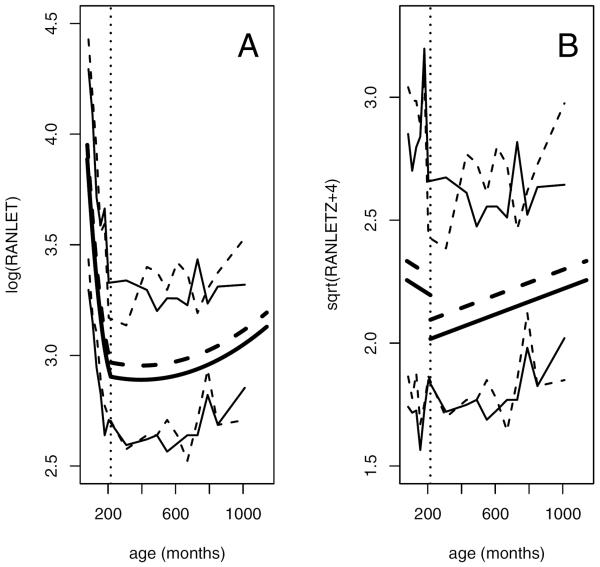
Models of this form were used for each of the raw score outcomes. Estimated values of the coefficients are found in Table III. This model indicates that on average, males take more time to finish the tasks than females at all ages in our sample (Figure 1A). Time to complete the tasks decreases with age in youths, with a slower rate of decrease in older youths than in younger youths. The time to completion increases in all but the youngest adults, with a faster rate of increase in older adults than younger adults. Grade was not found to be a significant predictor with age already included in the model. As expected, probands and their close relatives have higher adjusted phenotypic values than unrelated and distantly related individuals on average (Supplementary Figure 2). This relationship is consistent with the phenotypes having a genetic component.

Table III.

Covariate adjustment coefficients with 95% CIs using the raw score outcomes.

Outcome	Intercept	Age*	Age2	Sex	(Age)(cohort)	(Age2)(cohort)
RANCOL	3.25 (3.21, 3.29)	−0.00429 (−0.00553, −0.00305)	1.13e-05 (2.28e-06, 2.04e-05)	0.0879 (0.0696, 0.106)	0.00405 (0.00266, 0.00545)	−1.04e-05 (−1.93e-05, −1.43e-06)
RANNUM	2.91 (2.86, 2.96)	−0.00208 (−0.00353, −0.000632)	3.46e-05 (2.4e-05, 4.52e-05)	0.0536 (0.0321, 0.0752)	0.00181 (0.000171, 0.00344)	−3.41e-05 (−4.46e-05, −2.36e-05)
RANLET	2.90 (2.86, 2.95)	−0.00242 (−0.0039, −0.000939)	3.35e-05 (2.27e-05, 4.43e-05)	0.0641 (0.0422, 0.086)	0.00226 (0.000597, 0.00393)	−3.31e-05 (−4.38e-05, −2.24e-05)
RANLNavg	2.91 (2.87, 2.95)	−0.00221 (−0.00361, −0.00082)	3.46e-05 (2.44e-05, 4.48e-05)	0.0593 (0.0387, 0.0799)	0.00199 (0.000425, 0.00356)	−3.42e-05 (−4.42e-05, −2.41e-05)
RASCLN	3.19 (3.14, 3.24)	−0.00482 (−0.00635, −0.00329)	2.06e-05 (9.36e-06, 3.18e-05)	0.0478 (0.0252, 0.0705)	0.00445 (0.00273, 0.00617)	−1.97e-05 (−3.07e-05, −8.64e-06)
RASLN	3.05 (3, 3.1)	−0.00395 (−0.00549, −0.0024)	3.14e-05 (2.01e-05, 4.28e-05)	0.0489 (0.026, 0.0717)	0.00364 (0.0019, 0.00538)	−3.08e-05 (−4.2e-05, −1.96e-05)
RASavg	3.13 (3.08, 3.17)	−0.00437 (−0.00584, −0.0029)	2.64e-05 (1.56e-05, 3.72e-05)	0.0486 (0.0268, 0.0704)	0.00404 (0.00238, 0.0057)	−2.57e-05 (−3.63e-05, −1.5e-05)

^*Age was re-centered at 216 months (18 years) old.

Figure 1.

Illustration of the relationship between the observed RAN letters scores and age. A raw scores, B grade-normed scores, with (- - -) representing males and (—) representing females. The best fitting model is represented by the thicker middle lines, while the thinner top and bottom lines represent a summary of the data computed by finding the 95^th and 5^th percentiles of the RAN letters scores binned by age. Bin sizes are 24 months in youths and 60 months in adults, with larger bins of size 184 and 260 months in the youngest and oldest adults, due to the small number of individuals sampled in these age ranges. For an illustration using all data points, see Supplementary Figure 1. The vertical dotted line delineates the age (18 years) used to separate youths and adults.

To illustrate the form of this model, we use RANLET as an example (Table III). In the youngest youths (age 72 months), individuals who are one month older are predicted to have a 0.65 lower RANLET score. In the oldest youths (age 215 months), individuals who are one month older are predicted to have only a 0.05 lower RANLET score. In the youngest adults (216 months), individuals who are one month older have very little difference in RANLET score on average (a change of less than 0.01), while in the oldest adults (1139 months), individuals who are one month older are predicted to have a 0.16 higher RANLET score.

When considering the grade-normed score outcomes, the predictors that were found to be significant for the majority of the seven phenotypic adjustment models were age, sex, and cohort, with age fit as a linear term in this model. Not all of these predictors were significant at the 0.05 level for every outcome measure. However, the same model was used for each outcome measure because the model fit each measure well, and interpretation is easier when applying the same model to each outcome. The form of this model for each grade-normed score is as follows:

$$\mathrm{sqrt}(\text{grade-normed score}+4)={\beta }_0+{\beta }_1\left(\text{age}\right)+{\beta }_2\left(\text{cohort}\right)+{\beta }_3\left(\text{sex}\right)+{\beta }_4\left(\right(\text{age}\left)\right(\text{cohort}).$$

Estimated values of the coefficients are found in Table IV. This model also indicates that on average, males take more time to finish the tasks than females at all ages in the sample (Figure 1B). Although the scores had already been normed by grade, we still found significant effects of age, but we did not need as complex an adjustment for age as when using the raw scores. This model suggests that the time to complete the task decreases with age in youths and slightly increases with age in adults – a pattern consistent with the model obtained using the raw score outcomes.

Table IV.

Covanate adjustment coefficients with 95% CIs using the grade-normed outcomes.

Outcome	Intercept	Age	Cohort	Sex	(Age)(cohort)
RANCOLZ	2.20 (2.12, 2.29)	−0.000915 (−0.00152, −0.000314)	−0.705 (−0.809, −0.601)	0.118 (0.0921, 0.144)	0.00169 (0.00108, 0.0023)
RANNUMZ	2.27 (2.17, 2.37)	−0.000418 (−0.00111, 0.000272)	−0.333 (−0.452, −0.213)	0.0695 (0.04, 0.0989)	0.000549 (−0.000152, 0.00125)
RANLETZ	2.29 (2.19, 2.39)	−0.000437 (−0.00114, 0.000269)	−0.328 (−0.45, −0.206)	0.0779 (0.0478, 0.108)	0.000695 (−2.07e-05, 0.00141)
RANLNavgZ	2.29 (2.2, 2.38)	−0.000466 (−0.00113, 0.000194)	−0.339 (−0.453, −0.225)	0.0742 (0.046, 0.102)	0.000664 (−5.33e-06, 0.00133)
RASCLNZ	2.49 (2.38, 2.6)	−0.000952 (−0.00173, −0.000176)	−0.615 (−0.749, −0.48)	0.0648 (0.0317, 0.0979)	0.00141 (0.000618, 0.00219)
RASLNZ	2.66 (2.55, 2.78)	−0.00189 (−0.00271, −0.00107)	−0.657(−0.799, −0.514)	0.0696 (0.0345, 0.105)	0.0022 (0.00136, 0.00303)
RASavgZ	2.59 (2.48, 2.7)	−0.00151 (−0.00228, −0.000747)	−0.649 (−0.782, −0.517)	0.0681 (0.0356, 0.101)	0.00189 (0.00111, 0.00266)

To illustrate the form of the model with grade-normed score outcomes, we use RANLETZ as an example (Table IV). In the youths, individuals who are one month older are predicted to have a 0.002 lower RANLETZ score. Adults are predicted to have a 0.328 lower RANLETZ score than youths. Among adults, individuals who are one month older are predicted to have a 0.001 higher RANLETZ score.

The resulting models suggest that grade may be functioning as an imperfect measure of age. When using the raw scores, grade does not appear to be an important predictor when age is included in the model. Thus grade does not appear to add information beyond the age of the individual. However, when using the grade-normed scores, age is included in the best-fitting model with a simpler form than in the raw score model. This suggests that grade may be encompassing some, but not all, of the effects of age on the RAN and RAS scores.

The interpretation of the adjusted grade-normed scores is more challenging than that of the adjusted raw scores. The adjusted raw scores are simply the log of the time taken to complete the RAN or RAS task, adjusted for both sex and a straightforward function of age. The grade-normed scores, however, use a two-stage adjustment procedure, with an age adjustment after adjusting for the subject's grade. Therefore we might think of this as the effect on the trait of being older or younger than an average individual in the same grade as the subject.

Joint Linkage-Segregation Analysis

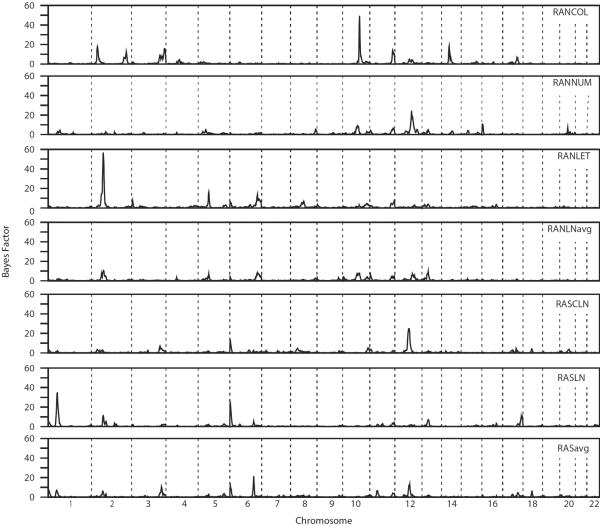
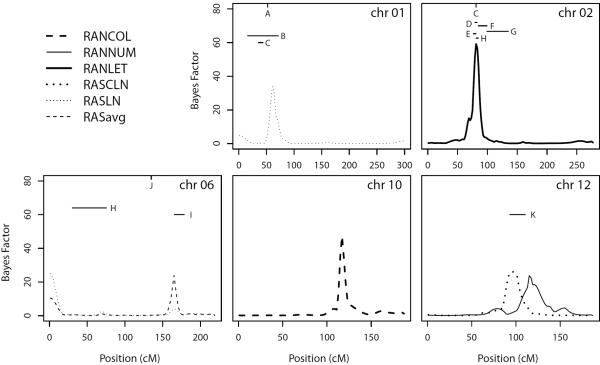
Genome scans of the raw scores identified strong evidence for linkage of RANLET to chromosome 2, and RANCOL to chromosome 10 (Figure 2). The maximum Bayes Factor (BF) for RANLET was 59.13 (Figure 3), at 81 cM, flanked by markers D2S1352 and D2S337. Under the null hypothesis of no linkage, a region-wide empirical p-value for this BF was 0.002. The maximum BF for RANCOL was 47.30 (p-value = 0.005), found at 117 cM, with closest flanking markers D10S677 and D10S1239.

Figure 2.

Genome scans for each of the raw score phenotypes. The strongest evidence for linkage is found on chromosome 2 with the RAN letters scores, and on chromosome 10 with the RAN colors scores.

Figure 3.

Evidence for linkage on chromosomes with maximum BF>20. Regions with evidence for linkage in selected studies are represented by a horizontal line covering the implicated region if multiple markers were reported. Evidence for linkage at a single marker is represented by a tic mark at the location of the marker at the top of the figure. Previous evidence of linkage is shown for: A dyslexia (Rabin et al. 1993), B RAN colors and objects composite score, phonemic awareness, phonological decoding, single word reading, and dyslexia (Grigorenko et al. 2001), C dyslexia (chr 1) and non-word reading (chr 2) (de Kovel et al. 2008), D dyslexia (Fagerheim et al. 1999), E phonological coding dyslexia and spelling (Petryshen et al. 2002), F phonological awareness (Fisher et al. 2002), G dyslexia (Kaminen et al. 2003), H orthographic coding (chr 2) and RAN colors and objects composite score (chr 6) (Konig et al. 2011), I spelling (Rubenstein et al. 2011), J irregular word spelling (Bates et al. 2007), and K real word reading (Igo et al. 2006a).

Two QTL models were identified in the same region of chromosome 2 using the RANLET scores, while only one model was identified on chromosome 10 using the RANCOL scores (Table VI). One of the RANLET models on chromosome 2 estimates that an average individual heterozygous for the risk allele requires 13% more time to complete the RANLET task, and an average individual homozygous for the risk allele requires 32% more time. The estimated risk allele frequency for this QTL is 0.32. The second RANLET model estimates that an average heterozygous individual requires 12% more time to complete the RANLET task, and an average homozygous individual requires 43% more time, with an estimated risk allele frequency of 0.64. That these two QTL models lie in nearly the same position on chromosome 2 indicates that there may in truth be a multiallelic QTL at this position that is being modeled by two diallelic QTLs. The RANCOL model on chromosome 10 estimates that an average heterozygous individual requires 12% more time to complete the RANCOL task, and an average homozygous individual requires 57% more time. The estimated risk allele frequency for this QTL is 0.82.

Table VI.

Estimated QTL model parameters for all loci with Bayes Factor > 40.

Trait	Chr	Location (cM)	pA (95% CI)	μAa − μaa (95% CI)	μAA − μaa (95% CI)
RANLET	2	81.29	0.32 (0.02, 0.62)	0.12 (0.08, 0.16)	0.28 (0.24, 0.31)
RANLET	2	82.40	0.64 (0.49, 0.79)	0.11 (0.08, 0.14)	0.36 (0.33, 0.40)
RASavgZ	6	143.65	0.85 (0.79, 0.90)	0.01* (−0.10, 0.11)	0.94* (0.73, 1.15)
RANCOL	10	121.56	0.82 (0.73, 0.91)	0.11 (0.06, 0.17)	0.45 (0.36, 0.54)

^*Effect sizes are on a different scale than for the raw score traits

More modest evidence for linkage was also found for the RASLN, RASavg, RANNUM, and RASCLN scores (Table V). Bayes factors of at least 20 were identified on chromosome 1 for RASLN (BF = 33.85, p-value = 0.012), on chromosome 6 for RASLN (BF = 25.07, p-value = 0.006) and RASavg (BF = 23.83, p-value = 0.010), and on chromosome 12 for RANNUM (BF = 23.75, p-value = 0.024) and RASCLN (BF = 26.31, p-value = 0.005). The linkage signal for RASLN on chromosome 6 may be a false positive, as it is close to the edge of the chromosome, and the only marker near this edge is not very informative. There were a number of other potentially notable signals (20 > BF > 10) identified in the genome scan (Supplementary Table I), but these were not pursued further.

Table V.

Regions of the genome with Bayes Factor of at least 20. Closer marker is in bold.

Chr	Outcome	Peak position (cM)	left flanking marker	left flanking marker position	right flanking marker	right flanking marker position	Bayes Factor	Empirical p-value
1	RASLN	61	D1S234	25023987	ATA79C10	34553130	33.85	<0.012
2	RANLET	81	D2S1352	50687218	D2S337	61523359	59.13	<0.002
6	RASLN	1	D6S942	765304	F13A1	6144162	25.07	<0.006
6	RASavg	165	D6S2436	154177748	D6S1035	159946991	23.83	<0.010
6	RASavgZ	165	D6S2436	154177748	D6S1035	159946991	54.17	<0.004
10	RANCOL	117	D10S677	95954428	D10S1239	103196353	47.30	<0.005
12	RASCLN	95	D12S1052	73895728	D12S1064	89347398	26.31	<0.005
12	RANNUM	115	D12S1300	97025074	PAH	103232906	23.75	<0.024

Genome scans of the grade-normed scores identified many of the same regions (Supplementary Figure 3). The linkage signals were generally similar or slightly smaller than the signals identified using the raw scores (Supplementary Figure 4). However, there were a few notable differences between the linkage signals resulting from the raw scores and grade-normed scores. The region identified using the RANCOL raw scores on chromosome 10 with BF 47.30 had a BF of only 4.91 using the corresponding grade-normed scores. Similarly, the region identified using the RASCLN raw scores on chromosome 12 with BF 26.31 had a BF of only 8.44 with the grade-normed scores. The region identified using the RASavg scores on chromosome 6 was the only region that exhibited the opposite pattern. The raw score BF was 23.83 (p-value 0.010), but the grade-normed score BF was 54.17 (p-value = 0.004).

One QTL model was identified on chromosome 6 using the RASavgZ scores (Table VI). This model appears to be recessive, with an estimated risk allele frequency of 0.85. Interpretation of the magnitude of the parameter for the homozygote effect is difficult due to the nature of the grade-norming and the adjustment model used.

Discussion

Here we present evidence for several genomic regions containing loci that contribute to genetic variation in measures of rapid naming and switching. One of these processes, rapid naming ability, has been shown to predict reading fluency independent from phonological awareness (Savage and Frederickson 2005), and another, rapid switching ability, was the most consistently unique predictor of various literacy outcomes for elementary school children with or without dyslexia (Altemeier et al. 2008). These features, coupled with their applicability across languages, usefulness even in pre-readers and stability across multiple ages support the importance of RAN and RAS as endophenotypes for genetic studies, especially those that include adults as well as children. This is further supported by results from our genome scans: after covariate adjustment, the joint linkage-segregation analysis of the RANLET scores provided strong evidence for a locus on chromosome 2p, with strong evidence also found on chromosome 10q using the RANCOL scores. More modest evidence for linkage was found on chromosome 1p using the RASLN scores, chromosome 6q using the RASavg scores, and two regions of chromosome 12q using the RANLET and RASCLN scores. In general, maximum evidence of linkage was obtained with the raw scores, with only the RASavgZ grade-normed scores on chromosome 6q giving stronger evidence than the corresponding raw scores.

The strongest linkage signal in our study overlaps a locus that has been well established as associated with related dyslexia traits in separate samples. The region identified on chromosome 2p using the RAN letters scores overlaps the DYX3 locus, identified by six previous studies (Figure 3), with the regions shown reflecting only the markers that were reported as significant. However, the location of the underlying QTLs may be more uncertain due to lack of marker information. We therefore do not rule out overlap of nearby signals that do not strictly appear to overlap our linkage signals. Several other loci that we detected in this study were previously also reported by our group and others in genome scans for related traits (Figure 3 chr 1, chr 6, and chr 12), and the linkage signal that we identified here on chromosome 1p using the RASLN scores overlaps the DYX8 locus (Figure 3, chr 1). We also found evidence for linkage in the 6q and 12q regions previously identified in the same subject sample (Igo et al. 2006a; Rubenstein et al. 2011). We expect that previously analyzed traits within our sample would result in some overlapping linkage signals with the RAN and RAS traits because of correlation between these sets of traits. However, another sample has also been found to support the 6q locus (Bates et al. 2007), providing added support.

A genome scan of the traits RAN letters, RAN numbers, and RAN objects/colors was conducted previously by König et al. (Konig et al. 2011). Strong evidence of a locus at 6p21 was found in their scan for a composite score of RAN objects and RAN colors, but no other findings reached the same level of genome-wide significance. Our results do not show significant evidence for linkage in this same region of 6p21 (Figure 3, chr 6). This may be due to differences in the phenotype measured: the RAN colors trait in our study does not have an object-naming component. In addition, the grade-norms used for our data were pre-publication, and may therefore differ from those used by König et al. Differences in the findings may also be attributed to the ascertainment of the samples: probands in the König et al. study were identified by spelling deficits, whereas probands in our study were identified based upon one or more of several types of deficits including spelling and reading. Furthermore, König et al. collected phenotype data only on siblings. They had genotypes of the parents, but no extended pedigrees beyond nuclear families. Our data may therefore have allowed us to detect different models of inheritance.

The regions of the genome implicated in our study differed across RAN and RAS measures, despite the high correlations between these phenotypes in our sample. A similar observation was made in a dyslexia study by Fisher et al. (Fisher et al. 2002) who identified a region on chromosome 18 using single word reading, but found no significant linkage signal using the correlated phenotypes orthographic coding, phoneme awareness, or phonological decoding. The differing evidence for linkage across phenotypes may be due to each phenotype being influenced by a separate gene. However, the evidence for linkage may also vary due to factors other than the underlying genes, such as the sensitivity of the RAN or RAS test, random variation in the sample (Marlow et al. 2003), or whether genetic and environmental covariance effects have the same or opposite sign (Evans and Duffy 2004). Even in the highly correlated case of the raw scores and grade-normed scores of the same phenotype, differences in the way that we quantify these RAN and RAS scores caused by the two covariate adjustments may result in a disparity in how well each score captures the relevant QTL effects.

Choice of either the raw score outcomes or the grade-normed score outcomes led to some different conclusions in the joint linkage-segregation analyses. Most of the regions identified were the same, with similar evidence for linkage that tended to be somewhat stronger when using the raw scores. However, because we generally do not further pursue linkage signals with Bayes Factors less than 10, two regions were identified with the raw scores that were missed with the grade-normed scores. One region had a much stronger linkage signal with the grade-normed scores than with the raw scores, but would have been identified using either set of scores. Although it appears that the raw scores identify more linkage regions than the grade-normed scores, we cannot be sure which set of results is more accurate without knowledge of the underlying truth.

Other factors may be used to inform the choice of outcome variable. The grade-normed scores have the advantage that they are used in diagnosis of some learning disabilities, and may be more familiar to clinicians. However, we may prefer to use the raw scores to maintain easy interpretability of the QTL model effect sizes. The raw scores also provide some advantages over the grade-normed scores when using the joint linkage-segregation analysis model of Loki 2.4.7. For example, we assume that all of the observations have the same variance. Departures from this assumption appeared to be less extreme when using the raw scores than with the grade-normed scores. The raw scores had inflated variances in the first and second graders, possibly due to the sample ascertainment method, or because we did not adequately adjust for covariates in this group. The grade-normed scores had inflated variances in both the grade 1 and 2 subjects and in the grade 8 subjects for most of the measures, suggesting that the covariate adjustment model was inadequate.

It is best to avoid over-interpreting the parameter estimates of any of the models estimated here. The sample was selected through a proband with a reading disability, and we were unable to apply an ascertainment correction due to the complex nature of this sample collection. Therefore, certain parameters are likely to be highly biased. In particular, the allele frequencies describing the genotypes attributable to the adjusted RAN or RAS scores are likely to be severely inflated. It is also possible that the apparent “recessivity” of some of the models may be in part a result of ascertainment through children.

Our analyses show evidence for both previously identified and novel loci associated with learning disabilities, and also that the choice of analysis, including the adjustment model, can have a large impact on the strength of evidence for linkage. This is not surprising, because with use of full multipoint linkage analysis and highly polymorphic markers, as we had here, marker information is very high. When marker information is high, the strength of the evidence for linkage is influenced almost entirely by ability of the linkage analysis model to accurately infer the trait genotype from the trait phenotype (Atwood and Heard-Costa 2003). This can be strongly influenced by the covariate-adjustment model, so careful choice of the analysis model may help to avoid missing important linkage signals.

Future study with dense markers obtained from sequence data will be needed to identify the causal genes underlying the genomic regions implicated here. With recent dramatic decreases in sequencing costs, it is no longer either efficient or necessary to first attempt fine-scale localization prior to obtaining the sequence data, especially because fine-scale mapping is relatively ineffective for QTLs (Atwood and Heard-Costa 2003) and provides, at best, modest resolution (Yang et al. 2005; Yu et al. 2005). Instead, methods that can be used to evaluate all sequence variants in pedigree data for a region of interest are now a highly attractive option, particularly with methods that accommodate multiple rare and/or common variants in family-based data within a functional unit (Chen et al. 2013). Together with pedigree-based imputation data derived from observed sequence data and existing genome scan markers (Cheung et al. 2013), significant gains in power to identify putative causal variants are now possible even if only a relatively small number of subjects are sequenced (Saad and Wijsman 2014). A data set such as this one, with a rich set of phenotypes and existing genome scan markers, therefore remains an important resource for leveraging information from such sequence data in the search for biological mechanisms that affect risk for learning disabilities.