A unified framework for glaucoma progression detection using Heidelberg Retina Tomograph images

Abstract

Glaucoma, the second leading cause of blindness worldwide, is an optic neuropthy characterized by distinctive changes in the optic nerve head (ONH) and visual field. The detection of glaucomatous progression is one of the most important and most challenging aspects of primary open angle glaucoma (OAG) management. In this context, ocular imaging equipment is increasingly sophisticated, providing quantitative tools to measure structural changes in ONH topography, an essential element in determining whether the disease is getting worse. In particular, the Heidelberg Retina Tomograph (HRT), a confocal scanning laser technology, has been commonly used to detect glaucoma and monitor its progression.

In this paper, we present a new framework for detection of glaucomatous progression using HRT images. In contrast to previous works that do not integrate a priori knowledge available in the images, particularly the spatial pixel dependency in the change detection map, the Markov Random Field is proposed to handle such dependency. To our knowledge, this is the first application of the Variational Expectation Maximization (VEM) algorithm for inferring topographic ONH changes in the glaucoma progression detection framework. Diagnostic performance of the proposed framework is compared to recently proposed methods of progression detection.

1. Intruduction

Glaucoma is characterized by structural changes in the optic nerve head (neuroretinal rim thinning and optic nerve cupping are usually the first visible signs) and visual field defects. Elevated intraocular Pressure (IOP) is a major risk factor for the disease [1].

However, some subjects with moderately high IOP may never develop glaucoma while others may have glaucoma without ever having an elevated IOP. Initially asymptomatic for several years, the first clinical symptoms related to glaucoma is a loss of peripheral vision and, in advanced disease, irreversible blindness [2]. Because most people with glaucoma have no early symptoms or pain, it is crucial to develop clinical routines to diagnose the disease before permanent damage to the optic nerve head occurs.

Since the introduction of the ophthalmoscope by Helmholtz in 1851, ophthalmologists have been able to view changes in optic nerve head topography associated with glaucoma. Nevertheless, the clinical examination of the ONH remains subjective (inter-observer diagnosis variability) and non-reproducible [3].

Because of this, ocular imaging instruments have been developed as potential tools to quantitatively measure ONH topography, which is essential for clinical diagnosis. For instance, the Heidelberg Retina Tomograph (HRT; Heidelberg Engineering, Heidelberg, Germany), a confocal scanning laser technology, has been commonly used for glaucoma diagnosis since its commercialization 20 years ago[4].

In order to assist the expert in qualitative and quantitative analysis, automatic image processing methods have been proposed. These methods aim to facilitate the interpretation of the obtained images by objectively measuring the ONH structure and detecting changes between a reference image (baseline exam) and other images (follow-up exams).

A limited number of studies have been published that deal with the change detection/classification problems for HRT images. In [5], the Topographic Change Analysis (TCA) was proposed for assessing glaucomatous changes. This technique has been shown to classify progressing and stable eyes with reasonably good sensitivity and specificity. However, TCA does not exploit additional available knowledge, such as spatial dependency among neighboring pixels ( i.e, the status of a pixel will depend on the status of its neighborhood). The POD method indirectly utilizes the spatial relationship among pixels by controlling the family-wise Type I error rate. In [6], a retinal surface reflectance model and a homomorphic filter were used to detect progression from changes in retinal reflectance over time. Similar to POD, dependency among spatial locations was only indirectly considered by controlling family-wise Type I error rate. In order to accommodate the presence of false positive change detection, a threshold-based classifier is generally used [7]. Nevertheless, the choice of the threshold (usually 5% of the number of pixels within the optic disc) may affect the robustness of the classification method. Indeed, if we decrease the threshold value, the risk of false negative classifications increases and similarly if we increase the threshold value, the risk of false positive classifications will increase.

In this paper, we propose a new strategy for glaucoma progression detection. We are particularly interested in determining if directly modeling and integrating the spatial dependency of pixels within the change detection model can improve glaucoma detection. Specifically, the Markov Random Field (MRF) is proposed to exploit the statistical correlation of intensities among the neighboring pixels [8]. Moreover, in order to account for noise in the estimation scheme, we consider the change detection problem as a missing data problem where we jointly estimate the noise hyperparameters and the change detection map. The most widely used procedure to estimate different problem parameters is the Expectation-Maximization EM algorithm [9]. However, the optimization step is intractable in our case because of the MRF prior we use for the change detection map. In order to overcome this problem, the Variational Expectation Maximization (VEM) algorithm is proposed. The VEM has been successfully employed for blind source separation [10], image deconvolution [11] and image superresolution [12].

Once the change detection map is estimated, a classification step is performed. This step aims at classifying a HRT image into “non-progressing” and “progressing” glaucoma classes, based on the estimated change detection map. In contrast to previous works which used the threshold-based classifier [7], a two layer fuzzy classifier is proposed. The importance of fuzzy set theory stems from the fact that much of the information on which human decisions are based is possibilistic, rather then deterministic [13]. We show that the proposed classifier increases the non-progressing versus progressing accuracy.

The paper is divided into three sections. In the next section, the proposed glaucoma progression detection scheme is presented. The classification step is described is section 3. Then, in section 4, results obtained by applying the proposed scheme to real data are presented and we compare the diagnostic accuracy, robustness and the efficiency of this novel proposed approach with three existing progression detection approaches, topographic change analysis (TCA) [5], proportional orthogonal decomposition (POD) [7] and the reflectance based method [6].

2. Glaucoma progression detection scheme

2.1. Intensity normalization

The curvature of the retina and differences in the angle of imaging the eye between exams may lead to an inhomogeneous background (illuminance) and introduce changes among follow-up exams [6]. Although this problem is not due to glaucomatous progression, it would have an influence on subsequent statistical analysis and quantitative estimates of progression. To this end, a reflectance-based normalization step is performed. Assuming that the optic nerve head is Lambertian, each HRT image I can be simplified and formulated as a product I = L × F where F is the reflectance and L is the illuminance. Because illumination varies slowly over the field of view, the illuminance L is assumed to be contained in the low frequency component of the image. Therefore, the reflectance F can be approximated by the high frequency component of the image. The reflectance component F describes the surface reflectivity of the retina, whereas the illumination component L models the light sources. The reflectance image can then be used as an input to the change detection algorithm [14, 15, 6].

Several methods have been proposed to solve the problem of reflectance and illuminance estimation including homomorphic filtering [14], the scale retinex algorithm [16, 17, 18] and the isotropic diffusion approach [19]. The reflectance based method of detecting progression uses a homomorphic filter to estimate retinal reflectance [6]. In our new glaucoma progression detection scheme presented in this study, we used the scale retinex approach. The retinex approach has been successfully utilized in many applications, including medical radiography [20], underwater photography [21] and weather images enhancement [22].

2.2. Change detection

Let us consider the detection of changes in a pair of amplitude images. Change-detection can be formulated as a binary hypothesis testing problem where the null hypothesis of “H₀: No change” is tested against the alternative hypothesis of “H₁: Change”. We denote by I₀ and I₁ two images acquired over the same scene at times t₀ and t₁, respectively (t₁ > t₀), and coregistered. A difference image R with M pixels was estimated as the pixelwise difference between images I₀ (a baseline image) and I₁ (a follow-up image): R = abs(I₀ – I₁). The difference image R(i) = {R(i)∣, i = 1, 2, …, M} can be modeled as R = X + N, where X is the true (or ideal) difference image and N is the noise (assumed to be white and normally distributed). Finally, the change detection is handled through the introduction of change class assignments Q, Q = {Q_i∣Q_i ∈ {H₀, H₁}, i = 1, 2, …, M} represent the change class assignment at each pixel.

The Bayesian model aims at estimating the model variables (R, X, Q) and parameters Θ. This requires the definition of the likelihood and prior distributions. The model is given by the joint distribution:

$$\begin{array}{cc}\hfill p(R,X,Q;ϴ)& =p(R\mid X,Q;ϴ)p(X,Q;ϴ)\hfill \\ \hfill & =p(R\mid X,Q;ϴ)p(X\mid Q;ϴ)p(Q;ϴ)\hfill \end{array}$$ (1)

We now present each term of the Bayesian model.

Likelihood

The definition of the likelihood depends on the noise model. In this study, we assume that the noise is white and normally distributed:

$$p(R\mid X,Q,{ϴ}_N)=N(0,{\sigma }_N)$$ (2)

where N is the normal distribution and σ_N is the noise standard deviation.

Model prior

To describe the marginal distribution of X conditioned to H_l, with l ∈ {0, 1}, we opted for the Normal distribution:

$$p(X\mid Q=H_l,{ϴ}_X)=N({\mu }_l,{\sigma }_l)$$ (3)

where μ_l and σ_l stand for the mean and the standard deviation respectively.

Concerning the change variable, we assume that p(Q; Θ) is a spatial Markov prior. In this study we adopt the Potts model with interaction parameter β:

$$p(Q;\beta )=\frac{1}{Z}\exp (-\beta U(Q\left)\right),U\left(Q\right)=\sum _{i~j}\delta (Q_i,Q_j)$$ (4)

where Z is the normalization constant and δ the delta Kroneker function. Hence, the definition of the energy function favors the generation of homogeneous areas reducing the impact of speckle noise, which could affect the classification results of the HRT images [23]. β allows us to tune the importance of the spatial dependency constraint. In particular, high values of β correspond to a high spatial constraint. Note that we have opted for the 8-connexity neighboring system. The estimation procedure of the model parameters (X, Q) and hyperparameters Θ = {σ_N, μ_l, σ_l, β} is presented in the next section.

Variational Expectation-Maximization

Once our model is established, we now address the inference problem. This step consists in estimating the model parameters and hyperparameters. However, exact inference is intractable due to the Markov prior we adopted for the change detection map, so we turn to approximate algorithms that search for distributions that are close to the correct posterior distribution. One of the most commonly used procedures is the Monte Carlo Markov Chain (MCMC) technique [24]. Unfortunately, this technique requires large computational resources and fine tuning of model hyperparameters. To overcome this problem, the Iterative Conditional Mode (ICM) [25] procedure is widely used because it is easy to implement [25]. However, the ICM does not take into account uncertainties in hidden variables (i.e; Q) during inference, so it may converge to poor local minima [26]. In this study, the variational approximations of the Expectation Maximization (EM) algorithm is proposed to alleviate the computational burden associated with stochastic MCMC approaches. In contrast to the MCMC procedure, the proposed VEM approach does not require priors on the model parameters for inference to be carried out. Indeed, the EM procedure can be viewed as an alternating maximization procedure of a function F : F (p, Θ) = E_p[log(p(R, X, Q; Θ)] + T(p) where E_p denotes the expectation with respect to p and T(p) = −E_p[log p(X, Q)] is the entropy of p. At iteration [r], and given the current hyperparameters values Θ^[r–1], the EM procedure consists of:

$$\begin{array}{cc}\hfill & \text{E-step}{p}_{X,Q}^{\left[r\right]}=\underset{p\in P}{\arg \max }F(p,{ϴ}^{[r-1]})\hfill \\ \hfill & \mathbf{M}-\mathbf{step}{ϴ}^{\left[r\right]}=\underset{ϴ}{\arg \max }F(p_{X,Q}^{\left[r\right]},ϴ)\hfill \end{array}$$

where P is the set of all probability distribution on X × Q. The optimization step leads to maximize p(X, Q∣R, Θ^[r–1]). Unfortunately, this posterior is intractable for X and Q for our model. Hence, the VEM procedure can be derived from the EM in which p(X, Q∣R, Θ^[r–1]) is approximated as a product of two probability density functions on X and Q: q_X,Q = q_Xq_Q where q_X and q_Q are probability distributions on X and Q, respectively. At iteration [r], the updating rules become:

E-step

$$\text{E-step}{q}_X^{\left[r\right]}\left(X\right)=\mathit{exp}\left(E\left(\mathit{log}p(X\mid R,Q,{ϴ}^{[r-1]})\right)\right)$$

The approximate posterior distribution q can be computed as follows. Keeping only the terms of log p(X∣R, Q, Θ^[r–1]) that depend on X we have:

$$\begin{array}{cc}\hfill \mathit{log}p(X\mid R,Q,{ϴ}^{[r-1]})& \propto \frac{{(X-R)}^T(X-R)}{2{\sigma }_N^2}+\frac{{(X-{\mu }_1)}^T(X-{\mu }_1)}{2{\sigma }_1^2}+\frac{{(X-{\mu }_2)}^T(X-{\mu }_2)}{2{\sigma }_2^2}\hfill \\ \hfill & \propto X^{T}X(\frac{1}{2{\sigma }_N^2}+\frac{1}{2{\sigma }_1^2}+\frac{1}{2{\sigma }_2^2})-X(\frac{R}{2{\sigma }_N^2}+\frac{{\mu }_1}{2{\sigma }_1^2}+\frac{{\mu }_2}{2{\sigma }_2^2})-{\left[X(\frac{R}{2{\sigma }_n^2}+\frac{{\mu }_1}{2{\sigma }_1^2}+\frac{{\mu }_2}{2{\sigma }_2^2})\right]}^T\hfill \\ \hfill & +\text{const}\hfill \end{array}$$ (5)

Notice that this is the exponent of a Gaussian distribution with mean μ_X and covariance matrix ∑_X given by: ${\Sigma }_X={\left(\frac{1}{2{\sigma }_N}+\frac{1}{2{\sigma }_1}+\frac{1}{2{\sigma }_2}\right)}^{-1}\times I,{\mu }_X={\Sigma }_X^{-1}\left(\frac{R}{2{\sigma }_N}+\frac{{\mu }_1}{2{\sigma }_1}+\frac{{\mu }_2}{2{\sigma }_2}\right)$ and I is the identity matrix. The analytic expression of the distribution that minimizes F is given by: qx ~ N (μ_x, Σ_x);

$$\mathbf{E}-\mathbf{step}{q}_Q^{\left[r\right]}\left(Q\right)=\exp \left(E\left(\mathit{log}p(Q\mid X,R,{ϴ}^{[r-1]})\right)\right)$$

Due to the Markov prior, $q_Q^{\left[r\right]}\left(Q\right)$ is intractable. To overcome this problem, many studies proposed the use of the Mean Field algorithm [27, 8]. According to this theory, given a single element in a random field, the effect of other elements can be approximated by the effect of their mean. The mean field approximation is a particular case of the mean field-like approximation when the neighborhood of a site at position i is set to constants [27]. $q_Q^{\left[r\right]}$, approximated by the mean field likely algorithm, is given by [28]:

$$\begin{array}{cc}\hfill q_Q^{\left[r\right]}(Q=l)& =\prod _i{q}_{Q_i}^{\left[r\right]}(Q_i=l)\hfill \\ \hfill & \propto \prod _{i}N(X_i,{\mu }_l^{[r-1]},{\sigma }_l^{[r-1]})\exp \left({\beta }^{[r-1]}\sum _{i~j}\delta ({\tilde{Q}}_j,l)\right)\hfill \end{array}$$ (6)

where $\tilde{Q}$ is a given configuration of Q created basing on X^[r] and updated at each iteration.

M-step

This step aims at estimating the model hyperparameters Θ = {σ_N, μ_l, σ_l, β}:

$$\mathbf{M}-\mathbf{step}{\sigma }_N^{\left[r\right]}=\underset{{\sigma }_N}{\arg \max }\left(E_{{\mathit{q}}_X}\left(\mathit{log}p(R\mid X^{\left[r\right]},ϴ)\right)\right)$$

Let us denote by ${\sigma }_n^{\prime }$ the inverse of σ_n (i.e; ${\sigma }_n^{\prime }=\frac{1}{{\sigma }_n}$). The derivation of E_qX (log p(R∣X^[r], Θ)) with respect to ${\sigma }_n^{\prime }$ is given by:

$$\frac{\delta E_{q_X}\left(\mathit{log}p\right(R\mid X^{\left[r\right]},ϴ\left)\right)}{\delta {\sigma }_n^{\prime }}=\frac{\text{size}\left(R\right)}{2{\sigma }_n^{\prime }}=-\frac{1}{2}({\Vert R-{\mu }_X\Vert }^2+\text{trace}({\Sigma }_X\left)\right)$$ (7)

Setting to zero the derivation, we obtain the following updated expression:

$$\begin{array}{cc}\hfill & {\sigma }_n^{\left[r\right]}=\frac{{\Vert R-\mu X\Vert }^2+\text{trace}\left({\Sigma }_X\right)}{\text{size}\left(R\right)}\hfill \\ \hfill \mathbf{M}=\mathbf{step}({\mu }_l^{\left[r\right]},& {\sigma }_l^{\left[r\right]})=\underset{({\mu }_l,{\sigma }_l)}{\arg \max }\left(E_{q_X,q_Q}\left(\mathit{log}p(X^{\left[r\right]}∕Q^{\left[r\right]}\right)\right)\hfill \end{array}$$ (8)

Setting to zero the derivation of E_qX,qQ (log p(X^[r]/Q^[r], μ_l, σ_l) with respect to (μ_l, σ_l), we get:

$${\mu }_l^{\left[r\right]}=\frac{{\sum }_i{X}_i{q}_Q(Q_i=1)}{{\alpha }_l},{\sigma }_l^{\left[r\right]}=\frac{{\sum }_i{\left(X_i-{\mu }_l^{\left[r\right]}\right)}^2{q}_Q(Q_i=l)}{{\alpha }_l}$$ (9)

where α_l = ∑_i q_Q(Q_i = l).

$$\mathbf{M}-\mathbf{step}{\beta }^{\left[r\right]}=\underset{\left(\beta \right)}{\arg \max }\left(E_{q_Q}\right(\mathit{log}p(Q;\beta )\left)\right)$$

The estimation of β^[r] is carried out using a gradient algorithm.

3. Classification

Once the change detection maps are estimated, we now tackle the glaucoma progressor image classification problem. This step aims at assigning an image to the non-progressor or the progressor classes. To this end, a two-layer fuzzy classifier is proposed. On one hand, in contrast to [7], no threshold is required. In our case, the fuzzy set theory is used to quantify the membership degrees of a given image to each class (i.e; progressor and non-progressor). On the other hand, the use of a two-layer classifier instead of one-layer allows better modeling of the classification function [29]. Moreover, the fuzzy classifier we propose can be trained using only the control data (non-progressor eyes) as in some cases, no prior knowledge of the changes due to glaucoma progression is available.

As in [7], we considered two features as input for the classifier: 1) feature1: the number of changed sites and 2) feature2: the residual image intensity R of changed sites. Note that only the loss of retinal height in neighboring areas is considered change due to glaucomatous progression because an increase in retinal height is considered improvement (possibly due to treatment or tissue rearrangement).

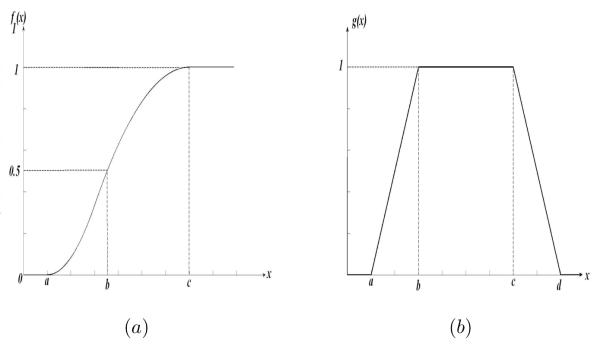
We now calculate the elementary membership degree to the non-progressor class given each feature γ_nor,o∈{feature1,feature2} using a S-membership function f whose expression is given in Eq. 10. Note that the range [a, c] defines the fuzzy region.

$$f(x;a,b,c)=\{\begin{array}{cc}0\hfill & x<a\hfill \\ \frac{{(x-a)}^2}{(b-a)(c-a)}\hfill & a\le x<b\hfill \\ 1-\frac{{(x-c)}^2}{(c-b)(c-a)}\hfill & b\le x<c\hfill \\ 1\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (10)

where a < b < c. The shape of f for a given triplet (a, b, c) is presented in Fig. 1.(a).

Figure 1.

Different fuzzy membership functions used in the classification scheme: (a) S membership function and (b) trapezoidal membership function. The hyperparameters of these fuzzy membership functions are estimated with the Genetic algorithm using a training HRT dataset which contains 7 non-progressor eyes and 7 progressor eyes.

$${\gamma }_{\text{nor}}={\gamma }_{\text{nor},\text{feature}1}\times {\gamma }_{\text{nor},\text{feature}2}$$ (11)

where γ_nor,feature1 = f(N_c; a₁, b₁, c₁), γ_nor,feature2 = f(∑_i∈C R_i; a₂, b₂, c₂), N_c and C stand for the number of changed sites and the changed site class respectively and (a₁, b₁, c₁, a₂, b₂, c₂) are the hyperparameters of the S-membership functions. The hyperparameters (a₁, b₁, c₁, a₂, b₂, c₂) are estimated with the Genetic algorithms (see Appendix A) using longitudinal HRT data from a training dataset which contains 7 non-progressor eyes and 7 progressor eyes. Note that the training dataset is independent of the test dataset described in section 4.1.

The membership degree to the glaucoma class γ_glau is given by:

$${\gamma }_{\mathit{glau}}=1-{\gamma }_{\text{nor}}$$ (12)

To decide if a given HRT image belongs to the glaucoma progressor class, another membership function is used. We opted for the trapezoidal function denoted by g as a membership function. The expression of g is given by :

$$g(x;a_3,b_3,c_3,d_3)=\{\begin{array}{cc}\left(\frac{x-a_3}{b_3-a_3}\right)\hfill & a_3\le x<b_3\hfill \\ 1\hfill & b_3\le x<c_3\hfill \\ \left(\frac{d_3-x}{d_3-c_3}\right)\hfill & c_3\le x<d_3\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (13)

where a₃ < b₃ < c₃ < d₃. The shape of g for a given quadruple (a₃, b₃, c₃, d₃) is presented in Fig. 1.(b). Alternately, the Genetic algorithm was used to estimate this quadruple. The decision to classify an image into the glaucoma class depends on the output of the function g(γ_glau). As can be observed, g function depends on the quadruple (a₃, b₃, c₃, d₃) as well as on (a₂, b₂, c₂) and (a₁, b₁, c₁). If g(γ_glau) = 1 the image is assigned to the glaucoma progressor class.

4. Experiments

This section aims at validating the proposed framework. Different datasets used for validation are presented in the next sub-section. In sub-section 4.2, the reliability of the intensity normalization algorithm is discussed. Change detection results on simulated and semi-simulated datasets are presented in sub-section 4.3. In order to corroborate the effectiveness of the variational estimation algorithm, comparisons with other estimation algorithms will be conducted throughout the present section. Finally, the classification results on real datasets are presented in sub-section 4.4.

4.1. Datasets for experiments

The proposed framework was experimentally validated on clinical, semi-simulated and simulated datasets. Our clinical dataset consists of 36 eyes from 33 participants with progressed glaucoma and 210 eyes from 148 participants considered non-progressing. It’s important to note that the glaucomatous progression in the patient eyes was not defined based on the HRT images but based on two other techniques: 1) likely progression by visual field (based on longitudinal standard automated perimetry testing) or 2) progression by stereo-photographic assessment of the optic disk. Progressive changes in the stereo-photographic appearance of the optic disk between baseline and the most recent available stereo-photograph (patient name, diagnosis, and temporal order of stereo-photographs were masked) were assessed by two observers based on a decrease in the neuroretinal rim width, appearance of a new retinal nerve fiber layer (RNFL) defect, or an increase in the size of a pre-existing RNFL defect. A third observer adjudicated any differences in assessment between these two observers. Therefore, no ground truth for glaucomatous change in the HRT images is available. An additional 21 eyes from 20 participants were normal eyes with no history of IOP > 22 mmHg, normal appearing optic disk by stereo-photography and visual field exams within normal limits. Note that all eligible participants were recruited from the University of California, San Diego Diagnostic Innovations in Glaucoma Study (DIGS) with at least 4 good quality HRT-II exams and at least 5 good quality visual field exams to ensure an accurate diagnosis.

Because no change detection map is available for the clinical dataset, we generated two semi-simulated datasets to assess the proposed change detection method. The first one (dataset1) was constructed from four normal HRT images. Changes were simulated by the permutation of 5%, 7%, 10% and 12% of image regions in the four images, respectively. In order to emphasize the robustness of the proposed approach compared to the high level of noise, an additive Gaussian noise with different values of peak signal to noise ratio (PSNR) (30, 28, 25, and 23 dB) (PSNR = 10 log₁₀(max(Image)²/E[(Noise)²])) was introduced to both the original image and the image with translated regions. Fig 2 presents an example of a semi-simulated image.

Figure 2.

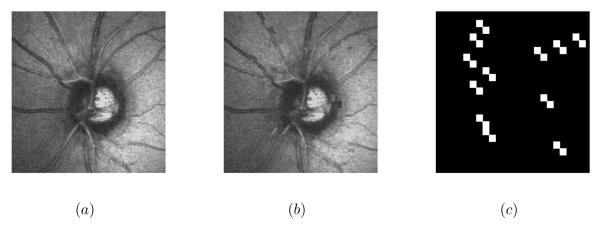
Semi-simulated image by the permutation of image regions: (a) the original image (b) the simulated image (PSNR=28 dB) and (c) the ground truth.

The second simulated dataset (dataset2) was constructed from four other HRT images. Changes were simulated by modifying the intensities of each 15 × 15 pixel-sized regions in the four images randomly with 0.5%, 0.75%, 1% and 1.25% probabilities, respectively. The intensities were modified by randomly multiplying the real intensities by 0.5, 0.75, 1.5 or 2 with a 0.25% probability. As for the first semi-simulated dataset, a Gaussian noise was added to each image. Fig 3 presents an example of a semi-simulated image.

Figure 3.

Semi-simulated image by the modification of image intensities: (a) the original image (b) the simulated image (PSNR=28 dB) and (c) the ground truth.

Concerning the simulated dataset, we have generated four images according to the proposed model (Eq. 1) with different values of PSNR (30, 28, 25 and 23 dB). Fig 4 presents an example of a simulated image.

Figure 4.

Simulated image: (a) the simulated image (PSNR=28 dB) and (b) the ground truth.

Note that for each exam, the baseline image and the follow-up image are co-registered using built in instrument software and saved together.

4.2. Intensity normalization algorithm assessment

To assess the proposed illumination correction normalization algorithm and particularly the use of the retinex method for reflectance estimation, five different methods were used to normalize the image intensities: the proposed method [17] (filter size=20 pixels), the homomorphic filtering method [30] (standard deviation=2 and filter size=20 pixels), the isotropic diffusion method [19] (smoothness constraint=7 pixels), the Discrete Cosine Transform (DCT) method [31] (number of components is 40) and the wavelet-based method (with Daubechies wavelet and three level decomposition) [20]. Fig.5 presents the intensity normalization of a baseline and a follow-up image using the five methods.

Figure 5.

Intensity normalization results of a baseline (left column) and a follow-up (right column) images respectively using : (a) (b) the proposed method, (c) (d) the homomorphic filtering, (e) (f) the isotropic diffusion method, (g) (h) the DCT method and (i) (j) the wavelet method.

The proposed change detection method is then applied to dataset1 and dataset2. In order to perform the change detection evaluation, we use the Percentage of False Alarm PFA, the Percentage of Missed Detection PMD and the Percentage of Total Error PTE measurements defined by:

$$\mathit{PFA}=\frac{FA}{N_F}\times 100\%;\mathit{PMD}=\frac{MD}{N_M}\times 100\%;\mathit{PTE}=\frac{MD+FA}{N_M+N_F}\times 100\%$$

where FA stands for the number of unchanged pixels that were incorrectly determined as changed ones, N_F the total number of unchanged pixels, MD the number of changed pixels that were mistakenly detected as unchanged ones, and N_M the total number of changed pixels.

Table. 1 presents the false detections, the missed detections and the total errors for both datasets. The retinex normalization and the DCT normalization perform similarly (with the retinex method performing slightly better). Moreover, the retinex-based method for reflectance estimation allows us to obtain better results than other reflectance estimation methods. Specifically, we obtained 0.98 % of total error with the retinex method while the homomorphic filtering method led to 1.43 % of total errors.

Table 1.

False detection, missed detection and total errors resulting from: the proposed initialization method, the homomorphic filtering, the isotropic diffusion method, the DCT method and the wavelet method.

dataset1	False detection	Missed detection	Total Errors
Retinex	0.71 %	4.61 %	0.99 %
DCT	0.74 %	4.96 %	1.07 %
Isotropic diffusion	0.79 %	5.39 %	1.28 %
Homomorphic filtering	0.87 %	6.32 %	1.38 %
Wavelet	1.98 %	7.24 %	2.69 %
dataset2	False detection	Missed detection	Total Errors
Retinex	0.62 %	3.85 %	0.89 %
DCT	0.69 %	4.72 %	1.02 %
Isotropic diffusion	0.72 %	5.19 %	1.26 %
Homomorphic filtering	0.86 %	6.98 %	1.43 %
Wavelet	1.59 %	6.25 %	2.38 %

4.3. Change detection results

In order to emphasize the benefit of the proposed change detection algorithm and particularly the use of the Markov model to handle pixel spatial dependency, we compared the proposed method with two kernel-based methods and a threshold-based method:

• The Support Vector Data Description (SVDD) [32] with the Radial Basis Function (RB) kernel using positive and negative examples,

• The Support Vector Machine (SVM) [33] with the RBF Gaussian kernel,

• A Bayesian threshold-based method [34],

Note that we used the retinex-based intensity normalization for all methods. First, we applied these methods on the four semi-simulated images from dataset1 with PSNR=30dB and the four semi-simulated images from dataset 2 with PSNR=30dB (Table 2). The proposed method tends to perform better than the SVDD, SVM and the Bayesian threshold-based methods. This means that the proposed Markov priori we considered improves the change detection results by taking the spatial dependency of pixels into the detection scheme. Note the results on dataset2 are similar to those obtained on dataset 1, so they are omitted for the sake of brevity.

Table 2.

False detection, missed detection and total errors resulting from: the proposed change detection method, the SVM method, the SVDD method and the threshold method.

Image 1 from dataset1 (PSNR=30dB)	False detection	Missed detection	Total Errors
Proposed method	0.62 %	4.28 %	0.95 %
SVM	0.97 %	6.47 %	1.68 %
SVDD	1.26 %	7.39 %	2.21 %
Threshold	2.14 %	9.34 %	3.05 %
Image 2 from dataset1 (PSNR=30dB)	False detection	Missed detection	Total Errors
Proposed method	0.68 %	4.01 %	0.81 %
SVM	0.91 %	5.98 %	1.42 %
SVDD	1.68 %	7.35 %	2.38 %
Threshold	2.13 %	9.31 %	3.04 %
Image 3 from dataset1 (PSNR=30dB)	False detection	Missed detection	Total Errors
Proposed method	0.65 %	4.68 %	0.83 %
SVM	0.94 %	6.24 %	1.71 %
SVDD	1.51 %	7.03 %	2.09 %
Threshold	2.10 %	9.43 %	3.17 %
Image 4 from dataset1 (PSNR=30dB)	False detection	Missed detection	Total Errors
Proposed method	0.75 %	4.62 %	1.08 %
SVM	0.96 %	6.98 %	1.73 %
SVDD	1.39 %	7.90 %	2.36 %
Threshold	2.21 %	10.32 %	3.57 %

In order to assess the noise robustness of the proposed approach, three different methods were applied on the semi-simulated datasets with different values of PSNR: the proposed method, the SVM method and the threshold method. (Table 3). We observe that the proposed method performed better than both the kernel based-method and the threshold-based method. Specifically, even with PSNR=25dB, we obtained a total error inferior to 1 % which is two times smaller than that obtained by the SVM method. This can be explained by the fact that we took into account in our change detection scheme both the uncertainty (the noise) and the spatial dependency of pixels.

Table 3.

False detection, missed detection and total errors resulting from: the proposed change detection method, the SVM method and the threshold method using the semi-simulated datasets.

(PSNR=30dB)	False detection	Missed detection	Total Errors
Proposed method	0.58 %	3.81 %	0.86 %
SVM	0.84 %	4.58 %	1.12 %
Threshold	1.51 %	6.58 %	2.03 %
(PSNR=28dB)	False detection	Missed detection	Total Errors
Proposed method	0.62 %	3.85 %	0.88 %
SVM	1.18 %	6.91 %	1.61 %
Threshold	1.98 %	6.92 %	2.71 %
(PSNR=25dB)	False detection	Missed detection	Total Errors
Proposed method	0.75 %	4.61 %	0.97 %
SVM	1.91 %	6.8 %	2.68 %
Threshold	2.32 %	8.17 %	3.18 %
(PSNR=23dB)	False detection	Missed detection	Total Errors
Proposed method	0.91 %	4.77 %	1.20 %
SVM	2.68 %	8.39 %	3.88 %
Threshold	2.73 %	8.63 %	3.97 %

In order to emphasize the benefit of the variational approximation used in the change detection scheme, we compared the proposed VEM estimation procedure with two other procedures:

• MCMC procedure,

• The Iterative Conditional Mode (ICM) [25],

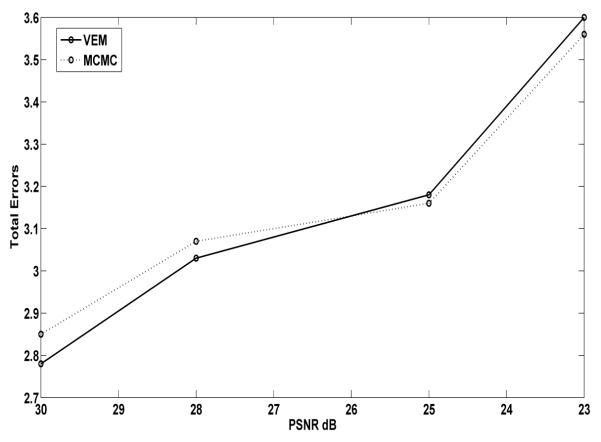
The change detection results obtained on dataset1 and dataset2 with different PSNR values are presented in Table 4. As can be seen, the proposed variational procedure performs better than the MCMC and the ICM procedure for PSNR=30, 28 and 25 dB and the MCMC approach performs slightly better for a PSNR=23dB. These results are similar to those obtained on the simulated dataset (cf. Fig. 6). This means that our variational estimation represents a good alternative to the MCMC procedure requiring a large computational burden and the fine tuning of model hyper-parameters.

Table 4.

False detection, missed detection and total errors resulting from: the proposed VEM procedure, the MCMC procedure and the ICM procedure using the semi-simulated datasets.

(PSNR=30dB)	False detection	Missed detection	Total Errors
Proposed VEM	0.58 %	3.81 %	0.86 %
MCMC	0.73 %	4.12 %	0.93 %
ICM	0.97 %	5.02 %	1.29 %
(PSNR=28dB)	False detection	Missed detection	Total Errors
Proposed VEM	0.62 %	3.85 %	0.88 %
MCMC	0.83 %	4.32 %	1.02 %
ICM	1.98 %	6.92 %	2.71 %
d(PSNR=25dB)	False detection	Missed detection	Total Errors
Proposed VEM	0.75 %	4.61 %	0.97 %
MCMC	0.85 %	4.46 %	1.04 %
ICM	2.3 %	7.58 %	3.03 %
(PSNR=23dB)	False detection	Missed detection	Total Errors
Proposed VEM	0.91 %	4.77 %	1.20 %
MCMC	0.88 %	4.71 %	1.16 %
ICM	2.69 %	8.61 %	3.82 %

Figure 6.

The total errors resulting from: the proposed VEM procedure and the MCMC procedure on the simulated dataset.

4.4. Classification results

We are now faced with the problem of framework validation on the clinical dataset. We have retained the sensitivity and the specificity measurements to perform the classification evaluation. In order to emphasize the benefit of the proposed glaucoma progression detection scheme, we have compared the proposed framework with three other published methods: the Topographic Change Analysis (TCA) method [35], the Proper Orthogonal Decomposition (POD) method [7] and the reflectance based method [6] (Table 5). Moreover, to emphasize the benefit of the proposed classification algorithm and particularly the use of the fuzzy set theory, we compared the proposed two-layer fuzzy classifier with two kernel-based methods, the SVM [36] and the SVDD [37] classifiers with the RBF Gaussian kernel. We obtained higher specificity and sensitivity with the proposed classifier compared to the SVM and the SVDD. This is due to the fact that the fuzzy set classifier leads to a better result when the training dataset is small. Moreover, we obtained the same progressor sensitivity as the TCA method while conserving a higher non-progressor specificity. This can be explained by the fact that the TCA technique does not include an intensity normalization step in the progression detection scheme, which makes the method less robust to the illuminance variation compared to the proposed scheme. Indeed, the TCA compares the topographic height variability at superpixels (4 × 4 pixels) in a baseline examination with the height change between baseline and follow-up examinations. A change map of P-values, indicating the probability of change at each superpixel is created, and contiguous superpixels showing significant (P<0.05) decreases in retinal height are clustered.

Table 5.

Diagnostic Accuracy of the proposed framework, the POD method, the reflectance based method and the TCA method.

	Progressor sensitivity	Non-progressor specificity
Proposed framework	86 %	88 %
Proposed framework  with SVM	79 %	85 %
Proposed framework  with SVDD	80 %	83 %
POD	78 %	45 %
TCA	86 %	25 %
reflectance based  method	64 %	76 %

The POD and the reflectance based methods led to a superior non-progressor specificity compared to the TCA. This is due in part that for both methods, dependency among spatial locations were indirectly used by controlling family-wise Type I error rate. However, the proposed method led to higher specificity and sensitivity than the POD and the reflectance based methods. This is likely because of the fact that we explicitly modeled the spatial dependency of classification among pixels whereas dependency is only implicitly accounted for by the two other methods.

Our results suggest that the detection of structural glaucomatous changes within the VEM framework, by taking into account the noise variations within the framework as well as the dependency among pixels using the MRF prior, shows promise for reducing the number of necessary follow up exams (i.e; only one follow-up exam is required for the proposed framework whereas at least 3 for the TCA technique) while maintaining high diagnostic specificity.

5. Conclusion

In this paper, a unified framework for glaucoma progression detection has been proposed. We particularly focus on the formulation of the change problem as a missing data problem. The task of inferring the topographic ONH changes is tackled with a Variational Expectation Maximization algorithm that is used for the first time, to our knowledge, in the glaucomatous progression detection framework. The handling of both spatial dependency of pixels and uncertainty increased the robustness of the proposed change detection scheme, compared with the kernel-based method and the threshold method. The real validation of the proposed approach is shown by its ability to perform more accurate glaucomatous progression detection compared with existing methods.

Appendix A. Genetic Algorithm

Genetic Algorithms (GA) are adaptive heuristic search algorithm premised on the evolutionary ideas of natural selection and genetics [38]. The basic concept of GA is designed to simulate processes in natural system necessary for evolution, specifically those that follow the principles first laid down by Charles Darwin of survival of the fittest. As such they represent an intelligent exploitation of a random search within a defined search space to solve a problem. The aim of genetic algorithm is to use simple representations to encode complex structures and simple operations to improve these structures. Let us denote by:

$$(a_1,b_1,c_1,a_2,b_2,c_2,a_3,b_3,c_3,d_3)$$

the population representing the parameters of the used fuzzy membership functions. We apply real coding to encode the chromosomes of the population. Therefore, each individual is represented by a vector of {0, 1}. The different steps of GA are:

1. Generating in an experimental way the initial population:

   $$(a_1^{\left[0\right]},b_1^{\left[0\right]},c_1^{\left[0\right]},a_2^{\left[0\right]},b_2^{\left[0\right]},c_2^{\left[0\right]},a_3^{\left[0\right]},b_3^{\left[0\right]},c_3^{\left[0\right]},d_3^{\left[0\right]})$$
2. Define individual fitness function to indicate the fitness of every chromosome. The proposed function is expressed as:

   $$f_{\mathit{opt}}=\{\begin{array}{cc}{\left(g\right({\gamma }_{\text{glau}})-0)}^2\hfill & \text{for}\text{non}-\text{progressing}\mathrm{HRT}\text{images}\hfill \\ {\left(g\right({\gamma }_{\text{glau}})-1)}^2\hfill & \text{for progressing}\mathrm{HRT}\text{images}\hfill \end{array}\phantom{\}}$$ (A.1)

   where g is given by Eq. 13, γ_glau is given by Eq. 13 and 1 or 0 is the expected result. Note that we used a training HRT dataset different from the test dataset and which contains 7 nonprogressor eyes and another 7 progressor eyes. Each eyes consists of one baseline and 4 to 8 follow-up exams (mean =5.5 exams). The change detection maps were estimated using the VEM algorithm presented in section 2.2.

3. Generating offspring by selection and crossover: 20% of the population which has best fitness is copied directly to next generation to keep the best gene. The other 80% of the population is obtained by crossover operation with a probability P_c = 0.8. We select randomly one cut-point and then we exchange the right part of two chromosomes.

4. Mutation operation: only the Chromosomes having undergone crossover can be affected by the mutation. It consists in modifying a gene with a probability Pm = 0.008.

5. Ending condition: if the maximal evolutionary epoch (maximal number of iterations 500) is reached, the GA end.