Abstract
This paper describes a Bayesian model for the assessment of inhalation exposures in an occupational setting; the methodology underpins a freely available web-based application for exposure assessment, the Advanced REACH Tool (ART). The ART is a higher tier exposure tool that combines disparate sources of information within a Bayesian statistical framework. The information is obtained from expert knowledge expressed in a calibrated mechanistic model of exposure assessment, data on inter- and intra-individual variability in exposures from the literature, and context-specific exposure measurements. The ART provides central estimates and credible intervals for different percentiles of the exposure distribution, for full-shift and long-term average exposures. The ART can produce exposure estimates in the absence of measurements, but the precision of the estimates improves as more data become available. The methodology presented in this paper is able to utilize partially analogous data, a novel approach designed to make efficient use of a sparsely populated measurement database although some additional research is still required before practical implementation. The methodology is demonstrated using two worked examples: an exposure to copper pyrithione in the spraying of antifouling paints and an exposure to ethyl acetate in shoe repair.
KEYWORDS: Bayesian exposure assessment, chemical regulation, occupational exposure, REACH
INTRODUCTION
Legislation on the Registration, Evaluation, Authorization and Restriction of Chemicals (REACH) entered into force within the member states of the European Union (EU) on 1 June 2007. The legislation makes industry responsible for assessing and managing the risk posed by chemicals. Under the REACH legislation, it is mandatory for any company manufacturing or importing chemicals to complete a chemical risk assessment for each chemical they handle, for substances produced or imported in quantities of 1 tonne or more per year per company. Whilst nominally the REACH legislation affects only the member states of the EU, in reality, due to global supply, the legislation has a global impact. Due to the very large number of chemicals covered by the regulations, phased deadlines for registration have been introduced with the recent deadline of 31 May 2013 addressing chemicals used in volumes of between 100 and 1000 tonnes.
Exposure assessments are critical to the risk assessment process. Many thousands of exposure scenarios need to be assessed under the REACH legislation. In comparison, exposure measurements are available for only a small fraction of exposure scenarios. It is clear that industry will be unable to comply with REACH without a significant input from exposure modelling (Tielemans et al., 2011). In order to decrease the burden on industry, a tiered approach to risk assessment has been proposed. Tier one approaches cover broad exposure scenarios and progressively more complex and specific exposure assessments are performed for substances where there is an overlap between the typically wide and conservative exposure ranges obtained from tier approaches and measures of the potential hazard of a substance, quantified by a metric such as a derived no-effect level.
A number of generic screening tools are available for assessing occupational inhalation exposures (Schinkel et al., 2010) . Screening tools provide conservative exposure estimates and are designed to filter out exposure scenarios of little concern from those that require further investigation. However, whilst well-validated and efficient screening tools may substantially reduce the pool of exposure scenarios to be investigated, a case-by-case assessment for every exposure scenario where a tier one tool is insufficient, based entirely upon exposure measurements, is impractical due to the time and expense of such assessments. Various authors (Creely et al., 2005; Hewett et al., 2006; Ramachandran, 2008) have proposed the use of Bayesian methods so that mathematical models of exposure can be combined with the limited data available from exposure measurements and utilized in risk assessments. A Bayesian framework allows the various disparate sources of information that are relevant to an exposure scenario to be integrated within a statistically rigorous framework.
The Advanced Reach Tool (ART) (www.advancedreachtool.com) is a higher tier tool for inhalation exposures that follows a Bayesian approach, making use of mechanistically modelled estimates of exposure for a range of substance classifications, information on exposure variability from meta-analyses in the literature, and any available exposure measurements. An overview of the ART version 1.0 is given in Tielemans et al. (2011). Technical details on various aspects of the ART 1.0 have been published elsewhere (Cherrie et al., 2011; Fransman et al., 2011; Marquart et al., 2011; Schinkel et al., 2011; Van Tongeren et al., 2011). Whilst the Bayesian approach was described in broad terms in Tielemans et al. (2011), a detailed methodology has not been previously published.
Version 1.5 of the ART has recently been released. The technical aspects are consistent with the original version (Tielemans et al., 2011); however, the software currently links to a library of exposure scenarios with associated measurements. Summary statistics and a brief description of the exposure scenario are provided for each scenario in the library and the source of the measurements (the relevant study) is referenced. Based upon the exposure scenario described by a user, the ART identifies related exposure scenarios which a user may utilize. Where appropriate, concentration adjustments to the exposure measurements are applied [measurements are rescaled such that they are appropriate for use in a user’s assessment scenario (AS)]. The development of the database is described in Schinkel et al. (2013) where at the point of publication the library consisted of 1944 measurements relating to 117 exposure scenarios. As with version 1.0, the software also accommodates measurements on the AS which are uploaded by users.
This paper provides technical details on the statistical model that underpins the ART version 1.5. A Bayesian approach is followed due to the complex hierarchical model of exposure, the disparate sources of information available, and the technical advantages of the approach (a full and complete treatment of uncertainty, the ability to resolve problems that are ill-posed in the classical sense, and treatment of censored observations). The technical details within the paper go beyond the methodology supported by the current version of the software. In particular, we introduce a model which accommodates partially analogous (PA) data, which is defined as data from exposure scenarios that share some similar characteristics to the AS of interest. This is a novel aspect of the model which is devised to maximize the information in a sparsely populated measurement database. PA data will be supported by version 2.0 of the ART once the final technical and programming issues have been resolved.
MATERIALS AND METHODS
Exposure model
The underlying statistical model of the ART assumes that every relevant exposure scenario has a distinct exposure distribution that is adequately represented by a log-normal mixed effects model, with random effects representing between-company and between-worker variability, and a residual error representing within-worker variability. The model is written
| (1) |
| (2) |
| (3) |
| (4) |
where Y (i)jkl is the lth observation on the kth worker within the jth company for the ith exposure scenario with μ (i) the mean natural log exposure, σ (i)bc and σ (i)bw between-company and between-worker standard deviations, respectively, and σ (i)ww the within-worker standard deviation. The AS is the specific exposure scenario for which inference is required. Exposure measurements for the AS are not necessarily available.
The model assumes that both between- and within-worker variability are constant over all companies. This is a strong assumption as it is possible to infer these components using data from a single company. Whilst a more elaborate model is theoretically appealing occupational hygiene data sets are usually too sparse to facilitate a hierarchical model for the variance components. However, the model assumptions are valid for the scenarios within the ART database. Whilst the model may apparently contradict the practical experience of some hygienists, model and experience can be reconciled with the concept of PA scenarios (Specifying analogy section).
Prior specification
A joint prior distribution for the model parameters corresponding to the AS is required. A priori the parameters are taken to be independent and distributions are specified for each of the four parameters. The parameters of the prior distributions are generated based upon user input and are regarded as known for any given AS. The form adopted for the mean (natural log) exposure is
| (5) |
The central estimate of equation (5) is and is provided by a mechanistic model. The mechanistic source–receptor model of the ART (Tielemans et al., 2011) is described in detail elsewhere (Fransman et al., 2008, 2011; Marquart et al., 2008). The uncertainty in the mean exposure for the AS is quantified by an exposure class-specific standard deviation (Schinkel et al., 2011). The four specific values that θ (AS) may take corresponding to the exposure classes that are currently supported by the ART are given in Table 1. A multiplicative 90% interval for the geometric mean (GM) is also given in Table 1. Example scenarios for the different exposure classes are given in Table 2 of Marquart et al. (2011).
Table 1.
Standard deviations representing uncertainty in the mechanistic model prediction for different substance classifications.
| Substance class |
|
Multiplicative 90% interval for GM | |
|---|---|---|---|
| Dusts | 0.89 | 0.23, 4.3 | |
| Vapours | 0.97 | 0.20, 4.9 | |
| Mists (low-volatiles) | 1.06 | 0.17, 5.7 | |
| Solid object/abraision | 0.46 | 0.47, 2.1 |
The prior distributions for the variance components are specified using log-normal distributions parameterized by a GM and geometric standard deviation (GSD); for a concise presentation of the model, the subscripts are suppressed and a general form is given
| (6) |
There are substantial differences in within- and between-worker variability for different types of exposure scenarios. The components of variability may even vary across groups within the same industry (Rappaport et al., 1999; Symanski et al., 2006; Van Tongeren et al., 2006). Kromhout et al. (1993) found that production factors (such as outdoors versus indoors, intermittent versus continuous processes) had a clear influence on within-worker variability but less of an impact on between-worker variability. Recent meta-analyses by Symanski et al. (2006) and Spaan et al. (2008) have been informative about further factors that influence within- and between-worker variability. The distinct scenarios supported by the ART at present and the parameters of the priors are given in Table 2. The priors for between-worker and within-worker variability are based upon regression models fitted to data on variance components taken from Kromhout et al. (1993). There is little information in the literature on between-company variability. At present a single prior for between-company variability is common to all scenarios. The prior for between-company variability was derived using information from Table 4 in Symanski et al. (2006). Technical detail on the derivation of these priors is given in supplementary material (available at Annals of Occupational Hygiene online).
Table 2.
Hyper-parameters for the variance components.
| Component | Scenario | GM | GSD |
|---|---|---|---|
| σ (i)bc | All cases | 0.44 | 1.29 |
| σ (i)bw | Vapours | 0.26 | 2.82 |
| Non-vapours | 0.32 | 2.82 | |
| σ (i)ww | Vapours, outdoors | 1.16 | 1.64 |
| Vapours, indoors | 0.48 | 1.64 | |
| Non-vapours, outdoors | 1.57 | 1.64 | |
| Non-vapours, indoors | 0.65 | 1.64 |
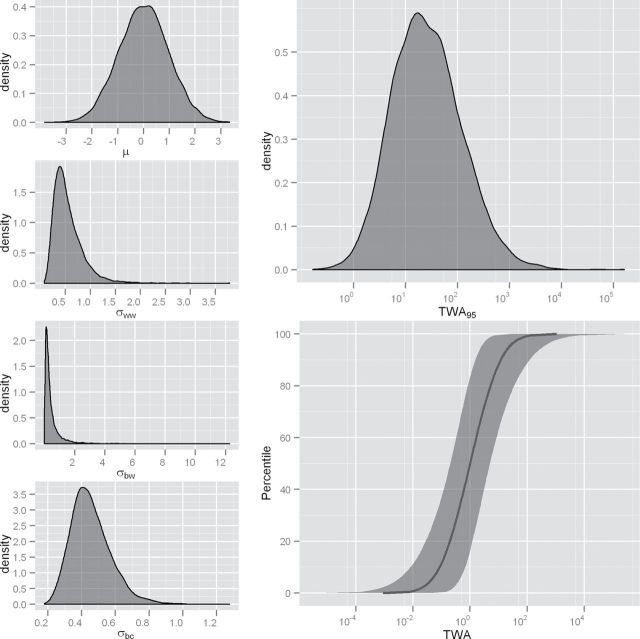
Based upon the prior alone, a point estimate and a distribution that captures the uncertainty in the model parameters are available. Furthermore, summary statistics based upon the model parameters also have implied prior distributions. Two important summaries for occupational exposures are the 8-h time weighted average (TWA) and the long-term average (LTA) exposure distributions given in equations (7) and (8) where z α denotes a critical value of the normal cumulative distribution function corresponding to a particular percentile. These implied prior distributions are calculated numerically by substituting values sampled from the prior distributions of μ (AS), σ (AS)bc, σ (AS)bw, and σ (AS)ww into equations (7) and (8), respectively. This process is illustrated in Fig. 1 for exposure to a vapour in an indoor AS. For the example, the mechanistic model is assumed to estimate a GM exposure of 1 with the remaining parameters of the prior distributions given in Tables 1 and 2, respectively (‘vapour, indoors’). The four panels of the left of Fig. 1 show the prior distributions for μ (AS), σ (AS)bc, σ (AS)bw, and σ (AS)ww. A total of 10000 samples were drawn from the prior distributions and two summaries calculated. The top right panel shows the implied prior distribution for the 95th percentile of the TWA. The data for this plot were generated by substituting the 10000 parameter sets into equation (7) with z α = 1.645. The bottom right plot shows the median and a 90% interval for cumulative TWA exposure distribution evaluated between the 0.1 and 99.9 percentiles of exposure. The data in this figure were generated by substituting the 10000 parameter sets into equation (7) for each percentile (and associated value of z α), sorting the resulting values, and extracting the 5000th, 500th, and 9500th values (for the median and interval, respectively).
1.
The propagation of uncertainty in a Bayesian calculation. Panels on the left represent prior distributions for the model parameters which are inputs to the calculation for percentiles of the exposure distribution. The panels on the right show the implied prior distribution for the 95th percentile of exposure and the central estimate (median) and a 90% interval for the TWA exposure distribution.
| (7) |
| (8) |
Specifying analogy
In a conventional Bayesian analysis, experimental data are observed and combined with parameters through the likelihood [defined through equations (2) to (5)], and the prior distribution is updated using these measurements. Indeed, this is the current mode of inference supported by version 1.5 of the ART. Inference for this case is presented in the first two examples in the paper.
The novel feature of the ART, as implemented in version 2.0, will be its ability to utilize available exposure measurements from other exposure scenarios that share some similarity to the AS, data from such scenarios are referred to as PA. Similarity is defined within but not across exposure classes; e.g. two processes involving dusts and vapours, respectively, would not be classed as PA, whereas two processes involving dusts would have some (perhaps small) degree of analogy. Analogy is modelled through a second tier to the prior specification.
The relationship between the central estimates of exposure in the AS and in the ith PA scenario is initially specified. The central estimates are linked by the expression
| (9) |
The motivation for equation (9) is that if the two scenarios differ in terms of only a few determinants, it might be possible to specify more precise information about the ratio of GMs in the two scenarios [which in equation (9) is represented as a difference in natural logs] than about the GM in either scenario. Bayesian inference has the flexibility to support indirect information about model parameters. Through equations (5) and (9), a bivariate normal distribution for μ (i) and μ (AS) is specified.
Briefly, parameter δ (i) represents the difference in the natural logs of mean exposure in the AS and PA scenarios. The mechanistic model which can be applied to both the AS and PA scenarios offers a logical framework for determining δ (i). Parameter ω (i) conveys information about to what extent knowing the mechanistic model error in estimating μ (AS) informs about the likely error in the estimate of μ (i). The upper bound on ω (i) is and occurs if the errors from the mechanistic model applied to the two scenarios are independent in which case μ (AS) provides no useful information about μ (i). Smaller values of ω (i) infer that knowledge about an under (over) estimate from the mechanistic model in the AS scenario conveys information about the under (over) estimate in the mechanistic model estimate for a PA scenario. Smaller values of ω (i) result in progressively larger correlations between μ (AS) and μ (i).
The relationships between the standard deviations of the AS and the ith PA scenario are modelled through bivariate normal distributions; specifically, ln(σ (AS)) and ln(σ (i)) have a bivariate normal distribution. Because analogy is only considered within exposure classes, ln(σ (AS)) and ln(σ (i)) share a common marginal distribution [equation (6)] (with class-specific parameters given in Table 2). A correlation ρ (i) quantifies the degree of analogy between the AS and PA scenarios and ranges from zero for scenarios that are not at all analogous to unity for fully analogous scenarios. Using a well-known property of the bivariate normal distribution, the relationship between the standard deviation in the AS and PA scenarios is modelled using
| (10) |
At present the correlation between the AS and PA data sets is assumed to be common for all the variance components; individualized correlations may be used in further versions of the ART if practical experience supports this. In a practical sense ρ (i) quantifies a reduction in the uncertainty of σ (i) if σ (AS) were known.
Expressions of the forms (9) and (10) for each of the PA scenarios complete this second tier to the prior specification. The correlations between the parameters of the AS and PA scenarios induced in this second phase mean that observations on the PA scenarios update both the parameters of the PA scenario and those of the AS. The extent to which the parameters of the AS are updated depends upon the strength of correlations. Whilst this is a conceptually sound approach, it is clear that reliable algorithms for determining δ (i), ω (i), and ρ (i) are critical; this is an area of ongoing research.
Computation
The joint posterior distribution of the model parameters, comprising of the parameters of both the AS and PA scenarios, cannot be calculated analytically. A Markov Chain Monte Carlo (MCMC) algorithm (Brooks, 1998) is used to draw samples from the joint posterior distribution of the model parameters. Inference about the model parameters is based upon these samples. The MCMC routine has been implemented using the OpenBugs software (Lunn et al., 2009), executed within the ART. As noted earlier, functions of the model parameters have priors and posteriors in a Bayesian model. Posterior distributions of the TWA and LTA exposure distributions [equations (7) and (8)], are calculated by the ART by repeatedly substituting sampled parameter sets into equations (7) and (8).
WORKED EXAMPLES
Simulated data
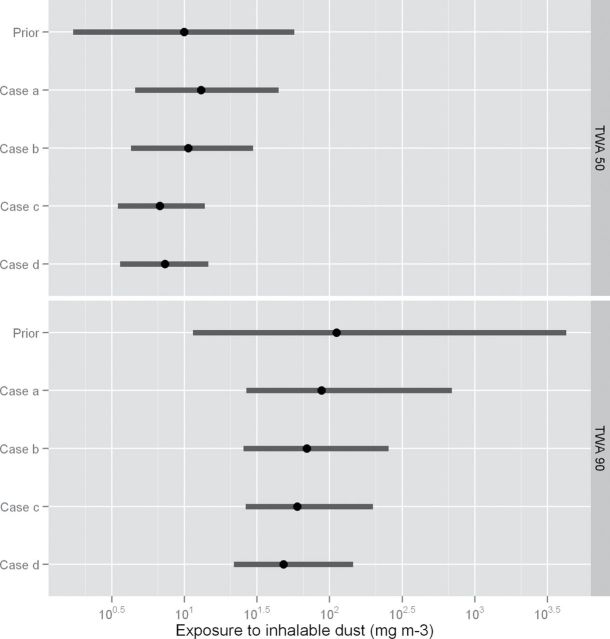
The first example is based upon simulated data and it demonstrates how the different qualities of information available from exposure measurements influence the precision of the posterior estimates. The hypothetical AS is for an exposure to dust in a process conducted in an outdoor setting. The assumed mechanistic model central estimate is 10mg m−3. Based upon the information presented, the remaining parameters of the prior are populated from Tables 1 and 2 (‘non-vapours, outdoors’). Four cases, each with 20 measurements, were considered corresponding to a) all measurements from a single worker; b) a single measurement on each of 20 workers at a single company; c) a single measurement on each of 20 workers from 20 companies and d) 20 measurements in total with two measurements on two workers at five companies. Data were simulated with μ (0) = log(10) and the three standard deviations set equal to their GM values for this scenario (Table 2). For each case, the posterior distributions of the 50th and 90th percentiles of the 8-h TWA were calculated [equation (7) with z α = 0 and z á = 1.2816, respectively].
The central estimate and a 90% interval from the prior distributions for these two summaries and the posterior distributions under scenarios a) to d) are given in Fig. 2. A central estimate and 90% credible interval for the parameters of the statistical model are given in Table 3.
2.
A comparison of the median and 90% credible intervals for the 50th and 90th percentiles of the full-shift exposure distribution. Results are shown for the prior and the posterior resulting from updates using four different data sets.
Table 3.
Posterior median and a 90% interval (brackets) for model parameters for the cases in example 1.
| Parameter | Prior | Case a | Case b | Case c | Case d |
|---|---|---|---|---|---|
| μ (0) | 2.29 (0.82, 3.76) | 2.56 (1.67, 3.64) | 2.36 (1.62, 3.18) | 1.92 (1.35, 2.51) | 1.99 (1.42, 2.57) |
| σ (0)bc | 0.44 (0.29, 0.68) | 0.44 (0.29, 0.68) | 0.44 (0.28, 0.68) | 0.45 (0.29, 0.75) | 0.42 (0.28, 0.64) |
| σ (0)bw | 0.31 (0.06, 1.77) | 0.30 (0.06, 1.54) | 0.35 (0.07, 1.10) | 0.29 (0.05, 1.24) | 0.29 (0.06, 0.89) |
| σ (0)ww | 1.56 (0.71, 3.56) | 1.29 (1.02, 1.73) | 1.29 (0.87, 1.75) | 1.54 (1.03, 2.11) | 1.33 (1.02, 1.78) |
| σ (0)total | 1.77 (0.92, 3.83) | 1.47 (1.16, 2.17) | 1.46 (1.17, 1.89) | 1.69 (1.35, 2.20) | 1.47 (1.17, 1.91) |
The example demonstrates that the degree of uncertainty in summaries depends upon the context of the data; all measurements are not of equal value. Many measurements on a single worker allow for a very precise determination of a personal exposure but convey no information about the personal exposure of other workers at the same or indeed at other companies. Measurements from a single company convey no information about between-company variability. A lack of repeat measurements on workers means that between- and within-worker variability cannot be uniquely identified. Cases a) to c) would be ‘ill-posed’ in classical statistical analysis, as the data are insufficient for a likelihood-based approach, whereas the Bayesian approach yields a posterior distribution with greater uncertainty about the parameters than would be the case had information on all sources of variability been available. The reduction in uncertainty about the model parameters was greatest in scenario d); however, there was also a large reduction in uncertainty in case c) as there was information on all three variance components even though the individual components could not be identified. A reduction in uncertainty about model parameters does not necessarily translate into reduced uncertainty about summaries calculated from those parameters. This is particularly important for a log-normal model as calculations of summaries of interest involve the exponential function [equations (7) and (8)].
Antifouling paints
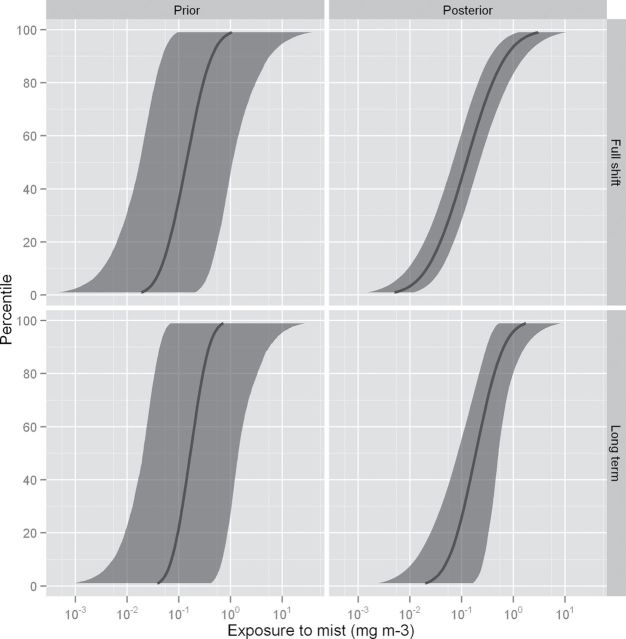
The first real-data AS concerns the spraying of antifouling paints onto boats. The exposure is to a mist containing copper pyrithione. Contextual information about this AS which is sufficient to reproduce our results is provided as supplementary information (available at Annals of Occupational Hygiene online). Contextual information would be elicited from a user of the ART based upon their answers to a series of multiple-choice questions. This information is used to produce a central estimate (from the mechanistic model) and associated uncertainty (Table 1, ‘mists’) and to specify the priors for all the variance components (Table 2, ‘non-vapours, indoors’). The estimated GM exposure and 90% credible interval were calculated by the ART as 0.13mg m−3 and 0.022–0.74mg m−3. The central estimate and 90% credible interval for the cumulative distribution of exposures for full-shift (8-h TWA) and LTA exposures based upon the prior alone are shown in Fig. 3.
3.
A comparison of the prior and posterior distributions for the full-shift and long-term average cumulative distributions of exposure for copper pyrithione in the antifouling paints example. The solid line represents the central estimate for a given percentile and the shaded region denotes the 90% credible interval.
The ART identified 22 exposure scenarios from the database which shared some similarities to the AS. Two scenarios were selected ‘Spraying operators of antifouling paints’ (HSE, 1999) and ‘Antifouling spraying’ (Hughson and Aitken, 2004) offering a single measurement from each of 21 workers at 11 companies and a measurement from each of four workers a single company, respectively. The median exposure from measurements alone was 0.14mg m−3 with measurements ranging from 0.01 to 1.3mg m−3. The Bayesian module was executed. The estimated GM exposure and 90% credible interval were calculated as 0.062mg m−3 and 0.035–0.11mg m−3. The central estimate and 90% credible interval for the cumulative distribution of exposures for the 8-h TWA and LTA based upon the prior and measurements are shown in Fig. 3.
This example corresponds to a classically ‘ill-posed’ problem as the within- and between-worker variability components are not estimable from the data; occupational hygiene data sets such as this are common. Based on the data alone, the LTA exposure cannot be estimated without some judgement as to the relative magnitudes of these two components. The Bayesian model presented in the paper naturally accommodates such scenarios. The unusual shape of the LTA posterior distribution (Fig. 3) is due to the bimodality of the posterior distributions for within- and between-worker variability, which is a consequence of observing a single measurement per worker.
Shoe repair
The second of the real-data case studies relates to exposure to solvents in glue, in particular ethyl acetate, for shoe repair in small and medium-sized enterprises. The example is based upon the study reported in Hertsenberg et al. (2007); data from this study are held within the ART database. Contextual information about this AS is provided as supplementary information (available at Annals of Occupational Hygiene online). The example was carefully chosen as PA data from a very similar exposure scenario in the orthopaedic sector were available. The results from using PA data could therefore be compared against a well-characterized exposure scenario. In this example, results from the mechanistic model are initially presented, before results from using PA data and finally results obtained from the fully analogous data from the Hertsenberg study are presented.
This information provided to the ART is used to produce a central estimate (from the mechanistic model) and associated uncertainty (Table 1, ‘vapours’) and to specify the priors for all the variance components (Table 2, ‘vapours, indoors’). The estimated GM exposure and 90% credible interval were calculated using the ART as 17mg m−3 and 3.5–84mg m−3. The central estimate and 90% credible interval for the parameters of the underlying statistical model and some summary statistics are given in the first column of results in Table 4.
Table 4.
Central estimates and 90% intervals for model parameters and selected summary statistics from the prior alone, from an update using PA data, and from an update using FA data for the shoe repair example.
| Summary | Prior | PA data | FA data | |||
|---|---|---|---|---|---|---|
| Estimate | 90% interval | Estimate | 90% interval | Estimate | 90% interval | |
| μ (0) | 2.8 | 1.2, 4.4 | 4.00 | 3.11, 5.05 | 3.51 | 3.09, 3.94 |
| σ (0)bc | 0.44 | 0.29, 0.66 | 0.70 | 0.49, 0.96 | 0.48 | 0.31, 0.75 |
| σ (0)bw | 0.26 | 0.05, 1.43 | 0.55 | 0.28, 0.99 | 0.77 | 0.34, 1.17 |
| σ (0)ww | 0.48 | 0.21, 1.08 | 0.43 | 0.33, 0.57 | 0.59 | 0.55, 0.63 |
| Median | 17 | 3.5, 84 | 56.2 | 22.4, 155.7 | 33 | 22, 51 |
| 90th percentile | 52 | 9.6, 365 | 101 | 39, 263 | 136 | 90, 239 |
| 90th percentile LTA | 46 | 8.6, 342 | 207.8 | 82, 568 | 130 | 83, 240 |
A study from the orthopaedic sector (Van Niftrik et al., 2006) was considered to be PA to the AS. The data set consisted of 62 measurements taken from 32 workers at 12 companies and thus provided information on all the variance components. The median and the range of these measurements were 139mg m−3 and 6.6–990mg m−3, respectively. These data are contained within the ART library, with the measurements within three data sets partitioned by the duration of the exposure ‘Spreading of glue [<1.5h, local exhaust ventilation (LEV)]’, ‘Spreading of glue [1.5–3h, LEV]’, ‘Spreading of glue [>3h, LEV]’. However, as the ART version 1.5 does not yet support PA data, the ART was used to provide the mechanistic model estimate and the Bayesian model was executed using OpenBugs (Lunn et al., 2009) called from a local environment. At present similarity algorithms for automating the generation of parameters that link the AS and PA scenarios are not available. For this example, the authors therefore determined the three parameters that linked the PA and AS by considering the determinants in the two scenarios in the ART mechanistic model. The central estimate in the two scenarios was equivalent (hence δ (i) = 0). The ratio of GMs was judged to be in the multiplicative interval 1/3 to 3 with 90% probability (hence ω (i) = 0.67) and ρ (i) was taken to be 0.9 [for this value of the correlation, a 90% interval for the conditional distribution (σ (i)|σ (AS)) corresponds to the interquartile range (a 75% interval) of the marginal distribution of σ (i) when σ (AS) takes its GM value]. The central estimate and 90% credible interval for the parameters of the model and some summary statistics after updating using these data are given in the second column of results in Table 4. The posterior median and a 90% interval for the exposure distribution are given in Fig. 4.
4.
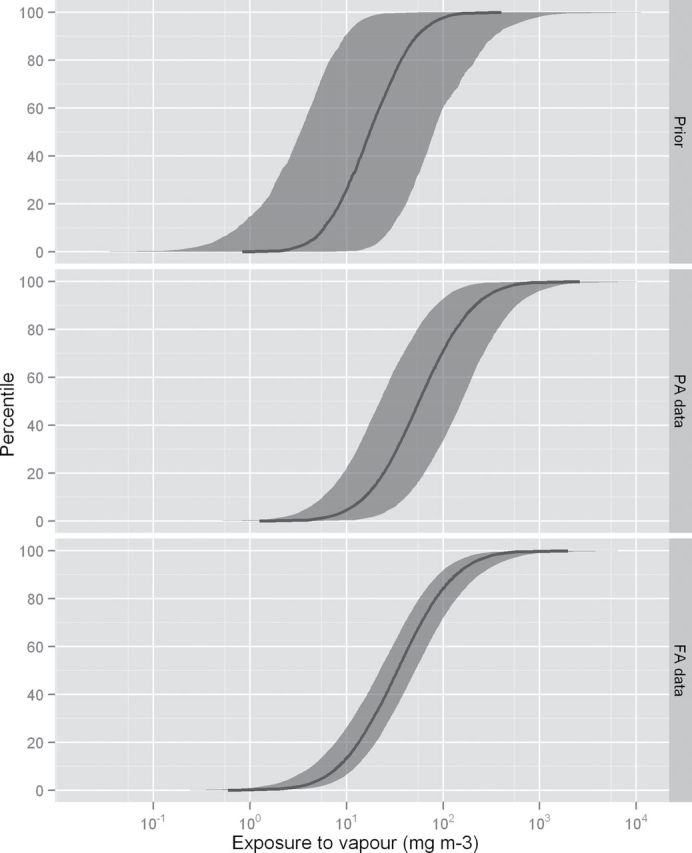
A comparison of the central estimate and a 90% credible interval for the full-shift cumulative distribution of exposure resulting from the prior alone and updates using partially analogous and fully analogous data for the shoe repair example.
The ART version 1.5 identified 16 exposure scenarios that shared some similarities to the AS. In practical use of the ART, a user would have to judge the most appropriate data for their AS based upon the contextual information that supplements each data set. For this example, the three data sets corresponding to the study reported in Hertsenberg et al. (2007) were selected. These data sets ‘Spreading of glue <1h, LEV’, ‘Spreading of glue 1–2h, LEV’, and ‘Spreading of glue >2h, LEV’ related to the same study; however, the measurements were partitioned by the exposure duration. A total of 294 measurements from 16 workers at 16 companies were available. The measurements in the three scenarios were from the same small subset of workers; the measurements on each worker were over varying durations and not all measurements on a particular worker appear in the same data set in the exposure library. Due to the labelling system in the underlying database, the ART correctly recognized and ascribed the exposure measurements to the correct worker when pooling the three data sets prior to executing the Bayesian update. The pooled data were regarded as being fully analogous to the AS and the ART was used for inference. A central estimate and 90% interval for parameters and summaries are given in the third column of results in Table 4. The posterior median and a 90% interval for the exposure distribution are given in Fig. 4.
The update using PA data resulted in narrower intervals for the model parameters and some movement in the central estimates for the parameters compared with the prior (Table 4, Fig. 4). The intervals for the 90th percentile were substantially narrower than under the prior, which reflects large uncertainty from the mechanistic model alone in calculations of percentiles in the upper tail of the exposure distribution. Tighter intervals for parameters and summaries were achieved when updating the prior using the fully analogous data, which resulted from the greater volume of data in this scenario and the removal of an important source of uncertainty (the degree of analogy). Whilst the between-company and between-worker variance components could not be uniquely identified using fully analogous data, their sum could be determined with high precision; therefore, the impact on calculations of the exposure distribution was negligible in this example. The central estimate for the cumulative distribution of exposures using fully analogous data was contained in the 90% interval derived using PA data, although the central estimate of the exposure distribution was higher when using the PA data.
It should be noted that the example was carefully chosen with the AS and PA scenarios sharing a number of important determinants and a subsequent high degree of similarity. In the absence of validated similarity algorithms, the chosen values of δ, ω, and ρ can clearly be questioned; however, the example is sufficient to demonstrate an application of the methodology. Smaller changes compared with the prior would have been achieved with PA data had a lower degree of analogy been assumed.
DISCUSSION
Contribution to exposure and risk assessment
The paper has described a methodology for estimating inhalation exposures that makes use of data from various disparate sources within a Bayesian framework. The methodology is implemented in a free web-based programme (www.advancedreachtool.com), although at present it does not support PA data. The use of Bayesian methods so that mechanistic exposure models and exposure measurements can be utilized in risk assessments has been proposed by others (Creely et al., 2005; Ramachandran, 2008) and implemented in software (Sottas et al., 2009) but as far as we are aware, the ART application offers the first practical online implementation. However, alternative Bayesian approaches have been used, for example Hewett et al. (2006) proposed the combination of elicited expert judgements about likely exposures with exposure measurements. This approach suffers from a considerable practical difficulty in training occupational hygienists such that they can express their beliefs about likely exposures using probability. In contrast the ART requires a user to describe the process and the calibrated mechanistic model automates the generation of priors. The ART is considerably more transparent in terms of defining the prior compared with Hewett et al. (2006).
The primary limitation of the ART version 1.5 is that whilst the software returns exposure scenarios that share some analogy with an AS, at present the burden of assessing the degree of analogy falls upon the user. Summary statistics and a description of the scenarios are provided to aid the user although a degree of judgement does need to be applied. Clearly there is some scope for error in this process. This can be mitigated against to an extent through the selection of a number of PA data sets when executing the Bayesian update; in the third example presented in this paper, this approach was adopted. Whilst at this stage of development the scenarios are not ranked by their similarity to the AS, the use of multiple scenarios will increase the variability in exposure estimates. Moreover, a comparison of the prior and posterior, both of which are provided in summary assessments generated by the ART, will reveal whether the data are consistent with the mechanistic model. A further safeguard could be achieved by using a conservative upper bound for a high percentile of the exposure distribution in risk assessments. In version 2 of the ART, the burden of assessing (and parameterizing) analogy will fall upon the developers and at this stage an important source of uncertainty will be removed.
Testing and robustness
MCMC is a powerful sampling technique; however, it is important to test that the sampling algorithm is error free, stable, and that it converges to the posterior distribution before samples are retained for inference. Usually the burden of these checks falls upon the user, typically an expert in Bayesian statistics. The MCMC algorithm within the ART is executed by a call to the OpenBugs software (Lunn et al., 2009) and is hidden from the user behind the web-based interface of the ART. In this instance, the burden of testing therefore falls upon the developers.
Extensive checks took place prior to the launch of the ART version 1.0 and a further battery of tests were conducted prior to the launch of the ART version 1.5 to ensure that the MCMC algorithm was correctly generated, and the data passed to the OpenBugs module were correct. The behaviour of the model has been extensively tested using simulated data using a locally run version of the Bayesian module so that the behaviour of the parameters of the statistical model and summaries calculated from these could be evaluated. The test programme considered cases where the prior distributions were consistent with measurements and cases where there were prior-data conflicts. Conflicts between two PA data sets were also studied as errors in the similarity algorithms that generate the model parameters could in principle result in such conflicts. It is important to have an understanding of the behaviour of the model in such situations so that conflicts can be identified and corrected. The challenges presented in the testing programme were far more extreme than we anticipate in routine use of the ART. In all test cases, the changes to parameters were consistent with our expectations and supported by statistical theory. In cases where some measurement series were inconsistent with each other, or the prior, we developed procedures to identify the conflicts; however, further testing is required before these are implemented in version 2.0 of the ART.
Censoring
Many occupational hygiene data sets contain a proportion of measurements that are below the threshold sensitivity of the equipment (the limit of detection). Such measurements are referred to as left censored. Depending upon the substance (and equipment), a large proportion of measurements may be below the limit of detection. Hewett and Ganser (2007) and Helsel (2010) discussed the merits of various simplistic methods for treating such observations. A more advanced imputation method was applied in Krishnamoorthy et al. (2009) and Schinkel et al. (2011). A classical likelihood-based treatment of censored measurements involves estimating the underlying measurement, with the resulting estimated measurements being treated as equivalent to observed measurements; as a consequence, classical methods underestimate the uncertainty in a measurement series. A Bayesian approach (Wild et al., 1996; Morton et al., 2010) naturally accommodates left-censored measurements as observations on the distribution function. The underlying unobserved measurements have both prior and posterior distributions, truncated at the limit of detection and these data are thus weaker than observed measurements. Testing of the Bayesian module of the ART in the presence of measurements below a limit of detection has considered censoring rates of up to 50% of observations at a common limit of detection (the poorest quality censored data). Whilst there was inevitably some impact on the uncertainty in the parameters, explicitly captured within the posterior distributions, the central estimates of parameters were relatively insensitive to the censoring. The MCMC numerical algorithm was stable in all test cases.
Value of measurements
The context of exposure measurements is important as this determines how informative a measurement series is about the model parameters. There is an interesting counterbalance between the size and scope of a measurement series. A small data set containing data from multiple workers at multiple companies and repeat measurements on a subset of workers may result in a larger reduction in overall uncertainty than a much larger data set that conveys weak or indeed no information about components of variance (J. Schinkel et al.). The degree of analogy adds an additional dimension to this comparison as there is a further counterbalance between the information in a PA data set with which to estimate the parameters specific to that data set, and the strength of the relationship between the AS and PA scenarios. When data from a series of PA data sets are available, those with the highest degrees of analogy are the most influential so long as the size and scope of the measurement series are similar.
For the majority of ASs, it is unlikely that a data-rich PA scenario will be available, although smaller measurement series with weaker analogy are likely to be available for a large range of exposure scenarios. The power of the model is in its ability to effectively pool the data from a range of such scenarios in order to improve the precision of estimates. The shoe repair example highlighted the value of PA data although it also demonstrated that observations on the AS provide a greater reduction in uncertainty; clearly this is desirable behaviour. So long as each of the variance components can be uniquely identified from at least one PA source, all parameters in the AS are updated. However, an important feature of the model is that exposure estimates are available in the absence of any data using the mechanistic model and priors for the variance components.
ART version 2.0
Tielemans et al. (2011) noted that the ART is considered to be an evolving system with a firm conceptual basis. The development of an exposure database (Schinkel et al., 2013) and the launch of version 1.5 of the ART are important recent developments; however, the ART does not currently support PA data. The conceptual basis for determining analogy is justified but is an unexplored field within Bayesian exposure assessment. Similarity algorithms for automating the process of parameterizing analogy are the subject of ongoing research.
In the longer term, there will be an ongoing review of the methodology. Large changes to the underpinning methodology are not anticipated, but subtle changes such as independent updating of the variance components via individualized correlations could be implemented and more substance classes will be supported. Future developments will be informed by extensive testing using real-data measurement series, and user feedback. Hence, populating the ART exposure database with high quality data is a priority area to actually progress this research field.
SUPPLEMENTARY DATA
Supplementary data can be found at http://annhyg.oxfordjournals.org/.
FUNDING
UK Health and Safety Executive; Dutch Ministry of Social Affairs and Employment; French agency for environmental and occupational health safety (Afsset); Cefic LRI; Royal Dutch Shell plc (Shell); GlaxoSmithKline; Eurometaux; British Occupational Hygiene Society.
Supplementary Material
DISCLAIMER
The contents of the paper, including any opinions and/or conclusions expressed, are those of the authors alone and do not necessarily reflect HSE policy.
REFERENCES
- Brooks S. (1998). Markov Chain Monte Carlo method and its application. J R Stat Soc D 47: 69–100. [Google Scholar]
- Cherrie JW, Maccalman L, Fransman W, et al. (2011). Revisiting the effect of room size and general ventilation on the relationship between near- and far-field air concentrations. Ann Occup Hyg; 55: 1006–15. [DOI] [PubMed] [Google Scholar]
- Creely KS, Tickner J, Soutar AJ, et al. (2005). Evaluation and further development of EASE model 2.0. Ann Occup Hyg; 49: 135–45. [DOI] [PubMed] [Google Scholar]
- Fransman W, Schinkel J, Meijster T, et al. (2008). Development and evaluation of an exposure control efficacy library (ECEL). Ann Occup Hyg; 52: 567–75. [DOI] [PubMed] [Google Scholar]
- Fransman W, Van Tongeren M, Cherrie JW, et al. (2011). Advanced Reach Tool (ART): development of the mechanistic model. Ann Occup Hyg; 55: 957–79. [DOI] [PubMed] [Google Scholar]
- Helsel D. (2010). Much ado about next to nothing: incorporating nondetects in science. Ann Occup Hyg; 54: 257–62. [DOI] [PubMed] [Google Scholar]
- Hertsenberg S, Brouwer D, Lurvink M, et al. (2007). Quantitative self-assessment of exposure to solvents among shoe repair men. Ann Occup Hyg; 51: 45–51. [DOI] [PubMed] [Google Scholar]
- Hewett P, Ganser GH. (2007). A comparison of several methods for analyzing censored data. Ann Occup Hyg; 51: 611–32. [DOI] [PubMed] [Google Scholar]
- Hewett P, Logan P, Mulhausen J, et al. (2006). Rating exposure control using Bayesian decision analysis. J Occup Environ Hyg; 3: 568–81. [DOI] [PubMed] [Google Scholar]
- HSE. (1999) Dermal exposure to non-agricultural pesticides. HSE guidance document EH74/3. ISBN 0-7176-1718-1. [Google Scholar]
- Hughson GW, Aitken RJ. (2004). Determination of dermal exposures during mixing, spraying and wiping activities. Ann Occup Hyg; 48: 245–55. [DOI] [PubMed] [Google Scholar]
- Krishnamoorthy K, Mallick A, Mathew T. (2009). Model-based imputation approach for data analysis in the presence of non-detects. Ann Occup Hyg; 53: 249–63. [DOI] [PubMed] [Google Scholar]
- Kromhout H, Symanski E, Rappaport SM. (1993). A comprehensive evaluation of within- and between-worker components of occupational exposure to chemical agents. Ann Occup Hyg; 37: 253–70. [DOI] [PubMed] [Google Scholar]
- Lunn D, Spiegelhalter D, Thomas A, et al. (2009). The BUGS project: evolution, critique and future directions. Stat Med; 28: 3049–67. [DOI] [PubMed] [Google Scholar]
- Marquart H, Heussen H, Le Feber M, et al. (2008). ‘Stoffenmanager’, a web-based control banding tool using an exposure process model. Ann Occup Hyg; 52: 429–41. [DOI] [PubMed] [Google Scholar]
- Marquart H, Schneider T, Goede H, et al. (2011). Classification of occupational activities for assessment of inhalation exposure. Ann Occup Hyg; 55: 989–1005. [DOI] [PubMed] [Google Scholar]
- Morton J, Cotton R, Cocker J, et al. (2010). Trends in blood lead levels in UK workers, 1995-2007. Occup Environ Med; 67: 590–5. [DOI] [PubMed] [Google Scholar]
- Ramachandran G. (2008). Toward better exposure assessment strategies–the new NIOSH initiative. Ann Occup Hyg; 52: 297–301. [DOI] [PubMed] [Google Scholar]
- Rappaport SM, Weaver M, Taylor D, et al. (1999). Application of mixed models to assess exposures monitored by construction workers during hot processes. Ann Occup Hyg; 43: 457–69. [PubMed] [Google Scholar]
- Schinkel J, Fransman W, Heussen H, et al. (2010). Cross-validation and refinement of the Stoffenmanager as a first tier exposure assessment tool for REACH. Occup Environ Med; 67: 125–32. [DOI] [PubMed] [Google Scholar]
- Schinkel J, Ritchie P, Goede H, et al. (2013). The Advanced REACH Tool (ART): incorporation of an exposure measurement database. Ann Occup Hyg; 57: 717–27. [DOI] [PubMed] [Google Scholar]
- Schinkel J, Warren N, Fransman W, et al. (2011). Advanced REACH Tool (ART): calibration of the mechanistic model. J Environ Monit; 13: 1374–82. [DOI] [PubMed] [Google Scholar]
- Sottas PE, Lavoué J, Bruzzi R, et al. (2009). An empirical hierarchical Bayesian unification of occupational exposure assessment methods. Stat Med; 28: 75–93. [DOI] [PubMed] [Google Scholar]
- Spaan S, Schinkel J, Wouters IM, et al. (2008). Variability in endotoxin exposure levels and consequences for exposure assessment. Ann Occup Hyg; 52: 303–16. [DOI] [PubMed] [Google Scholar]
- Symanski E, Maberti S, Chan W. (2006). A meta-analytic approach for characterizing the within-worker and between-worker sources of variation in occupational exposure. Ann Occup Hyg; 50: 343–57. [DOI] [PubMed] [Google Scholar]
- Tielemans E, Warren N, Fransman W, et al. (2011). Advanced REACH Tool (ART): overview of version 1.0 and research needs. Ann Occup Hyg; 55: 949–56. [DOI] [PubMed] [Google Scholar]
- TNO. (2006) De blootstelling van orthopedisch schoentechnici aan Vluchtige Organische Stoffen: niveaus en modellering. In van Niftrik M, Schinkel J, le Feber M, Lurvink M, Meijster T, Tielemans E. editors. TNO report V6894. [Google Scholar]
- Van Tongeren M, Burstyn I, Kromhout H, et al. (2006). Are variance components of exposure heterogeneous between time periods and factories in the European carbon black industry? Ann Occup Hyg; 50: 55–64. [DOI] [PubMed] [Google Scholar]
- Van Tongeren M, Fransman W, Spankie S, et al. (2011). Advanced REACH Tool: development and application of the substance emission potential modifying factor. Ann Occup Hyg; 55: 980–8. [DOI] [PubMed] [Google Scholar]
- Wild P, Hordan R, Leplay A, et al. (1996). Confidence intervals for probabilities of exceeding threshold limits with censored log-normal data. Environmetrics; 7: 247–59. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.