Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 May 20;14(6):3453–3458. doi: 10.1021/nl5009713

Fabrication of 200 nm Period Hard X-ray Phase Gratings

Houxun Miao †,*, Andrew A Gomella †, Nicholas Chedid †, Lei Chen ‡, Han Wen †,*
PMCID: PMC4055044  PMID: 24845537

Abstract

graphic file with name nl-2014-009713_0008.jpg

Far field X-ray grating interferometry achieves extraordinary phase sensitivity in imaging weakly absorbing samples, provided that the grating period is within the transverse coherence length of the X-ray source. Here we describe a cost-efficient process to fabricate large area, 100 nm half-pitch hard X-ray phase gratings with an aspect ratio of 32. The nanometric gratings are suitable for ordinary compact X-ray sources having low spatial coherence, as demonstrated by X-ray diffraction experiments.

Keywords: X-ray grating far-field interferometer, X-ray phase contrast imaging, nanoimprint lithography, cryogenic reactive ion etch, atomic layer deposition, electroplating

X-ray modalities account for the majority of medical imaging procedures today, owing to the penetrating power of hard X-ray photons (energies >20 keV) through the human body.1 The partial absorption of X-rays that pass through an opaque object is responsible for the first shadow grams observed by W. Roentgen in 18952 and still is the primary contrast mechanism in X-ray imaging today. Inherently, this mechanism involves the absorption of radiation by the sample medium, leading to harmful ionization effects. This is a growing concern in healthcare due to the rising prescription of computed tomography (CT) scans. Phase contrast provides a fundamental solution to the problem. Phase contrast methods detect the refractive bending of the X-rays instead of their attenuation. In the wave picture, phase contrast refers to sensing the distortion of the wavefront after propagation through a sample.

Some of the first demonstrations of phase contrast are achromatic visible light two-beam interferometers, such as the Michelson–Morley3 and the Mach–Zehnder4 interferometers. They are sensitive to the relative phase shift between two light paths of nearly equal lengths. The X-ray embodiment of a two-beam interferometer is the Bonse–Hart interferometer, which uses monolithic crystals to split and direct the beams.5 It achieves the highest phase sensitivity among common hard X-ray techniques6 and can reveal subtle soft tissue structures with low radiation exposure.7,8 However, the crystals reject most of the flux of a broadband source (Δλ/λ ∼ 10–4), which restricts applications with ordinary X-ray tube sources.

Recently, methods based on the near-field self-imaging (Talbot) phenomenon of microgratings have been extensively investigated for X-ray phase contrast imaging with compact sources.9−15 Although suitable for polychromatic sources, they do not rival the sensitivity of the classic far-field interferometer.16 More recently, with the development of nanofabrication techniques, prototype 200 nm period hard X-ray phase gratings have been fabricated that can replace the monolithic crystals in the classic Bonse–Hart interferometer,17 thus releasing the bandwidth restrictions on the X-ray source. The first grating Bonse–Hart interferometer demonstrated exquisite sensitivity approaching those of crystal interferometers while operating at a source bandwidth that is 2 orders of magnitude higher.18

A key requirement of a grating far-field interferometer is that the transverse coherence of the incident beam exceeds the grating period. Common X-ray tubes in the hard X-ray range have transverse coherence lengths of 1 μm or less within a 0.5 m distance. Thus, nanometric gratings are a prerequisite. Alternatively, the pitch of the gratings should be sufficiently small such that adjacent diffraction orders of an incident beam are fully separated after propagating over a reasonable distance. As an example, assuming normal incidence, in order to separate two adjacent diffraction orders by 50 μm after a propagation distance of 0.5 m, the diffraction angle between the two beams (∼ X-ray wavelength/grating pitch) must be greater than 10–4 radians. For typical photon energies in radiological imaging of 25 to100 keV, the pitch of the grating must be as small as 500 to 124 nm to have a first order diffraction angle of 1 × 10–4 radians. Additionally, the efficiency of the phase gratings is measured by the fraction of the incident energy that is diffracted into higher orders, typically the ±1 orders. This depends on the amplitude of the phase modulation by the gratings. For example, a 50% duty cycle, π-phase shift binary phase grating diffracts 100% of incident energy to higher orders, of which 40.5% goes into the ±1 orders each. For a binary grating with alternating Au and Si strips, a strip height of 5.8 to 23.4 μm is required to get a π-phase shift for 25 to 100 keV X-rays, corresponding to an aspect ratio (gold strip height-to-width ratio) of 23 to 377. The difficulties imposed by the combination of small periods and high aspect ratios make the fabrication particularly challenging. The first prototype gratings met the requirements with multilayer stacks viewed from the side. However, the multilayer stacks took lengthy coating runs that were difficult to control precisely.17

The fabrication of hard X-ray gratings and zone plates typically involves creating a free-standing high aspect ratio mold and then filling the trenches of the mold with high atomic number metals via electroplating. For trenches that are several micrometers wide, both bottom-up and full-surface electroplating are used to fill them. The molds are either made in polymer layers of tens of micrometers thickness using deep X-ray lithography or optical lithography19,20 or in silicon wafers through direct etching (reactive ion etch (RIE) or wet KOH etch). To allow bottom-up electroplating, the polymer resist is spin coated on a predeposited conductive layer, while the seed layer is coated on the bottom of the trenches in the silicon wafers with a combination of electron-beam depositions and a lift-off process.20,21 The alternative full-surface electroplating has been used with molds made in silicon wafers, where the seed layer is formed on the mold surface with a combination of electron-beam depositions and a lift-off process.20 For nanoscale trenches such as in X-ray zone plates, only bottom-up plating is realized in molds typically patterned in a polymer resist layer (<2 μm) using X-ray lithography,22,23 electron beam lithography,23−26 or dry etching a polymer (<1 μm)27 or diamond layer.28 The reported aspect ratios of the trenches in the nanoscale zone plates approaches 25.25,28

The bottom-up plating for nanoscale zone plates is difficult to adapt to the deeper trenches of large-area nanometric hard X-ray phase gratings, because the polymer molds are not able to support the required aspect ratios without cross-bridges that reduce X-ray diffraction efficiency, and e-beam lithography is comparatively costly for large areas. The alternative full-surface electroplating from physically deposited seed layers works in trenches of several micrometer periods, but physical vapor deposition (PVD) has inherent difficulties accessing the interior surface of nanoscale deep trenches.

Here, we present a cost-efficient fabrication process based on atomic layer deposition (ALD) of a seed layer (Figure 1) for large-area, 200 nm pitch hard X-ray phase gratings with walls having an aspect ratio of 32. We demonstrate void-free filling of 100 nm wide, 3.2 μm deep trenches with full-surface electroplating of gold from a uniform platinum seed layer.

Figure 1.

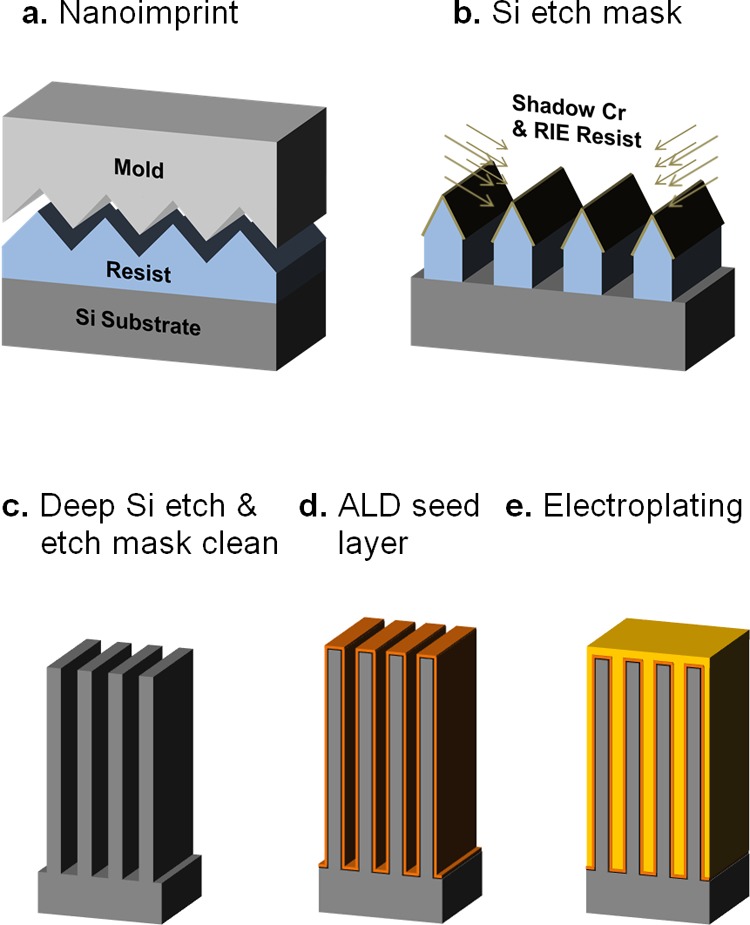
Figure 1

Open in a new tab

Illustration of the fabrication process for 200 nm period hard X-ray phase gratings. (a) The grating lines are patterned on a polymer resist layer on the silicon wafer by nanoimprint lithography. (b) Chromium shadowing and reactive ion etching of the resist layer forms the etch mask for the silicon wafer. (c) Cryogenic deep silicon etching produces a grating mold of high aspect ratio, followed by plasma cleaning of the etch mask. (d) Atomic layer deposition of Al2O3 and Pt lays the electroplating seed layer. (e) Electroplating of gold fills the trenches of the mold.

Single crystal silicon is selected as the mold material for its superior mechanical properties. In the first step, etch masks of 200 nm period are patterned on the silicon wafer via nanoimprint lithography,29 bidirectional chromium shadowing,30 and RIE of the nanoimprint resist layer. This is followed by cryogenic RIE31,32 to create deep trenches in the silicon, then O2 plasma removal of the mask materials. A seed layer for electroplating is formed on the silicon mold by ALD of a thin platinum layer (∼10 nm).33−36 Proper thickness of the seed layer is essential: too thick and the excessive stress may collapse the walls of the mold; too thin will not provide electrical connectivity. The trenches between the walls are then filled with gold via conformal electroplating,20,37−39 mainly from the sidewalls. The performance of the product as an X-ray grating is tested by X-ray diffraction experiments on a tabletop device.

The common options for patterning etch masks of 100 nm features on the silicon wafers are electron beam lithography, optical interference lithography and nanoimprint lithography. Considering the time and cost of electron beam lithography over centimeter areas and the high environmental stability requirement of optical interference lithography for the small grating period, we chose nanoimprint lithography to pattern the mask. The grating master template (Polarization Solutions, LLC) is a 4 in. Si wafer with a thermally grown SiO2 layer on top, patterned via optical interference lithography and RIE of SiO2. The master template has a pitch of 200 nm, an approximately triangular cross section with a depth of 100 nm and a base of approximately 75% the pitch. The grating pattern is transferred to a resist layer (Nanonex NXR-1025) spin-coated on a 4 in. (100) Si wafer via nanoimprint lithography, at a temperature of 120 °C and a pressure of 200 psi for 5 min 30 s. Figure 2a shows a cross-section scanning electron microscopy (SEM) image of the printed pattern, which represents an inverted pattern of the master template. The triangular shape of the imprinted cross sections provides a convenient way to adjust the duty cycle of the subsequent etch mask for deep silicon etching. This is accomplished in the next step of chromium shadowing by changing the incident angle of the Cr deposition beam onto the wafer surface (Figure 1b). Figure 2b–d shows cross-section SEMs of the etch masks after RIE of the resist with shadowing angles of 30, 33.4, and 36.9°, respectively. The line width increased from 115 to 142 nm over the range of the shadowing angles. The flexibility of adjusting the line width is valuable for cryogenic deep silicon etching, becuase there is an undercut of the silicon material immediately below the mask lines, which is one of the factors that limit deep RIE of silicon.

Figure 2.

Figure 2

Open in a new tab

Cross-sectional scanning electron microscopy images showing the production of the etch mask on the silicon wafer. (a) The resist layer is patterned with nanoimprinting. (b) A top chromium protection mask is formed by e-beam deposition at 30° angle from both sides (chromium shadowing). RIE then removes the unprotected resist. (c) Chromium shadowing at 33.4° produces wider resist lines than (b). (d) Chromium shadowing at 36.9° further widens the resist lines. In all cross-section samples, a thin layer of Au/Pd was sputtered on the surface to remove charging effects on the polymer resist.

Two recipes were created for cryogenic deep silicon etching. The first recipe has operating parameters of −110 °C temperature, 3.8 mT pressure, ICP power of 700 W, RF bias power of 10 W, SF6 flow rate of 24 sccm, and O2 flow rate of 7 sccm. The second recipe has parameters of −110 °C temperature, 6 mT pressure, ICP power of 700 W, RF bias power of 30 W, SF6 flow rate of 36 sccm, and O2 flow rate of 10 sccm. To give sufficient directionality and kinetic energy to the ion flux for deep etching either a lower pressure of 3.8 mT (first recipe) or a higher RF bias power of 30 W (second recipe) is used. Both lead to overablation of the polymer resist layer without additional protection, which is solved by the chromium top mask. The parameters of the O2 plasma clean are −110 °C temperature, 20 mT pressure, ICP power of 2000 W, RF bias power of 100 W, and O2 flow rate of 100 sccm. Figure 3a shows cross-sectional SEM of a sample that was Cr shadowed at 33.4°, followed by 7 min of Si etch with the first recipe and 8 min of O2 plasma clean. Figure 3b shows a sample that was Cr shadowed at 35.1° and Si etched for 9 min using the second recipe, followed by 8 min of O2 plasma clean. The two samples have trenches of 3.2 and 4.0 μm depths, corresponding to aspect ratios of 32 and 40, respectively. The larger Cr shadowing angle of the second sample was more effective in slowing the undercut of material below the mask lines, allowing for a deeper etch. More details on the cryogenic silicon etching are described in the Supporting Information.

Figure 3.

Figure 3

Open in a new tab

Cross-sectional scanning electron microscopy images of cryogenically etched silicon grating molds of 200 nm period. (a) This mold has 3.2 μm trenches, giving a depth-to-wall thickness ratio (aspect ratio) of 32. (b) This mold has a depth of 4.0 μm and an aspect ratio of 40.

To fill the trenches with electroplating, the first step is to cover the mold surface with an electrically contiguous metal seed layer. In micrometer period gratings, the seed layer can be formed with PVD followed by a lift-off process.20 Typically, a PVD layer of few tens of nanometers is needed to have electrical continuity over the mold surface. The PVD process is less suitable for the nanometric gratings, since the trench width is too narrow for a seed layer of tens of nanometers, and the stress in the PVD metal layer may collapse the walls. Therefore, the ALD technique is used to form the seed layer. Since ALD lays one atomic layer at a time, a total thickness of about 10 nm is sufficient to form an electrically contiguous film for electroplating. A 10 nm adhesion layer of Al2O3 is first coated by exposing the sample to 20 ms of trimethyl aluminum (TMA) and 40 ms of H2O at 300 °C and 80 mT chamber pressure. The Al2O3 layer also increases the wall thickness of the grating, allowing for adjustment of the trench width (detailed information is provided in Supporting Information). A Pt layer is added by using 1 s trimethyl (methylcyclopentadienyl)-platinum(IV) (MeCpPtMe3) and 50 s O2 at 240 mT chamber pressure and 300 °C. An idle time of 1 min 20 s is programmed after MeCpPtMe3 injection to allow the precursor to fill the deep trenches. The idle time and other ALD parameters have been optimized to improve the Pt coating into high-aspect ratio structures. Figure 4a shows a cross-section view of the grating after ALD of Al2O3 and Pt. Figure 4b is a face-on view of the Pt film on the surface of a trench wall from 400 cycles of Pt ALD. The film appears to be a tightly packed mosaic. The requirement for the Pt seed layer is that the mosaic grains are in electrical contact, which is easily tested with an ohmmeter. More details on the ALD of Pt and Al2O3, including an example of less densely packed grains, are provided in the Supporting Information.

Figure 4.

Figure 4

Open in a new tab

Scanning electron microscopy images of the platinum and Al2O3 layers on the silicon mold. The Pt layer is the seed layer for electroplating. (a) Cross-sectional view shows conformal and uniform coating of the silicon mold. (b) In a face-on view of a side wall of a trench, the Pt layer appears to be a tightly packed mosaic of 10 to 30 nm patches.

With the Pt seed layer in place, gold is electroplated to fill the trenches of the grating. Plating is done in Auruna 556 electrolyte solution at a temperature of 50 °C and a direct current density of 0.0175 mA/cm2. Figure 5a is an SEM cross-section image of a gold-plated grating with a trench depth-to-width ratio of 32. The trenches are fully filled with gold, which grew from the side surfaces of the walls.20 Another sample was split along a trench to expose a face-on view of the trench wall (Figure 5b). Part of the wall is covered with a solid gold film, while the rest of the film was detached during cleaving, revealing the silicon surface underneath. Part of the Pt seed layer adhered to the gold film and is also visible in the image. The granular structure of the plated gold can be seen in Figure 5a. This resulted in reduced density and refractive index relative to bulk gold, which is quantified in the X-ray diffraction experiments. Lastly, the gratings are backside-thinned to 170 μm to reduce X-ray attenuation in the silicon substrate.

Figure 5.

Figure 5

Open in a new tab

Scanning electron microscopy images of 200 nm period gratings with the trenches filled by electroplated gold. (a) The cross-sectional view and inset reveals the granular structure of the gold filling. (b) A face-on view of the side wall of a trench shows a contiguous layer of gold film covering the silicon surface. In the bottom area of the gold film, the Pt layer is attached and visible.

The performance of the finished gratings is tested in a tabletop X-ray diffraction device. Figure 6a schematically illustrates the experimental setup. The X-ray source is a tungsten-target X-ray tube (SB-80-1k, Source Bay Inc.) operating at various peak voltages ranging from 30 to 80 kV and 1.0 mA tube current. The size of the focal spot of the tube is approximately 100 μm. Two tungsten slits of 20 μm widths are placed along the beam at 0.44 m spacing to collimate the cone beam into a fan beam. The grating is placed at 0.82 m from the first slit. An X-ray camera is placed at 0.59 m from the grating. The camera consists of a GdOs phosphor that converts X-rays to green emission that is captured by a digital camera of 20 μm pixel size. The camera is tilted around x-axis by 82.5° to give an effective pixel size of 2.6 μm in the y-direction.40

Figure 6.

Figure 6

Open in a new tab

X-ray diffraction test of a fabricated grating. (a) The cone beam from an X-ray tube is collimated by two slits of 20 μm widths and 0.44 m spacing, diffracted by the grating and captured on an X-ray camera. The grating is rotated around the vertical axis by an angle θ to increase the effective depth of the gold trenches. (b) The diffraction profiles at various X-ray tube voltages at θ = 45° are normalized to the intensity of the beam without the grating. As the tube voltage decreases, its output spectrum shifts to lower photon energies, resulting in greater phase modulation by the grating and greater fraction of the flux into the +1 and −1 diffraction orders. The diffraction angles also increase with lower photon energies. (c) At θ = 60°, the effective depth of the gold trenches is increased to twice the depth at normal incidence, leading to higher phase modulation by the grating and higher diffraction efficiency. (d) Increasing θ to 65° further increases the phase shifts incurred by the grating. (e) The diffraction profiles are fitted to three Gaussian peaks representing the zeroth undiffracted order and the ±1 diffraction orders. The fitted curve over the measured profile for θ = 65° and 40 kV tube voltage is shown. (f) On the basis of the separation of the +1 and −1 diffraction orders, the mean photon energy of the X-ray spectrum as a function of the tube voltage is calculated for the three rotation angles of the grating. (g) The ratio between the intensities of the ±1 diffraction order and the zeroth order is a measure of the phase modulation amplitude by the grating. A binary π-phase shift grating completely suppresses the zeroth order leading to a ratio of infinity. Practically, residual zeroth order intensity exists due to the broad spectrum of the X-ray beam and grating imperfections. At θ = 65°, the ratio peaks at 40 kV tube voltage, indicating that the phase modulation reaches π at this tube voltage and exceeds π for lower tube voltages.

To observe X-ray diffraction by the grating the transverse coherence length of the beam (ξ ∼ X-ray wavelength/angular divergence of the beam) should exceed the grating period. In our setup, the coherence length at the grating is approximately 1.7 μm for 30 keV X-rays, which is well over the 200 nm grating period. The grating can be rotated around the vertical y-axis to increase the X-ray path length through the gold trenches and the accumulated phase shift.14,41 Figure 6b–d summarizes the measured diffraction profiles at a range of tube voltages and at the y-rotation angles of 45, 60, and 65°, respectively.

For quantitative analysis, the diffraction profiles are fitted to a superposition of three Gaussian peaks representing the ±1 diffraction and the zeroth undiffracted orders. An example of fitted curves versus measured profiles is shown in Figure 6e for the y-rotation angle of 65° and tube voltage of 40 kV. The widths of the diffraction peaks are the result of the broad spectrum of the X-ray tube and the angular divergence of the incident beam. The diffraction angles of the ±1 orders relate to the X-ray wavelength λ and the grating period P as ±λ/P. Thus, it is possible to estimate the mean wavelength of the transmitted beam from the angular separation between the +1 and −1 orders. Figure 6f shows the transmitted mean photon energy versus the tube voltage at three y-rotation angles. The mean photon energy increased not only with the tube voltage but also with the rotation angle of the grating. The cause for the latter is that the vertical rotation increases the light paths through the gold and silicon material, leading to more attenuation of the lower energy photons and a “hardening” of the transmitted spectrum toward higher photon energies.

A measure of the performance of the gratings is the ratio of the diffracted intensity into the ±1 orders over the undiffracted zeroth order (±first/zeroth). In a phase grating designed to modulate the phase distribution of the wavefront without substantial intensity attenuation, how much of the incident flux is diffracted depends on the amplitude of the phase modulation. The refractive index difference between gold and silicon decreases with photon energy, thus higher energy photons experience less phase modulation. The ±first/zeroth ratio approaches infinity for an ideal binary π-phase shift grating. On the basis of the measured diffraction profiles, the ratio is calculated from the aforementioned peak fitting. Figure 6g shows the ratio as a function of the tube voltage at the three rotation angles. At 45° rotation, the ratio monotonically increased with decreasing tube voltage, indicating that the phase modulation was less than π at all voltage levels. The ratio is higher at 60°, showing a nearly vanished zeroth order peak at 30 kV tube voltage (mean photon energy 23.6 keV). At 65° rotation angle, the ±first/zeroth ratio peaks at 40 kV tube voltage (mean photon energy 27.7 keV), indicating that the phase modulation reaches π at this photon energy and exceeds π for lower photon energies. From the phase shift estimates, the effective depth of the gold trenches can be calculated based on the reference values of the refractive indices of gold and silicon for specific photon energies (http://physics.nist.gov/PhysRefData/FFast/html/form.html). The effective gold depth is estimated to be 2.78 ± 0.15 μm from the 65° data, taking as the lower and upper bounds the required depth for a π-phase shift at 35 and 45 kV tube voltages. This effective depth is less than the physical depth of 3.2 μm from the SEM images, due to the granular pattern of the plated gold. The gaps between the grains accounts for 13% of the trench volume. Coherent X-ray scattering from the grain structure can account for the weak and broad baseline peak in the diffraction profile, visible in Figure 6e.

When compared with the previous multilayer coating fabrication,17 this process saves substantial time and cost. The main challenge of the previous process is the multilayer deposition step. It involves e-beam deposition of alternating layers of tungsten and silicon (100 nm single layer thickness) on a staircase silicon substrate to build up multilayer stacks that exactly match the height of the stairs (3.5 μm). Because of the stress mismatch between silicon and tungsten that accumulates in the thick stack, extensive surface preparation both outside and inside the e-beam chamber was needed to improve layer adhesion. This was followed by a 28 h uninterrupted deposition run using an experimental high temperature deposition protocol. This was then followed by a careful annealing protocol in the e-beam chamber to ensure layer adhesion before the temperature was lowered and vacuum broken. The combined challenges of mismatched film stresses, lengthy deposition run, and precise layer thickness control to 0.5% over a thick stack meant that the yield of useful gratings was relatively low, further increasing the time it took to produce a satisfactory grating. In comparison, the current process involves an atomic layer deposition step of 16 h, followed by gold electroplating of about 40 nm in thickness that took 45 min. Both are well-controlled processes without much room for error. The major cost of the ALD process is the precursor MeCpPtMe3 injection that lasts only 400 s. The time and cost to produce a useful grating is thus substantially reduced.

In summary, a reactive ion etching and electroplating process has been developed to fabricate 200 nm period gold-in-silicon gratings. The grating areas are 5 cm long and 1 cm wide. The demonstrated capability of conformal electroplating to fully fill high aspect ratio 100 nm wide trenches provides a new approach for nanometer scale high aspect ratio X-ray grating fabrication. X-ray diffraction experiments show that at the appropriate photon energy and incident angle the gratings modulate the phase of the wavefront by π radians, thus delivering most of the transmitted flux into the first diffraction orders. A slit-collimated beam from an X-ray tube is split into two separated beams by the grating. The ability to split and redirect beams offer possibilities of far-field X-ray interferometry with off-the-shelf tube sources, opening the door to highly sensitive phase detection and imaging methods with compact sources.

The first products of this fabrication process have defects to be corrected and there is ample room for improvement. For example, the effective width of the gold-filled trenches as a percentage of the grating period (the duty cycle) is not precisely controlled. A duty cycle other than 50% leads to incomplete suppression of the zeroth diffraction order. Asymmetry of the cross-sectional shape of the grating leads to asymmetry between the +1 and −1 diffraction orders. The depth of the trenches and the density of the gold filling should be improved to reduce the required rotation of the grating, and thereby reduce the path length and attenuation in the silicon substrate. Lastly, exploring smaller grating periods may lead to further relaxed requirements on the transverse coherence of the incident beam, allowing more flux into an imaging device and shorter exposure times.

Acknowledgments

We sincerely thank Eric Bennett, Gary Melvin, and Dumitru Mazilu of the National Heart, Lung, and Blood Institute of National Institutes of Health for their assistance in mechanical engineering and the staff of the Center for Nanoscale Science and Technology of National Institute of Standards and Technology for assistance on the fabrication. This work was supported by the Intramural Research Program of National Heart, Lung, and Blood Institute, National Institutes of Health, U.S. Certain commercial equipment, instruments, or materials (or suppliers) are identified in this paper to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.

Supporting Information Available

Nanoscale cryogenic silicon etch, atomic layer deposition of Al2O3 and Pt, Figures S1–S7. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

nl5009713_si_001.pdf (1.7MB, pdf)

References

  1. Smith-Bindman R. Use of diagnostic imaging studies and associated radiation exposure for patients enrolled in large integrated health care systems, 1996–2010. JAMA 2012, 307222400–2409. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Roentgen W. C. On a new kind of rays. Nature 1896, 53, 274–276. [Google Scholar]
  3. Michelson A. A.; Morley E. W. LVIII On the relative motion of the earth and the luminiferous Æther. London, Edinburgh Dublin Philos. Mag. J. Sc. 1887, 24151449–463. [Google Scholar]
  4. Born M.; Wolf E.. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Cambridge University Press: New York, 1999. [Google Scholar]
  5. Bonse U.; Hart M. An X-Ray Interferometer. Appl. Phys. Lett. 1965, 68155. [Google Scholar]
  6. Bonse U.; Hart M. Moiré patterns of atomic planes obtained by X-ray interferometry. Z. Phys. 1966, 1904455–467. [Google Scholar]
  7. Momose A.; Fukuda A. Phase-contrast radiographs of nonstained rat cerebellar specimen. Med. Phys. 1995, 224375–379. [DOI] [PubMed] [Google Scholar]
  8. Yoneyama A.; Takeda T.; Tsuchiya Y.; Wu J.; Thet T. L.; Koizumi A.; Hyodo K.; Itai Y. A phase-contrast X-ray imaging system - with a 60 × 30 mm field of view - based on a skew-symmetric two-crystal X-ray interferometer. Nucl. Instrum. Methods Phys. Res., Sect A 2004, 5231–2217–222. [Google Scholar]
  9. David C.; Nohammer B.; Solak H. H.; Ziegler E. Differential x-ray phase contrast imaging using a shearing interferometer. Appl. Phys. Lett. 2002, 81173287–3289. [Google Scholar]
  10. Momose A.; Kawamoto S.; Koyama I.; Hamaishi Y.; Takai K.; Suzuki Y. Demonstration of X-Ray Talbot interferometry. Jpn. J. Appl. Phys., Part 2 2003, 427BL866–L868. [Google Scholar]
  11. Weitkamp T.; Diaz A.; David C.; Pfeiffer F.; Stampanoni M.; Cloetens P.; Ziegler E. X-ray phase imaging with a grating interferometer. Opt. Express 2005, 13166296–6304. [DOI] [PubMed] [Google Scholar]
  12. Pfeiffer F.; Weitkamp T.; Bunk O.; David C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat. Phys. 2006, 24258–261. [Google Scholar]
  13. Tapfer A.; Bech M.; Velroyen A.; Meiser J.; Mohr J.; Walter M.; Schulz J.; Pauwels B.; Bruyndonckx P.; Liu X.; Sasov A.; Pfeiffer F. Experimental results from a preclinical X-ray phase-contrast CT scanner. Proc. Natl. Acad. Sci. U.S.A. 2012, 1093915691–15696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Miao H.; Chen L.; Bennett E. E.; Adamo N. M.; Gomella A. A.; DeLuca A. M.; Patel A.; Morgan N. Y.; Wen H. Motionless phase stepping in X-ray phase contrast imaging with a compact source. Proc. Natl. Acad. Sci. U.S.A. 2013, 1104819268–19272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Momose A.; Yashiro W.; Kido K.; Kiyohara J.; Makifuchi C.; Ito T.; Nagatsuka S.; Honda C.; Noda D.; Hattori T. X-ray phase imaging: from synchrotron to hospital. Philos. Trans. R. Soc., Ser. A 2014, 372201020130023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Modregger P.; Pinzer B. R.; Thnring T.; Rutishauser S.; David C.; Stampanoni M. Sensitivity of X-ray grating interferometry. Opt. Express 2011, 191918324–18338. [DOI] [PubMed] [Google Scholar]
  17. Lynch S. K.; Liu C.; Morgan N. Y.; Xiao X.; Gomella A. A.; Mazilu D.; Bennett E. E.; Assoufid L.; Carlo F. d.; Wen H. Fabrication of 200 nm period centimeter area hard x-ray absorption gratings by multilayer deposition. J. Micromechan. Microeng. 2012, 2210105007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wen H.; Gomella A. A.; Patel A.; Lynch S. K.; Morgan N. Y.; Anderson S. A.; Bennett E. E.; Xiao X.; Liu C.; Wolfe D. E., Subnanoradian X-ray phase-contrast imaging using a far-field interferometer of nanometric phase gratings. Nat. Commun. 2013, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Noda D.; Tanaka M.; Shimada K.; Yashiro W.; Momose A.; Hattori T. Fabrication of large area diffraction grating using LIGA process. Microsyst. Technol. 2008, 149–111311–1315. [Google Scholar]
  20. David C.; Bruder J.; Rohbeck T.; Grunzweig C.; Kottler C.; Diaz A.; Bunk O.; Pfeiffer F. Fabrication of diffraction gratings for hard X-ray phase contrast imaging. Microelectron. Eng. 2007, 845–81172–1177. [Google Scholar]
  21. Rutishauser S.; Bednarzik M.; Zanette I.; Weitkamp T.; Börner M.; Mohr J.; David C. Fabrication of two-dimensional hard X-ray diffraction gratings. Microelectron. Eng. 2013, 101, 12–16. [Google Scholar]
  22. Divan R.; Mancini D. C.; Moldovan N.; Lai B.; Assoufid L.; Leonard Q.; Cerrina F. In Progress in the Fabrication of High-Aspect-Ratio Zone Plates by Soft X-ray Lithography; SPIE: Bellingham, WA, 2002; pp 82–91. [Google Scholar]
  23. Liu L.; Liu G.; Xiong Y.; Chen J.; Li W.; Tian Y. Fabrication of X-ray imaging zone plates by e-beam and X-ray lithography. Microsyst. Technol. 2010, 168–91315–1321. [Google Scholar]
  24. Gorelick S.; Guzenko V. A.; Vila-Comamala J.; David C. Direct e-beam writing of dense and high aspect ratio nanostructures in thick layers of PMMA for electroplating. Nanotechnology 2010, 2129295303. [DOI] [PubMed] [Google Scholar]
  25. Gorelick S.; Vila-Comamala J.; Guzenko V. A.; David C. High aspect ratio nanostructuring by high energy electrons and electroplating. Microelectron. Eng. 2011, 8882259–2262. [Google Scholar]
  26. Gorelick S.; Vila-Comamala J.; Guzenko V. A.; Barrett R.; Salome M.; David C. High-efficiency Fresnel zone plates for hard X-rays by 100 keV e-beam lithography and electroplating. J. Synchrotron Radiat. 2011, 183442–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Chubarova E.; Nilsson D.; Lindblom M.; Reinspach J.; Birch J.; Vogt U.; Hertz H. M.; Holmberg A. Platinum zone plates for hard X-ray applications. Microelectron. Eng. 2011, 88103123–3126. [Google Scholar]
  28. Wojcik M. J.; Mancini D. C.; Divan R.; Ocola L. E. X-ray zone plates with 25 aspect ratio using a 2-μm-thick ultrananocrystalline diamond mold. Microsyst. Technol. 2014, 1–6. [Google Scholar]
  29. Chou S. Y.; Krauss P. R.; Renstrom P. J. Nanoimprint lithography. J. Vac. Sci. Technol. B 1996, 1464129–4133. [Google Scholar]
  30. Yu Z.; Chou S. Y. Triangular profile imprint molds in nanograting fabrication. Nano Lett. 2004, 42341–344. [Google Scholar]
  31. Welch C.; Goodyear A.; Wahlbrink T.; Lemme M. C.; Mollenhauer T. Silicon etch process options for micro-and nanotechnology using inductively coupled plasmas. Microelectron. Eng. 2006, 8341170–1173. [Google Scholar]
  32. Wu Y.; Olynick D.; Goodyear A.; Peroz C.; Dhuey S.; Liang X.; Cabrini S. Cryogenic etching of nano-scale silicon trenches with resist masks. Microelectron. Eng. 2011, 8882785–2789. [Google Scholar]
  33. George S. M. Atomic layer deposition: an overview. Chem. Rev. 2009, 1101111–131. [DOI] [PubMed] [Google Scholar]
  34. Narayan R. J.; Adiga S. P.; Pellin M. J.; Curtiss L. A.; Hryn A. J.; Stafslien S.; Chisholm B.; Shih C.-C.; Shih C.-M.; Lin S.-J. Atomic layer deposition-based functionalization of materials for medical and environmental health applications. Philos. Trans. R. Soc. London, Ser. A 2010, 36819172033–2064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Baker L.; Cavanagh A.; Seghete D.; George S.; Mackus A.; Kessels W.; Liu Z.; Wagner F. Nucleation and growth of Pt atomic layer deposition on Al2O3 substrates using (methylcyclopentadienyl)-trimethyl platinum and O2 plasma. J. Appl. Phys. 2011, 1098084333. [Google Scholar]
  36. Pardon G.; Gatty H. K.; Stemme G.; van der Wijngaart W.; Roxhed N. Pt–Al2O3 dual layer atomic layer deposition coating in high aspect ratio nanopores. Nanotechnology 2013, 241015602. [DOI] [PubMed] [Google Scholar]
  37. Green T. A. Gold electrodeposition for microelectronic, optoelectronic and microsystem applications. Gold Bull. 2007, 402105–114. [Google Scholar]
  38. Hu Z.; Ritzdorf T. Superconformal electrochemical deposition of gold for metallization in microelectronic devices. J. Electrochem. Soc. 2006, 1537C467–C471. [Google Scholar]
  39. Josell D.; Moffat T. P. In Superconformal Deposition of Au in a Sulfite Electrolyte, Meeting Abstracts, The Electrochemical Society, San Francisco, CA, Oct. 27–Nov. 1,2013; pp 2393–2393. [Google Scholar]
  40. Wen H.; Kemble C. K.; Bennett E. E. Theory of oblique and grazing incidence Talbot-Lau interferometers and demonstration in a compact source x-ray reflective interferometer. Opt. Express 2011, 192525093–25112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Hoshino M.; Uesugi K.; Yagi N. Phase-contrast x-ray microtomography of mouse fetus. Biol. Open 2012, 1, 269–274. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl5009713_si_001.pdf (1.7MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES