A model actin cortex is constituted in vitro and used to monitor the relative movements of actin and myosin under conditions that promote or abrogate network contraction. Myosin II molecular motors efficiently drive contraction of a disordered, cortical F-actin network with attenuated relative actomyosin sliding.
Abstract
Myosin II motors embedded within the actin cortex generate contractile forces to modulate cell shape in essential behaviors, including polarization, migration, and division. In sarcomeres, myosin II–mediated sliding of antiparallel F-actin is tightly coupled to myofibril contraction. By contrast, cortical F-actin is highly disordered in polarity, orientation, and length. How the disordered nature of the actin cortex affects actin and myosin movements and resultant contraction is unknown. Here we reconstitute a model cortex in vitro to monitor the relative movements of actin and myosin under conditions that promote or abrogate network contraction. In weakly contractile networks, myosin can translocate large distances across stationary F-actin. By contrast, the extent of relative actomyosin sliding is attenuated during contraction. Thus actomyosin sliding efficiently drives contraction in actomyosin networks despite the high degree of disorder. These results are consistent with the nominal degree of relative actomyosin movement observed in actomyosin assemblies in nonmuscle cells.
INTRODUCTION
The actin cortex in nonmuscle cells is an apolar, disordered network of cross-linked filamentous actin (F-actin) coupled to the plasma membrane (Svitkina and Borisy, 1998). The network is decorated with the molecular motor myosin II and, together, the actomyosin cortex is responsible for generating the contractile stresses that mediate cortical flows and change cell shape during cell polarization, migration, and division (Bray and White, 1988; Vicente-Manzanares et al., 2009; Pollard, 2010). As wide ranging as the cellular processes that use actomyosin contraction are the myriad ways in which cells modulate contraction itself. Cells actively regulate actomyosin contraction spatially and temporally by altering the concentrations and activities of numerous factors (Stendahl et al., 1980; Kane, 1983; Salbreux et al., 2012). Thus understanding the mechanisms that underlie actomyosin force generation within the cortex requires a systematic approach for evaluating the contributions of individual components toward network contraction under controlled biochemical conditions.
The myosin II–generated movement of F-actin underlies contraction of actomyosin assemblies. In highly organized sarcomeres, the relative sliding of antiparallel F-actin on bipolar myosin filaments increases the extent of actomyosin overlap, and thus the extent of relative sliding is directly correlated to the extent of myofibril contraction (Huxley, 1957). For a disordered network such as the actin cortex, the F-actin movements generated by bipolar myosin filaments may not be as efficiently coordinated with its contraction. Previous simulations of this process reveal large relative motion of actomyosin with no net contraction (Kohler et al., 2011). On the other hand, recent reports demonstrated nominal relative actomyosin motions within actomyosin assemblies in nonmuscle cells, including the cytokinetic ring (Ma et al., 2012) and the lamella (Lim et al., 2010). Thus, despite a solid understanding of sarcomeric contraction for decades, contraction in nonsarcomeric assemblies, in particular the degree to which myosin translocation contributes to contraction in disordered networks, remains poorly understood.
In this article, we use a reconstituted, biomimetic cell cortex to observe the movements of myosin II and F-actin in both weakly and strongly contractile two-dimensional networks. First, we demonstrate that actomyosin network contraction varies strongly with myosin filament density, indicating that maximal contraction occurs above a critical myosin density. We then measure how the relative motions between myosin filaments and F-actin quantitatively change at different extents of contraction. In weakly contractile networks, myosin thick filaments can translocate large distances along a stationary F-actin network substrate. Myosin motions are fast and intermittent, and myosin filaments may change direction or orientation along the F-actin. By contrast, in contractile networks, large-distance translocation of myosin with respect to F-actin is not observed. These results demonstrate that the transition from weakly to strongly contractile is punctuated by large differences in the extent of relative actomyosin motion.
RESULTS
Assembly of a reconstituted actomyosin cortex
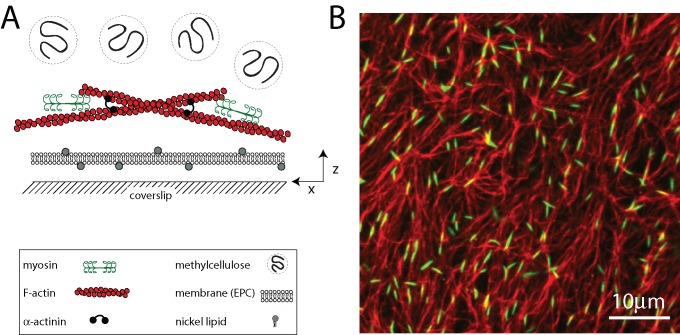
To monitor quantitatively the movements of F-actin and myosin, we use a recently developed in vitro model of the cortex that is amenable to high-resolution imaging of fluorescently tagged proteins (Murrell and Gardel, 2012). The reconstituted cortex comprises a minimal set of components, including F-actin, thick filaments of skeletal muscle myosin II, the F-actin cross-linker α-actinin, and a lipid bilayer (Figure 1A). F-actin is polymerized in the presence of phalloidin and subsequently crowded to the surface of the bilayer using methylcellulose (MC). As F-actin sediments, it entangles into a quasi-two-dimensional network that is <1 μm in thickness and highly concentrated (∼100 μM). After network formation, dimers of skeletal muscle myosin II are added to the sample chamber and polymerize into thick filaments between 0.5 and 2.0 μm (∼100–500 molecules) in length (Figure 1B). The number density of myosin filaments in the cortex is defined as r.
FIGURE 1:
Reconstituted cell cortex in vitro. (A) Schematic of the experimental system. F-actin is crowded down to the surface of a multicomponent phospholipid bilayer via methylcellulose, after which myosin II motors and cross-linkers are added. (B) F-actin network (red) decorated with thick filaments of skeletal muscle myosin II (green; ρ = 0.07 μm−2). Bulk concentration of F-actin is 1.3 μM (Rxlink = 0, Radh = 0).
F-actin network reorganization and contraction depend critically on myosin thick filament density
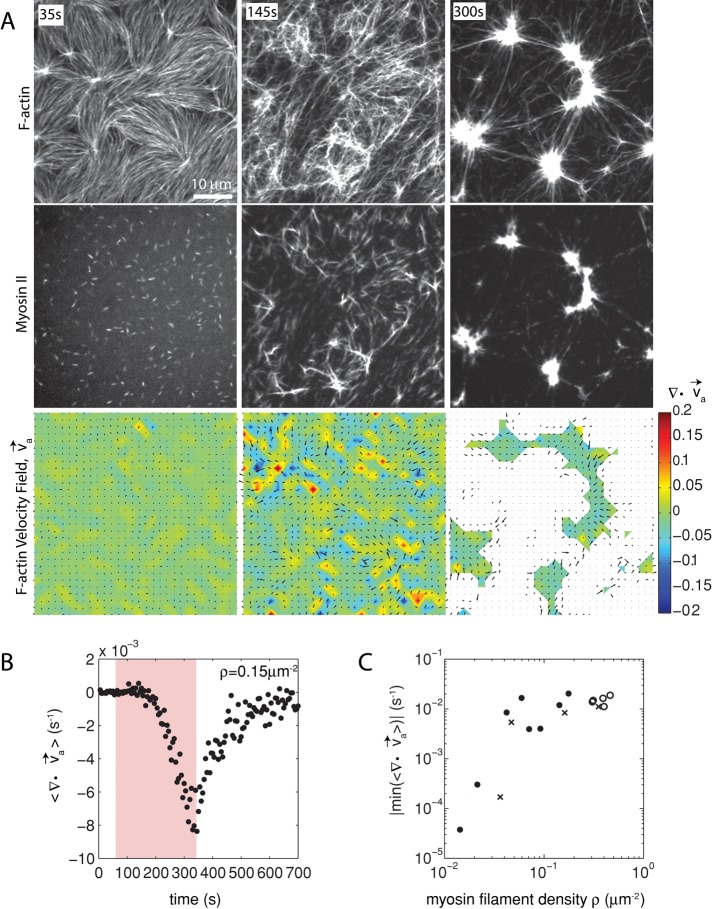
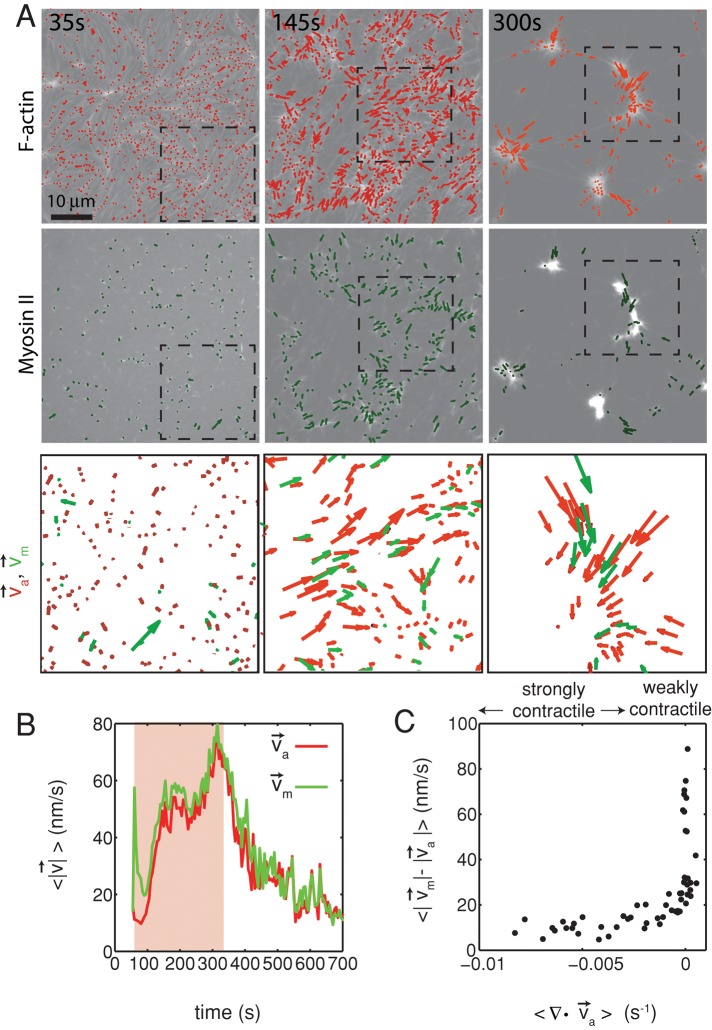
Because the formation of the F-actin network adjacent to the membrane is modulated predominantly by MC-mediated depletion forces, we consider the interaction between the F-actin and the membrane to be weak. Owing to this weak interaction, the activity of myosin thick filaments induces large density fluctuations of the F-actin network. Myosin drives the formation of domains, each of which decreases in area (contracts) and increases F-actin density over time (Figure 2A, top, and Supplemental Movie S1). The motion of the myosin thick filaments follows that of the F-actin, irreversibly coalescing into dense foci (Figure 2A, middle, and Supplemental Figure S1).
FIGURE 2:
Two-dimensional F-actin network contraction varies with myosin density. (A) Images of actin (top), myosin II (middle), and F-actin velocity field (bottom) for a contractile 2D network (ρ = 0.15 μm−2). Myosin II addition occurs at 0 s. Filled contours are drawn over the vector fields and represent the divergence of the vector field, 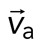 (red-blue). Hot colors indicate positive divergence (expansion) and cold colors indicate negative divergence (contraction). (B) Mean divergence of the actin velocity field,
(red-blue). Hot colors indicate positive divergence (expansion) and cold colors indicate negative divergence (contraction). (B) Mean divergence of the actin velocity field, 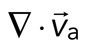 , as a function of time. Shaded region indicates time over which contraction of the network occurs, before foci coalescence. (C) Magnitude of the minimal divergence of the F-actin velocity field,
, as a function of time. Shaded region indicates time over which contraction of the network occurs, before foci coalescence. (C) Magnitude of the minimal divergence of the F-actin velocity field, 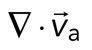 , as a function of the density of myosin thick filaments. Open symbols refer to blebbistatin inhibition experiments (Rxlink = 0, Radh = 0), ×’s represent cross-linked F-actin (Rxlink = 0.003, Radh = 0), and solid circles have no cross-linker (Rxlink = 0, Radh = 0).
, as a function of the density of myosin thick filaments. Open symbols refer to blebbistatin inhibition experiments (Rxlink = 0, Radh = 0), ×’s represent cross-linked F-actin (Rxlink = 0.003, Radh = 0), and solid circles have no cross-linker (Rxlink = 0, Radh = 0).
The movement of the F-actin network during contraction is quantified by particle image velocimetry (PIV). By PIV, an F-actin vector field is generated that measures the frame-to-frame velocity 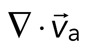 , where the magnitude of each vector is the instantaneous F-actin speed, and the angle indicates the direction of movement. The net contractile or extensile behavior of the network is determined by the magnitude and sign of the divergence
, where the magnitude of each vector is the instantaneous F-actin speed, and the angle indicates the direction of movement. The net contractile or extensile behavior of the network is determined by the magnitude and sign of the divergence 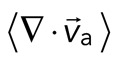 of the F-actin velocity field. Regions of the grid that are contractile have vectors pointing inward to a point (
of the F-actin velocity field. Regions of the grid that are contractile have vectors pointing inward to a point (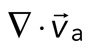 < 0), whereas regions that are extensile have arrows emanating from a point (
< 0), whereas regions that are extensile have arrows emanating from a point (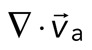 > 0). Thus, henceforth, our measure of network contraction is quantified by the magnitude of the mean divergence of the F-actin velocity field,
> 0). Thus, henceforth, our measure of network contraction is quantified by the magnitude of the mean divergence of the F-actin velocity field, 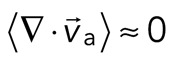 .
.
With the polymerization of myosin thick filaments, the F-actins within the network are deformed from their initial configuration (Figure 2A, bottom). Initially, these deformations are local (<1 μm) and may be either expansive (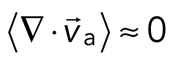 > 0) or contractile (
> 0) or contractile (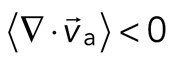 < 0), although no net behavior dominates (Figure 2A, bottom). Each behavior is transient and, at the network level, averages to a net zero divergence,
< 0), although no net behavior dominates (Figure 2A, bottom). Each behavior is transient and, at the network level, averages to a net zero divergence, 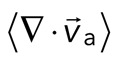 , for times between 0 and 145 s (Figure 2B). After contraction starts (t ≈ 145 s), the net movement is inward, with a negative divergence field (Figure 2B and Supplemental Movie S2). The mean divergence reaches a minimum until the F-actin is depleted from the space surrounding the foci, leaving negative divergence values for only the remaining areas that contain F-actin. As the network condenses further, the velocity of the F-actin network decreases, and the divergence returns to zero. At this stage, the remaining foci continue to coalesce through the contraction of connecting bundles (Silva et al., 2011). Because this last stage does not reflect the contractile strain of a disordered, two-dimensional network, we do not quantify these dynamics and confine our analysis to earlier times. Thus there are three phenotypic stages of structural reorganization of a disordered network. First, there are the local deformations of the network that result in no net contraction (
, for times between 0 and 145 s (Figure 2B). After contraction starts (t ≈ 145 s), the net movement is inward, with a negative divergence field (Figure 2B and Supplemental Movie S2). The mean divergence reaches a minimum until the F-actin is depleted from the space surrounding the foci, leaving negative divergence values for only the remaining areas that contain F-actin. As the network condenses further, the velocity of the F-actin network decreases, and the divergence returns to zero. At this stage, the remaining foci continue to coalesce through the contraction of connecting bundles (Silva et al., 2011). Because this last stage does not reflect the contractile strain of a disordered, two-dimensional network, we do not quantify these dynamics and confine our analysis to earlier times. Thus there are three phenotypic stages of structural reorganization of a disordered network. First, there are the local deformations of the network that result in no net contraction (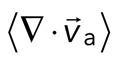 ). Second, these deformations become more widespread and result in net inward flow of the F-actin and net contraction of the network (
). Second, these deformations become more widespread and result in net inward flow of the F-actin and net contraction of the network (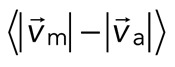 ). Finally, after the bulk of the material has contracted, the divergence returns to nearly zero. The peak network contraction can be parametrized by the minimum of the mean divergence of the actin velocity field, min
). Finally, after the bulk of the material has contracted, the divergence returns to nearly zero. The peak network contraction can be parametrized by the minimum of the mean divergence of the actin velocity field, min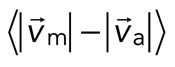 .
.
Next we sought to evaluate how the contraction was affected by the myosin thick filament density. We calculated how min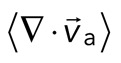 varies as a function of thick filament density, ρ. Changing the concentration of myosin dimer varies ρ from 0.01 to 0.5 μm−2. Strikingly, the relationship between ρ and contraction is highly nonlinear, as a change in myosin filament density over one order of magnitude increases the contraction by two orders of magnitude, which then leads to a plateau (Figure 2C and Supplemental Figure S2). This suggests a critical density, ρc ∼ 0.04 μm−2, to reach the maximum contraction of a network with skeletal muscle myosin II for the given experimental conditions.
varies as a function of thick filament density, ρ. Changing the concentration of myosin dimer varies ρ from 0.01 to 0.5 μm−2. Strikingly, the relationship between ρ and contraction is highly nonlinear, as a change in myosin filament density over one order of magnitude increases the contraction by two orders of magnitude, which then leads to a plateau (Figure 2C and Supplemental Figure S2). This suggests a critical density, ρc ∼ 0.04 μm−2, to reach the maximum contraction of a network with skeletal muscle myosin II for the given experimental conditions.
Myosin filaments execute diverse motions through disordered networks
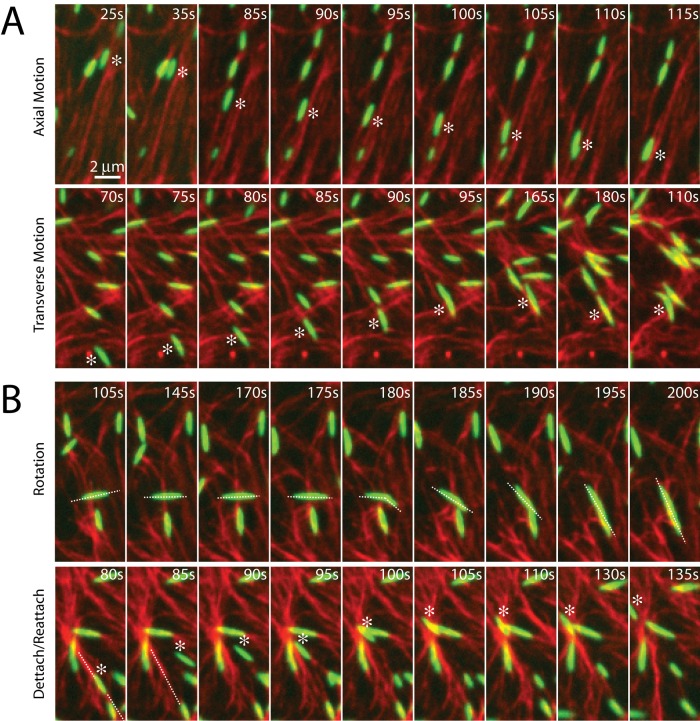
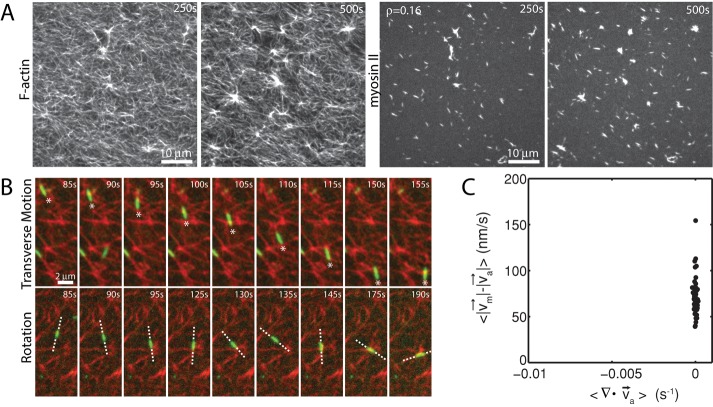
Before contraction, thick filaments execute diverse movements through the F-actin network. Filament motions can be sustained over long ranges (>5 μm), as can be seen in their translocation either along or across individual F-actin (Figure 3A). In this case, myosin filaments move in the direction of their long axis at speeds of ∼100 nm/s. This speed is 10-fold slower than observed for the translocation of individual F-actin against surface-immobilized myosin (Yamada et al., 1997), potentially due to the binding of multiple F-actin of mixed polarity and the added drag of moving through an entangled F-actin network. Nevertheless, this motion may be unidirectional over many micrometers, likely reflecting the length and polarity of the local F-actin. Conversely, motions may be short ranged and nonpersistent, as occurs when the filaments change orientation, direction, or F-actin substrate (Figure 3B). The speed of myosin filament motion in this case is nominal, as they accrue nearly no net displacement. This type of motion is likely associated with regions of high F-actin density or mixed polarity. Thus there is a large variation in the dynamics of myosin motion within a population. We next sought to explore whether these dynamics were significantly different in strongly versus weakly contractile networks.
FIGURE 3:
Myosin motion within the F-actin network is highly diverse and dynamic. Myosin thick filaments (green) at a density of ρ = 0.07 μm−2 move within an F-actin network (red; Radh = 0, Rxlink = 0). (A) Persistent myosin filament motions, such as translocation along F-actin (top) or across F-actin (bottom). (B) Nonpersistent myosin filament motions, such as filament rotation (top) or switching F-actin substrates (bottom). White asterisks refer to myosin filament of interest. White line refers to the orientation of the thick filament. Myosin polymerized at 0 s.
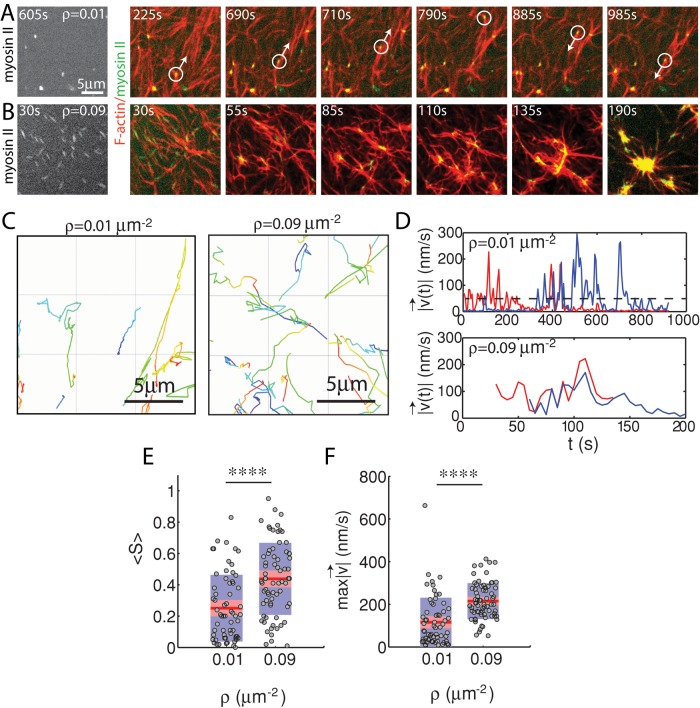
The effect of myosin filament motions on the F-actin network depends strongly on myosin density. At low myosin density (ρ = 0.01 μm−2), on average, neither the organization nor the dynamics of the F-actin network are significantly altered by myosin activity over long times (∼1400 s; Figure 4A). At high density (ρ = 0.09 μm−2) the F-actin network contracts and densifies quickly (∼200 s; Figure 4B). In both cases, however, myosin filaments are highly mobile (Figure 4, C and D). We use particle tracking to identify the centroids of myosin thick filaments, follow them over time, and calculate ensemble-averaged statistics of their trajectories. We then measure the maximum speed and straightness (Eq. 1) of the thick filament trajectories. We find that at high densities (ρ = 0.09 μm−2), myosin thick filaments execute more persistent, directed motions at high speeds than at low density (ρ = 0.01 μm−2) when measured over equivalent time intervals (τ = 450 s; Figure 4, E and F).
FIGURE 4:
Myosin motion in strongly and weakly contractile networks. Overlay of F-actin (red) and myosin (green) at myosin density (A) ρ = 0.01 and (B) 0.09 μm−2 (Rxlink = 0, Radh = 0). White circle highlights an individual myosin thick filament within the F-actin network. White arrow indicates the direction of movement. Myosin polymerized at 0 s. (C) Trajectories of myosin thick filaments within F-actin network (left) at ρ = 0.01 and (right) at 0.09 μm−2. Color indicates time, from purple to yellow. (D) Instantaneous speeds for two selected myosin thick filaments embedded within the samples in A and B. The dotted line represents our minimum threshold for identifying moving myosins of 50 nm/s. (E) Mean straightness, S, and (F) maximum velocity over the course of a myosin trajectory for equivalent time frames (p < 0.0001). For ρ = 0.09 μm−2, the times were between 0 and 450 s to encompass the times over which contraction into dense foci occurred. For ρ = 0.01 μm−2, time was taken from 535 to 985 s to confirm that steady state had been achieved.
However, the extent to which these differences in myosin dynamics reflect differences in overall network motions or altered relative motion between actomyosin is not clear.
Relative sliding of actin and myosin is attenuated in contractile networks
To quantify relative actomyosin sliding as a function of F-actin network contraction, we track the instantaneous velocities of individual myosin thick filaments and F-actin (Figure 5, A and B) and calculate the mean difference in their speeds, 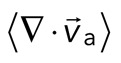 . We then plot
. We then plot 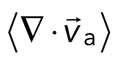 as a function of mean divergence of the F-actin network,
as a function of mean divergence of the F-actin network, 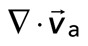 , at each point in time (Figure 5C) from the assembly of myosin filaments to the minimum in F-actin network divergence (Figures 2B and 5B, shaded region). We consider only data for which the myosin speed is >50 nm/s to ensure that only mobile myosins are considered (Figure 4D, top).
, at each point in time (Figure 5C) from the assembly of myosin filaments to the minimum in F-actin network divergence (Figures 2B and 5B, shaded region). We consider only data for which the myosin speed is >50 nm/s to ensure that only mobile myosins are considered (Figure 4D, top).
FIGURE 5:
Relative actomyosin motion decreases during contraction. (A) Contraction of a cross-linked F-actin network (Rxlink = 0.003, Radh = 0) and corresponding F-actin velocity vectors (top), myosin II thick filament density of ρ = 0.15 μm−2 and corresponding myosin velocity vectors (middle), and an overlay of F-actin and myosin velocity vectors (bottom). The dotted squares in the top and middle are zoomed in on the bottom. This is the same experiment as that in Figure 2. (B) Average velocity for F-actin (red) and myosin (green) puncta during contraction. Shaded region indicates time over which contraction of the network occurs, before foci coalescence. (C) The average relative speeds between individual myosin and F-actin (interpolated onto the myosin position) as a function of the F-actin network contraction. Each dot pertains to the average of the relative motions between actin and myosin velocity vectors (for 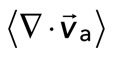 > 50 nm/s), and the mean divergence of the F-actin velocity vector field at each point in time, as indicated in B and Figure 2B. The data are taken between 60 and 330 s (shaded region in B).
> 50 nm/s), and the mean divergence of the F-actin velocity vector field at each point in time, as indicated in B and Figure 2B. The data are taken between 60 and 330 s (shaded region in B).
We find that the relative motion between actin and myosin depends strongly on the degree of F-actin network contraction (Figure 5C). When the network contraction is low (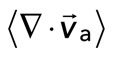 > −0.001), the relative motions between F-actin and myosin on average are large, up to 100 nm/s. However, during periods of large contraction (
> −0.001), the relative motions between F-actin and myosin on average are large, up to 100 nm/s. However, during periods of large contraction (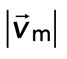 < −0.001), the difference in speeds is reduced and approaches zero. Thus, as the F-actin network becomes increasingly contractile, the relative motion between actin and myosin decreases (Supplemental Movie S3).
< −0.001), the difference in speeds is reduced and approaches zero. Thus, as the F-actin network becomes increasingly contractile, the relative motion between actin and myosin decreases (Supplemental Movie S3).
Inhibiting network contraction induces myosin thick filament mobility
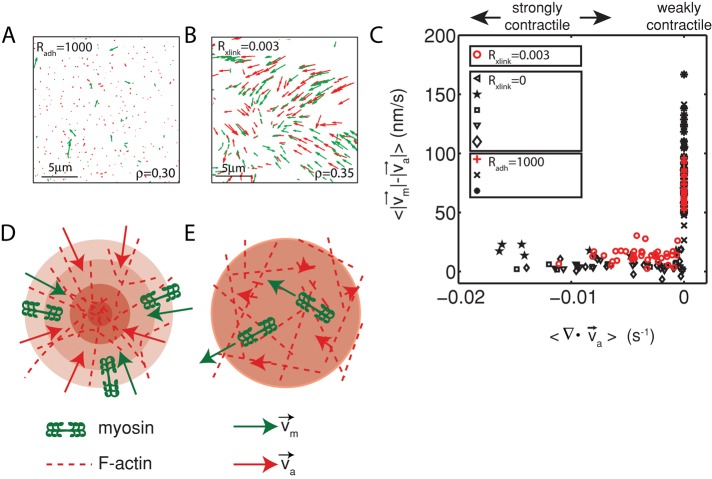
To probe whether changes in relative motion actomyosin at different extents of contraction is observed over a large range of network conditions, we constructed networks that contained similar densities of myosin but whose contraction was altered by changing network parameters. First, we coupled the F-actin to the membrane using His-FimA2, a mutant form of the F-actin cross-linker fimbrin (Skau et al., 2011). FimA2 comprises a single F-actin–binding domain and a histidine tag that binds to nickel lipids present in the bilayer. Because the F-actin is strongly coupled to the membrane, its displacement by myosin activity is resisted by enhanced viscous drag of the membrane. We estimate that the viscosity of the bare membrane is 10−9 N ⋅ s/m, and similarly the viscous drag added to F-actin of average length of 15 μm is 5.2 pN. We previously showed that FimA2 impairs network contraction (Figure 6A; Murrell and Gardel, 2012). By contrast, the motion of the myosin filaments is not impaired and remains highly dynamic (Figure 6B). Myosin filaments execute sustained and long-range motions (> 5 μm; Figure 6B, top), as well as transient, short-range (<1 μm) motions (Figure 6B, bottom). Because F-actin contraction is impaired, myosin filaments executed these movements on a stationary F-actin substrate such that relative motions between actin and myosin were large (Figures 6C and 7, A and C, and Supplemental Movie S4).
FIGURE 6:
Coupling of F-actin to membrane inhibits contraction but not myosin motion. (A) F-actin (left) and myosin (right) within a network bound to the membrane (Rxlink = 0.003, Radh = 10). (B) Myosin thick filaments (green) move within an F-actin network (red). (B) Persistent myosin filament motions, such as translocation along or across F-actin (top) and nonpersistent myosin filament motions, such as filament rotation (top) or switching F-actin substrates (bottom). White asterisks refer to myosin filament of interest. White line refers to the orientation of the thick filament. (C) F-actin network contraction vs. relative motion. Each point corresponds to the mean difference in actin and myosin speed as a function of the mean F-actin network velocity field divergence for a single time point. Only relative motions that correspond to 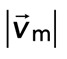 > 50 nm/s are included.
> 50 nm/s are included.
FIGURE 7:
Diminished relative motion is observed over a range of parameters. (A, B) Overlay of F-actin and myosin velocities for strongly contractile F-actin networks (Rxlink = 0.003, Radh = 0) and weakly contractile F-actin networks (Rxlink = 0, Radh = 1000). (C) F-actin network contraction vs. relative motion for strongly contractile networks (Rxlink = 0 and 0.003, Radh = 0) and weakly contractile networks (Rxlink = 0, Radh = 1000). Each point corresponds to the mean difference in actin and myosin speed, as well as mean F-actin velocity field divergence for a single time point. Only relative motions that correspond to 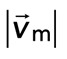 > 50 nm/s are included. In addition, the divergence of strongly contractile networks is only plotted for
> 50 nm/s are included. In addition, the divergence of strongly contractile networks is only plotted for 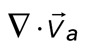 < −0.001. The data for the contractile samples are taken from the formation of myosin thick filaments to the peak contraction (≤280 s). The FimA2 samples are taken for the first 280 s. All myosin densities are >0.3 μm−2. (D, E) Schematics of actomyosin motion in (D) strongly contractile and (E) weakly contractile networks.
< −0.001. The data for the contractile samples are taken from the formation of myosin thick filaments to the peak contraction (≤280 s). The FimA2 samples are taken for the first 280 s. All myosin densities are >0.3 μm−2. (D, E) Schematics of actomyosin motion in (D) strongly contractile and (E) weakly contractile networks.
We and others showed that introduction of an actin cross-linking protein, α-actinin, can potentiate contraction (Janson et al., 1991; Murrell and Gardel, 2012). In the networks formed with α-actinin, myosin and actin flowed concomitantly, with similar speeds and directions (Figure 7B). Similarly, the relative actomyosin was attenuated in comparison to the weakly contractile networks formed with FimA2 (Figure 7, C–E). Thus the different actomyosin movements observed are not solely a consequence of specific network conditions but appear to depend strongly on the extent to which the network is contracting.
DISCUSSION
In this study, we explore the relationship between actomyosin interactions and contraction in disordered F-actin networks, as found in the cell cortex. Consistent with previous reports, we find that the rate and extent of contraction increase with myosin motor content (Janson et al., 1991; Bendix et al., 2008). We find a nonlinear dependence on myosin density, with maximal contraction emerging above a critical density of ρc ≈ 0.04 μm−2. It will be interesting to explore how ρc depends on network parameters. For instance, we would expect an increase in F-actin concentration to increase network viscosity and therefore require an increase in myosin motor concentration in order to contract, in accordance with previous work (Silva et al., 2011).
We suggest that the dependence of F-actin network contraction on a critical myosin density may be due to either of two related factors. First, the critical myosin density may correspond to a minimal threshold in myosin-generated mechanical stress. A myosin density of ρc ≈ 0.04 μm−2 would yield a stress of ∼1.8 Pa (see Materials and Methods). The lack of contraction at low myosin density (ρ < ρc) or at elevated F-actin viscosity would support a critical stress needed to contract. However, the critical density of myosin may also be important for the length scale that it confers. A density of ρc ≈ 0.04 μm−2 corresponds to one myosin thick filament per 25 μm2. Binding or motor activity across this area may create a percolation length scale or fluctuations in F-actin polarity that may facilitate contraction.
In weakly contractile networks formed either at low myosin density or high levels of membrane attachment, the F-actin retains a nearly constant spatial density over long times. Yet the myosin filaments within the networks are highly dynamic and exhibit a wide range of distinct motions. Individual thick filaments can quickly and persistently translocate over long distances, either along or across individual F-actin. Thick filament motions may also include cycles of detachment and reattachment, as well as frequent rotation of the filament with respect to the F-actin substrate. Owing to constant change in direction or orientation, these motions are short ranged and not processive. In these networks, myosin moves relative to F-actin at speeds up to 200 nm/s.
In strongly contractile networks, myosin activity induces density fluctuations of the F-actin network, which evolve over time into a net contraction, or an inward flow of actomyosin. During contraction, the motions of F-actin and myosin filaments are strongly correlated and exhibit minimal relative motion between them (<20 nm/s on average). Thus relative actomyosin motion is attenuated in strongly contractile networks.
The decrease in relative motion between actin and myosin for contractile network may be related to the accumulation of active stresses within the network that alter its mechanical properties, thereby modifying the behavior of the myosin itself. Higher myosin content may stiffen the F-actin network (Koenderink et al., 2009), inducing mechanical feedback, placing the myosin motors under an additional load that will increase their processivity and decrease their speed (Veigel et al., 2003). Thus, although generating sufficient stresses to contract the network, there is less motion of the myosin thick filaments with respect to F-actin. This mechanism would suggest that F-actin network contraction is enhanced as myosin behaves more as a cross-linker, being maximized as myosin approaches its stall load. Alternatively, the accumulation of active stresses may facilitate the reorganization and densification of F-actin, which, in turn, alters thick filament processivity. During contraction, the density of F-actin in the vicinity of the myosin increases as the network contracts into foci. The increase in the F-actin density may drive a decrease in processivity of myosin, as the potential of binding of many F-actin would reduce the probability of sliding with respect to a single F-actin, thereby reducing the net relative motion. By minimizing the displacement of the F-actin (via membrane coupling), the network cannot densify (Carvalho et al., 2013), and the average number of F-actin binding partners remains sufficiently low for myosin to slide with respect to individual F-actin.
Disordered F-actin networks may be poised to resist filament sliding during contraction. Disordered networks are apolar, and thus myosin binds both parallel and antiparallel filament pairs, although they preferentially slide the latter (Yamada et al., 1990). Misaligned binding and preferential motor activity may result in the variation in nonprocessive motions we observe, serving as effective F-actin cross-linking. Thus the sliding of F-actin may be frustrated by the misaligned cross-linking that occurs in an apolar network, allowing only minimal sliding to occur. Furthermore, F-actin is known to buckle under very low myosin-induced compressive loads resulting in large network strains (Murrell and Gardel, 2012), making persistent sliding unnecessary. Thus contraction and the generation of mechanical forces are determined by the organizational structure of the network and the balance of stresses that result from this organization. In the future, we seek to explore the effects of dissipation on stress accumulation and contraction by complementing the disorder in network organization to the dynamics of F-actin assembly and disassembly.
MATERIALS AND METHODS
Buffer preparation
G-buffer was 2 mM Tris-HCl, pH 8.0, and 0.1 mM CaCl2, 0.2 mM ATP, 1 mM NaN3, and 0.5 mM dithiothreitol. F-buffer was 10 mM imidazole, 1 mM MgCl2, 50 mM KCl, 0.2 mM ethylene glycol tetraacetic acid, and 0.5 mM ATP, pH 7.5. The vesicle buffer was 100 mM NaCl and 20 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid, pH 7.3. The storage buffer for the myosin was 0.5 mM 1,4-piperazinediethanesulfonic acid, pH 7.0, and 0.45 M KCl. All chemicals were purchased from Sigma-Aldrich (St. Louis, MO).
Bilayer preparation
Egg phosphatidyl choline (EPC; Avanti Polar Lipids), the nickel lipid 1,2-di-(9Z-octadecenoyl)-sn-glycero-3-([N-(5-amino-1-carboxypentyl)iminodiacetic acid)succinyl] (NTA; Avanti Polar Lipids, Alabaster, AL), and Oregon green 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (DHPE; Molecular Probes, Eugene, OR) were combined in chloroform and dried in a glass container under N2 gas. Bilayers were prepared in either a 99.6% EPC/0.4% EPC ratio or a 91% EPC/8.6% NTA/0.4% DHPE proportion for FimA2 attachment. They were then resuspended in vesicle buffer and vortexed for 10 s. The solution was then sonicated for upward of 5 min to generate small, unilamellar vesicles (SUVs). The SUVs were then added to Piranha-treated coverslips to coat them with a phospholipid bilayer in a custom-built imaging chamber (Quorum Technologies, Guelph, Canada). The phospholipid bilayer was maintained hydrated in ∼500 μl of ATP-free F-buffer.
Reconstituted cortex assembly
Dark F-actin, 2.0 μM (prepared from chicken breast; gift of Yujie Li and Dave Kovar, University of Chicago), and 0.64 μM Alexa 568–actin (Molecular Probes) were polymerized in the presence of 6 μM dark phalloidin (Molecular Probes) in F-buffer for 1–2 h on ice. The F-actin was then crowded to the phospholipid bilayer surface with 0.25% methylcellulose (molecular weight 14,000; Sigma-Aldrich, St. Louis, MO) for 15 min at 25°C in an equal volume of ATP-free F-buffer, yielding a final bulk F-actin concentration of 1.3 μM. The two-dimensional (2D) concentration of F-actin at the surface of the bilayer is ∼100 μM. To attach the F-actin to the membrane, before F-actin sedimentation, various concentrations of a histidine-tagged mutant of fimbrin, FimA2 (gift of Dave Kovar) were added in solution (Radh = [FimA2]/[G-actin]). FimA2 binds nickel lipids in the bilayer membrane and the sedimented F-actin. After F-actin sedimentation, various concentrations of α-actinin (Sigma-Aldrich) were added in solution (Rxlink = [α-actinin]/[G-actin]). Finally, Alexa 642–labeled skeletal muscle (Cytoskeleton, Denver, CO) myosin dimers were added at variable bulk concentrations (4–40 nM) to the sample to polymerize. The polymerization yields a density of myosin thick filaments embedded within the 2D F-actin network that is variable across different 60× fields of view (even at identical concentrations). We therefore measure the thick filament density before onset of contraction within the field of view in each experiment (ρ = 0.01–0.5 μm−2). Above a myosin thick filament density of 0.2 μm−2, the F-actin network may begin to contract before complete myosin polymerization. Thus, for these densities, 20 μM blebbistatin was added before myosin addition to prevent contraction during myosin polymerization. Contraction was then induced by imaging with 488-nm light before 568 (F-actin) or 642 nm (myosin) at every time step. Further details can be found in Murrell et al. (2014).
Imaging
The 25-mm coverslips were sandwiched in a custom-built chamber (Quorum Technologies). Sample fluorescence was monitored using a Ti-E microscope (Nikon Instruments, Melville, NY) with a spinning disk confocal head (Yokagawa), a HQ2 CoolSNAP charge-coupled device camera (Photometrics, Tucson, AZ), and a 60×/1.4 numerical aperture oil immersion objective lens (Nikon). The microscope and confocal head were controlled using MetaMorph software (Molecular Devices, Sunnyvale, CA).
Analysis of actin and myosin velocity
The velocity of the F-actin and myosin was calculated using two types of PIV: 1) a grid-based method (mPIV; www.oceanwave.jp/softwares/mpiv/) and 2) a non–grid-based method termed quantitative fluorescent speckle microscopy (qFSM; Danuser and Waterman-Storer, 2006). mPIV uses a regular mesh whose coordinates are static in time and assesses the velocity of F-actin that enters each individual unit of the mesh. This code is available at www.oceanwave.jp/softwares/mpiv/. The divergence was calculated using mPIV and custom-written Matlab routines (MathWorks, Natick, MA). A 3.4-μm grid spacing was chosen because it minimizes the deviation in divergence (Supplemental Figure S3). The mean divergence was taken over the entire field of view (130 by 100 μm) for each successive 5-s interval (the frame rate) over the entire time course of contraction. For the interval at which the smallest divergence is found, a mean of the divergence was taken over time from 10 s before 10 s after this minimum value. This mean is what we call the “contraction” of the network. qFSM tracks the movement of individual diffraction-limited spots of high intensity. The F-actin velocities were interpolated onto the myosin velocity field (Gardel et al., 2008). The difference in the speeds was used to assess the degree of relative motion. We measured only relative motions that correspond to myosin speeds >50 nm/s to ensure that only moving myosins were included in the measurements and that motion was not thermally driven (Supplemental Figure S4). qFSM and mPIV yield different values of velocity due to differences in their measurement methods (Supplemental Figure S4).
Particle tracking was performed using Imaris (Bitplane, South Windsor, CT) to identify the spatial coordinates of the peaks of fluorescence intensity of the myosin thick filaments. These coordinates were recorded for all times and used to calculate the mean speed and straightness of the trajectories. The density of myosin filaments was calculated by counting the total tracked myosin thick filaments and dividing that number by the total area of the sample that they occupy.
Analysis of myosin trajectories
The straightness, S, of an individual myosin thick filament is calculated as
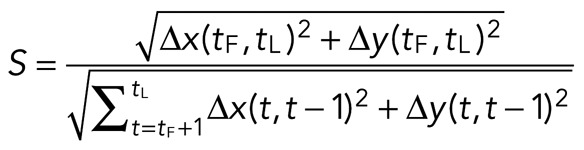 |
The straightness is the total displacement divided by the track length. The total displacement is the distance traveled between the first time point tF and the last time point tL. The track length is the sum of the displacement between each two time points taken over time, t. If the path is straight, the two distances are equal, and S = 1. The more the path deviates from straight, the closer S is to zero.
Stress analysis
The minimal stress required to yield maximum contraction in the network is estimated from the myosin thick filament density, as well as the thick filament size at that density. The lowest density of skeletal muscle myosin that contracts the network is 0.042 μm−2, pertaining to a single thick filament in a 24.4 μm2 area. The mean size of the thick filaments at this density is 1158 ± 235 nm. There is ∼1 myosin molecule/3.6 nm in a skeletal muscle myosin filament (Skubiszak and Kowalczyk, 2002). This yields ∼320 ± 65 heads in our filaments. Given that each dimer has an unloaded duty ratio of 4% (Harris and Warshaw, 1993), as a lower bound, there are 12.8 ± 2.6 dimers attached at any given time. Because each dimer can produce up to 3.4 pN force under isometric conditions (Finer et al., 1994), this yields a total force of 43.6 ± 8.8 pN. This corresponds to a stress of 1.8 ± 0.4 Pa required to reach maximum contraction in a network with skeletal muscle myosin.
Supplementary Material
Acknowledgments
We thank Gaudenz Danuser (Harvard University) for use of qFSM software and David Kovar (University of Chicago) for reagents. We acknowledge funding from National Science Foundation Grant DMR-0844115 for postdoctoral fellowship support to M.M., as well as from the Institute for Complex Adaptive Matter Branches Cost Sharing Fund. M.L.G. acknowledges support from the Burroughs Wellcome Fund Career Awards at the Scientific Interface, the American Asthma Foundation, the Packard Foundation, and the University of Chicago Materials Research Science and Engineering Center. We also thank Martin Lenz and Patrick MacCall for critical reading of the manuscript.
Abbreviations used:
- F-actin
filamentous actin
- F-buffer
buffer for filamentous actin
- G-actin
globular actin
- G-buffer
buffer for globular actin
- MC
methylcellulose
- PIV
particle image velocimetry
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E13-08-0450) on April 23, 2014.
REFERENCES
- Bendix PM, Koenderink GH, Cuvelier D, Dogic Z, Koeleman BN, Brieher WM, Field CM, Mahadevan L, Weitz DA. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys J. 2008;94:3126–3136. doi: 10.1529/biophysj.107.117960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray D, White JG. Cortical flow in animal cells. Science. 1988;239:883–888. doi: 10.1126/science.3277283. [DOI] [PubMed] [Google Scholar]
- Carvalho K, Tsai FC, Lees E, Voituriez R, Koenderink GH, Sykes C. Cell-sized liposomes reveal how actomyosin cortical tension drives shape change. Proc Natl Acad Sci USA. 2013;110:16456–16461. doi: 10.1073/pnas.1221524110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danuser G, Waterman-Storer CM. Quantitative fluorescent speckle microscopy of cytoskeleton dynamics. Annu Rev Biophys Biomol Struct. 2006;35:361–387. doi: 10.1146/annurev.biophys.35.040405.102114. [DOI] [PubMed] [Google Scholar]
- Finer JT, Simmons RM, Spudich JA. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. 1994;368:113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- Gardel ML, Sabass B, Ji L, Danuser G, Schwarz US, Waterman CM. Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. J Cell Biol. 2008;183:999–1005. doi: 10.1083/jcb.200810060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris DE, Warshaw DM. Smooth and skeletal muscle myosin both exhibit low duty cycles at zero load in vitro. J Biol Chem. 1993;268:14764–14768. [PubMed] [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- Janson LW, Kolega J, Taylor DL. Modulation of contraction by gelation/solation in a reconstituted motile model. J Cell Biol. 1991;114:1005–1015. doi: 10.1083/jcb.114.5.1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kane RE. Interconversion of structural and contractile actin gels by insertion of myosin during assembly. J Cell Biol. 1983;97:1745–1752. doi: 10.1083/jcb.97.6.1745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenderink GH, Dogic Z, Nakamura F, Bendix PM, MacKintosh FC, Hartwig JH, Stossel TP, Weitz DA. An active biopolymer network controlled by molecular motors. Proc Natl Acad Sci USA. 2009;106:15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohler S, Schaller V, Bausch AR. Structure formation in active networks. Nat Mater. 2011;10:462–468. doi: 10.1038/nmat3009. [DOI] [PubMed] [Google Scholar]
- Lim JI, Sabouri-Ghomi M, Machacek M, Waterman CM, Danuser G. Protrusion and actin assembly are coupled to the organization of lamellar contractile structures. Exp Cell Res. 2010;316:2027–2041. doi: 10.1016/j.yexcr.2010.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X, Kovacs M, Conti MA, Wang A, Zhang Y, Sellers JR, Adelstein RS. Nonmuscle myosin II exerts tension but does not translocate actin in vertebrate cytokinesis. Proc Natl Acad Sci USA. 2012;109:4509–4514. doi: 10.1073/pnas.1116268109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell M, Thoresen T, Gardel M. Reconstitution of contractile actomyosin arrays. Methods Enzymol. 2014;540:265–282. doi: 10.1016/B978-0-12-397924-7.00015-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murrell MP, Gardel ML. F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex. Proc Natl Acad Sci USA. 2012;109:20820–20825. doi: 10.1073/pnas.1214753109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD. Mechanics of cytokinesis in eukaryotes. Curr Opin Cell Biol. 2010;22:50–56. doi: 10.1016/j.ceb.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salbreux G, Charras G, Paluch E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 2012;22:536–545. doi: 10.1016/j.tcb.2012.07.001. [DOI] [PubMed] [Google Scholar]
- Silva MS, Depken M, Stuhrmann B, Korsten M, Mackintosh FC, Koenderink GH. Active multistage coarsening of actin networks driven by myosin motors. Proc Natl Acad Sci USA. 2011;108:9408–9413. doi: 10.1073/pnas.1016616108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skau CT, Courson DS, Bestul AJ, Winkelman JD, Rock RS, Sirotkin V, Kovar DR. Actin filament bundling by fimbrin is important for endocytosis, cytokinesis, and polarization in fission yeast. J Biol Chem. 2011;286:26964–26977. doi: 10.1074/jbc.M111.239004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skubiszak L, Kowalczyk L. Myosin molecule packing within the vertebrate skeletal muscle thick filaments. A complete bipolar model. Acta Biochim Pol. 2002;49:829–840. [PubMed] [Google Scholar]
- Stendahl OI, Hartwig JH, Brotschi EA, Stossel TP. Distribution of actin-binding protein and myosin in macrophages during spreading and phagocytosis. J Cell Biol. 1980;84:215–224. doi: 10.1083/jcb.84.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svitkina TM, Borisy GG. Correlative light and electron microscopy of the cytoskeleton of cultured cells. Methods Enzymol. 1998;298:570–592. doi: 10.1016/s0076-6879(98)98045-4. [DOI] [PubMed] [Google Scholar]
- Veigel C, Molloy JE, Schmitz S, Kendrick-Jones J. Load-dependent kinetics of force production by smooth muscle myosin measured with optical tweezers. Nat Cell Biol. 2003;5:980–986. doi: 10.1038/ncb1060. [DOI] [PubMed] [Google Scholar]
- Vicente-Manzanares M, Ma X, Adelstein RS, Horwitz AR. Non-muscle myosin II takes centre stage in cell adhesion and migration. Nat Rev Mol Cell Biol. 2009;10:778–790. doi: 10.1038/nrm2786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada A, Ishii N, Takahashi K. Direction and speed of actin filaments moving along thick filaments isolated from molluscan smooth muscle. J Biochem. 1990;108:341–343. doi: 10.1093/oxfordjournals.jbchem.a123203. [DOI] [PubMed] [Google Scholar]
- Yamada A, Yoshio M, Nakayama H. Bi-directional movement of actin filaments along long bipolar tracks of oriented rabbit skeletal muscle myosin molecules. FEBS Lett. 1997;409:380–384. doi: 10.1016/s0014-5793(97)00558-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.