Can streamlined multi-criteria decision analysis be used to implement shared decision making for colorectal cancer screening?

Abstract

Background

Current US colorectal cancer screening guidelines that call for shared decision making regarding the choice among several recommended screening options are difficult to implement. Multi-criteria decision analysis (MCDA) is an established methodology well suited for supporting shared decision making. Our study goal was to determine if a streamlined form of MCDA using rank order based judgments can accurately assess patients’ colorectal cancer screening priorities.

Methods

We converted priorities for four decision criteria and three sub-criteria regarding colorectal cancer screening obtained from 484 average risk patients using the Analytic Hierarchy Process (AHP) in a prior study into rank order-based priorities using rank order centroids. We compared the two sets of priorities using Spearman rank correlation and non-parametric Bland-Altman limits of agreement analysis. We assessed the differential impact of using the rank order-based versus the AHP-based priorities on the results of a full MCDA comparing three currently recommended colorectal cancer screening strategies. Generalizability of the results was assessed using Monte Carlo simulation.

Results

Correlations between the two sets of priorities for the seven criteria ranged from 0.55 to 0.92. The proportions of absolute differences between rank order-based and AHP-based priorities that were more than ± 0.15 ranged from 1% to 16%. Differences in the full MCDA results were minimal and the relative rankings of the three screening options were identical more than 88% of the time. The Monte Carlo simulation results were similar.

Conclusion

Rank order-based MCDA could be a simple, practical way to guide individual decisions and assess population decision priorities regarding colorectal cancer screening strategies. Additional research is warranted to further explore the use of these methods for promoting shared decision making.

Background

Current US guidelines call for screening patients at average risk for colorectal cancer with one of up to six options that differ across multiple dimensions. They recommend that screening decisions be made through a shared decision making process that incorporates individual patient preferences and values. [1, 2]

Shared decision making differs from conventional patient education and clinical decision making activities in its emphasis on engaging patients and integrating their preferences into clinical decisions. Evidence exists suggesting that shared decision making is associated with both improved health care quality and reduced healthcare costs. [3–5] Although the principles of shared decision making apply to many healthcare decisions, they are particularly important in preference-sensitive situations, like colorectal cancer screening for average risk patients, where no clearly dominant strategy exists. [6]

Patient decision aids, developed to facilitate shared decision making, have been shown to increase patients’ knowledge, reduce decisional conflict, and foster patient involvement in decisions about their care but are difficult to implement in a busy practice. [7] Commonly identified implementation barriers include lack of time, inadequate provider expertise, and care systems that discourage their adoption. [4, 8] Successful dissemination of shared decision making therefore depends on the development of tools, processes, and systems of care that will make shared decision making feasible within the constraints imposed by clinical settings.

Tools that could effectively catalyze this process already exist. Multi-criteria decision analysis (MCDA) provides decision makers with a logical, structured, and transparent approach for eliciting decision-related preferences and integrating them into the decision making process. We and others have shown that they can be applied to clinical decisions, are well accepted by patients, and can foster effective doctor-patient communication. [9–13] A variety of multi-criteria methods are available that range from simple, a-theoretical assessments to sophisticated, theory-based procedures. [14, 15] Although methods in the latter category could be expected to provide more valid and reliable information, they typically are more complicated and require significantly more time and effort. Consequently they are more difficult to implement and may result in higher rates of user errors that can limit or even negate their effectiveness. [16]

For these reasons, there has been increasing interest in the development of easier to use methods that still provide decision makers with the benefits of a multi-criteria analysis. Rank ordering, which only involves ranking decision criteria from most to least important, is the simplest assessment procedure. Methods based on rank ordering have received considerable attention and have been recommended for general use. [16–19]

The procedural simplicity of rank order MCDA combined with the close correspondence between the MCDA framework and the requirements of shared decision making suggest that it could be a useful way to implement shared decision making in busy practice settings. The first step in exploring this hypothesis is to determine if rank order MCDA can accurately assess patient decision priorities. To date, studies examining the accuracy of rank order methods have relied on simulations to determine a “correct” decision that is then used as the reference standard for comparison. [20–22] The ability of these methods to accurately assess healthcare decision priorities of patients is unknown. To address this question, we compared patient rank order-based decision priorities regarding the choice of a colorectal cancer screening program with priorities obtained using the analytic hierarchy process (AHP), a widely used, theoretically grounded MCDA method.

Methods

Brief summary of the original study

To determine how people at average risk for colorectal cancer view the advantages and disadvantages of alternative screening strategies, we used the Analytic Hierarchy Process (AHP) to assess decision priorities of people at average risk for colorectal cancer in a multi-center study. The AHP is a widely used, theory-based multi-criteria method that derives decision priorities from a series of pairwise comparisons. A description of the AHP is beyond the scope of this report. Full details are available elsewhere. [15, 23–27]

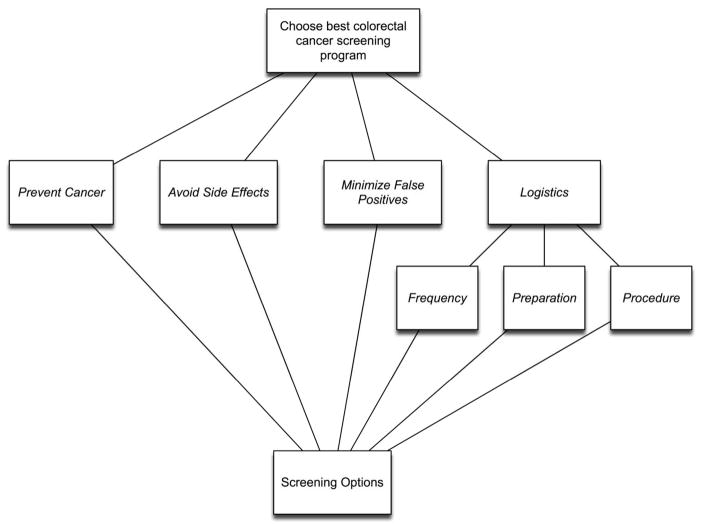
After a brief introduction, study participants performed a full AHP analysis using the four major decision criteria and three sub-criteria shown in Figure 1 to compare colorectal cancer screening options. A standard AHP-assessment procedure was used for the study that instructed participants to first rank order the criteria in order of importance, and then perform the pairwise comparisons needed to calculate the AHP priorities. [28] Full details and study results have been published. [11]

Figure 1.

The decision model.

Calculation of rank order-based priorities

The use of rank order centroids to create priority weights for decision criteria was first proposed by Barron and Hutton and incorporated in a MCDA method called SMARTER (Simple Multi-attribute Rating Technique Exploiting Ranks). [16] Subsequent research has found this approach to be the most accurate of several alternative methods for converting rank order decision criteria priorities into priority weights. [20–22] Rank order centroids are calculated using the formula:

$$w_i=\frac{1}{n}{\mathrm{\sum }}_k^n\left(1/k\right)$$

Where i= 1,2,…n, k is the rank order for each criterion, w is the rank order centroid priority weight of rank k, and n is the number of criteria. For example:

$$\begin{array}{l}{\mathrm{W}}_1=(1+1/2+1/3+\dots +1/k)/k\\ {\mathrm{W}}_2=(1/2+1/3+\dots +1/k)/k\\ {\mathrm{W}}_3=(1/3+\dots +1/k)/k\end{array}$$

Table 1 shows rank order centroid weights for sets of 3 and 4 items.

Table 1.

Description of method used to derive rank order-based decision priorities from the original AHP priorities.

		Major Decision Criteria				Logistical sub-criteria
		Prevent Cancer	Avoid Side Effects	Minimize False positives	Logistics	Frequency	Preparation	Procedure
I	Original AHP priority	0.66	0.21	0.09	0.04	0.67	0.07	0.26
II	Rank order priority	1	2	3	4	1	3	2
III	Rank-based priority weight	0.52	0.27	0.15	0.06	0.61	0.11	0.28

This table shows the method used to derive one of the study participant’s Rank order-based priority weights for the major decision criteria and sub-criteria used in this study. The original AHP-based priorities, shown in row I, were first converted to ranks. The results are illustrated in row II. Standard Rank order-based weights were then assigned according to the priority ranks as shown in row III. Note that separate sets of priorities are assigned to the major decision criteria and logistical sub-criteria.

For this study we derived rank order-based priorities for the decision criteria and sub-criteria from the AHP-based priority scores generated by the participants in the previous study. We first ordered the AHP-based priority scores from best to worst and then assigned the rank order weight associated with each ranking. If ties existed, we averaged the rank order weights of the adjacent ranks. [18] An example of this conversion using one of the study participant’s priorities is shown in Table 1.

Decision Priority Comparison Method

We compared the absolute differences between the original AHP-based decision criteria priority weights generated by the 484 participants in the previous study (the standard measure) with the derived rank order-based priorities (the experimental measure) by subtracting the rank order-based priority from the original AHP-based priority for each study participant. Both sets of priorities are measured on a 0–1 scale with 0 indicating no influence on the decision and 1 indicating absolute influence. Because the measurement differences are not normally distributed, we examined the relationship between the two sets of priorities using Spearman rank order correlation analysis. To examine the extent to which the two measures differ, we used the non-parametric form of Bland-Altman limits of agreement analysis. The Bland-Altman method is currently the standard approach for comparing two measurement methods but assumes that the differences in measurement values being examined are normally distributed. [29, 30] The non-parametric version involves calculating the proportion of measurements that fall within a defined interval, chosen based on clinically important differences, rather than calculated 95% confidence limits used in the standard Bland-Altman procedure. [31]

We calculated the differences between the two sets of priorities using the formula AHP-based – rank order-based priority and tallied the frequency of differences that were greater than ± 0.10, and ± 0.15 of the AHP-based value which we tentatively defined as possible and probable clinically important discrepancies. We then summarized the results using a discordance proportion plot, which illustrates the percentage of measurements that fall within various limits using a modified Kaplan-Meier survival analysis with the absolute difference between the two measures used in place of the more usual survival time. [32]

Decision comparison method

To further determine the significance of differences between the two sets of decision priorities, we compared the results of using them in a full multi-criteria decision analysis comparing the three screening options currently recommended by the US Preventive Service Task Force for average risk patients aged 50 to 75 years: colonoscopy every 10 years, annual immunochemical fecal occult blood tests, and immunochemical fecal occult blood tests every three years combined with flexible sigmoidoscopy every 5 years. [1]

The results of a multi-criteria analysis are a function of both the criteria decision priorities and assessments regarding how well the decision options meet the criteria. We therefore used a standard set of option assessments to isolate the effects of the differences between the AHP-based and rank order-based priorities on the results. We used the estimated outcomes for 50 year old patients used in the original study to compare the three screening options with regard to preventing cancer, minimizing serious side effects, and avoiding false positive screening tests. (These data are included in an online supplemental file: “Information about the screening options used for analysis for 50 year old patients”.) To assess cancer prevention, we created a normalized score by dividing each option’s estimated number of prevented cancers by the sum of all three options. We followed the same procedure for minimizing side effects and avoiding false positives except we used the reciprocals of the outcome estimates because better programs minimize rather than maximize these criteria. Because there is no objective way to measure how well the screening options meet the three logistical sub-criteria, we used the mean responses obtained from the participants in the original study. The resulting standard set of screening option assessments is shown in Table 2.

Table 2.

Standard set of screening option assessments

	Decision criteria
	Prevent Cancer	Avoid Side Effects	Minimize False positives	Frequency	Preparation	Procedure
Colonoscopy	0.371	0.124	0.996	0.182	0.335	0.459
iFOBT & Flex Sig *	0.351	0.433	0.002	0.410	0.438	0.140
iFOBT	0.278	0.443	0.002	0.408	0.227	0.401

^*Abbreviations: iFOBT: immunochemical fecal occult blood test; Flex Sig: flexible sigmoidoscopy.

This table shows the scores summarizing the abilities of three recommended colorectal cancer screening strategies to meet the criteria included in the decision model that were used in the full multi-criteria decision analysis comparing AHP-based and Rank order-based decision priorities. Assessments regarding Prevent Cancer, Avoiding Side effects and Minimizing false positives were based on data used in the original study for 50 year old patients. (These data are included in supplemental file: “Information about the screening options used for analysis for 50 year old patients”.) Assessment scores regarding Screening Frequency, preparation and procedure are the mean values obtained from the prior study.

We then calculated AHP-based and rank order-based overall scores for the three screening options for each study participant by multiplying the option assessments by the priorities assigned to each criterion and summing the results using the following formula:

$$\mathit{Option}\mathit{score}=\sum _{k=1}^n(p_k)(o_k)$$

where p_k represents the priority assigned to criterion k, o_k represents the score describing how well option o meets criterion k, and n equals the number of criteria.

We measured the differential effects of the two sets of priorities by comparing the rank order of the decision options and the differences between the overall option scores generated using the two sets of priorities.

Generalizability analysis

To estimate the generalizability of the findings from the study data, we conducted a Monte Carlo simulation. We first created AHP comparison matrices consisting of three and four rank-ordered criteria. For each matrix, each pairwise comparison entry consisted of a variable constrained to maintain the original rank order of the two criteria involved in the comparison. For example, in the four criteria matrix the variable representing the comparison between the 3^rd and 4^th ranked criteria, 3vs4, was input into the simulation as a variable with a uniform distribution varying from 0.1 (indicating that the 3^rd criterion was minimally preferable to the 4^th) to 8.8. The variable representing the comparison between the 2^nd and 4^th ranked criteria, 2vs4, was then input as a uniform distribution ranging from (3vs4 + 0.1) to 8.9. The variable representing the comparison between the 1^st and 4^th ranked criteria, 1vs4, was then input as a uniform distribution ranging from (2vs4 + 0.1) to 9. (The reductions in the full 1–9 conventional AHP pairwise comparison scale were made to simplify the simulation and are very unlikely to affect the results significantly.) The rest of the comparisons needed to complete the comparison matrix were created similarly. We chose to use uniform distributions for all variables to simulate the entire range of possible pairwise comparison matrices.

Ten thousand iterations were run. Simulation outputs included the criteria priorities derived from the AHP comparison matrix calculated using the geometric mean method [28, 33], differences between the simulated AHP-based priorities and the fixed rank order based-priorities, and the number of times the AHP-based and rank order-based criteria priorities resulted in differences in the rankings assigned to the three recommended CRC screening strategies described earlier using the most common rank ordering of criteria in the data set: Prevent Cancer > Avoid Side Effects > Minimize False Positives > Logistics and Procedure > Preparation > Frequency.

All statistical analyses were performed using MEDCALC. [34] The Monte Carlo simulation was performed using @Risk 6.0. [35]

Results

Description of the study population

The study sample consists of 484 patients at average risk for colorectal cancer. Their demographic characteristics are summarized in Table 3. Their mean age was approximately 62 years, 65% were female, 49% were black, and 42% were white.

Table 3.

Description of the study population, n = 484

Parameter	Number (percent)
Gender
Male	166 (34%)
Female	315 (65%)
Missing	3 (1%)
Age
50–54	87 (18%)
55–59	86 (18%)
60–64	88 (18%)
65–69	88 (18%)
70–74	54 (11%)
75–79	44 (9%)
80–84	37 (8%)
Missing	0
Race
African-American	238 (49%)
American Indian	1 (0.2%)
Asian	2 (0.4%)
White	202 (42%)
Missing or Other	41 (9%)
Ethnicity
Non-Hispanic	405 (91%)
Hispanic	3 (0.7%)
Missing or Other	76 (8%)
Education
< 7 years	2 (0.4%)
Junior high school	24 ( 5%)
Partial high school	54 (11%)
High school	152 (31%)
Partial college	121 (25%)
College	64 (13%)
Graduate	60 (12%)
Missing	7 (1%)

Comparisons between AHP and Rank order priorities

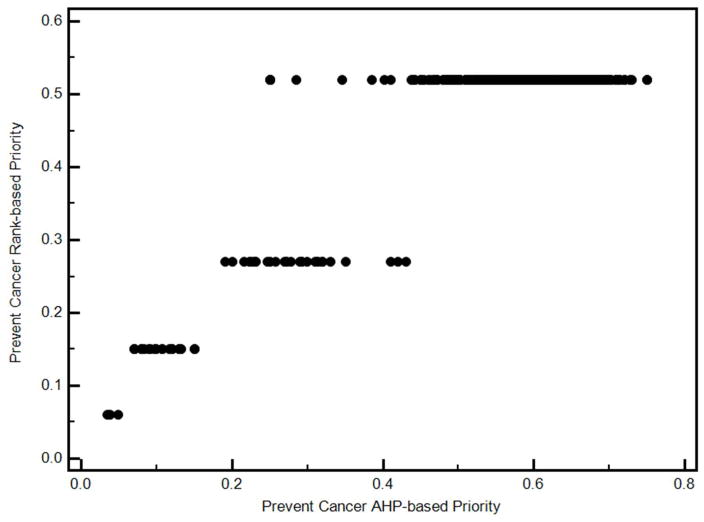
The relationship between the two sets of priorities is illustrated in Figure 2. The biggest difference is the fixed nature of the values associated with the rank order-based priorities versus the more continuous AHP-based priorities. It is also apparent that the differences between the two are more pronounced at higher priorities.

Figure 2.

Example of the relationship between AHP and rank order based decision priorities

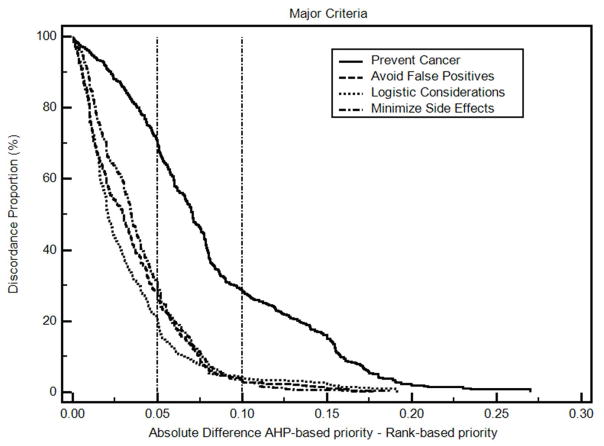
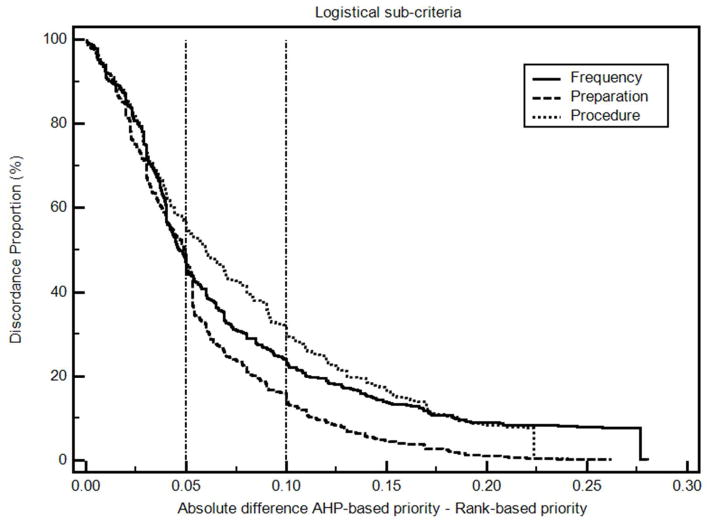
The differences between the AHP-based colorectal cancer decision priorities and the derived rank order-based priorities are summarized in Table 4. Absolute differences in mean priorities range from 0.01 to 0.07. The differences in individual priorities are illustrated in Figures 3 and 4 and summarized in a supplemental file “Non-parametric analysis results”. The percentage of differences within ± 0.10 ranged from 70% to 95%, and the percentage of differences within ± 0.15 ranged from 84% to 99%. Based on our proposed classification system, these results indicate that at least some of the differences in criteria decision priorities are probably clinically significant. Spearman’s coefficients of rank correlation are 0.86 or higher except for Prevent Cancer, which has a correlation coefficient of 0.55

Table 4.

AHP-based versus Rank order-based decision priorities

	AHP priority		Rank-based priority		AHP-Rank priority difference		Spearman’s coefficient of correlation
n = 484
Major Criteria	Mean	95% CI	Mean	95% CI	Mean	95% CI	rho	95% CI
Prevent Cancer	0.55	0.53 – 0.56	0.48	0.48 – 0.49	0.061	0.05 to 0.07	0.55	0.49 – 0.61
Minimize Side Effects	0.17	0.16 – 0.18	0.20	0.19 – 0.21	−0.028	−0.03 to −0.02	0.89	0.87 – 0.91
Avoid False Positives	0.15	0.14 – 0.16	0.17	0.16 – 0.18	−0.019	−0.023 to −0.015	0.91	0.89 – 0.93
Logistical considerations	0.14	0.13 – 0.15	0.15	0.14 – 0.16	−0.013	−0.017 to −0.01	0.88	0.86 – 0.90
Subcriteria
Screening frequency	0.32	0.30 – 0.34	0.35	0.33 – 0.37	0.076	0.069 to 0.083	0.92	0.91 – 0.94
Preparation for screening	0.25	0.23 – 0.26	0.27	0.25 – 0.28	0.056	0.052 to 0.06	0.87	0.85 – 0.89
Screening procedure	0.43	0.41 – 0.45	0.39	0.37 – 0.41	0.08	0.075 to 0.086	0.86	0.84 – 0.88

Figure 3. Discordance-proportion plot, major decision criteria priorities.

The discordance proportion refers to the proportion of differences that equal or exceed the value on the x-axis. More concordant measurements will have curves farther to the left of this graph. More discordant measures will have curves farther to the right.

Figure 4. Discordance-proportion plot, logistical sub-criteria.

The discordance proportion refers to the proportion of differences that equal or exceed the value on the x-axis. More concordant measurements will have curves farther to the left of this graph. More discordant measures will have curves farther to the right.

Comparisons between AHP-based and Rank order-based decision analyses

The results of the decision analyses using the two sets of decision criteria priorities are summarized in Table 5. The relative rankings of the three screening options were the same more than 88% of the time and there were only minimal differences between the AHP-based and rank order-based scores.

Table 5.

Comparisons between AHP-based and Rank order-based decision analyses

	AHP-based rank = rank order-based rank		AHP-based rank & rank order-based rank differ by 1		AHP-based rank & rank order-based rank differ by 2
	Study participants	Simulation	Study participants	Simulation	Study participants	Simulation
Colonoscopy	446 (92.1%)	9,007 (90.1%)	33 (6.8%)	894 (8.9%)	5 (1.0%)	99 (1%)
iFOBT & Flex Sig*	428 (88.4%)	9,007 (90.1%)	55 (11.4%)	993 (9.9%)	1 (0.2%)	0
iFOBT	452 (93.4%)	9,901 (99.0%)	30 (6.2%)	99 (1%)	2 (0.4%)	0

^*Abbreviations: iFOBT: immunochemical fecal occult blood test; Flex Sig: flexible sigmoidoscopy.

“Study participants” refers to the 484 participants in the colorectal cancer screening priorities study. “Simulation” refers to the Monte Carlo simulation consisting of 10,000 iterations.

Generalizability analysis

The differences between the simulated AHP priority values and the fixed rank order values for comparisons involving 3 and 4 criteria are shown in Table 6. For both sets of comparisons, the rank order priority weights tend to underestimate the AHP-based weight of the top ranked priority and overestimate the AHP-based weights of all others. Despite these differences, as shown in Table 5, the full multi-criteria analysis of the three standard colorectal cancer screening options using the AHP-based and rank order-based criteria priorities yielded the identical rank orderings 90.1% of the time for two screening options - colonoscopy every 10 years and annual immunochemical fecal occult blood tests every three years combined with flexible sigmoidoscopy every 5 years - and 99% of the time for the third: annual immunochemical fecal occult blood tests.

Table 6.

Monte Carlo simulation: AHP-based versus Rank order-based decision priorities

	AHP priority		Rank-based priority	AHP-Rank priority difference
n = 10,000 iterations
Four Ranked Criteria	Mean	95% CI	Value	Mean	95% CI
Criterion Rank 1	0.608	0.606 to 0.609	0.52	0.0875	0.0864 to 0.0887
Criterion Rank 2	0.253	0.252 to 0.254	0.27	−0.0174	−0.0184 to −0.0163
Criterion Rank 3	0.099	0.0984 to 0.0996	0.15	−0.051	−0.0516 to −0.0504
Criterion Rank 4	0.0408	0.0405 to 0.0410	0.06	−0.0192	−0.0195 to 0.0190
Three Ranked Criteria
Criterion Rank 1	0.693	0.692 to 0.695	0.61	0.0831	0.0817 to 0.846
Criterion Rank 2	0.231	0.229 to 0.232	0.28	−0.0495	−0.0509 to −0.0481
Criterion Rank 3	0.0764	0.0757 to 0.0770	0.11	−0.0336	−0.0343 to −0.0330

Discussion

In absolute terms, the extent of agreement between the rank order-based and AHP-based decision priorities in this study varied from excellent to fair. The mean priorities were almost identical for all the decision criteria but the congruence between participants’ individual priorities was more variable. The biggest difference in individual priorities occurred relative to the criterion Prevent Cancer, where the correlation between the two sets of priorities was 0.55, 28% of the differences were greater than ± 0.10, and 15% were greater than ± 0.15. Discrepancies were also found among priorities assigned to the two of the three logistical sub-criteria. Although highly correlated, 14% of the measurements for Screening Frequency and 16% of the measurements for Screening Procedure disagreed by more than ± 0.15. These results indicate that, in this dataset, the rank order-based priorities are good approximations of group mean decision criteria priorities regarding colorectal cancer screening but less accurate at the individual level.

The importance of the differences in individual priorities depends on the clinical context and the adequacy of alternative methods for implementing shared decision making in practice. Despite the variance in criteria priorities, the results of full multi-criteria analyses using individual rank order-based and AHP-based priorities using both the study data and simulation data were the same at least 88% of the time. Moreover, since the purpose of the rank based MCDA is to promote shared decision making, rather than prescribe a specific course of action, the primary objective is to assess patient and provider decision priorities and identify differences in need of further discussion. The relative magnitude of the differences therefore becomes less important than being able to assess them quickly, easily, and transparently. Multiple studies have found that patient and provider preferences for colorectal cancer screening frequently differ and we currently do not have the tools needed to adequately implement shared decision making in practice. [36–44] From this perspective our findings suggest that simple rank order-based methods could provide a clinically feasible method for eliciting patient preferences regarding colorectal cancer screening options and incorporating them into a shared clinical decision making process.

Our results are consistent with several prior studies that have found good agreement between rank order-based priorities and decision quality. These studies have all defined quality decisions using “hit rates” of different weighting methods, i.e., the proportion of correct decisions identified using simulated cases as the reference standard. Reported hit rates for rank order-based priorities are approximately 85%, quite consistent with our results. [20–22] To our knowledge, this is the first study to assess both the accuracy of rank order-based decision priorities obtained from a sample of real decision stakeholders with those obtained using a more conventional MCDA priority assessment method and the impact of using them in a multi-criteria decision analysis of a clinical decision.

A key assumption in our analysis is the appropriateness of using the AHP-derived weights to define the study participants’ “true” decision priorities. We believe that this approach is well supported by previous research. Decision priorities generated using the AHP pairwise comparison process have been extensively validated and determined to be quite accurate when compared with measurable physical properties and forecasted future events. [45] They have also been shown to accurately reflect subjective preferences and enhance the decision making process. [46]

This study is subject to several limitations. The first is that the results were obtained from a single study sample using one particular implementation of a sole MCDA method. Therefore the results may not be generalizable to other populations or decision making situations. They do, however, adequately represent differences in priorities within the context of the original study and are consistent with the results of our simulated generalizability analysis. It is also possible that variations in how the study participants performed their AHP analyses could have affected the results. To explore this possibility we repeated the analysis using only the 379 participants who met a common standard for a technically adequate AHP analysis as described in our earlier paper and found similar results. (Data not reported) Another possible limitation is the definitions used to identify possible and probable clinically important discrepancies in the Bland-Altman analysis. These tentative definitions were needed because standard measures are not available. Although they worked well in the current study, they may not be as applicable in other contexts. We also used only one set of decision option assessments to compare the impact of the two sets of priorities on a full multi-criteria decision analysis. As noted above, we used a standard set of option assessments in order to focus our analysis on the impact of the different priorities. Because of the interrelationship between criteria priorities and option assessments in MCDA, it is possible that the differences between the two sets of criteria priorities would have a greater impact on the results if they were combined with different sets of option assessments. Finally, because they were beyond the scope of the current analysis, we did not determine if the use of either of these two priority assessment methods would result in better colorectal cancer screening decisions than those that are currently made or examine if they facilitate and foster use of shared decision making in practice.

Despite these limitations, the results of this study suggest that the use of rank order-based decision priorities in lieu of more precisely determined priorities obtained using the AHP or an alternative MCDA method could be a simple, practical way to both guide individual decisions and assess population criteria priorities regarding colorectal cancer screening. Additional research is warranted to determine if rank order-based methods can be used to facilitate shared decision making regarding colorectal cancer screening in practice and to further explore the advantages and disadvantages of simpler versus more rigorous MCDA methods for assessing individual and aggregate patient preferences and incorporating them into additional preference-sensitive healthcare decisions.