Reconstruction of the human cerebral cortex robust to white matter lesions: Method and validation

Abstract

Cortical atrophy has been reported in a number of diseases, such as multiple sclerosis and Alzheimer's disease, that are also associated with white matter (WM) lesions. However, most cortical reconstruction techniques do not account for these pathologies, thereby requiring additional processing to correct for the effect of WM lesions. In this work, we introduce CRUISE⁺, an automated process for cortical reconstruction from magnetic resonance brain images with WM lesions. The process extends previously well validated methods to allow for multichannel input images and to accommodate for the presence of WM lesions. We provide new validation data and tools for measuring the accuracy of cortical reconstruction methods on healthy brains as well as brains with multiple sclerosis lesions. Using this data, we validate the accuracy of CRUISE⁺ and compare it to another state‐of‐the‐art cortical reconstruction tool. Our results demonstrate that CRUISE⁺ has superior performance in the cortical regions near WM lesions, and similar performance in other regions. Hum Brain Mapp 35:3385–3401, 2014. © 2013 Wiley Periodicals, Inc.

INTRODUCTION

Cortical reconstruction is the task of obtaining a mathematical representation of the cerebral cortex from image data. Analysis of the cortex plays an important role in neuroimaging studies. Anatomical measures like cortical thickness, sulcal depth, and gyrification index, which can be directly derived from this mathematical representation, have been widely used in the study of both healthy and diseased brains [Goldman et al., 2009; Im et al., 2008; Nordahl et al., 2007; Schmitt et al., 2007; Thambisetty et al., 2010; Thompson et al., 2007]. Cortical reconstruction is also the first step in many neuroimaging algorithms including but not limited to cortical labeling [Desikan et al., 2006; Destrieux et al., 2010; Fischl et al., 2004], surface based registration [Fischl et al., 1999; Lyttelton et al., 2007; Tosun and Prince, 2008; Tosun et al., 2004; Yeo et al., 2010], and surface based morphometry [Chung et al., 2003, 2008; Fornito et al., 2008].

Magnetic resonance imaging (MRI) provides superior contrast for finding the cerebral cortex in comparison to other imaging modalities. In particular, T1‐weighted images generally provide the best contrast for cortical geometry. Many algorithms have been developed for cortical reconstruction [Dale et al., 1999; Fischl and Dale, 2000; Han et al., 2004; Kim et al., 2005; MacDonald et al., 2000; Shattuck and Leahy, 2002], and not surprisingly, most of them use T1‐weighted images as the basis of the reconstruction. Using only T1‐weighted images inherently assumes that the brain does not have any pathology with similar contrast to the cortical interfaces. This is not a valid assumption in many diseases. For instance subjects with Alzheimer's disease (AD) develop white matter (WM) lesions that are hypointense on T1‐weighted images, and their boundary with normal WM is similar to the inner boundary of the cortex (in terms of intensity). Another example is multiple sclerosis (MS), which causes focal lesions throughout the WM that can even extend to, and across, the boundary of WM and gray matter (GM). Similar to AD, MS WM lesions also appear with intensity similar to GM on T1‐weighted images. Other MR contrasts (T2‐weighted, proton density (PD) weighted, and FLuid Attenuated Inversion Recovery (FLAIR) T2‐weighted) are required to segment these pathologies but do not provide adequate contrast for segmenting the WM and GM structures.

Most of the current automated algorithms are affected by the presence of the WM lesions and therefore cannot be directly applied to the brains with WM hypointensities. A manual or semiautomated step is required to correct for the effect of the WM lesions. This is not desirable for cortical analysis in a large group of subjects. Recent findings about cortical atrophy in MS [Calabrese et al., 2010; Charil et al., 2007; Chen et al., 2004; Ramasamy et al., 2009; Sailer et al., 2003] highlight the need for a fully automated and pathology robust cortical reconstruction algorithm even more. Among these reports, only [Charil et al., 2007] used a method that provides tools for accounting for WM lesions before the cortical reconstruction step; however, they reported limitations in the segmentation of lesions near the cortex. In most other studies [including reports by Calabrese et al., 2010; Ramasamy et al., 2009; Sailer et al., 2003], Fressurfer [Dale et al., 1999] followed by a semiautomated lesion correction step was used for the cortical analysis.

In this work, we extend upon the previously proposed CRUISE approach [Han et al., 2004; Lucas et al., 2010; Tosun et al., 2006] to develop an automated cortical reconstruction process that accounts for WM lesions. CRUISE is an accurate, robust, anatomically consistent, and computationally efficient algorithm that generates three cortical surfaces: inner surface, defined as the interface between cortical GM and WM; outer or pial surface, defined as the interface between cortical GM and sulcal cerebrospinal fluid (CSF); and central surface, defined as the surface lying at the geometric center between the inner and outer surfaces. The center layer approximates cytoarchitectonic Layer 4 and provides a single surface approximation to the cortical sheet. In this work, several steps in CRUISE are replaced by the Lesion‐TOADS algorithm [Shiee et al., 2010] which makes the process robust to the presence of the WM lesions. Lesion‐TOADS uses the desirable properties of T1‐weighted and FLAIR images simultaneously to generate an accurate segmentation of brain structures as well as WM lesions. Moreover, the resulting segmentation of Lesion‐TOADS is guaranteed to be topologically correct. In other words, every segmented structure and grouping of structures does not have any holes or handles unless they are dictated by the underlying anatomy. The voxel‐level segmentation of Lesion‐TOADS is followed by topology‐preserving level set deformable models to reconstruct the inner, central, and pial cortical surfaces to a subvoxel accuracy. Thickness or other geometric measures of the cortex may be computed from the reconstructed surfaces. Because topology is preserved, cortical unfolding algorithms may also be used for performing group analyses. We call the pathology robust CRUISE algorithm CRUISE⁺ and make it freely available as part of the TOADS‐CRUISE software package [Lucas et al., 2010; http://www.nitrc.org/projects/toads-cruise].

The validation of cortical reconstruction algorithms is not trivial. Evaluating the accuracy of reconstructed cortices on real data has been performed by means of checks on the topological properties of the surfaces and reproducibility of the results [see, for example, Dale et al., 1999; Kim et al., 2005; Tosun et al., 2006]. Although these are necessary properties of a good cortical reconstruction algorithm, they do not provide a quantitative measure of surface accuracy. Lee et al. 2006 performed a quantitative evaluation of several reconstruction algorithms based on surface distances, but their approach is based on a simulated phantom data created from the result of each algorithm. Their approach measures the reproducibility and relative robustness properties of a method but not the actual accuracy of the reconstructed surfaces. Here, similar to the validation performed for CRUISE [Tosun et al., 2006], we use surface landmarks manually placed by human raters to measure the accuracy of the automatically generated inner and outer surfaces in both healthy regions and lesion areas. Our validation data consists of two different data sets of healthy and MS subjects with multi sequence MR scans. We have made this validation data and software freely available to provide the neuroimaging community with unified tools for validation of cortical reconstruction algorithms (https://www.iacl.ece.jhu.edu/cortical_data/).

Parts of this work have been previously presented in conferences [Shiee et al., 2009, 2011]. Here, we present a complete description of the algorithm, provide new validation data, and conduct a more thorough analysis of the method accuracy.

METHODS

CRUISE [Han et al., 2004] was developed for reconstructing the cortex from single channel T1‐weighted images with extracted brain tissue. Similar to most of the current cortical reconstruction algorithms, it assumes a brain with a healthy anatomy. Although the original CRUISE approach only creates a segmentation of CSF, GM, and WM throughout the brain along with the cortex itself, when the TOADS segmentation algorithm is incorporated into the process the two together label many brain regions as well [Bazin and Pham, 2007, 2008]. CRUISE⁺ augments CRUISE in two aspects. First, CRUISE⁺ includes a fully automated brain extraction (skull stripping) algorithm, making it a completely automated tool. Second, and most importantly, CRUISE⁺ is robust to the presence of the WM lesions by allowing the use of multi‐contrast input images, enabling it to model such brain abnormalities.

Taking both T1‐weighted and FLAIR images as input, CRUISE⁺ consists of four major steps: (i) the brain volume is extracted from the T1‐weighted image using an automated skull stripping method; (ii) Both T1‐weighted and FLAIR images are used to segment the brain into its different structures and WM lesions; (iii) The segmentation is then enhanced in the deep sucal regions; (iv) Topology preserving geometric deformable models are used to generate the inner, central, and outer cortical surfaces. As the details of each individual algorithm have been previously published, here we mainly focus on describing how these methods fit in CRUISE⁺ to automatically segment the cortex in brains with WM lesions. In particular, we highlight the important considerations necessary for dealing with the WM lesions where applicable. In the description of these steps, we assume that T1‐weighted and FLAIR images are already coregistered; this can be easily accomplished by any rigid registration software such as FLIRT [Jenkinson and Smith, 2001].

Skull Stripping

In the first step, the brain volume is extracted by a two‐level approach. First, the brain tissue and CSF are extracted using the SPECTRE skull‐stripping algorithm [Carass et al., 2011]. SPECTRE is specifically designed to retain a layer of CSF around the brain, making sure that all the brain tissue (cortical GM in particular) is included in the mask. This is an essential property of the brain extraction step since we are interested in preserving the pial surface.

The SPECTRE mask might include parts of the dura, so we developed a new refinement stripping step to make sure that there is no nonbrain tissue attached to the brain mask. To this end, a geometric deformable model is used to estimate a surface that includes brain and a part of sulcal‐CSF but not any dura. An atlas‐based EM algorithm is used to generate posterior probabilities for GM, WM, sulcal CSF, ventricles, and subcortical GM structures. A geometric deformable model is then initialized by the boundary of GM and WM estimated from this segmentation. Using the union of the WM and GM posteriors, the initial surface is evolved toward the outer boundary of the brain. During the evolution, an additional force is applied to regularize the distance between the WM and GM memberships isosurfaces. As the dura is usually attached to the brain via irregular or thin connections, this regularization removes any part of the dura that is included in the SPECTRE mask.

Figure 1 shows the stripping mask from a T1‐weighted image computed by the above procedure. It is worth mentioning that the mask is computed from the T1‐weighted image only and then applied to the coregistered FLAIR image. We have verified that the stripping procedure is robust to the presence of the WM lesions.

Figure 1.

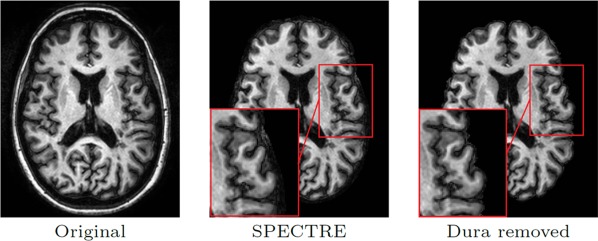
The result of automatic brain extraction using SPECTRE and the refinement step for removing the dura. The red boxes show an area where the dura retained by SPECTRE has been removed in the refinement step. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Simultaneous Lesion and Tissue Segmentation

A necessary step in most cortical reconstruction algorithms is the segmentation of GM and WM. Because the cortical surface has a spherical topology, specific constraints are necessary to either preserve the topology of an initial surface with a spherical topology [Han et al., 2004; MacDonald et al., 2000], or correct the topology of the generated surfaces after finding the cortical boundaries [Dale et al., 1999; Shattuck and Leahy, 2002].

CRUISE⁺ uses the first approach by incorporating Lesion‐TOADS algorithm [Shiee et al., 2010]. Lesion‐TOADS incorporates spatial and topological priors along with intensity information from the stripped T1‐weighted and FLAIR images to segment a brain with WM lesions. The segmentation is performed by minimization of a clustering energy function that allows for imposing topological, spatial, and smoothing priors. Lesion‐TOADS provides a fuzzy (soft) segmentation for each brain structure. This fuzzy segmentation is then followed by a homeomorphic fast marching algorithm to generate a topologically consistent “hard” segmentation. The segmented structures include sulcal and ventricular CSF, cerebellar, cortical, and subcortical GM (consisting of thalamus, putamen, and caudate), cerebral and cerebellar WM, and brain stem. Moreover, if the brain contains WM lesions, Lesion‐TOADS also segments them separately. The details of the algorithm are described in [Shiee et al., 2010]; here, we elaborate on two unique features of the algorithm important for the cortical reconstructions task.

The effect of having WM lesions in the segmentation process is two‐fold. First, the WM lesions result in inaccuracies in the segmentation of WM and GM based solely on T1‐weighted images because they typically have intensities similar to GM. The MR contrasts useful for lesion segmentation, on the other hand, do not provide good GM/WM contrast. Lesion‐TOADS addresses this issue by using a class dependent weighting scheme. In this model, channel and class‐dependent weights tune the effect of intensity information from each channel on the segmentation of each structure or lesions. Because of this novel weighting scheme, the segmentation of sulcal CSF is only affected by the T1‐weighted image, whereas other tissues use both images.

Second, lesions do not have a fixed topology and cannot be accounted for topologically. This is critical in the cortical reconstruction task as many subsequent processes such as cortical unfolding and surface mapping depend upon the spherical topology of the cortex. Lesion‐TOADS has a unique feature among the existing algorithms in that it generates topologically consistent segmentations even in the presence of the WM lesions. It does so by combining the lesions and healthy WM tissue into a single WM tissue class. The combined WM tissue shares the topological properties of the WM tissue in healthy anatomy; hence it can be modeled in a topology‐preserving framework. Note that other approaches typically guarantee topological consistency for a single structure (e.g., cortex), but in Lesion‐TOADS, consistency is guaranteed for every structure and all possible groupings of structures.

Figure 2 shows Lesion‐TOADS segmentation results for an MS subject. One can see that despite the similar intensity of GM and WM lesions on the T1‐wighted image and poor tissue contrast of the FLAIR image, Lesion‐TOADS generates an accurate segmentation of both healthy structures and lesions.

Figure 2.

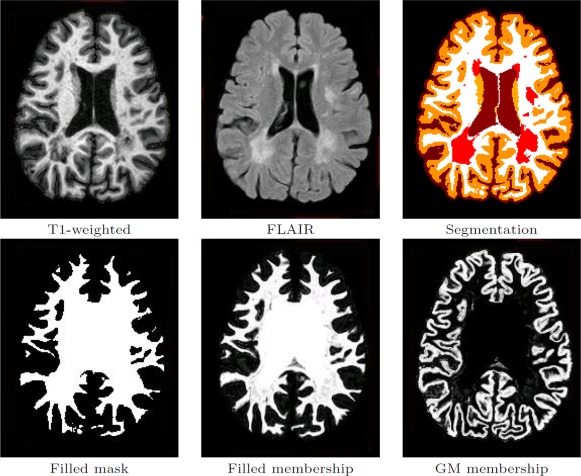
Lesion‐TOADS segmentation results. First row shows the brain‐extracted T1‐weighted and FLAIR images and the Lesion‐TOADS topologically correct hard segmentation (dark red: CSF, dark orange: cortical GM, light orange: caudate, white: WM, and light red: lesions). Second row shows the binary filled‐WM mask used as an initialization for TGDM (Topology‐preserving Geometric Deformable Models), the filled WM membership, and the cortical GM membership, which are used to drive the TGDM evolution. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Cortical Reconstruction

The inner, outer, and central surfaces are generated using nested Topology‐preserving Geometric Deformable Models (TGDM) [Han et al., 2003, 2004]. TGDM, is a member of the geometric deformable models family with a unique property: the zero level set of TGDM does not change topology during the evolution. In other words, the final deformed surface generated by TGDM is guaranteed to have the same topology as the initial surface. This is an essential requirement in generating surfaces like the brain cortex that has a known topology.

The topologically consistent segmentation generated by Lesion‐TOADS, provides the initial inner surface for TGDM. To be more specific, a filled WM mask is generated by combining the cerebral WM, ventricles, subcortical GM structures and lesions (see Fig. 2).

This initial surface is guaranteed to have the correct topology of the cortex, eliminating the need for elaborate topology correction algorithms. Nested TGDM algorithm then evolves this surface to generate the inner surface. The central and outer surfaces are then generated in a sequential fashion, each initializing from the previously reconstructed inner and central surfaces, respectively. TGDM evolves the initial surfaces using the fuzzy memberships from Lesion‐TOADS, a curvature force, and GVF [Xu and Prince, 1998] (in the case of central surface) to generate the final surfaces with a subvoxel accuracy. Before getting incorporated in TGDM, the fuzzy membership of the cortical GM is enhanced in the tight sulcal regions by ACE algorithm. Also, the lesion membership is added to the WM membership in order to provide TGDM with appropriate forces to evolve the surface “through” the WM lesions.

Figure 3 demonstrates how modeling the lesions in the clustering framework affects the reconstruction of the inner surface. Figure 4 shows the triangulated surfaces as well as their intersection with a T1‐weighted image for one of the MS subjects we used in our validation.

Figure 3.

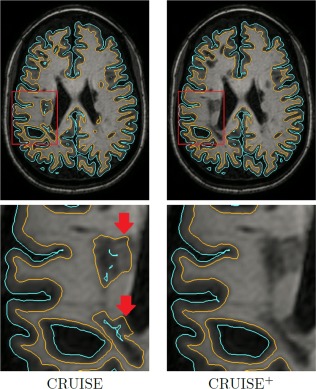
Comparison of CRUISE with CRUISE⁺ in the vicinity of the WM lesions (red arrows). The outer surface is cyan and the inner surface is orange. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 4.

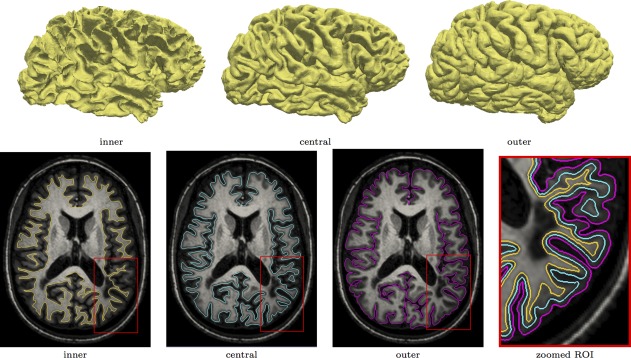
Inner, central, outer surfaces generated by CRUISE⁺ (top row) and their corresponding planar cuts overlaid on the T1‐weighted image. Notice that WM lesions do not affect the generated surfaces. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Cortical Mapping

Using the surfaces automatically generated by CRUISE⁺, a mapping of the cortical thickness in MS subjects and healthy volunteers can be computed in a common coordinate space. As the lesions do not affect the surfaces generated by CRUISE⁺, surface mapping tools can be directly applied to these results without any adaptation or manual interaction. As a demonstration, we first compute the cortical thickness values on the central surface using a level set subtraction method [Han et al., 2004]. We then used the approach described by [Tosun et al., 2004] to map the central surfaces of one MS subject and one healthy volunteer to a common coordinate space. Figure 5 shows the original and the transformed thickness maps of these two subjects.

Figure 5.

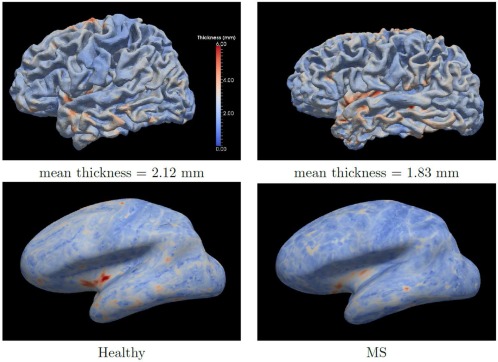
Surface mapping of central surfaces. First row shows the thickness maps of two subjects on the central surface computed by CRUISE⁺. Second row shows the thickness surfaces mapped to a common coordinate space. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

RESULTS

Surface Landmarks and Validation Data

Our validation data set consists of five healthy subjects (three women) with a mean age of 39.4 years (range: 30–49) from the “Multi‐Modal MRI Reproducibility Resource” [Landman et al., 2011] and five MS subjects (four women) with a mean age of 48.4 years (range: 40–59) recruited by the Johns Hopkins MS Center. All the MS subjects have moderate to high lesion load and contain lesions near the cortex. Both data sets of healthy and MS subjects include Magnetization Prepared RApid Gradient Echo (MPRAGE) T1‐weighted, T2‐weighted, PD‐weighted, and FLAIR images for each subject. This set of MR pulse sequences covers the input images required by almost any algorithm dealing with brain and lesion segmentation. The imaging parameters for each data set is as follows: MPRAGE (acquired resolution: 1.0 × 1.0 × 1.2 mm³; FOV: 240 × 204 × 256 mm³; sagittal acquisition), T2‐weighted and PD‐weighted (acquired resolution: 1.5 × 1.5 × 1.5 mm³; FOV: 212 × 212 × 143 mm³; axial acquisition; reconstructed to 0.83 × 0.83 mm² in plane), FLAIR (acquired resolution: 1.1 × 1.1 × 1.1 mm³; FOV: 242 × 180 × 200 mm³; sagittal acquisition; reconstructed to 0.55 × 0.42 × 0.42 mm³) for the healthy data set; MPRAGE (acquired resolution: 1.1 × 1.1 × 1.1 mm³; axial acquisition; reconstructed to 0.83 × 0.83 mm² in plane), T2‐weighted and PD‐weighted (acquired resolution: 1.1 × 1.1 × 2.2 mm³; axial acquisition; reconstructed to 0.83 × 0.83 mm² in plane), and FLAIR (acquired resolution: 0.83 × 0.83 × 2.2 mm³; axial acquisition) for the MS data set. To generate our validation data set, we isotropically interpolated the MPRAGE image to its finest reconstructed resolution in all dimensions (1 mm for the healthy data set; 0.83 mm for the MS data set). All the images for each subject were then registered to their corresponding resampled MPRAGE image. All landmark selection and error calculations were performed in this space.

To thoroughly evaluate the accuracy of a cortical reconstruction algorithm, we chose seven different regions of interest (ROIs) defined by a sulcal region or a gyrus on each hemisphere (see Table 1 and Supporting Information Figure 1). To this end, coarse regions of interest were drawn on three nonadjacent slices in the right and left hemispheres of the brain for each of these seven regions. Two raters (Raters A and B) then placed 10 landmark points upon the inner and outer boundaries of the cortex in each of the selected regions, for a total of 420 landmarks per surface for each subject. For the MS cases, the ROIs were carefully selected such that they are not near the lesion areas. Thus the errors computed in these ROIs are solely representative of the accuracy in the regions without any WM pathology for both of the data sets. For the MS subjects, in addition to the described ROIs, we specified five additional coarse ROIs on the cortex near the MS lesions. Raters A and B as well as a third Rater C were asked to put 10 landmarks on each of these regions for both inner and outer boundaries of the cortex, resulting in 50 total landmarks per surface for each MS subject. The errors in these regions are representative of the accuracy in areas near the WM lesions. There were no restrictions on the location of the landmarks on the selected ROIs. Hence the landmarks include sulcal fundui, sulcal banks, and gyral crowns. The landmark coordinates have floating point precision, which gives them a subvoxel accuracy. This allows an accurate evaluation of the performance of the cortical reconstruction algorithms.

Table 1.

Cortical regions of interest (ROI) used for validation

Acronym	ROI name
CALC	Calcarine fissure
CING	Cingulate gyrus
CS	Central sulcus
PO	Parieto‐occipital sulcus
SF	Superior frontal gyrus
ST	Superior temporal gyrus
SYL	Sylvian fissure

The raters have different levels of experience. Rater A is a technologist with more than 10 years of experience in delineating the anatomical structures and WM lesions. Rater B is an engineering graduate student with limited experience in identifying anatomical structures. This rater was first trained to identify the WM lesions to be able to place landmarks near these areas. Rater C is a neuroradiologist with 8 years of research experience. In placing the landmarks, raters used the same amount of image magnification (seven times of the original image size) but were free to adjust the local contrast for each image. Also, each rater used his or her own computer system. Landmarks were placed on the MPRAGE image. For the landmarks near the WM lesions, the raters were allowed to use coregistered FLAIR images as a reference.

Software

We have implemented and released the CRUISE⁺ software as well as the described landmark selection tool as part of the TOADS‐CRUISE software package freely available to download from the NITRC neuroimaging software resource (http://www.nitrc.org/projects/toads-cruise). The CRUISE⁺ software can be used as a plug‐in within the Medical Image Processing, Analysis and Visualization (MIPAV) software package [McAuliffe et al., 2001], as well as a module in the Java Image Science Toolkit (JIST) [Lucas et al., 2010]. The software allows reading of nearly all common file formats, including DICOM, Analyze, and NIFTI, and is available on Linux, Windows, and Mac platforms. The plug‐in provides a user friendly graphical user interface to execute the algorithm on a loaded data set or to easily change the default parameters.

We also developed a plug‐in for the MIPAV software package for selecting the surface landmarks. We have publicly released this tool within the TOADS‐CRUISE software package as well. As mentioned before, this tool supports floating point coordinates, allowing subvoxel accuracy in placing landmarks. Supporting Information Figure 2 shows the interface of the landmark selection tool.

We have also made the data we used for validation in this work (five healthy subjects, five MS subjects) as well as the manually placed landmarks associated with them freely available through https://www.iacl.ece.jhu.edu/cortical_data/.

Validation Results

In this section, we evaluate the performance of CRUISE⁺ quantitatively and compare its accuracy to FreeSurfer [Dale et al., 1999] (version 5.1.0), a state‐of‐the‐art cortical reconstruction tool. We measured the accuracy of each method by computing the closest distance from each landmark to the reconstructed inner and outer surfaces represented as a triangle mesh. By convention, a landmark located outside (inside) of a surface is assigned a positive (negative) distance. We report both signed and absolute surface distances from the manually picked landmarks described in the previous section.

Although our validation data set contains all the conventional structural MR pulse sequences, CRUISE⁺ only uses the MPRAGE and FLAIR images whereas FreeSurfer only uses the MPRAGE image. As FreeSurfer does not allow multiple MR contrasts, it cannot completely model the WM lesions. However, it does have an option to perform correction of its results if lesion masks are available. In addition to running FreeSurfer under default settings, we ran its postcorrection step using the lesion masks provided by Lesion‐TOADS.

Accuracy on Brains With Healthy Anatomy

On the first experiment, we applied CRUISE⁺ and FreeSurfer to the data set selected from the “Multi‐Modal MRI Reproducibility Resource.” As these subjects do not have any WM lesions, we ran CRUISE⁺ without the WM lesion model. Table 2 shows the mean and the standard deviation of the absolute surface errors for both methods. The absolute error shows the overall accuracy of each method in finding the correct surface. The total mean absolute error values are in the range of 0.44–0.51 mm for FreeSurfer and 0.49–0.69 mm for CRUISE⁺. Although both methods show subvoxel accuracy, FreeSurfer is more accurate by this metric and on this data set than CRUISE⁺. The overall total mean absolute error differences between CRUISE⁺ and FreeSurfer on both the inner and the outer surfaces are less than 0.12 mm according to Rater A and less than 0.25 mm according to Rater B (which are equivalent to 0.12 and 0.25 of a voxel, respectively, for this data set). Focusing on the surface errors from each rater's landmark separately, Table 2 suggests that CRUISE⁺ has better accuracy according to Rater A in comparison to Rater B, whereas the reverse is true for FreeSurfer.

Table 2.

Absolute surface errors on subjects with healthy anatomy and MS (mean ± standard deviation in mm)

	ROI	Healthy subjects				MS subjects
		FreeSurfer		CRUISE+		FreeSurfer		CRUISE+
		Rater A	Rater B	Rater A	Rater B	Rater A	Rater B	Rater A	Rater B
Outer surface	CALC	0.414 ± 0.286	0.446 ± 0.392	0.647 ± 0.636	0.897 ± 0.834	0.331 ± 0.288	0.349 ± 0.284	0.360 ± 0.312	0.471 ± 0.404
	CING	0.507 ± 0.366	0.425 ± 0.318	0.465 ± 0.330	0.515 ± 0.421	0.366 ± 0.325	0.373 ± 0.330	0.427 ± 0.463	0.460 ± 0.464
	CS	0.605 ± 0.316	0.381 ± 0.276	0.408 ± 0.310	0.499 ± 0.485	0.451 ± 0.277	0.276 ± 0.206	0.273 ± 0.217	0.282 ± 0.234
	PO	0.576 ± 0.349	0.408 ± 0.293	0.507 ± 0.389	0.549 ± 0.472	0.489 ± 0.290	0.347 ± 0.244	0.395 ± 0.339	0.427 ± 0.421
	SF	0.466 ± 0.356	0.513 ± 0.593	0.363 ± 0.317	0.666 ± 0.719	0.528 ± 0.350	0.395 ± 0.286	0.386 ± 0.320	0.383 ± 0.316
	ST	0.561 ± 0.435	0.457 ± 0.333	0.534 ± 0.538	0.536 ± 0.492	0.395 ± 0.319	0.369 ± 0.407	0.313 ± 0.232	0.335 ± 0.257
	SYL	0.453 ± 0.39	0.427 ± 0.348	0.553 ± 0.444	0.664 ± 0.555	0.369 ± 0.258	0.334 ± 0.287	0.295 ± 0.242	0.433 ± 0.371
	All	0.512 ± 0.365	0.437 ± 0.379	0.494 ± 0.446	0.618 ± 0.598	0.418 ± 0.309	0.350 ± 0.299	0.350 ± 0.318	0.397 ± 0.367
Inner surface	CALC	0.780 ± 0.54	0.566 ± 0.476	0.792 ± 0.897	1.025 ± 1.101	0.765 ± 0.619	0.651 ± 0.599	0.560 ± 0.387	0.533 ± 0.447
	CING	0.436 ± 0.33	0.452 ± 0.391	0.888 ± 0.885	0.937 ± 0.917	0.485 ± 0.350	0.510 ± 0.401	0.903 ± 0.893	1.040 ± 1.038
	CS	0.381 ± 0.333	0.415 ± 0.333	0.386 ± 0.289	0.408 ± 0.336	0.310 ± 0.228	0.349 ± 0.260	0.636 ± 0.495	0.659 ± 0.476
	PO	0.470 ± 0.338	0.423 ± 0.322	0.430 ± 0.361	0.526 ± 0.455	0.408 ± 0.295	0.375 ± 0.307	0.405 ± 0.269	0.371 ± 0.302
	SF	0.346 ± 0.276	0.370 ± 0.279	0.489 ± 0.399	0.671 ± 0.607	0.358 ± 0.329	0.429 ± 0.385	0.332 ± 0.278	0.404 ± 0.377
	ST	0.376 ± 0.277	0.340 ± 0.272	0.560 ± 0.577	0.591 ± 0.706	0.453 ± 0.356	0.434 ± 0.406	0.408 ± 0.346	0.411 ± 0.379
	SYL	0.500 ± 0.336	0.493 ± 0.395	0.570 ± 0.496	0.659 ± 0.761	0.318 ± 0.237	0.390 ± 0.359	0.412 ± 0.444	0.476 ± 0.463
	All	0.470 ± 0.382	0.437 ± 0.365	0.588 ± 0.626	0.688 ± 0.765	0.443 ± 0.393	0.448 ± 0.411	0.522 ± 0.519	0.556 ± 0.588

The signed distance is a measure of the surface bias and the consistency in estimating the cortical surfaces. A positive signed distance means that the automatically generated surface is located inside the interface that is estimated by a rater, whereas a negative value for the signed distance indicates that the estimated surface lies outside the cortical boundary identified by a rater. Table 3 shows these errors for both methods on subjects with healthy anatomy. According to Rater A, CRUISE⁺ generates surfaces with a smaller bias in comparison to FreeSurfer (a bias of −0.041 mm vs. 0.385 mm for the outer surface and a bias of 0.142 mm vs. −0.321 mm for the inner surface). The reverse is true based on the landmarks of Rater B: FreeSurfer shows less bias in estimating both surfaces in comparison to CRUISE⁺ (a bias of −0.042 mm vs. −0.464 mm for the outer surface and a bias of −0.101 mm vs. 0.407 mm for the inner surface).

Table 3.

Signed surface errors on subjects with healthy anatomy and MS (mean ± standard deviation in mm)

	ROI	Healthy subjects				MS subjects
		FreeSurfer		CRUISE+		FreeSurfer		CRUISE+
		Rater A	Rater B	Rater A	Rater B	Rater A	Rater B	Rater A	Rater B
Outer surface	CALC	0.229 ± 0.448	−0.121 ± 0.582	−0.439 ± 0.794	−0.788 ± 0.938	0.142 ± 0.415	−0.018 ± 0.450	−0.112 ± 0.463	−0.322 ± 0.530
	CING	0.380 ± 0.498	0.046 ± 0.529	0.017 ± 0.571	−0.309 ± 0.589	0.289 ± 0.395	0.118 ± 0.485	0.248 ± 0.579	0.013 ± 0.654
	CS	0.564 ± 0.385	0.063 ± 0.467	0.077 ± 0.507	−0.366 ± 0.592	0.421 ± 0.321	0.173 ± 0.297	0.107 ± 0.333	−0.137 ± 0.339
	PO	0.497 ± 0.455	0.139 ± 0.483	−0.070 ± 0.636	−0.399 ± 0.605	0.462 ± 0.331	0.178 ± 0.385	0.080 ± 0.514	−0.222 ± 0.557
	SF	0.438 ± 0.391	−0.228 ± 0.751	0.195 ± 0.441	−0.534 ± 0.821	0.489 ± 0.403	0.206 ± 0.443	0.148 ± 0.480	−0.151 ± 0.473
	ST	0.313 ± 0.637	−0.065 ± 0.562	0.038 ± 0.758	−0.341 ± 0.643	0.247 ± 0.443	−0.017 ± 0.549	0.086 ± 0.381	−0.194 ± 0.376
	SYL	0.254 ± 0.542	−0.128 ± 0.536	−0.139 ± 0.696	−0.512 ± 0.698	0.286 ± 0.348	0.000 ± 0.441	0.055 ± 0.378	−0.261 ± 0.507
	All	0.385 ± 0.497	−0.042 ± 0.577	−0.041 ± 0.665	−0.464 ± 0.724	0.334 ± 0.399	0.094 ± 0.451	0.088 ± 0.465	−0.179 ± 0.510
Inner surface	CALC	−0.762 ± 0.565	−0.392 ± 0.627	0.342 ± 1.148	0.826 ± 1.258	−0.490 ± 0.855	−0.234 ± 0.854	−0.462 ± 0.501	−0.113 ± 0.687
	CING	−0.106 ± 0.537	0.101 ± 0.590	0.686 ± 1.050	0.836 ± 1.010	−0.175 ± 0.573	0.042 ± 0.648	0.621 ± 1.108	0.853 ± 1.197
	CS	−0.248 ± 0.442	−0.007 ± 0.532	−0.304 ± 0.375	−0.091 ± 0.521	−0.052 ± 0.382	−0.026 ± 0.435	−0.560 ± 0.580	−0.537 ± 0.610
	PO	−0.388 ± 0.430	−0.083 ± 0.526	−0.122 ± 0.549	0.252 ± 0.649	−0.258 ± 0.432	−0.191 ± 0.445	−0.129 ± 0.469	−0.073 ± 0.473
	SF	−0.165 ± 0.411	−0.004 ± 0.464	0.250 ± 0.580	0.508 ± 0.749	−0.020 ± 0.487	0.184 ± 0.546	0.018 ± 0.433	0.216 ± 0.509
	ST	−0.194 ± 0.425	−0.116 ± 0.420	0.139 ± 0.793	0.304 ± 0.869	−0.226 ± 0.530	−0.086 ± 0.589	−0.102 ± 0.525	−0.023 ± 0.559
	SYL	−0.381 ± 0.467	−0.206 ± 0.597	0.004 ± 0.757	0.209 ± 0.985	−0.109 ± 0.381	−0.058 ± 0.527	0.048 ± 0.605	0.085 ± 0.660
	All	−0.321 ± 0.514	−0.101 ± 0.560	0.142 ± 0.847	0.407 ± 0.946	−0.190 ± 0.561	−0.053 ± 0.606	−0.081 ± 0.732	0.058 ± 0.807

Another quantity that can be computed from the signed distances is the combined bias of a method. We define it as the absolute value of the differences between the signed distances of inner and outer surfaces generated by an algorithm. The combined bias affects the cortical thickness values estimated by each algorithm. Consistent with the individual signed distances, the combined bias of CRUISE⁺ is lower according to Rater A (0.183 mm vs. 0.706 mm) whereas FreeSurfer has smaller combined bias according to Rater B (0.059 mm vs. 0.871 mm).

Accuracy on Brains With WM Lesions

The MS data set includes landmarks in both regions far from lesions and cortical areas near the WM lesions. This allowed us to evaluate the performance of CRUISE⁺ and FreeSurfer in each of these regions separately and to study the effect of the WM lesions on the reconstructed surfaces. Table 2 shows the absolute surface error statistics on the ROIs away from the WM lesions. In comparison to the previous data set, the mean overall errors, which range between 0.35 and 0.45 mm for FreeSurfer and 0.35–0.56 for CRUISE⁺, are smaller and quite comparable for this data set, which might be related to its higher resolution. Table 3 shows the signed errors for this data set. Similar to the subjects with healthy anatomy, CRUISE⁺ has a smaller individual (0.088 mm vs. 0.334 mm for the outer surface and −0.081 mm vs. −0.190 mm for the inner surface) and combined (0.169 mm vs. 0.524 mm) biases according to Rater A whereas FreeSurfer has smaller individual (0.094 mm vs. −0.179 mm for the outer surface and −0.053 vs. 0.058 mm for the inner surface) and combined (0.147 mm vs. 0.237 mm) biases according to Rater B.

As mentioned in the description of the validation data, three raters picked 50 extra landmarks near the WM lesions, which allowed us to measure the effect of these lesions on each of the two methods. As presented in Tables 4 and 5, FreeSurfer has larger errors in these regions in comparison to CRUISE⁺, with mean errors in the range of 0.48–1.08 mm in comparison to CRUISE⁺ error range of 0.38–0.59 mm). FreeSurfer performs particularly poorly on Subject 5, but even disregarding this subject, CRUISE⁺ generally performs as well or better than FreeSurfer at the subject level. Moreover, CRUISE⁺ surface errors near the WM lesions are very close to the errors in the other regions, which is not the case for FreeSurfer (see Fig. 6). These results show that in the cortical regions near the WM lesions, CRUISE⁺ has a superior performance over FreeSurfer.

Table 4.

Absolute surface errors near WM lesions (mean ± standard deviation in mm)

	Subject	Rater A			Rater B			Rater C
		FreeSurfer	Corrected FreeSurfera	CRUISE+	FreeSurfer	Corrected FreeSurfera	CRUISE+	FreeSurfer	Corrected FreeSurfera	CRUISE+
Outer surface	S1	0.398 ± 0.410	0.385 ± 0.385	0.457 ± 0.297	0.376 ± 0.333	0.351 ± 0.308	0.420 ± 0.332	0.593 ± 0.435	0.579 ± 0.411	0.526 ± 0.336
	S2	0.540 ± 0.304	0.448 ± 0.276	0.240 ± 0.193	0.277 ± 0.276	0.262 ± 0.218	0.427 ± 0.322	0.654 ± 0.345	0.586 ± 0.332	0.440 ± 0.259
	S3	0.642 ± 0.370	0.613 ± 0.379	0.376 ± 0.324	0.407 ± 0.301	0.390 ± 0.309	0.317 ± 0.239	0.565 ± 0.387	0.566 ± 0.361	0.346 ± 0.250
	S4	0.419 ± 0.289	0.446 ± 0.333	0.568 ± 0.687	0.462 ± 0.453	0.355 ± 0.343	0.554 ± 0.612	0.574 ± 0.442	0.498 ± 0.377	0.592 ± 0.506
	S5	1.017 ± 0.990	0.422 ± 0.276	0.259 ± 0.212	0.865 ± 0.851	0.342 ± 0.286	0.373 ± 0.387	1.125 ± 0.842	0.715 ± 0.375	0.348 ± 0.267
	All	0.603 ± 0.582	0.463 ± 0.340	0.380 ± 0.403	0.478 ± 0.528	0.340 ± 0.296	0.418 ± 0.403	0.702 ± 0.560	0.589 ± 0.376	0.450 ± 0.349
Inner surface	S1	0.608 ± 0.305	0.651 ± 0.326	0.650 ± 0.373	0.501 ± 0.463	0.473 ± 0.382	0.588 ± 0.448	0.861 ± 0.440	0.728 ± 0.399	0.683 ± 0.367
	S2	0.398 ± 0.278	0.347 ± 0.211	0.276 ± 0.200	0.538 ± 0.628	0.369 ± 0.338	0.548 ± 0.474	0.678 ± 0.623	0.537 ± 0.396	0.469 ± 0.346
	S3	0.572 ± 0.678	0.603 ± 0.705	0.610 ± 0.808	0.531 ± 0.566	0.518 ± 0.557	0.610 ± 0.641	0.607 ± 0.557	0.591 ± 0.577	0.684 ± 0.734
	S4	0.650 ± 1.002	0.311 ± 0.284	0.256 ± 0.257	0.763 ± 0.821	0.471 ± 0.398	0.495 ± 0.331	0.906 ± 0.991	0.666 ± 0.556	0.559 ± 0.424
	S5	2.164 ± 2.360	0.432 ± 0.262	0.630 ± 0.717	2.069 ± 2.281	0.480 ± 0.550	0.673 ± 0.707	2.359 ± 2.229	0.607 ± 0.573	0.540 ± 0.473
	All	0.879 ± 1.356	0.469 ± 0.419	0.484 ± 0.557	0.881 ± 1.305	0.462 ± 0.453	0.583 ± 0.537	1.082 ± 1.330	0.626 ± 0.508	0.587 ± 0.493

^aFreeSurfer after correction with the WM lesion masks generated by Lesion‐TOADS.

Table 5.

Signed surface errors near WM lesions (mean ± standard deviation in mm)

	Subject	Rater A			Rater B			Rater C
		FreeSurfer	Corrected FreeSurfera	CRUISE+	FreeSurfer	Corrected FreeSurfera	CRUISE+	FreeSurfer	Corrected FreeSurfera	CRUISE+
Outer surface	S1	0.341 ± 0.460	0.305 ± 0.452	−0.010 ± 0.549	0.209 ± 0.459	0.153 ± 0.443	−0.215 ± 0.493	0.496 ± 0.545	0.466 ± 0.538	0.168 ± 0.606
	S2	0.540 ± 0.304	0.446 ± 0.280	0.056 ± 0.305	0.140 ± 0.367	0.044 ± 0.340	−0.333 ± 0.420	0 647 ± 0.359	0.574 ± 0.353	0.158 ± 0.489
	S3	0.637 ± 0.378	0.605 ± 0.392	0.081 ± 0.492	0.287 ± 0.418	0.275 ± 0.416	−0.122 ± 0.380	0.530 ± 0.434	0.520 ± 0.426	0.143 ± 0.405
	S4	0.405 ± 0.309	0.294 ± 0.476	−0.402 ± 0.797	0.350 ± 0.546	0.175 ± 0.464	−0.458 ± 0.689	0.555 ± 0.466	0.446 ± 0.439	−0.158 ± 0.767
	S5	0.997 ± 1.011	0.407 ± 0.299	−0.125 ± 0.312	0.838 ± 0.878	0.285 ± 0.344	−0.332 ± 0.424	1.114 ± 0.857	0.715 ± 0.375	0.221 ± 0.381
	All	0.584 ± 0.601	0.411 ± 0.401	−0.080 ± 0.548	0.365 ± 0.612	0.186 ± 0.411	−0.292 ± 0.503	0.668 ± 0.600	0.544 ± 0.438	0.106 ± 0.560
Inner surface	S1	−0.545 ± 0.410	−0.599 ± 0.415	−0.580 ± 0.476	0.119 ± 0.675	0.027 ± 0.611	0.161 ± 0.726	−0.136 ± 0.965	−0.343 ± 0.762	−0.263 ± ± 0.735
	S2	−0.170 ± 0.458	−0.293 ± 0.283	−0.122 ± 0.320	0.399 ± 0.726	0.188 ± 0.466	0.456 ± 0.565	0.223 ± 0.898	−0.151 ± 0.655	0.079 ± 0.581
	S3	−0.082 ± 0.887	−0.055 ± 0.930	0.085 ± 1.013	0.232 ± 0.744	0.232 ± 0.728	0.347 ± 0.818	0.055 ± 0.826	−0.024 ± 0.830	0.127 ± 1.000
	S4	0.337 ± 1.149	−0.200 ± 0.372	−0.061 ± 0.359	0.755 ± 0.828	0.392 ± 0.477	0.457 ± 0.382	0.391 ± 1.289	−0.338 ± 0.804	−0.298 ± 0.639
	S5	1.576 ± 2.795	−0.310 ± 0.401	0.146 ± 0.947	1.710 ± 2.567	0.130 ± 0.721	0.363 ± 0.910	2.042 ± 2.529	0.022 ± 0.839	0.115 ± 0.713
	All	0.223 ± 1.601	−0.292 ± 0.557	−0.107 ± 0.731	0.643 ± 1.437	0.194 ± 0.618	0.357 ± 0.708	0.515 ± 1.636	−0.167 ± 0.789	−0.048 ± 0.766

^aFreeSurfer after correction with the WM lesion masks generated by Lesion‐TOADS.

Figure 6.

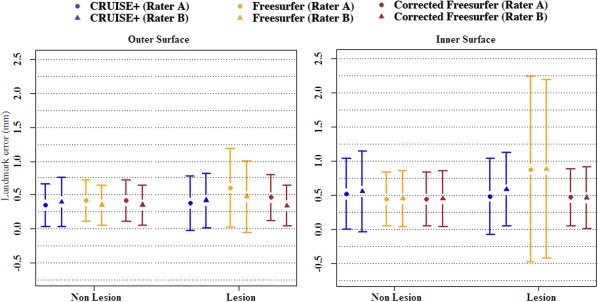
Comparison of the absolute surface errors (mean ± std. err.) in the areas close to the WM lesions (labeled as lesion) vs. the areas far from the lesions (labeled as nonlesion). The error bars represent the standard error computed over all five MS subjects. Each color represents one of the methods. Rater A is represented by a circle and Rater B is represented by a triangle. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Although FreeSurfer only uses T1‐weighted images, which does not provide a unique contrast for WM lesions, it still aims to segment WM hypointensities to avoid surface misrepresentations. This modeling is often inaccurate in MS cases as the lesions are usually large and their contrast varies to a great extent. WM lesions sometimes get segmented as ventricles or GM (see Fig. 7). To address this known issue, FreeSurfer allows for postprocessing of the surfaces to correct for the effect of lesions if a lesion mask is available. We used lesion masks generated by Lesion‐TOADS to correct the results of FreeSurfer. This includes a step for correcting the WM mask estimated by FreeSurfer and then rerunning a part of the surface generation algorithm. This correction step improves the performance of FreeSurfer to a great extent, as presented in Tables 4 and 5 and Figure 6. After correction, the absolute surface errors of FreeSurfer on both surfaces become close to those of CRUISE⁺, but the signed surface error of CRUISE⁺ is still smaller according to Raters A and C.

Figure 7.

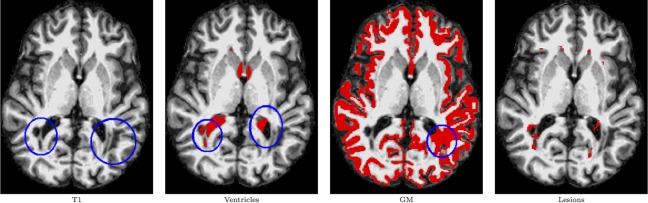
FreeSurfer MS segmentation results. The first column shows a slice from an MS subject with lesions areas highlighted within the blue circles. Subsequent columns show the FreeSurfer segmentation result for the ventricles, gray matter (GM), and WM hypointensinty (lesions) classes. MS lesions near the ventricles or cortex are sometimes mis‐segmented as ventricles. The presence of MS lesions can introduce errors in the segmentation of other structures (ventricles in this case) by FreeSurfer. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 8 shows a planar cut of the inner surface from CRUISE⁺, FreeSurfer, and corrected FreeSurfer near the lesion areas as well as the manually picked landmarks from Rater C. Although using the lesion masks generated by our algorithm significantly improved the performance of FreeSurfer in the lesion areas, there is still a misrepresentation of the cortex apparent in the corrected FreeSurfer results which is not present in the CRUISE⁺ results.

Figure 8.

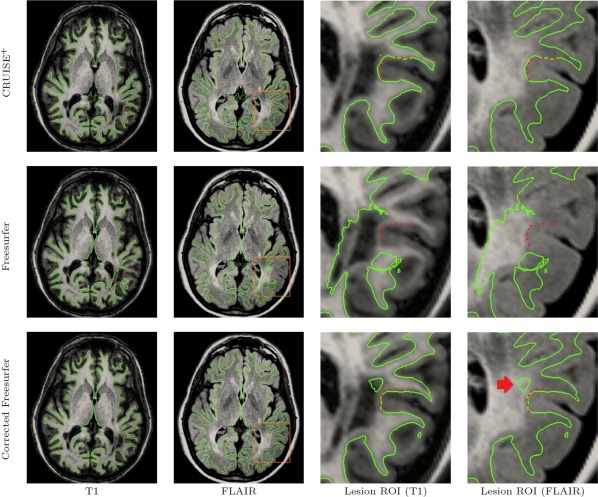
A planar cut of the inner surface near the lesion landmarks from Rater C. CRUISE⁺ (first row) correctly found the inner surface in the vicinity of the WM lesions whereas FreeSurfer (second row) included the WM lesions as a part of the GM. Third row shows the FreeSurfer results after correcting for the lesions (provided by Lesion‐TOADS). Although the results of corrected FreeSurfer are substantially improved, there are still some errors in the lesion areas (red arrow). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Computational Efficiency

CRUISE⁺ has a major advantage over FreeSurfer in the data processing time. The CRUISE⁺ algorithm for processing of a two channel 205 × 256 × 256 image with 1 × 1 × 1 mm³ resolution on a modern Linux workstation takes about 2 h. The analysis of a similar input (but single channel) with FreeSurfer requires about 9 h. Moreover, for subjects with WM lesions, the postprocessing step in FreeSurfer, which is required for the correction of the results, takes an additional 1.5 h. This does not include the time required for segmenting the lesions (either manually or automatically).

DISCUSSION

Many methods have been developed for reconstruction of the human cerebral cortex using MRI. However, most of these methods do not account for brain pathologies such as WM lesions that are present in diseases like multiple sclerosis or Alzheimer's. In this article, we extended the CRUISE algorithm to inherently model the lesions in the cortical reconstruction process, eliminating any need for postprocessing or manual editing of the results. The new algorithm, CRUISE⁺, uses multichannel data (T1‐weighted and FLAIR images) to reconstruct the cortical surface on brains with and without WM lesions. Using manually placed landmarks on data sets of healthy and MS brains, we demonstrated that CRUISE⁺ provides a high level of accuracy in reconstruction of the cortex in both healthy regions and areas near WM lesions. Compared to FreeSurfer, a widely used cortical reconstruction algorithm, our method achieves a similar level of accuracy in the healthy regions, whereas in the areas with WM pathologies CRUISE⁺ has better accuracy. In addition, CRUISE⁺ is computationally much faster than FreeSurfer.

The main advantage of CRUISE⁺ over other cortical reconstruction tools is its consistency in segmenting the cortex throughout the brains with WM lesions. As Figure 6 demonstrates, unlike FreeSurfer, the accuracy of CRUISE⁺ is not affected by the presence of the WM lesions. So far, there has been no cortical reconstruction algorithm that is fully optimized for brains with WM lesions. The common approach for dealing with lesions is to correct the holes in the WM segmentation (due to the presence of lesions) as a separate step and then to run a cortical reconstruction algorithm developed for healthy brains. Both FreeSurfer and the method proposed by [Kim et al., 2005] have been used in this fashion [see, for instance, Charil et al., 2007; Sailer et al., 2003].

There are two fundamental differences between this masking approach and the CRUISE⁺ approach in modeling the lesions. First, the masking approach models the lesions in a voxel‐based fashion and as the intensity values of the WM lesions on a T1‐weighted image are similar to that of GM, the accuracy of the generated surfaces near the lesion areas cannot attain a subvoxel level. Second and most importantly, the reconstruction algorithm is not aware of the presence of the lesions. In other words, after correction of the initial WM surface, these methods still do not account for the intensity similarities between the WM lesions and GM. In Charil et al. 2007, the authors acknowledged the inaccuracy of their approach in areas where lesions are very close to the cortex. CRUISE⁺ on the other hand uses a regional force modulated by the fuzzy memberships in the surface evolution. The lesion fuzzy membership enables the modeling of the lesions in a subvoxel level. It also overcomes the similarity of lesions to GM as it is computed from a multichannel input. The lesion membership pushes the surface out towards the correct boundary if the initial surface lies just inside the lesion boundary, or it prevents the surface from moving inside the lesions if the initial surface lies just outside the lesion. It is worth emphasizing that the notions of inside and outside here are at a subvoxel level; the initial surface already includes the lesions at a voxel level. Figure 8 demonstrates that even after correcting the results of FreeSurfer by the lesion masks, the surface can still leak into the WM lesions. This can even happen in the presence of smaller lesions (see Fig. 9).

Figure 9.

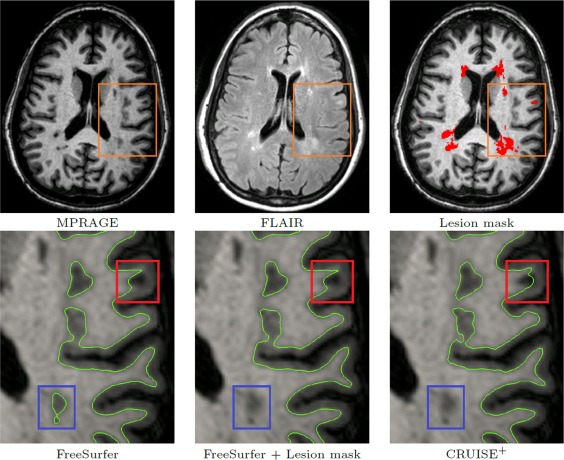
Inner surface near a small lesion attached to the cortex. Top row shows the location of the WM lesions and the automated mask generated by CRUISE⁺. The bottom row shows that although the FreeSurfer result improved in some regions after correcting for the lesions (the blue box), there are still some regions that the surface generated by Freesuerfer leaks into the lesion (the red box). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Another advantage of CRUISE⁺ lies in its ability to provide brain structure volumes, lesion load, and cortical measures in a well‐integrated software tool. In many studies involving subjects with WM lesions, it is of interest to analyze the association of these measurements with scores from different tests. The CRUISE⁺ software provides the neuroimaging community with a tool for conducting these analyses in a large scale and completely automated fashion.

Our validation data provides tools for analyzing the effect of different parameters on the accuracy of the cortical reconstruction algorithms. First, we computed the accuracy of each method in seven separate regions of the brain. MR intensities and tissue contrasts could vary in different parts of the brain. We can investigate the effect of these variations by the landmark errors in each of these regions. Second, we used two data sets with different resolutions and acquisition parameters for the validation which can help us to measure the sensitivity of the methods to the image acquisition parameters. We now briefly describe these effects on our methodology by analyzing the results reported in the previous section.

Tables 2 and 3 show that CRUISE⁺ has larger errors in the calcarine fissure and the cingulate cortex in comparison to other regions. FreeSurfer has also its largest inner surface error in the calcarine fissure. Note that the poorer performance of CRUISE⁺ in these regions also affects the variability of the surface accuracy. This can be seen by the increased standard deviations in Tables 2 and 3, particularly in the inner surface measurements. After visually inspecting the data and the results, we noticed that in the calcarine fissure, the contrast between WM and GM is lower in comparison to other regions of the brain in our data set. In particular, the intensity of GM in this area is higher. This can introduce some errors in the cortical surfaces estimated by CRUISE⁺. As the centroid of the GM cluster is computed globally, the GM fuzzy membership in this region acquires lower values which affect the results. The lower contrast in these regions also decreases the gradient value at the interface of WM and GM which is used by FreeSurfer, decreasing the accuracy of the method in this region. FreeSurfer is not affected as much in the outer surface, because the edge between GM and CSF becomes stronger.

CRUISE⁺ has also large errors in the cingulate region on the inner surface. This is likely a result of the FLAIR intensity variability in the limbic lobe of the cortex as reported previously by Hirai et al. 2000. They observed consistently higher signal intensities on the FLAIR image in the cingulate cortex of neurologically normal brains. This variability affects the membership values and results in error in estimating the cortical boundaries. In our current approach, we target a fixed (i.e., not regionally variable) isovalue of the membership functions in order to estimate the positions of cortical surfaces. If we were to incorporate our knowledge about the variability of T2 in different regions of the cortex [see Georgiades et al., 2001] for instance), then we could specify variable regional forces to accommodate such intensity variability in our multichannel approach. This could be an area for future improvement.

Comparing the errors for healthy subjects and MS patients in Tables 2 and 3, we notice that the surface errors are smaller for the MS cohort in comparison to the healthy cohort. This difference is more pronounced in the outer surface errors. The error standard deviations are also lower in the MS patients. Visual observation of the data suggests that overall, the contrast of the T1‐weighted images are better in the MS cohort which could explain the higher surface accuracy on this data set. The MPRAGE pulse sequence is optimized for better GM/WM contrast and has a slightly higher native resolution. This causes the CSF/GM boundary to be more sensitive to the choice of the segmentation parameters. We believe this is the main reason for error differences between the two data sets. FreeSurfer shows more consistent performance across the two data sets. This could be attributed to its use of a parametric deformable model and gradient‐based forces that potentially make it more robust to differences in resolution and contrast.

Among the outcomes of a cortical reconstruction algorithm, cortical thickness is probably the one that is used the most in neuroscience studies. The accuracy of the computed thickness values heavily relies on the consistency of an algorithm in the estimation of the cortex. One way to measure this consistency is to compute the bias of the algorithm. Our validation data can be used to measure the bias of each algorithm by means of the combined bias computed from the signed distances. According to Rater A, who is the more experienced rater, CRUISE⁺ has a smaller signed distance error on both inner and outer surfaces in comparison to the FreeSurfer. Moreover, CRUISE⁺ has a smaller combined bias too. The overall mean signed distance values for FreeSurfer have different signs (for instance 0.385 mm for the outer surface and −0.321 mm for the inner surface in the healthy dataset). The difference in the sign of the bias (i.e., the combined bias) could lead to larger errors in the thickness values even if the individual biases are small.

Based on the signed distances reported in Table 3, the CRUISE⁺ outer surface lies outside the FreeSurfer outer surface whereas the inner surface generated by CRUISE⁺ lies inside the FreeSurfer inner surface. Hence we expect that the thickness values computed by FreeSurfer to be different from and smaller than CRUISE⁺. Using the built in thickness computation method in each software, the mean thickness values of the healthy and MS subjects in our validation data set are 2.45 mm and 2.12 mm, respectively, as computed by FreeSurfer, and they are 2.10 mm and 1.79 mm, respectively, as computed by CRUISE⁺. This seems contradictory to our expectation from the computed signed distances. However, it is explained by the different methodologies that each algorithm uses to compute the cortical thickness [see Fischl and Dale, 2000; Han et al., 2004]. When we used a method similar to the one implemented in FreeSurfer, the estimated thickness values from the cortical surfaces generated by CRUISE⁺ were larger than FreeSurfer, approximately in the amount that would be predicted by the landmark validation results on both groups.

Despite the differences in the computed cortical thickness values, it is worth mentioning that in most studies involving cortical thickness analysis, group differences are the important outcome. As long as the bias toward either higher or lower cortical thickness values are the same between the study groups, this bias has limited effect on the result of the study. Investigating whether or not the bias of each method is the same for both healthy and MS subjects requires more extensive study. However, in our limited number of subjects, both methods estimated higher thickness values for the healthy group in comparison to the MS group, a fact which is widely reported elsewhere [Calabrese et al., 2010; Charil et al., 2007; Chen et al., 2004; Ramasamy et al., 2009; Sailer et al., 2003]. The landmark errors reported here do not necessarily reflect the error of thickness measurements across the brain surface that may be desired for characterizing outcome measures and power analyses. A full validation of thickness accuracy is beyond the scope of this article but is an area of interest for future work. The challenge of such a validation lies in defining a suitable gold standard for cortical thickness.

There are some differences in the landmark errors computed from each rater's data, which can be due to several reasons. The unrestricted nature of our protocol for selecting landmarks might have affected the landmark selection results for several reasons. First, the use of different monitors by the raters could have an effect on the contrast of the cortical boundaries which could have been propagated in the landmark data. Second, our protocol heavily relies on the judgment of the raters and does not describe a procedure to locate the boundaries. The identification of the cortical interfaces is a subjective task, to an extent, and can be judged differently by different raters. For instance, it is apparent in our validation results that CRUISE⁺ and FreeSurfer consistently have lower errors with respect to Rater A and Rater B, respectively. Defining a rigorous protocol for determining the interfaces at a subvoxel level is a challenging task. After all, the raters are dealing with digitized data with a finite resolution, and there is no correct way of defining where in the voxel the cortex boundary lies. Finally, the variability in the raters' data could be explained by the different experience levels of the raters. Naturally, we expect Rater A, who is more experienced, to generate higher quality landmarks. Despite these limitations, we believe the provided validation data in this work can be used as a standard way to validate and compare cortical reconstruction algorithms.

Finally, we demonstrated an application of the CRUISE⁺ process in the study of the cortical thickness in MS. To date, these studies could not have been performed without a great deal of manual interaction to account for lesions, which decreases both the efficiency and the reproducibility of these studies. Although we only presented the results of the cortical thickness analysis and surface mapping here, any subsequent processing algorithms developed for the analysis of the cortical surfaces of healthy brains can be directly applied to the result of our algorithm on subjects with WM lesions. Moreover, CRUISE⁺ provides the location of lesions, which could be very helpful in the study of their effect on the cortical atrophy.

Supporting information

Supporting Information Figure 1.

Supporting Information Figure 2.