Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 13;4:5281. doi: 10.1038/srep05281

Tug-of-war of microtubule filaments at the boundary of a kinesin- and dynein-patterned surface

Junya Ikuta 1, Nagendra K Kamisetty 1, Hirofumi Shintaku 1, Hidetoshi Kotera 1, Takahide Kon 2,3, Ryuji Yokokawa 1,3,a
PMCID: PMC4055898  PMID: 24923426

Abstract

Intracellular cargo is transported by multiple motor proteins. Because of the force balance of motors with mixed polarities, cargo moves bidirectionally to achieve biological functions. Here, we propose a microtubule gliding assay for a tug-of-war study of kinesin and dynein. A boundary of the two motor groups is created by photolithographically patterning gold to selectively attach kinesin to the glass and dynein to the gold surface using a self-assembled monolayer. The relationship between the ratio of two antagonistic motor numbers and the velocity is derived from a force-velocity relationship for each motor to calculate the detachment force and motor backward velocity. Although the tug-of-war involves >100 motors, values are calculated for a single molecule and reflect the collective dynein and non-collective kinesin functions when they work as a team. This assay would be useful for detailed in vitro analysis of intracellular motility, e.g., mitosis, where a large number of motors with mixed polarities are involved.

Among the highly organized functions in a living cell, molecular motors play essential roles in intracellular transport by converting chemical energy, arising from ATP hydrolysis, into mechanical work. There are two main microtubule (MT)–based motors, kinesin, which moves to the plus end of MTs, and cytoplasmic dynein, which moves to the minus end. Cargo such as organelles and protein bodies is carried by multiple motors with opposite polarities, resulting in bidirectional transport with frequent reversals. This type of transport has been observed in vivo, such as with the movement of lipid droplets in Drosophila embryos, which is a well-known example of bidirectional motion along MTs1. Other types of cargo, such as endosomes2,3, mitochondria4, melanosomes5, and secretory vesicles6 have also been reported.

Along with numerical simulations, several models that explain how motors work in bidirectional transport have been proposed. In the tug-of-war model, two opposite-polarity motors carry cargo and work to move it to their respective ends of the MT, resulting in the tug-of-war conditions7,8. When one of the two motor groups exerts more force, the “winning” motor unidirectionally transports the cargo. Another is the coordination model in which both motors carry the cargo, but one of the motors is inactivated without interfering with the function of the other motor to carry the cargo9, resulting in unidirectional transport. In both models, a regulatory mechanism is likely to exist that controls the activity of the motors by binding to both opposite-polarity motors. In the exclusionary presence model, the motors of each polarity are capable of binding to cargo, but only one of them can bind and work at a time. This necessitates frequent binding and unbinding of motors, which occur in endosome transport and which are reversed by binding of dynein to the kinesin-coated endosome2.

Bidirectional transport has been extensively studied in vivo. However, such a study in vitro is limited. Using purified motors in vitro enables segregation of possible factors that induce switching of the cargo direction. However, until now, only a few attempts have been made using a bead assay in which cargo is carried by multiple motors on an immobilized MT10,11,12,13. With the minimum configuration comprised of a bead (i.e., the cargo), one kinesin, and one dynein molecule, back-and-forth motion was observed with optical trapping10. Combined western blotting and photobleaching also showed a number of motors attached to purified vesicles11. More recently, a DNA origami12 or strand13 configuration was used to demonstrate tug-of-war by kinesin and/or dynein motors. These bead assay–based approaches are applicable to in vitro models that include several but not >10 motors. Compared with the bead assay format, the gliding assay is more appropriate for studies with >10 motors such as intracellular motility. However, it has not been used to investigate the cooperative activities of motors with different polarities except in one study in which Vale et al. demonstrated bidirectional MT gliding on a substrate that was randomly coated with kinesin and dynein14.

Here, to explore applicability of the gliding assay format to a multi-motor study, we present a tug-of-war molecular model consisting of a single MT filament at a boundary that is defined by the patterning of conventional kinesin and cytoplasmic dynein motors. Based on microfabrication and self-assembled monolayer (SAM) technologies15,16, we describe a method to selectively immobilize kinesin and dynein in two different regions. After evaluation of the selective coating, we study MT behavior at the boundaries and categorize these MTs into one of four groups based on their behaviors. One of the most interesting behaviors among the groups includes MTs that initially bridge the boundary and experience the tug-of-war phenomena: MTs are stationary when the force exerted by the two motor groups is balanced, they begin to glide once the balance is broken, and finally glide to the “winning” motor region. The number of motors pulling the MTs is determined by measuring the MT length and the distance between motors, which enables us to plot the velocity against the ratio of motor numbers. Those plots are fitted by three models to discuss whether the models that were previously proposed for the bead assay fit the gliding assay–based tug-of-war. As a result, though our tug-of-war involves >100 motors, the detachment force and motor backward velocity calculated for a single motor reflect the tenacious nature of dynein and non-collective kinesin function when they work as a team12,17,18,19. The proposed assay also has a potential to be utilized for detailed in vitro analysis of intracellular motility, e.g., chromosome oscillations in mitosis where multiple kinds of numerous mitotic motors (>100 motors) are working with spindle MTs20,21.

Results

Selective kinesin and dynein patterning

Two motor proteins, kinesin and dynein, were patterned on a fused silica substrate using conventional photolithography and SAM grafting methods. Chromium and gold were patterned using the lift-off process to create a boundary between the gold and the bare glass surfaces (Fig. 1a-1). The glass substrate cleaning process including the use of acetone, ethanol, 2-propanol, and an ammonia-peroxide mixture was critical to form the SAM that reduces nonspecific protein binding. Then, the substrate was immersed in a SAM solution (HS-(CH2)11-EG3-biotin) and stored in ethanol until use. This processing step introduces biotinylated SAM on the gold-coated surface, while leaving the bare glass surface uncoated (Fig. 1a-1). A flow cell was constructed using the patterned substrate as the top substrate.

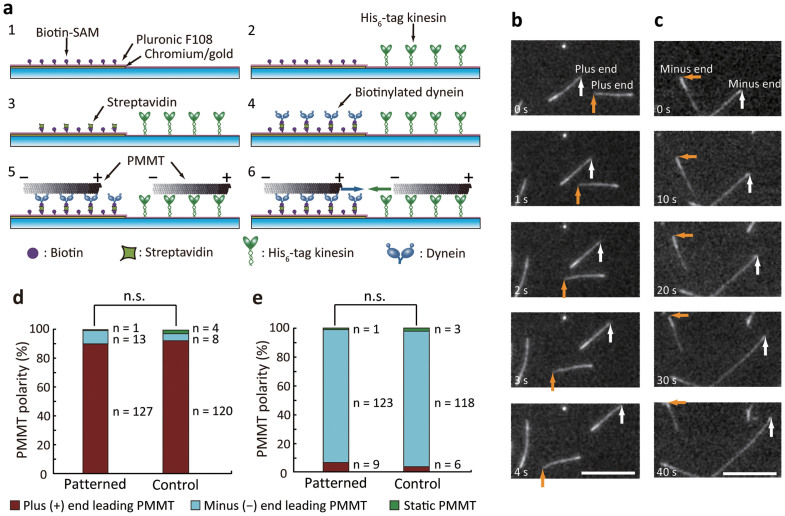
Figure 1. Selective kinesin and dynein patterning.

Figure 1

Open in a new tab

(a) Schematic for selective coating procedure of kinesin and dynein. (1) Biotinylated SAM grafting on the gold patterned region. (2) Kinesin, (3) streptavidin, and (4) dynein were immobilized sequentially. Selective coating was examined by injecting (5) PMMT, and the gliding direction was evaluated (6). (b), (c) PMMTs gliding on the selectively immobilized motors in the (b) SAM-coated region (led by dimmer plus end) and (c) glass region (led by brighter minus end). Scale bar, 10 μm. (d), (e) Polarity of PMMTs gliding on the (d) SAM-coated region and (e) glass region. Control surfaces were prepared by omitting kinesin in (d) or dynein in (e) from the optimum assay for the selective coating. In both cases, polarity distribution was not significantly different (p > 0.05) from control experiments as determined with the chi-square test. n.s. = not significant.

We optimized the condition for introducing protein solutions to selectively immobilize genetically modified Dictyostelium discoideum cytoplasmic dynein (biotinylated, GST380)22 onto the SAM-coated gold region and human kinesin (His6-tagged K573)23 onto the glass region while avoiding nonspecific protein binding. The optimum sequence starts with filling the flow cell with BRB80 solution (80 mM PIPES, 1 mM EGTA, 1 mM MgCl2, pH 6.8). Next, 2 mg ml−1 Pluronic F108, 0.2 mg ml−1 kinesin (Fig. 1a-2), 0.5 mg ml−1 streptavidin (Fig. 1a-3), and 0.06 mg ml−1 dynein (Fig. 1a-4) were introduced sequentially into the flow cell, with a 5-min incubation period and washing step involving BRB80 solution for each (see the Method section for detail). In this sequence, the combination of the polyethylene glycol fraction of SAM and Pluronic prevented nonspecific binding of kinesin to the gold surface so that kinesin bound only to the glass surface. Streptavidin was specifically immobilized on the biotinylated SAM, which results in the binding of biotinylated dynein only to the gold surface. When we changed even one of the orders of injection, nonspecific binding of molecules to unexpected regions caused mixed immobilization of kinesin and dynein on both the glass and gold-coated regions. Other sequences examined for this optimization are listed in the Supplementary Table S1 and discussed in the Supplementary Discussion.

To evaluate if the SAM-coated surface has dynein and if the glass surface has kinesin, we introduced polarity-marked MTs (PMMTs) prepared according to a standard method24. Polarity and the velocity of gliding PMMTs on the SAM-coated and glass surfaces were observed (Fig. 1a-5,6). For control experiments, kinesin- or dynein-coated control surfaces were prepared using the optimum sequence while omitting the other motor. Most MTs were led by the plus end in the SAM-coated region (Fig. 1b, see Supplementary Video S1) and by the minus end in the glass region (Fig. 1c, see Supplementary Video S2). Statistical analysis also proves that ratio of PMMT polarities are not significantly different (p > 0.05 for graphs in Fig. 1d,e) from the control surfaces. The following gliding velocities were measured: 1.43 ± 0.20 (mean ± s.d.) μm s−1 (n = 40) on the SAM-coated surface, 1.45 ± 0.14 μm s−1 (n = 40) on the dynein-coated control surface, 0.30 ± 0.11 μm s−1 (n = 100) on the glass surface, and 0.49 ± 0.05 μm s−1 (n = 100) on the kinesin-coated control surface. No significant differences (p > 0.05) were noted between the SAM-coated surface and the control, but the glass surface showed a decrease compared with the kinesin-coated control surface (p < 0.05). By evaluating the influence of streptavidin and dynein, we recognized that the decrease in velocity may have been caused by dynein bound to the glass surface together with kinesin or to kinesin immobilized on the glass surface (see Supplementary Fig. S1 and Supplementary Discussion). There was a concern that on the glass surface, MTs can be captured and/or propelled by nonspecifically immobilized dynein molecules, even at the single-molecule level, as demonstrated by Howard et al. for single kinesin molecules25. As detailed in the Supplementary Discussion, however, no MT attachment or movement was observed when dynein was injected onto streptavidin that was nonspecifically bound to the Pluronic-treated glass surface. The results show that on the glass surface, dynein hindered kinesin-driven MT gliding not by binding to MTs, but presumably as steric hindrance or a “roadblock”. Collectively, although the velocity in the kinesin-coated region was decreased, polarity evaluation revealed that dynein and kinesin were selectively coated on the SAM-coated and glass surfaces, respectively, without losing their functions.

Behavior of MTs at the boundary

The boundary created by kinesin and dynein patterning was evaluated by observing the behavior of gliding MTs. Such an evaluation has been used to study the boundary between kinesin-coated and kinesin-free regions26,27, and the physical boundary generated by microfabricated structures28,29,30,31. Here, we categorized MTs into one of four groups based on their behaviors (Fig. 2a): group 1, MTs that were gliding in the dynein-coated region across the boundary toward the kinesin-coated region; group 2, MTs that were gliding in the kinesin-coated region across the boundary toward the dynein-coated region; group 3, MTs that were initially bridging the two regions and then buckled as a result of kinesin and dynein motility upon ATP injection; group 4, MTs that were initially bridging two regions and that experienced a tug-of-war upon ATP injection.

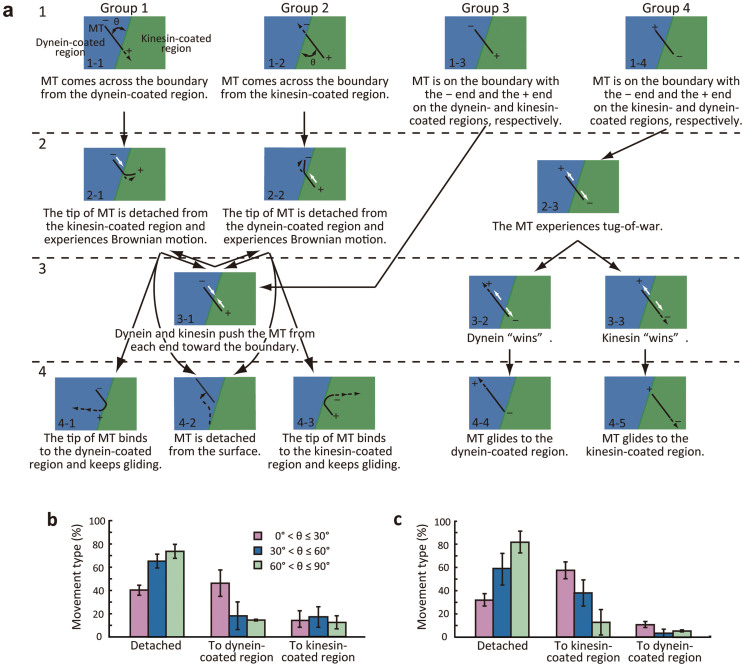
Figure 2. Behavior of MTs at the dynein-kinesin boundary.

Figure 2

Open in a new tab

(a) Schematic diagram for grouping MT behavior. MTs approached the boundary from the dynein-coated region (group 1) or the kinesin-coated region (group 2). The tip of the MT was at the boundary with the minus end in the dynein-coated region (group 3) or in the kinesin-coated region (group 4). θ is the approach angle of the tip of the MT to the boundary. (b), (c) The behavior of MTs with respect to the approach angle, θ. MTs approached from (b) the dynein-coated region and (c) the kinesin-coated region. Values are the mean ± s.d. (n = 286 for (b) and n = 168 for c).

The MTs in groups 1 and 2 were initially gliding on either a kinesin- or dynein-coated region and occasionally encountered a boundary. We observed several transient conditions as summarized in Fig. 2a that were due to the existence of the other motor beyond the boundary. When the leading tip of a MT driven by dynein detached at the boundary while leaving its tail gliding (Fig. 2a, 2-1), the tip swiveled around until it landed on the kinesin region (Fig. 2a, 3-1), returned to the original dynein region (Fig. 2a, 4-1), or detached from the surface (Fig. 2a, 4-2). When a MT was in the 3-1 condition, two different polarity motors pushed the MT from each end toward the boundary, resulting in buckling and detachment of one end of the MT (Fig. 2a, 2-1 or 2-2). Group 3 is equivalent to the 3-1 condition, and hence, we do not discuss this group further. MTs moved between these states in a dynamic manner, as indicated by the arrows, and eventually reached the final three conditions: detaching from the surface, returning to the original region, and passing the boundary to the other region. The third classification has not been seen in previous studies in which only kinesin was involved27,28. Whether MTs approached the boundary from dynein- or kinesin-coated regions, the majority (64.3%, Fig. S2a and 58.9%, Fig. S2b, respectively) of them were detached. However, those values are much lower than that measured at the boundary of kinesin-coated and kinesin-free regions (~88%)28. This discrepancy is most likely to be caused by the other motor immobilized on the opposite region beyond the boundary, which powered the movement of some MTs that otherwise would have detached.

As the approach angle, θ, of MTs to the boundary increased, the percentage of detached MTs increased and that of MTs returning to the original regions decreased (Fig. 2b,c). When the approach angle from the kinesin-coated region was ≤30°, 57.4% of MTs were guided to the original region (Fig. 2c). This result agrees with measurements of MTs at a chemical boundary, as reported by Clemmens et al.28. The same trend was seen for MTs approaching from the dynein-coated region (Fig. 2b). However, the third group in which MTs went over the boundary to continue gliding on the other region did not show a significant difference in relation to the approach angles (to the kinesin-coated region in Fig. 2b and to the dynein-coated region in Fig. 2c, respectively). This is because most MTs categorized in this group experienced the transient back-and-forth conditions depicted in Fig. 2a. Although MTs underwent changes in their conditions, their approach angles were drastically altered from their initial approach angles due to thermal fluctuations.

MT gliding assay–based tug-of-war

MTs categorized in group 4 showed tug-of-war behavior in which kinesin and dynein pulled the MT in opposite directions (see Supplementary Video S3). This type of movement has been seen previously with the bead assay. Based on only those MTs that finally glided to the kinesin-coated region (Fig. 3a), the time course of the ratio of MT length in the kinesin-coated region with respect to the total MT length is plotted in blue together with the velocity in red (Fig. 3c). When MTs were pulled evenly by the two motor groups, the ratio remained constant and the velocity was near zero. However, once the ratio exceeded ~0.6, kinesin dominantly propelled the MT and cleaved dynein-MT binding until the MT glided to the kinesin-coated region. The velocity increase followed the change in the ratio and reached the normal velocity driven by kinesin. Corresponding plots were obtained for MTs that glided to the dynein-coated region (Fig. 3b,d). Non-normalized data for one of MTs gliding to the kinesin- and dynein-coated regions are plotted in Supplementary Fig. S3a and Fig. S3b, respectively.

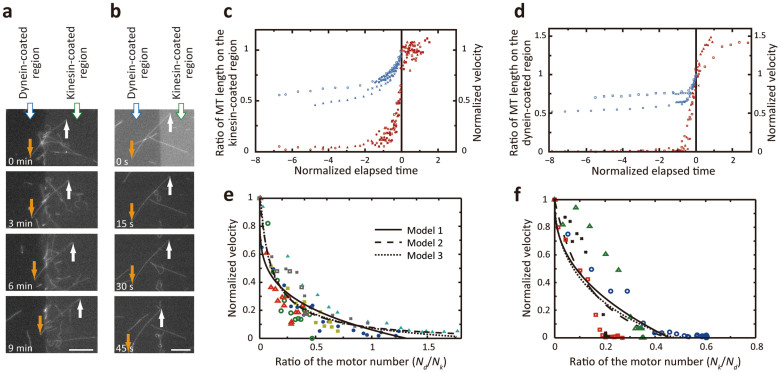
Figure 3. Tug-of-war of MTs at the boundary of a kinesin- and dynein-patterned surface.

Figure 3

Open in a new tab

(a), (b) MTs experiencing tug-of-war and glide to the (a) kinesin-coated region and (b) dynein-coated region. Scale bar, 10 μm. (c), (d) Normalized MT length and velocity during tug-of-war for MTs gliding to (c) the kinesin-coated region (n = 7) and (d) the dynein-coated region (n = 4). Ratio of the MT length attached to the “winning” motor region (blue plots) and normalized velocity (red plots). The standard velocity for each MT that was measured when the MT passed the boundary and was propelled only by the “winning” motors at t = 0 was used to calculate the normalized velocity. Dimensionless time is defined as (elapsed time)/(MT length)/(standard MT velocity). The same symbols are used for a MT in each graph. (e), (f) Relationship between velocity and ratio of the motor number. (e) Nd/Nk–velocity and (f) Nk/Nd–velocity relationships for MTs gliding to the kinesin- and dynein-coated regions, respectively. Velocity was normalized as described above. MTs that were analyzed here correspond to those that were tracked in Fig. 3c,d and are coded accordingly. Fitted curves based on the three models are shown.

To investigate the number of kinesin or dynein motors pulling a MT, we measured the average spacing between motors. Among several methods to determine the distance between surface-immobilized motors32,33,34, we adopted the method by Van den Heuvel et al.33: the mean distance, <d>, between motors was calculated through the mean distance, <S>, that a short MT travels between successive rotations, and the MT length, L (see Supplementary Methods and Supplementary Fig. S4). The mean distance on the kinesin-coated surface, <dk> = 0.16 ± 0.04 μm, was obtained with L = 0.66 ± 0.03 μm (n = 10) and <S> = 2.5 ± 1.1 μm. The corresponding values for the dynein-coated surface were <dd> = 0.10 ± 0.02 μm, L = 0.52 ± 0.02 μm (n = 10), and <S> = 4.0 ± 2.3 μm.

Relationship between the ratio of motor number and velocity

Although the load to a MT was not directly measured as is usually done with optical tweezers, velocity transition can be investigated by comparison with the conventional force-velocity (F-V) relationship by assuming that the mean-field theory can be applied to our gliding assay–based system35. Several models have been proposed when the motor number (N) involved in the tug-of-war is small (N < 3), including a cooperative mechanism9,35 and stochastic models36. However, when the motor number is large (N > 4), correlations between motors weaken, and the load is shared equally among motors, i.e., the mean-field model is applicable18. Assuming that motors are uniformly distributed on the surface, we derived the number of kinesin and dynein motors, Nk and Nd, involved in the tug-of-war as follows: Nk = Lk/<dk> and Nd = Ld/<dd>, where Lk and Ld are the MT lengths on the kinesin-coated and dynein-coated regions, respectively. For instance, Nk = 78 and Nd = 94 bound to a MT (blue circle, Fig. 3c) prior to the tug-of-war. In the following calculation of three models that fit our experimental data, we focused on a MT gliding to the kinesin-coated region. One can simply exchange suffixes k and d in the equations to consider a MT gliding to the dynein-coated region.

The proportional load model (Model 1, see Supplementary Methods) stems from a conventional F-V relationship focusing on a target motor against an external load such as optical tweezers37,38. As the relationship has been also used to model a bead carried by multiple motors35, we applied it as a potential model that fit to our results. To apply the F-V relationship, we considered that Nk kinesins propelled the MTs evenly against the load by Nd dyneins. The important assumption, which is different from that of the other two models, is that the total load is proportional to the number of dynein molecules. Therefore, the total load was defined as FTotal = Ndfd*, where fd* is the load (detachment) force of a dynein molecule in the retrograde direction9,35,36. As the total load is shared by Nk kinesins with a stall force of fk, the load felt by a kinesin is F = FTotal/Nk. A conventional F-V equation for a single motor18,

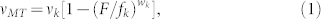graphic file with name srep05281-m1.jpg

can be rewritten as

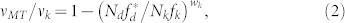graphic file with name srep05281-m2.jpg

where vMT is the apparent MT velocity, vk is the load-free MT velocity driven by kinesin, and wk determines whether the F-V curve is linear (wk = 1), convex up (wk > 1), or concave up (wk < 1). When the experimental results were plotted in the Nd/Nk − vMT/vk (normalized velocity) relationship (Fig. 3e), fd*/fk = 0.94 and wk = 0.24 were obtained with the least-squares method (Model 1, Table 1).

Table 1. Parameters obtained by fitting the F-V relationships to experimental results.

Model type fd*/fk fk*/fd fk (pN) fd (pN) fk* (pN) fd* (pN) wk wd vkb (nm s−1) vdb (nm s−1)
Model 1 (Proportional load model) 0.94 1.4 635,37 1.117 1.5 5.6 0.24 0.41 NA NA
Model 2 (Linear F-V model) 0.27 2.2 635,37 1.117 2.4 1.6 19 19 503 9.5
Model 3 (Non-linear F-V model) 0.5 2.1 635,37 1.117 2.3 3.0 217,36 0.517,36 456 56
Kunwar et al.36 0.19 2.9 4.7 1.4 4.0 0.87 2 0.5 NA NA
Muller et al.9 0.13 2.7 6 1.1 3 0.75 1 1 6 72
Open in a new tab

fd, dynein stall force, fk, kinesin stall force, fd*, dynein detachment force, fk*, kinesin detachment force, wk, linear/nonlinear parameter for kinesin, wd, linear/nonlinear parameter for dynein, vkb, kinesin backward velocity, vdb, dynein backward velocity, NA, not applicable.

In the following two models, we regarded dynein as a motor that makes backward steps not as a simple load as modeled in Model 1. Hence, we incorporated the backward velocity of dynein, vdb, under superstall loads according to previous studies9,36. When each kinesin and dynein molecule propels a MT against load F+ and F–, respectively, vMT can be expressed as

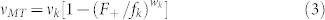graphic file with name srep05281-m3.jpg

for kinesin and

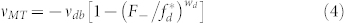graphic file with name srep05281-m4.jpg

for dynein. Here, we consider two assumptions that can be applied to our gliding assay–based format: (i) the presence of opposing motors induces a load force, and (ii) each kinesin and dynein experiences the load F+ and F–9,36. This yields the force balance as NkF+ = NdF–. Therefore, normalized velocity, vMT/vk, can be a function of Nd/Nk. Until recently, linear F-V relationships for both kinesin and dynein have been used to model bead assay–based tug-of-war9,36. Although the molecular geometry is converted in our system, we expect the linear model can be the second candidate to explain our results (Model 2 is the linear F-V model)9,36,37, i.e., wk = wd = 1. The function of normalized velocity,

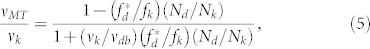graphic file with name srep05281-m5.jpg

provides fd*/fk = 0.27 and vdb = 9.5 nm s−1 by fitting to the experimental results shown in Fig. 3e (Model 2, Table 1). Very recently, a nonlinear relationship has been also discussed, for example, with kinesin-like convex up (wk > 1) or dynein-like concave up (wd < 1) curves17,18,32. Rai et al. reported that the difference between two motor groups attributed to their behavior when they work as a team17. Therefore, we also fit the normalized velocity using wk = 2 and wd = 0.5 as a nonlinear F-V model (Model 3)17,36. The resulting values were fd*/fk = 0.50 and vdb = 56 nm s−1 (Model 3, Table 1). Applying the corresponding analysis to MTs gliding to the dynein-coated region (Fig. 3f), we obtained fk*/fd and vkb, which are summarized in Table 1 along with the reported values.

Discussion

Regardless of which was the “winning” motor, the velocity markedly changed at low loads, as MT transport became dominated by the “winning” motor (Nd ≪ Nk, in Fig. 3e and Nd ≫ Nk, in Fig. 3f), and the change was small at high loads when the two motor groups were pulling the MT evenly. This implies that our fully reconstructed MT tug-of-war assay reflects a gradual velocity change due to the tug-of-war by two motor groups as observed using cell extract (see below for detailed comparison with Soppina et al.3), which indicates that the number of “losing” motors decreases with an increasing number of “winning” motors. Here, we note that our assay uses kinesin and dynein from different species that do not match to the in vivo experiments3. The characteristic has been also reported by numerical simulation in the bead assay–based tug-of-war35. F-V curves recently measured with optical tweezers are represented by wk ≥ 1 (convex up) and wd ≤ 1 (concave up), which implies that kinesin velocity is insensitive to load, whereas dynein velocity is sensitive to load17,32. In our Model 1, however, wk = 0.24 (i.e., wk < 1) does not agree with either the linear or nonlinear models (wk ≥ 1), and wd = 0.41 is in good agreement with the nonlinear model (wd = 0.49)17. The conventional mean field model assumes that the total load is evenly generated by Nd dyneins with a detachment force, fd*, for MTs gliding to the kinesin-coated region, and Model 1 cannot explain our tug-of-war phenomenon because of the large discrepancy of the wk value as compared with previous results17,32,36. Therefore, in the other two models, we assumed typical linear and nonlinear models by applying wk = wd = 1 for Model 2 and wk = 2 and wd = 0.5 for Model 3, because our gliding assay–based molecular system is simply inverted compared with the bead assay–based system. This setting of w-values fulfills the characteristics of a single kinesin or dynein motor, i.e., the sensitivity of velocity to load.

Because all three models yield fd*/fk and fk*/fd, and stall forces, fk and fd, are widely measured by manipulating a motor-coated bead with optical tweezers, we were able to calculate detachment forces for a single motor in the retrograde direction. When we used typical values fk ~ 6 pN35,37 and fd ~ 1.1 pN17, the detachment forces for kinesin and dynein were calculated as fk* = 2.3–2.4 pN and fd* = 1.6–3.0 pN from our Model 2 and 3 (Table 1). The value for fk* was in close agreement to the value of 3 pN that was previously used to model kinesin detachment9,39. However, values for fd* that had been reported previously are below 1 pN9,36, which shows slight discrepancy from our result. Compared with kinesin, dynein is more tenacious in the superstall catch-bonded state when ~10 dyneins are used17. As our tug-of-war involves ~100 dyneins, the tenacity may be greatly enhanced, leading to higher fd* values.

The other two values obtained in Models 2 and 3 are backward velocities for kinesin, vkb, and dynein, vdb, both of which are highly deviated from the values obtained by single-molecule measurements. When stall forces of 7–8 pN were applied, a vkb of 6 nm s−1 was previously measured for a single kinesin molecule40. However, at high forces above 10 pN, kinesin detached after a few or no backward steps. As >10 pN is calculated even for 10 kinesins pulling cargo35, multiple “winning” dynein motors propel a MT against >10 pN in our molecular configuration, in which several tens of kinesins are working as a load. This implies that the “losing” kinesin motors are simply detached from the MT. Therefore, the calculated vkb values (503 nm s−1 from Model 2 and 456 nm s−1 from Model 3) are much larger than that measured at a single molecule and simply indicate the detachment velocity without steps in the retrograde direction. It is also obvious that vkb values are much smaller than original MT gliding velocity on a dynein-coated surface (1.45 ± 0.14 μm s−1) due to load generated by kinesins. In contrast to vkb, vdb values (9.5 nm s−1 from Model 2 and 56 nm s−1 from Model 3) are smaller than a reported value (72 nm s−1)9. This decrease can also be explained by the catch-bond state of dynein, because dynein sustains a load because of its tenacious characteristics when multiple dyneins pull a MT that eventually glide to the kinesin-coated region.

To examine the validity of Model 2 and 3, we compared ratios of the motor number, Nd/Nk in Fig. 3e and Nk/Nd in Fig. 3f, when a MT is balanced at the boundary, i.e. the normalized velocity is equal to zero. For Model 2, when MTs glide to the kinesin- and dynein-coated regions, Nd/Nk are 3.8 and 2.2, respectively. For Model 3, the corresponding values for Nd/Nk are 2.0 and 2.1. As Nd/Nk values are supposed to match regardless of which regions a MT glide to, we conclude that Model 3 depict our molecular system better than Model 2. In return, we apply Model 3 to a bead assay–based tug-of-war to derive a ratio of the motor number when velocity is determined. When average velocities of 2.3 μm s−1 in dynein-driven transport and 0.4 μm s−1 in a tug-of-war measured for Dictyostelium endosomes were used3, their normalized velocity of 0.17 provides Nk/Nd = 0.3 in our Model 3 (Fig. 3f). This ratio falls in the range of their results, as they reported an endosome was transported by one to two kinesins and four to eight dyneins. Taken together, although our vkb and vdb cannot be directly compared with values that were measured with optical tweezers for a single motor, other values fall within a reasonable range compared with those reported using the bead assay–based system for a countable number of molecules.

In summary, we have shown the tug-of-war of MTs by using the boundary between kinesin- and dynein-patterned regions that were defined by combining photolithography and SAM coating. With the optimum sequence of protein injection into the flow cell, the two regions were completely segregated by the opposite polarity motors, which was confirmed by the behavior of PMMTs. MTs experienced many different states at the boundary because of their multiple attachments and detachments to the two regions, which ultimately resulted in detachment from or gliding in one of the regions. Group 4 MTs showed tug-of-war that was due to simultaneous motility of the two motor groups. Whether kinesin or dynein was the “winner” in the tug-of-war, MTs were not motile when the force generated by the two motors was balanced. Finally, velocity increased exponentially during gliding to either region. Based on the conventional F-V relationship, the relationship between the ratio of the motor number and the velocity was applied to explain the phenomena by assuming that the “loser” contributes the load to the MT. Adopting values of stall force and linear/nonlinear parameters from previous studies, the backward detachment force and velocity for a single molecule were derived, although >100 motors are involved in the assay. More interestingly, as nonlinear F-V relationship (Model 3) best fits our results, the tenacious nature of dynein and non-collective characteristic of kinesin are preserved even in the teamwork with >100 motors12,17,18,19. Apart from tug-of-war studies based on the bead-assay format using an immobilized MT in vitro, the proposed molecular configuration introduces a way to explore the phenomena in further detail.

Methods

Microfabrication

Fused quartz silica substrate (20 mm × 30 mm, Corning 7980) was immersed in a piranha solution (H2SO4/H2O2 = 7:3) for at least 1 h and then washed thoroughly with deionized water. For dehydration, the substrate was baked for 5 min at 200°C. A negative photoresist (ZPN1150-90, Zeon Corp.) was spincoated at 3,000 rpm for 20 s and baked at 90°C for 90 s. Conventional photolithography by UV exposure (90 mJ cm−2) and development in NMD-3 (2.38% TMAH, Tokyo Ohka Kogyo Co.) solution for 60 s created a 100-μm line-and-space pattern based on the resist. Chromium (3 nm) and gold (12 nm) layers were thermally deposited and partially removed using a lift-off process in acetone (>20 min).

Self-assembled monolayer (SAM) formation

Substrate cleaning was critical for selective immobilization of the SAM on the gold surface. The gold-patterned fused silica substrate was immersed in an ultrasonic bath filled with acetone for 10 min, ethanol for 2 min, and isopropanol for 2 min. Then, the substrate was transferred to a bath with ammonium hydroxide solution (NH4OH/H2O2/H2O = 1:1:5) at 90°C for 20 min and then washed thoroughly with deionized water. This is the substrate cleaning process that we optimized for the following SAM coating.

A thiol solution of 20 μM HS-(CH2)11-EG3-biotin (TH 004-m11.n3-0,1, Altec Group) was prepared in ethanol. The cleaned substrate was immersed in the solution for >12 h and then rinsed ultrasonically in ethanol for 5 min to remove excess molecules. The substrate was stored in ethanol in the dark until use. This process resulted in the SAM grafting onto the gold-coated surface only, while leaving the other fused silica substrate uncoated.

Protein preparation

Tubulin was purified from porcine brains using two assembly-disassembly cycles and phosphocellulose chromatography41 and was labeled with tetramethyl rhodamine (TMR) (C1711, Molecular Probes) to generate labeled tubulin42. Protein concentrations were determined by the Bradford method using bovine serum albumin as the standard. The microtubule (MT) concentration was expressed as the tubulin dimer concentration. TMR-labeled MTs were prepared by polymerizing unlabeled and labeled tubulin (10:1) for 30 min at 37°C. Polarity marked microtubules (PMMTs) were polymerized according to a conventional method43. Briefly, short and bright seeds, which are the minus ends of long MTs, were polymerized using 1 mM guanylyl 5′-α,β-methylenediphosphonate (GMPCPP) (NU-405S, Jena Bioscience). The seeds were elongated in the presence of rhodamine-labeled tubulin, unlabeled tubulin, and N-ethylmaleimide (NEM)-treated tubulin (at a molar ratio of 2:30:5, respectively). As NEM-treated tubulin inhibits minus end polymerization, the dimmer plus end becomes elongated, resulting in PMMTs with a brighter minus end and a dimmer plus end. All polymerized MTs were stabilized by adding 20 μM paclitaxel (T1912, Sigma). The kinesin construct for MT gliding consisted of human kinesin (amino acid residues 1–573) with an N-terminal histidine tag that was purified as described23.

The expression and purification of recombinant dynein motor domains were carried out as described44,45. We used the 380-kDa motor domain (amino acids V1388–I4730) of the cytoplasmic dynein heavy chain isolated from Dictyostelium discoideum Ax2 strain. We used a GST380 construct22, in which the gene encoding the motor domain (380 kDa) was fused with a His6-FLAG-BioEase GST tandem tag at its N terminus and a SNAP-tag at the interior of the AAA2 module of the motor domain. The expression construct was introduced into D. discoideum cells, which were selected for construct expression, cultivated, and harvested. The expressed motor domain was purified with two-step affinity chromatography using Ni-NTA agarose and FLAG agarose44,45.

Selective kinesin and dynein patterning

A flow cell was constructed by placing two pieces of double-sided tape 5 mm apart on a blank coverslip (24 mm × 36 mm, Matsunami Glass) to act as spacers, and the SAM-patterned coverslip was attached to the top. The optimum protocol was derived after functional evaluation of the proteins in the two regions, the SAM-coated surface and the bare glass surface, as described in the Supplementary Discussion. The flow cell was filled with BRB80 buffer (80 mM PIPES, 1 mM EGTA, 1 mM MgCl2, pH 6.8). Then, Pluronic F108 (2 mg ml−1, BASF Corp.), a triblock copolymer (in BRB80), was introduced and incubated for 5 min to prevent nonspecific binding of proteins on the SAM surface. After unbound material was rinsed away with BRB80 buffer, a mixture of 0.1 mg ml−1 casein (C7078, Sigma) and 0.2 mg ml−1 kinesin in BRB80 buffer was introduced to the flow cell and incubated for 5 min. The flow cell was washed with BRB80 and incubated for 5 min with 0.5 mg ml−1 streptavidin (194-11643, Wako) in BRB80 with 0.5 mg ml−1 casein. Finally, 62 μg ml−1 biotinylated dynein was introduced with a 5-min incubation. MTs at 0.02 mg ml−1 in BRB80 with 20 μM paclitaxel were immobilized for 5 min, and excess MTs were washed out with BRB-O2 (BRB80 containing 36 μg ml−1 catalase, 25 mM glucose, 216 μg ml−1 glucose oxidase, 1% β-mercaptoethanol, and 20 mM DTT). Once the 1 mM ATP in the BRB-O2 buffer was introduced, MTs began gliding on the kinesin- or dynein-coated surfaces.

Optical imaging and image processing

MTs were visualized using a fluorescence microscope (IX71, Olympus) equipped with a 100× oil objective (NA 1.3) and a charge-coupled device camera (ORCA-R2, Hamamatsu). Fluorescent images were stored with an exposure time of 200 ms (5 fps) using recording software (HDR-35, Hamamatsu). As motor proteins were not fluorescently labelled, we defined the boundary between two regions under bright-field microscopy. Acquired images and videos were processed using MARK 213, ImageJ (NIH), Matlab and FIESTA46 software to measure incident angle, velocity, and length of MTs.

Author Contributions

R.Y. and J.I. designed research; R.Y., J.I. and N.K.K. performed research; J.I., H.S., H.K., T.K. and R.Y. analyzed data; and J.I., T.K. and R.Y. wrote the paper.

Supplementary Material

Supplementary Information

Supplementary Info

srep05281-s1.pdf (363.5KB, pdf)
Supplementary Information

Video S1

Download video file (453.5KB, avi)
Supplementary Information

Video S2

Download video file (216.4KB, avi)
Supplementary Information

Video S3

Download video file (5.6MB, avi)

Acknowledgments

This research was supported by PRESTO from JST. We thank Takashi Ichii for supporting SAM grafting and Fumie Oda for useful discussions.

References

  1. Welte M. A., Gross S. P., Postner M., Block S. M. & Wieschaus E. F. Developmental regulation of vesicle transport in Drosophila embryos: forces and kinetics. Cell 92, 547–557 (1998). [DOI] [PubMed] [Google Scholar]
  2. Schuster M., Lipowsky R., Assmann M. A., Lenz P. & Steinberg G. Transient binding of dynein controls bidirectional long-range motility of early endosomes. Proc. Natl. Acad. Sci. USA 108, 3618–3623 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Soppina V., Rai A. K., Ramaiya A. J., Barak P. & Mallik R. Tug-of-war between dissimilar teams of microtubule motors regulates transport and fission of endosomes. Proc. Natl. Acad. Sci. USA 106, 19381–19386 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Pilling A. D., Horiuchi D., Lively C. M. & Saxton W. M. Kinesin-1 and Dynein are the primary motors for fast transport of mitochondria in Drosophila motor axons. Mol. Biol. Cell 17, 2057–2068 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Wu X., Bowers B., Rao K., Wei Q. & Hammer J. A. 3rd Visualization of melanosome dynamics within wild-type and dilute melanocytes suggests a paradigm for myosin V function In vivo. J. Cell Biol. 143, 1899–1918 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Wacker I. et al. Microtubule-dependent transport of secretory vesicles visualized in real time with a GFP-tagged secretory protein. J. Cell Sci. 110 (Pt 13), 1453–1463 (1997). [DOI] [PubMed] [Google Scholar]
  7. Gross S. P. Hither and yon: a review of bi-directional microtubule-based transport. Phys. Biol. 1, R1–11 (2004). [DOI] [PubMed] [Google Scholar]
  8. Leidel C., Longoria R. A., Gutierrez F. M. & Shubeita G. T. Measuring molecular motor forces in vivo: implications for tug-of-war models of bidirectional transport. Biophys. J. 103, 492–500 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Muller M. J., Klumpp S. & Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc. Natl. Acad. Sci. USA 105, 4609–4614 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Toba S., Watanabe T. M., Yamaguchi-Okimoto L., Toyoshima Y. Y. & Higuchi H. Overlapping hand-over-hand mechanism of single molecular motility of cytoplasmic dynein. Proc. Natl. Acad. Sci. USA 103, 5741–5745 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hendricks A. G. et al. Motor coordination via a tug-of-war mechanism drives bidirectional vesicle transport. Curr. Biol. 20, 697–702 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Derr N. D. et al. Tug-of-war in motor protein ensembles revealed with a programmable DNA origami scaffold. Science 338, 662–665 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Furuta K. et al. Measuring collective transport by defined numbers of processive and nonprocessive kinesin motors. Proc. Natl. Acad. Sci. USA 110, 501–506 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Vale R. D., Malik F. & Brown D. Directional instability of microtubule transport in the presence of kinesin and dynein, two opposite polarity motor proteins. J. Cell Biol. 119, 1589–1596 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kane R. S., Takayama S., Ostuni E., Ingber D. E. & Whitesides G. M. Patterning proteins and cells using soft lithography. Biomaterials 20, 2363–2376 (1999). [DOI] [PubMed] [Google Scholar]
  16. Thakur G., Prashanthi K. & Thundat T. Directed self-assembly of proteins into discrete radial patterns. Sci. Rep. 3, 1923 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Rai A. K., Rai A., Ramaiya A. J., Jha R. & Mallik R. Molecular adaptations allow dynein to generate large collective forces inside cells. Cell 152, 172–182 (2013). [DOI] [PubMed] [Google Scholar]
  18. Kunwar A. & Mogilner A. Robust transport by multiple motors with nonlinear force-velocity relations and stochastic load sharing. Phys. Biol. 7, 16012 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jamison D. K., Driver J. W., Rogers A. R., Constantinou P. E. & Diehl M. R. Two kinesins transport cargo primarily via the action of one motor: Implications for intracellular transport. Biophys. J. 99, 2967–2977 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Sharp D. J., Rogers G. C. & Scholey J. M. Microtubule motors in mitosis. Nature 407, 41–47 (2000). [DOI] [PubMed] [Google Scholar]
  21. Campas O. & Sens P. Chromosome oscillations in mitosis. Phys. Rev. Lett. 97, 128102 (2006). [DOI] [PubMed] [Google Scholar]
  22. Numata N., Shima T., Ohkura R., Kon T. & Sutoh K. C-sequence of the Dictyostelium cytoplasmic dynein participates in processivity modulation. FEBS Lett. 585, 1185–1190 (2011). [DOI] [PubMed] [Google Scholar]
  23. Yokokawa R., Tarhan M. C., Kon T. & Fujita H. Simultaneous and bidirectional transport of kinesin-coated microspheres and dynein-coated microspheres on polarity-oriented microtubules. Biotechnol. Bioeng. 101, 1–8 (2008). [DOI] [PubMed] [Google Scholar]
  24. Howard J. & Hyman A. A. Preparation of marked microtubules for the assay of the polarity of microtubule-based motors by fluorescence microscopy. Methods Cell Biol. 39, 105–113 (1993). [DOI] [PubMed] [Google Scholar]
  25. Howard J., Hudspeth A. J. & Vale R. D. Movement of microtubules by single kinesin molecules. Nature 342, 154–158 (1989). [DOI] [PubMed] [Google Scholar]
  26. Clemmens J., Hess H., Howard J. & Vogel V. Analysis of Microtubule Guidance in Open Microfabricated Channels Coated with the Motor Protein Kinesin. Langmuir 19, 1738–1744 (2003). [Google Scholar]
  27. Yoshida Y. et al. Biomolecular linear motors confined to move upon micro-patterns on glass. J. Micromech. Microeng. 16, 1550–1554 (2006). [Google Scholar]
  28. Clemmens J. et al. Mechanisms of Microtubule Guiding on Microfabricated Kinesin-Coated Surfaces: Chemical and Topographic Surface Patterns. Langmuir 19, 10967–10974 (2003). [Google Scholar]
  29. Hiratsuka Y., Tada T., Oiwa K., Kanayama T. & Uyeda T. Q. Controlling the direction of kinesin-driven microtubule movements along microlithographic tracks. Biophys. J. 81, 1555–1561 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Nitta T., Tanahashi A., Hirano M. & Hess H. Simulating molecular shuttle movements: towards computer-aided design of nanoscale transport systems. Lab Chip 6, 881–885 (2006). [DOI] [PubMed] [Google Scholar]
  31. Lin C. T., Meyhofer E. & Kurabayashi K. Predicting the stochastic guiding of kinesin-driven microtubules in microfabricated tracks: a statistical-mechanics-based modeling approach. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 81, 011919 (2010). [DOI] [PubMed] [Google Scholar]
  32. Fallesen T. L., Macosko J. C. & Holzwarth G. Force-velocity relationship for multiple kinesin motors pulling a magnetic bead. Eur. Biophys. J. 40, 1071–1079 (2011). [DOI] [PubMed] [Google Scholar]
  33. Van Den Heuvel M. G., De Graaff M. P. & Dekker C. Microtubule curvatures under perpendicular electric forces reveal a low persistence length. Proc. Natl. Acad. Sci. USA 105, 7941–7946 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Fallesen T. L., Macosko J. C. & Holzwarth G. Measuring the number and spacing of molecular motors propelling a gliding microtubule. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83, 011918 (2011). [DOI] [PubMed] [Google Scholar]
  35. Klumpp S. & Lipowsky R. Cooperative cargo transport by several molecular motors. Proc. Natl. Acad. Sci. USA 102, 17284–17289 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Kunwar A. et al. Mechanical stochastic tug-of-war models cannot explain bidirectional lipid-droplet transport. Proc. Natl. Acad. Sci. USA 108, 18960–18965 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Svoboda K. & Block S. M. Force and velocity measured for single kinesin molecules. Cell 77, 773–784 (1994). [DOI] [PubMed] [Google Scholar]
  38. Kojima H., Muto E., Higuchi H. & Yanagida T. Mechanics of Single Kinesin Molecules Measured by Optical Trapping Nanometry. Biophys. J. 73, 2012–2022 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Schnitzer M. J., Visscher K. & Block S. M. Force production by single kinesin motors. Nat. Cell Biol. 2, 718–723 (2000). [DOI] [PubMed] [Google Scholar]
  40. Carter N. J. & Cross R. A. Mechanics of the kinesin step. Nature 435, 308–312 (2005). [DOI] [PubMed] [Google Scholar]
  41. Williams R. C. Jr & Lee J. C. Preparation of tubulin from brain. Methods Enzymol. 85 Pt B, 376–385 (1982). [DOI] [PubMed] [Google Scholar]
  42. Hyman A. et al. Preparation of modified tubulins. Methods Enzymol. 196, 478–485 (1991). [DOI] [PubMed] [Google Scholar]
  43. Hyman A. A. Preparation of marked microtubules for the assay of the polarity of microtubule-based motors by fluorescence. J. Cell Sci. Suppl. 14, 125–127 (1991). [DOI] [PubMed] [Google Scholar]
  44. Kon T., Nishiura M., Ohkura R., Toyoshima Y. Y. & Sutoh K. Distinct functions of nucleotide-binding/hydrolysis sites in the four AAA modules of cytoplasmic dynein. Biochemistry 43, 11266–11274 (2004). [DOI] [PubMed] [Google Scholar]
  45. Kon T., Shima T. & Sutoh K. Protein engineering approaches to study the dynein mechanism using a Dictyostelium expression system. Methods Cell Biol. 92, 65–82 (2009). [DOI] [PubMed] [Google Scholar]
  46. Ruhnow F., Zwicker D. & Diez S. Tracking Single Particles and Elongated Filaments with Nanometer Precision. Biophys. J. 100, 2820–2828 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Info

srep05281-s1.pdf (363.5KB, pdf)
Supplementary Information

Video S1

Download video file (453.5KB, avi)
Supplementary Information

Video S2

Download video file (216.4KB, avi)
Supplementary Information

Video S3

Download video file (5.6MB, avi)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES