Modeling US Adult Obesity Trends: A System Dynamics Model for Estimating Energy Imbalance Gap

Abstract

Objectives. We present a system dynamics model that quantifies the energy imbalance gap responsible for the US adult obesity epidemic among gender and racial subpopulations.

Methods. We divided the adult population into gender–race/ethnicity subpopulations and body mass index (BMI) classes. We defined transition rates between classes as a function of metabolic dynamics of individuals within each class. We estimated energy intake in each BMI class within the past 4 decades as a multiplication of the equilibrium energy intake of individuals in that class. Through calibration, we estimated the energy gap multiplier for each gender–race–BMI group by matching simulated BMI distributions for each subpopulation against national data with maximum likelihood estimation.

Results. No subpopulation showed a negative or zero energy gap, suggesting that the obesity epidemic continues to worsen, albeit at a slower rate. In the past decade the epidemic has slowed for non-Hispanic Whites, is starting to slow for non-Hispanic Blacks, but continues to accelerate among Mexican Americans.

Conclusions. The differential energy balance gap across subpopulations and over time suggests that interventions should be tailored to subpopulations’ needs.

The energy imbalance gap (EIG) is an important factor in the development of obesity and a key target of public health interventions to reduce obesity.¹ The EIG captures the average daily excess energy intake, defined as total energy intake minus total energy expenditure for some unit of time, and is a critical control parameter in the energy system; it governs the speed of change in body mass.² A related concept, maintenance energy gap (MEG), captures the increased energy intake needed to maintain higher average body weights compared with an initial (e.g., the early 1970s) distribution of body weight (i.e., heavier individuals expend more energy as a result of their body mass and hence need higher energy intake to keep their weight in equilibrium).^3,4 The MEG captures the extent of change in energy intake that is needed to turn back the obesity epidemic, and as such relates to the long-term accumulation of energy imbalance in the body mass index (BMI, defined as weight in kilograms divided by the square of height in meters) distribution and is often larger than the EIG.³ Previous studies have pointed to the importance of quantifying both the EIG and MEG to explain the magnitude of changes required to reverse the obesity epidemic, provide intervention targets, and estimate the contribution of different drivers of obesity,^3–6 but concerns have also been raised about the effectiveness of using overly simplified models of the EIG as tools to design obesity interventions.¹

Estimating the EIG at the population level requires the use of models that can capture the feedback relationships between body weight and different body tissues that store and expend energy (e.g., fat mass vs fat-free mass) as well as nonlinear changes over time.⁷ For example, the models must account for differential mortality rates by weight class to avoid underestimation of the EIG because of higher mortality among the very obese. To date, the literature has focused on estimates of the EIG and MEG for entire populations averaged over long time horizons.^3–6,8,9 These estimates lack detail on changes in the EIG and MEG over time and across subpopulations and weight groups. Correct specification of these variations is essential because people of different gender and racial/ethnic subpopulations or BMI classes may be affected differentially by the environment and may respond differently to interventions.⁷ There is also evidence that secular trends may be diverging among demographic subpopulations in the United States.¹⁰ As such, there is a clear public health need for models that are able to distinguish finer trends and provide more nuanced EIG and MEG estimations to develop and test targeted interventions.

We used system dynamics modeling to address the limitations of previous EIG models and leveraged those estimates to also calculate MEG trends for different subpopulations. Although system dynamics methodology is increasingly used in public health research to explain the complex etiology of health and disease^11–16 and to test intervention effectiveness,^17–20 we provide one of the first applications of system dynamics to the population dynamics of EIG and MEG over time as an important first step for the design of obesity prevention interventions targeting specific subpopulations. Many system dynamics applications have been based solely on simulated agents or artificial populations. To inform public health practice, models can be strengthened by connecting what we know about the biology of obesity from clinical and lab-based studies to population dynamics in a way that is explicitly linked to existing empirical data.

We used an innovative method²¹ to connect a validated individual-level model of weight dynamics²² to population-level obesity dynamics and estimate the EIG associated with different gender and race/ethnicity subpopulations, without the need to simulate a large number of individuals explicitly.¹⁶ Finally, we calculated the MEG values by using the EIG and population BMI profile dynamics. This allowed us to address 3 key questions: (1) How can the dynamics of the average EIG help explain observed changes in the prevalence of obesity in the US adult population in the past 4 decades?; (2) How do these dynamics differ across different gender, race/ethnicity, and BMI groups?; and (3) How have MEG values changed over the past 4 decades across different subpopulations?

METHODS

To estimate the EIG among adults in the United States, we carried out 3 main steps: (1) developing a population-level system dynamics model that captures BMI distribution and obesity prevalence, (2) modeling the EIG, and (3) calibrating the system dynamics model with the data from National Health and Nutrition Examination Surveys (NHANES)²³ to estimate the EIG that is consistent with the prevalence shifts of obesity in the past 4 decades by gender, race/ethnicity, and BMI groups. We then calculated the MEG trajectories by using the estimates from steps 1 to 3.

Developing the Model of Body Mass Index Distribution

We used nationally representative data from NHANES for adults aged 20 to 74 years from 1971 through 2010 and matched that with our system dynamics model to estimate the EIG across gender (male or female) and racial/ethnic (Mexican American, non-Hispanic White, non-Hispanic Black) subpopulations. For each subpopulation, we used the method developed and validated by Fallah-Fini et al.²¹ to efficiently simulate the dynamics of population BMI distribution over time. Underlying this method is an established individual-level model of body weight dynamics derived from previous work by Hall et al.²² This novel method allows us to model BMI distribution dynamics based on a validated individual-level model of body weight dynamics,²² while avoiding the computational costs that would render calibrating a detailed agent-based model infeasible for the problem at hand.

This method approximates the BMI distribution for each of J gender and racial/ethnic subpopulations by disaggregating each subpopulation into M classes corresponding to distinct BMI ranges (e.g., people with BMI corresponding to ranges such as 15 ≤ BMI < 18, 18 ≤ BMI < 20, and so on). In this study, we used 14 BMI classes after careful evaluation of a range of possible values of M. A representative individual for each of the BMI classes is modeled explicitly. These individuals represent average BMI of people in the corresponding BMI classes.

We used Hall et al.’s model of human metabolism and body-weight change²² to capture the dynamics of weight gain and loss for representative individuals over time when exposed to some average EIG. We then used the rate of change in the weight of each representative individual to formulate the rates by which population moves across different BMI classes. As a result, to represent a population of P individuals, we only need to explicitly model the representative individuals for the M different BMI classes and the corresponding population flows, rather than P explicit individuals. Because we modeled the US adult population, P is hundreds of millions whereas M is 14.

This method accurately estimates the BMI distribution and its changes over time,²¹ cuts the computational costs by more than a million times compared with the equivalent agent-based model, and allows us to calibrate the model and estimate the EIG for different subpopulations efficiently. Appendix A (available as a supplement to the online version of this article at http://www.ajph.org) provides more details on this method along with fully documented system dynamics models (Appendix C, available as a supplement to the online version of this article at http://www.ajph.org); Fallah-Fini et al.²¹ provide additional details and validation on this methodology.

Figure 1 summarizes our model’s overall structure in which the population stock-flow structure is broken by BMI classes. To make sure our model is demographically representative of the US adult population, we modeled both the rate of transition from childhood into adulthood as well as the deaths. To capture the former, we calculated the rate of 19-year-old individuals entering into the simulated (adult) population in different BMI classes for different gender and race/ethnicity subpopulations by using the weighted population fractions from each successive NHANES wave (NHANES I to 2009–2010),²³ and interpolated for intervening years for which direct population estimates from NHANES did not exist. We also used the Centers for Disease Control and Prevention’s census and vital statistics data²⁴ to capture the overall death rates. In calculating the death rates from each BMI class we took into account the differential mortality attributable to very low or high BMI by using the mortality adjustment curves developed by Gray²⁵ for men and women. Further detail regarding the calculation of mortality rates is available in Appendix B (available as a supplement to the online version of this article at http://www.ajph.org).

FIGURE 1—

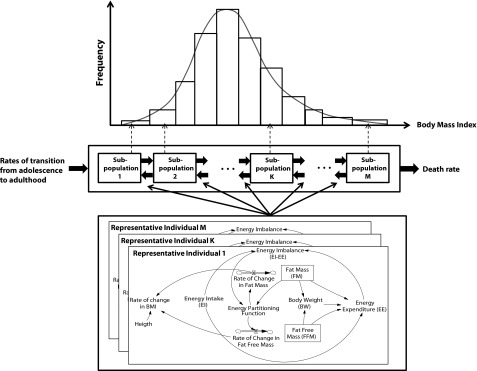
Overall structure of the system dynamics model for replicating population-level prevalence of obesity among US adults in different gender and racial/ethnic subpopulations: National Health and Nutrition Examination Survey, United States, 1971–2010.

Note. BMI = body mass index (defined as weight in kilograms divided by height in meters squared).

Source. Adapted from Fallah-Fini et al.²¹

Modeling the Energy Imbalance Gap

The energy intake and expenditure data from the NHANES food frequency and physical activity questionnaires are not precise enough to estimate the EIG precisely and reliably. Instead, we indirectly estimate the EIG with our model by inferring from observed changes in BMI.^3,4,6

We defined the EIG associated with a representative individual of any BMI class k in any subpopulation j at any time t, represented by 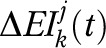as a function of the equilibrium energy expenditure, 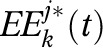of that representative individual calculated at time t (i.e., the energy required for normal activity and maintenance of the body) and an “energy gap multiplier,” represented by 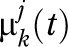, for subpopulation j and BMI class k (Equation 1).

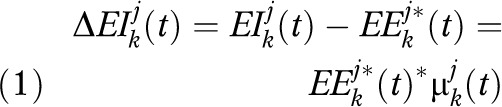The equilibrium energy expenditure of each representative individual was equal to the energy expenditure necessary for maintaining the body weight and we calculated it by using Hall et al.’s model of body weight regulation.²² We then calculated energy intake for each representative individual by adding the energy gap to the equilibrium energy expenditure for that individual. Essentially, the BMI distribution for a subpopulation will remain in equilibrium if the energy gap multiplier is zero. A multiplier greater than zero will lead to BMI growth and less than zero will reduce the BMI for that group.

We defined the energy gap multiplier 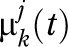as a function of 3 main components representing (1) the effect of time on energy intake of individuals, (2) the effect of BMI of individuals, and (3) the effect of the interaction between BMI of individuals and time. Equation 2 shows the structure of the equation associated with energy gap multiplier .

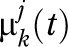We normalized the Time and BMI variables used in Equation 2 with respect to their maximum values. The BMI effect measures the relationship between the levels of individual BMI and daily EIG. Our approach differs from traditional regression-based approaches in several important ways. We specify a general model that allows very flexible, nonlinear relationships with time and BMI in the model. Parameters are not estimated by using a standard closed-form equation but through a process of calibration.

Model Calibration and Parameter Estimation

Data from NHANES²³ provide information about the distributions of BMI for different subpopulations over time. A good population-level model should be able to closely replicate those distributions observed in the past after taking into account the sampling errors. Parameter estimation and hypothesis testing can be pursued by matching the simulated BMI distributions to those observed empirically. We followed this basic intuition for parameter estimation. Specifically, the parameters forming the energy gap multiplier 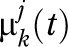were estimated such that the BMI distributions over the past 4 decades generated by the model for each subpopulation j got as close as possible to the subpopulation’s BMI distribution according to data from NHANES.

We used a maximum likelihood method for estimating the unknown model parameters. Let P_1j(t), P_2j(t), …, P_Mj(t) be the probabilities of an individual in subpopulation j falling within BMI classes 1 to M based on our simulation model of the US adult population. If a random sample of n_j(t) people is drawn from this subpopulation (in our case the NHANES samples), the probability that we observe x_1j(t),…, x_Mj(t) individuals in BMI classes 1,…,M of the sample is given by this multinomial distribution:

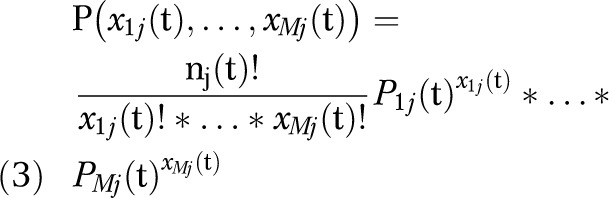We initialized the model by using BMI distributions from the first survey in which data for that subpopulation is available (1971 for non-Hispanic Whites and non-Hispanic Blacks; 1988 for Mexican Americans). (For NHANES I and NHANES II only White and Black races were identified; non-Hispanic Whites and Blacks were identified only after NHANES III. However, for simplicity we use the terms non-Hispanic Whites and Blacks in referring to the trends over the whole study period.) We then simulated the model through 2010 and calculated the likelihood of observing the BMI distributions in NHANES sample according to Equation 3. The overall log-likelihood function summed up the logarithm of these likelihood values across different survey waves (NHANES I, NHANES II, NHANES III, 1999–2000, 2001–2002, 2003–2004, 2005–2006, 2007–2008, 2009–2010). We used a nonlinear optimization method to find the parameters for energy gap multiplier that maximized the likelihood function. Those parameters inform the calculation of gender, race/ethnicity, and BMI-specific EIG values.

We repeated this process for the different gender and racial/ethnic subpopulations to provide subpopulation-specific estimates of the EIG. We conducted all simulations and optimizations in Vensim software, version 6 (Ventana Systems Inc, Harvard, MA). We conducted data processing in Stata (StataCorp LP, College Station, TX). Full system dynamics model documentation is available based on standard model reporting criteria²⁶ and provided in Appendix B (available as a supplement to the online version of this article at http://www.ajph.org).

RESULTS

Using the system dynamics model described previously and data from NHANES,²³ we estimated the EIG among US adults across different demographic subpopulations over the past 4 decades. The estimated EIG represents the average daily imbalance between energy intake and energy expenditure needed to produce observed changes in BMI distributions. These results explain, in part, the shifting prevalence of obesity in the United States. We obtained the results reported here by using the calibrated parameters reported in Table 1.

TABLE 1—

Estimated Parameter Values for Different Adult Racial/Ethnic and Gender Subpopulations: National Health and Nutrition Examination Survey, United States, 1971–2010

	Time Effect Parameters				BMI Effect Parameters			Interaction Effect Parameter
Subpopulations	B1	B2	B3	B4	B5	B6	B7	B8
Non-Hispanic White
Female	−0.0036	0.0003	0.0296	−0.0317	0.0181	−0.1470	7.8743	−0.0004
Male	−0.0999	−0.0034	0.0263	−0.0270	0.0588	0.0570	−0.3421	0.0095
Non-Hispanic Black
Female	0.0440	0.0007	0.0174	−0.0182	−0.0459	−0.0088	−0.8185	0.0059
Male	0.0306	0.0060	0.0032	−0.0060	−0.0513	−0.0819	−0.1860	0.0010
Mexican American
Female	−0.0127	0.0431	0.0165	−0.0243	0.0967	−0.0964	1.1851	−0.0602
Male	0.0999	−0.0073	0.0993	−0.0301	0.0876	0.0391	−0.6908	−0.0008

Note. BMI = body mass index (defined as weight in kilograms divided by height in meters squared).

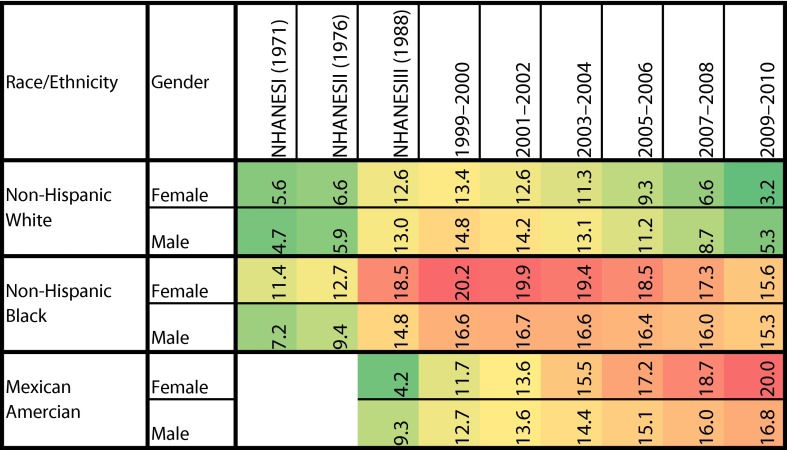
We estimated the EIG associated with each BMI class in each demographic subpopulation separately over time; results are shown in Figure 2. For each subpopulation, we also calculated the average energy gap across different BMI classes weighted by the population in that class (Figure 3). These figures are heat maps that are color-coded for intensity (green shows small or negative values for estimated EIG, yellow shows intermediate values, and red shows larger values). An EIG value of zero suggests that that group is in equilibrium and its BMI distribution is not changing. A positive value, present for most subpopulations and times, indicates increasing obesity; a negative value suggests that those subpopulations are losing weight on average. The pattern that emerges across BMI classes and subpopulations over time suggests clues about the processes that result in disparities in obesity rates.

FIGURE 2—

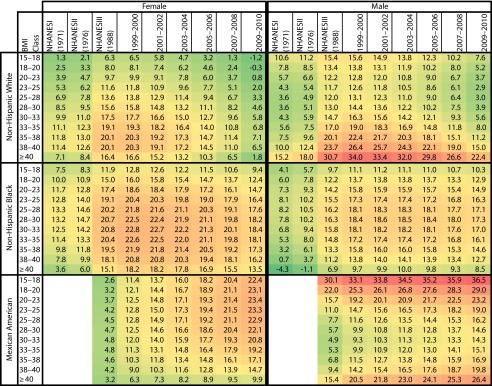
Energy imbalance gap (kcal/day) over time estimated for different gender, race/ethnicity, and body mass index groups: National Health and Nutrition Examination Survey, United States, 1971–2010.

Note. BMI = body mass index (defined as weight in kilograms divided by the square of height in meters); NHANES = National Health and Nutrition Examination Survey. Green shows small or negative values for estimated EIG, yellow shows intermediate values, and red shows larger values.

FIGURE 3—

Weighted average energy imbalance gap (kcal/day) estimated for different adult race/ethnicity and gender subpopulations: National Health and Nutrition Examination Survey, United States, 1971–2010.

Note. NHANES = National Health and Nutrition Examination Survey. Green shows small or negative values for estimated EIG, yellow shows intermediate values, and red shows larger values.

It is important to note that we could have stable BMI distributions over the population while the energy imbalance gap is positive. In essence, the energy imbalance gap leads to both changes in BMI distributions over time and the gap between the BMI distribution of individuals entering the population versus those leaving it (through death).

Energy Imbalance Gap With Respect to Time

For both non-Hispanic Whites and non-Hispanic Blacks, Figure 2 demonstrates an increase in the estimated EIG in NHANES III (late 1980s to early 1990s) in comparison with NHANES I (early 1970s) and NHANES II (late 1970s). The increase in the magnitude of the EIG continues over the next 2 survey waves (i.e., 1999–2000 and 2001–2002), followed by a gradual drop in the estimated energy gap in the last 4 waves (i.e., 2003–2004 until 2009–2010). However, none of these groups showed a negative or zero EIG, suggesting that obesity continues to increase, albeit at a slower rate.

The magnitude of the drop in the energy gap was larger in non-Hispanic Whites in comparison with non-Hispanic Blacks, so that, despite the slowdown, the EIG of the latter group is by 2010 growing at rates higher than the peak trends for non-Hispanic Whites by 2010 (Figure 3). On the other hand, Mexican Americans showed an increase in the estimated EIG over all periods (i.e., NHANES III until 2009–2010) and we observed no drop in EIG. The current EIG for this subpopulation was as large as the peak for non-Hispanic Blacks and is still increasing.

Overall women showed a larger EIG than men. However, non-Hispanic White men had a larger energy surplus in the past 3 decades, suggesting a more rapid pace of the obesity epidemic. For all subpopulations EIG trends continued to accelerate over the first 3 decades (1970–2000). The general trend over the past decade has been slowing for non-Hispanic Whites, is starting to slow for non-Hispanic Blacks, and is accelerating among Mexican Americans.

Energy Imbalance Gap Across Different Body Mass Index Classes

If individuals in different BMI classes had similar energy gaps, then the obesity trend would have resulted in an even shift of the entire distribution to the right. The observed patterns suggest that the epidemic operates at varying paces across BMI classes. Among non-Hispanic White men, the 2 tails of the distribution (BMI < 18 and BMI > 40) showed larger energy surpluses than their neighboring classes (18 ≤ BMI < 20 and 30 ≤ BMI < 40); among non-Hispanic White women, the trend was the reverse; the peak was observed among the very (but not extremely) obese class (35 ≤ BMI < 40).

For non-Hispanic Blacks, the magnitude of the energy gap was relatively high across all BMI classes in both genders. We observed the peak surplus in the overweight and obese classes. Last, among Mexican Americans, the energy gap was initially larger in the overweight and obese classes. In the past decade, this pattern has gradually shifted: the underweight, normal, and overweight classes have begun to show a larger energy gap in comparison with the obese and severely obese classes.

Estimated Maintenance Energy Gap

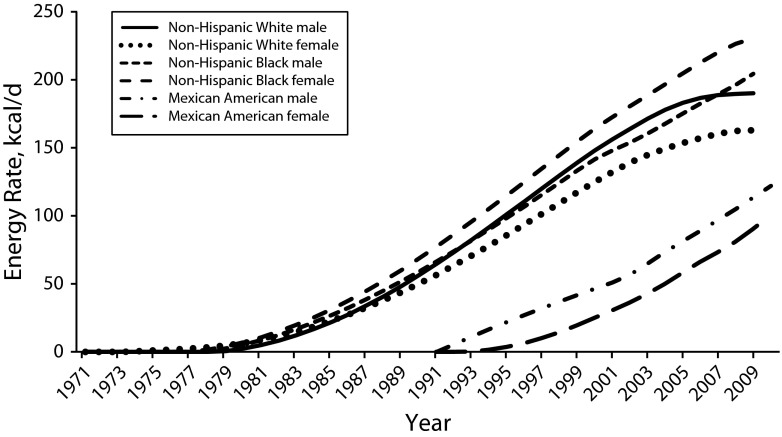
The small EIG estimated previously is the persistent excess daily energy intake over energy expenditure required to drive the weight gain over time. However, we require a substantially larger change to reverse the obesity trends.^3,5 This change can be measured by the MEG. Figure 4 shows the magnitude of MEG associated with different subpopulations, compared with the first date for which data are available. For example, comparing the BMI distribution in 2009–2010 with the NHANES I data (early 1970s), the magnitude of the MEGs associated with non-Hispanic White men (solid line) and women (dotted line) were estimated at 190 kilocalories per day and 163 kilocalories per day, respectively. Similarly, the corresponding numbers for non-Hispanic Black men and women (represented by different dashed lines) were estimated as 213 kilocalories per day and 233 kilocalories per day, respectively. These numbers characterize challenges facing public health efforts to reverse obesity rates back to the 1970s values for non-Hispanic Whites and Blacks. For Mexican American men and women, the magnitude of change required to reverse obesity rates back to those of the early 1990s were estimated as 122 kilocalories per day and 100 kilocalories per day, respectively. The MEGs associated with the past 4 decades estimated in our model are comparable with the 220 kilocalories per day MEG estimated by Hall et al.³ for US adults when comparing data between 1978 and 2005.

FIGURE 4—

The simulated maintenance energy gap associated with different adult racial/ethnic and gender subpopulations (rescaled to start from zero): National Health and Nutrition Examination Survey, United States, 1971–2010.

Another important insight gained from Figure 4 is the increase in health disparities by race and ethnicity over the past 10 years. The difference between the MEGs associated with non-Hispanic White women and non-Hispanic Black women has increased in the past decade. Similar trends are observed between MEGs associated with non-Hispanic White men and non-Hispanic Black men in the past 5 years. This observation is consistent with concerns that disparities persist or may be worsening for disadvantaged minority groups compared with Whites.²⁷

Validation of Results

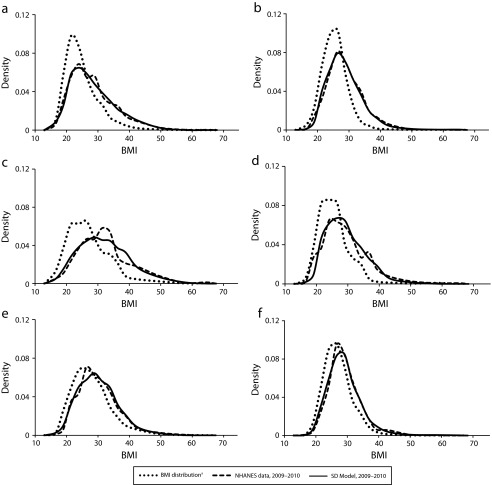
Figure 5 shows the empirical BMI distribution at the start of the simulation (i.e., NHANES I for the non-Hispanic Blacks and non-Hispanic Whites and NHANES III for Mexican Americans) along with empirical and simulated BMI distribution at the end of the simulation period (i.e., 2009–2010). The significant shifts in the BMI distributions are indicative of the progression of the obesity epidemic across different subpopulations. The model started from the initial empirical distributions, and without access to additional data, closely replicated the observed distributions 3 to 4 decades later.

FIGURE 5—

Body mass index distribution associated with first available wave of National Health and Nutrition Examination Survey data compared with empirical and model outcomes in 2009–2010 for (a) non-Hispanic White women, (b) non-Hispanic White men, (c) non-Hispanic Black women, (d) non-Hispanic Black men, (e) Mexican American women, and (f) Mexican American men: National Health and Nutrition Examination Survey, 1971–2010.

Note. BMI = body mass index, defined as weight in kilograms divided by the square of height in meters; NHANES = National Health and Nutrition Examination Survey; SD = system dynamics.

^a1971 for Non-Hispanic Blacks and Non-Hispanic Whites, 1988 for Mexican American.

We used the 1-sample Kolmogorov–Smirnov test to evaluate whether there was a statistically significant difference between the BMI distribution of the sample obtained from NHANES data and the BMI distribution generated by the system dynamics model for each subpopulation in each wave of the survey. Table 2 shows the values of the test statistics as well as the 95% significance level to test the null hypothesis that NHANES sample data has been drawn from the same BMI distribution generated by the system dynamics model. The null hypothesis is rejected only when the value of test statistics is larger than the critical value. Out of 50 possible tests, only 1 was rejected at the 95% confidence level, suggesting that there is minimal difference between the empirical distributions and those generated by the model. This increases our confidence in the ability of the model to capture the key changes in energy gap responsible for generating the observed trends in BMI.

TABLE 2—

The Results of Kolmogorov–Smirnov Test Over Time for Different Adult Racial/Ethnic and Gender Subpopulations: National Health and Nutrition Examination Survey, United States, 1971–2010

	NHANES I		NHANES II		NHANES III		1999–2000		2001–2002		2003–2004		2005–2006		2007–2008		2009–2010
Subpopulations	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value	K-S Test Statistics	Critical Value
Non-Hispanic White
Female	0.007	0.018	0.007	0.018	0.012	0.015	0.033a	0.029a	0.015	0.027	0.014	0.028	0.022	0.028	0.018	0.028	0.009	0.028
Male	0.000	0.018	0.018	0.018	0.015	0.015	0.025	0.029	0.016	0.027	0.012	0.029	0.019	0.028	0.026	0.029	0.019	0.029
Non-Hispanic Black
Female	0.000	0.051	0.044	0.050	0.015	0.037	0.064	0.069	0.048	0.065	0.052	0.067	0.016	0.065	0.058	0.066	0.029	0.064
Male	0.000	0.057	0.026	0.055	0.032	0.041	0.070	0.076	0.059	0.073	0.024	0.074	0.058	0.072	0.039	0.073	0.040	0.071
Mexican American
Female	. . .	. . .	. . .	. . .	0.000	0.057	0.046	0.093	0.040	0.085	0.047	0.085	0.037	0.083	0.011	0.083	0.021	0.079
Male	. . .	. . .	. . .	. . .	0.000	0.055	0.041	0.091	0.041	0.082	0.041	0.080	0.049	0.078	0.030	0.076	0.037	0.074

Note. K-S =  Kolmogorov–Smirnov; NHANES = National Health and Nutrition Examination Survey.

^aSignificance level = 95%.

DISCUSSION

System dynamics models offer a tool for researchers modeling complex public health issues such as the obesity epidemic. By combining nationally representative surveillance data with a state-of-the art model of individual-level energy metabolism, we demonstrate a system dynamics modeling approach that characterizes the dynamic EIG patterns that underlie the rise in obesity over the past 4 decades. We demonstrate how these dynamics differ across different gender, race/ethnicity, and BMI groups. We also show how those estimates can be leveraged to calculate MEG trends for different subpopulations. This model can be used as a base model to test hypotheses about the population drivers of the obesity epidemic and to conduct simulations testing the effects of different public health interventions on the prevalence of obesity among different demographic groups.

Our results are comparable to those documented by previous studies. According to Hall et al.,³ the EIG underlying the development of obesity in US adults in the past 3 decades is about 30 kilojoules or 7.2 kilocalories per day. Swinburn et al.⁴ reported that an increase in total energy intake of 5.5% per decade (i.e., average increase of 0.55% per year), would have been needed to drive the observed average weight gain for US adults since the early 1970s. Hill et al.⁵ estimated that 15 kilocalories per day of positive energy balance can explain the median weight gain (about 1–2 pounds per year) of US adults in the past 2 decades. However, our results show more nuanced and detailed energy gap trends than previously published studies.^3–5

A key finding is that the pattern of EIG change over time is heterogeneous across demographic groups. Our results suggest an earlier onset of energy surplus among non-Hispanics. We also show differences between non-Hispanic Blacks and non-Hispanic Whites in rates of decline in energy surplus in the past decade that may have exacerbated subpopulation disparities in obesity. These findings confirm the persistence of health disparities during the past 10 years as reported by May et al.²⁷

The relatively large EIG across all BMI groups among non-Hispanic Blacks suggests that interventions targeting only the obese and severely obese groups are less likely to succeed at the population level because of the driving energy surplus among those in the lower BMI classes. By contrast, among non-Hispanic Whites, lower BMI classes face a slower upward pressure and obese and severely obese BMI classes show a much larger EIG. The trend for Mexican Americans is striking; the energy surplus is high among all BMI classes and shows no sign of abating. Widespread and significant behavioral changes are needed to decrease the EIG and slow the obesity epidemic in this subpopulation. These findings are consistent with the report by Ogden and Carroll²⁸ that, despite a leveling of the trend in overweight adults, there has been a substantial increase in extreme obesity in the past 20 years, and illustrate that the recent stabilization of this trend reflects differences in trends among demographic groups.

Implications

The EIG poses a significant challenge to public health researchers because it is driven by major economic and social trends with significant inertia.^29,30 The current EIG trajectories provide some indication of the near future. First, as a matter of basic energy balance law, population groups will continue to gain weight until their average EIG is zero; only then will the obesity epidemic abate. Furthermore, a decline in obesity will require negative EIG values, which we did not find for any subpopulation or period in our study.

Although there is some evidence that obesity trends may be leveling off,³¹ our results suggest that the plateau may not be as close as anticipated and that, to increase effectiveness, public health interventions should target specific subpopulations. In 2010 all groups demonstrated positive energy gaps, with non-Hispanic White women being closest to a real plateau, followed by non-Hispanic White men. If the EIG decline has continued among these groups over the past 3 years, they may currently be approaching peak population obesity. Should the decline in EIG continue over the coming years, a gradual decline in BMI and obesity is conceivable. However, our results suggest that the EIG for the other 2 racial/ethnic subpopulations remains high, suggesting potential for a widening of obesity disparities. Non-Hispanic Blacks show a slower decline in EIG than non-Hispanic Whites. If this decline continues, it will take another 10 to 20 years to reach the peak obesity prevalence. The trends for Mexican Americans show an increasing EIG and thus continued acceleration in the obesity epidemic. Without effective, targeted policies and interventions, if processes similar to those that have slowed the growth of the EIG in other racial/ethnic subpopulations are to change the trends for Mexican Americans, another 2 to 3 decades may pass before we see obesity peak in this subpopulation.

Conclusions

Despite reports of a plateau in population-level obesity prevalence in the United States,^27,28,32 we have demonstrated substantial variation in the EIG, an important factor in the development of obesity, across multiple subpopulations. This highlights the need for an analytic tools, such as the system dynamics model described here, that allow public health researchers to isolate EIG and MEG differences in separate subpopulations, rather than in the entire population.^3-6,8,9 A national trend toward slowing or flat increases in average BMI may mask continued increases among the most obese.²⁸ Our model is able to test hypotheses about how policy or environmental changes may contribute to this uneven progress. Our model can also be used to determine the extent by which the reported obesity plateau is a compositional phenomenon, an artifact of higher transition of less obese adolescence to adult population, or the first wave of higher mortality in the most obese.

Our results demonstrate the strengths of a multidisciplinary, systems science approach to the study of energy imbalance and suggest several areas for future public health research. First, although we have demonstrated heterogeneity in the EIG and MEG trends, the behavioral and environmental factors that explain these trends have not been identified. This is a ripe area for further research using system dynamics models that allow for different social and environmental mechanisms to be measured and tested. Another fruitful direction is to assess the differential impact of public health interventions on subgroups and BMI classes to identify those interventions that may have the greatest potential impact and design for subgroups. Future public health research should focus on understanding the differences in EIG among multiple subpopulations to inform the design and testing of future interventions to address the subpopulation differences underlying the obesity epidemic.