Bending of the Looping Heart: Differential Growth Revisited

Short abstract

In the early embryo, the primitive heart tube (HT) undergoes the morphogenetic process of c-looping as it bends and twists into a c-shaped tube. Despite intensive study for nearly a century, the physical forces that drive looping remain poorly understood. This is especially true for the bending component, which is the focus of this paper. For decades, experimental measurements of mitotic rates had seemingly eliminated differential growth as the cause of HT bending, as it has commonly been thought that the heart grows almost exclusively via hyperplasia before birth and hypertrophy after birth. Recently published data, however, suggests that hypertrophic growth may play a role in looping. To test this idea, we developed finite-element models that include regionally measured changes in myocardial volume over the HT. First, models based on idealized cylindrical geometry were used to simulate the bending process in isolated hearts, which bend without the complicating effects of external loads. With the number of free parameters in the model reduced to the extent possible, stress and strain distributions were compared to those measured in embryonic chick hearts that were isolated and cultured for 24 h. The results show that differential growth alone yields results that agree reasonably well with the trends in our data, but adding active changes in myocardial cell shape provides closer quantitative agreement with stress measurements. Next, the estimated parameters were extrapolated to a model based on realistic 3D geometry reconstructed from images of an actual chick heart. This model yields similar results and captures quite well the basic morphology of the looped heart. Overall, our study suggests that differential hypertrophic growth in the myocardium (MY) is the primary cause of the bending component of c-looping, with other mechanisms possibly playing lesser roles.

1. Introduction

For more than a century, researchers have studied the physical mechanisms of cardiac looping [1–4]. During looping, the initially straight HT transforms into a curved tube, laying out the basic pattern of the future four-chambered pump. This paper focuses on the first phase of this process, called c-looping, as the HT bends and twists into a c-shaped tube [1,3]. Experiments have suggested that the bending and torsional components of c-looping are driven primarily by forces intrinsic and extrinsic to the HT, respectively [4–8]. Although the external forces that drive cardiac torsion are now becoming clear, the internal forces that cause the HT to bend remain poorly understood [3,4,7–9].

Some of the early theories for bending of the HT focused on growth. Patten [1] proposed that the HT is forced to bend simply because it outgrows the distance between its constrained ends. This idea was contradicted three decades later, however, when Butler [5] found that the isolated HT bends in culture (see also Ref. [6]). Others speculated that differential growth causes bending [10], but Sissman [11], and Stalsberg [12] measured mitotic rates in the MY and found no clear spatial patterns. Differential growth was thus ruled out as a causal mechanism because it was generally thought that the embryonic heart grows primarily by hyperplasia (more cells), rather than by hypertrophy (bigger cells) as it does after birth [13,14]. Finally, Manasek et al. [15] postulated that growth (or swelling) of the acellular cardiac jelly (CJ), combined with the constraint of a relatively stiff dorsal mesocardium (DM), drives bending of the HT, but later experiments showed that looping occurs even when CJ is chemically removed [16,17].

These results led most researchers, including us, to conclude that growth does not play a major role in looping. Other potential bending mechanisms include differential contraction [18], differential adhesion [17,19], and active changes in myocardial cell shape [8,20]. Considering all of the various possibilities in light of both old and new data, we recently postulated that HT bending is caused by active cell-shape changes driven by the forces of actin polymerization [8]. This hypothesis, however, has not yet undergone definitive testing.

A recent study by Soufan et al. [21] has caused us to reconsider growth as a potential driver for HT bending. These investigators constructed detailed maps of cell proliferation and cell size in the embryonic chick heart [21]. They found that relatively little cell division occurs in the HT during c-looping (stages 10–12- of Hamburger and Hamilton [22]), although relatively high mitotic rates were found in the DM and parts of the omphalomesenteric veins (primitive atria). These results support the generally accepted view that cellular hyperplasia does not bend the HT. In contrast, they found clear patterns of cellular hypertrophy, with cells at the outer curvature (OC) of the looped tube becoming significantly larger than those at the inner curvature (IC). This pattern is consistent with differential growth being a possible mechanism for bending.

Here, we use experiments with isolated embryonic chick hearts, along with computational models, to explore differential hypertrophic growth as a mechanism for the bending component of c-looping. Isolated hearts bend in culture without the complicating effects of external loads, which alter the shape of the HT near its ends [5,6]. Our results indicate that patterns of growth measured by Soufan et al. [21] are sufficient to cause the observed deformation, as quantified by measured morphogenetic strains. However, experimental wall stress distributions are not completely consistent with those given by the model, suggesting that other mechanisms also may be involved. Further study indicated that HT bending is driven primarily by differential growth, with CJ swelling, DM tension, and active changes in myocardial cell shape playing secondary roles. We suggest that these results add new understanding to this important problem in cardiac development.

2. Background

2.1. Structure of the Early Heart Tube.

At Hamburger-Hamilton (HH) stage 10 (33–38 h of a 21-day incubation period) [22], the chick heart is a relatively straight tube consisting of three layers (Figs. 1(a) and 1(a′))—an outer two-cell-thick layer of MY, a one-cell-thick inner layer of endocardium, and a relatively thick middle layer of CJ (extracellular matrix). The HT is connected cranially to the outflow tract (conotruncus), and its posterior end gradually lengthens during c-looping by fusion of the two lateral omphalomesenteric veins. The MY layer is initially anchored to the foregut of the embryo by the DM, which ruptures as the HT loops. An endodermal membrane called the splanchnopleure presses against the ventral surface of the HT.

Fig. 1.

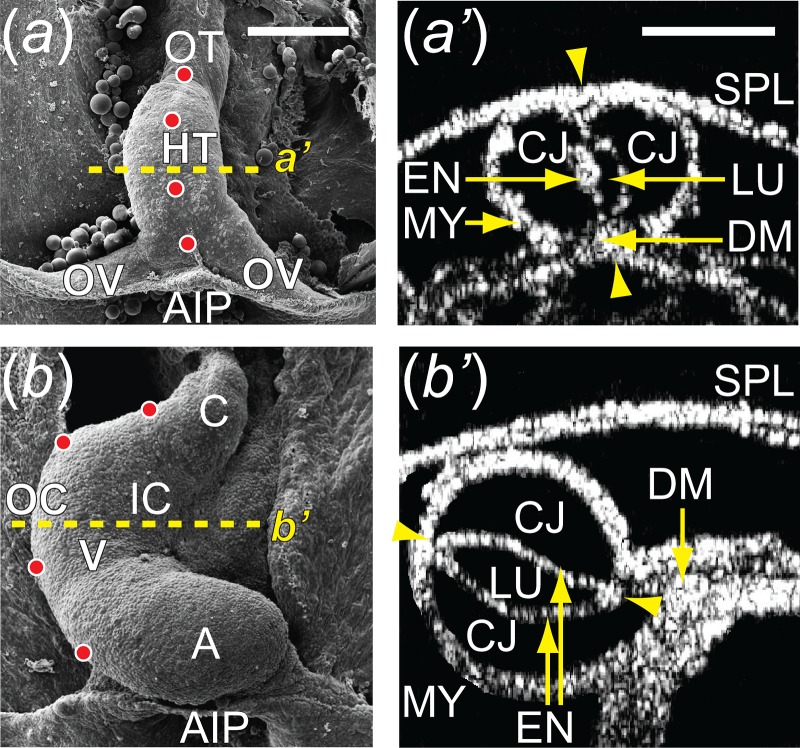
Cardiac c-looping of chick embryo. ((a) and (b)) SEM images of embryonic chick hearts during c-looping (ventral view). The originally straight HT at HH10 (a) bends ventrally and rotates rightward, transforming into a c-shaped tube at HH12 (b). To help visualize rotation, artificial labels (dots) along the ventral midline of the HT at HH10 move to the outer curvature of the HH12 heart. The splanchnopleure membrane was removed to reveal the HT. ((a′) and (b′)) Rotation of the HT is shown by the orientation of the elliptical lumen (arrowheads) in OCT cross sections taken midway along the length of the HT (dashed lines in (a) and (b)). A = atrium, AIP = anterior intestinal portal, C = conotruncus, CJ = cardiac jelly, DM = dorsal mesocardium, EN = endocardium, IC = inner curvature, LU = lumen, HT = heart tube, MY = myocardium, SPL = splanchnopleure, OC = outer curvature, OT = outflow tract, OV = omphalomesenteric veins, V = ventricle. Scale bars: 200 μm.

During approximately the next 12 h (to HH12), the HT gradually bends ventrally and twists rightward, transforming into the shape of the letter “c” as the original ventral and dorsal sides become the OC and IC, respectively (Figs. 1(b) and 1(b′)). Although bending and twisting are coupled to some extent, studies have shown that the torsional component of c-looping is caused by external forces exerted by the splanchnopleure and the omphalomesenteric veins, while bending is driven by forces generated within the HT [5–7].

2.2. Possible Bending Mechanisms During C-Looping.

Over the years, several hypotheses have been proposed for the mechanism of heart bending [4]. Some of the most prominent hypotheses are summarized below.

CJ Swelling With DM Constraint.

Cardiac jelly is secreted by the MY and can change its volume in response to alterations in ambient osmolarity [23]. Manasek et al. [15] speculated that CJ swelling pressure inflates the HT with a relatively stiff DM locally restricting longitudinal extension along the dorsal side, causing the HT to bend ventrally. This idea was later supported by two pieces of evidence: (1) the MY is in a state of tension, likely due to CJ pressure [7,24]; and (2) the DM at the IC is 2–3 times stiffer than the rest of the HT [25]. However, other studies seemingly contradicted this hypothesis by showing that dissolving the CJ with hyaluronidase does not prevent looping [16,17]. On the other hand, these studies were done on whole embryos in which the results are complicated by the effects of torsion, and the lack of CJ made the hearts appear flaccid and abnormally shaped. Here, to help clarify this issue, we repeated these experiments using isolated hearts and obtained similar results.

DM Tension.

Experiments have shown that the MY and DM are under tension in the HT during c-looping [7,24] (see also Fig. 6(c)). Taber et al. [26] speculated that pre-existing tension in the DM causes the dorsal side of the HT to shorten as the DM ruptures, resulting in ventral bending of the HT. The authors used a mathematical model to demonstrate the plausibility of this mechanism, but they also suggested that other mechanisms probably are involved.

Fig. 6.

Residual stresses in the myocardium as revealed by microsurgical cuts. (a) Linear cut in heart tube cultured for 24 h. Opening of the circumferential cut indicates tensile longitudinal stress. Cut aspect ratio (α), defined as opening width (w) divided by cut length (l) in the local myocardial plane (see panel (c)), characterizes tension in the myocardium. (b) Aspect ratios for cuts made near the OC or IC of control hearts before (0 h) or after (24 h) culture. Subscripts z and θ denote longitudinal and circumferential tensions, respectively (${\hspace{0.17em}}^{*}p\hspace{1em}<\hspace{1em}0.001,{\hspace{0.17em}}^{**}p\hspace{1em}=\hspace{1em}0.011$). (c) Opening (dashed ellipses) and closure (dashed lines) of representative cuts show residual stress states in control hearts before (0 h) and after (24 h) culture. Outward and inward arrows indicate tension and compression, respectively. Since cuts made near the IC of bent hearts usually do not open, aspect ratios were reported as 0 in (b). Scale bars: 200 μm.

Cytoskeletal Contraction.

Myosin-based contraction serves as a fundamental force-generating process during morphogenesis [27–29]. Recent studies have shown, however, that c-looping in both whole chick embryos and isolated hearts does not require either sarcomeric contraction, which causes the heartbeat, or nonsarcomeric contraction, which drives morphogenesis [9]. Nevertheless, contraction likely plays a role in the formation of the HT before looping begins [9,29], and Nerurkar et al. [30] showed that contraction can play a backup role in cardiac torsion when normal loads supplied by the splanchnopleure are removed. Hence, it remains possible that cytoskeletal contraction also has some effect on bending, and we explore this prospect here.

Active Cell-Shape Change.

It has been observed that myocardial cells undergo changes in shape during c-looping [20], but it is not clear whether these shape changes are actively generated and cause bending or whether they are a passive response to bending driven by some other mechanism. Manasek et al. [20] speculated that the former is true. Using scanning electron microscopy (SEM), they found relatively small cells randomly orientated in the prelooped HT; in the looped heart, myocardial cells at the OC were larger in surface area with arbitrary orientations, whereas those near the IC were elongated in the circumferential direction. We used computer modeling to illustrate how these changes in cell shape can cause the HT to bend [8,26] and suggested that these shape changes may be driven by actin polymerization, because drugs that inhibit polymerization prevent looping [8]. However, since blocking actin polymerization can affect a variety of cellular activities [31–34], these results are not conclusive.

Differential Growth.

As mentioned in the Introduction, researchers in general have ruled out differential growth as a possible cause of looping after failing to find significant differences in cell proliferation and death over the HT [2,11,12]. Recently, however, Soufan et al. [21] found that, whereas cells proliferate at a relatively slow and uniform rate in the HT, cells increase in volume significantly during c-looping in spatial patterns that are consistent with a causal role for ventral bending. (The significant cell proliferation found in the DM and omphalomesenteric veins is more likely to affect torsion than bending [7,30,35].) Their results show that from HH10 to HH12-, when most of the bending occurs, myocardial cell volume increases 2–3 times more on the ventral side than on the dorsal side of the HT. A main goal of this paper is to reevaluate hypotheses for bending in light of these new findings.

In all, we have given a brief review of five proposed mechanisms for the bending component of c-looping. It is important to emphasize that evolution has led to redundancy in morphogenesis, and normal looping may require multiple mechanisms [2,4]. In the current study, we consider these mechanisms individually as well as collectively.

3. Experimental Methods

3.1. Preparation and Culture of the Embryonic Heart.

Fertile white Leghorn chicken eggs (Sunrise Farms, Catskill, NY) were incubated in a humidified atmosphere at 38 °C for 36–48 h to yield embryos at HH stages 10–12. Embryos were extracted from the eggs using filter paper rings (Waterman, No.2) [36] and rinsed in PBS. The sandwich structure of embryo and filter paper rings was covered with liquid culture media to a depth of approximately 5 mm to eliminate surface tension artifacts [36], and a stainless steel ring was placed on top of the paper rings to hold them in place.

To eliminate the complicating effects of external loads, as well as to allow better access for manipulation, we studied bending in isolated hearts. First, the splanchnopleure was removed using a fine glass needle. Then, the cranial, caudal and dorsal connections of the HT to surrounding tissues were severed with microscissors (Fine Science Tools, Foster City, CA), and the isolated heart was transferred by pipette to a sterile culture dish (Fisher Scientific, 35 mm) containing media. To prevent cell adhesion and spreading over the stiff plastic substrate, the culture dish was covered with a relatively soft agarose gel (0.3% agar, Sigma, Sigma-Aldrich, St. Louis, MO) [8]. Culture dishes were then sealed in plastic bags filled with a humidified mixture of 95% O₂ and 5% CO₂, and put into an incubator for continued 24 h culture [36].

For controls, we used media consisting of 89% Dulbecco's modified Eagle's medium (DMEM, Sigma), 10% chick serum (Sigma), and 1% antibiotics [36]. For chemical perturbation, one of the following drugs was added to the culture media: blebbistatin (Bleb, 30 µM, Sigma), a myosin-II inhibitor, to inhibit cell contractility [9]; cytochalasin D (CytoD, 100 nM, Sigma) to block actin polymerization [8]; or ovine hyaluronidase (Hyal, 20 UTR/mL, Sigma) to dissolve the CJ [16,17]. To prevent Bleb from being photoinactivated, tin foil was used to cover the media and dishes during culture and manipulation. In this study, we used 176 isolated chick hearts: 81, 52, 35, and 8 for the control group and hearts treated with Bleb, CytoD, or Hyal, respectively. In some samples, to examine the short-term effects of drug perturbations, culture was stopped briefly at 1 h and resumed immediately after images were taken.

3.2. Optical Coherence Tomography.

Optical coherence tomography (OCT) is a noninvasive imaging technique that can provide sub-surface structural information of living tissues with high spatial resolution (∼10 µm) and relatively good penetration depth (up to ∼2 mm) [37]. Therefore, OCT is ideal for imaging the early development of chick embryos [37]. Images were obtained with a commercial OCT system (Thorlabs, Newton, NJ), and 3D tissue geometries were reconstructed using image analysis software (Volocity, PerkinElmer, Waltham, MA).

3.3. Strain Measurements.

Morphogenetic strains in the MY were measured by tracking the movements of fluorescent tissue labels. Prior to heart isolation, DiI (D282, Life Technologies, Carlsbad, CA) labels were injected into the MY via pulled glass micropipettes using a pneumatic pump (PicoPump PV830, World Precision Instruments, Sarasota, FL) and a micromanipulator (Sutter Instrument, Novato, CA) [7]. To quantify myocardial deformation along the longitudinal direction, three labels were evenly placed along either the ventral or dorsal side of the HH10 HT (see Fig. 5(a)). To do this, we first removed the splanchnopleure over the heart in the intact embryo and injected ventral labels along the midline of the HT. Then, we dissected the DM on one side to expose the dorsal side to the injection apparatus and injected labels near the remnant of the DM. Lastly, the DM on the other side was severed, and the conotruncus and omphalomesenteric veins were cut to remove the HT from the embryo.

Fig. 5.

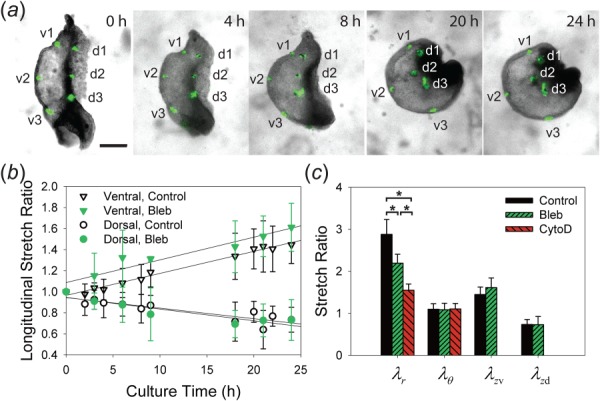
Morphogenetic strains measured during bending of the isolated heart. (a) Fluorescent labels were injected on the ventral (v) and dorsal (d) sides of the HT to measure longitudinal strains. (b) Longitudinal stretch ratios (${\lambda }_{zv}\hspace{1em}>\hspace{1em}1,{\lambda }_{zd}\hspace{1em}<\hspace{1em}1$) indicate ventral elongation and dorsal shortening in both control hearts and hearts treated with 30 μM blebbistatin (Bleb). Linear regressions (solid lines) suggest longitudinal stretch ratios change linearly with time (for control and Bleb-treated hearts, R ²= 0.9839, 0.9157 for ${\lambda }_{zv}$ and R ²= 0.7831, 0.8409 for ${\lambda }_{zd}$, respectively). (c) Summary of all myocardial stretch ratios after 24 h culture: radial ${\lambda }_r$, circumferential ${\lambda }_{\theta }$, longitudinal on the ventral side ${\lambda }_{zv}$, and longitudinal on the dorsal side ${\lambda }_{zd}$. The myocardial wall thickened less in Bleb-treated hearts than that in control, and even less in hearts treated with 100 nM cytochalasin D (CytoD; ${\hspace{0.17em}}^{*}p\hspace{1em}<\hspace{1em}0.001$, one-way ANOVA). Note that longitudinal stretch ratios were not measured in CytoD-treated hearts, where bending was inhibited. Scale bar: 200 μm.

Images were acquired immediately after isolation and every few hours thereafter during culture using a fluorescence microscope (Leica Camera Inc., Allendale, NJ) and a high magnification camera (Canon USA Inc., Melville, NY). Label tracking was performed later using image analysis software (ImageJ, NIH). Arc lengths between adjacent labels were measured over time, and longitudinal stretch ratios were computed as the current length divided by the reference length immediately after isolation.

Radial and circumferential strains in the MY were estimated from OCT time-lapse images. Since the myocardial wall thickness was relatively uniform around the HT (see Fig. 4(b)), cross sections midway along the length of the HT were selected as representative sections for analysis. Through image cropping, reslicing, and thresholding (ImageJ), the myocardial wall was traced and used to calculate its average circumference and thickness. Average radial and circumferential stretch ratios in the MY were computed by dividing the average myocardial thickness and circumference during culture by their values immediately after isolation. In hearts treated with Hyal for 24 h, however, this analysis was not feasible because the cross section collapsed, making the inner boundary of the MY ambiguous (see Fig. 4(b)).

Fig. 4.

Bending of isolated hearts in different culture conditions. (a) Ventral view of a representative HH10 chick embryo before heart dissection. (b) Lateral views and OCT cross sections of hearts isolated at HH10 (0 h) and cultured for 24 h in various conditions: control, 30 μM blebbistatin (Bleb), 20 UTR/mL hyaluronidase (Hyal), and 100 nM cytochalasin D (CytoD). Bending occurred in all cases except the CytoD-treated hearts. Significant thickening of the myocardial wall was observed in the cross sections of bent hearts (solid arrowheads), while the myocardium thickened less in the CytoD-treated heart (hollow arrowheads). DM = remnant dorsal mesocardium, IC = inner curvature, OC = outer curvature. Scale bar: 200 μm in (a) (the same for (b)).

3.4. Stress Measurements.

Myocardial stresses were estimated by introducing microsurgical incisions in the tissue [24]. The isolated heart was submerged under PBS and held by a glass micropipette with a small suction (see Fig. 6(a)). Small linear cuts were made in the MY using a Gastromaster microdissection device (Xenotek Engineering, Belleville, IL). To avoid the complication of stress alteration introduced by a second cut, only one cut was made in each heart. Immediately after cutting, OCT was used to image the wounds, which were relatively elliptical in the myocardial plane (see Fig. 6(c)). The geometry of the cut opening was obtained using image analysis software (Volocity and ImageJ), and the aspect ratio of the cut (opening width divided by cut length) was used to characterize the tension in the tissue normal to the cut direction [24]. Longitudinal and circumferential stresses correspond to circumferential and longitudinal cuts, respectively (see Fig. 6(c)).

3.5. Statistical Analysis.

Statistical analysis was performed using SigmaPlot software (Systat Software Inc., San Jose, CA). The Holm-Sidak method (one-way or two-way ANOVA) was used to compare strain and stress data among different groups. All experimental measurements are presented as mean ± SD, with statistical significance assumed for p < 0.05.

4. Computational Methods

4.1. Modeling of Morphogenesis.

For more than 30 yr, computational models have been used to simulate various morphogenetic processes [38], including some used to test other hypotheses for c-looping [26,30,35,39]. Several of these models, as well as the present model, are based on the theory for finite volumetric growth of Rodriguez et al. [40]. The detailed theoretical framework has been described previously [40], and only a short summary is given here.

Consider an elastic body that is initially in a stress-free reference configuration β (to a first approximation) when it is created in the embryo (Fig. 2). We imagine that the body is first cut into infinitesimal pieces, which undergo morphogenesis (growth, cell-shape change, etc.) defined by the morphogenesis tensor M (analogous to the growth tensor G in Rodriguez et al. [40]). This yields an intermediate stress-free configuration B. Finally, reassembly and loading of the body through the elastic deformation gradient tensor F ^* gives the current configuration b. If the distribution of M is geometrically incompatible, then the unloaded body B _R will contain residual stress. The total deformation gradient tensor is given by the relation

Fig. 2.

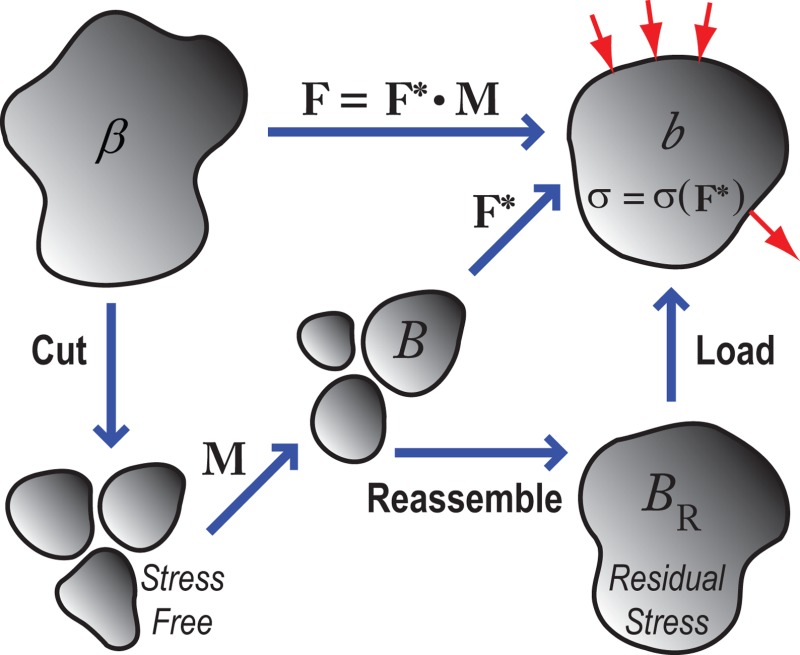
Schematic of configurations in computational modeling. Intermediate states (B, B _R) are defined between the initial unstressed (β) and the current stressed (b) configurations. The total deformation gradient tensor (F) is decomposed into morphogenetic (M) and elastic (F ^*) deformations. The Cauchy stress ($\sigma$) only depends on the elastic deformation (F ^*).

$$\mathbf{F}={\mathbf{F}}^{*}·\mathbf{M}$$ (1)

In this theory, the Cauchy stress tensor $\mathbf{\sigma }$ is a function of F ^*. The constitutive relation for a compressible material can be expressed as

$$\mathbf{\sigma }=\frac{1}{J^{*}}{\mathbf{F}}^{*}·\frac{\partial W}{\partial {\mathbf{E}}^{*}}·{\mathbf{F}}^{*\mathrm{T}}$$ (2)

where W is the strain-energy density function, $J^{*}=det{\mathbf{F}}^{*}$ is the volume ratio, and ${\mathbf{E}}^{*}=({\mathbf{F}}^{*\mathrm{T}}·{\mathbf{F}}^{*}-\mathbf{I})/2$ is the Lagrangian strain tensor, with I being the identity tensor, and T denoting the transpose. Computational models were developed using the commercial finite-element code ABAQUS (v. 6.9, SIMULIA, Providence, RI). With F being a solution variable and M specified, Eqs. (1) and (2) were implemented using a user subroutine UMAT [41], as described by Young et al. [42].

4.2. Cylindrical Model for Heart Bending.

To simulate bending of the isolated chick heart, two types of models are considered. First, to explore basic behavior, we used a cylindrical tube model for the HT. Then, we constructed a model based on realistic heart geometry. This subsection discusses the tubular model; the other model is considered later.

The idealized model for the HT at HH10 is a straight cylinder consisting of a relatively thin outer layer of MY filled with a core of CJ (Figs. 3(a)–3(c)). The lumen is omitted, as it collapses when blood pressure is lost upon isolation. The cross-sectional dimensions are scaled according to representative OCT images. Here, it is important to note that the outflow tract and a small portion of the omphalomesenteric veins are incorporated as part of the HT, since they are part of the isolated heart in the experiments. The myocardial layer is further divided into three regions of interest—ventral myocardium (VMY), dorsal myocardium (DMY), and DM. Note that the ventral and dorsal sides become the OC and IC, respectively, of the bent HT.

Fig. 3.

Finite-element models for bending of the isolated heart. ((a)–(c)) Idealized cylinder model. Due to symmetry, only the top half of the model is shown, i.e., the heart is actually about 1 mm long. ((a′)–(c′)) Model based on realistic geometry. The undeformed geometries and meshes are shown in lateral ((a), (a′)), ventral ((b), (b′)), and cross-sectional views ((c), (c′)). In both models, the heart tube consists of ventral myocardium (VMY), dorsal myocardium (DMY), dorsal mesocardium (DM), and cardiac jelly (CJ). The outflow tract and the remnant omphalomesenteric veins are considered part of the heart tube in the cylinder model, but they are included as passive structures in the realistic geometry model. The lumen is included in the realistic model but not in the cylinder model. Shown separately in (b) and (b′), a global cylindrical coordinate system {$R,\Theta ,Z$} and principal directions (${\mathbf{e}}_R,{\mathbf{e}}_{\Theta },{\mathbf{e}}_Z$) are defined in the undeformed configurations. Symmetry planes of the cylinder model are shown as dashed-dot lines in (b) and (c).

Because of symmetry, only a quarter of the HT is modeled, with symmetry conditions enforced and no external loads. In addition, a cylindrical coordinate system $\{R,\theta ,Z\}$ is defined in the undeformed tube with Θ defined as the circumferential angle relative to the DM (Fig. 3(c)). The mesh consists of quadratic brick elements with reduced integration (C3D20R). We used a moderately fine mesh (21,662 nodes, 4785 elements) that roughly follows the undeformed cylindrical geometry.

4.3. Material Properties.

Mechanical properties for MY and CJ were previously determined for the HH12 heart, and an exponential strain-energy density function was proposed [24]. At stage 12, material nonlinearity is relatively mild, and studies suggest that it increases during development [9,24,25]. Since the present study focuses on earlier stages (HH10 to HH12), we assume that the properties for both MY and CJ are nearly linear and take the strain-energy density function in the neo-Hookean form

$$W=C({\overline{I}}_1-3)+\frac{1}{D}[\frac{1}{2}(J^{*2}-1)-\ln (J^{*})]$$ (3)

where C and D are material constants, and ${\overline{I}}_1=J^{*-2/3}\mathrm{tr}{\mathbf{C}}^{*}$ is a modified invariant of the elastic right Cauchy-Green deformation tensor ${\mathbf{C}}^{*}={\mathbf{F}}^{*\mathrm{T}}·{\mathbf{F}}^{*}$. For relatively small values of D, this form of W includes slight material compressibility as fluid flows in and out of soft tissues when they deform.

From the results of Zamir and Taber [24], we take $C_{\mathrm{MY}}=4C_{\mathrm{CJ}}=13\mathrm{Pa}\equiv C_0$ and D _MY = D _CJ = 0.1. Unless stated otherwise, the material properties in the DM are taken the same as those in the MY. In this paper, all stresses are reported as dimensionless values normalized by C ₀. As discussed later, choosing an exponential form for the strain-energy density function does not significantly change the results.

4.4. Looping Simulation.

With the morphogenesis tensor M specified as a function of position and time, the simulation for bending of the HT consists of a series of five sequential steps: CJ swelling, DM dissection, MY contraction, MY growth, and active MY cell-shape change. In each step, we assume that morphogenetic processes occur primarily along principal directions relative to the tube geometry and take

$$\mathbf{M}=M_R{\mathbf{e}}_R{\mathbf{e}}_R+M_{\theta }{\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+M_Z{\mathbf{e}}_Z{\mathbf{e}}_Z$$ (4)

where M_I and e _I are the morphogenetic stretch ratio and the unit vector along direction I of the undeformed cylinder $(I=R,\theta ,Z)$. Below, we discuss the rationale and specialize M for each simulation step. The following subsection then details how experimental data were used to determine the values for the M_I in each step.

CJ Growth.

During looping, CJ continues to be created by myocardial cells, and it may also swell due to changes in osmolarity [23]. Together, these processes are simulated by isotropic growth, i.e.,

$${\mathbf{M}}_{\mathrm{j}}=M_{\mathrm{j}}({\mathbf{e}}_R{\mathbf{e}}_R+{\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+{\mathbf{e}}_Z{\mathbf{e}}_Z)\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}(M_{\mathrm{j}}>1)$$ (5)

where M _j is the CJ growth parameter, with $det{\mathbf{M}}_{\mathrm{j}}=M_{\mathrm{j}}^3$ being the relative volumetric increase of CJ. Growth of CJ inflates and stretches the MY both circumferentially and longitudinally.

The value taken for M _j is based on results from Zamir and Taber [24], who used cutting experiments and modeling to estimate the residual strain (relative to the zero-stress state) in the MY of the HH12 chick heart. They found that the residual stretch ratio is approximately isotropic in the myocardial plane with a value of about 1.3. In our experiments, the circumference of the HT remained relatively constant during looping, suggesting that CJ undergoes little additional growth as the isolated heart bends (see Fig. 4(b)). We therefore set M _j = 1.3 (Table 1) at t = 0 and hold it constant thereafter (unless noted otherwise).

Table 1.

Morphogenetic parameters of finite-element models

	M j	M t	M c	M g	M s
Cardiac jelly growth model	$1.3\to 2.0$ 1	—	1.0	—	—
Dorsal mesocardial tension model	1.3	0.3	1.0	—	—
Myocardial cell-shape change model	1.3	—	1.0	—	1.7
Myocardial differential growth model	1.3	—	1.0, 0.9 2	1.3	—
Baseline model	1.3	0.8	1.0, 0.9	1.3	1.3

¹Initial cardiac jelly growth M _j = 1.3 used in all models as the initial condition. Cardiac jelly growth model includes additional growth of 1.5 to generate bending during looping, and the total growth is 1.3 × 1.5 = 2.0.

² M _c = 1.0 for blebbistatin-treated heart and 0.9 for control.

DM Dissection.

Until about HH11, the HT is attached to the foregut of the embryo through the DM [3,4], which is in a state of tension (see Fig. 6(c)). When the heart is removed from the embryo, the DM is severed, and the remnants of the DM shorten, similar to a stretched rubber band when its ends are released. This effect is simulated by shortening the zero-stress length of the DM as given by

$${\mathbf{M}}_{\mathrm{t}}={\mathbf{e}}_R{\mathbf{e}}_R+{\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+M_{\mathrm{t}}{\mathbf{e}}_Z{\mathbf{e}}_Z\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}(M_{\mathrm{t}}<1)$$ (6)

where M _t is the DM tension parameter defined as the stress-free DM length divided by its length before dissection.

Unfortunately, the value of M _t is neither available in the literature nor trivial to measure experimentally. This is because the DM is not accessible for label injection in the HH10 embryo, unless one side of the DM is dissected to allow the HT to rotate lateral side up. This dissection, however, disturbs the stress in the DM. Hence, the value of M _t was estimated by matching the longitudinal stress and the deformed HT shape between our model and experiments. This gave M _t = 0.8 for control hearts (see Table 1 and supplemental Fig. S7*).

MY Contraction.

In previous work, we have found that the MY undergoes a general cytoskeletal contraction in response to the removal of compressive loads normally exerted by the splanchnopleure [30,43]. In contrast to the sarcomeric contraction that generates the heartbeat, cytoskeletal contraction is likely produced by actomyosin fibers localized at or near cell borders [27,28]. Our experimental observations of short-term Bleb-exposure suggest that contraction decreases the length and diameter of the HT while increasing the thickness of the myocardial wall (see supplemental Fig. S2*). Consequently, we assume that this contractile response is isotropic at the tissue level within the plane of the MY as observed, for example, during dorsal closure in the Drosophila embryo [27]. Simulating contraction as negative growth, we take

$${\mathbf{M}}_{\mathrm{c}}=M_{\mathrm{c}}^{-2}{\mathbf{e}}_R{\mathbf{e}}_R+M_{\mathrm{c}}({\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+{\mathbf{e}}_Z{\mathbf{e}}_Z)\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}(M_{\mathrm{c}}\le 1)$$ (7)

which satisfies the cellular incompressibility condition $det{\mathbf{M}}_{\mathrm{c}}=1$.

Since Bleb inhibits actomyosin contraction, we set M _c = 1 (passive tissue) to simulate the Bleb-treated heart with the other parameters remaining unchanged (Table 1). The value of M _c for the control case was chosen from our experimental estimates of radial strain caused by contraction. As discussed later, compared to the heart treated with Bleb, the MY of control hearts had approximately 30% more radial thickening (see Fig. 5(c)). We assume this difference can be attributed to cytoskeletal contraction of the MY and choose M _c = 0.9 $(M_{\mathrm{c}}^{-2}\approx 1.3)$ for the control heart (see Table 1).

MY Growth.

Experimental evidence indicates that significant cell proliferation occurs during c-looping in the foregut near the DM and in parts of the omphalomesenteric veins, which eventually are incorporated into the HT [17,21,44]. However, relatively little proliferation occurs within the MY of the HT from HH10 to HH12-, when most of the bending occurs [11,12,21]. The mitotic rate begins to increase significantly in the HT only as c-looping nears completion at HH12 [21]. Hence, we neglect the effects of cell division on cardiac bending and assume, to a first approximation, that all growth in the MY can be attributed to cellular hypertrophy.

The specific form of the morphogenesis (growth) tensor M _g is chosen based on existing data and our own experimental observations. Soufan et al. [21] found that between HH10 and HH12-, myocardial cells at the IC grow relatively little, while those at the OC become 2–3 times larger than those at the IC. Accordingly, we assume that a dorsal-to-ventral gradient exists in the spatial pattern of myocardial growth and take a linear distribution around the circumference, i.e.,

$$G(\theta )=det{\mathbf{M}}_{\mathrm{g}}=G^{\mathrm{IC}}+(G^{\mathrm{OC}}-G^{\mathrm{IC}})(\theta /\pi )$$ (8)

where $G(\theta )$ is the volumetric-growth function, with G ^IC= 1 and G ^OC= 3 at the IC $(\theta =0)$ and OC $(\theta =\pi )$, respectively, (see Fig. 3(c)).

However, since Soufan et al. [21] measured only changes in volume without considering the possibility of anisotropic growth, the spatial distribution of each component of M _g (G_R, G _Θ, G_Z) remains unknown. Thus, we must make additional assumptions.

First of all, as discussed later, our measurements show that the myocardial wall thickness increases almost uniformly during bending of the isolated heart while its circumference remains essentially constant (see Figs. 4(b) and 5(c)). These observations suggest that growth in the radial and circumferential directions is relatively uniform, and it follows that the differences in cell size measured by Soufan et al. [21] reflect dimensional changes occurring primarily in the longitudinal direction. These considerations lead us to propose a morphogenesis tensor for MY growth of the form

$${\mathbf{M}}_{\mathrm{g}}=G_R{\mathbf{e}}_R{\mathbf{e}}_R+G_{\theta }{\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+\frac{G(\theta )}{G_R{G}_{\theta }}{\mathbf{e}}_Z{\mathbf{e}}_Z$$ (9)

where G_R and G _Θ are uniform growth parameters, G/(G_R G _Θ) = G_Z, and $det{\mathbf{M}}_{\mathrm{g}}=G(\theta )$ is the volumetric growth given by Eq. (8).

Various possibilities exist for the values of G_R and G _Θ. At first thought, it may seem that the measured change in myocardial thickness dictates the value of G_R. However, this matter is complicated by the fact that both circumferential and longitudinal growth can cause myocardial thickening, because the CJ constrains myocardial expansion, causing the MY to become compressed with an accompanying thickness increase. Moreover, since the inner myocardial circumference changes little during culture, radial growth alone would increase circumferential tension near the outer myocardial surface as it grows outward. Our results indicate that the amount of radial growth needed to match our data would increase myocardial circumferential stress to an extent that cannot be overcome by other factors, contrary to our observations that show a decrease in myocardial tension during bending (see Fig. 6 and supplemental Fig. S6*). These considerations lead to the alternative assumption $G_R=G_{\theta }\equiv M_{\mathrm{g}}$, leaving M _g as the only free growth parameter (with $G(\theta )$ known).

We do not know how to justify this assumption based on microstructure. However, we note that, like the mature heart, the embryonic heart adapts to changes in loading conditions by altering its radius and wall thickness [45]. Hence, the increased CJ volume may trigger a response similar to that of elevated end-diastolic volume, i.e., the unloaded circumference grows. In addition, the increased wall tension caused by CJ pressure induces an increase in myocardial thickness that tends to return wall stress toward normal levels. Taking $G_R=G_{\theta }$ then represents the simplest assumption.

A parameter study was used to determine M _g. As shown below, the best match to the bending strains in control hearts is given by taking M _g = 1.3 (see Table 1 and supplemental Fig. S7*).

Active MY Cell-Shape Change.

According to Manasek et al. [20], myocardial cells at the OC increase in apical surface area but remain randomly oriented during c-looping, while cells near the IC become elongated and aligned in the circumferential direction. The changes in cell surface area measured by these investigators are generally consistent with the volumetric data of Soufan et al. [21]. Taken together, these results suggest that cells near the IC become shorter longitudinally than those near the OC. Manasek et al. [20] speculated that these cell-shape changes drive rather than being a consequence of looping, and results obtained by Latacha et al. [8] suggest that polymerizing actin filaments cause the observed changes in cell morphology.

These effects are included in the model through the shape-change tensor

$${\mathbf{M}}_{\mathrm{s}}={\mathbf{e}}_R{\mathbf{e}}_R+S{\mathbf{e}}_{\theta }{\mathbf{e}}_{\theta }+S^{-1}{\mathbf{e}}_Z{\mathbf{e}}_Z$$ (10)

which satisfies the constraint $det{\mathbf{M}}_{\mathrm{s}}=1$, i.e., changes in cell shape occur isovolumetrically. The shape-change function S is assumed to depend on Θ. The SEM images of Manasek et al. [20] suggest that the gradient in cell morphology increases toward the IC, and thus we take

$$S(\theta )=(M_{\mathrm{s}}-1)·{[(\theta /\pi )-1]}^2+1\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}(M_{\mathrm{s}}>1)$$ (11)

where M _s is the shape-change parameter. From Eq. (10), we can consider $S^2(\theta )$ as the change in the aspect ratio of circumferential to longitudinal length for a cell, which monotonically decreases from $M_{\mathrm{s}}^2$ at the IC $(\theta =0)$ to unity at the OC $(\theta =\pi )$.

To estimate M _s, we quantified cell shapes from the SEM images of Manasek et al. [20] and chose M _s = 1.3 for the baseline model for control hearts (see Table 1, supplemental Fig. S1*, and supplemental Results 2.1*).

Timing of Events.

The steps outlined above are assumed to occur sequentially, with CJ swelling occurring before dissection of the DM. This sets the reference state (t = 0 h) for experimental correlations from the beginning of the culture period. The MY then contracts after the heart is isolated. Finally, MY growth and cell-shape changes occur over the next 24 h of culture. The total morphogenesis tensor is given by

$$\mathbf{M}={\mathbf{M}}_{\mathrm{s}}·{\mathbf{M}}_{\mathrm{g}}·{\mathbf{M}}_{\mathrm{c}}·{\mathbf{M}}_{\mathrm{t}}·{\mathbf{M}}_{\mathrm{j}}$$ (12)

Evaluation of Strain and Stress.

For comparison with acquired data, we quantify the myocardial strains and stresses in the same way as in our experiments (see Experimental Methods). Briefly, longitudinal stretch ratios were calculated as the changes in myocardial length (on the outer surface) at the OC $(\theta =\pi )$ and near the IC $(\theta =\pi /6)$ of the HT, respectively, where our labels were placed in the experiments. Radial and circumferential stretch ratios were computed from the average myocardial thickness and circumference, respectively, at the cross-sectional plane of symmetry (see Fig. 3(c)). To evaluate myocardial stresses, we introduced virtual cuts in the cylinder model by freeing nodal connections on the plane of the cut. All cuts were made approximately 150 µm long and 75 µm deep with their centers located on the cross-sectional plane of symmetry. The OC and IC cuts were located at the center of the VMY $(\theta =\pi )$ and DMY $(\theta =\pi /3)$, respectively, where we made the cuts in the experiments. The tension in the MY perpendicular to the cut was quantified by the aspect ratio of the cut opening. It is important to note that the stretch ratios and decreases in cut aspect ratios are defined relative to the configuration at the beginning of culture, i.e., after CJ growth and DM dissection.

4.5. Model Based on Realistic Heart Geometry.

After using the idealized cylinder model to determine the morphogenesis tensor for each simulation step, we extrapolated these results to a heart model based on realistic 3D geometry.

We reconstructed the geometry for an isolated HH10 heart from a stack of OCT cross sections (Figs. 3(a′)–3(c′)). Anatomic structures, such as the MY, CJ, and lumen, were segmented out from the images. Then, voxel surfaces at the interface of two entities were extracted and smoothed to remove any sharp changes in curvature at the voxel edges and vertices, which could cause stress concentrations and convergence difficulties. After adjusting the position of each vertex by its weighted average over neighboring vertices, the triangular mesh on the congruent surface was further smoothed and coarsened using the PATRAN Mesh-on-Mesh routine (PATRAN, MSC Software, Santa Ana, CA). Finally, the closed triangular surface mesh was converted to a solid tetrahedral mesh using ABAQUS/CAE. This model consists of 11,914 nodes and 51,405 elements (C3D4), and the MY contains at least two layers of elements in the thickness direction.

For convenience, the model was partitioned into the following segments: CJ, DM, DMY, VMY, outflow tract, and remnants of omphalomesenteric veins (Figs. 3(a′) and 3(c′)). Unlike the cylinder model, the lumen space was included, and frictionless contact conditions were defined to model the collapse of the lumen due to the loss of blood pressure and myocardial contraction. The parameters from the cylinder model were used to compute average input parameters, which were taken as uniform in each region. Such an approximation has its drawbacks, as stress concentrations arise due to the mismatch between adjacent regions. Hence, to achieve a finer spatial variation and to reduce stress concentrations, the MY was further partitioned into 24 subregions.

Principal directions $({\mathbf{e}}_R,{\mathbf{e}}_{\theta },{\mathbf{e}}_Z)$ were defined for each element following anatomic features of the undeformed HT. For boundary conditions, the cranial end of the outflow tract was fixed while all other boundaries were free. Material properties for both MY and CJ were adopted from the cylinder model (see Eq. (3)). As an approximation, the outflow tract and the remnant omphalomesenteric veins were taken as passive, while the rest of the MY layer was assumed to undergo the same morphogenetic processes (contraction, growth, cell-shape change, etc.) as defined by the parameter values extrapolated in each region from those given by the cylinder model.

5. Experimental Results

To test the plausibility of the differential growth hypothesis for cardiac bending, we conducted experiments on isolated chick hearts. Measurements were made from images acquired at various times during a 24 h culture period from about HH10. First, we explored the fundamental idea that myocardial growth can drive HT bending. Then, we collected strain and stress data to be used in testing our computational models.

5.1. Perturbations of HT Growth and Bending.

To determine whether growth of the MY is required for HT bending, we compared the amount of growth in hearts that bend normally to growth in hearts in which bending is perturbed. For this purpose, we note that looping is inhibited by exposure to relatively low doses of CytoD or latrunculin A, which block actin polymerization [8]. In contrast, looping in both whole embryos and isolated hearts continues unimpeded when actomyosin contraction is blocked by BDM, Y-27632, ML-7, or Bleb after looping begins [9]. Hence, if differential growth provides the main driving force for bending, then it follows that actin inhibitors should have a greater effect on HT growth than myosin inhibitors.

Published studies suggest that this is generally the case for various cell types. Since cell division requires the formation and contraction of an actomyosin ring, both actin and myosin inhibitors reduce hyperplasia [31,32]. But whereas blocking actin polymerization decreases hypertrophy [33,34], inhibiting contraction via Bleb, for example, has relatively little effect on increases in cell size [46]. In fact, rather than dividing into two cells, stem-cell-derived cardiomyocytes exposed to Bleb often end up with two nuclei following mitosis [46,47]. Taken together, these results are consistent with the view that inhibiting actin polymerization hinders both tissue growth and looping more than inhibiting contraction. However, we still need to verify this for embryonic hearts.

To check for a correlation between myocardial growth and heart bending, we cultured isolated HH10 hearts in media containing 100 nM CytoD or 30 µM Bleb. After 24 h of culture, CytoD prevented significant bending in 89% of the hearts (n = 35), while all of the Bleb-treated hearts (n = 52) bent approximately the same amount as controls (n = 81; Fig. 4). (Effectiveness of drug treatments was verified by diminished but not abolished heartbeat and reduced tension in the MY.) OCT cross sections near the center of the HT showed that the thickness of the myocardial wall increased by a factor of about 2.9 in control hearts, but only 2.2 and 1.5 in Bleb-treated and CytoD-treated hearts, respectively (Fig. 4(b) and ${\lambda }_r$ in Fig. 5(c)). Changes in cross-sectional area of the MY showed similar trends (supplemental Fig. S3*). As discussed below, the difference in myocardial thickness and cross-sectional area between control and Bleb-treated hearts is likely caused by contractile effects rather than growth, and since both drugs inhibit contraction, decreased growth likely accounts for the further reduction in thickness in CytoD-treated hearts. These results suggest a link between cell growth and looping but do not rule out other possible contributing factors.

As a side issue, since CJ expansion can affect growth in the MY though mechanical feedback [48], we examined the effects of removing the CJ in isolated hearts. Previous studies suggest that looping occurs in intact embryos devoid of CJ, although the heart becomes flaccid [16,17]. We exposed isolated hearts to 20 UTR/mL ovine Hyal. After 24 h of culture, all hearts (n = 8) were bent significantly (Fig. 4(b)). Despite the noticeable overall shrinkage of the HT, the cross-sectional area of the myocardial wall increased similarly to control and Bleb-treated hearts (Fig. 4(b) and supplemental Fig. S3*), consistent with results for whole embryos [16]. We reason that shrinkage of the HT is caused by the loss of CJ pressure, but the myocardial growth that drives bending is unaffected by CJ removal.

Taken together, the results of these drug perturbation experiments support the hypothesis that differential growth plays a role in heart bending through myocardial hypertrophy. However, these experiments do not address the issue of how growth causes the HT to bend. That is the objective of the following experiments and modeling.

5.2. Morphogenetic Strains.

Average longitudinal stretch ratios relative to HH10 were computed along the ventral and dorsal sides of the HT by tracking the motions of three tissue labels on each side during culture (Fig. 5(a)). Consistent with the results of Butler [5], the ventral side of the heart elongated, while the dorsal side shortened as the heart bent. In control hearts (n = 13), the stretch ratio on the ventral side $({\lambda }_{z\mathrm{v}})$ increased from unity to 1.45 ± 0.18, while the dorsal value $({\lambda }_{z\mathrm{d}})$ decreased to 0.73 ± 0.12 after 24 h (Fig. 5(c)). These values are relatively consistent with those reported by Butler [5], which were based on length measurements of a single heart. The deformation rates during culture remained relatively constant (Fig. 5(b)). In Bleb-treated hearts (n = 8), ${\lambda }_{z\mathrm{v}}$ increased more (1.61 ± 0.23), but the dorsal side shortened approximately the same amount as controls $({\lambda }_{z\mathrm{d}}=0.73\hspace{1em}\pm \hspace{1em}0.19)$. Since bending was inhibited by CytoD (see Fig. 4(b)), longitudinal stretch ratios were not measured in CytoD-treated hearts.

We computed average radial $({\lambda }_r)$ and circumferential $({\lambda }_{\theta })$ stretch ratios in the MY from measured myocardial thickness and circumference, respectively. After 24 h, the change in circumference was relatively small and nearly the same for all three groups (${\lambda }_{\theta }\approx 1.1$; Fig. 5(c) and supplemental Fig. S3*), suggesting that the CJ volume increased relatively little during culture. In contrast, compared to controls $({\lambda }_r=2.88\hspace{1em}\pm \hspace{1em}0.36)$, the wall thickened significantly less in Bleb-treated $({\lambda }_r=2.19\hspace{1em}\pm \hspace{1em}0.21)$ and even less in CytoD-treated hearts $({\lambda }_r=1.52\hspace{1em}\pm \hspace{1em}0.13)$ (Fig. 5(c); $n\ge 6$ for each group; p < 0.001, one-way ANOVA). Since Bleb specifically inhibits actomyosin contractility, we attributed the differences in ${\lambda }_r$ between control and Bleb groups to myocardial contraction, i.e., as the lumen closes in isolated hearts (see Fig. 4(b)), the circumference of the MY decreases while its thickness increases due to near incompressibility. Because some boundaries of the myocardial wall became indistinguishable without CJ (see Fig. 4(b)), stretch ratios were not computed for Hyal-treated hearts. However, the measured areas of the myocardial cross sections suggest that losing CJ pressure does not significantly affect growth of the MY (supplemental Fig. S3*).

5.3. Myocardial Stresses.

Circumferential and longitudinal microsurgical cuts near the OC or the IC were used to probe myocardial stress in the HT (Fig. 6(c)). We used the aspect ratios ${\alpha }_z^{\mathrm{OC}},{\alpha }_{\theta }^{\mathrm{OC}},{\alpha }_z^{\mathrm{IC}}$, and ${\alpha }_{\theta }^{\mathrm{IC}}$ of the cut openings to characterize the stresses ${\sigma }_z^{\mathrm{OC}},{\sigma }_{\theta }^{\mathrm{OC}},{\sigma }_z^{\mathrm{IC}}$ and ${\sigma }_{\theta }^{\mathrm{IC}}$, respectively.

After isolation at HH10 (t = 0 h), all cuts opened immediately after being made (Fig. 6(c)). The aspect ratios indicate that initial longitudinal stress near the IC $({\alpha }_z^{\mathrm{IC}}=0.46\hspace{1em}\pm \hspace{1em}0.03)$ was considerably smaller than the other three measured stresses (${\alpha }_z^{\mathrm{OC}}\hspace{1em}=\hspace{1em}0.65\mathrm{\hspace{1em}\hspace{1em}}\pm \mathrm{\hspace{1em}\hspace{1em}}0.08,\hspace{1em}\hspace{1em}{\alpha }_{\theta }^{\mathrm{OC}}\hspace{1em}=\hspace{1em}0.65\mathrm{\hspace{1em}\hspace{1em}}\pm \mathrm{\hspace{1em}\hspace{1em}}0.13,\hspace{1em}\hspace{1em}{\alpha }_{\theta }^{\mathrm{IC}}\hspace{1em}=\hspace{1em}0.73\mathrm{\hspace{1em}\hspace{1em}}\pm \mathrm{\hspace{1em}\hspace{1em}}0.14$) (Fig. 6(b); n = 5 for each type of cut). The difference between ${\alpha }_z^{\mathrm{IC}}$ and ${\alpha }_z^{\mathrm{OC}}$ was statistically significant (p = 0.011, two-way ANOVA), suggesting that ${\sigma }_z^{\mathrm{IC}}<{\sigma }_z^{\mathrm{OC}}$ at t = 0 h. Interestingly, additional data show that ${\alpha }_z^{\mathrm{OC}}$ (and ${\sigma }_z^{\mathrm{OC}}$) was significantly larger in the isolated heart than in the intact heart at HH10 (supplemental Fig. S4^*; n = 6), consistent with an increase in OC tension that would be expected if the DM shortens and bends the heart somewhat after dissection. Here, it is important to note that the cuts in the isolated HH10 hearts were made just after removal from the embryo, before the active contractile response became significant.

At the end of the culture period (t = 24 h; Figs. 6(b) and 6(c)), the stresses at the OC of control hearts dropped by nearly 50% (${\alpha }_z^{\mathrm{OC}}=0.36\hspace{1em}\pm \hspace{1em}0.08,{\alpha }_{\theta }^{\mathrm{OC}}=0.35\hspace{1em}\pm \hspace{1em}0.09;n=7$ for each type of cut) relative to those in hearts at HH10 (p < 0.001, two-way ANOVA). Cuts at the IC hardly opened at all (Fig. 6(c); $n\ge 5$ for each type of cut). These results indicate that both longitudinal and circumferential myocardial tensions decrease throughout the MY as the HT bends.

In some hearts, circumferential cuts were made in remnants of the DM (Fig. 6(c)). We did not measure the aspect ratio for these cuts, because access to the DM was sometimes difficult as it became packed tightly inside the bent HT. But generally speaking, strong longitudinal tension seemed to be present along the DM before and after culture (n = 4 for each), supporting one of the assumptions in our model.

It is also worth noting that exposure to Bleb or CytoD further diminished myocardial stresses during culture (data not shown). Therefore, we often used cutting to test the efficacy of these drug treatments.

Taken together, these results indicate the following: (1) tension was present everywhere in the MY of the straight HH10 heart before culture; (2) after culture for 24 h, the tension decreased significantly or even disappeared in control hearts; and (3) treatment with Bleb or CytoD relaxed almost all the initial tension.

6. Computational Results

As described above, two types of finite-element models were developed (Fig. 3). Our strategy is (1) to investigate possible bending mechanisms individually using a cylinder model; (2) to obtain a baseline cylinder model that can best recapitulate our experimental data; and (3) to extend our analysis to a model based on realistic heart geometry. As in the experiments, morphogenetic stretch ratios in all models were calculated relative to the configuration at the onset of culture, i.e., following CJ growth and dissection of the DM.

6.1. Single-Mechanism Models.

To better understand fundamental behavior and limitations, we first created a separate model for each bending mechanism. Each model is based on idealized cylindrical geometry and contains one free morphogenetic parameter (see Eqs. (5)–(11)) that changes linearly in time as suggested by the time-history plot of longitudinal stretch ratios (see Fig. 5(b)). The input value of each model-specific parameter was adjusted to match our strain data as much as possible (Table 1 and Fig. 7(b)). To avoid the complication of myocardial contraction, only Bleb-treated hearts (M _c = 1) are considered in this subsection (supplemental Movie S1*). Please note that our comparisons focus on stresses near the middle of the HT, where our measurements were made.

Fig. 7.

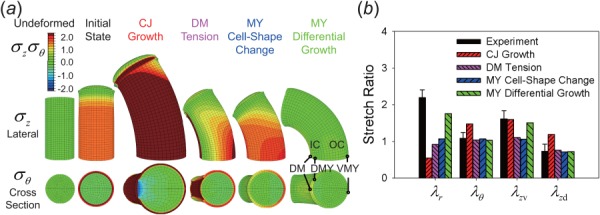
Single-mechanism cylinder models for bending of blebbistatin-treated heart. (a) Deformed shapes and stress distributions shown in lateral and cross-sectional views. Because of symmetry, only the top half of the model is shown. The initial configuration for each model includes CJ growth that occurs prior to HH10. Simulations then include one of the following mechanisms: additional CJ growth with DM constraint; DM tension; active cell-shape changes in the MY; or MY differential growth. Only the differential growth model produces deformation and stresses comparable to experimental results (DM = dorsal mesocardium, DMY = dorsal myocardium, VMY = ventral myocardium, IC = inner curvature, OC = outer curvature). (b) Experimental and numerical stretch ratios in the MY: radial ${\lambda }_r$, circumferential ${\lambda }_{\theta }$, longitudinal on ventral side λ_zv, and longitudinal on dorsal side λ_zd. The differential growth model yields the closest agreement with experiment.

CJ Growth With DM Constraint.

In both whole embryos and isolated culture, the HT apparently always bends with the DM located along the IC, consistent with the CJ swelling hypothesis of Manasek et al. [15]. This mechanism requires the DM (i.e., IC of the HT) to be stiffer than the MY, as verified by the microindentation measurements of Zamir et al. [25]. Here, the DM is represented by a relatively narrow region of the outer cell layer along the dorsal side of the HT (Figs. 3(a) and 3(c)). Guided by published stiffness data for HH12 chick hearts [25], we set the DM modulus to five times of that of the MY. In this single-mechanism model, we took M _j = 1.5 relative to t = 0 h (the total growth is M _j = 1.3 × 1.5 ≈ 2.0) to match the longitudinal strain on the ventral side of the HT (Table 1 and ${\lambda }_{z\mathrm{v}}$ in Fig. 7(b)).

Similar to a previous model based on this idea [48], the HT bends as expected (Fig. 7(a)). However, although the longitudinal stretch at the OC matches our data, the IC also elongates, contrary to our measured IC shortening (${\lambda }_{z\mathrm{d}}$ in Fig. 7(b)). This behavior leads to relatively modest bending (Fig. 7(a)).

The stress patterns predicted by this model also are not consistent with our experimental data. Without the DM, CJ growth would generate myocardial tension in both the circumferential and longitudinal directions. With the DM, superimposed bending increases this tension at the OC and decreases it at the IC, whereas our experiments indicate that stresses decrease throughout the MY as the HT bends (see Figs. 6(b) and 6(c)). Hence, along with the present and other published studies of Hyal-treated hearts [16,17] (see Fig. 4(b)), these results suggest that CJ swelling can contribute to the bending, but other factors likely play a more prominent role.

DM Tension.

Until about HH11, the DM connects the dorsal side of the HT to the foregut of the embryo [3,4]. Since our experiments indicate that the DM is initially under tension (see Fig. 6(c)), this structure would shorten when it ruptures during normal looping or is severed for isolated heart experiments. This shortening, modeled as negative longitudinal growth of the DM, causes the HT to bend ventrally with the DM located along the IC. In agreement with trends in our measurements, the computed longitudinal strain decreases at the IC and increases a little at the OC (Fig. 7(b)). However, whereas the longitudinal myocardial stress near the IC (not in the DM) decreases as in cultured hearts, the OC stress increases (Fig. 7(a)), contrary to our data. In addition, even very strong DM shortening (M _t = 0.3) does not generate enough bending, as reflected in ${\lambda }_{z\mathrm{v}}$ (Figs. 7(a) and 7(b)).

Active Cell-Shape Change.

As discussed below Eq. (11), we stipulate active changes in cell shape to simulate the observed circumferential elongation and longitudinal shortening of myocardial cells near the IC. These shape changes cause the HT to bend ventrally (Fig. 7(a)). Here, we choose M _s = 1.7, which corresponds to a maximum increase in cell aspect ratio of approximately 2.9 (much larger than our estimate of M _s = 1.3 from the cell-shape data of Manasek et al. [20]). With this value, the model matches the longitudinal stretch ratio on the dorsal side $({\lambda }_{z\mathrm{d}})$ but not on the ventral side $({\lambda }_{z\mathrm{v}})$ of the HT (Fig. 7(b)). In addition, the CJ restricts the increase in myocardial circumference, causing circumferential tension to decrease, in agreement with our data, but the longitudinal tension in the MY increases in regions near the IC and OC (Fig. 7(a)), contrary to our data. Taken together, these results suggest that a bending mechanism based on active changes in myocardial cell shape alone is not consistent with all of our newly acquired data.

Differential Growth.

Unlike the other mechanisms, our model shows that differential growth based on the measurements of Soufan et al. [21] is capable of not only generating sufficient bending but also relaxing the initial tensions in the MY (Figs. 7(a) and 7(b)). For Bleb-treated hearts, the differential growth model yields results that agree reasonably well with all of our experimental strain and stress data (Fig. 7).

Next, we explored whether differential growth alone can also reproduce our experimental results for control hearts, which undergo cytoskeletal contraction after isolation (supplemental Fig. S5*). For the same amount of growth, myocardial contraction was added (M _c = 0.9, see Eq. (7)). Although the nearly incompressible CJ keeps the myocardial circumference relatively unchanged, contraction causes the MY to shorten longitudinally and to thicken radially (supplemental Fig. S5A*). All strains agree reasonably well with our data (supplemental Fig. S5B*), but contraction elevates myocardial tensions (${\sigma }_z$ and ${\sigma }_{\theta }$) so that they remain unrealistically high near the IC after bending is complete (supplemental Figs. S5A, S5C*). Taken together, these results suggest that differential growth is the primary driver of bending in isolated hearts, with other mechanisms possibly playing a lesser role.

In summary, all of the studied mechanisms for the bending component of c-looping cause the HT to bend with the DM located along the IC, as observed both in intact embryos and in isolated heart culture. However, of the various proposed mechanisms, our models indicate that only differential growth is capable of capturing the regional changes in stress and strain in Bleb-treated hearts. As a step toward understanding the situation in ovo, we next combine mechanisms to develop a baseline model for isolated hearts cultured under control conditions.

6.2. Baseline Model.

Our simulation for bending of the isolated heart under control conditions consists of five steps: (1) CJ growth, which also occurs in ovo; (2) DM dissection (to isolate the HT from the embryo); (3) MY contraction, which is a response to the removal of normal external loads; (4) MY differential growth; and (5) active changes in MY cell shape. As described above, the parameter values in the model were chosen using a combination of existing data and manual iteration to obtain agreement between model predictions and our experimental results (Table 1). It is important to note that the primary driving mechanism in our model, differential growth, is based on the measurements of Soufan et al. [21].

Results are shown for each step of the model in Figs. 8(a), 8(c), and 8(d), as well as supplemental Movie S2*. As expected, the initial tensions generated by CJ growth are almost uniform in the MY, except near the ends of the HT. Shortening of the DM upon dissection then causes the HT to bend a little toward the ventral side, increasing ${\sigma }_z^{\mathrm{OC}}$ and decreasing ${\sigma }_z^{\mathrm{IC}}$ (defined in the DMY region near the IC, not at the DM where tension is large, see Fig. 8(c)). Next, MY contraction shrinks the outer layer slightly and uniformly elevates tension in both directions by approximately 30–50%. Differential growth then produces considerable bending while lowering tension levels globally. To this point, the strains and stresses given by the model show the correct trends (see control, differential growth in Figs. 8(e) and 8(f)) with one notable exception: the myocardial stresses near the IC (${\sigma }_z^{\mathrm{IC}}$ and ${\sigma }_{\theta }^{\mathrm{IC}}$) decrease much less during the simulation than our cutting data suggest (see $\Delta {\alpha }_z^{\mathrm{IC}}$ and $\Delta {\alpha }_{\theta }^{\mathrm{IC}}$ in Fig. 8(f)).

Fig. 8.

Baseline cylinder model for bending of the isolated heart. (a) This model includes five steps: CJ growth, DM dissection, MY contraction, MY differential growth, and active MY cell-shape change. Deformed shape and longitudinal stress distribution after each step in simulation are shown (lateral view; DM = dorsal mesocardium, DMY = dorsal myocardium, VMY = ventral myocardium, IC = inner curvature, OC = outer curvature). (b) MY contraction is turned off to simulate bending of hearts treated with blebbistatin (Bleb). (The scale and legend are the same as in (a).) ((c) and (d)) Stress distributions after each step along the MY circumference at center of the heart tube. (e) Experimental and numerical stretch ratios in the MY for control and Bleb-treated hearts: radial ${\lambda }_r$, circumferential ${\lambda }_{\theta }$, longitudinal on ventral side λ_zv, and longitudinal on dorsal side λ_zv. Model results are shown after the differential growth and cell-shape change steps. (f) Decrease in MY tension after 24 h culture as characterized by decrease in aspect ratios of cut ($\Delta \alpha \hspace{1em}=\hspace{1em}\alpha (0\hspace{1em}h)-\alpha (24\hspace{1em}h)$). Although most bending is produced by differential growth, cell-shape change significantly lowers the circumferential stress (${\sigma }_{\theta }$), especially near the IC (panels (d) and (f)).

Introducing MY cell-shape changes further reduces myocardial stresses to levels consistent with our data while increasing the amount of bending somewhat (Figs. 8(a), 8(c)–8(f); see control, cell-shape change in Figs. 8(e) and 8(f)). Taken together, these results suggest that most of the bending is caused by differential growth, but cell-shape changes may provide a supplementary mechanism. This model represents our baseline cylindrical model for bending of isolated hearts under control conditions.

To test our model, we use it to simulate bending of Bleb-treated hearts (Fig. 8(b)). The only change we make here is to remove the contraction step by setting M _c = 1. Notably, all of the predicted stretch ratios match the data quite well, with ${\lambda }_r$ showing better agreement than in the control case (Fig. 8(e)). The decrease in stress also agrees reasonably well, though the drop in longitudinal stress is under predicted (Fig. 8(f)).

The baseline model includes five primary morphogenetic parameters: M _j (CJ growth), M _t (DM tension), M _c (MY contraction), M _g (MY growth), and M _s (MY cell-shape change). As discussed in the Sec. 4, the values for all of these parameters except for M _t were deduced rather directly from published data or our newly acquired data and are considered “known”. The value of M _t was chosen to make the change in longitudinal stress match approximately the experimental treads and is considered “free”. In addition, the components of M _g, i.e., G_R, G _Θ, and G_Z, are based on the assumption $G_R=G_{\theta }$ with $G=G_R{G}_{\theta }{G}_Z$. Hence, we explored the sensitivity of the computational results to the values of M _t, G_R, and G_Θ.

In general, the results of this sensitivity analysis show that the solution is relatively robust (supplemental Results 2.3*). The magnitudes of the stresses and strains change, but the qualitative trends remain the same. Hence, we conclude that the behavior of the model is relatively insensitive to the precise values of the free parameters.

In this study, we used the neo-Hookean form of strain-energy density function (Eq. (3)), which is relatively linear compared to the exponential form used in Zamir and Taber [24]. To evaluate how material nonlinearity affects the final results, we reran the simulation with the exponential strain-energy density function. The difference between the results given by these two models is very little (supplemental Fig. S8*).

6.3. Model Based on Realistic Heart Geometry.

Models based on simple geometries are useful for studying general behavior of biomechanical systems. They often provide qualitatively correct results and can be surprisingly accurate quantitatively. Nevertheless it is important to examine the effects of realistic geometry when feasible. Hence, we developed a model for a representative isolated HH10 chick heart based on 3D geometry reconstructed from a stack of OCT images (Figs. 3(a′)–3(c′)). The simulation includes the same morphogenetic steps and model parameters as the cylinder model with one important difference: the realistic-geometry model includes the outflow tract and remnants of the omphalomesenteric veins explicitly as passive segments, whereas these structures are incorporated into the cylindrical model as part of the active HT. Hence, in comparing results between the two models and with experiments, the reader should focus on the HT located between the dashed lines in Fig. 9.

Fig. 9.

Model for bending of control heart based on realistic geometry. Lagrangian strains ($E_Z,E_{\Theta }$) and myocardial stresses (${\sigma }_z,{\sigma }_{\theta }$) are shown in the initial (0 h) and final (24 h) shapes of the heart (lateral view). To help visualize the bending deformation, the passive outflow tract and remnant omphalomesenteric veins are separated from the rest of the heart tube by dashed lines. When growth of CJ occurs, the lumen decreases significantly, as shown in cross-sectional view. (CJ = cardiac jelly, DM = dorsal mesocardium, MY = myocardium, DMY = dorsal myocardium, VMY = ventral myocardium)

In general, the myocardial stresses and strains produced by this model are qualitatively consistent with those given by the baseline cylinder model (Fig. 9) and supplemental Movie S3*. Notably, the initial tensions in the MY decrease significantly during bending, with only a small amount left at the OC (except near the boundaries between adjacent subregions, where stress concentrations occur). We found similar agreement for single-mechanism simulations (results not shown). Because the end segments in this model are taken as passive, the final deformed shape of the model appears to be bent less than control hearts after 24 h culture (compare with Fig. 5(a)). Note, however, that the model strongly resembles hearts cultured for a shorter period of time (see 8 h heart in Fig. 5(a)).

We also note that CJ growth reduces the lumen space included in this model (see myocardial cross sections in Fig. 9). In fact, contraction closes the lumen almost completely (see Fig. 4(b)). This supports our simplification of neglecting the lumen in the cylinder model.

7. Discussion

The heart is the first functioning organ to develop in the vertebrate embryo. Immediately after the HT forms, cardiac looping begins with the heart undergoing dramatic changes in morphology while simultaneously beginning to pump blood to the developing embryo [4,49]. Looping represents the first large-scale marker of left-right asymmetry in the embryo, and abnormalities during this process often lead to congenital heart defects [50,51]. For these reasons, cardiac looping has long intrigued developmental biologists.

Despite decades of study, however, looping has remained a poorly understood biophysical process [1–4]. For c-looping in particular, misperceptions have contributed to this state of affairs. For example, it has been known for more than 60 yr that the directionality of the c-looped HT is caused by torsion rather than rightward bending [5]. Nevertheless, many researchers apparently did not appreciate the significance of this fact [4], leading Männer [3] to emphasize that looping comprises both bending and torsional components. One consequence is that, while torsion may depend on differences between the anatomic left and right sides of the heart [4,7,35], dorsal-ventral differences should be more important for bending [5,8,20]. All of the bending mechanisms considered here are based on dorsal-ventral variations within the HT.

Another possible misconception led indirectly to the present study. It has been known that the heart grows primarily by cardiomyocyte hyperplasia before birth and by hypertrophy after birth [13], and a recent study suggests that the “on-off switch” for cell division is controlled by myocardial fibroblasts [14]. Accordingly, when early studies found no significant spatial patterns of cellular proliferation in the looping HT, researchers essentially eliminated differential growth from their list of potential looping mechanisms [11,12]. Recent studies have challenged this view, however, by showing that some cellular hypertrophy occurs before birth [21] and some hyperplasia occurs after birth [52].

As mentioned in the Introduction, Soufan et al. [21] carefully measured cell size and proliferation rates in the embryonic chick heart and reconstructed 3D maps of myocardial growth throughout the looping stages. Their measurements indicate that hypertrophic growth dominates hyperplastic growth in the MY during the time when most of the bending of c-looping occurs. Significantly, they found that cells located at the OC of the HT become 2–3 times larger than those near the IC. This finding suggests that differential growth may be a mechanism for bending after all.

Examining this idea from a mechanics perspective, we have found that differential myocardial growth likely is the primary mechanism that drives bending of the HT during c-looping. Evidence supporting this conclusion is discussed below.

7.1. Hypertrophic Myocardial Growth Correlates With Bending.

Prior experiments have shown that blocking actin polymerization inhibits c-looping in both intact embryos and isolated heart culture [8], while inhibiting actomyosin contraction has little or no effect on looping once it begins at HH10 [9]. It is well documented that an intact actin network is required for both cellular hypertrophy and hyperplasia. Exposure to actin polymerization inhibitors, such as cytochalasins and latrunculins, can prevent protein synthesis and cytokinesis, which are important for increasing cell size and cell division, respectively [31–34]. On the other hand, actomyosin contraction is only required by the latter, as treatment with the myosin inhibitor Bleb often results in binucleated cells without affecting cell size [46, 47]. Hence, we reasoned that if hypertrophic differential growth drives looping, then inhibiting actin polymerization but not contraction should decrease myocardial growth rates as well as looping progression.

Consistent with this idea, our measurements of myocardial thickness, circumference, and cross-sectional area show that myocardial growth in control, Bleb-treated, and Hyal-treated hearts, all of which bent, was significantly greater than in hearts exposed to CytoD, which did not bend (Fig. 5 and supplemental Fig. S3*). These results suggest a correlation between myocardial growth and bending. Although we did not measure mitotic rates or changes in cell size, we postulate that both Bleb and CytoD decrease myocardial hyperplasia but only the latter also decreases myocardial hypertrophy, in agreement with previous studies [31–34,46, 47]. Further work is needed, however, to test this hypothesis at the cell level.

7.2. Differential Myocardial Growth is the Primary Bending Mechanism.

It is not surprising that the dorsal-ventral gradient in myocardial hypertrophy measured by Soufan et al. [21] can cause the HT to bend with the DM located along the IC, as observed experimentally (Fig. 4(b)). However, as shown by our single-mechanism models, several other processes can produce similar shapes (Fig. 7(a)). Hence, we used stress and strain measurements to help determine the most plausible mechanism(s).

Of the various individual looping mechanisms, our models show that differential growth comes the closest to matching all of our data (Fig. 7 and supplemental Fig. S5*). In particular, a model based on growth alone captures the increase in myocardial wall thickness, the respective increase and decrease in longitudinal strain at the OC and IC, and the overall reduction in myocardial tension given by the experiments. Quantitative comparison of results reveals, however, that this model underestimates the temporal decay in myocardial tension near the IC of control hearts. Matching this result required adding active changes in cell shape (see below), establishing our baseline model (Fig. 8).

In summary, our baseline model predicts the correct trends in stress and strain distributions, as well as curvature of the deformed HT (Fig. 8). This is not a trivial result, as the model contains relatively few free parameters. Initial geometry and material properties were taken from representative data [24]; CJ growth (M _j) was determined from myocardial tensions estimated by local tissue dissection [24]; MY contraction (M _c) was determined from myocardial thickening of control relative to Bleb-treated hearts; volumetric MY growth $(G=det{\mathbf{M}}_{\mathrm{g}})$ was taken from the measurements of Soufan et al. [21]; and active cell-shape changes (M _s) were estimated from data in Manasek et al. [20]. Only the morphogenetic parameters defining DM tension (M _t) and MY growth anisotropy (G_R and G _Θ or the assumed $M_{\mathrm{g}}\equiv G_R=G_{\theta }$) were determined by fitting model results to experimental data. Moreover, sensitivity analysis shows that the values of these free parameters affect the final results quantitatively but not qualitatively (supplemental Results 2.3*).

To test our baseline model further, we used data from Bleb-treated hearts. For the same parameter values, our model with contraction turned off predicts reasonably well the results from Bleb experiments (Fig. 8). Finally, when the same morphogenetic parameters are input into a model based on realistic heart geometry, the same trends occur, illustrating the robustness of our model (Fig. 9).

7.3. Other Mechanisms Contribute to the Bending Process.

Since looping plays a central role in cardiac development, multiple backup mechanisms probably have evolved over time [2,4]. In previous work, we have found that myocardial contraction may provide one such mechanism for the torsional component of c-looping [7,30,35]. For bending, active contraction in the DM when it ruptures may increase DM tension in both whole embryos and isolated hearts [26]. Although this contraction may contribute to the bending, Bleb exposure has shown that contractility is not necessary for normal looping [9].

Cardiac jelly pressure may provide another backup mechanism. During the 1980s, Manasek and colleagues postulated that growth of CJ drives both bending and torsion during c-looping [15,23]. In their view, CJ inflates the HT with the DM locally constraining longitudinal expansion, causing the HT to bend. They also speculated that spiraling fibers in the MY cause the HT to twist as it inflates [15]. Since that time, several new pieces of evidence have added credence to their hypothesis, including experiments showing that CJ can swell substantially via osmotic pressure [15] and that the IC (where the DM is located) is stiffer than the rest of the MY [25]. In addition, physical and computer models have shown that their proposed mechanism is plausible [15,48]. However, other experiments have indicated that the heart loops in chick embryos when CJ is digested by Hyal [16,17]. Here, we further confirmed this result for bending of isolated chick hearts (Fig. 4(b)). While these results show that CJ is not necessary for HT bending, our model suggests that constrained CJ growth still contributes to the bending process and also increases myocardial tension (Fig. 7(a)), which helps to stabilize the HT as a structure, especially in whole embryos where cytoskeletal contraction does not normally occur [30,43]. Without this added tension, the MY may buckle during looping (supplemental Fig. S6*).

Another possible backup mechanism is active changes in cell shape. This mechanism was originally proposed by Manasek et al. [20], who found that myocardial cells elongate in the circumferential direction near the IC and spread near the OC of the looping HT. Computer models, including the single-mechanism model presented here, show that such shape changes are consistent with the observed bending pattern [8,26] (see also Fig. 7). Considering this and other available studies (prior to the time that [21] was published), we speculated that polymerizing actin filaments generate myocardial cell-shape changes that cause the HT to bend [8]. However, when we include shape changes based on measured changes in cell aspect ratio from Manasek et al. [20], our single-mechanism model produces considerably less bending than observed in isolated hearts (Fig. 7). The model also shows, however, that myocardial cell-shape changes can significantly lower circumferential stress, making this mechanism an essential component of our baseline model (Figs. 7(a) and (8)).

Taken together, our results suggest that locally constrained CJ growth, DM tension, and active changes in myocardial cell shape all contribute to the bending process, but they likely play a more minor role than differential growth. If myocardial growth is perturbed, however, these backup mechanisms may upregulate to restore normal looping.

7.4. Limitations.

Our quantitative analyses of myocardial growth and cell-shape change are based on experimental studies of hearts from whole embryos [20,21]. Although the tissue growth estimated from isolated hearts appears to be consistent with these data, our numbers warrant further study using detailed measurements at the cell level. Such measurements, which are beyond the scope of the present work, are needed for isolated hearts under both control and perturbed conditions. It also would be extremely useful to acquire time-lapse data from living samples during looping.

Studying bending in isolated hearts has several advantages over conducting experiments with whole embryos. Devoid of the complicating effects of torsion, isolated hearts are not affected by mechanical loads external to the HT and can be manipulated relatively easily for strain and stress measurements. However, it is important to note that the shape of the heart in ovo is affected by boundary conditions at the ends of the HT. On the other hand, as shown by Flynn et al. [53], freeing one end of the looped heart in the embryo allows it to assume a bent configuration similar to that seen in isolated culture. This observation suggests that the intrinsic bending mechanism in ovo is the same as that in isolated hearts cultured in vivo.

Another consequence of isolation is that (nonsarcomeric) cytoskeletal contraction occurs in the MY in response to the removal of compressive loads normally exerted by the splanchnopleure [30,43]. However, our model suggests that, although this contraction increases myocardial tension considerably, it has little effect on bending (Fig. 8). Since this contractile response does not occur in ovo, it may be more appropriate to consider Bleb-treated hearts as “controls” and those with this elicited contraction as “perturbed” hearts. Notably, our baseline model captures the behavior of both reasonably well.

Although the final shape of the heart is relatively consistent between individuals within a given species, there is quite a bit of variability in heart morphology during development. The geometry of our realistic-geometry model is based on a single representative chick heart at HH10. In general, the specific geometry of a given heart would affect the trends in the numerical results quantitatively, but not qualitatively.

Our model provides one possible solution to the bending problem. While this solution fits a relatively wide range of supporting data, other solutions involving the same or other mechanisms may exist. Perhaps cell-cell adhesion, for instance, plays a role [17,19]. The built-in redundancy in morphogenesis combined with the relatively high variability in the normal form of the developing embryo [54], especially at early stages, makes finding a unique solution impractical. The best we can do is to insist that model results are consistent with trends in the experimental data under various conditions.

In conclusion, our study on bending of isolated hearts has provided new evidence supporting differential hypertrophic myocardial growth as the driving mechanism for the bending component of c-looping. Other morphogenetic processes likely play a lesser role. Future work is needed to further test this hypothesis, for example, by quantifying cell-level growth and shape changes in living hearts under various experimental conditions.