Controlled Support MEG imaging

Abstract

In this paper, we present a novel approach to imaging sparse and focal neural current sources from MEG (magnetoencephalography) data. Using the framework of Tikhonov regularization theory, we introduce a new stabilizer that uses the concept of controlled support to incorporate a priori assumptions about the area occupied by focal sources. The paper discusses the underlying Tikhonov theory and its relationship to a Bayesian formulation which in turn allows us to interpret and better understand other related algorithms.

Introduction

The brain’s neuronal activity generates weak magnetic fields (10 fT-pT). Magnetoencephalography (MEG) is an non-invasive technique for characterizing these magnetic fields using an array of superconducting quantum interference devices (SQUIDs). SQUID magnetometers can measure the changes in the brain’s magnetic field on a millisecond timescale, thus, providing unique insights into the dynamic aspects of the brain’s activity. The goal of biomagnetic imaging is to use MEG data to characterize macroscopic dynamic neural information by solving an electromagnetic source localization problem.

In the past decade, the development of source localization algorithms has significantly progressed (Baillet et al., 2001). Currently, there are two general approaches to estimating MEG sources: parametric methods and tomographic imaging methods (Hamalainen et al., 1993). With parametric methods, a few current dipoles of unknown location and moment represent the sources. In this case, the inverse problem is a non-linear optimization in which one estimates the position and magnitude of the dipoles.

In this paper, we use the tomographic imaging method, where a grid of small voxels represents entire brain volume. The inverse problem then seeks to recover a whole brain activation image, represented by the moments and magnitudes of elementary dipolar sources located at each voxel. The advantage of such a formulation is that the forward problem becomes linear. However, the ill-posed nature of the imaging problem constitutes considerable difficulty, most notably due to the non-uniqueness of the solution.

A common way to constrain the non-uniqueness is to use the weighted minimum norm methods. Such methods find solutions that match the data while minimizing a weighted l₂ norm of the solution (Hamalainen et al., 1993; Sarvas, 1987; Wang et al., 1992; Pascual-Marqui and Biscay-Lirio, 1993). Unfortunately, these techniques tend to “smear” focal sources over the entire reconstruction region.

There are three basic approaches for creating less smeared solutions to the MEG focal imaging problem: (1) use of l_p norms, (2) Bayesian estimation procedures with sparse priors, and (3) iterative reweighting methods. The first approach that produces sparse solutions uses an l₁, or an l_p norm. Although, the l₁ norm solution can be formulated as a linear programming problem which converges to the global solution, other l_p norm methods are calculated using multidimensional iterative methods which often do not converge to the correct solution. Furthermore, all l_p methods are sensitive to noise (Matsuura and Okabe, 1995; Uutela et al., 1999). The second approach is a Bayesian framework with sparse priors derived from Gibbs distributions (Schmidt et al., 1999). However, these methods are very computationally intensive since full a posteriori estimation is solved using the Markov-chain Monte-Carlo or mean-field approximation methods (Bertrand et al., 2001a,b; Phillips et al., 1997). The third approach is iterative reweighted minimum norm method. The method uses a weighting matrix which, as the iterations proceed, reinforces strong sources and reduces weak ones (Gorodnitsky and Rao, 1997; Gorodnitsky and George, 1995). The problems associated with this method are sensitivity to noise, high dependency on the initial estimate and tendency to accentuate the peaks of the previous iteration. In addition, the method often produces an image of a focal source as a scattered cloud of multiple sources that exist near each other.

In this paper, we combine features of all three approaches outlined above and derive a novel Controlled Support MEG imaging algorithm, using Tikhonov regularization theory. The advantages of our algorithm are the quality of focal source images as well as robustness and speed. We first formulate the MEG inverse problem under the framework of Tikhonov regularization theory, and introduce a way to constrain the problem using specially selected stabilizing functionals. We then describe the relationship of this formulation to the minimum norm methods and Bayesian methods. Subsequently, we revisit minimum support stabilizing functional which obtains the sparsest possible solutions, but may produce an image of a focal source as a cloud of points. To remedy this problem, we derive a new controlled support functional, by adding an extra constraining term to the minimum support and then explain details of computationally efficient method of reweighted optimization. The minimization algorithm section explains how the numerical minimization is carried out. In Results and discussion section, we demonstrate performance of the algorithm using results from Monte-Carlo simulation studies with realistic sensor geometries and variety of noise levels.

Formulation of the MEG inverse problem using Tikhonov regularization

Let the three Cartesian coordinates of the current dipole strength for each one of the N_s/3 voxels be denoted by the length N_s vector s. The data consist of a vector b that contains magnetic field measurements at all receivers. The length of the b is determined by the number of sensor sites, as denoted by N_b. The forward modeling operator L connects the model to the data:

$$L_s=b,$$ (1)

where L is also known as the “lead field.” The lead field is a matrix of size N_b×N_s that connects the spatial distribution of the dipoles s to measurements at the sensors b. According to Hadamard (1902), the three difficulties in an inverse problem are: (1) the solution of the inverse problem may not exist, (2) the solution may be non-unique, (3) the solution may be unstable. The Tikhonov regularization theory resolves these difficulties using the notions of misfit, the stabilizer and the Tikhonov parametric functional.

The notion of misfit minimization resolves the first difficulty, the non-existence of the solution. In the event that an exact solution does not exist, we search for the solution that fits the data approximately, using the misfit functional as a goodness-of-fit measure. Following tradition (Eckhart, 1980), we use a quadratic form of the misfit functional, denoted as φ:

$$\varphi (s)={\Vert L_s-b\Vert }^2/{\Vert b\Vert }^2.$$ (2)

When the model produces a misfit that is smaller than the noise level (Tikhonov discrepancy principle), this model could be a solution of the problem.

The second difficulty, the non-uniqueness, is a situation where many different models have misfits smaller than the noise level. All of these models could be solutions of the problem. In practice, we need only one solution that is good. The stabilizing functional, enoted S(s), measures goodness of the solution. Designing the stabilizer S is a difficult task which we will discuss in detail in the next two sections. In simplest terms, S is small for “good” models and large for “bad” models. Therefore, the weighted sum of misfit and stabilizer (denoted as P) measures both the goodness of data fit and goodness of the model:

$$P(s)=\varphi (s)+\lambda S(s),$$ (3)

where λ is regularization parameter and P is Tikhonov parametric functional. Both difficulties considered so far (non-uniqueness and non-existence) are resolved by posing the minimization of parametric functional:

$$s={\text{argmin}}_{s}P(s)$$ (4)

The third difficulty, the ill conditioning, is a situation where small variation in the data results in large variation in the solution. Careful choice of regularization parameter λ resolves this difficulty. In short, the Tikhonov discrepancy principle defines the choice of λ, which is discussed in The minimum support stabilizer section.

In summary, the formulation of MEG inverse problem using Tikhonov regularization reduces to minimization of the Tikhonov parametric functional to (4).

Finally, we note that a probabilistic framework provides a similar view on the inverse problem (Baillet and Garnero, 1997). A Bayesian approach poses the maximum a posteriori (MAP) problem:

$$s={\text{argmax}}_s(\text{exp}(-{(Ls-b)}^T(Ls-b))·\text{exp}(-\lambda S(s))).$$ (5)

Note that the logarithm of (5) is (4). While using different underlying axioms, the Tikhonov problem results in a formulation similar to the Bayesian approach. In the Bayesian framework, the functional exp (−λS(s)) incorporates prior assumptions on distribution of s. A stabilizer function in the Tikhonov framework can be viewed as the log of the prior probability drawn from an exponential distributions on the sources, without the normalization terms for probability distributions. For example, a quadratic functional would correspond to a Gaussian prior, a linear functional corresponds to a Laplacian prior and a P-norm functional would correspond to a sparse distribution drawn from the exponential family.

The minimum support stabilizer

As discussed in the previous section, the role of a stabilizer is especially important for a situation in which many different models produce similar data. Clearly, the misfit functional alone cannot discriminate between these models. Therefore, this situation requires using additional discriminatory measure, such as the stabilizing functional.

The choice of the stabilizing functional S is difficult. S should be small for good models and large for bad models, so that the minimum of S determines the solution. Unfortunately, the definition of a good model relies upon empirical knowledge and depends upon each particular problem.

The good model for MEG inverse problem should adequately represent focal current sources, i.e., sources that occupy a small volume (or, sources with small support). Therefore, the minimum support functional (Last and Kubik, 1983) (Portniaguine and Zhdanov, 1999) (denoted as S_min) is one possible choice for the stabilizer:

$$S_{\text{min}}(s)=\frac{1}{N_s}\sum _1^{N_s}\frac{s_k^2}{s_k^2+{\beta }^2}$$ (6)

where s_k is a component of vector s.

To better understand physical meaning of the minimum support stabilizer consider the following form of S_min:

$$S_{\text{min}}(s)=\frac{1}{N_s}\Vert \mathit{\text{Sign}}(s)\Vert ,$$ (7)

where sign denotes signature function

$$\text{sign}(x)=\left[\begin{array}{cc}1.\hfill & \hfill \text{if}x>0\hfill \\ 0,\hfill & \hfill \text{if}x=0\hfill \\ -1,\hfill & \hfill \text{if}x<0\hfill \end{array}\right]$$ (8)

Continuous approximation of the sign₂ function is better for numerical implementation:

$$\text{sign}{(s_k)}^2=\frac{s_k^2}{s_k^2+{\beta }^2}·{\beta }^2={10}^{-16}·\text{max}{(s)}^2,$$ (9)

where constant 10⁻¹⁶ is machine precision. Note that, substituting (9) into (7) leads to (6). The form (7) is convenient to understand the physical meaning of S_min. Functional S_min measures a fraction of non-zero parameters. In other words, S_min measures support. If we use S_min as a stabilizer, we define the good model as one with the small support.

However, not all images with small support are suitable for imaging of focal MEG sources. As indicated in Fig. 1, sometimes the minimum support method represents a single focal source as a cloud of scattered points which can be misinterpreted as multiple local sources located near each other (panel a). What we ideally want in this situation is an image of a single patch, as depicted in panel (b) of Fig. 1. We note that this problem has also been reported by the researchers working with other types of sparse priors (Phillips et al., 1997). In the next section, we deal with this problem by introducing additional restrictive term to the minimum support stabilizer.

Fig. 1.

This Figure illustrates outcomes of two attempts to image a single focal source with two different stabilizers. (a) Image obtained with minimum support stabilizer is a cloud of disconnected multiple focal sources located near each other. (b) Image obtained with controlled support stabilizer is a single patch.

Controlled support stabilizer

The controlled support stabilizer (denoted as S_con) is a functional that reaches its minimum for images with a predetermined support value α. That value should be small, but not so small that it creates the undesirable of producing scattered sources. In other words, the image in Fig. 1 case b, which we consider to be good, produces a minimum of the stabilizer S_con. The undesirable (scattered) image (case a in the same figure) corresponds to a larger value of stabilizer S_con. This discriminative effect of S_con happens because S_con is a weighted sum of the previously introduced minimum support stabilizer S_min and an additional restricting term S_reg:

$$S_{\text{con}}(s)=(1-\alpha )·S_{\text{min}}(s)+\alpha ·S_{\text{reg}}(s),$$ (10)

where the restricting term S_reg is:

$$S_{\text{reg}}(s)=\frac{1}{\text{max}|s|\sum _{k=1}^{N_s}|s_k|}\sum _{k=1}^{N_s}{s}_k^2=\frac{{\Vert s\Vert }_{l_2}^2}{\Vert s{\Vert }_{l_{\infty }}\Vert s{\Vert }_{l_1}}.$$ (11)

Upon examining expression (11) we notice that the functional S_reg has opposing properties to S_min, S_reg has a maximum where S_min has a minimum. Obviously, the choice of the weighting factor α determines the balance between terms (1−α)S_min and αS_reg. In summary, S_min favors minimum support solutions, S_reg favors solutions with large support, and S_con favors solutions with support controlled by the value of α.

The remainder of this section addresses two important details. First, we must explain why the effect of S_reg is opposite to that of S_min. Second, we will discuss the normalizations of S_min and S_reg, which leads to their invariance to discretization. We must note that S_reg is the square of the l₂ norm weighted by the product of l_l and l₁ norms (11).We think of S_reg as a normalized l₂ norm. Therefore, the minimum of S_reg is reached at the minimum l₂ norm solution (a solution with large support where S_min has maximum). The maximum of S_min is 1, which happens for a case with one nonzero parameter, where S_con is at its minimum. Strictly speaking, the maximum of S_reg is also possible for other cases. However, opposing properties of the minimums are more important for our purposes.

Now, we consider the normalizations of S_min and S_reg. Factor 1/N_s normalizes S_min (6), while divisions by l₁ and l_∞ norms normalize stabilizer S_reg (11). Normalizations are important for the meaningful summation of S_min and S_reg in expression (10), because they make the terms bounded:

$$0\le S_{\text{min}}\le \mathrm{1\; 0}\le S_{\mathit{\text{reg}}}\le 1.$$ (12)

In addition, normalizations make functionals S_min and S_reg invariant to discretization and grayscale of the image. To illustrate this property, consider an example 2D image with a total of 100 pixels, where 96 pixels are zero, and a compact domain in the middle contains 4 pixels all with the value of a. The left panel in Fig. 2 illustrates this case. The following calculations find values of S_min and S_reg for this case:

$$N_s=100,\sum _{k=1}^{N_s}\mathit{\text{abs}}(s_k)=4a,\text{max}(s)=a,\sum _{k=1}^{N_s}\text{sign}{(s_k)}^2=4,\sum _{k=1}^{N_s}{s}_k^2=4a^2,S_{\text{min}}=\sum _{k=1}^{N_s}\text{sign}{(s_k)}^2/100=0.04S_{\text{reg}}=\sum _{k=1}^{N_s}{(s_k)}^2/(\sum _{k=1}^{N_s}\mathit{\text{abs}}(s_k)·\text{max}(s))=\frac{4a^2}{4a·a}=1$$ (13)

Fig. 2.

Functionals S_min and S_reg are invariant to image level and discretization. For illustration, consider a 2D model depicted in this figure. Model has a non-zero domain in the middle. Left panel, shows case with 100 pixels and 4 non-zeros. Functional values for this model are S_min=0.04 and S_reg=1. Right panel, same case with finer discretization, 400 pixels and 16 non-zero values.

According to (13), S_min=0.04 (which is a fraction of the non-zero pixels in the image from Fig. 2) and S_reg=1. Now, we refine the discretization twice. The resulting image has total of 400 pixels with 16 pixels containing the value of a, as shown in the right panel of Fig. 2. Calculations similar to (13) show that S_min and S_reg did not change (S_min=0.04 and S_reg=1). This example also shows that functional values are invariant to a (image level, or grayscale). Note that the same properties hold true for 3D grids and volume models that we consider in this paper.

The method of reweighted optimization

In this section, we discuss how to solve minimization problem using the method of reweighted optimization. To obtain the final form of the objective functional (denoted as P_con), we substitute definitions (2), (6), (10), (11) into (3):

$$P_{\text{con}}=\frac{{\Vert L_s-b\Vert }^2}{{\Vert b\Vert }^2}+\lambda (\frac{1-\alpha }{N_s}\sum _{k=1}^{N_s}\frac{s_k^2}{s_k^2+{\beta }^2}+\frac{\alpha }{\Vert s{\Vert }_{l_{\infty }}·\Vert s{\Vert }_{l_1}}\sum _{k=1}^{N_s}{s}_k^2).$$ (14)

In this section, we discuss the idea of how to solve the minimization problem:

$$s={\text{argmin}}_s{P}_{\text{con}}(s).$$ (15)

Arguably, the minimization of P_con is difficult, because it is a non-linear (non-quadratic) functional of s. We have two feasible options for the numerical solution of our non-quadratic problem. The first uses gradient-type inversion methods, and the second uses the method of reweighted optimization. While the gradient-type minimization method is well known (Fletcher, 1981), this method requires computing the gradient of a functional (14). Computing such a gradient is problematic since we previously used sign while constructing P_con (see formulas (8) and (9)).

In this paper, we use the method of reweighted optimization, a historical choice for related minimum support problem (Last and Kubik, 1983; Portniaguine and Zhdanov, 1999; Portniaguine, 1999). In addition, a number of researchers have found the reweighted optimization convenient (Wolke and Schwetlick, 1988; O’Leary, 1990; Farquharson and Oldenburg, 1998), especially for cases where non-linearity is represented by weights to the quadratic term. This is exactly our case. Notice that the term $s_k^2$ in (14) can be taken out of the brackets

$$P_{\text{con}}=\frac{{\Vert L_s-b\Vert }^2}{{\Vert b\Vert }^2}+\lambda \sum _{k=1}^{N_s}(\frac{1-\alpha }{N_s}\frac{1}{s_k^2+{\beta }^2}+\frac{\alpha }{\Vert s{\Vert }_{l_{\infty }}·\Vert s{\Vert }_{l_1}})s_k^2.$$ (16)

Thus, model-dependent weighting of the quadratic functional represents the non-linearity in (14):

$$P_{\text{con}}=\frac{{\Vert L_s-b\Vert }^2}{\Vert b\Vert }+\lambda \sum _{k=1}^{N_s}{w}_k^{-2}·s_k^2,$$ (17)

where w_k is model-dependent weight

$$w_k^{-2}=\frac{1-\alpha }{N_s}\frac{1}{s_k^2+{\beta }^2}+\frac{\alpha }{\Vert s{\Vert }_{l_{\infty }}·\Vert s{\Vert }_{l_1}}.$$ (18)

It is convenient to assemble weights into a sparse diagonal matrix W(s) with terms w_k in the main diagonal, and write (17) in matrix notations:

$$P_{\text{con}}=\frac{{\Vert L_s-b\Vert }^2}{{\Vert b\Vert }^2}+\lambda \Vert W{(s)}^{-1}s{\Vert }^2$$ (19)

To understand our optimization algorithm in detail, it is necessary to convert the parametric functional to a purely quadratic form, which has a known analytic solution. This form is obtained by transforming the problem into a space of weighted model parameters. To do that, we insert W(s)W(s)⁻¹ term into (19):

$$P_{\text{con}}=\frac{{\Vert LW(s)W{(s)}^{-1}s-b\Vert }^2}{{\Vert b\Vert }^2}+\lambda {\Vert W{(s)}^{-1}s\Vert }^2.$$ (20)

Then, we transform (20) by replacing the variables:

$$s=W(s)s_w,L_w=LW(s).$$ (21)

After substituting (21), expression (20) results in a purely quadratic form of the functional with respect to s_w:

$$P(s_w)=\frac{{\Vert L_w{s}_w-b\Vert }^2}{{\Vert b\Vert }^2}+\lambda {\Vert s_w\Vert }^2.$$ (22)

Since P_con (s_w) is purely quadratic with respect to s_w, the minimization problem for P_con (s_w) has an analytical solution, known as the Riesz representation theorem (Aliprantis and Burkinshaw, 1978):

$$s_w=L_w^T{(L_w{L}_w^T+\lambda {\Vert b\Vert }^2{I}_b)}^{-1}b,$$ (23)

where I_b is unit matrix in the space of data (of size N_b×N_b).

Thus, the idea of reweighted optimization is to solve (15) iteratively, assuming the weights are constant on each iteration. Starting from the initial guess for the weights, we can use the Riesz representation theorem to find weighted solution. We can then convert back to original space, update the weights depending on the solution, and repeat the iterative process. The next section discusses the details of this process. The above equation is identical to the MAP estimator with Gaussian priors for the sources and the noise, where the source variance is assumed to be an unknown diagonal matrix and the noise variance is known and parameterized by λ.

The minimization algorithm

The algorithm for minimizing a parametric functional is iterative. On each iteration (enumerated with index n), we compute the updates of: the weights W_n, the weighted lead fields L_wn, the weighted model s_wn, and the update of the model s_n. These quantities depend upon values from previous iteration (denoted with index n−1). Inputs to the algorithm include the data b, noise level estimate φ₀, as well as the support parameter α. Before the first iteration, we precompute the lead fields L, set weights to one W₀=I_s, and set the current model update to zero s₀=0. The important additional step are incorporated in the final algorithm. The first is the choice of regularization parameter, the second is the line search correction, and the third is termination criterion.

According to Tikhonov condition, the choice of the regularization parameter λ should be such that the misfit (2) at the solution equals an a priori known noise level φ₀ (Tikhonov and Arsenin, 1977):

$$\frac{{\Vert L_w{s}_w-b\Vert }^2}{{\Vert b\Vert }^2}={\varphi }_0.$$ (24)

Substituting (23) into (24) yields the equation

$$\Vert L_{w_n}{L}_{w_n}^T{(L_{w_n}{L}_{w_n}^T+\lambda \Vert b{\Vert I_b)}^{-1}b-b\Vert }^2={\varphi }_0{\Vert b\Vert }^2$$ (25)

which we solve with a fixed point iteration method. In Eq. (25) the only unknown variable is the scalar parameter λ. Since the Gramm matrix $L_{w_n}{L}_{w_n}^T$ is small (N_b×N_b, where N_b is small), the fixed point iteration method easily solves Eq. (25) for λ. For the cases where the data dimension N_b is large, which makes the direct inversion of a Gramm matrix impractical, solving Eq. (22) using the Riesz theorem (23) can be substituted by solving (22) via a conjugate gradient method (Portniaguine, 1999). In this paper, we consider processing of MEG data from an array of 102 sensors, so the dimension of data is small N_b=102 and therefore the Gramm matrix is easily invertible with direct methods. Such a choice of the regularization term is analogous to setting the noise variance in the Bayesian MAP estimation procedure.

Second, to ensure convergence of the algorithm, we incorporate a line search procedure. Convergence of the reweighted optimization depends upon how accurately the Eq. (22) approximates the original non-quadratic Eq. (19). That, in turn, depends on assumption of constant weights, which, in our case, are dependent on s. The usual assumption for any iterative method is that the changes in a model are small from one iteration s_n−1 to the next s_n. That assumption may not always hold, and therefore, steps which converge on Eq. (22) may be divergent on the original Eq. (16) due to significant changes in W(s). The well-known method of line search (Fletcher, 1981) serves to correct this problem. Once the next approximate update S_n' is found from the previous update s_n−1 using the approximate formula (22), we check the value of original non-linear objective functional P_con (s_n′). If the objective functional decreases, the line search is not deployed. If the objective functional increases (which signifies the divergent step), we perform a line search.

If P_con (s_n−1)<P_con (s_n), we perform a line search, by searching for the minimum of P_con with respect to the scalar variable t (the step length):

$$t={\text{argmin}}_t{P}_{\text{con}}(s_{n-1}+t(s_n^{\prime }-sn-1))$$

If P_con (s_n−1)<P_con (s_n), then we set t=1 and do not perform the line search. Note that the smaller step size t is, the closer the corrected update s_n is to the previous update s_n−1 from which the weights W_n were derived. Thus, the smaller t has the less weights change from n−1 iteration to n, and therefore, our quadratic approximation becomes more accurate. With small enough t, a smaller value of P_con will always be found somewhere between s_n−1 and s′. Minimization of the scalar functional P_con with respect to scalar argument t is a simple 1D problem. That problem is solved by sampling the function at a few points (usually three or four), fitting the parabola into it, and finding the argument of a minimum. Such sampling is fast, for one estimate of the functional we only need to solve one forward problem. In many previously conducted studies with minimum support functional S_min, the reweighted optimization has never diverged (Last and Kubik, 1983; Portniaguine and Zhdanov, 1999). Our new controlled support functional, S_con, is dominated by term S_min. Therefore, we expected the same good convergence for S as was reported for S_min. However, in the Monte-Carlo simulations carried out in this paper and with some limited datasets, the algorithm has never called the line search routine because the divergence was never detected.

Third, the termination criterion was formulated based on the following two observations.

First, we must observe that all updates s_n produce the same misfit φ₀ (due to enforcement of the Tikhonov condition). Therefore, only the second term S_con determines the minimum of P_con (s_n) on a given set of arguments s_n. This second term consists of two parts: (1−α) S_min (s_n), and αS_reg (s_n). The second observation is that the S_min (s_n) term decreases with n, and the S_reg (s_n) term increases with n. This happens because on the first iteration n=1 we produce the minimum norm solution, and then progress towards more focused solutions (see discussion about opposing properties of S_min and S_reg in The minimum support stabilizer section). So, the dominance of αS_reg term over (1−α)S_min term signifies close proximity to the minimum of P_con. We summarize the complete algorithm as follows:

1. Compute L_wn using (21)

   $$L_{w_n}=L{W}_{n-1}.$$

2. Determine regularization parameter by fixed point iteration of Eq. (25).

3. Find the weighted model s_wn using (23):

   $$s_{w_n}=L_{w_n}^T{(L_{w_n}{L}_{w_n}^T+\lambda \Vert b\Vert I_b)}^{-1}b.$$
4. Find preliminary update of the model s_n using (21),

   $$s_n^{\prime }=W_{n-1}{s}_{w_n}.$$

5. Check for divergence and incorporate line search.

6. Corrected update s_n is found from the previous update s_n−1 using step length t:

   $$s_n=s_{n-1}+l(s_n^{\prime }-s_{n-1}).$$
7. Check for termination criterion. We stop iterations if

   $$(1-\alpha )S_{\text{min}}(s_n)<\alpha S_{\text{reg}}(s_n).$$

8. Find the updated weight W_n using (18) and go to Step 1, repeating all steps in the loop.

Results and discussion

In simulations we demonstrate the algorithm performance, estimate localization accuracy and speed of the method. The geometry for all simulations was from an MR (magnetic resonance) image of a subject. Fig. 3 shows a head surface extracted from the MR volume image. We transformed the MEG sensor array to MRI coordinates by matching the reference points (measured on the subjectTs head) and the extracted head surface (Kozinska et al., 2001). Fig. 3 shows the MEG array as a “helmet” consisting of 102 square sensor “plates.” Each plate has magnetic coils that measure the normal (to the plate) component of the magnetic field. The middle of the plate serves as a reference point. In order to parameterize the inverse problem, we divided the volume of the brain into 30,000 cubic voxels of size 4×4×4 mm. Vector s consists of strengths of three components of current dipoles within each voxel. This produces N_s=90,000 free inversion parameters (unknowns). This parameterization takes into account both gray matter and white brain matter. We did not use the alternative parameterization with the cortical surface constraint because the final reconstruction result would strongly depend on the accuracy of the cortical surface extraction procedure. The controlled support algorithm is the point of our investigation. So, we did not use cortical surface extraction since it may mask the evaluation of the algorithmTs performance.

Fig. 3.

Geometry that was used in the model study. An outer head surface was extracted from the subject's MRI. MEG sensor array (a “hat” consisting of square receiver “plates”, as shown here) was positioned in MRI coordinates by matching the reference points to the head surface. Each “plate” measures normal component of a magnetic field.

We built the underlying forward model (lead field operator) using the formula for a dipole in a homogeneous sphere (Sarvas, 1987). We computed the sensitivity kernel for each sensor (a row of matrix L), using an individual sphere locally fit to the surface of the head near that particular sensor site (Huang et al., 1999).

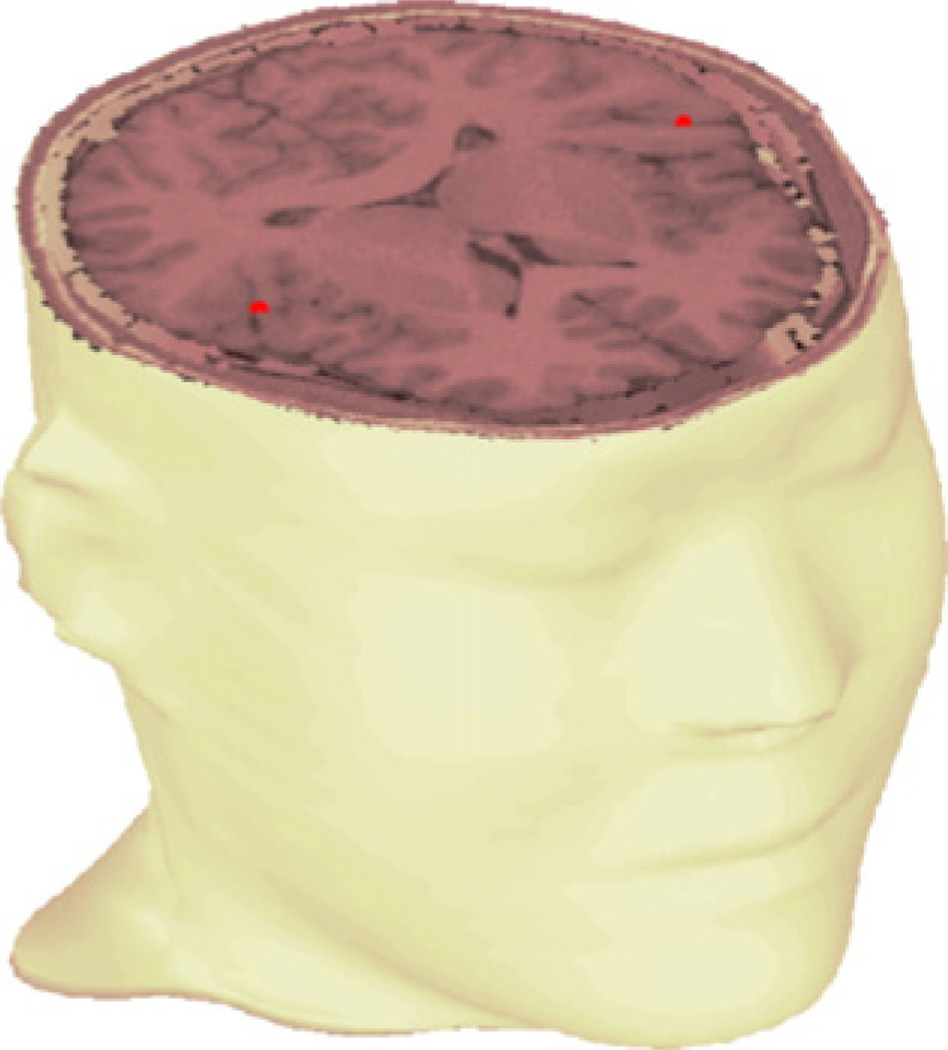
As a first numerical experiment, we placed two dipoles within the brain, approximately at the level of the primary auditory cortex.

Fig. 4 shows the location of dipoles within the brain. That setup defines the vector s as zeros everywhere except the specified dipole locations. We generate the data b using the forward Eq. (1), adding Gaussian random noise such that the SNR is 400. The level of noise is set relative to the data and measured in the same units as a normalized misfit, as defined by the formula

$$b_{\text{noise}}=b+n\frac{\Vert b\Vert }{\Vert n\Vert ·\text{SNR}}$$ (26)

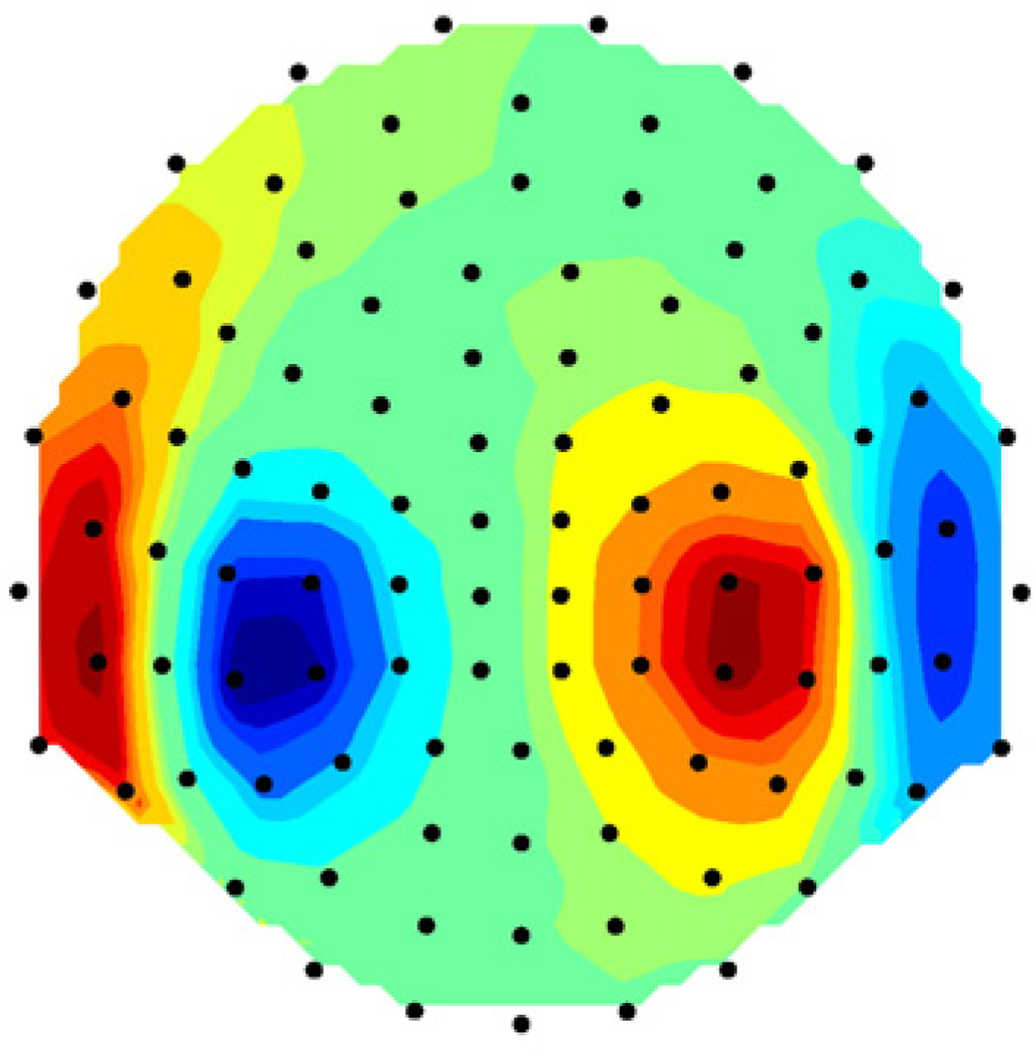
where SNR is the signal-to-noise ratio defined by the ratio of the average signal power across channels divided by the average noise power, and n is the noise vector. Fig. 5 shows the resulting data as a flat projection.

Fig. 4.

Location of two test dipoles (stars) within the head.

Fig. 5.

Magnetic field data for two-dipole model (the model from Fig. 4). Data are shown by color map superimposed on flat projection of measuring array (the helmet from Fig. 3). Dots show the locations of the sensors, each sensor corresponds to one plate in Fig. 3. Data contain Gaussian random noise such that the SNR=400.

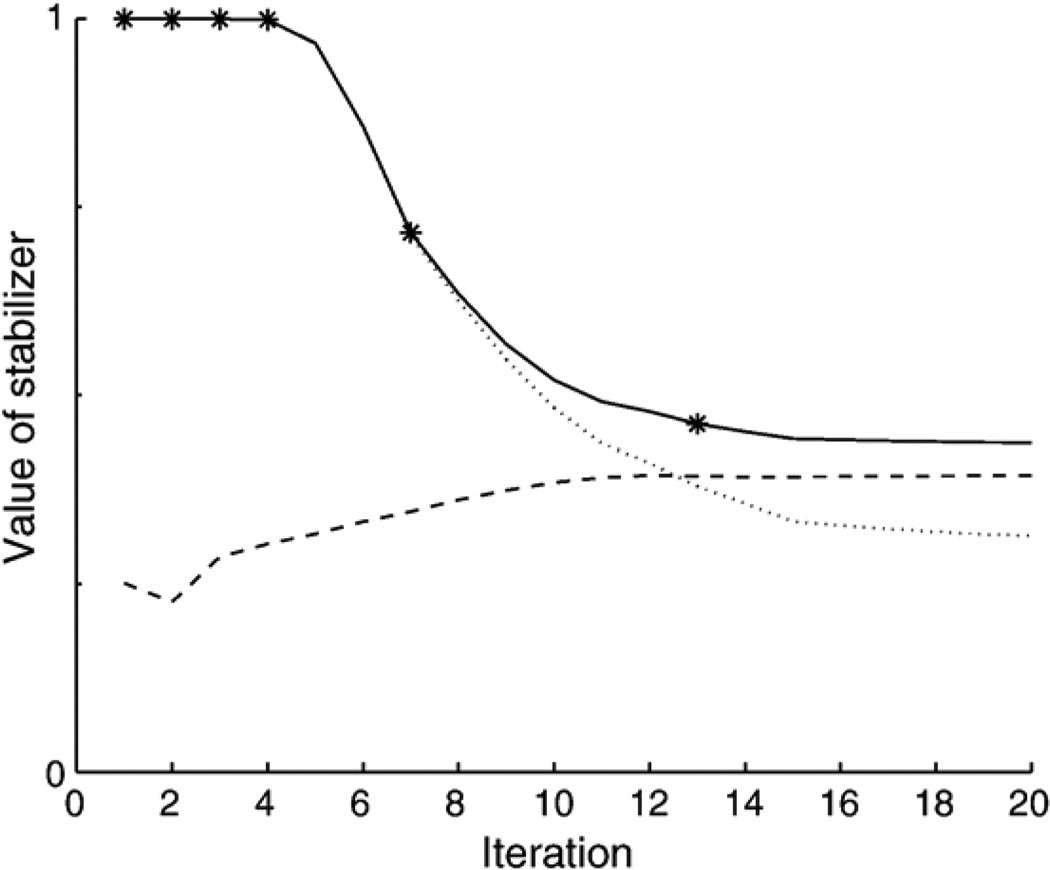
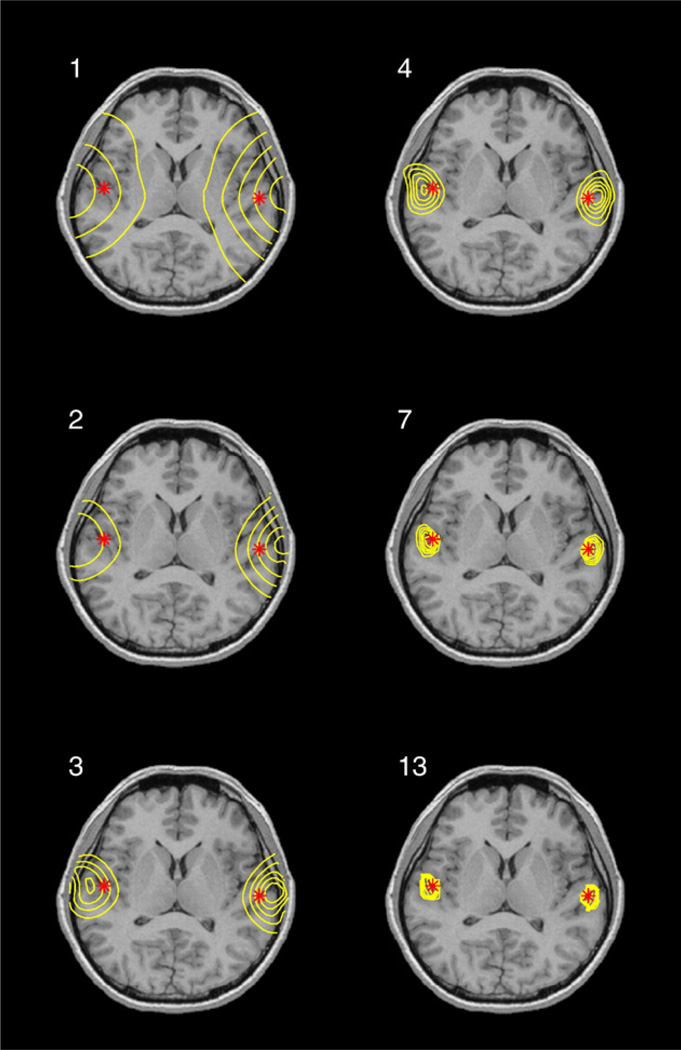
To illustrate convergence, Fig. 6 shows the evolution of stabilizers during iterations, and Fig. 7 shows the evolution of the solution. The isolines in Fig. 7 display the magnitudes of the dipoles in the solutions, superimposed on a corresponding MRI slice.

Fig. 6.

Evolution of stabilizers during reweighted iterations. Solid line shows evolution of S, dashes show evolution of αS_reg and dots show the evolution of (1−α)S_min. Stars show the stopping point, where term (1−α)S_min becomes less than term αS_reg. After that point term αS_reg (dashes) dominates, and S_con (solid line) flattens, as illustrated by this figure.

Fig. 7.

Evolution of solution during reweighted iterations. The case corresponds to example discussed in Fig. 6. Stars show “true” location of dipoles (location of dipoles within the head is shown in Fig. 4). Solution is superimposed on corresponding MRI slice as isolines. Panels numbered 1, 2, 3, 4, 7, 13 show the solutions at the corresponding iteration.

Fig. 7 displays six solutions produced on each iteration. The first solution (panel 1) is a minimum norm solution that is smooth, and maximums are far away from the true dipole locations. In contrast to a common misconception about reweighted optimization methods, observe how the location of maximum activation shifts during reweighted iterations (panels 1–6 in Fig. 7). Note that the method discussed here does not simply accentuate the peaks of the previous iteration. The size and shape of the estimated source area are mainly due to the model and the noise level and do not directly relate to the size and shape of the original source.

Each of these solutions describe the data equally well, but they do not describe the prior expectations that the activity is focused. The solutions are indistinguishable in terms of the data fit, however, they have different values of the stabilizer. Fig. 6 shows evolutions of a stabilizer S (solid line) and its individual components (α−1)S_min (dots) and αS_reg (dashes). We see that the first solution has a large value of a stabilizer, and on the next iterations, the stabilizer decreases to a minimum.

We have empirically determined, from our Monte-Carlo experiments, that the best estimate of the dipole location is not the maximum of the image, but rather the location of the maximum of a local weighted average of the image around its maximum solution. Such a technique is better since it provides estimates located away from the grid nodes, and is, therefore, less sensitive to a given inversion grid. We estimate the dipole locations by thresholding the whole image at 10% to the maximum, separating the individual maximums by clustering, and determining the center of each cluster as the average of a position of cluster points with weights corresponding to the intensity of the image. This procedure is very fast for our compact images (fractions of a second) and does not increase the overall computation time.

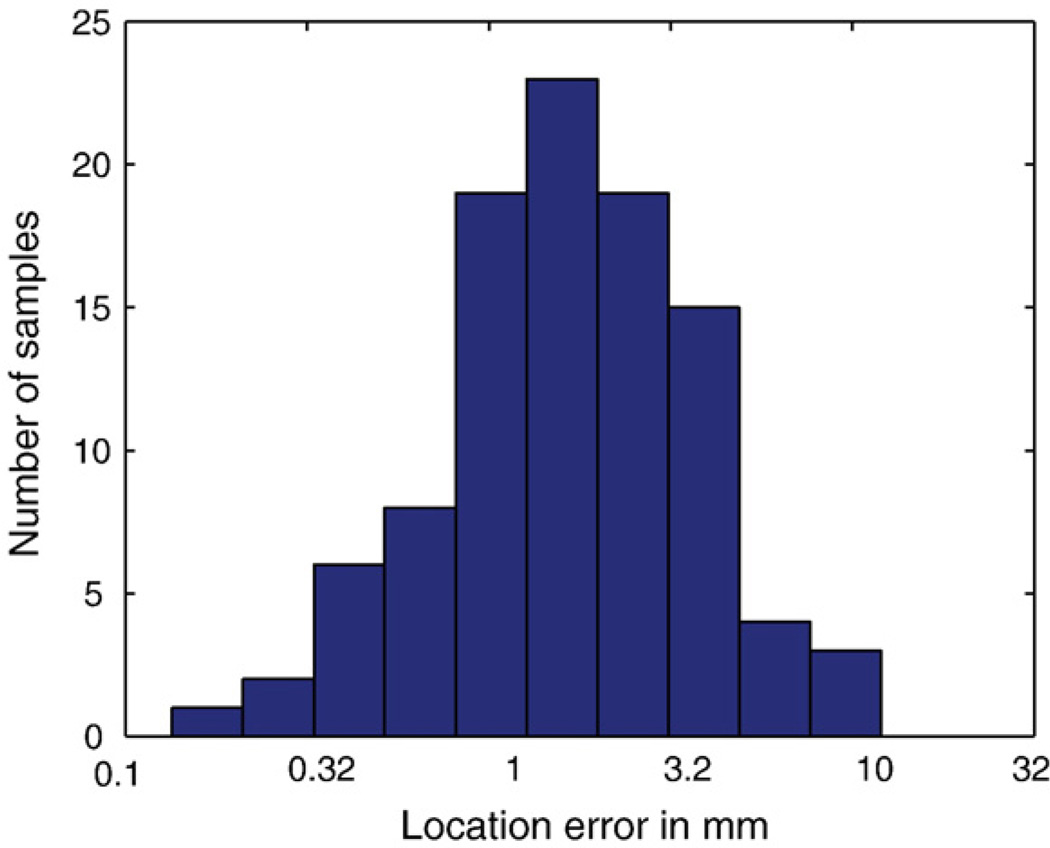
Second, we estimate the localization accuracy and speed of our algorithm using the Monte-Carlo study with 100 simulations. Each experiment is a separate round of inversion run on a data generated by a dipole with a random orientation and a random location within the brain. Fig. 8 shows a histogram of the root–mean–square localization error. The mean error was 2.1 mm, the three largest errors were 8,10 and 12 mm, all for dipoles located very deep within the brain or at the corners of the mesh. Four errors were below 8 mm, and the rest of 93 errors were below 4 mm. These results are consistent with performance reported in the literature for single-dipole parametric inversion (Leahy et al., 1998). With the geometrical setup described above, and using a 700 MHz PC, the localization runs for 30 s.

Fig. 8.

Histogram of localization errors for 100 experiments with a randomly located dipole. Average error is 2.1 mm, seven errors are above 4 mm.

Third, we run the source localization with different levels of noise, ranging from small (SNR=400) to high (= 4). Table 1 summarizes the results. Each column in the table is averaged from 100 Monte-Carlo trials. Expectedly, under high levels of noise localization accuracy as well as errors in orientation deteriorates. However, the method performed robustly and converged well even under 25% of noise and even in this case exhibited localization accuracy of 10 mm.

Table 1.

Results from Monte-Carlo simulation study

Error/Noise	400	100	67	33	16	8	4
Location [mm]	2.55	2.76	3.80	4.36	6.43	8.58	10.90
Orientation [degree]	1.35	1.50	1.94	2.62	4.13	4.78	6.18