Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jul 18.
Published in final edited form as: J Biomech. 2014 Apr 16;47(10):2483–2489. doi: 10.1016/j.jbiomech.2014.04.010

Image based weighted center of proximity versus directly measured knee contact location during simulated gait

Hongsheng Wang 1, Tony Chen 1, Matthew F Koff 2, Ian D Hutchinson 1, Susannah Gilbert 1, Dan Choi 1, Russell F Warren 3, Scott A Rodeo 3, Suzanne A Maher 1,§
PMCID: PMC4057892  NIHMSID: NIHMS586758  PMID: 24837219

Abstract

To understand the mechanical consequences of knee injury requires a detailed analysis of the effect of that injury on joint contact mechanics during activities of daily living. Three-dimensional (3D) knee joint geometric models have been combined with knee joint kinematics to dynamically estimate the location of joint contact during physiological activities – using a weighted center of proximity (WCoP) method. However, the relationship between the estimated WCoP and the actual location of contact has not been defined. The objective of this study was to assess the relationship between knee joint contact location as estimated using the image-based WCoP method, and a directly measured weighted center of contact (WCoC) method during simulated walking. To achieve this goal, we created knee specific models of six human cadaveric knees from magnetic resonance imaging. All knees were then subjected to physiological loads on a knee simulator intended to mimic gait. Knee joint motion was captured using a motion capture system. Knee joint contact stresses were synchronously recorded using a thin electronic sensor throughout gait, and used to compute WCoC for the medial and lateral plateaus of each knee. WCoP was calculated by combining knee kinematics with the MRI-based knee specific model. Both metrics were compared throughout gait using linear regression. The anteroposterior (AP) location of WCoP was significantly correlated with that of WCoC on both tibial plateaus in all specimens (P < 0.01, 95% confidence interval of Person’s coefficient r > 0), but the correlation was not significant in the mediolateral (ML) direction for 4/6 knees (P > 0.05). Our study demonstrates that while the location of joint contact obtained from 3D knee joint contact model, using the WCoP method, is significantly correlated with the location of actual contact stresses in the AP direction, that relationship is less certain in the ML direction.

Keywords: Tibiofemoral contact, cartilage contact, weighted center, 3D knee model

INTRODUCTION

It has been postulated that alterations in knee kinematics lead to an increased risk for the development of posttraumatic osteoarthritis (Andriacchi and Mundermann, 2006; Chaudhari et al., 2008). Thus, to understand the mechanical consequences of knee injury requires a detailed analysis of the effect of that injury on joint contact mechanics during activities of daily living. While gait analysis provides information about the tibiofemoral motion (Andriacchi and Alexander, 2000), it was not until the advent of image-based knee specific models that the location of contact between the tibial and femoral articular surfaces could be assessed.

Several knee joint contact models have been developed for quantifying dynamic joint contact location based on three-dimensional (3D) bone geometry (Anderst and Tashman, 2003; Asano et al., 2001; Li et al., 2004), and cartilage geometry (DeFrate et al., 2004; Li et al., 2005). Briefly, Asano et al. and Li et al. estimated the tibiofemoral contact location by finding the shortest distance between the tibia and femur in the superior-inferior direction (so called shortest distance method) (Asano et al., 2001; Li et al., 2004). Subsequently, DeFrate et al. reported that during the weight-bearing phase of a forward lunge, the shortest distance method overestimated the translation of the contact point. So, they developed a cartilage-overlap method, in which the location of contact was determined as the geometric centroid of the cartilage overlapping area (DeFrate et al., 2004). Instead of depending solely on a single measurement of the shortest distance, Anderst and Tashman proposed a method of using weighted center of proximity between the tibial and femoral bone surfaces to define the contact point. In this method, vertices on the tibial plateau with shorter tibia-femur distances were assigned higher weights and therefore considered more important for determining the location of contact (Anderst and Tashman, 2003). Beveridge et al. found that the weighted center of proximity can detect subtle changes in tibiofemoral contact resulting from combined ligament transection (Beveridge et al., 2013b), and a connection between the altered tibiofemoral contact and the extent of cartilage degeneration at the site of contact has also emerged (Anderst and Tashman, 2009; Beveridge et al., 2013a). Despite this connection, the relationship between the estimated location of contact using the weighted center of proximity method and the actual location of contact experienced by the knee during daily activities has not been quantified.

The purpose of this study was to assess the relationship between the tibiofemoral contact location as estimated using the image-based weighted center of proximity and a directly measured weighted center of contact for the human knee during the stance phase of simulated walking. Our hypothesis is that the location of contact as quantified using both methods on each plateau would be significantly correlated throughout the stance phase of gait.

MATERIAL AND METHODS

Overview

To test the hypothesis, we created knee specific models for six cadaveric knees, which were then subjected to physiological loads intended to mimic gait. The weighted center of contact was directly measured throughout gait using a thin electronic sensor placed on the tibial plateau as reported in our previous studies (Gilbert et al., 2013; Wang et al., 2014). Marker-based kinematic analysis of the physical experiment was used as input to the knee-specific in silica models to enable the weighted center of proximity to be computed.

Magnetic Resonance Imaging

Six human cadaveric knees with no history of surgery or trauma were acquired and stored at −20°C (Anatomy Gifts Registry), the demographics of which are shown in Table 1. The knees were thawed for 12 hours at room temperature and were then scanned using Magnetic Resonance Imaging (MRI). All scanning was performed on a clinical 3T scanner (GE Healthcare, Waukesha, WI) using an 8 channel phased array knee coil (Invivo, Gainesville, FL). A 3D CUBE (Gold et al., 2007) series was acquired to generate an image dataset for segmentation of the menisci: echo time (TE) = 31 ms, repetition time (TR) = 2500 ms, echo train length = 35–40, receiver bandwidth (RBW) = ± 41.7 kHz, number of excitations (NEX) = 0.5 with voxel dimensions: 0.3 × 0.3 × 0.6 mm3. A 3D SPGR with frequency selective fat suppression image series was acquired to segment cartilage and osseous geometries: TE = 3.2 ms, TR = 13.9 ms, RBW = ±41.7 kHz, NEX = 2, voxel dimensions = 0.3 × 0.3 × 0.7 mm3. Images were manually segmented using custom software (Fig. 1a). Note: the articular cartilage surfaces were extracted so that the knee model could be appropriately aligned with the physical digitization of the articular surfaces (see Cadaveric Model and Physical Experiments section).

Table 1.

Demographics of the knee joint donors.

Specimen Side Gender Age Weight (kg) Height (m)
1 R Female 39 64 1.68
2 L Male 53 91 1.73
3 R Female 56 104 1.7
4 R Male 58 90 1.78
5 R Female 62 41 1.63
6 L Female 27 59 1.57
Mean ± SD 49.2 ± 13.4 74.8 ± 23.9 1.68 ± 0.07
Open in a new tab

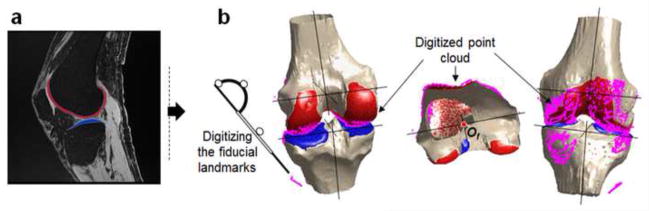
Figure 1.

Figure 1

Open in a new tab

(a) Segmentation of bone and cartilage from knee joint sagittal MR images. (b) The reconstructed 3D knee joint models were aligned with the digitized point clouds using an iterative closet-point (ICP) technique.

Cadaveric Model and Physical Experiments

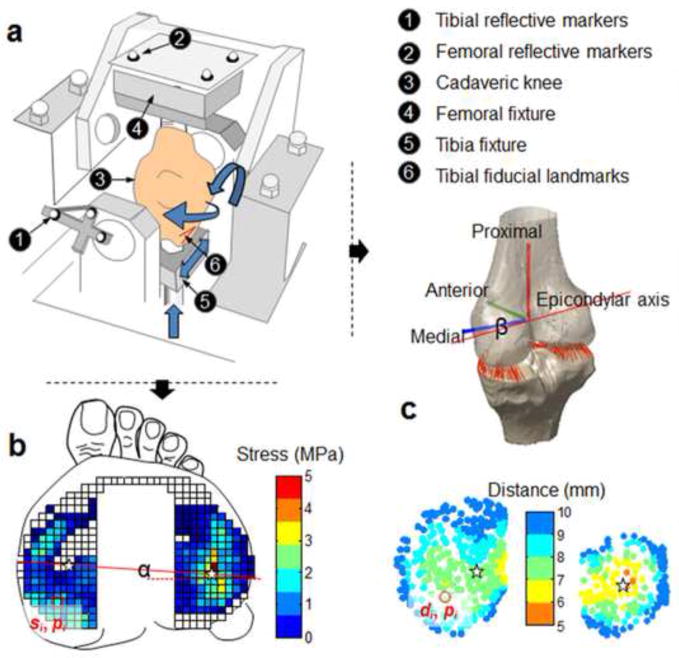
After stripping the surrounding soft tissue (fat, musculature), the specimens were fixed to a modified load-controlled Stanmore Knee Simulator (University College London, Middlesex, UK) (Fig. 2a) (Bedi et al., 2010; Gilbert et al., 2013; Wang et al., 2014). The normal contact stresses across the tibial plateaus were measured using a thin electronic sensor (4010N, Tekscan Inc., MA) which is a matrix of 23 by 34 sensing elements (Fig. 2b). The sensor was inserted underneath the meniscus and the placement was adjusted to capture loads across the entire plateau under a static 1000 N axial load. The sensor was fixed to the tibial plateau by suturing the augment tabs to the tibial insertion of the anterior cruciate ligament (ACL) and the posteroinferior capsule, as detailed in our previous studies (Gilbert et al., 2013; Wang et al., 2014). The knee was then driven under prescribed femur flexion/extension angles and cyclic multidirectional loads (period = 2s) including axial force, anterior/posterior force and internal/external torque applied on the tibia to mimic the activity of gait (ISO 14243-1) (Bedi et al., 2013; Gilbert et al., 2013). The medial/lateral translation and varus/valgus rotation were unconstrained. Reflective markers were rigidly attached to the femoral and tibial fixtures (Fig. 2a).

Figure 2.

Figure 2

Open in a new tab

Schematic diagrams of the data collection. (a) Experimental setup for the cadaveric model on a modified Stanmore Knee Simulator. The femur and tibia were potted into fixtures with PMMA bone cement. The specimen was driven by multidirectional gait inputs (axial force, anteroposterior force, internal/external torque, flexion angle) while the kinematics was measured with the reflective markers fixed to each segment and the contact stress was measured with the electronic sensor. (b) The contact stress on tibial plateau was collected using a Tekscan™ sensor. The location of weight center of contact (WCoC) was calculated on each plateau, as shown by the star (★). The rotation of WCoC was defined as an angle (α). (c) Closest proximities (the shortest tibiofemoral distance) were calculated at each vertex on the tibial plateau during gait. Angle-α is the internal/external rotation angle of the femoral trans-epicondylar axis by kinematic analysis. di – distance at vertex-i on the tibial plateau, si – local contact stress at vertex-i, pi –coordinate of vertex-i.

Anatomical bony landmarks and fiducial landmarks were digitized at neutral position (0° flexion and under an axial force of 1000 N) using a digitizing pointer (Fig. 1b). Specifically, the medial and lateral femoral epicondyles, medial and lateral edges of tibial plateau and tibial spine were identified. Reference frames of the femur and the tibia were defined based on the bony landmarks to describe the motion of the femur relative to the tibia (Wang et al., 2012; Wang and Zheng, 2010). Meanwhile, the fiducial landmarks rigidly attached to the bones were also traced using the digitizing pointer. For each knee, we also digitized a set of point clouds from the following surface areas: the anterior portion of femoral articular cartilage, central region of tibial articular cartilage, and medial/lateral portion of the femur and tibia (Fig. 1b). The surfaces were digitized using a commercial 3D digitizer (accuracy: 0.23 mm) (MicroScribe, Immersion, San Jose, California). Again, the fiducial landmarks were traced using the MicroScribe digitizer, which would be used to transform the digitized point clouds into the Laboratory coordinate frame of the motion capture system. After collecting all the data at neutral position, the motion data (MotionAnalysis Inc., CA) and the contact stress data (Tekscan Inc., MA) were synchronously recorded at 50 Hz and 100 Hz respectively during simulated walking. Data from twenty continuous gait cycles were collected and the average of the last three cycles was used for analysis to ensure the electronic sensor and the knee simulator reached steady-state (Cottrell et al., 2008).

Aligning the Physical and In Silica Models

To align the MRI models with the physical location of the femur and tibia on the knee simulator, first, the digitized joint surfaces (point clouds) were reconstructed at the neutral position in the Laboratory coordinate frame of the motion capture system by coordinate transformation based on the fiducial landmarks using a custom program (MATLAB R2012b, MathWorks, Natick, MA). The MRI models were then aligned to the point clouds which included a minimum of 6,000 points using an iterative closet-point (ICP) technique (Abebe et al., 2009; Besl and McKay, 1992; Defrate et al., 2006) (Fig. 1b). After alignment, the root mean square errors were calculated by measuring the minimum distances from the point clouds to the respective MRI model surfaces.

Direct Measure of Weighted Center of Contact

The weighted center of contact (WCoC) was quantified by assigning different weights to each sensing element (sensel) on the tibial plateau according to the magnitude of contact stress recorded by each sensel (Eq. 1)(Fig. 2b) (Gilbert et al., 2013). Sensels with higher stresses were assigned greater weights, and vice versa. In this way, WCoC is less influenced by lower stresses that occur at the periphery of the contact area. The trajectories of WCoC on each plateau were calculated throughout the stance phase of gait. In this study, the location of WCoC was defined in local Cartesian coordinate systems on the medial and lateral tibial plateaus. The origin of each local coordinate system was located at the center of a best fit circle to the periphery of each meniscus on the contact stress map (Fig. 3a). The stress maps at the static trial (under a 1000 N axial load) for each knee were selected to approximate the circles. In the mediolateral (ML) direction, locations lateral to the origin were considered positive. In the anteroposterior (AP) direction, a location anterior to the origin was considered positive. This idea was similar to a previous study (Hosseini et al., 2012), in which the posterior edge of tibial compartment was used as the reference. The procedure of defining a local coordinate system was repeated three times. The location of the coordinate origin was taken as the mean of three repeated measures. The rotation of WCoC was defined as an angle-α between mediolateral axis and the line connecting the WCoC on the medial and lateral plateaus (Fig. 2b). As a comparison, the axial femoral rotation (β) (rotation of trans-epicondylar axis) was determined from kinematic analysis (Fig. 2c).

Figure 3.

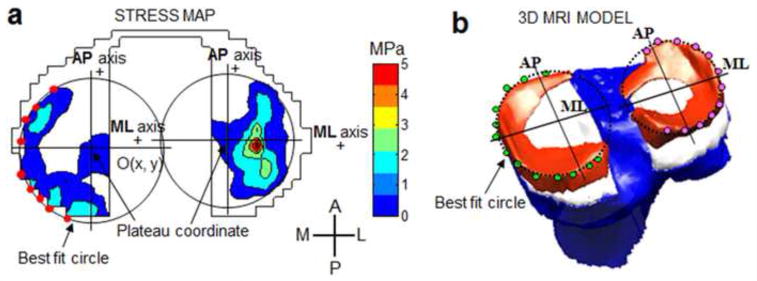
Figure 3

Open in a new tab

(a) Peripheral points on the stress map were manually identified and used to fit a circle on each plateau. A local Cartesian coordinate system was defined on each tibial plateau. (b) On the reconstructed 3D model, the local Cartesian coordinate systems were defined in the same way. The lateral and anterior directions were considered positive.

WCoC=∑i=1n(si∗pi)∑i=1nsi (1)

where pi denotes the location of sensel-i in the local coordinate system of tibial plateau, si denotes the contact stress at sensel-i (Gilbert et al., 2013).

Image-based Weighted Center of Proximity

The weighted center of proximity (WCoP) was calculated using previously developed and validated techniques (Anderst and Tashman, 2003; Beveridge et al., 2013b). On the tibial plateau, points closer to the femoral surface were assigned greater weights (Fig. 1c), therefore considered more important for determining the location of contact. The regulation of weights was adopted from the previous study (Beveridge et al., 2013b)(Eq. 2). In our study, the location of WCoP was defined in local Cartesian coordinate systems on the medial and lateral tibial plateaus. The origin of each local coordinate system was located at the center of a best fit circle to the periphery of each meniscus selected from the 3D meniscus model (Fig. 3b). Likewise, the lateral and anterior directions were considered positive.

{WCoP=∑i=1n(wi∗pi)∑i=1nwiwi=4,di≤2wi=2,2<di≤4wi=0.5,4<di≤6 (2)

where pi denotes the location of vertex-i on the tibial plateau, wi denotes the weight assigned to the vertex with shortest distance of di (unit: mm) to the coupled femoral condyle surface. Since the position of WCoP is dependent on the knee kinematics, the axial femoral rotation angle-β (counterpart to angle-α of WCoC) is directly determined from kinematic results, rather than from WCoP on the medial and lateral plateaus.

Statistical Analysis

An intra-class correlation (ICC) coefficient was calculated for assessing the intra-observer reliability of defining the local coordinate system on each plateau. Pearson correlation coefficients were used to test the relationship between WCoC and WCoP in both directions. Twenty equally spaced time points were interpolated along the gait cycle, and the points (n = 13) during the stance phase (0% ~ 60%) were used for data analysis. The confidence intervals of Pearson’s correlation coefficient were calculated using a Bootstrap resampling algorithm (Statistics Toolbox, Matlab). In the same way, the axial femoral rotation (relative to the tibia) was compared to the rotation of WCoC. Level of significance was set at p < 0.05.

RESULTS

The root mean square errors in aligning the in silica model created from the MRI scans to the digitized point cloud of the physical models using ICP technique were 0.6 ± 0.4 mm in all specimens. The ICC of repeatability in determining the origin of tibial plateau local coordinate system was 0.92 (95% confidence interval, 0.904 to 0.937) on the medial plateau, and 0.95 (95% CI, 0.937 to 0.965) on the lateral.

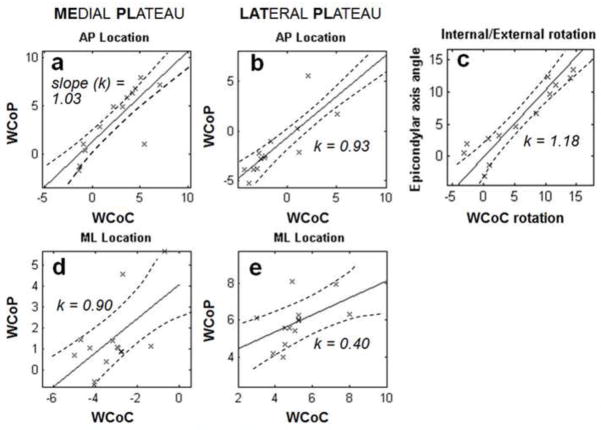
The line drawn through the medial and lateral WCoC (trans-WCoC) first translated posteriorly during the load acceptance phase (0–15% of gait cycle) (Fig. 4), and then externally rotated from mid-stance to terminal stance phases (15–45% of gait cycle). During the pre-swing phase (45–60% of gait cycle), the axis started to rotate internally. The axial femoral rotation (trans-epicondylar axis) from kinematic analysis (2nd row, Fig. 4) replicated the rotation of the trans-WCoC axis (1st row, Fig. 4) and their correlation was statistically significant (p < 0.05) in 5 out of 6 specimens (Table 2) (Fig. 5c). The WCoC had a greater AP displacement on the medial plateau than on the lateral between 15% and 45% of gait (1st row, Fig. 4).

Figure 4.

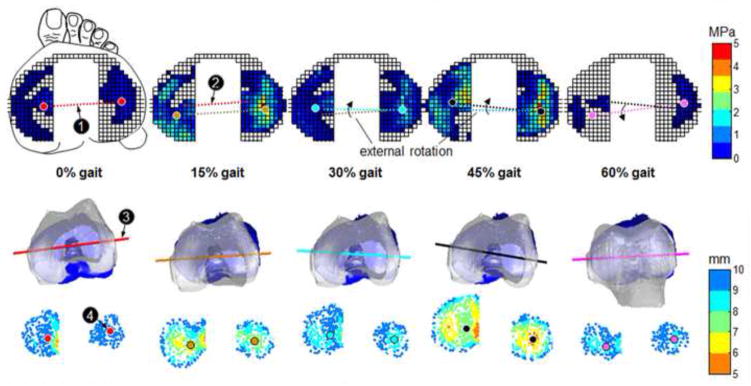
Figure 4

Open in a new tab

Color map of the directly measured knee joint contact stress (1st row) and the closest proximity (3rd row) on tibia plateaus at different time of gait cycle for a typical specimen. The 2nd row represents the relative tibiofemoral position in the tibial local coordinate system during the stance phase of gait cycle. ‘1’-axis connecting the medial and lateral weight center of contact (WCoC), ‘2’-the axis at the previous timing, ‘3’-transepicondylar axis of femur, ‘4’ – weighted center of proximity (WCoP).

Table 2.

Correlation coefficients (Pearson - r) between the weighted center of proximity (WCoP) and weighted center of contact (WCoC), with respect to internal/external rotation, anteroposterior and mediolateral translations.

Specimen IE Rotation AP Translation ML Translation
r (95% CI) p Medial Plateau Lateral Plateau Medial Plateau Lateral Plateau
r (95% CI) p r (95% CI) p r (95% CI) p r (95% CI) p
1 0.48, 0.91 0.006 0.72, 0.98 <0.001 0.46, 0.98 <0.001 0.03, 0.85 0.32 0.52, 0.94 0.003
2 0.33, 0.90 0.012 0.13, 0.91 0.025 0.81, 0.99 <0.001 −0.63, 0.75 0.30 −0.22, 0.87 0.017
3 0.86, 0.98 <0.001 0.43, 0.99 <0.001 0.66, 0.97 <0.001 0.02, 0.86 0.04 0.10, 0.89 0.09
4 −0.19, 0.61 0.41 0.59, 0.93 0.002 0.76, 0.97 <0.001 −0.73, 0.87 0.35 −0.58, 0.91 0.017
5 0.69, 0.98 <0.001 0.93, 0.99 <0.001 0.74, 0.99 <0.001 −0.20, 0.84 0.02 0.20, 0.91 0.027
6 0.43, 0.96 0.004 0.40, 0.88 0.01 0.58, 0.96 0.001 −0.08, 0.89 0.15 −0.21, 0.69 0.53
Open in a new tab

CI: confidence interval. Shade indicates an inadequate correlation with a negative lower limit of 95% CI or p-value greater than 0.05.

Figure 5.

Figure 5

Open in a new tab

Significant correlations were found between the location of image-based measure of weighted center of proximity (WCoP) from knee joint contact model and directly measured Weighted Center of Contact (WCoC) in the anterior-posterior (AP) direction on each plateau (a, b), but not in the mediolateral (ML) direction (d, e). The correlation was also significant between the internal/external (IE) rotation angles of epicondylar axis and trans-WCoC axis (c). The slope (k) of best fitting line was close to 1 in AP location and IE rotation.

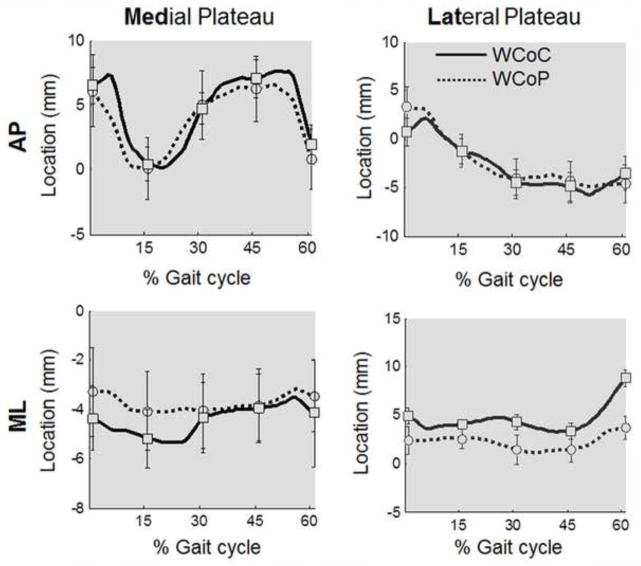
In the AP direction, the calculated WCoP was significantly correlated with WCoC on both the medial and lateral tibial plateaus (Table 2), and the slope of the best fitting lines were close to 1 (Fig. 5a, b). However, the correlations were not as strong in the ML direction (Fig. 5d, e). The direction-dependent difference was also observed from the plot of average positions of WCoC and WCoP at different time points of gait (Fig. 6), in which the curves were close to each other in the AP direction but not in the ML direction.

Figure 6.

Figure 6

Open in a new tab

A plot of anteroposterior (AP) and mediolateral (ML) positions (mean ± SEM) of WCoC and WCoP on the medial and lateral tibial plateau at different time points of gait (heel strike-0%, 15%, 30%, 45%, and toe off-60%) through the stance phase for all 6 specimens.

DISCUSSION

The purpose of this study was to assess the relationship between the tibiofemoral contact location as estimated using an image-based calculation of weighted center of proximity (WCoP) and a directly measured weighted center of contact (WCoC) for the human knee during simulated walking. Our results show that WCoP is significantly correlated with WCoC in the AP direction on both tibial plateaus during simulated walking, which supports our hypothesis. Moreover, the axial femoral rotation from kinematic analysis provides an accurate prediction of the rotation of WCoC. However, WCoP provides a relatively poor prediction (insignificant correlation for 5/6 specimens) of the WCoC in the ML direction, which rejects the hypothesis.

It has been shown that the knee joint articular cartilage experiences variable contact stresses at different regions across the articular surface (e.g. peripheral vs. central) (Wang et al., 2014). Alterations in knee kinematics associated with sports injuries (e.g. ACL rupture) (Gao and Zheng, 2010; Georgoulis et al., 2003; Scanlan et al., 2010; Shefelbine et al., 2006; Wang et al., 2013) may distort the ambulatory loading and further alter the distribution of contact stresses, as suggested by Chaudhari et al. (Chaudhari et al., 2008). Due to our inability of directly measuring joint contact stresses in the general population, a reliable surrogate is needed to allow us to better understand the biomechanical environment of the knee joint after injury. Towards this goal, our study is the first to assess the relationship between the location of joint contact as estimated from 3D image-based models, and the actual location of contact as directly measured across the tibial plateau during simulated walking.

From the direct measurements of contact, we found that there was greater amount of anteroposterior displacement of WCoC on the medial tibial plateau than on the lateral during 15~45% of gait cycle when the axial force was high. This finding was consistent with previously reported lateral pivoting phenomenon of the femoral epicondylar axis during human walking by Kozanek et al. (Kozanek et al., 2009) using dual-fluoroscopic and Koo et al. (Koo and Andriacchi, 2008) using skin markers. When these measurements were compared to the model-based WCoP measures, we found strong relationships for the anteroposterior location and internal/external rotation of the center of contact. The poor relationship between WCoC and WCoP to in the mediolateral direction may be due to the fact that WCoP method does not take into account the contribution of meniscal-cartilage contact. In addition, more asymmetry exists in the meniscus anatomy in the mediolateral direction than the anteroposterior direction. Given that the meniscus plays an important role in load carrying (Gilbert et al., 2013), the absence of meniscus in current methods may hinder the accurate estimation of joint contact. Since the meniscus deforms and translates on tibial surface during walking (Vedi et al., 1999), a more sophisticated kinematic model that incorporates a deformable meniscus model would help improve the accuracy in predicting the contact location in mediolateral direction. In current cartilage-overlap method as the authors did in previous studies (DeFrate et al., 2004; Li et al., 2005), the cartilage-to-meniscus contact was ignored, thus it represents an unfair comparison to the WCoC which takes account of the contact stresses across the whole tibial plateau including both the cartilage-to-cartilage and cartilage-to-meniscus contact regions.

Our study has limitations. Our method of directly measuring contact stresses on the tibial plateau, and then using those measures to establish the location of contact, required that the magnitude of contact stress recorded by each sensel be weighted. In this way, WCoC is less influenced by lower stresses that occur at the periphery of the contact area. Different selections of weighting factors (eq. 2) could cause differences in the results of WCoC. For this reason, we performed three different combinations of weighting factors adapted from literature (Beveridge et al., 2013b), and the ICC coefficient of “inter-combination” repeatability was 0.91, which indicated the results were also insensitive to weighting factors in human knee model. Furthermore, we used a prescribed input of loads in all knees irrespective of the demographics and activity levels of the donor. Therefore, for some specimens (undersized or oversized), the joint load may not fully replicate the actual “physiological” load during gait.

In summary, the knee joint contact model based on the closest proximity between bony surfaces provides an accurate measurement of the location of contact in the anteroposterior direction on both tibial plateaus, but not in the mediolateral direction. The axial knee joint rotation from kinematic analysis predicts the internal/external rotation of the axis connecting the center of contact on both tibial plateaus. Validation of the knee joint contact model gives us more confidence in using it as a surrogate measurement of the distribution of knee joint contact stress in human subjects.

Acknowledgments

Research reported in this publication was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases, part of American Orthopaedic Society for Sports Medicine, under Meniscus Allograft Transplantation Grant, part of Clinical and Translational Science Center at Weill Cornell Medical College (KL2RR000458), part of the National Institutes of Health (R01AR057343 and T32-AR007281-27). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. We thank the Clark & Kirby Foundations and the Russell Warren Chair in Tissue Engineering.

Footnotes

CONFLICT OF INTEREST

The authors have no conflicts of interest to disclose in relation to this study.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Abebe ES, Moorman CT, 3rd, Dziedzic TS, Spritzer CE, Cothran RL, Taylor DC, Garrett WE, Jr, DeFrate LE. Femoral tunnel placement during anterior cruciate ligament reconstruction: an in vivo imaging analysis comparing transtibial and 2-incision tibial tunnel-independent techniques. The American journal of sports medicine. 2009;37 (10):1904–1911. doi: 10.1177/0363546509340768. [DOI] [PubMed] [Google Scholar]
  2. Anderst WJ, Tashman S. A method to estimate in vivo dynamic articular surface interaction. J Biomech. 2003;36 (9):1291–1299. doi: 10.1016/s0021-9290(03)00157-x. [DOI] [PubMed] [Google Scholar]
  3. Anderst WJ, Tashman S. The association between velocity of the center of closest proximity on subchondral bones and osteoarthritis progression. J Orthop Res. 2009;27 (1):71–77. doi: 10.1002/jor.20702. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andriacchi TP, Alexander EJ. Studies of human locomotion: past, present and future. J Biomech. 2000;33 (10):1217–1224. doi: 10.1016/s0021-9290(00)00061-0. [DOI] [PubMed] [Google Scholar]
  5. Andriacchi TP, Mundermann A. The role of ambulatory mechanics in the initiation and progression of knee osteoarthritis. Current opinion in rheumatology. 2006;18 (5):514–518. doi: 10.1097/01.bor.0000240365.16842.4e. [DOI] [PubMed] [Google Scholar]
  6. Asano T, Akagi M, Tanaka K, Tamura J, Nakamura T. In vivo three-dimensional knee kinematics using a biplanar image-matching technique. Clin Orthop Relat Res. 2001;(388):157–166. doi: 10.1097/00003086-200107000-00023. [DOI] [PubMed] [Google Scholar]
  7. Bedi A, Chen T, Santner TJ, El-Amin S, Kelly NH, Warren RF, Maher SA. Changes in dynamic medial tibiofemoral contact mechanics and kinematics after injury of the anterior cruciate ligament: A cadaveric model. Proc Inst Mech Eng H. 2013;227 (9):1027–1037. doi: 10.1177/0954411913490387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bedi A, Kelly NH, Baad M, Fox AJ, Brophy RH, Warren RF, Maher SA. Dynamic contact mechanics of the medial meniscus as a function of radial tear, repair, and partial meniscectomy. The Journal of bone and joint surgery American volume. 2010;92 (6):1398–1408. doi: 10.2106/JBJS.I.00539. [DOI] [PubMed] [Google Scholar]
  9. Besl PJ, McKay ND. A method for registration of 3-D shapes. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1992;14 (2):239–256. [Google Scholar]
  10. Beveridge JE, Heard BJ, Shrive NG, Frank CB. Tibiofemoral centroid velocity correlates more consistently with Cartilage damage than does contact path length in two ovine models of stifle injury. J Orthop Res. 2013a doi: 10.1002/jor.22429. [DOI] [PubMed] [Google Scholar]
  11. Beveridge JE, Shrive NG, Frank CB. Repeatability and precision of a weighted centroid method for estimating dynamic in vivo tibiofemoral surface interactions in sheep. Computer methods in biomechanics and biomedical engineering. 2013b doi: 10.1080/10255842.2013.772592. [DOI] [PubMed] [Google Scholar]
  12. Chaudhari AM, Briant PL, Bevill SL, Koo S, Andriacchi TP. Knee kinematics, cartilage morphology, and osteoarthritis after ACL injury. Med Sci Sports Exerc. 2008;40 (2):215–222. doi: 10.1249/mss.0b013e31815cbb0e. [DOI] [PubMed] [Google Scholar]
  13. Cottrell JM, Scholten P, Wanich T, Warren RF, Wright TM, Maher SA. A new technique to measure the dynamic contact pressures on the Tibial Plateau. Journal of biomechanics. 2008;41 (10):2324–2329. doi: 10.1016/j.jbiomech.2008.04.024. [DOI] [PubMed] [Google Scholar]
  14. Defrate LE, Papannagari R, Gill TJ, Moses JM, Pathare NP, Li G. The 6 degrees of freedom kinematics of the knee after anterior cruciate ligament deficiency: an in vivo imaging analysis. The American journal of sports medicine. 2006;34 (8):1240–1246. doi: 10.1177/0363546506287299. [DOI] [PubMed] [Google Scholar]
  15. DeFrate LE, Sun H, Gill TJ, Rubash HE, Li G. In vivo tibiofemoral contact analysis using 3D MRI-based knee models. J Biomech. 2004;37 (10):1499–1504. doi: 10.1016/j.jbiomech.2004.01.012. [DOI] [PubMed] [Google Scholar]
  16. Gao B, Zheng N. Alterations in three-dimensional joint kinematics of anterior cruciate ligament-deficient and -reconstructed knees during walking. Clin Biomech (Bristol, Avon) 2010;25 (3):222–229. doi: 10.1016/j.clinbiomech.2009.11.006. [DOI] [PubMed] [Google Scholar]
  17. Georgoulis AD, Papadonikolakis A, Papageorgiou CD, Mitsou A, Stergiou N. Three-dimensional tibiofemoral kinematics of the anterior cruciate ligament-deficient and reconstructed knee during walking. The American journal of sports medicine. 2003;31 (1):75–79. doi: 10.1177/03635465030310012401. [DOI] [PubMed] [Google Scholar]
  18. Gilbert S, Chen T, Hutchinson ID, Choi D, Voigt C, Warren RF, Maher SA. Dynamic contact mechanics on the tibial plateau of the human knee during activities of daily living. J Biomech. 2013 doi: 10.1016/j.jbiomech.2013.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gold GE, Busse RF, Beehler C, Han E, Brau AC, Beatty PJ, Beaulieu CF. Isotropic MRI of the knee with 3D fast spin-echo extended echo-train acquisition (XETA): initial experience. AJR American journal of roentgenology. 2007;188 (5):1287–1293. doi: 10.2214/AJR.06.1208. [DOI] [PubMed] [Google Scholar]
  20. Hosseini A, Van de Velde S, Gill TJ, Li G. Tibiofemoral cartilage contact biomechanics in patients after reconstruction of a ruptured anterior cruciate ligament. J Orthop Res. 2012;30 (11):1781–1788. doi: 10.1002/jor.22122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Koo S, Andriacchi TP. The knee joint center of rotation is predominantly on the lateral side during normal walking. Journal of biomechanics. 2008;41 (6):1269–1273. doi: 10.1016/j.jbiomech.2008.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kozanek M, Hosseini A, Liu F, Van de Velde SK, Gill TJ, Rubash HE, Li G. Tibiofemoral kinematics and condylar motion during the stance phase of gait. J Biomech. 2009;42 (12):1877–1884. doi: 10.1016/j.jbiomech.2009.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Li G, DeFrate LE, Park SE, Gill TJ, Rubash HE. In vivo articular cartilage contact kinematics of the knee: an investigation using dual-orthogonal fluoroscopy and magnetic resonance image-based computer models. The American journal of sports medicine. 2005;33 (1):102–107. doi: 10.1177/0363546504265577. [DOI] [PubMed] [Google Scholar]
  24. Li G, Wuerz TH, DeFrate LE. Feasibility of using orthogonal fluoroscopic images to measure in vivo joint kinematics. J Biomech Eng. 2004;126 (2):314–318. doi: 10.1115/1.1691448. [DOI] [PubMed] [Google Scholar]
  25. Scanlan SF, Chaudhari AM, Dyrby CO, Andriacchi TP. Differences in tibial rotation during walking in ACL reconstructed and healthy contralateral knees. J Biomech. 2010;43 (9):1817–1822. doi: 10.1016/j.jbiomech.2010.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Shefelbine SJ, Ma CB, Lee KY, Schrumpf MA, Patel P, Safran MR, Slavinsky JP, Majumdar S. MRI analysis of in vivo meniscal and tibiofemoral kinematics in ACL-deficient and normal knees. Journal of orthopaedic research: official publication of the Orthopaedic Research Society. 2006;24 (6):1208–1217. doi: 10.1002/jor.20139. [DOI] [PubMed] [Google Scholar]
  27. Vedi V, Williams A, Tennant SJ, Spouse E, Hunt DM, Gedroyc WM. Meniscal movement. An in-vivo study using dynamic MRI. The Journal of bone and joint surgery. 1999;81 (1):37–41. doi: 10.1302/0301-620x.81b1.8928. British volume. [DOI] [PubMed] [Google Scholar]
  28. Wang H, Chen T, Torzilli P, Warren R, Maher S. Dynamic contact stress patterns on the tibial plateaus during simulated gait: A novel application of normalized cross correlation. J Biomech. 2014;47 (2):568–574. doi: 10.1016/j.jbiomech.2013.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wang H, Fleischli JE, Nigel Zheng N. Effect of lower limb dominance on knee joint kinematics after anterior cruciate ligament reconstruction. Clin Biomech (Bristol, Avon) 2012;27 (2):170–175. doi: 10.1016/j.clinbiomech.2011.08.006. [DOI] [PubMed] [Google Scholar]
  30. Wang H, Fleischli JE, Zheng NN. Transtibial versus anteromedial portal technique in single-bundle anterior cruciate ligament reconstruction: outcomes of knee joint kinematics during walking. The American journal of sports medicine. 2013;41 (8):1847–1856. doi: 10.1177/0363546513490663. [DOI] [PubMed] [Google Scholar]
  31. Wang H, Zheng NN. Knee joint secondary motion accuracy improved by quaternion-based optimizer with bony landmark constraints. J Biomech Eng. 2010;132 (12):124502. doi: 10.1115/1.4002856. [DOI] [PubMed] [Google Scholar]

RESOURCES