A hierarchical finite mixture model that accommodates zero-inflated counts, non-independence, and heterogeneity

Abstract

A number of mixture modeling approaches assume both normality and independent observations. However, these two assumptions are at odds with the reality of many data sets, which are often characterized by an abundance of zero-valued or highly skewed observations as well as observations from biologically related (i.e., non-independent) subjects. We present here a finite mixture model with a zero-inflated Poisson regression component that may be applied to both types of data. This flexible approach allows the use of covariates to model both the Poisson mean and rate of zero-inflation and can incorporate random effects to accommodate non-independent observations. We demonstrate the utility of this approach by applying these models to a candidate endophenotype for schizophrenia, but the same methods are applicable to other types of data characterized by zero inflation and non-independence.

1. Introduction

One of the major statistical analytic challenges faced by researchers concerns the distributions of observed count values characterized by a plethora of zero values (or a functional equivalent, lowest possible values). Examples include rating scale data (e.g., symptom severity) and objectively measured neurocognitive or motor processes where zero values occur frequently and are thought to reflect either the absence of pathology or poor performance, respectively. This abundance of “zero” values typically results in markedly skewed positive distributions with long extended right tails. Clearly, zero-inflated data produce distributions that fall well short of normality. This type of data is not well-modeled using methods developed for normally distributed data [1, 2]; the application of such techniques to zero-inflated count data can yield biased, inefficient results [3]. Further, when multiple variables are characterized by actual or potential zero-inflation, multivariate normality cannot be expected to model these data well. Thus, count data with skewed distributions with an excess of zero values point to a need for data analytic methods that explicitly take the possibility of zero-inflation into account.

The application of finite mixture modeling to data from psychopathology investigations has been gaining momentum over the years. The utility of the mixture modeling approach, especially as contrasted with traditional clustering methods and other data reduction approaches, has been reviewed elsewhere [4]. Despite its utility and potential (c.f., Gibbons et al. [5]; Levy et al. [6]), mixture modeling has seen only modest application in psychopathology research [4] and usually focuses on only one index of interest (i.e., univariate mixture analysis). Examples include psychosis-proneness [7], ventricle size [8], age-at-admission [9], and smooth pursuit eye movement parameters [10]. Mixture modeling methods have also been developed to take into account both between-subject and within-subject factors that impact performance on laboratory tasks [11–14].

As interest in laboratory methods for the measurement of putative psychiatric endophenotypes [15] has grown, especially in connection with efforts to resolve the nature and influence of genetic factors in liability for illness, the utility of finite mixture modeling approaches has become more salient [16]. Family data are especially relevant to the analysis of putative endophenotypes, because first-degree biological relatives of affected individuals would be expected to be a mixture of gene carriers and non-gene carriers if the trait is subject to genetic influences. In order to capitalize on data from multiple individuals in the same family, mixture models that take into account the non-independence of observations from biologically related individuals are a necessity. Early mixture modeling approaches typically made two core assumptions: multivariate normality, and statistical independence (or conditional independence given covariates) of observations. These two assumptions are not met in many data sets, which are often zero-inflated and include observations from biologically related subjects, both of which affect the structure of the data. Thus, in order for many areas of research to take full advantage of finite mixture modeling, there is a need for methods that simultaneously take into account both zero-inflation in data values and the non-independence of observations within a sample.

In this paper, we present a series of mixture models that can be applied to zero-inflated count data. This method is useful not only for the specific example of count data with an over-abundance of zeros, but also for more general applications that result in data that, while not strictly being count data, can nevertheless be well-modeled using a zero-inflated Poisson (ZIP) distribution (e.g., values obtained from a symptom severity rating scale). In Section 2, we review the definition and notation for the zero-inflated Poisson distribution, a distribution that is well equipped to handle zero-inflated observations. In Section 3, we discuss finite mixture models and in Section 4 we present the ZIP mixture model, a model that can be applied to zero-inflated data with non-independent observations. Section 5 contains details on how to fit and choose from among these models as well as information about how to assess the goodness of fit of a model. In Section 6 we apply these models to a candidate endophenotype for schizophrenia.

2. The Zero-inflated Poisson Distribution

In this paper we use the zero-inflated Poisson (ZIP) distribution to model event count data that may contain more zero-valued observations than would be expected for data arising from a Poisson distribution. The definition of the ZIP distribution is as follows:

Definition

If a random variable Y with probability π equals zero and with probability (1−π) follows a Poisson distribution with mean λ, that is,

$$\begin{array}{l}P(Y=0)=\pi +(1-\pi )e^{-\lambda }\\ P(Y=y)=(1-\pi )\frac{{\lambda }^y{e}^{-\lambda }}{y!},\mathit{\text{for}}y>0,\end{array}$$

then we say that Y is distributed as a zero-inflated Poisson with Poisson mean λ and probability of zero-inflation π and use the following notation: Y ~ ZIP(λ, π). Event count data that are distributed as ZIP can be conceptualized as arising from one of two sources: 1) a proportion π of the time that no event will occur; 2) for the remaining 1-π proportion of the time that the number of events arises from a Poisson process with mean λ (see also Ridout et al [17] for an overview of methods for zero-inflated count data).

Lambert [18] developed the ZIP regression model, which allows both the Poisson mean and probability of zero-inflation to depend on covariates. Lee et al. [19] extended this model to accommodate repeated measures and/or clustered data, adding the flexibility obtained by including random effects:

$$\begin{array}{l}{Y}_{\mathit{ij}}~\mathit{ZIP}({\lambda }_{\mathit{ij}},{\pi }_{\mathit{ij}})\\ \log ({\lambda }_{\mathit{ij}})=\beta ·x_{\mathit{ij}}+u_{\mathit{ij}}\\ \mathrm{logit}({\pi }_{\mathit{ij}})=\psi ·x_{\mathit{ij}}+w_{\mathit{ij}}\\ u_{\mathit{ij}}~N(0,{\sigma }_u^2),w_{\mathit{ij}}~N(0,{\sigma }_v^2),\end{array}$$

where, x_ij is a vector of covariates for the j^th subject within the i^th cluster. We note here that the same set of covariates is not necessarily used to model λ and π. Cluster-level random effects can easily be included in the model, for example by setting u_ij = u_i for all subjects within the i^th cluster.

For other examples of hierarchical Poisson models, see Tsutakawa [20], Christiansen and Morris [21], or Geoffroy and Weerakkody [22].

3. Finite Mixture Models

For data with n observations, let Y_ij be the outcome for the j^th subject within the i^th cluster. Let the probability density function of Y_ij be

$$\begin{array}{l}f(y_{\mathit{ij}})={\displaystyle \sum _{k=1}^m{p}_{\mathit{ij},k}·g_k(y_{\mathit{ij}}),}\\ {\displaystyle \sum _{k=1}^m{p}_{\mathit{ij},k}=1\mathit{\text{and}}{p}_{\mathit{ij},k}\ge 0,\forall k,}\end{array}$$

where m is the number of components or risk classes, p_ij = (p_ij,1, …, p_ij,m) is the vector of mixing proportions, p_ij,k is the mixing proportion for the j^th subject within the i^th cluster and component k, and the g_k are density functions [23–25]. When Y_i follows this distribution, we can interpret the data Y as arising from a mixture of m components, or risk classes, where the density of the k^th component is g_k(·). For this paper we turn our attention to the specific case where the g_k(·) are either Poisson or ZIP density functions.

Although for some applications, it may be appropriate to assume that the prior probability of belonging to a given risk class is the same for all individuals, the vector of mixing proportions, p_ij, need not be identical for all subjects. For example, a first-degree relative of an individual with a disease may be more likely to show abnormal performance or an abnormal trait than a person with no family history of that disease; indeed, such a difference is one of the criteria for an endophenotype. For such applications, the mixing proportions can be allowed to depend on covariates, typically by modeling p_ij using multinomial logistic regression:

$$\begin{array}{l}\log \left(\frac{p_{\mathit{ij},k}}{p_{\mathit{ij},1}}\right)={\gamma }_k{x}_{\mathit{ij}}\\ k=2,\dots ,m\end{array}$$

[25, 26].

Note that while it is not required that the same covariates be used to model the Poisson mean, rate of zero-inflation, and the mixing proportions, there may exist applications where it is necessary to include a subset of the covariates in all three regression models. The methods presented here are still applicable in these settings.

In the finite mixture models described above we assumed that the number of components, m, is a known quantity. Although methods for estimating the number of components do exist [27–29] [27–29], in this paper we take the more common approach of fitting multiple finite mixture models with varying values of m and then comparing the fits of those models. See also MacLachlan and Khan [30] for a comparison of methods for selecting the number of components.

4. The ZIP Mixture Model

In this section we describe a model that can be used to fit heterogeneous, zero-inflated count data. This model takes into account two possible sources of heterogeneity: 1) the heterogeneity resulting from the presence of distinct subpopulations, or mixture components, and 2) the heterogeneity arising from variability within those subpopulations. We model the data using a finite mixture model composed of m classes. Without loss of generality, we order the classes so that the probability, or “risk,” of an event increases with the class label. That is, subjects belonging to the first risk class are at lowest risk and subjects belonging to the m^th component have the highest probability of an event. In order for the model to be statistically identifiable (i.e., parameters for the model are estimable), only one component can be subject to zero-inflation. Since zero-inflation results in an event not occurring, it is reasonable to assume that those subjects who are susceptible to zero-inflation should be at low risk for the event (assuming that zero values reflect the most normal score). Thus, we assume that only subjects belonging to the first class are subject to zero-inflation; observations from these subjects are modeled using a ZIP regression.¹ Observations arising from each of the remaining risk classes are assumed to follow Poisson distributions with increasing means.

A random effects structure such as the one suggested by Lee et al [19] is incorporated into all Poisson and ZIP regression models to handle the presence of non-independent observations in the data (e.g., repeated measurements taken on the same individual or data obtained from members of the same family).²

The structure of this model is summarized in Table 1:

Table 1.

Structure of the ZIP Mixture Model^*

Component 1	Component k (k = 2, …, m)
Yij ~ ZIP(λij1, πij)	Yij ~ Poisson(λijk)
log(λij1) = β1 + β·xij + uij	log(ijk) = βk + β·xij + uij
logit(πij) = ψ·xij + wij
uij ~ N(0, σu2), wij ~ N(0, σu2)	uij ~ N(0, σu2)

^*We require β_{1 <} β_{2 < … <} β_m to ensure the identifiability of the model.

The ZIP mixture model belongs to the larger class of mixture regression models (see Wedel and DeSarbo [31] for a review) and is an extension of a model proposed by Lenk and DeSarbo [32], who noted that an approach that combines finite mixture modeling with mixed effect regression modeling could well model data comprised of distinct, heterogeneous subpopulations or mixture classes.

5. Model Fitting and Comparison

In taking a Bayesian approach, we use the posterior distributions of the model parameters to make inferences. Guidance on Bayesian methods for finite mixture models can be found in Lenk and DeSarbo [32]. Models are compared using the Bayesian Information Criterion (BIC; [33]). See Nagin [34] for a discussion of the use of BIC to select the number of components for a finite mixture model. When comparing models using the BIC, the model that yields the smallest BIC value when fitted to the data is selected as the best-fitting.³

Once a final model has been selected, the goodness of fit of that model can be assessed using posterior predictive checks (PPC) [37] to determine whether the model reproduces key features of the data. Under this approach, a test statistic that captures some important aspect of the data is selected. Parameter values are drawn from their posterior distribution and a replicate of the data is simulated using the drawn values. The chosen test statistic is then calculated from the replicated data. The observed value of the test statistic is compared to a sample of test statistics calculated from replicated data sets. For each statistic, a posterior predictive p-value is calculated by computing the proportion of simulated statistics that are at least as extreme as the observed value. A well-fitting model will yield several replicated statistics that are comparable to the observed value, and thus the associated p-value will be large.

6. Example

We demonstrate this approach by applying these models to an example relevant to schizophrenia family data. Linkage and association studies of schizophrenia have so far yielded weak and inconsistent results [39–41]. Indeed, common variants account for only about a third of the genetic variance in risk for schizophrenia and show substantial shared genetic liability for bipolar disorder [42]. Such pleiotropic effects of specific SNPs were recently confirmed across both adult and childhood onset psychiatric disorders [43]. A number of traits have been identified that are both associated with schizophrenia and that aggregate in relatives of schizophrenia patients at a rate much higher than that of the clinical disorder. These traits, provisionally identified endophenotypes, may be alternative manifestations of schizophrenia risk genes that are more penetrant than schizophrenia itself. These endophenotypes may help to identify relatives who are non-penetrant carriers of one or more of the genes that increase susceptibility for schizophrenia, thereby improving power to detect disease loci. In this worked example, we use thought disorder as a candidate endophenotype for schizophrenia.

Thought disorder was described by Bleuler [44] as a “loosening of associations” and both Bleuler [44] and Kraepelin [45] considered this symptom to be a core feature of schizophrenia psychopathology. An individual who suffers from thought disorder may exhibit difficulties in concept formation, cognitive focus, reasoning, and/or reality testing [46]. Meehl [47, 48] suggested that mild thought disorder should also be found in those who harbor the genetic liability for schizophrenia, but who may never display the clinical disorder (see also Lenzenweger [16]; Levy et al. [49]).

The data set considered in these analyses included 286 participants. Of these participants, 173 (66 males and 107 females) were first-degree biological relatives of schizophrenia and schizo-affective patients (RelSZ) who did not meet diagnostic criteria for a psychotic disorder, bipolar disorder without psychotic features, or a schizophrenia spectrum personality disorder (schizoid, schizotypal, or paranoid). A detailed description of the clinical assessment and diagnostic procedures can be found elsewhere [50, 51]. The non-psychiatric control (NC) group was comprised of 113 individuals (45 males and 68 females). The NC met the same clinical exclusion criteria described for RelSZ above but also did not have a family history of psychosis, psychiatric hospitalization, or suicide. Demographic characteristics of the subject groups are presented in Table 1. The two groups did not significantly differ in estimated verbal IQ (p = 0.29), socio-economic status (SES, p = 0.44), years of education (p = 0.75), or sex ratio (p = 0.87). The NC group was significantly younger (M = 42.78 years) than the RelSZ group (M = 49.27, p < 0.001).

The majority of the participants (63.41%) were related to at least one other participant in the study. The RelSZ group consisted of a total of 88 families. Three families had five members each, four families had four members each, 19 families had three members each, 23 families had two members each and 39 families had one member. In the NC group there were a total of 84 families. Four families had four members each, two families had three members each, 13 families had two members each, and 65 families consisted of one member.

Measures

Verbal responses to ten cards of the Rorschach Inkblot [54] were tape recorded and transcribed verbatim. Three experienced raters scored the verbatim transcript for thought disorder using the Thought Disorder Index (TDI) [55, 56] without knowledge of group membership. The TDI is a reliable and valid scale used to assess twenty-three categories of thought disorder; the intra-class correlation coefficient (ICC) for four teams of raters for Total TDI score was 0.74; Spearman correlations among six pairs of rating teams were between 0.81 and 0.90 [55, 57]. Use of the TDI to characterize thought disorder in different patient groups and in relatives has been described extensively [55, 58–65] (see Holzman et al. [66] for a review). Four of these categories (peculiar verbalization, queer response, absurd response, neologism) refer to successively more severe idiosyncratic use of language, or “deviant verbalizations.” Deviant verbalizations are characteristic of the thought disorder associated with schizophrenia in all clinical states [58–60] and are also over-represented in clinically unaffected relatives [55, 59, 61, 63]. More deviant verbalizations signify stronger evidence of schizophrenia-related thought disorder. The number of deviant verbalizations in each subject’s verbatim responses was the outcome variable.

The RelSZ made a significantly higher number of deviant verbalizations ( $\overline{x}$= 4.0, s.d. = 4.84) than the NC ( $\overline{x}$ = 2.11, s.d. = 3.84) (p < 0.001, Wilcoxon rank sum test). The two groups did not differ significantly in variance of deviant verbalizations scores (p > 0.10, Z = 1.20 from Miller’s [67] jackknife test for equality of variance). Figure 1 displays histograms showing the distributions of the deviant verbalization score in RelSZ and NC. At least one deviant verbalization was present in 128 (74.0%) of the RelSZ and in 60 NC (53.1%), a statistically significant difference (χ₍₁₎² = 12.33, p < 0.001). Age was not significantly correlated with number of deviant verbalizations in either the RelSZ (r = −0.08, p > 0.10) or the NC (r = 0.07, p > 0.10). Among NC, male subjects ( $\overline{x}$ = 3.44, s.d. = 4.79) made significantly more deviant verbalizations than female subjects ( $\overline{x}$ = 1.22, s.d. = 2.75) (p < 0.001, Wilcoxon rank sum test); this relationship was not observed among RelSZ (p > 0.10). The distribution of deviant verbalizations in the RelSZ appears to be bimodal, suggesting that a finite mixture model may be suitable for these data. Figure 1 also shows the relatively large proportion of zero-valued observations (i.e., no deviant verbalizations) in both groups.

Figure 1.

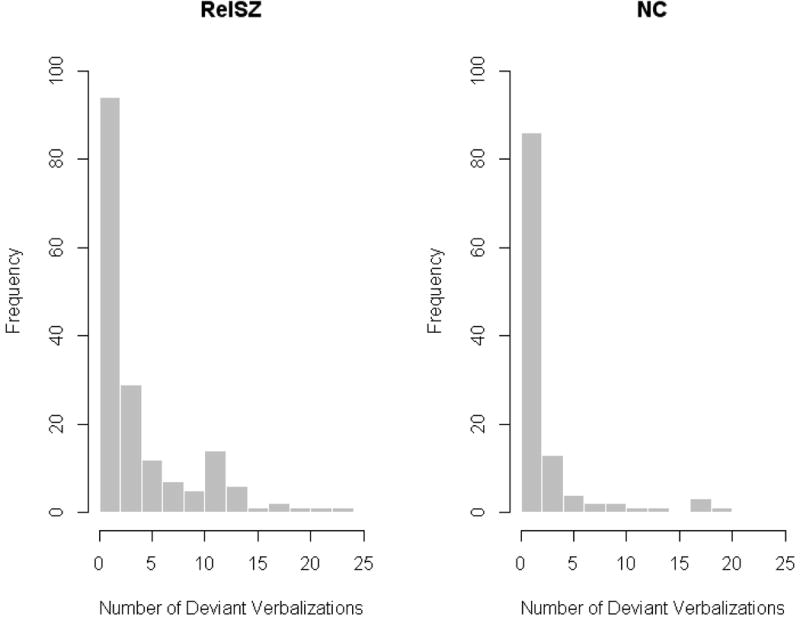
Histograms Comparing the Distribution of the Number of Deviant Verbalizations in First-Degree Relatives of Schizophrenia Patients and Non-psychiatric Controls

Method

Since this particular data set does not include any repeated measurements, we do not need to include any subject level effects into our model; however, because this data set contains related individuals, we incorporated cluster (i.e., family) level effects, u_i, in the model. We note that since the data consist of only first-degree relatives, a simple random effect for each family should be sufficient to handle the non-independence introduced by the inclusion of related individuals. Although not needed here, covariates could potentially be included into the random effects portion of the model to handle data comprised of subjects with differing degrees of relatedness (for example, second- versus first-degree relatives or dizygotic versus monozygotic twins).

Since we observed a sex difference in rate of deviant verbalizations in NC, and sex effects have been found in previous studies of thought disorder [68], for our model we allow the deviant verbalization rate to depend on sex,

$$\begin{array}{l}\log ({\lambda }_{\mathit{ijk}})={\beta }_k+{\beta }_S·S_{\mathit{ij}}+u_i\\ u_i~N(0,{\sigma }_u^2)\end{array}$$

where S is an indicator variable for sex.

Recall that we assume that only subjects belonging to the lowest-risk class are subject to zero-inflation. However, it may be the case that subjects with a high verbal IQ may be more likely to show no deviant verbalizations that those with lower verbal IQ. In order to test this hypothesis, we include a measure of verbal IQ in our model for the rate of zero-inflation:

$$\mathrm{logit}({\pi }_{\mathit{ij}})={\psi }_0+{\psi }_V·V_{\mathit{ij}}$$

where V_ij is the verbal IQ for the j^th subject in the i^th cluster.

We also note that equality constraints over groups on the mixing proportions would clearly not be an appropriate if the quantitative trait in question were, indeed, a valid schizophrenia endophenotype. For example, relatives may be a mixture of gene carriers and non-gene carriers (e.g., 60% and 40%, respectively) and controls may all be non-gene carriers. Or, controls may also be a mixture but with very different mixing proportions from those observed in RelSZ (e.g., 5% and 95%, respectively). We use the following multinomial logistic model for the mixing proportions:

$$\begin{array}{l}\log \left(\frac{p_{\mathit{ij},k}}{p_{\mathit{ij},1}}\right)={\gamma }_{k0}+{\gamma }_{k1}·x_{\mathit{ij}}\\ k=2,\dots ,m\end{array}$$

where

$$x_{\mathit{ij}}=\{\begin{array}{cc}1& \text{if}{j}^{\mathit{th}}\text{subject within}{i}^{\mathit{th}}\text{cluster is RelSZ}\\ 0& \text{otherwise}\end{array}.$$

We can then examine the posterior distribution of the covariates γ_k1 to determine whether different mixing proportions for the RelSZ and NC are necessary to adequately model these data.

We also fit Lambert’s ZIP regression model [18] to these data:

$$\begin{array}{l}{\mathrm{Y}}_{\mathrm{ij}}~\mathit{ZIP}({\lambda }_{\mathit{ij}},{\pi }_{\mathit{ij}})\\ \log ({\lambda }_{\mathit{ij}})={\beta }_1+{\beta }_S·S_{\mathit{ij}}+{\beta }_x{x}_{\mathit{ij}}+u_i\\ \mathrm{logit}({\pi }_{\mathit{ij}})={\psi }_0+{\psi }_V·V_{\mathit{ij}}\\ u_i~N(0,{\sigma }_u^2)\end{array}$$

as well as a standard Poisson regression model that was identical to the ZIP regression model described above, except that it did not allow for zero inflation (i.e., π_ij = 0, for all i, j). Note that for these regression models, mixture within the RelSZ is not modeled. That is, for a given sex, all RelSZ are assumed to have the same Poisson mean. This assumption is equivalent to assuming that all RelSZ belong to the same risk class and is clearly inappropriate for an endophenotype since at most, half of relatives would be expected to be gene carriers.⁴ Thus, failure of the data to support the ZIP mixture model in favor of either the ZIP or Poisson regression model would be inconsistent with the idea that the level of risk varies among RelSZ according to genetic liability and would provide evidence against the use of deviant verbalizations as a schizophrenia endophenotype.

Results

The data for this example were analyzed using the openBugs software package [69]; an example of BUGS code useful for fitting these types of models is provided in the Appendix. The prior distributions for all model parameters were uniform over a suitably large interval. This approach was taken to ensure that all prior distributions were proper, while providing little prior information. More information on the specific priors used can be found in the Appendix. Convergence was assessed using the Gelman-Rubin statistic, $\widehat{R}$ [36]. The Gibbs sampler was used to simulate draws from the posterior distributions of the different models. Starting points for the Gibbs samplers were randomly selected and each chain was iterated until approximate convergence ( $\widehat{R}$ < 1.1). We fit versions of the ZIP mixture model with different numbers of mixing components. The log posterior density, log-likelihood, and BIC at the posterior modes for each of these models are displayed in Table 3.

Table 3.

Results of Model Fitting

Model	# of Risk Classes	Log Posterior Density	Log-Likelihood	# of Parameters	BIC
Poisson Regression	–	−818.4	−988.3	4	1999.22
ZIP Regression	–	−716.5	−832.2	6	1698.34
ZIP Mixture	1	−721.4	−854.4	5	1737.02
ZIP Mixture	2	−499.0	−642.0	8	1329.15
ZIP Mixture	3	−471.3	−640.6	11	1343.46

The ZIP mixture model with two components returned a smaller BIC (1329.15) than the one-component model (BIC = 1737.02), providing evidence that the data were better explained using a finite mixture model than a one-component model. The BIC for the model with two classes was also smaller than that of the model with three classes (BIC = 1343.46); thus we conclude that two mixture components were sufficient to adequately model the data and did not fit the ZIP mixture model with four or more risk classes.

Table 3 also gives the results from fitting the ZIP and Poisson regression models. The BIC values from fitting these models were larger than that of the two-component model. We see that the ZIP mixture model provided a better fit to the data than both the ZIP regression model (BIC = 1698.34) and the Poisson regression model (BIC = 1999.22), further confirming the need for using a finite mixture model.

We now report results for the two-component ZIP mixture model. One of the two mixture components corresponded to a low-risk group (Risk Class 1) whose deviant verbalization counts follow a zero-inflated Poisson distribution; the other mixture component represented the high-risk group (Risk Class 2), whose observations were distributed as Poisson. We drew 5000 values of the model parameters from their posterior distribution; Table 4 gives the 95% posterior intervals for these parameters.

Table 4.

Estimated Parameters (95% Posterior Intervals) for the Final Model

Parameter		Low-Risk Class (Component 1)	High-Risk Class (Component 2)
Poisson mean	Males	2.09 (1.66 to 2.57)	12.38 (10.54 to 14.43)
	Females	1.56 (1.15 to 2.04)	9.22 (7.58 to 11.26)
Rate of Zero-inflation		28.3% (17.3% to 37.8%)	—

The estimated odds ratio for RelSZ versus NC for membership in the high-risk component is 3.42 (95% posterior interval: 1.72 to 7.80); as the posterior interval (PI) for the odds ratio did not contain one, we concluded that the relationship between family type (i.e., RelSZ vs. NC) and deviant verbalization risk is statistically significant. Participants who are at high risk for deviant verbalizations represent an estimated 27.6% of the first-degree RelSZ, and 10.1% of the NC. That RelSZ are indeed at higher risk than NC for deviant verbalizations provides support for the use of thought disorder as a schizophrenia endophenotype.

The effect of sex on the deviant verbalization rate can be estimated using the posterior distribution for β_S. We estimated that male subjects make on average 1.34 times as many deviant verbalizations as female subjects (95% PI for this effect: 1.08 to 1.68). The effect of verbal IQ on the rate of zero-inflation was not statistically significant (95% PI for ψ_V: −0.31 to 0.47). The estimated mean number of deviant verbalizations for a high-risk participant is 12.38 for males and 9.22 for females. The number of deviant verbalizations for a low-risk participant is assumed to follow a zero-inflated Poisson distribution with an estimated Poisson mean of 2.09 for males and 1.56 for females, and estimated rate of zero-inflation of 28.3%. 95% posterior intervals for the model parameters are given in Table 4.

We next performed PPC to assess the fit of the final model; we selected the maximum number of deviant verbalizations, the variance, and the percentage of zeros as the test statistics. We also evaluated the final model’s ability to replicate the familial structure present in these data by performing PPC on two additional test statistics: the intra-family correlation coefficient and the median intra-family variance. Each of these statistics was calculated for the entire sample as well as for the RelSZ and NC separately. All of the PPC p-values are greater than 0.05, indicating that the final model can adequately reproduce all of the summary statistics considered. Thus, we conclude that the final model performs well for both family and global statistics.

7. Discussion

Datasets that contain a large proportion of zero-valued observations are common in many areas of research. Such data can be too skewed for statistical methods that assume normality to perform well, motivating the use of data analytic methods that accommodate zero-inflated data. Furthermore, datasets that include related family members will be characterized by non-independent observations. Finite mixture models are a useful tool for resolving the heterogeneity in these types of data. Mixture analytic methods for including related individuals and families of different size have been developed [70, 71] based on models that are similar in structure to models developed for repeated-measures data [11, 13]. At the time the work described here was being done (2010), there appeared to be no commercial software available to fit correlated zero-inflated Poisson models using a Bayesian approach. However, it appears that Mplus has recently been expanded to include that functionality [72].

The models we present can be adapted to many different kinds of data sets by adjusting the number of risk classes, selecting which risk class is subject to zero-inflation, or by removing the zero-inflated component altogether. In addition, the need for each adjustment to the basic model can be assessed by conducting a likelihood ratio test and using posterior predictive checks to test the resulting increase in likelihood for statistical significance. That these models can be further adjusted to allow for the analysis of correlated data provides additional flexibility and has considerable utility.

This method offers an advantage over the classic Poisson or ZIP regression model in that heterogeneity within groups is explicitly modeled. This feature is especially helpful when analyzing data from a proposed endophenotype. Use of the ZIP mixture model allows us to estimate the proportion of subjects who exhibit an abnormal behavior or trait, and thus, may be potential gene carriers.

The method presented here should only be applied to data that can be well modeled by a mixture of Poisson models with a zero-inflated component. Furthermore, in order for the parameters of the model to be estimable, only one of the mixture components may be zero-inflated; thus this model should not be applied to data that are subject to multiple sources of zero-inflation. Several steps can be taken to avoid the inappropriate application of the ZIP mixture model. Much work has been devoted to verifying the appropriateness of the Poisson assumption [73–75] as well as correctly identifying zero-inflation [19, 76]. We also advocate first fitting a version of the model with only one component and comparing the fit of that model to versions with two components to determine whether a finite mixture model is necessary to adequately model the data. Finally, as demonstrated above, posterior predictive checks [37] can be useful in assessing model fit and diagnosing model misspecifications. This approach can be applied to any dataset that meets the above criteria for a ZIP mixture model and can incorporate random effects and covariates as needed.

In our worked example, we apply our method to a provisionally identified endophenotype – a quantitative measure of “thought disorder with schizophrenic features” – in samples of clinically unaffected first-degree relatives of schizophrenia patients and nonpsychiatric controls. In the finite mixture modeling of the thought disorder data, we started with relatively simple models and successively incorporated more complex models in order to illustrate the model testing sequence and strategy and how to evaluate the goodness of fit of the various models to the data. This approach showed that a mixture model succeeds in fitting the deviant verbalizations data and that simple models do not fit the data as well as more complex ones. We also demonstrated that the probability of being identified at high risk for thought disorder, based on the best-fitting model, is significantly greater for first-degree relatives of schizophrenics than for controls. These results provide support for the potential usefulness of deviant verbalizations as a schizophrenia endophenotype.

Figure 2.

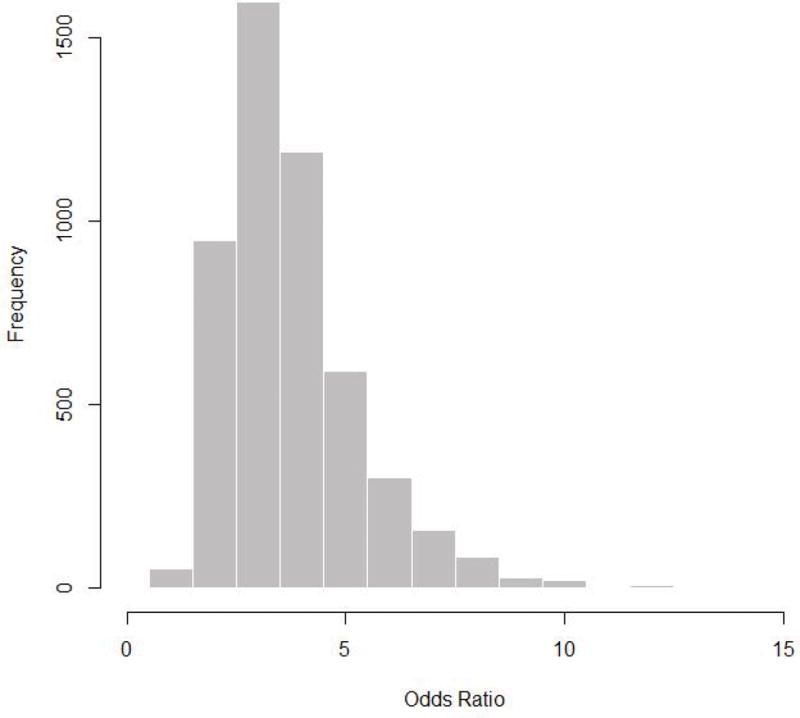
Posterior Distribution of Odds Ratio for Membership in the High-Risk Class for RelSZ versus NC

Table 2.

Demographic Characteristics of the Sample

	RelSZ		NC
	Mean	(SD)	Mean	(SD)
Age (yrs)	49.27	(15.94)	42.78	(15.37)
Estimated Verbal IQ*	107.86	(12.78)	106.33	(11.52)
Education (yrs)	15.21	(2.66)	15.31	(2.40)
SES**	2.25	(0.95)	2.16	(0.96)
GAS	74.98	(10.57)	76.59	(10.56)
% Male	38.15%		39.82%
n	173		113

^*Estimated from the vocabulary subtest of the WAIS-R [52].

^**Estimated from the Hollingshead scale [53], as revised by our group.