Infection dynamics in HIV-specific CD4 T cells: does a CD4 T cell boost benefit the host or the virus?

Abstract

Recent experimental data have shown that HIV specific CD4 T cells provide a very important target for HIV replication. We use mathematical models to explore the effect of specific CD4 T cell infection on the dynamics of virus spread and immune responses. Infected CD4 T cells can provide antigen for their own stimulation. We show that such auto-catalytic cell division can significantly enhance virus spread, and can also provide an additional reservoir for virus persistence during anti-viral drug therapy. In addition, the initial number of HIV-specific CD4 T cells is an important determinant of acute infection dynamics. A high initial number of HIV-specific CD4 T cells can lead to a sudden and fast drop of the population of HIV-specific CD4 T cells which results quickly in their extinction. On the other hand, a low initial number of HIV-specific CD4 T cells can lead to a prolonged persistence of HIV specific CD4 T cell help at higher levels. The model suggests that boosting the population of HIV-specific CD4 T cells can increase the amount of virus-induced immune impairment, lead to less efficient anti-viral effector responses, and thus speed up disease progression, especially if effector responses such as CTL have not been sufficiently boosted at the same time.

1. Introduction

CD4 T helper cells are a major target for the replication of human immunodeficiency virus (HIV). On the other hand, CD4 T cells are also a central component which orchestrates the generation of specific immune responses through the delivery of help. Recent studies have shown that a significant proportion of HIV-specific CD4 T cells are infected by the virus, and that this specific population of T cells might be preferentially infected [1]. This has important implications for understanding the dynamics between HIV and immune responses. Infection of HIV-specific CD4 T cells can have several consequences for the dynamics between the virus and the immune system. For example, it enables the virus to spread via the division of infected T cells. Moreover, this spread can be considered autocatalytic, since T cells proliferate in response to antigenic stimulation. (The higher the virus load, the more efficient the rate of mitotic spread). Infection of HIV-specific CD4 T cells can also result in efficient impairment of effector responses, such as cytotoxic T lymphocytes (CTL) or antibodies, because the ability to deliver help may be subverted [2–4].

Mathematical models have provided important insights into the dynamics between HIV replication and immune responses [5–7]. While some models have analyzed the effect of specific helper cell infection and immune impairment [8], the detailed dynamics of virus spread in HIV-specific CD4 T cells has so far not been taken into account explicitly. Here, we construct mathematical models which describe the infection dynamics in HIV-specific CD4 T cells in detail, and ask how this affects the dynamics between virus spread and effector responses. We start by examining the dynamics of autocatalytic virus spread via the division of infected CD4 T cells. We then expand the model to include infectious spread of the virus and alternative target cells which do not react against HIV (T cells with other specificities or antigen presenting cells). We ask how a change in the initial number of HIV-specific CD4 T cells can influence the outcome of the dynamics during the initial stages of the infection. Further, we explore how infection of HIV-specific CD4 T cells influences virus dynamics during drug treatment.

The general approach to the article is as follows. We start from very a very simple model that forms the core for understanding the effect of autocatalytic virus spread. Although this very simple model lacks much of HIV biology, it allows us to obtain some basic analytical insights into the properties of autocatalytic virus spread. Once we have analyzed and understood this system, we will subsequently include more biological reality and complexity. That is, several models are discussed, ranging from simple to complex. The models are investigated analytically and by numerical simulations. The aim is to demonstrate potential consequences of autocatalytic virus spread and the dual role of CD4 T cells in HIV infection. At this stage, not enough parameter values are known, and not enough details are known about the biological processes underlying the model assumptions for quantitative predictions to be possible. However, a general analysis of the dynamics is a first step for a better understanding, and can provide valuable information for the design of vaccines. Also, please note that the models presented here are specifically tailored to investigate the questions posed here, and thus do not take into account aspects of HIV dynamics that are not directly relevant to these questions (e.g. immune escape and antigenic variation, or aspects of long term progression of the disease).

2. Basic dynamics of autocatalytic virus spread

We start by looking at the simplest model of autocatalytic virus spread. We assume the existence of infected HIV specific CD4 T cells which can produce new virions, and ask under which circumstances this population of cells will grow and expand. The model is given by the following differential equations which describe the development of the cells over time.

$$\begin{array}{l}\frac{dy}{dt}=\mathit{ryv}\left(1-\frac{y}{k}\right)-ay\\ \frac{dv}{dt}=\eta y-uv\end{array}$$ (1)

The infected HIV-specific CD4 T cells are denoted by y, and free virus particles are denoted by v. The CD4 T cells are assumed to proliferate at a rate proportional to the amount of virus recognized (ryv). This proliferation is density dependent, limited by the so called carrying capacity, k. This means that as the number of infected CD4 T cells increases, the proliferation rate slows down. This is because we assume that the number of specific CD4 T cells cannot grow beyond a level given by k, determined by homeostatic mechanisms. Density dependence is modeled in a phenomenological way, and this could also be modeled with other mathematical expressions. Numerical simulations, however, indicate that the results discussed here do not depend on the exact mathematical formulation of density dependence. The infected CD4 T cells die at a rate ay. The infected cells produce free virus at a rate ηy and free virus decays at a rate uv. For now, we do not include spread of these virus particles to uninfected cells because we ask under which circumstances autocatalyitc growth alone can drive virus spread.

The model is characterized by two outcomes: (EQ1) The infected CD4 T cells fail to expand where y=v=0. (EQ2) The infected CD4 T cells do expand and grow towards an equilibrium which is described by $y=\frac{r^{\prime }k+\sqrt{{r^{\prime }}^2{k}^2-4r^{\prime }ak}}{2r^{\prime }}$ and v=ηy/u, where r′=rη/u. The stability properties have been determined by standard techniques and are described as follows. Outcome EQ1 describing failure to expand is always stable. If the basic rate of T cell proliferation lies above a threshold such that r′ > 4a/k, the outcome describing T cell expansion is also stable. Thus, if this condition is fulfilled, both outcomes are possible. Which outcome is observed depends on the initial conditions. If the initial abundance of the infected CD4 T cells lies above a threshold, the CD4 T cells expand. If the initial abundance of infected CD4 T cells lies below a threshold, the T cells fail to expand. This threshold abundance of infected CD4 T cells is given by $y_{\mathit{thr}}=\frac{r^{\prime }k-\sqrt{{r^{\prime }}^2{k}^2-4r^{\prime }ak}}{2r^{\prime }}$. The reason for this dependence on the initial number of T cells is that the cells need to receive sufficient antigenic stimulation so that the rate of proliferation is greater than the death rate. This can only be achieved if the number of infected T cells lies above a threshold. Therefore, autocatalytic virus growth via antigen-induced division of infected T cells is inefficient at low virus loads, but can contribute significantly to virus spread at higher virus loads.

3. Infectious and autocatalytic virus spread in T cells

In the previous section, we examined virus spread by the division of HIV-specific CD4 T cells. We ignored virus transmission to susceptible and uninfected HIV-specific CD4 T cells. We now expand the model to include this. We assume that uninfected CD4 T cells proliferate in response to antigenic stimulation at a rate rx, die at a rate dx, and become infected at a rate βxv. The rate of infection is thus proportional to the amount of virus present. Note that the proliferation rate of the T cells is density dependent and slows down as the total number of T cells (infected + uninfected) reaches a homeostatic set-point described by the parameter k. Virus is produced from infected cells at a rate η and decays at a rate u. The model is based on previous work which investigated virus spread via the mitotic division of T cells [9,10] and is given by the following set of differential equations.

$$\begin{array}{l}\frac{dx}{dt}=\mathit{rxv}\left(1-\frac{x+y}{k}\right)-dx-\beta xv\\ \frac{dy}{dt}=\beta xv+\mathit{ryv}\left(1-\frac{x+y}{k}\right)-ay\\ \frac{dv}{dt}=\eta y-uv\end{array}$$ (2)

The dynamics may converge to two different stable equilibria. (i) The CD4 T cell response, and thus virus replication in specific T cells, does not become established. That is, x=y=v=0. (ii) The response and thus the infection does become established. We do not, however, observe the presence of uninfected CD4 T cells. The entire population of HIV-specific CD4 T cells carries the virus. This is described the by the following equilibrium expressions. x=0; $y=\frac{r^{\prime }k+\sqrt{{r^{\prime }}^2{k}^2-4r^{\prime }ak}}{2r^{\prime }}$. Note, that the system is characterized by a third equilibrium that describes the coexistence of infected and uninfected cells. The equilibrium, however, is always unstable.

Which outcomes are observed depends both on the parameters of the model and the initial conditions (Figure 1). The stability properties of the equilibria are as follows. The outcome describing the absence of the response and the failure of infection in HIV-specific CD4 T cells is always stable. The equilibrium describing the establishment of infection is stable if r′ > 4a/k and $\beta >\frac{2r^{\prime }(a-d)}{r^{\prime }k\sqrt{{r^{\prime }}^2{k}^2-4r^{\prime }ak}}$. In words, the division rate of the CD4 T cells, as well as the rate of infection need to lie above a threshold. Therefore, if these two conditions are fulfilled, the dynamics may result in either failure of infection, or the establishment of infection in specific T cells. Which outcome is achieved depends on the initial conditions (Figure 1). Establishment of infection is promoted by a high initial number of uninfected CD4 T cells, as well as a high initial number of infected CD4 T cells.

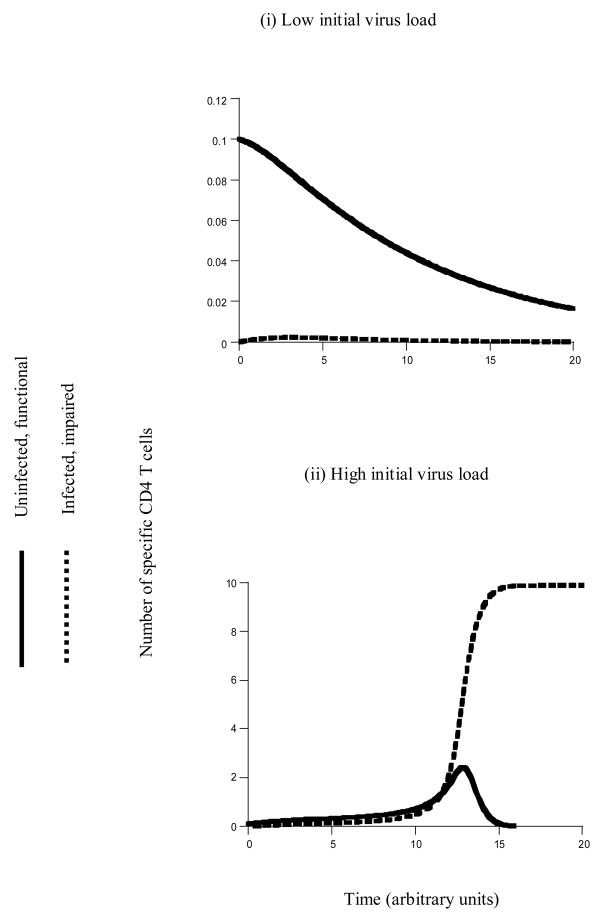
Figure 1.

Basic dynamics of HIV in specific CD4 T cells. The figure is based on model (2). It shows the outcome of infection depending on the initial conditions. (i) If the initial virus load is low, there is not enough antigenic stimulation to establish a CD4 T cell response. Consequently, infection in the specific CD4 T cell population also goes extinct. (ii) If the initial virus load is high, there is enough antigenic stimulation to establish the CD4 T cell response. Consequently, the infection is also established. The virus spreads through the entire population of HIV-specific CD4 T cells and attains 100% prevalence in this population (that is, all specific T cells are infected). Parameters were chosen as follows. r=1, d=0.1, k=10, β=0.2, a = 0.2, η=1, u=0.5. Initial conditions were as follows: x₀=0.1, y₀=0; for (i) v₀=0.1; for (2) v₀=1.

A high initial number of infected T cells provides high degrees of antigenic stimulation for expansion. A high initial number of uninfected T cells provides targets for the virus which accelerates virus growth and the generation of antigenic drive. If, on the other hand, the initial number of infected T cells is low, and there are only few susceptible T cells to infect, then the initial level of antigenic stimulation is not sufficient for the response and the infection to be initiated.

These requirements for establishment of infection are different from those derived from the basic reproductive ratio of the virus, R₀, in standard virus dynamics models. This quantity denotes the number of newly infected cells that arise from any one infected cell when almost all cells are uninfected [11]. If R₀ < 1, then one infected cell gives rise on average to less than one newly infected cell and the virus population cannot spread. If R₀ > 1, then one infected cell gives rise on average to more than one newly infected cell and the virus population grows. The basic reproductive ratio of the virus cannot be clearly defined in the model describing virus replication in HIV-specific T cells because initial virus growth depends on the initial amounts of antigenic stimulation.

As noted above, if virus replication in HIV-specific CD4 T cells is established, the model suggests that all CD4 T cells are infected with HIV (100% prevalence). The reason is that both susceptible and infected T cells proliferate, but that infectious spread of the virus reduces the number of susceptible T cells, and increases the number of infected T cells. Data suggest that uninfected T cells may coexist with infected cells. This can be caused by additional factors which are discussed below, such as the existence of target cells which do not specifically react to HIV, or the presence of immune effector responses. This result does, however, highlight the ability of HIV to quickly impair T cell responses against itself via the infection of its own specificities.

4. Virus replication in HIV-specific and non-specific cells

Here, we include the specific T cell infection model into a larger mathematical framework which takes into account virus replication in cells which do not react against HIV. These are T cells which are not specific to HIV, or antigen presenting cells such as macrophages and dendritic cells. We will refer to them as non-specific target cells.

We denote susceptible non-specific target cells as T, and infected non-specific target cells as I. As before we denote susceptible HIV-specific CD4 T cells as x, infected specific T cells as y, and free virus as v. We assume that susceptible non-specific target cells are produced at a constant rate λ, die at a rate δ, and become infected by virus at a rate γ. Infected non-specific cells die at a rate α. The dynamics of virus infection in HIV-specific T cells remains the same as in the last section. Finally, free virus is produced by both types of infected cells (specific and non-specific) at a rate η and decays at a rate u. The model is given by the following set of differential equations.

$$\begin{array}{l}\frac{dT}{dt}=\lambda -\delta T-\gamma Tv\\ \frac{dI}{dt}=\gamma Tv-\alpha I\\ \frac{dx}{dt}=\mathit{rxv}\left(1-\frac{x+y}{k}\right)-dx-\beta xv\\ \frac{dx}{dt}=\beta xv+\mathit{ryv}\left(1-\frac{x+y}{k}\right)-ay\\ \frac{dv}{dt}=\eta (y+I)-uv\end{array}$$ (3)

A similar model was published by [8] in the context of studying the strength of the CD4 cell response in relation to the clonality of the immune response and the ability of the immune system to control HIV. This model, however, did not take into account autocatalytic virus spread of HIV, and thus did not separately consider populations of infected HIV-specific T cells and infected alternative target cells.

Due to its complexity, this model was studied mostly by numerical simulations. In contrast to specific T cell infection, establishment of viral replication in non-specific target cells does not depend on the initial conditions and occurs if the basic reproductive ratio of the virus, R₀, is greater than one. The basic reproductive ratio in the non-specific target cells is given by R₀ = γηλ/δαu. If the virus can establish infection in the population of non-specific target cells, we can observe three different outcomes regarding the dynamics of the specific CD4 T cells. (i) If virus load in the non-specific target cells lies below a threshold and is not sufficient to trigger a CD4 T cell response, the dynamics of the specific CD4 T cell response behave in the same way as those in the model which only includes the population of specific CD4 T cells studied in the previous section. This scenario will not be considered further. (ii) Virus load in the non-specific target cells is sufficiently high to trigger CD4 cell expansion, and we observe the coexistence between susceptible and infected HIV-specific CD4 T cells. This occurs if the infection rate of specific T cells lies below a threshold and the rate of virus-induced cell death of specific T cells lies above a threshold. Under these circumstances virus replication in specific T cells is not efficient enough for the virus to achieve 100% prevalence in the specific CD4 cell population. (iii) Virus load in the non-specific target cells is sufficiently high to trigger specific CD4 cell expansion, and we observe 100% prevalence of HIV in the specific T cells (that is all HIV-specific T cells are infected). This is observed if the infection rate of specific T cells lies above a threshold and the rate of virus-induced death of specific T cells lies below a threshold. Now, virus replication in specific CD4 T cells is efficient enough so that the virus can reach 100% prevalence in this cell population. This is an interesting result in the context of data that indicate preferential infection of HIV-specific CD4 T cells [1], and highlights the efficiency with which HIV infection can result in the impairment of immune responses against itself.

5. Initial numbers of specific CD4 T cells and impairment of help

Here we use the above model to explore how the initial number of HIV-specific CD4 T cells can influence initial virus growth and the impairment of CD4 T cell help. We assume that uninfected CD4 T cells can deliver help, but that infection impairs helper function. For now, we consider the number of HIV-specific CD4 T cells as a general measure of immunity, because CD4 T cell are needed to activate effector responses such as antibodies and CTL. In Section 6, CD4 T cell help will be considered specifically in the context of CTL responses against HIV. The effect of the initial number of HIV-specific CD4 T cells on virus growth and the kinetics of functional helper cells is shown in Figure 2. Consider the virus growth kinetics first. The initial rate of virus growth is the same regardless of the number of specific T cells (Figure 2). This is because virus growth is initiated by replication in non-specific target cells. The slope of this initial growth reflects the intrinsic growth rate of the virus in the non-specific T cells and therefore the basic reproductive ratio, R₀. The subsequent growth kinetics depend on the initial number of specific CD4 T cells (Figure 2). The higher the initial number of specific T cells, the faster this phase of virus growth. These growth kinetics have important implications for measuring the basic reproductive ratio of HIV from the virus dynamics during initial stages of the infection [12, 13]. The phase of virus growth which reflects the basic reproductive ratio of the virus might occur only at relatively low virus loads, possibly below the level of detection. As virus load increases, the kinetics of virus growth change and are not described by the standard infection models used to estimate R₀.

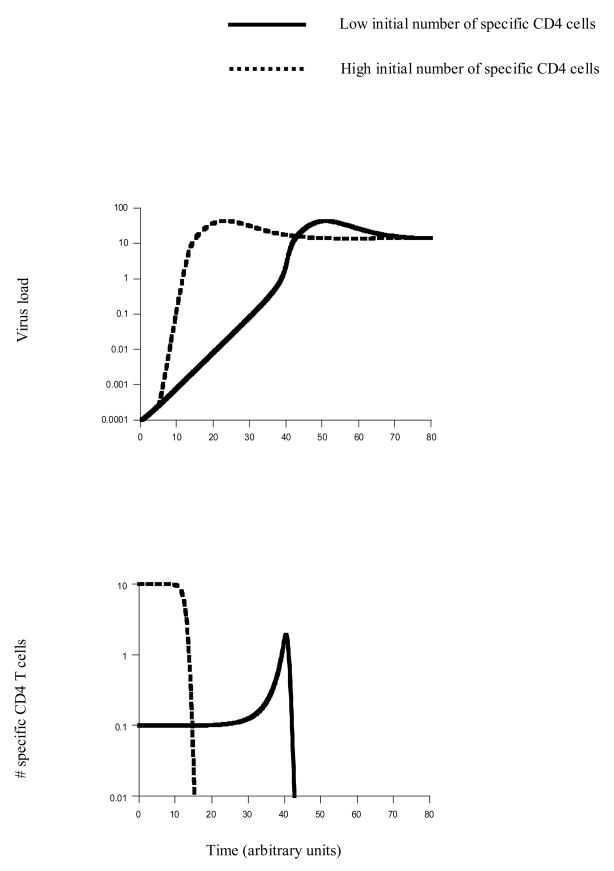
Figure 2.

Virus growth and the impairment of help as a function of the initial number of specific CD4 T cells. The figure is based on model (3) which contains both specific and non-specific target cells. (i) Virus growth: The very first phase of virus growth is the same, regardless of the initial number of specific CD4 T cells. This is because the infection is initiated in the non-specific target cells and it is assumed that specific T cells only become infected after a certain time threshold, because it will take some time for virus to meet the majority of HIV-specific T cells (the virus enters through mucosal surfaces and then makes its way to the blood where the majority of T cells are located). Subsequently, the rate of virus growth depends on the initial number of specific CD4 T cells. The higher the initial number of CD4 T cells, the faster the rate of virus growth. Both time series eventually converge to the same equilibrium. The reason is that this model does not contain any immune effector responses. (ii) Dynamics of functional specific CD4 T cells. We define this population as uninfected T cells. This assumes that infected T cells are impaired. A high initial number of specific CD4 T cells results in a fast decline of functional helper cells. If the initial number of specific CD4 T cells is lower, functional helper cells remain at higher levels for a longer period of time. In the simulation shown here, the population of specific CD4 T cells actually expands before declining to low levels. Parameters were chosen as follows. λ=1, r=1, δ=0.01, α=0.2, γ=0.005, β=0.3, d=0.001, a=0.2, k=10, η=1, u=1. Initial conditions were as follows: T₀=λ/d, I₀=0.0001, x₀=0.1 or x₀=10, y₀=0, v₀=ηI₀/u.

Next, we consider the kinetics of functional helper cells (Figure 2). We distinguish between two scenarios. First we assume that the virus can spread efficiently enough in specific T cells to eventually achieve 100% prevalence. That is, the eventual outcome is complete impairment of help. We then investigate the more benign scenario where not all HIV-specific CD4 T cells are infected.

1. Assume that the virus can achieve 100% prevalence in the specific helper cell population once the dynamics have reached a steady state. The dynamics before this steady state is reached are as follows. The dynamics of the uninfected specific T cells can strongly depend on the initial number of these cells (Figure 2). Of course, the higher the initial number of specific T cells, the more help is available as the virus enters the host. As the virus starts to grow, however, the uninfected helper cells decline (Figure 2). Interestingly, the higher the initial number of specific T cells, the faster the decline of functional helpers. On the other hand, if we start with a lower initial number of specific T cells, a higher number of functional helpers remains present for a longer period of time (Figure 2). If we start from a sufficiently low initial number of T cells, we can even observe a significant temporary increase in the number of functional helpers before they decline and the infection achieves 100% prevalence (Figure 2). In summary, while at the time of infection, a higher initial number of specific T cells provides more help, elevated numbers of functional helpers are retained for longer if the initial number of specific T cells is lower. This observation does, however, depend on the parameter values. In particular it depends on the parameters that determine the extent to which the virus impairs its specific immune responses, i.e. the parameters that describe the rate of virus spread in the HIV-specific CD4 T cells. Of particular importance is the infection rate of HIV specific T cells, β. As the value of β is reduced, the virus infects the HIV specific T cells less efficiently, and thus the degree of immune impairment is less strong. Therefore, the difference in the timing of HIV-specific CD4 T cell elimination becomes less pronounced. If the value of β is even lower and crosses a threshold, then virus-induced immune impairment is so weak that the specific CD4 T cells do not go extinct, and this is described in section (ii) below. Also, note that the above described observation can disappear if the viral rate of spread in non-specific target cells is very fast compared to the rate of spread in HIV-specific CD4 T cells. In this case, the virus immediately attains high prevalence in the non-specific target cells, and this leads to instant infection and killing of the HIV specific CD4 T cells. This is not likely to be a realistic scenario.

2. Now, consider the more benign scenario where the virus population cannot achieve 100% prevalence in the specific CD4 T cell population. That is, when steady state is reached, we observe the persistence of uninfected and functional HIV-specific helper cells. If the number of persisting functional helpers is relatively low, the dynamics are similar to the scenario described above. The lower the initial number of specific T cells, the longer the duration during which the number of functional helper cells remains at elevated levels before declining to relatively low numbers. As the infectivity of specific T cells is decreased and the virus-induced death rate of specific T cells is increased, the spread of the virus in the specific T cell population becomes less efficient, and more functional helpers remain at steady state. In this case, the initial number of specific T cells does not significantly alter the availability of help. As steady state is reached, the same relatively high number of functional helpers is maintained. This scenario corresponds to only limited amounts of virus-induced immune impairment and might not apply to typical HIV infection.

6. Generation of effector responses

The generation of sustained effector responses can depend on the availability of help [14–16]. This applies both to antibody and to cytotoxic T lymphocyte (CTL) responses. As an example, we consider a CTL response which kills infected cells. CTL dynamics are modeled as follows. We assume that upon antigenic stimulation, naïve CTL undergo a phase of programmed proliferation which results in the differentiation into effector and memory cells [17,18]. We start with a (small) population of naïve specific CTL which have been activated by antigen. They are denoted by m₀. These CTL undergo n rounds of proliferation, and this is independent of antigenic stimulation. Proliferation occurs with a rate 2ρm_i, where m_i denotes CTL which have undergone i divisions (i=1..n−1). The n^th division gives rise to effector cells, denoted by w. They can kill infected cells. Effectors die at a rate φw and differentiate into memory cells at a rate ξw. These processes are described by the following set of differential equations (This approach is described in detail by [19,20]):

$$\begin{array}{l}\frac{dw}{dt}=2\rho m_{n-1}-\xi w-\varphi w\\ \frac{d{m}_{n-1}}{dt}=2\rho m_{n-2}-\rho m_{n-1}\\ •••\\ \frac{d{m}_1}{dt}=2\rho m_0-\rho m_1\\ \frac{d{m}_0}{dt}=-\rho m_0\end{array}$$ (4)

Other mathematical models of programmed CTL proliferation have also been considered by [21,22].

In accord with experimental data we assume that effectors differentiate into effector memory cells [23], and that in HIV infection central memory cells are not created at normal levels [24]. Instead, the effector memory cells continuously become activated by antigen and give rise to new effectors which again differentiate into effector memory cells. This cycle is continuously repeated during the course of infection. We assume that activation of the memory cells requires not only antigen, but also CD4 T cell help [25–27]. Because not much is known about the CTL proliferation kinetics (involving effector memory and central memory cells) during chronic infection, we take a simplified approach. We can capture the populations of effector and effector memory cells during chronic infection in a single variable, denoted by z. Based on previous models [28], these dynamics are described by the following differential equation:

$$dz/dt=\xi w+cx(y+I)z/(\epsilon x+1)-bz$$ (5)

Effector memory cells are generated during acute infection with a rate ξ. In addition, they become reactivated, expand and develop effector activity. This requires antigen, derived from both infected HIV specific and alternative cells (y+I), and CD4 T cell help, x. It occurs with a rate cx(y+I)z/(εx+1). The dependence on help saturates at high numbers of helper cells. The CTL die during chronic infection with a rate bz. CTL-mediated lysis is described in the model by adding the death terms −py(z+w) and −pI(z+w) to the equation for the respective infected cell dynamics.

This model was studied by numerical simulations, assuming that the virus can successfully establish an infection. If HIV significantly reduces the number of functional helper cells, or even drives them extinct, we find that the outcome of the CTL dynamics can depend on the initial conditions (Figure 3). The CTL response may either become established and control the infection; or the CTL response is impaired and does not become fully established. Which outcome is attained can crucially depend on the initial number of specific helper cells. We distinguish between two scenarios. (i) Assume that CTL effectors are generated with a fast rate when the virus infects the host (Figure 3i). In the model this corresponds to a high value of ρ. This is unlikely to apply to a naïve host. It may correspond to the existence of CTL memory, for example induced by boosting CD8 T cell responses. In this case, establishment of a CTL response is promoted by a higher initial number of specific helper cells (Figure 3i). This is because at the time of infection, a higher initial number of specific helper cells results in more availability of help for the CTL. (ii) Next assume that there is a certain delay in the induction of the CTL effectors (Figure 3ii). This is likely to apply to naïve hosts because the process of antigenic stimulation, programmed proliferation, and migration of the cells to the site of infection takes time (low value of ρ). Now, we find the opposite result. A lower initial number of specific helper cells promotes the establishment of a sustained CTL response (Figure 3ii). This is because with a lower initial number of specific helper cells, elevated numbers of functional helpers remain present for a longer period of time before declining to low levels or extinction. Since we assume a naïve host which needs time to activate CTL and to mount a response, the prolonged availability of help is crucial for the maintenance of the response once it has been induced. Note that this effect also depends on viral parameters, in particular those that determine the degree of virus-induced immune impairment. These are parameters that describe the rate of viral spread in HIV-specific T cells, such as the rate of infection or the life-span of infected specific T cells. For example, if the infection rate of HIV-specific CD4 T cells, β, is reduced, the difference in the timing of T cell decline gets smaller. In other words, the difference in outcome between low and high initial numbers of specific CD4 T cells becomes less pronounced. If the infection rate of specific CD4 T cells falls below a threshold, then the specific CD4 T cell population does not go extinct anymore. This corresponds to minimal immune impairment, a scenario that is not typical of HIV infection. In this case, the initial number of specific CD4 T cells has no effect in the outcome of the dynamics.

Figure 3.

CTL dynamics as a function of the initial number of specific CD4 T cells. The figure is based on models (4,5). We distinguish between two scenarios. (i) Effectors are generated at a relatively fast rate. In this case, a high initial number of specific CD4 T cells is beneficial for the immune response. (ii) Effectors are generated with a slower rate. In this case, a low initial number of specific CD4 T cells is beneficial for immunity. Parameters were chosen as follows. (i) λ=1, r=1, δ=0.01, α=0.2, γ=0.01, β=0.3, d=0.001, a=0.2, p=45, c=1, b=0.1, k=10, η=1, u=1, φ=1.5, ξ=0.01, ε=1, n=10. For (i) ρ=1 and for (ii) ρ=0.3. Initial conditions were as follows: T₀=λ/d, I₀=0.0001, x₀=0.1 or x₀=10, y₀=0, v₀=ηI₀/u, m₀=0.1, mi₀=0, w₀=0, z₀=0.

Therefore, the dependency of the dynamics on the initial number of specific helper cells can be complex and can depend on the viral replication kinetics and on the exact CTL kinetics. If the CTL give rise to effectors immediately upon infection, boosting the specific CD4 T cells is beneficial for the host. This may occur if in addition to the helper cell response, the CD8 cell response has also been boosted by vaccination. Whether CD8 cell vaccination can lead to this outcome may, however, also depend on the details of the vaccination [29]. If vaccination maintains active effector responses by providing continuous antigenic stimulation, this argument would certainly apply. If, on the other hand, vaccination just boosts the number of resting memory CTL, effectors might not be generated sufficiently fast for this argument to apply. If there is a significant delay between the time of infection and the generation of CTL effectors, boosting the specific CD4 T cells is beneficial for the virus and can potentially accelerate disease progression. This may correspond to the scenario where only helper cells, but not CD8 T cells have been boosted by vaccination; or if the boosted CTL response persists in the form of resting CTL which require a certain amount of time to differentiate into effectors. It has been documented that specific vaccination approaches which increased the number of SIV-specific CD4 T cells can accelerate disease progression rather than prolong or prevent it [30].

7. Specific CD4 T cell dynamics during drug therapy

Here we investigate the dynamics of the HIV-specific T cells during a phase of drug therapy. Antiviral drugs essentially block viral replication. In terms of the model, this can be expressed as a reduction in the parameters γ and β; in words [31], a reduction in the infectivity of non-specific target cells and specific T cells. As expected, drug therapy in the model results in a reduction of virus load in the non-specific target cells (Figure 4). The dynamics of virus replication during drug therapy in the specific T cell population is more complicated. This is because the virus can also spread by antigen-driven division of infected T cells, and this is not inhibited by drug therapy. We distinguish between two scenarios. In the first case, we assume that before therapy, the virus is 100% prevalent in the specific T cell population. Then we consider the case where both infected and uninfected specific T cells co-exist before the start of treatment.

Figure 4.

Virus dynamics during drug therapy. Phase of drug therapy is indicated by shading. This figure is based on model (3), and does not include immune effectors for simplicity. We make the extreme assumption that there are no latently infected cells and that therapy can eradicate HIV from the non-specific target cells. We do this in order to demonstrate that the auto-catalytic virus spread via antigen driven division of specific CD4 T cells can present a separate reservoir which can prevent eradication of HIV from the host. Upon treatment, virus load is significantly reduced in the simulation, but settles at a persistent equilibrium. This happens, although the number of infected non-specific target cells is eradicated, and no latency is assumed. The key lies in the dynamics of the infected specific CD4 T cells. Because drug therapy reduces infectious spread of HIV, the amount of antigenic stimulation is reduced. Consequently, the number of infected specific helper cells declines. However, this population of infected specific helper cells provides enough antigenic stimulation itself to keep these cells dividing. Because drug therapy does not inhibit the mitotic spread of the infection, the virus persists. Parameters were chosen as follows. λ=100, r=1.5, δ=0.01, α=0.3, γ=0.01, β=0.3, d=0.01, a=0.3, k=1, η=1, u=1. During treatment, γ=β=0. Regarding initial conditions upon start of therapy, the system was run until all populations equilibrated, and then treatment was initiated in the model.

Consider the scenario where the virus has attained 100% prevalence in the specific T cell population before the start of treatment. We further assume that during drug therapy, new susceptible specific T cells are not produced. In this case, the population of infected specific T cells can keep cycling during drug therapy and can be maintained at a steady state (Figure 4). This steady state may be small and below the level of detection. Thus, while drug treatment can significantly reduce virus load, continued antigen-driven proliferation of infected T cells can provide a reservoir of mitotic virus spread which is not affected by therapy and which hinders further elimination of the infection (Figure 4). This is a separate and additional barrier to treatment from latently infected cells which are known to persist during therapy [32].

Now, assume that the virus has not attained 100% prevalence in the specific T cell population, and that uninfected specific T cells are observed before the start of treatment. That is, virus spread is slower than above, and virus-induced helper cell impairment is weaker. In this case, the dynamics of specific T cells are different. Therapy reduces the infection rate of susceptible T cells and thus the degree of impairment. Consequently, functional (uninfected) CD4 T helper cells temporarily expand upon treatment, and infected T cells decline. This is because before the virus has declined to low levels, the T cells receive antigenic stimulation without being infected at a significant rate. While the infected T cells also receive antigenic stimulation, they are killed by the virus and therefore decline relative to the number of uninfected cells. If virus load is reduced to sufficiently low levels during therapy, the specific CD4 T cells are expected to eventually vanish during treatment. On the other hand, if sufficient amounts of antigenic stimulation remains during therapy due to elevated residual replication in non-specific target cells, this can maintain elevated levels of specific T cells which are active and divide during treatment. Both infected and uninfected cells persists. The higher the amount of antigenic stimulation during treatment, the higher the number of infected relative to uninfected specific cells which persist during the phase of therapy.

8. Conclusion

This paper has used mathematical models to show that the ability of HIV to infect and perhaps preferentially infect HIV-specific CD4 T cells has important consequences for the dynamics of the infection. The auto-catalytic spread of infected HIV-specific CD4 T cells contributes significantly to the rate of virus spread at higher virus loads, and also provides an additional reservoir which prevents elimination of infected cells during drug therapy. Because the ability of HIV-specific CD4 T cells to divide is not hindered by anti-viral drugs, the cells can stimulate themselves during therapy, and thus persist at a certain steady state rather than declining. The ability of HIV to infect its specific CD4 T cells also has important implications for vaccination approaches. Especially if CD8 T cells are not boosted at the same time, an elevation of the initial numbers of CD4 T cells can be advantageous for the virus and not for the host, and such vaccination approaches are likely to speed up disease progression rather than to prevent it, as found in a case study with SIV-infected macaques [30]