Estimation of the CSA-ODF using Bayesian Compressed Sensing of Multi-shell HARDI

Abstract

Purpose

Diffusion MRI provides important information about the brain white matter structures and has opened new avenues for neuroscience and translational research. However, acquisition time needed for advanced applications can still be a challenge in clinical settings. There is consequently a need to accelerate diffusion MRI acquisitions.

Methods

A multi-task Bayesian compressive sensing (MT-BCS) framework is proposed to directly estimate the constant solid angle orientation distribution function (CSA-ODF) from under-sampled (i.e., accelerated image acquisition) multi-shell high angular resolution diffusion imaging (HARDI) datasets, and accurately recover HARDI data at higher resolution in q-space. The proposed MT-BCS approach exploits the spatial redundancy of the data by modeling the statistical relationships within groups (clusters) of diffusion signal. This framework also provides uncertainty estimates of the computed CSA-ODF and diffusion signal, directly computed from the compressive measurements. Experiments validating the proposed framework are performed using realistic multi-shell synthetic images and in-vivo multi-shell high angular resolution HARDI datasets.

Results

Results indicate a practical reduction in the number of required diffusion volumes (q-space samples) by at least a factor of four to estimate the CSA-ODF from multi-shell data.

Conclusion

This work presents, for the first time, a multi-task Bayesian compressive sensing approach to simultaneously estimate the full posterior of the CSA-ODF and diffusion-weighted volumes from multi-shell HARDI acquisitions. It demonstrates improvement of the quality of acquired datasets via CS de-noising, and accurate estimation of the CSA-ODF, as well as enables a reduction in the acquisition time by a factor of two to four, especially when “staggered” q-space sampling schemes are used. The proposed MT-BCS framework can naturally be combined with parallel MR imaging to further accelerate HARDI acquisitions.

INTRODUCTION

Diffusion magnetic resonance imaging (MRI) can characterize the anisotropic thermal motion of water molecules in biological tissues, such as brain white matter. This information can be used to estimate the local orientation of white matter fiber bundles. Diffusion tensor imaging (DTI) (1) was introduced to describe the three-dimensional nature of anisotropic diffusion in biological tissues. However, the diffusion tensor model is inadequate when two or more fiber bundles cross (at the acquisition resolution). It is estimated that between one third and two-thirds of imaging voxels in the human brain’s white matter contain multiple fiber crossings (2). High angular resolution diffusion imaging (HARDI) overcomes limitations of DTI for characterizing complex tissue geometries such as fiber crossings, by measuring the diffusion-weighted signal along tens to hundreds of directions (q-space). The high angular resolution of HARDI allows estimating the orientation distribution function (ODF), which is the average probability of diffusion along any diffusion direction, therefore enabling fiber crossing detection (3).

HARDI requires a relatively large number of diffusion encodings to accurately recover the ODF (4), limiting its applicability to clinical studies. The use of more complex excitation techniques combined with parallel imaging techniques (pMRI) (5–8) has reduced acquisition times of diffusion weighted MRI (DW-MRI), typically by a factor of three. Recently, pMRI and compressed sensing (CS)¹ methods have been combined to reduce the acquisition time of structural MRI (9–16), diffusion spectrum imaging (DSI) [14–19], HARDI (23–25), and dynamic MRI (26–34), leading to combined acceleration factors of 9 and higher.

Compressed sensing of HARDI data sets has been proposed in the past (24,35–37), where the diffusion directions are pseudo-randomly under-sampled and the skipped directions are recovered (interpolated) using sparse representation models and CS reconstruction methods. However, these under-sampled measurements are not linear combination of the diffusion signal (just a subsample of them), and hence, do not fully exploit the power of CS as an inverse model reconstruction technique. More recent work directly estimated the ODF from under-sampled single-shell (38) and multi-shell HARDI data (21–23,25,39) using CS methods. Under-sampled HARDI data can be seen as a CS measurement of the ensemble average propagator (EAP) (21–23,25,39) or the ODF (38), fully exploiting the power of CS. However, most of these previous works rely on the classical definition of the ODF (3). In this work, we develop a multi-task Bayesian compressive sensing framework for DW-MRI, following our previous work by Duarte-Carvajalino et al. (37), to directly estimate the constant solid angle ODF (CSA-ODF) (40) from multi-shell compressed sensed HARDI data sets. The CSA-ODF was recently introduced to update the commonly used ODF definition (3), providing a mathematically correct probabilistic distribution function (PDF) expression for the ODF. The classical definition of the ODF ignores the quadratic growth of the volume element in q-space with respect to its distance from the origin, leading to an inaccurate formulation that requires artificial post-processing such as normalization and sharpening (40–43). The CSA-ODF accounts for this quadratic growth, leading to a correct PDF formulation that does not require artificial normalization (integrating to one) or sharpening.

Compared to the work by Tristán-Vega et al. (38), we use multi-shell data, with signal-to-noise ratios (SNRs) commonly found in in-vivo HARDI data,² and a Bayesian CS approach (37,44). In addition, previous work on CS of the CSA-ODF provide only maximum a posteriori (MAP) (45) estimates of the ODF and/or diffusion-weighted volumes. We use here Bayesian inference to estimate the full posterior distributions of the CSA-ODF and diffusion-weighted volumes, providing point estimates, as well as uncertainty estimates of those quantities. The uncertainty estimates allow us to evaluate the confidence on the reconstructed data. Since the reconstructed point estimates may have large variance, the additional characterization of full posterior distribution, information not available with classical MAP CS methods, is as important as the reconstructed point estimates.

In addition to the proposed Bayesian compressed sensing of the CSA-ODF (bcsCSA-ODF), we provide comparison with the CSA-ODF (40) implemented in the FSL library³ (46) to compute the ODFs from the original and under-sampled HARDI data sets. CSA-ODF relies on a bi-exponential model for the diffusion signal decay and analytic solution for multi-shell HARDI data (with b-values in arithmetic progression). We also compare with a generalized CSA-ODF (gCSA-ODF) bi-exponential algorithm (41) that can handle under-sampled HARDI, with arbitrary q-space sampling, and computes the CSA-ODFs and “missing” diffusion-weighted volumes by using optimally regularized SHs interpolation and the bi-exponential model. Both gCSA-ODF and CSA-ODF are established data-fitting techniques which do not explicitly exploit signal sparsity and have performances that can more readily be compared with the more sophisticated CS algorithm. The comparison with more conventional algorithms is used to illustrate the advantage of applying a sophisticated CS algorithm. The gCSA-ODF and bcsCSA-ODF models have been implemented in FSL and will be available on the NITRC web site.

The results demonstrate that, at realistic SNR levels, the proposed Bayesian CS framework performs better than using simpler angular interpolation methods such as the CSA-ODF and gCSA-ODFs for multi-shell images. We demonstrate the feasibility of acceleration factors equal to or greater than four.

METHODS

Constant Solid Angle ODF

For a given spatial location (voxel) of a HARDI dataset, the probability of diffusion along the direction û can be modeled by the constant solid angle orientation distribution function (CSA-ODF) ϕ(û) (38,40)

$$\varphi (\widehat{\mathbf{u}})=-\frac{1}{8{\pi }^2}{\mathcal{R}}_{\widehat{\mathbf{u}}}\{{\nabla }^{2}x(\mathbf{q})\},$$ [1]

where, {f(q)} = ∫∫f(q)δ(q̂^Tû)dq is the Funk-Radon transform, δ the Delta-Dirac function, x(q) = S(q)/S(0) the normalized signal attenuation at a given diffusion direction q̂ and magnitude q(q = qq̂), S(q) is the measured HARDI signal in q-space, and S(0) the non diffusion-weighted (q = 0) signal. Limiting the diffusion signal to concentric spheres and introducing a radial mono-exponential model, we obtain x(q) for any q from a given measurement x(q₀q̂) at a specific q₀ value as $x(\mathbf{q})={[x(q_0\widehat{\mathbf{q}})]}^{q^2/q_0^2}$ (40). With this assumption, it has been shown that [1] is equivalent to (40)

$$\varphi (\widehat{\mathbf{u}})=\frac{1}{4\pi }+\frac{1}{16{\pi }^2}{\mathcal{R}}_{\widehat{\mathbf{u}}}\left\{{\nabla }_b^{2}ln\left(-ln\left(x(\mathbf{q})\right)\right)\right\},$$ [2]

where ${\nabla }_b^2=\frac{1}{tan\theta }\frac{\partial }{\partial \theta }+\frac{{\partial }^2}{{\partial }^2\theta }+\frac{1}{{sin}^2\theta }\frac{{\partial }^2}{{\partial }^2\phi }$ is the Laplace-Beltrami operator in spherical coordinates (θ, φ). In practice, E in [2] is regularized in such a way that ln(−ln(x)) is smooth (40).

We should emphasize that there is, in practice, no need to carry the numerical derivation and integration indicated in [2] to compute the CSA-ODF. The computation of the CSA-ODF is greatly facilitated by the fact that the spherical harmonics (SH) basis are eigen-functions of the Funk Radon transform (47–49). Indeed, with Ẽ = ln(−ln(x(q))), Ẽ can be represented in the SH basis as

$$\stackrel{\sim }{x}=ln\left(-ln\left(x(\mathbf{q})\right)\right)\approx {\sum }_{r=1}^R{c}_r{Y}_r(\widehat{\mathbf{u}}),$$ [3]

where R is the number of elements of the SH basis used in the approximation, Y_r(û) the real and symmetric modified SH basis (49), and c_r the SH coefficients computed using least-squares. Then, the CSA-ODF can be obtained explicitly from the SH representation of Ẽ as (40,49)

$$\varphi (\widehat{\mathbf{u}})={\sum }_{r=1}^R{c}_r^{\prime }{Y}_r(\widehat{\mathbf{u}}),c_r^{\prime }=\{\begin{array}{ll}\frac{1}{2\sqrt{\pi }},\hfill & r=1\hfill \\ -\frac{1}{8\pi }{(-1)}^{\frac{k_r}{2}}\frac{1\times 3\times \cdots \times (k_r+1)}{2\times 4\times \cdots \times (k_r-2)}{c}_r,\hfill & r>1\hfill \end{array},$$ [4]

where −k_r(k_r + 1) are the eigenvalues of the Laplace-Beltrami operator. This result indicates that there is an explicit linear relationship between the SH representation of the CSA-ODF and the SH representation of the double logarithm of the diffusion signal. We build on this in the next sections.

Bayesian Compressed Sensing of the CSA-ODF (bcsCSA-ODF)

Consider a multi-shell HARDI experiment, with a total of M diffusion directions (encodings) spread over B shells and N voxels. Let x be the M × 1 measured HARDI attenuations at a given voxel in vector form and Y_M×R the SH basis, with R harmonic coefficients. Then [3] and [4] can be expressed in the SH basis using matrix-vector notation as⁴

$${(\mathbf{\varphi })}_{\text{SH}}\approx {\left[\begin{array}{ll}0\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathbf{\Lambda }\hfill \end{array}\right]}_{R\times R}{\mathbf{Y}}_{R\times M}^{+}\stackrel{\sim }{\mathbf{x}}+{\left[\begin{array}{c}1/\left(2\sqrt{\pi }\right)\\ \mathbf{0}\end{array}\right]}_{R\times 1},\stackrel{\sim }{\mathbf{x}}={\left[ln\left(-ln(x_j)\right)\right]}_{1\le j\le M},$$ [5]

where (ϕ)_SH corresponds to the SH representation of the CSA-ODF, and Y⁺ = (Y^TY)⁻¹Y^T is the pseudo-inverse of the SH basis Y. Hence, Y⁺x̃ provides the (least-squares) estimated SH coefficients c_r indicated in [3], and Λ provides the scaling factors multiplying the SH coefficients c_r in [4], for r > 1. Notice that for r = 1, the scaling factor is zero, since the Laplace-Beltrami operator eliminates the first harmonic coefficient c₁ corresponding to the (constant) average component of the signal x̃. Hence, the $1/\left(2\sqrt{\pi }\right)$ term in [5] is required to obtain $c_1^{\prime }=\frac{1}{2\sqrt{\pi }}$ in [4].

Equation [5] is also equivalent to

$${(\mathbf{\varphi })}_{\text{SH}}\approx \left[\begin{array}{ll}{\gamma }^{-1}\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathbf{\Lambda }\hfill \end{array}\right]{\mathbf{Y}}^{+}\stackrel{\sim }{\mathbf{x}}+\left[\begin{array}{c}1/\left(2\sqrt{\pi }\right)-{\gamma }^{-1}{c}_1\\ \mathbf{0}\end{array}\right],$$ [6]

for any γ ≠ 0. We introduce here the variable γ in order to make the matrix $\left[\begin{array}{cc}{\gamma }^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{\Lambda }\end{array}\right]$ invertible.

Given that one key component in compressive sensing is the sparse representation of the signal in a sparsifying basis or dictionary,⁵ and the SH basis does not constitute a good sparsifying basis for HARDI data (24,35,50), we represent the measured HARDI attenuations x using a more adequate sparsifying dictionary

$$\mathbf{x}={\mathbf{\Psi }}_{M\times L}\mathbf{\vartheta }+\mathit{\eta },$$ [7]

where ϑ(L × 1) is the sparse representation of the attenuation signal at a given voxel in a sparsifying dictionary Ψ, and η is the representation noise at that voxel. As previously reported (24,35,37,50), we choose Ψ to be the Ridgelets basis (though we could learn this from data if desired), since it has been shown that it constitutes a good sparsifying dictionary for HARDI data (24,35,50). Replacing x given by [7] in [1]

$$\mathbf{\varphi }\approx -\frac{1}{8{\pi }^2}{\mathcal{R}}_{\widehat{\mathbf{u}}}\{{\nabla }_b^2(\mathbf{\Psi }(\widehat{\mathbf{u}})\mathbf{\vartheta })\},$$ [8]

where we have used the fact that Ψ(û) has no radial component, hence the Laplacian reduces to the Laplace-Beltrami operator. Since the Laplace-Beltrami and Funk-Radon transforms commute,

$$\mathbf{\varphi }\approx -\frac{1}{8{\pi }^2}{\nabla }_b^2{\mathcal{R}}_{\widehat{\mathbf{u}}}\{\mathbf{\Psi }(\widehat{\mathbf{u}})\mathbf{\vartheta }\}=-\frac{1}{8{\pi }^2}{\nabla }_b^2(\mathcal{H}(\widehat{\mathbf{u}})\mathbf{\vartheta }),$$ [9]

where {Ψ(û)ϑ} = 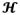(û)ϑ, and 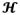(û) corresponds to the Funk-Radon transform of the Ridgelets basis, as specified in (50). We can use finite differences to approximate [9] (see Appendix) and express the CSA-ODF in vector form as ϕ ≈ Dϑ, where D is a dictionary for the CSA-ODF, derived from the Ridgelets basis. The equations to be derived here apply to any CSA-ODF dictionary (including learned ones); we use the Ridgelets basis for convenience (see next section).

We have now two representations of the CSA-ODF. The first in terms of the SH basis ([6]), and another one in terms of a sparsifying dictionary ([9]) that can be represented in matrix-vector form as ϕ ≈ Dϑ. Since, it is the same CSA-ODF, both representations should be equivalent. However, since ϕ ≈ Dϑ is in a different basis, we need to transform this representation in terms of the SH coefficients so that both representations are in the same basis. The SH representation of ϕ ≈ Dϑ can be obtained with the pseudo-inverse as (ϕ)_SH ≈ Y⁺(Dϑ). Representing ϕ ≈ Dϑ in terms of the SH basis does not affect the sparse representation ϑ, (ϕ)_SH ≈ (Y⁺D)ϑ, where Y⁺D corresponds to the new sparsifying dictionary in the SH basis. Hence, [6] and [9] must correspond to the CSA-ODF in SH coordinates,

$${(\mathbf{\varphi })}_{\text{SH}}\approx \left[\begin{array}{ll}{\gamma }^{-1}\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathbf{\Lambda }\hfill \end{array}\right]{\mathbf{Y}}^{+}\stackrel{\sim }{\mathbf{x}}+\left[\begin{array}{c}1/\left(2\sqrt{\pi }\right)-{\gamma }^{-1}{c}_1\\ \mathbf{0}\end{array}\right]\approx {\mathbf{Y}}^{+}\mathbf{D}\mathbf{\vartheta }.$$ [10]

We can solve for x̃ in [10] as (see Appendix)

$${\mathbf{x}}^{\ast }\approx \mathbf{PDJ},{\mathbf{x}}^{\ast }\approx (\stackrel{\sim }{\mathbf{x}}-{\mathrm{c}}_1{\mathbf{Y}}_1)+\gamma /\left(2\sqrt{\pi }\right){\mathbf{Y}}_1,\mathbf{P}=\mathbf{Y}\left[\begin{array}{cc}\hfill \gamma \hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{\Lambda }}^{-1}\hfill \end{array}\right]{\mathbf{Y}}^{+},$$ [11]

where Y₁ corresponds to the first column of the SH basis. (x̃ − c₁Y₁) in [11] corresponds to the variable component of x̃, since the term c₁Y₁ is the mean value of x̃. $\left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]$ corresponds to the inverse of $\left[\begin{array}{cc}{\gamma }^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{\Lambda }\end{array}\right]$ in [6], explaining the auxiliary variable γ ≠ 0 in [5].

Eq. [11] implicitly uses a set of M diffusion directionsU_M = {û₁, ···, û_M} that define the CSA-ODF signal x^*(U_M). However, this equation applies to any number of diffusion directions. Let U_m = {û₁, ···, û_m} ⊂ U_m be the diffusion directions of an under-sampled HARDI experiment, with m < M diffusion directions. Let ${\mathbf{x}}_s^{\ast }={\mathbf{x}}^{\ast }(U_m)$, P_s = P(U_m), D_s = D(U_m) be respectively, the under-sampled HARDI diffusion signal, and P_s, D_s the projection matrix and dictionary of the CSA-ODF ϕ(U_m), then [11] for under-sampled data becomes

$${\mathbf{x}}_s^{\ast }\approx {\mathbf{P}}_s{\mathbf{D}}_s\mathbf{\vartheta },{\mathbf{x}}_s^{\ast }=\stackrel{\sim }{\mathbf{x}}(U_m)-{\mathrm{c}}_1{\mathbf{Y}}_1(U_m)+\gamma /\left(2\sqrt{\pi }\right){\mathbf{Y}}_1(U_m).$$ [12]

A key requirement in CS is that the sampling should be incoherent with the signal of interest (here, the CSA-ODF). This requirement is satisfied with high probability when the sampling is random or pseudo-random (see, for instance (10,17–19,21,22,24,25,35,38,45,50)). As in our previous work (37), we use the optimal pseudo-random Dirac sampling of multi-shell HARDI data proposed by Caruyer et al. (4), which provides diffusion directions that uniformly cover the unit sphere when truncated before the acquisition is complete and satisfy the incoherence principle (35).

Notice that since the signal of interest is the CSA-ODF ϕ ≈ Dϑ. Then with respect to the CSA-ODF, P_s corresponds to the CS matrix and ${\mathbf{x}}_s^{\ast }$ corresponds to the compressed samples of the CSA-ODF, i.e., ${\mathbf{x}}_s^{\ast }$ is an under-sampled linear combination of the full CSA-ODF ([12]), as required to exploit CS. Note that it is not just a sub-sampled signal as in more standard approaches (21–23,25,38,39). On the other hand, x^* is also a signal of interest and PD can be seen as its sparsifying dictionary. However, the samples ${\mathbf{x}}_s^{\ast }$ are not a linear combination of the full x^* signal, and hence the compressed sensed signal is the CSA-ODF, not the attenuations.

Another key requirement in CS is the sparse representation on a given dictionary, which can be exploited by using ℓ₀ or ℓ₁ minimization, sometimes in combination with additional regularizing constraints such as total variation (19,35). We use multi-task Bayesian compressed sensing (MT-BCS), (37), that enforces sparsity via sparsifying priors, provides spatial regularization via probabilistic clustering, and allows the estimation of the full posterior distribution of the signal of interest (while other approaches only give the maximum a posteriori or MAP).

Bayesian Compressed Sensing

We use MT-BCS (37,44,51) to obtain the full posterior distribution of the estimated CSA-ODF and diffusion signal using sparsity inducing priors and shared hyper-priors that model similar spatial sparsity patterns between diffusion signals from different spatial locations in the brain. Specifically,

$$p({\mathbf{\vartheta }}_i\mid {\mathbf{\alpha }}_i)~\mathcal{N}(\mathbf{0},{\mathbf{\Lambda }}_{{\mathbf{\alpha }}_i}),{\mathbf{\Lambda }}_{{\mathbf{\alpha }}_i}=\mathit{diag}\{\begin{array}{lll}{\alpha }_{i1}^{-1}\hfill & \cdots \hfill & {\alpha }_{iL}^{-1}\hfill \end{array}\},i=1,\dots ,N,$$ [13]

is the a priori distribution of ϑ_i ([7], [10]–[12]), modeled as a multidimensional Gaussian with zero mean and diagonal covariance Λ_{α_i}. This prior promotes sparse representations, when the hyper-priors follow a Gamma distribution (44,51). Hyper-parameters ${\left\{{\mathbf{\alpha }}_i\right\}}_{i=1}^N$ in [13] model information sharing among different diffusion signal. Specifically, diffusion signal from different voxels are clustered using a nonparametric Dirichlet process (DP) mixture model. A Dirichlet process G(λ, G₀) is a distribution of distributions with scaling variable λ and base distribution G₀. The DP prior models uncertainty in the distributions, hence, it is rich enough to approximate any possible distribution. This makes it more powerful than parametric probabilistic models (52). In particular, the DP is used here as a tool for non-parametric clustering, as explained next.

Hyper-parameters α_i are modeled as independent identically distributed random variables drawn from a distribution generated by G. Let ${\left\{{\mathbf{\alpha }}_k^{\ast }\right\}}_{k=1}^K$, K ≤ N, be the distinct values taken by ${\left\{{\mathbf{\alpha }}_i\right\}}_{i=1}^N$, then (44)

$$p\left({\mathbf{\alpha }}_i\mid {\mathbf{\alpha }}^{-i}\right)=\frac{\lambda }{\lambda +N-1}{G}_0+\frac{1}{\lambda +N-1}{\sum }_{k=1,k\ne i}^K{n}_k^{-i}{\delta }_{{\mathbf{\alpha }}_k^{\ast }},i=1,\dots ,N,$$ [14]

where α⁻ⁱ = {α₁ ··· α_i−1 ··· α_i+1 ··· α_N}, $n_k^{-i}$ is the number of times ${\mathbf{\alpha }}_k^{\ast }$ is in α⁻ⁱ, and ${\delta }_{{\mathbf{\alpha }}_k^{\ast }}$ the distribution concentrated at ${\mathbf{\alpha }}_k^{\ast }$. Eq. [14] explains the sharing and non-parametric properties of DPs: new hyper-parameters α_i+1 can either use the value of one of the existing hyper-parameters α⁻ⁱ or a new one (generated from G₀). The random variable λ controls the balance between the creation of new hyper-parameters and sharing with the existing hyper-parameters. Let z_i be a variable that indicates how much of each hyper-parameter ${\mathbf{\alpha }}_j^{\ast }$ is used in the mixture model ${\mathbf{\alpha }}_i={\sum }_{k=1}^K{z}_{ik}{\mathbf{\alpha }}_k^{\ast }$. Hence z_i provides a probabilistic clustering of the data, based on how much of each hyper-parameter ${\left\{{\mathbf{\alpha }}_k^{\ast }\right\}}_{k=1}^J$ is used at each voxel. Since G can be modeled as $G={\sum }_{k=1}^{\infty }{w}_k{\delta }_{{\mathbf{\alpha }}_k^{\ast }}$, using a stick-breaking process (53), the complete DP-MT-CS probabilistic model is given by

$$\begin{array}{lll}\hfill {\mathbf{x}}_{is}^{\ast }\mid {\mathbf{\vartheta }}_i,{\alpha }_0& ~\hfill & \mathcal{N}(\mathbf{\Phi }{\mathbf{\vartheta }}_i,{\alpha }_0\mathbf{I}),\mathbf{\Phi }\stackrel{\text{def}}{=}{\mathbf{P}}_s{\mathbf{D}}_s\hfill \\ \hfill {\mathbf{\vartheta }}_i\mid {\mathbf{z}}_i{\left\{{\mathbf{\alpha }}_k^{\ast }\right\}}_{k=1}^K& ~\hfill & \mathcal{N}\left(\mathbf{0},{\mathbf{\Lambda }}_{{\mathbf{\alpha }}_{{\mathbf{z}}_i}^{\ast }}\right),\hfill \\ \hfill {\mathbf{z}}_i\mid {\left\{w_k\right\}}_{k=1}^k& ~\hfill & \mathit{Multinomial}(w_1,\cdots ,w_K),\hfill \\ \hfill w_k& =\hfill & {\pi }_k\prod _{l=1}^{k-1}(1-{\pi }_l),\hfill \\ \hfill {\pi }_k\mid \lambda & ~\hfill & \mathit{Beta}(1,\lambda ),\hfill \\ \hfill \lambda \mid e,f& ~\hfill & \mathit{Gamma}(e,f),\hfill \\ \hfill {\mathbf{\alpha }}_k^{\ast }\mid c,d& ~\hfill & \prod _{k=1}^K\mathit{Gamma}(c,d),\hfill \\ \hfill {\alpha }_0& ~\hfill & \mathit{Gamma}(a,b),\hfill \end{array}$$ [15]

where 1 ≤ i ≤ N, 1 ≤ k ≤ K, and a, b, c, d, e, f are non-informative hyper-parameters determining the distribution of the random variables in the model.

Bayesian inference using the DP-MT-CS model is provided by Bayes rule

$$p(\mathbf{H}\mid {\mathbf{x}}_s^{\ast },\mathbf{\Upsilon })=\frac{p({\mathbf{x}}_s^{\ast }\mid \mathbf{H})p(\mathbf{H}\mid \mathbf{\Upsilon })}{\int p({\mathbf{x}}_s^{\ast }\mid \mathbf{H})p(\mathbf{H}\mid \mathbf{\Upsilon })d\mathbf{H}},$$ [16]

where $\mathbf{H}=\left\{{\left\{{\mathbf{\vartheta }}_i\right\}}_{i=1}^N,{\left\{{\mathbf{\alpha }}_j^{\ast }\right\}}_{k=1}^K,{\left\{{\mathbf{z}}_i\right\}}_{i=1}^N,{\left\{{\pi }_j\right\}}_{j=1}^J,{\alpha }_0,\lambda \right\}$ are the hidden model variables, ${\mathbf{x}}_s^{\ast }={\left[{\mathbf{x}}_{si}^{\ast }\right]}_{i=1}^N$ the M × N matrix of CS HARDI measurements, and ϒ = {a, b, c, d, e, f} the hyper-parameters determining the distribution of the hidden variables. Eq. [16] cannot be solved analytically, due to the mathematical intractability of the integration term in the denominator. An iterative variational method can be used to seek a distribution q(H) that approximates $p(\mathbf{H}\mid {\mathbf{x}}_s^{\ast },\mathbf{\Upsilon })$. Let us consider the logarithm of the marginal likelihood (44),

$$\mathit{log}(p({\mathbf{x}}_s^{\ast }\mid \mathbf{\Upsilon }))=\mathcal{L}(q(\mathbf{H}))+{\mathcal{D}}_{KL}(q(\mathbf{H}),p(\mathbf{H}\mid {\mathbf{x}}_s^{\ast },\mathbf{\Upsilon })),\mathcal{L}(q(\mathbf{H}))=\int q(\mathbf{H})\mathit{log}\left(\frac{p({\mathbf{x}}_s^{\ast }\mid \mathbf{\Upsilon })p(\mathbf{H}\mid \mathbf{\Upsilon })}{q(\mathbf{H})}\right),$$ [17]

where ${\mathcal{D}}_{KL}(q(\mathbf{H}),p(\mathbf{H}\mid {\mathbf{x}}_s^{\ast },\mathbf{\Upsilon }))$ is the Kullback-Leibler (KL) divergence between the approximate q(H) and the true posterior $p(\mathbf{H}\mid {\mathbf{x}}_s^{\ast },\mathbf{\Upsilon })$. The approximation of the true posterior $p(\mathbf{H}\mid {\mathbf{x}}_s^{\ast },\mathbf{\Upsilon })$ by q(H) can be achieved by minimizing ${\mathcal{D}}_{KL}(q(\mathbf{H}),p(\mathbf{H}\mid {\mathbf{x}}_s^{\ast },\mathbf{\Upsilon }))$. Since the KL divergence is non-negative and $p({\mathbf{x}}_s^{\ast }\mid \mathbf{\Upsilon })$ is fixed given ϒ, then minimizing the KL divergence is the same as maximizing 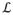(q(H)) in [17] (44).

Maximizing 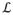(q(H)) is tractable using functional derivatives if we define

$$q(\mathbf{H})=q({\alpha }_0)q(\lambda ){\mathrm{\Pi }}_{k=1}^{K}q({\pi }_j){\mathrm{\Pi }}_{i=1}^{N}q({\mathbf{z}}_i){\mathrm{\Pi }}_{i=1}^{N}q({\mathbf{\vartheta }}_i){\mathrm{\Pi }}_{k=1}^{K}q({\alpha }_j^{\ast }).$$ [18]

In particular we assume q(ϑ_i)~ 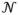(μ_i‚ Σ_i), where μ_i and Σ_i are estimated by iteratively maximizing 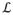(q(H)). Hence, by Eq. [8] and Eq. [11]

$$\{\begin{array}{c}{\widehat{\mathbf{x}}}_i^{\ast }~\mathcal{N}(\mathbf{PD}{\mathbf{\mu }}_i,\mathbf{PD}{\mathbf{\sum }}_i{(\mathbf{PD})}^{\mathrm{T}})\\ {\widehat{\mathbf{\varphi }}}_i~\mathcal{N}(\mathbf{D}{\mathbf{\mu }}_i,\mathbf{D}{\mathbf{\sum }}_i{\mathbf{D}}^{\mathrm{T}})\end{array},i=1,\dots ,N,$$ [19]

Eq. [19] provides the full posterior of ${\mathbf{x}}_i^{\ast }$ and CSA-ODF at each voxel. From here, it is simple to obtain (see Eq. [12])

$${\stackrel{\sim }{\mathbf{x}}}_i~\mathcal{N}({\stackrel{\sim }{\mathbf{\epsilon }}}_i,\mathbf{PD}{\mathbf{\sum }}_i{(\mathbf{PD})}^{\mathrm{T}}),{\stackrel{\sim }{\mathbf{\epsilon }}}_i\approx \mathbf{PD}{\mathbf{\mu }}_i+({\mathrm{c}}_1-\gamma /(2\sqrt{\pi })){\mathbf{Y}}_1.$$ [20]

It is easy to see that ε_i = [exp(−exp(ε̃_ij))]_1≤j≤M (see Eq. [5]) provides a point estimate of the diffusion-weighted signal, x_i. We did not use Eq. [7] here to obtain x_i, because there were several approximations made in Eqs. [10]–[12] and the mean value of x̃ was removed, so it is more accurate to estimate x_i as indicated above. However, it is difficult to obtain an estimate of the uncertainty of x_i, given the highly non-linear relationship between x̃_i and x_i. Here, we can use Eq. [7] to provide a reasonable estimate of the uncertainty (covariance matrix) in x_i as

$${\mathbf{x}}_i~\mathcal{N}({\mathbf{\epsilon }}_i,\mathbf{\Psi }{\mathbf{\sum }}_i{\mathbf{\Psi }}^{\mathrm{T}}).$$ [21]

An advantage of using a known dictionary Ψ for the attenuation signal x_i is that it is related to the CSA-ODF, Eqs. [7] and [9]. Compared to using directly a dictionary for the CSA-ODF, it allows us to obtain uncertainty estimates for both the CSA-ODF and attenuation signal.

HARDI Data Sets

We tested the proposed approach on two kinds of HARDI data sets:

• Synthetic multi-shell HARDI data with non-staggered (same diffusion directions on all shells) and staggered (complementary diffusion directions on all shells) protocols.

• In-vivo non-staggered multi-shell HARDI datasets.

The synthetic HARDI data was generated using the analytic Camino diffusion MRI toolkit⁶ that employs realistic diffusion models (54). Rician noise was added in Camino to produce SNRs of 25, and 15, where SNR = E/σ, E being the magnitude of the noise-free attenuation signal and σ the standard deviation of the noise (55). The diffusion model consists of two fibers crossing at angles 45°, 60°, and 90°, where one fiber was fixed at (45°, 45°) in spherical coordinates, while the other was rotated 45°, 60°, and 90° with respect to the first. Fiber crossings with angles around 30° could not be detected using the CSA-ODF. The reason for this is that the ODF requires the product of the mean apparent diffusion coefficient (ADC) and b-values to be close to one (40). This condition is satisfied in practice, for the range of b-values commonly used and the mean ADC in the brain parenchymia (0.7 μm²/ms). However, Camino produces lower ADC values (~0.07 μm²/ms) for all models and parameters tested (see also Figure 1b in (56)). Fiber crossings reported in the literature using the CSA-ODF and angles around 30 degrees (40,41) were obtained using ADC values close to those found in the brain, a much simpler model consisting of two anisotropic diffusion tensors, no noise, and a large SH order (8). We limit ourselves here to those angles that could be discriminated using Camino’s state-of-the-art analytic models, Rician noise, and a maximum SH order of six.

The volume fractions for each fiber were 0.3 for the intra-axonal, 0.05 for the extra-axonal components, and volume fraction of 0.3 for the isotropic compartment. Following (54), the intra-axonal compartment is modeled as a cylinder of radius 4 μm with a Gaussian phase distribution (GPD) and diffusivity 1.7 μm²/ms. The extra-axonal compartment is modeled as a zeppelin with diffusivity 1.7 μm²/ms along, and 0.2 μm²/ms across the fiber orientation. Finally, the isotropic component is modeled as a sphere of radius 4 μm and diffusivity 0.8 μm²/ms. Simulated standard Stejskal-Tanner pulse-gradient spin-echo pulse sequence was 50 mT/m, TE = 100ms, δ = 20ms. Multi-shell non-staggered synthetic HARDI signal was generated with three shells and a total of M=399 diffusion directions (133 gradients per shell), and three b-values, b=2000, 4000, and 6000 s/mm². Multi-shell staggered synthetic HARDI signal was generated with three shells and a total of M=400 diffusion directions (b=2000, 4000, and 6000 s/mm²), where 134 were allocated in the first shell, 133 in the second and 133 in the last one. The sampling protocol follows (4), which ensures that CS “partial” samples (taking the first m gradients) cover the whole shell almost uniformly. CS single and multi-shell HARDI datasets were generated with accelerations one (no CS), two, four, and eight, corresponding to m = M, M/2, M/4, and M/8.

In-vivo multi-shell HARDI data sets were obtained on the WU-UMN Human Connectome Project (57) 3T Connectome Skyra system (Siemens, Erlangen, Germany), with various spatial and angular resolutions. The scanner was equipped with SC72 gradients operating at 100 mT/m maximum gradient amplitude with a maximum slew rate of 91 T/m/s for diffusion encoding. Dataset 1, with spatial resolution 1.5×1.5×1.5 mm³, has three shells with 133 diffusion directions per shell at b=1000, 2000, and 3000 s/mm² and 10 additional b0s per shell. Dataset 2, with spatial resolution 1.25×1.25×1.25 mm³, has three shells with 128 diffusion directions per shell at b=1500, 2500, and 3500 s/mm² and 26 b0s. The third data set, with spatial resolution 1.25×1.25×1.25 mm³, has six shells with 128 diffusion directions per shell at b=1500, 2500, 3500, 5000, 7000, and 10,000 s/mm² and 28 b0s. Each dataset was corrected for geometric and eddy current distortions, using information from acquisitions in opposite phase-encoding directions, as well as head motion (58). The gradient table for these images follow the protocol proposed in (4). Simulated CS HARDI datasets were constructed with accelerations one, two, four, and eight. An acceleration factor of one means that all the data is used (no CS). Acceleration factors of two, four and eight means that only half, one quarter, and one eight of the diffusion-weighted volumes are used as input to the proposed algorithm.

The research protocol used in this investigation was approved by the Institutional Review Board of the University of Minnesota. All subjects provided informed written consent prior to participating in the research.

Finally, parameters a and b are defined as a = b = Variance{Ẽ}, while c, d, e, f in [15] are set initially to very small values and are estimated from the data. Experimentally, we found that ${\mathbf{z}}_i={\left[\begin{array}{ccc}\frac{1}{K}& \cdots & \frac{1}{K}\end{array}\right]}^{\mathrm{T}}$ provides a good initialization, with K = O(N). Also, the best γ in [6], [10]–[12], was found by trial and error as γ = 10⁻².

Ground Truth Definition and Evaluation

The ground truth for the fiber orientations in the synthetic data sets is given by the knowledge of the true fiber orientations. We also generated synthetic images without noise and a full set of diffusion directions (acceleration one) that provide ground truth for the corresponding diffusion-weighted volumes. The ground truth CSA-ODFs are computed from this “clean” data using each method and all the diffusion directions (acceleration one). Finally, the “ground truth” for the fiber orientations, CSA-ODFs, and diffusion-weighted volumes of the in-vivo HARDI datasets is obtained from each method studied in this work with the full dataset (acceleration one). Notice that there is obviously not a single ground-truth for the in-vivo HARDI datasets. Hence using the estimated CSA-ODFs using only one of these methods as ground truth is favorably biased towards that method. The best we can do to mitigate this caveat is to compare each method at accelerations two and higher with the same method using the full dataset (acceleration one). This allows us to evaluate their relative performance as the acceleration factor increases, with respect to the best-case scenario, i.e., without CS and a relatively high number of diffusion directions.

We evaluate results using the metrics (see Eq. [19])

$$\begin{array}{c}\mathit{FOE}(\mathbf{\varphi },\widehat{\mathbf{\varphi }})=\frac{1}{N}\sum _{i=1}^N\left|{cos}^{-1}\left(\frac{180}{\pi }\widehat{\mathbf{u}}{({\mathbf{\varphi }}_i)}^{\mathrm{T}}\widehat{\mathbf{v}}({\widehat{\mathbf{\varphi }}}_i)\right)\right|\\ KL(\mathbf{\varphi },\widehat{\mathbf{\varphi }})=\frac{1}{2N}\sum _{i=1}^N\left(\sum _{j=1}^{J}ln\left(\frac{{\varphi }_{ij}}{{\widehat{\varphi }}_{ij}}\right){\varphi }_{ij}\delta {\mathrm{\Omega }}_j+\sum _{j=1}^{J}ln\left(\frac{{\widehat{\varphi }}_{ij}}{{\varphi }_{ij}}\right){\widehat{\varphi }}_{ij}\delta {\mathrm{\Omega }}_j\right),\delta {\mathrm{\Omega }}_j=\mathrm{\Delta }\theta \mathrm{\Delta }\phi \mathit{sin}{\theta }_j\\ D_{SH}(\mathbf{\varphi },\widehat{\mathbf{\varphi }})=\frac{1}{N}{\sum }_{i=1}^N{\Vert {({\mathbf{\varphi }}_i)}_{\text{SH}}-{({\mathbf{\varphi }}_i)}_{\text{SH}}\Vert }_2^2,\end{array}$$ [22]

where FOE is the Fiber Orientation Error (degrees) computed from the known (synthetic images) or estimated (in-vivo data sets) fiber orientations û(ϕ_i) and the fiber orientations v̂(ϕ̂_i) from the known (ϕ_i) and estimated CSA-ODF (ϕ̂). Fiber orientations are approximated by the CSA-ODF peaks using functionality provided in CSA-ODF (FSL) (42)). KL(ϕ, ϕ̂) is the Kullback-Leibler divergence in spherical coordinates (59), between ϕ and ϕ̂, from the CS HARDI data sets. δΩ stands for the discrete approximation of the differential of the solid angle Ω, and J ≫ M stands for the number of tessellation points in the unit sphere. D_SH(ϕ, ϕ̂) stands for the mean Euclidean distance between the SH coefficients of ϕ_i and ϕ̂. These metrics are used routinely to compare ODFs (3,59–61). The order of the SH basis was six for the synthetic data and four for the in-vivo data (as recommended in (40,62,63)).

RESULTS

Synthetic Data

Multi-shell non-staggered

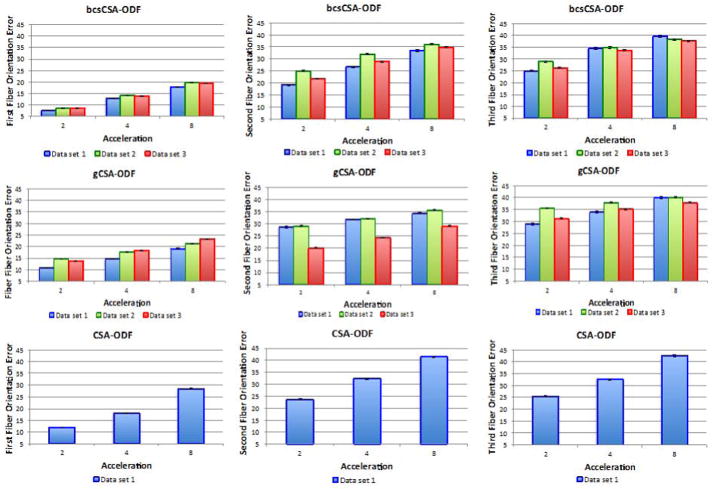
Figure 1⁷ compares the FOE of the estimated CSA-ODF from under-sampled HARDI synthetic multi-shell non-staggered HARDI data using bcsCSA-ODF, gCSA-ODF, and CSA-ODF at SNRs 15, 25 and fiber crossing angles: 45°, 60°, and 90°. CSA-ODF reconstructions cannot be obtained at acceleration eight, since at that acceleration the number of diffusion directions per shell is lower than the number of SH coefficients (28 in this case). bcsCSA-ODF significantly outperforms CSA-ODF and gCSA-ODF in terms of the FOE, for all acceleration factors up to eight, except for the case of SNR 15 and fiber crossing angle of 45°, where the CSA-ODF is better up to an acceleration factor of six. The CSA-ODF provides a reduction in the FOE of up to 10 degrees. The worst performance of the CSA-ODF corresponds to fibers crossing at 45°, SNR 15 and acceleration eight. This is due to the need of a better initialization of the variational Bayesian inference algorithm as the acceleration, SNR and order of the SH basis increase.

Figure 1.

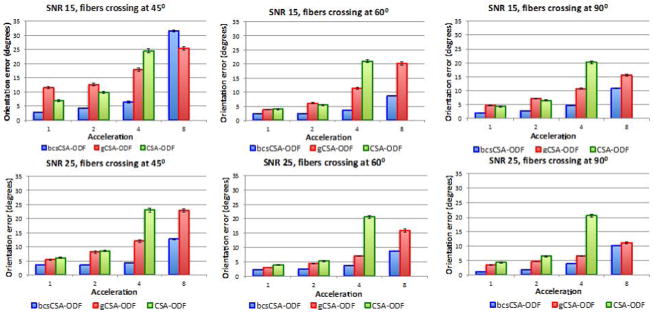
Fiber orientation errors (FOEs) estimated from under-sampled synthetic multi-shell non-staggered HARDI data. First row corresponds to the FOEs of the estimated ODFs for a signal to noise ratio (SNR) of 15, while the second row shows the FOEs for a SNR of 25. All the figures indicate the FOEs using the proposed bcsCSA-ODF, gCSA-ODF, and CSA-ODF for three fiber crossing angles: 45°, 60°, and 90°. Acceleration one corresponds here to the full 399 gradients.

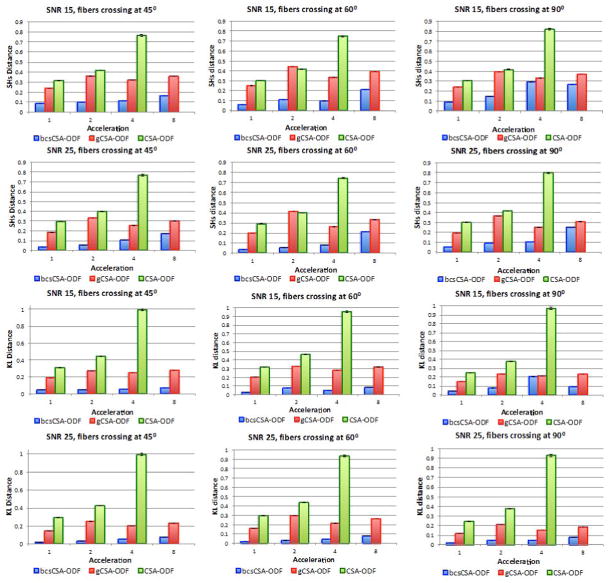
Figure 2 indicates that the SH distance and KL divergence are at least 70% lower for the proposed bcsCSA-ODF than CSA-ODF (even at acceleration one). The SH distance is 18–88% lower for the bcsCSA-ODF than the gCSA-ODF, while the KL divergence is up to 90% lower for the bcsCSA-ODF than the gCSA-ODF. As the acceleration increases, the difference between the bcsCSA-ODF and gCSA-ODF reduces. As the fiber crossing angle increases, the difference between the bcsCSA-ODF and gCSA-ODF reduces, since fiber crossings close to 90° have CSA-ODFs with more separated modes than smaller angles.

Figure 2.

Euclidean SH distance (first and second rows) and the Kullback-Leibler divergence (third and fourth rows) for the estimated ODFs from under-sampled synthetic multi-shell non-staggered HARDI data using bcsCSA-ODF, gCSA-ODF, and CSA-ODF (no CS algorithm) at two different signal to noise ratios, 15 and 25; and three fiber crossing angles, 45°, 60°, and 90°. Acceleration one corresponds here to 399 gradients.

Multi-shell staggered

Figure 3 compares the FOE of the estimated CSA-ODF from under-sampled HARDI synthetic multi-shell staggered HARDI data using bcsCSA-ODF, gCSA-ODF, and CSA-ODF at SNRs 15, 25 and fiber crossing angles 45°, 60°, and 90°. bcsCSA-ODF significantly outperforms CSA-ODF and gCSA-ODF in terms of the FOE, for all acceleration factors up to eight, except for the case of a fiber crossing angle of 45°, where the CSA-ODF is better up to an acceleration factor of five. The CSA-ODF provides a reduction in the FOE of up to 16 degrees. The worst performance of the CSA-ODF corresponds to fibers crossing at 45° and accelerations above five. Comparing with Figure 2, it can be seen that the differences with the gCSA-ODF are larger for staggered data than with non-staggered data, since the gCSA-ODF performs worse with staggered diffusion directions. The reason for this might be that the gCSA-ODF requires a preliminary SHs interpolation to obtain the same diffusion directions on all shells so that the bi-exponential model can be fitted for all diffusion directions. This interpolation is not necessary with non-staggered diffusion directions.

Figure 3.

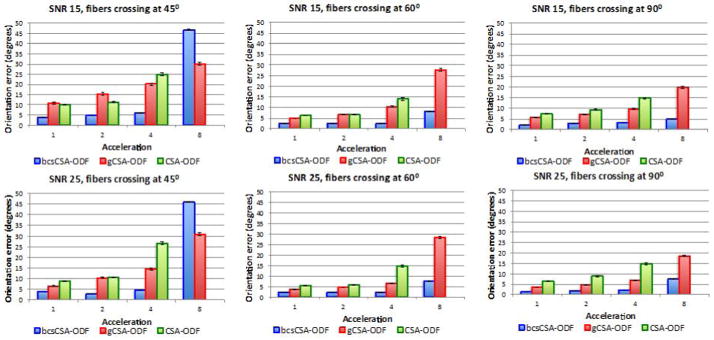
Fiber orientation errors (FOEs) estimated from under-sampled synthetic multi-shell staggered HARDI data. First row corresponds to the FOEs of the estimated ODFs for a signal to noise ratio (SNR) of 15, while the second row shows the FOEs for a SNR of 25. All the figures indicate the FOEs using the proposed bcsCSA-ODF, gCSA-ODF, and CSA-ODF for three fiber crossing angles, 45°, 60°, and 90°. Acceleration one corresponds here to the full 399 gradients.

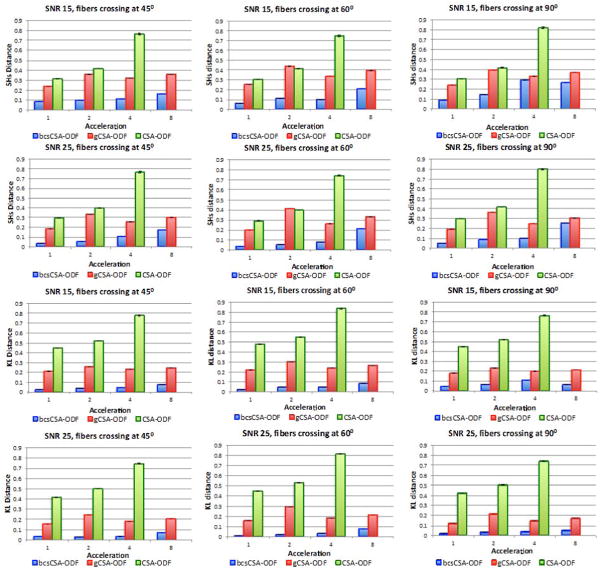
Figure 4 indicates that the SH distance and KL divergence are at least 73% lower for the proposed bcs-CSA-ODF than CSA-ODF (even at acceleration one). The SH distance is up to 92% lower for the bcs-CSA-ODF than the gCSA-ODF, while the KL divergence 45–93% lower for the bcsCSA-ODF than the gCSA-ODF. As the acceleration and fiber crossing angle increases, the difference between the bcsCSA-ODF and gCSA-ODF reduces too as with the non-staggered case.

Figure 4.

Euclidean SH distance (first and second rows) and the Kullback-Leibler divergence (third and fourth rows) for the estimated ODFs from under-sampled synthetic multi-shell staggered HARDI data using bcsCSA-ODF, gCSA-ODF, and CSA-ODF (no CS algorithm) at two different signal to noise ratios, 15 and 25; and three fiber crossing angles, 45°, 60°, and 90°. Acceleration one corresponds here to 399 gradients.

In-vivo Data

Figure 5 compares the FOE of the estimated CSA-ODF from under-sampled HARDI multi-shell data using the proposed bcsCSA-ODF, gCSA-ODF, and CSA-ODF. Notice that CSA-ODF was used only on one dataset, since the other datasets were not compatible with the CSA-ODF requirements.⁸ The results indicate that bcsCSA-ODF does perform better than gCSA-ODF (and CSA-ODF) up to acceleration four. The largest benefit of bcsCSA-ODF occurs at acceleration two.

Figure 5.

Fiber orientation errors estimated from under-sampled in-vivo multi-shell non-staggered HARDI data. First row shows the FOEs of the ODFs estimated using bcsCSA-ODF. Second row shows the FOEs computed using gCSA-ODF. Third row shows the FOEs using CSA-ODF on the under-sampled data, directly (no CS algorithm).

Figure 6 shows the KL divergence and SH distance for the three models considered here. Here, the bcsCSA-ODF has a 55–75% lower error than CSA-ODF and (17–50%) lower than gCSA-ODF, especially showing significant improvements at acceleration two. Notice that the KL divergence and SH distance metrics show bigger differences relative to acceleration one (Figure 6) than the differences observed on the fiber orientations (Figure 5). The reason for this is that KL divergence and SH distance are metrics that apply directly to the estimated “full” ODFs, which is the focus of the bcsCSA-ODF model, while fiber orientation depends on peak detection.

Figure 6.

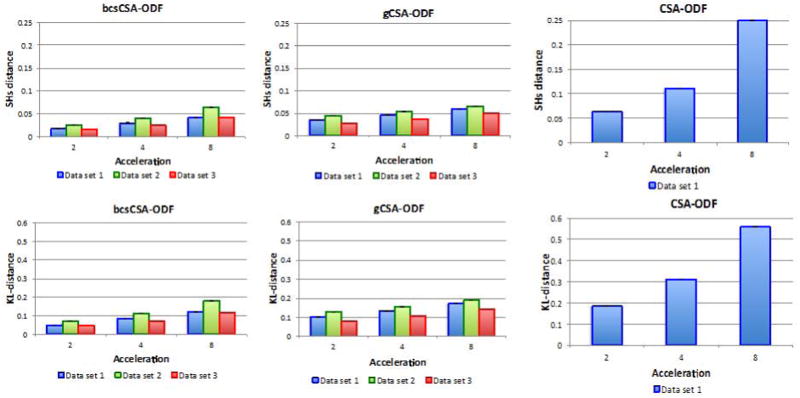
Euclidean SH distance (first row) and Kullback-Leibler divergence (second row) for the estimated ODFs from under-sampled in-vivo multi-shell non-staggered HARDI data using bcsCSA-ODF, gCSA-ODF, and CSA-ODF (no CS algorithm).

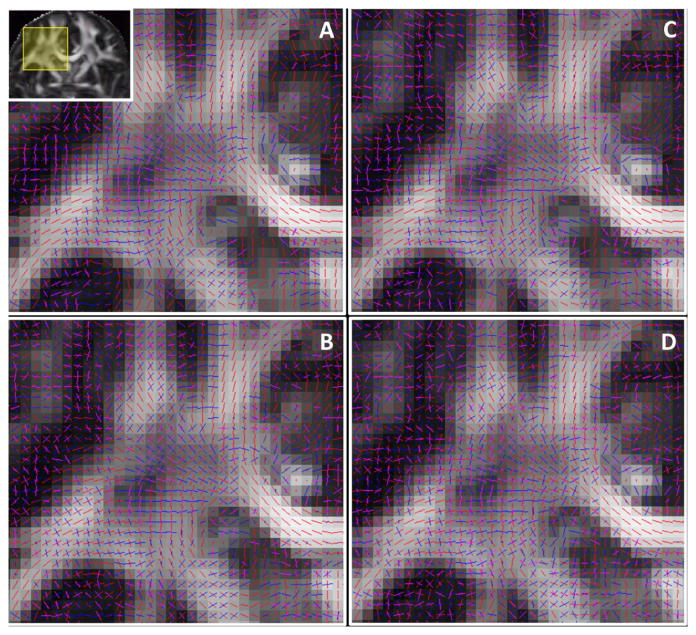
Figure 7 compares the CSA-ODFs estimated using gCSA-ODF and the proposed bcsCSA-ODF at acceleration one and acceleration four. Differences in the CSA-ODF between acceleration one and four are visually lower for the proposed bcsCSA-ODF.

Figure 7.

Visualization of the estimated three principal fiber orientations (ODF peaks) on a coronal view in the region of the centrum semiovale, and obtained using A) bcs-CSA-ODF at acceleration one, B) bcs-CSA-ODF at acceleration four, C) gCSA-ODF at acceleration one, D) gCSA-ODF at acceleration four.

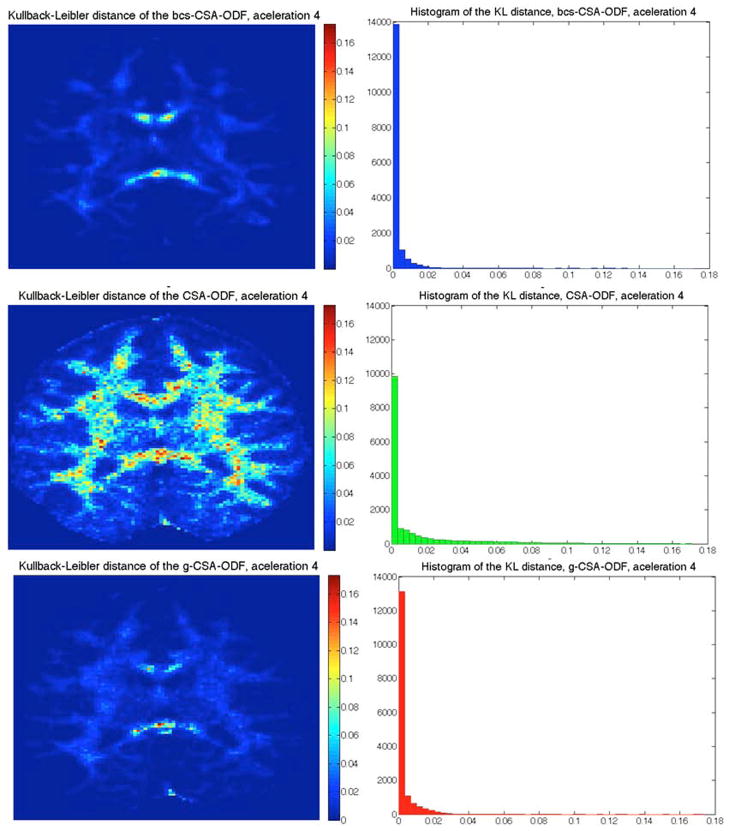
Figure 8 shows the KL divergence at acceleration four for these three methods, where we can see how the KL varies spatially (left) and its distribution (right). The lowest KL divergence is obtained by using bcs-CSA-ODF, followed by gCSA-ODF and then CSA-ODF.

Figure 8.

Kullback-Leibler divergence of the reconstructed ODF from under-sampled in-vivo HARDI data (acceleration four) using bcsCSA-ODF (top), gCSA-ODF (middle), and CSA-ODF (bottom). Left images correspond to a color-coded representation of the KL divergence that goes from cyan (low) to magenta (high). Right images correspond to the histogram of the KL divergence. Results shown are for dataset 1 (see Figure 6).

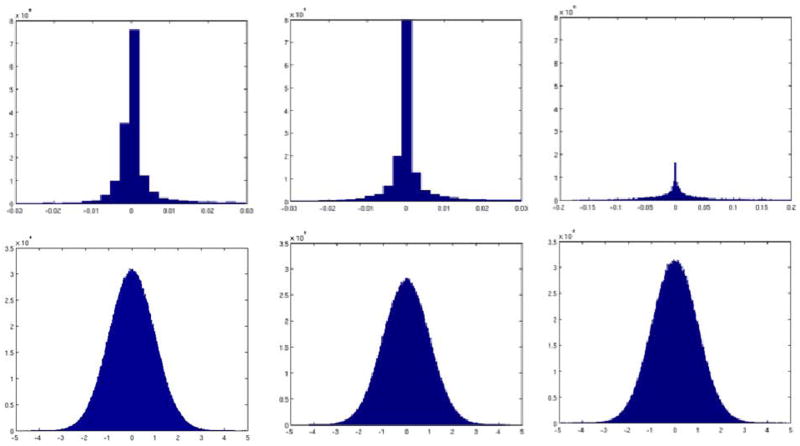
Figure 9 shows the histogram of the CSA-ODF and diffusion-weighted volumes uncertainties (see Eq. [22]) obtained by normalizing and averaging the covariance matrices and then using these covariances to generate zero-mean random variables, which distribution can be approximated via histograms. As can be seen from the histograms, the uncertainty (dispersion) of the CSA-ODF remains almost the same until acceleration four, growing to about 20 times for acceleration 8. On the other hand, the uncertainty for the estimated diffusion-weighted volumes seems to be fairly insensitive to acceleration.

Figure 9.

First row indicates the normalized ODF uncertainty for acceleration one (left), four (center), and eight (right). Second row indicates the normalized volume estimation uncertainty for acceleration one (left), four (center), and eight (right). Uncertainties were compute on dataset 1.

DISCUSSION

For under-sampled multi-shell HARDI data, the proposed bcsCSA-ODF model performs very well compared to the original CSA-ODF and the generalized CSA-ODF models when the number of diffusion-weighted volumes per shell is at least one quarter of the original image, corresponding to 32–33 volumes per shell, for the in-vivo data, i.e. 96–99 for the three shells. Further reduction in the acquisition time can be achieved using parallel imaging techniques (pMRI) (5–8). Even larger acceleration factors could also be achieved using trained dictionaries rather than pre-specified basis as indicated in (19).

Errors for the proposed bcsCSA-ODF increase with acceleration and noise, with the exception of the third fiber orientation error in Figure 6. There are several reasons for this. ODF peak detection is a hard problem that depends on the selected thresholds and is affected by spurious lobes in ODFs arising from noise. It has also been recognized that there are limits in CS in terms of acceleration and noise level (64,65).

Figures 1–4 show that even at acceleration one (no compression) it is advantageous to use CS since the estimated CSA-ODFs have lower errors than using CSA-ODF or gCSA-ODF. This is due in part to the denoising capabilities of sparse representation and also to the fact that the full dataset can be seen as the CS version of a larger dataset (say acceleration ½ for instance) so it may contain information not seen by the other algorithms.

The number of steps required to maximize (q(H)) in [17] depends on the tolerance used to determine convergence and the initialization. The time complexity of the variational Bayesian inference is determined by the cost of estimating the precision matrix Σ_i in [19], [20] on every voxel, which requires the inversion of an M×M matrix (44). Hence, the time complexity is O(κ₁NM³), where N is the number of voxels, M the number of samples, and κ₁ the number of iterations (20 in all our simulations). However, in contrast to (44,51) where the CS matrix is random, here Φ (see Eq. [15]) is fixed and Σ_i needs to be computed only once at each iteration, hence, the precision matrix can be computed in O(κ₁M³) time. On every voxel there are also matrix by vector operations, hence the time complexity of the proposed bcsCSA-ODF is O(κ₁M³) + O(κ₁NL²), where L correspond to the number of ridgelets basis. This reduces to O(κ₁NL²), since in general N≫L>M. The time complexity of the CSA-ODF is determined by the estimation of the SH coefficients, which requires only matrix by vector computations (see [5]), i.e. O(NMR), where R corresponds to the number of SH coefficients. The time complexity of gCSA-ODF is determined by the cost of fitting the bi-exponential model on each voxel and for each diffusion direction. Using an iterative nonlinear least squares fitting, the computational complexity is O(κ₂NMB³), with κ₂~10⁴ and B corresponds to the number of shells in the diffusion image.

The proposed bcsCSA-ODF is computationally more demanding than the CSA-ODF and the gCSA-ODF. The higher computational complexity of the proposed CSA-ODF is in agreement with the computational complexity of typical CS algorithms, CS signal reconstruction is more complex than traditional signal reconstruction. Computationally more efficient CS methods have being proposed recently and could also be employed here within the proposed CSA-ODF framework.

Comparisons with other CS algorithms that focus on the CSA-ODF should also be conducted in the future. The bcsCSA-ODF could be further improved by using dictionaries trained for CSA-ODFs and HARDI data, and also by changing the implicit diffusion signal decay (mono-exponential) model by a more accurate representation of the white matter microstructure in Eq. [2] such as the bi-exponential model or other more complex microstructure models.

CONCLUSION

In summary, this work presents, for the first time, a multi-task Bayesian compressive sensing approach to simultaneously estimate the full posterior of the CSA-ODF and diffusion-weighted volumes from multi-shell HARDI acquisitions. It demonstrates improvement of the quality of acquired datasets via CS de-noising, and accurate estimation of the CSA-ODF, as well as enables a reduction in the acquisition time by a factor of two to four, especially when “staggered” q-space sampling schemes are used.

Appendix

Discrete Approximation in Eq. [9]

Using finite differences to approximate ${\nabla }_b^2(\mathcal{H}(\widehat{\mathbf{u}})\mathbf{\vartheta })$ in Eq. [9]

$${\nabla }_b^2(\mathcal{H}(\widehat{\mathbf{u}}(\phi ,\theta ))\mathbf{\vartheta })\approx \mathbf{D}\mathbf{\vartheta }$$

where

$$\mathbf{D}=\frac{1}{\text{tan}\theta }\left(\frac{\mathcal{H}(\phi ,\theta +\mathrm{\Delta })-\mathcal{H}(\phi ,\theta -\mathrm{\Delta })}{2\mathrm{\Delta }}\right)+\frac{(\mathcal{H}(\phi ,\theta +\mathrm{\Delta })-2\mathcal{H}(\phi ,\theta )+\mathcal{H}(\phi ,\theta -\mathrm{\Delta })}{{\mathrm{\Delta }}^2}+\frac{1}{{sin}^2\theta }\frac{(\mathcal{H}(\phi +\mathrm{\Delta },\theta )-2\mathcal{H}(\phi ,\theta )+\mathcal{H}(\phi -\mathrm{\Delta },\theta ))}{{\mathrm{\Delta }}^2},$$

is the dictionary for the ODF. For sufficiently small Δ and Δ ≤ θ ≤ π, 0 ≤ φ ≤ 2π. 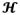is explicitly defined in (50).

Derivation of Eq. [11]

Let us rewrite Eq. [10] here for convenience

$$\left[\begin{array}{cc}{\gamma }^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{\Lambda }\end{array}\right]{\mathbf{Y}}^{+}\stackrel{\sim }{\mathbf{x}}+\left[\begin{array}{c}1/(2\sqrt{\pi })-{\gamma }^{-1}{c}_1\\ \mathbf{0}\end{array}\right]\approx {\mathbf{Y}}^{+}\mathbf{D}\mathbf{\vartheta },$$

multiplying both sides by $\left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]$

$$\begin{array}{c}{\mathbf{Y}}^{+}\stackrel{\sim }{\mathbf{x}}+\left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]\left[\begin{array}{c}1/(2\sqrt{\pi })-{\gamma }^{-1}{c}_1\\ \mathbf{0}\end{array}\right]\approx \left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]{\mathbf{Y}}^{+}\mathbf{D}\mathbf{\vartheta },\\ {\mathbf{Y}}^{+}\stackrel{\sim }{\mathbf{x}}+\left[\begin{array}{c}\gamma /(2\sqrt{\pi })-c_1\\ \mathbf{0}\end{array}\right]\approx \left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]{\mathbf{Y}}^{+}\mathbf{D}\mathbf{\vartheta }.\end{array}$$

Now x̃ ≈ YY⁺x̃., hence multiplying by Y

$$\begin{array}{c}\stackrel{\sim }{\mathbf{x}}+\left[\begin{array}{ccc}{\mathbf{Y}}_1& \dots & {\mathbf{Y}}_R\end{array}\right]\left[\begin{array}{c}\gamma /(2\sqrt{\pi })-c_1\\ \mathbf{0}\end{array}\right]\approx \mathbf{Y}\left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]{\mathbf{Y}}^{+}\mathbf{D}\mathbf{\vartheta },\\ \stackrel{\sim }{\mathbf{x}}+(\gamma /(2\sqrt{\pi })-c_1){\mathbf{Y}}_1\approx \mathbf{Y}\left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]{\mathbf{Y}}^{+}\mathbf{D}\mathbf{\vartheta }.\end{array}$$

and we arrive at Eq. [11] by defining ${\mathbf{x}}^{\ast }=(\stackrel{\sim }{\mathbf{x}}-{\mathrm{c}}_1{\mathbf{Y}}_1)+\gamma /(2\sqrt{\pi }){\mathbf{Y}}_1$ and $\mathbf{P}=\mathbf{Y}\left[\begin{array}{cc}\gamma & \mathbf{0}\\ \mathbf{0}& {\mathbf{\Lambda }}^{-1}\end{array}\right]{\mathbf{Y}}^{+}$.