Molecular Recognition in a Diverse Set of Protein-Ligand Interactions Studied with Molecular Dynamics Simulations and End-Point Free Energy Calculations

Abstract

End-point free energy calculations using MM-GBSA and MM-PBSA provide a detailed understanding of molecular recognition in protein-ligand interactions. The binding free energy can be used to rank-order protein-ligand structures in virtual screening for compound or target identification. Here, we carry out free energy calculations for a diverse set of 11 proteins bound to 14 small molecules using extensive explicit-solvent MD simulations. The structure of these complexes was previously solved by crystallography and their binding studied with isothermal titration calorimetry (ITC) data enabling direct comparison to the MM-GBSA and MM-PBSA calculations. Four MM-GBSA and three MM-PBSA calculations reproduced the ITC free energy within 1 kcal•mol⁻¹ highlighting the challenges in reproducing the absolute free energy from end-point free energy calculations. MM-GBSA exhibited better rank-ordering with a Spearman ρ of 0.68 compared to 0.40 for MM-PBSA with dielectric constant (ε = 1). An increase in ε resulted in significantly better rank-ordering for MM-PBSA (ρ = 0.91 for ε = 10). But larger ε significantly reduced the contributions of electrostatics, suggesting that the improvement is due to the non-polar and entropy components, rather than a better representation of the electrostatics. SVRKB scoring function applied to MD snapshots resulted in excellent rank-ordering (ρ = 0.81). Calculations of the configurational entropy using normal mode analysis led to free energies that correlated significantly better to the ITC free energy than the MD-based quasi-harmonic approach, but the computed entropies showed no correlation with the ITC entropy. When the adaptation energy is taken into consideration by running separate simulations for complex, apo and ligand (MM-PBSA_ADAPT), there is less agreement with the ITC data for the individual free energies, but remarkably good rank-ordering is observed (ρ = 0.89). Interestingly, filtering MD snapshots by pre-scoring protein-ligand complexes with a machine learning-based approach (SVMSP) resulted in a significant improvement in the MM-PBSA results (ε = 1) from ρ = 0.40 to ρ = 0.81. Finally, the non-polar components of MM-GBSA and MM-PBSA, but not the electrostatic components, showed strong correlation to the ITC free energy; the computed entropies did not correlate with the ITC entropy.

INTRODUCTION

Molecular Dynamics (MD) simulation-based free energy calculations have been used extensively to predict the strength of protein-ligand interactions. Accurate rank-ordering of small molecules bound to protein structures can benefit every step of drug discovery from hit identification to lead optimization. When applied to a compound docked to the human proteome, free energy calculations can be used for target discovery.¹ Several rigorous methods such as free energy perturbation and thermodynamic integration have been developed for accurate free energy calculations.^2-8 But these methods cannot easily be used for virtual screening of large chemical or combinatorial libraries that typically contain highly diverse compounds.⁹ End-point methods such as molecular dynamics (MD)-based MM-GBSA or MM-PBSA¹⁰ offer an alternative to rigorous free energy methods. Structurally diverse molecules can be considered in the calculations. The free energy consists of several terms that include a potential energy, a polar and non-polar solvation energy, and an entropy.

The MM-GBSA or MM-PBSA free energy consists of several components that can be determined independently. There exists more than one approach for each of these components. For example, the potential energy, which typically includes electrostatic and van der Waals energies, can be obtained using different force fields.¹¹ The electrostatic component of the solvation energy can be performed using either Poisson-Boltzmann¹² (PB) or Generalized-Born (GB) models.¹³ Two approaches are commonly used for the entropy, namely a normal mode analysis or a quasiharmonic approximation.^{14, 15} Finally, the calculations are performed on multiple snapshots collected from MD simulations.^16-18 The selection of different collections of structures is expected to affect the predicted free energy of binding.¹⁹

Here, we apply MM-GBSA and MM-PBSA calculations to determine the free energy of binding and rank-order a diverse set of protein-ligand complexes. The diversity in the structures of the ligand and targets distinguishes this work from previous efforts that have typically been limited to calculations on congeneric series of compounds on the same target protein. In addition, the use of structures whose binding was characterized with a single method, namely ITC, is expected to reduce the uncertainties in the comparisons between predicted and experimental data. We select 14 protein-ligand structures obtained from the PDBcal database (http://pdbcal.iu.edu) to provide high quality structural and thermodynamic binding data.²⁰ Extensive explicit-solvent MD simulations were performed and binding to these proteins was studied using various implementations of MM-GBSA and MM-PBSA. We also tested our previously-developed scoring functions for their ability to rank-order complexes by scoring MD structures. The effect of induced-fit conformational changes on rank-ordering these complexes was studied by performing separate simulations for ligand, protein and protein-ligand complexes. Components of the MM-GBSA and MM-PBSA free energy are compared with the ITC free energy, enthalpy and entropy. To the best of our knowledge, this is the first comparison of MM-GBSA and MM-PBSA calculations to ITC data for a diverse set of proteins.

MATERIALS AND METHODS

Scoring Protein Ligand Complexes

We previously reported the Support Vector Machine Target SPecific (SVMSP) model²¹ for enriching databases and Support Vector Regression Knowledge-Based (SVRKB) scoring²² for rank-ordering protein-compound complexes based on their binding affinity. Unlike SVRKB, SVMSP is developed for each individual target protein as described previously.²¹ SVMSP model was developed by using protein-ligand crystal structures from the sc-PDB database v2010 for the positive set and randomly selected compounds docked to the target of interest as the negative set. The positive set was refined by removing crystal structures in which the ligand contains highly charged moieties such as sulfate or phosphate groups, resulting in a set of 4,677 structures. The negative set consisted of docking 5,000 randomly selected compounds from the ChemDiv library to a pocket within the target of interest. The random selection of these compounds from a large chemical library reduces the likelihood that active compounds exist in the negative set.

To develop the SVMSP or SVRKB models, we extended on our previous work knowledge-based descriptors by using 14 distinct protein atom types and 16 ligand atom types (Table S1).²¹ This resulted in 224 atom-pairs based potentials. We used 76 pair potentials for the vectors of SVMSP. A higher SVMSP score corresponds to a higher probability that the compound is active.

MD Simulations

A set of 14 complexes of small molecules bound to a protein were selected from the PDBcal database (Table 1).²⁰ The structures of proteins were obtained from RCSB and prepared using BIOPOLYMER in SYBYL 8.0 (Tripos International, St. Louis, Missouri, USA). Hydrogen atoms were added. Missing gaps were modeled. Residue orientation and protonation states were further adjusted using the REDUCE²³ program to optimize the hydrogen bonding network. The ligand structures extracted from crystal structures were prepared and visually checked in SYBYL. The compound was assigned AM1-BCC²⁴ charges using the antechamber program from the AMBER9 package.²⁵ Water molecules from crystal structures within 5 Å to any atoms on the protein or compound were retained. To perform MD simulations, the protein-ligand complexes were immersed in a box of TIP3P²⁶ water molecules such that no atom on the protein or ligand was within 14 Å from any side of the box. The solvated box was further neutralized with Na⁺ or Cl⁻ counterions using the leap program from the AMBER9 package.

Table 1.

Calculated Free Energies of Selected Protein-Ligand Complexes (Set 1)

		Methods
Target	Complex PDB	ΔGMM-GBSA (kcal•mol−1 )	ΔGMM-PBSA (dielc = 1) (kcal•mol−1 )	ΔGMM-PBSA (dielc = 2) (kcal•mol−1 )	ΔGMM-SVRKB (kcal•mol−1 )	ΔGSVMSP// MM-PBSA (dielc = 1) (kcal•mol−1 )	ΔGSVMSP// MM-PBSA (dielc = 2) (kcal•mol−1 )	ΔGITC (kcal•mol−1 )	Ligand No.
human cyclophilin A	1CWA	−17.4±0.7	−13.1±0.8	−36.6±0.7	−7.3	−17.0±0.4	−41.0±0.7	−10.9±0.03	1
HIV-1 protease	1HPV	−18.9±0.8	−8.2±0.8	−38.5±0.8	−10.1	−15.6±0.3	−43.7±0.8	−12.6	2
HIV-1 protease	1HPX	−31.1±0.8	−12.5±0.8	−49.0±0.8	−11.5	−21.1±0.4	−58.9±0.8	−13.3	3
HIV-1 protease	1HXW	−32.4±0.8	−9.9±0.8	−49.3±0.8	−10.1	−24.6±0.4	−65.8±0.8	−13.63±0.07	4
leukocyte function-associated antigen-1	1RD4	−14.9±0.8	−9.8±0.8	−30.9±0.8	−11.1	−17.9±0.2	−39.5±0.8	−10.73	5
porcine odorant-binding protein	1DZK	−6.2±0.6	−5.9±0.6	−13.2±0.6	−5.8	−6.0±0.2	−13.0±0.6	−9.2	6
mouse major urinary protein	1I06	−4.4±0.7	−4.0±0.7	−9.1±0.7	−7.2	−3.2±0.2	−9.0±0.7	−8.38±0.52	7
mouse major urinary protein	1QY1	−7.5±0.7	−7.7±0.7	−13.9±0.7	−6.3	−8.8±0.3	−14.9±0.7	−8.1±0.07	8
DNA gyrase subunit B	1KZN	−24.1±0.9	−4.7±1.0	−41.7±0.9	−8.8	−14.0±0.6	−49.8±0.9	−9.785	9
hen lysozyme C	1LZB	−7.67±0.7	3.6±0.7	−28.5±0.8	−9.0	−5.7±0.3	−39.9±0.7	−7±0.01	10
human galectin-3	1KJL	−13.7±0.6	−8.1±0.7	−22.3±0.6	−5.2	−12.1±0.3	−25.1±0.6	−5.6	11
purine nucleoside receptor A	2FQY	−19.4±1.0	−13.1±1.1	−33.8±1.0	−6.9	−11.3±0.6	−35.3±1.0	−8.81±0.09	12
bovine pancreatic trypsin	1S0R	−6.6±0.8	−11.6±0.9	4.9±0.8	−5.5	−10.9±0.5	5.2±0.8	−6.35±0.07	13
human brain fatty acid-binding protein	1FDQ	−10.4±0.7	−12.8±0.9	−40.3±0.8	−9.8	−14.9±0.6	−41.7±0.7	−10.1	14

Simulations were carried out using the pmemd program in AMBER9 with ff03 force field²⁷ in periodic boundary conditions. All bonds involving hydrogen atoms were constrained by using the SHAKE algorithm,²⁸ and a 2 fs time step was used in simulation. The particle mesh Ewald (PME) method was used to treat long range electrostatics. Simulations were run at 298 K under 1 atm in NPT ensemble employing Langevin thermostat and Berendsen barostat. Water molecules were first energy-minimized and equilibrated by running a short simulation with the complex fixed using Cartesian restraints. This was followed by a series of energy minimizations in which the Cartesian restraints were gradually relaxed from 500 kcal·Å⁻² to 0 kcal·Å⁻², and the system was subsequently gradually heated to 298 K via a 48 ps MD run. By assigning different initial velocities, 6 independent simulations in length of 4 ns were performed for each of the crystal structure. The first 2 ns in each trajectory were discarded. MD snapshots were saved every 1 ps yielding 4,000 structures per trajectory.

MD-Based Free Energy Calculations

MM-PBSA and MM-GBSA calculations were carried out as described previously.^29-31 It combines internal energy, solvation energy based on electrostatic and nonpolar contributions, and the entropy. These calculations are carried out on snapshots collected from an MD simulation. The binding free energy is expressed as:

$$\begin{array}{c}\hfill \Delta G_{MM\text{-}PBSA}=\Delta E_{PBTOT}-T\Delta S_{\mathrm{NM}\mathrm{or}\mathrm{QHA}}\hfill \\ \hfill \Delta G_{MM\text{-}GBSA}=\Delta G_{GBTOT}-T\Delta S_{\mathrm{NM}}\hfill \end{array}$$

where ΔG_MM-PBSA and ΔG_MM-GBSA are binding free energies calculated by MM-PBSA and MM-GBSA method, ΔE_PBTOT and ΔE_GBTOT are the combined internal and solvation energies, T is system temperature. ΔS_{NM or QHA} is entropy determined by normal mode calculation or quasiharmonic analysis. The internal energy is determined using the Lennard-Jones and Coulomb potentials in the Amber force-field (ΔE_GAS). The solvation energy is determined using Poisson-Boltzmann or Generalized-Born solvation models (ΔE_PBSOL or ΔE_PBSOL):

$$\begin{array}{cc}\hfill \Delta E_{PBTOT}=& \Delta E_{PBSOL}+\Delta E_{GAS}\hfill \\ \hfill \Delta E_{GBTOT}=& \Delta E_{GBSOL}+\Delta E_{GAS}\hfill \end{array}$$

where ΔE_PBSOL and ΔE_GBSOL are the solvation free energies calculated with PB or GB model, and ΔE_GAS is the molecular mechanical energies. The molecular mechanical energies are composed of three components:

$$\Delta E_{GAS}=\Delta E_{ELE}+\Delta E_{VDW}+\Delta E_{INT}$$

where ΔE_ELE is the non-bonded electrostatic energy, ΔE_VDW is non-bonded van der Waals energy, and ΔE_INT is the internal energies composed of bond, angle, and dihedral energies.

The solvation free energies can be calculated using PB or GB model, expressed respectively by:

$$\begin{array}{cc}\hfill \Delta E_{PB\mathrm{SOL}}=& \Delta E_{PBSUR}+\Delta E_{PBCAL}\hfill \\ \hfill \Delta E_{GB\mathrm{SOL}}=& \Delta E_{GBSUR}+\Delta E_{GB}\hfill \end{array}$$

where ΔE_PBSUR and ΔE_GBSUR are hydrophobic contribution to desolvation energy, ΔE_PBCAL and ΔE_GB are reaction field energies.³²

All the binding energies are determined by:

$$\Delta E=E^{PL}-E^P-E^L$$

where E^PL, E^P and E^L are total energies corresponding to protein-ligand complex (PL), protein (P) and ligand (L), respectively.

The molecular mechanical gas phase energies were calculated by sander program from AMBER9 package, including the internal energy, van der Waals and electrostatic interactions. Dielectric constant for electrostatic interactions was set to 1.0. The polar contributions of the solvation free energy were calculated with Poisson-Boltzmann (PB) method using the pbsa program¹² and generalized Born (GB) method implemented in sander. The nonpolar contributions of the desolvation energy were determined with solvent-accessible surface area (SASA) dependent terms.³³ The surface area was calculated by molsurf program.³⁴ The surface tension used to calculate the non-polar contribution to the free energy of solvation is 0.0072. In the PB method, reaction field energy was calculated with dielectric constant for protein and solvent as 1.0 and 80.0 respectively. In the test of the contribution of dielectric constant, we use various dielectric constant for the solute from 1 to 10, 15 and 20. The default value of the dielectric constant is 1. Solvent probe radius was set to 1.6 Å, which was optimized by Tan and Luo.³⁵ Atomic radii used were also optimized by Tan and Luo.³⁵ The calculation based on GB method was performed with the Onufriev's GB model.^{36, 37} SASA calculation was switched to ICOSA method, surface area was computed by recursively approximating a sphere around an atom, starting from an icosahedra. Two different methods were applied for the calculation of entropies of the protein-ligand complexes. Quasiharmonic approximation was analyzed using the ptraj program in AMBER. Normal mode conformational entropies were estimated with the nmode module from AMBER. Distance-dependent dielectric constant was set to 4. Maximum number of cycles of minimization was set to 10,000. The convergence criterion for the energy gradient to stop minimization was 0.0001. Parameters for the MM-PBSA and MM-GBSA free energy calculation are summarized in Table S2.

For the MM-PBSA or MM-GBSA free energy calculations, a set of 500 structures for each protein-ligand complex was extracted from trajectories of MD simulations at regular intervals. For ΔG_{SVMSP//MMPBSA} and ΔG_{SVMSP//MM-GBSA}, all snapshots from MD simulations were first scored by SVMSP. The top scored 500 structures were selected for free energy. For ΔG_MM-SVRKB, all snapshots were scored by SVRKB first, the mean value of SVRKB score of all snapshots was used for calculated binding affinity (pK_d) of the complex using:

$$\Delta G=-2.303\mathrm{RT}\left(\mathrm{p}{K}_{\mathrm{d}}\right)$$

where R is the gas constant, T is room temperature (298.15 K).

Correlation Analysis

Three correlation metrics, Pearson's correlation coefficient R_p, Spearman correlation coefficient ρ, and Kendall tau τ, were used in model parameterization and performance assessment. All the correlation analysis was done using packages in R (version 1.12.1). The 95% confidence interval was calculated using 5000 replicate bootstrap sampling.

Pearson product-moment correlation coefficient R_p is a measure of linear dependence between two variables x and y, giving a value between +1 and −1 inclusive. It was given by:

$$R_p=\frac{{\sum }_i(x_i-\stackrel{‒}{x})(y_i-\stackrel{‒}{y})}{\sqrt{{\sum }_i{(x_i-\stackrel{‒}{x})}^2\cdot {\sum }_i{(y_i-\stackrel{‒}{y})}^2}}$$

where x̄ and ȳ are the mean value for x_i and y_i respectively. The Spearman's rank correlation coefficient ρ assesses how well the association of two variables can be described using a monotonic function. It was given by

$$\rho =1-\frac{6{\sum }_i{(x_i^{\prime }-y_i^{\prime })}^2}{n(n^2-1)}$$

where $x_i^{\prime }$ and $y_i^{\prime }$ denote the ranks of x_i and y_i, n is the total number of x-y pairs. A perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other. Kendall tau rank correlation coefficient τ is a measure of the association between two measured quantities. It was given by

$$\tau =\frac{{\sum }_{i<j}sign(x_j-x_i)\cdot sign(y_j-y_i)}{\frac{1}{2}n(n-1)}$$

when the values of x_i and y_i are unique.

RESULTS

Calculations of Binding Free Energies and Comparison to ITC Data

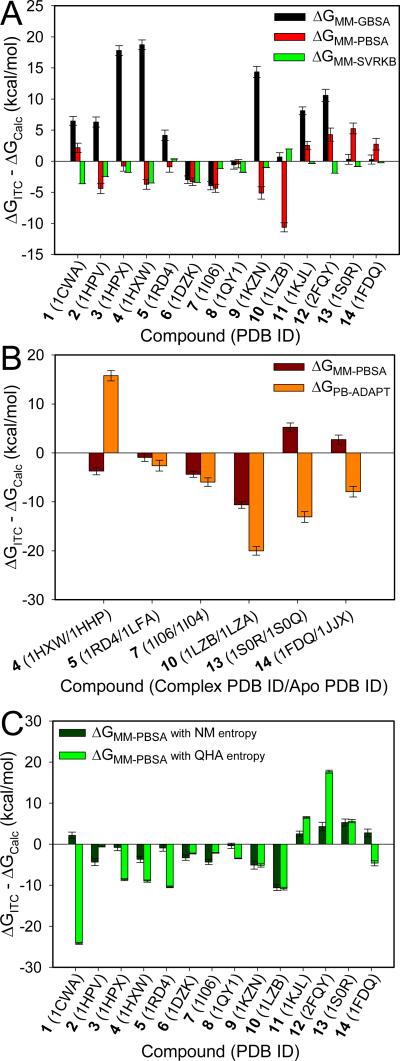
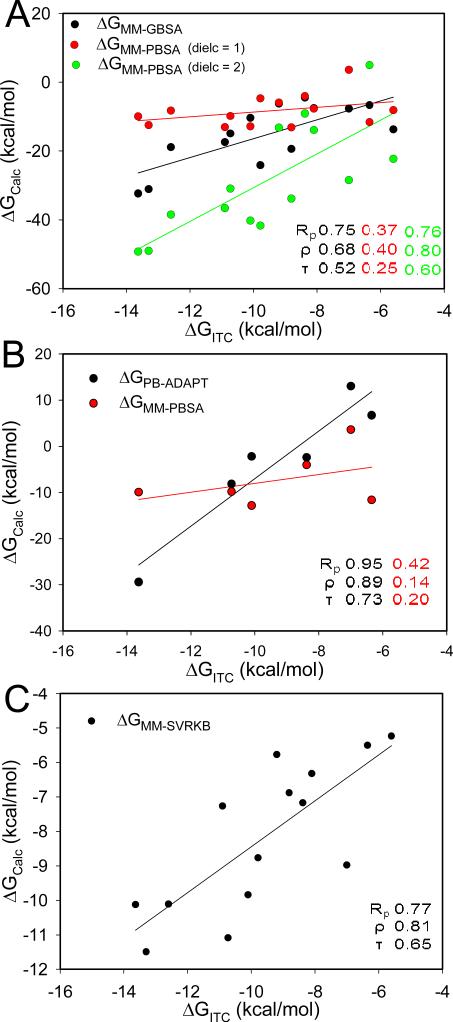
Free energy calculations were carried out for a set of 14 protein-ligand interactions using MM-GBSA and MM-PBSA (Fig. 2). The structure of these complexes was previously solved by crystallography and characterization of the binding was done by ITC. The set contains 11 unique proteins and 14 structurally different ligands. The ligands include a cyclic peptide (1), peptidomimetics (2-4), small organic molecules (5-10, and 13), carbohydrates (10 and 11), a nucleoside (12) and a fatty acid (14) (Fig. 1). Among the small organic molecules, four were fragment-like (6-8, and 13) with molecular weight less than 200 Da. Calculations were carried out using the MM-GBSA and MM-PBSA approach on multiple MD structures collected from 12 ns of simulation. The computed MM-GBSA or MM-PBSA free energies were compared to experimental binding affinity data ΔG_ITC (Table 1, Fig. 3A). Among the 14 complexes, the predicted ΔG_MM-PBSA were excellent (less than 1 kcal•mol⁻¹) for three of the ligands, namely for (i) 3 binding to HIV-1 protease (PDB code: 1HPX; |ΔΔG| = 0.8); (ii) 8 binding to mouse major urinary protein 1 (PDB code: 1QY1; |ΔΔG| = 0.4); and (iii) binding of 5 to human leukocyte function-associated antigen-1 (PDB code: 1RD4; |ΔΔG| = 0.9). The predicted binding affinities for another five ligands were between 2 and 4 kcal•mol⁻¹, namely for (i) 1 binding to human cyclophilin A (PDB code: 1CWA; |ΔΔG| = 2.2); (ii) 6 binding to porcine odorant-binding protein (PDB code: 1DZK; |ΔΔG| = 2.2); (iii) 14 binding to human brain fatty acid-binding protein (PDB code: 1FDQ; |ΔΔG| = 2.7); (iv) 4 binding to HIV-1 protease (PDB code: 1HXW; |ΔΔG| = 3.7); and (v) 11 bound to human galectin-3 (PDB code: 1KJL). The remaining predicted affinities for compounds 2, 7, 9, 10, and 13 were larger than 4 kcal•mol⁻¹. An overall measure of the deviation of the MM-PBSA free energy from the ITC free energy is provided by the root-mean-square of the calculated free energy deviation from experimental energy ΔΔG_RMS, which was 4.4 kcal•mol⁻¹. The median ΔΔG (ΔΔG_MED) for MM-PBSA is 3.5. The effect of the dielectric constant on the MM-PBSA calculations was also investigated (Table 5). Doubling the dielectric constant from 1 to 2 resulted in significantly worse agreement between the MM-PBSA and ITC free energy as evidenced by a five-fold increase in ΔΔG_RMS and a 7-fold increase in (ΔΔG_MED). This was also observed for calculations performed with larger dielectric constants (Table 5).

Figure 2. Stereoview of three-dimensional structures for apo proteins and protein-ligand complexes.

The protein structure in complex is illustrated as a cartoon representation in cyan. The apo protein structure (if available) is illustrated as a cartoon representation in blue. Atoms within 5.5 Å of the ligands in complex is considered as pocket atoms and illustrated in a surface representation in orange. The ligand is illustrated as sticks representation in the color-coded by atom types (yellow, red, and blue for carbon, oxygen and nitrogen). All illustrations were generated by PyMOL (The PyMOL Molecular Graphics System, Version 1.5.0.4 Schrödinger, LLC).

Figure 1.

Chemical structure of bound ligands in protein-ligand complexes.

Figure 3. Calculated free energy deviation from experimental energy in ΔG_ITC-ΔG_Calc of selected protein-ligand complexes with different methods.

(A) ΔG_MM-GBSA, ΔG_MM-PBSA, and ΔG_MM-SVRKB for complexes in Set 1; (B) ΔG_MM-PBSA and ΔG_PB-ADAPT for complexes in Set 2; and (C) ΔG_MM-PBSA with normal mode calculated entropy and ΔG_MM-PBSA with quasiharmonic analysis estimated entropy for complexes in Set 1.

Table 5.

Correlation Coefficients for MM-PBSA Calculations with Different Dielectric Constants

Dielectric Constant	Rp	ρ	τ	ΔΔGRMSa	ΔΔGMEDb
Set 1 complexes
1	0.37	0.40	0.25	4.37	3.51
2	0.76	0.80	0.60	23.53	23.24
3	0.81	0.83	0.65	25.04	23.69
4	0.84	0.85	0.69	24.63	23.13
5	0.85	0.89	0.76	24.03	21.89
6	0.86	0.89	0.76	23.49	20.44
7	0.87	0.89	0.76	23.04	19.29
8	0.88	0.89	0.76	22.67	18.36
9	0.88	0.91	0.78	22.36	17.59
10	0.89	0.91	0.78	22.10	16.96
15	0.89	0.91	0.76	21.26	14.92
20	0.90	0.91	0.76	20.82	13.83

^aRoot-mean-square deviation of the calculated free energy deviation from experimental energy

^bMedian of the calculated free energy deviation from experimental energy.

The above calculations are repeated using a GB model for the electrostatic solvation free energy (MM-GBSA). MM-GBSA free energies were significantly larger than MM-PBSA free energies. In some cases, MM-GBSA energies exceeded 18 kcal•mol⁻¹. Seven of the MM-GBSA free energies deviated from the ITC free energies by 5 kcal•mol⁻¹ compared with only two for MM-PBSA. Overall the MM-GBSA free energy showed greater deviation from the ITC free energy (ΔΔG_RMS = 9.2 kcal•mol⁻¹) compared with MM-PBSA (ΔΔG_RMS = 4.4 kcal•mol⁻¹). The median ΔΔG for MM-GBSA is 5.2 kcal•mol⁻¹. Despite the large absolute values, MM-GBSA reproduced the free energy of binding remarkably well in four cases with ΔΔG less than 1 kcal•mol⁻¹: (i) 7 binding to the mouse major urinary protein 1 (PDB code: 1QY1; |ΔΔG| = 0.6); (ii) 10 binding to hen lysozyme C (PDB code: 1LZB; |ΔΔG| = 0.7); (iii) 13 binding to the bovine pancreatic trypsin (PDB code: 1S0R; |ΔΔG| = 0.3); and finally (iv) 14 bound to human brain fatty acid binding protein (PDB code: 1FDQ; |ΔΔG| = 0.3).

Typically, MM-GBSA calculations are carried out by running a single simulation for the complex. Implicit in this approach is that the ligand will only select conformations of the apo protein that are similar to those that are sampled by the protein in the protein-ligand complex. However, there are numerous examples of ligand binding that leads to conformational change of the protein. The free energy of this conformational change, also known as adaptation energy, contributes to the overall free energy of binding.³⁸ We investigate the role of this adaptation energy for 6 of the 14 complexes (Table 2 and Fig. 3B) for which the crystal structure of the apo was solved independently from the complex structure. Starting with the structure of complex, apo and ligand, three separate MD simulations were carried out. The root-mean-square deviation (RMSD) of the free protein and ligand were determined with respect to the crystal structure of the protein and ligand in the complex crystal structure (Supporting Information Fig. S1). The protein and ligand sampled different structures in the free-state compared to the bound state.

Table 2.

Calculated Free Energies of Selected Protein-Ligand Complexes (Set 2)

			Methods
Target	Complex PDB	Apo PDB	ΔGPB-ADAPT (dielc = 1) (kcal•mol−1)	ΔGPB-ADAPT (dielc = 2) (kcal•mol−1)	ΔGMM-PBSA (dielc = 1) (kcal•mol−1)	ΔGMM-PBSA (dielc = 2) (kcal•mol−1)	ΔGITC (kcal•mol−1)	Ligand No.
HIV-1 protease	1HXW	1HHP	−29.4±1.1	−67.1±2.8	−9.9±0.8	−49.3±0.8	−13.63±0.07	4
leukocyte function-associated antigen-1	1RD4	1LFA	−8.1±1.1	−35.8±3.1	−9.8±0.8	−30.9±0.8	−10.73	5
mouse major urinary protein	1I06	1I04	−2.4±0.9	−9.7±3.1	−4.0±0.7	−9.1±0.7	−8.38±0.52	7
hen lysozyme C	1LZB	1LZA	13.0±0.9	−22.6±2.3	3.6±0.7	−28.5±0.8	−7±0.01	10
bovine pancreatic trypsin	1S0R	1S0Q	6.7±1.1	15.0±2.7	−11.6±0.9	4.9±0.8	−6.35±0.07	13
human brain fatty acid-binding protein	1FDQ	1JJX	−2.2±1.1	−30.6±2.8	−12.8±0.9	−40.3±0.8	−10.1	14

The snapshots from the three separate simulations of complex, apo and ligand are used to carry out MM-PBSA free energy calculations (ΔG_PB-ADAPT) (Table 2). These are compared with the standard MM-PBSA free energies (ΔG_MM-PBSA) (Table 2, Fig. 3B). Overall, the root-mean-square deviation of ΔG_PB-ADAPT from the ITC free energies is ΔΔG_RMS = 12.4 kcal•mol⁻¹ with a median ΔΔG of 7.6 kcal•mol⁻¹ (Table 3). Hence, ΔG_PB-ADAPT resulted in overall greater deviation from the experimental free energy than both MM-GBSA (ΔG_MM-GBSA) and MM-PBSA (ΔG_MM-PBSA). Only one out of the 6 complexes, namely 5 in complex with human leukocyte function-associated antigen-1 (PDB code: 1RD4; |ΔΔG| = 2.6), showed reasonable agreement with experiment (<3 kcal•mol⁻¹). The remaining five exhibited binding free energies that were substantially different from the ITC data.

Table 3.

Correlation Coefficients for Free Energy Calculations

Method	Rp	ρ	τ	ΔΔGRMSa	ΔΔGMEDb
Set 1c complexes
MM-GBSA	0.75	0.68	0.52	9.16	5.23
MM-PBSA (dielc = 1)	0.37	0.40	0.25	4.37	3.51
MM-PBSA (dielc = 2)	0.76	0.80	0.60	23.53	23.24
MM-SVRKB	0.77	0.81	0.65	2.09	1.79
SVMSP//MM-GBSA	0.74	0.74	0.56	15.14	10.94
SVMSP//MM-PBSA (dielc = 1)	0.76	0.81	0.63	5.53	4.67
SVMSP//MM-PBSA (dielc = 2)	0.75	0.78	0.60	29.84	29.45
Set 2d complexes
MM-PBSAADAPT (dielc = 1)	0.95	0.89	0.73	12.42	7.63
MM-PBSAADAPT (dielc = 2)	0.92	0.94	0.87	27.70	20.92
MM-GBSA	0.89	0.83	0.73	8.00	2.30
MM-PBSA (dielc = 1)	0.42	0.14	0.20	5.50	4.03
MM-PBSA (dielc = 2)	0.82	0.89	0.73	23.00	20.83
MM-SVRKB	0.74	0.89	0.73	1.76	1.03
Set 1 complexese
GBSA	0.44	0.47	0.27	2.32	1.49
PBSA	−0.51	−0.57	−0.45	2.22	1.64
SVRKB	0.83	0.82	0.69	1.43	0.59

^aRoot-mean-square deviation of the calculated free energy deviation from experimental energy

^bMedian of the calculated free energy deviation from experimental energy

^cComplexes listed in Table 1

^dComplexes listed in Table 2

^eCorrelation coefficients for free energy calculations with crystal structures.

A question of interest is whether scoring functions can generate reliable binding affinities when carried out on multiple structures sampled from MD simulations instead of crystal structures. To address this question, we applied our recently-developed scoring function, SVRKB,²² to snapshots from MD simulations. The empirical scoring function is trained on three-dimensional protein-ligand crystal structures and experimentally-measured binding affinity data. SVRKB is used to score MD snapshots of the 14 complexes considered for MM-GBSA and MM-PBSA calculations (Table 1 and 2). We refer to this approach as MM-SVRKB to emphasize the use of multiple MD structures in the scoring. MM-SVRKB (ΔΔG_RMS= 2.1 kcal•mol⁻¹) showed better agreement with the experimental free energies than MM-PBSA (ΔΔG_RMS = 4.4 kcal•mol⁻¹). In fact, |ΔΔG_MM-SVRKB| was less than 2 kcal•mol⁻¹ for 10 of the targets, compared with three for the MM-PBSA calculations. None of the predicted MM-SVRKB binding affinities were greater than 5 kcal·mol⁻¹ than the experimentally-measured affinity.

Finally, we compared calculations performed using harmonic versus quasiharmonic approaches for the entropy of binding. Two approaches were considered, namely normal mode analysis, or the use of a quasiharmonic approach where the entropies are determined by a covariance analysis of the fluctuations obtained from the MD simulations. The MM-PBSA free energies obtained with the normal mode analysis resulted in a ΔΔG_RMS= 4.4 kcal•mol⁻¹ when compared with the ITC free energy, and a median of 3.5 kcal•mol⁻¹ for ΔΔG (Fig. 3C). On the other hand, the MM-PBSA free energies for the quasiharmonic approach led to a ΔΔG_RMS of 10.1 kcal•mol⁻¹ and a median value of 6.1 kcal•mol⁻¹.

Rank Ordering Protein Ligand Complexes

Performance to rank-order complexes was evaluated using three correlation metrics, namely the Pearson's correlation coefficient (R_p), Spearman's rho (ρ), and Kendall's tau (τ). Pearson's coefficient is the more traditional metric used to measure the correlation between observed and predicted affinities. Spearman's rho is a non-parametric measure of the correlation between the ranked lists of the experimental binding affinities and the scores. It ranges between −1 and 1. A negative value corresponds to anti-correlation while a positive value suggests correlation between the variables. Kendall's tau (τ) was also considered to assess rank-ordered correlation as suggested by Jain and Nicholls.³⁹ τ has the advantage of being more robust and can be more easily interpreted. It corresponds to the probability of having the same trend between two rank-ordered lists.

It is interesting that despite the better performance of MM-PBSA in predicting the absolute free energy, the opposite is observed for rank-ordering. All three correlation coefficients metrics were significantly higher for MM-GBSA (R_p = 0.75; ρ = 0.68; τ = 0.52) compared with MM-PBSA (R_p = 0.37; ρ = 0.40; τ = 0.25) (Table 3, Fig. 4A). At higher dielectric constants, the correlations for MM-PBSA significantly improves (Table 5). A mere doubling of the dielectric onstant from 1 to 2 led to a similar increase in the correlation factors (R_p = 0.77; ρ = 0.81; τ = 0.65). Further increase of the dielectric beyond two results in smaller increases in performance, as illustrated by the correlations at a dielectric constant of 20 (R_p = 0.90; ρ = 0.91; τ = 0.76). But inspection of the components of the free energy (Table 6) reveals that this increase in performance is not due to more accurate representation of the electrostatic component of the free energy. Instead, it is attributed to the significantly smaller contributions of the electrostatic energy at higher dielectric constants. An increase in the dielectric constant reduced ΔE_ELE and ΔE_PB by a factor of 1/ε and 1/ε ², respectively, where ε is the dielectric constant. As a results, the lower contributions from the electrostatic component results in a free energy component that is dominated by the non-polar and entropy terms. SVRKB applied to MD structures (MM SVRKB) showed better performance than MM-GBSA (R_p = 0.77; ρ = 0.81; τ = 0.65) (Fig. 4C, Fig. 6A). Interestingly, free energies that included the adaptation energy (ΔG_PB-ADAPT) exhibited dramatic improvement over MM-PBSA (R_p = 0.95; ρ = 0.89; τ = 0.73) (Table 3, Set 2, Fig.4B). ΔG_PB-ADAPT correlations are also better than MM-SVRKB (R_p = 0.74; ρ = 0.89; τ = 0.73).

Figure 4. Regression plots between experimental free energy (ΔG_ITC) and different calculated free energy of selected protein-ligand complexes.

(A) ΔG_MM-GBSA, ΔG_MM-PBSA (dielc = 1) and ΔG_MM-PBSA (dielc = 2) for complexes in Set 1; (B) ΔG_MM-PBSA and ΔG_PB-ADAPT for complexes in Set 2; and (C) ΔG_MM-SVRKB for complexes in Set 1.

Table 6.

Components of Free Energy Calculations

PDB	Ligand No.	ΔEELE		ΔEVDW	ΔENP	ΔEPB		TΔSNM	TΔSQHA
		dielc = 1	dielc =2			dielc = 1	dielc =2
1CWA	1	−34.5±0.3	−17.2±0.2	−58.1±0.1	−6.7±0.01	54.9±0.3	14.4±0.1	−31.3±0.7	−54.7
1HPV	2	−35.2±0.3	−17.4±0.1	−60.4±0.2	−6.8±0.01	63.4±0.2	15.2±0.0	−30.9±0.8	−14.9
1HPX	3	−43.9±0.4	−21.3±0.2	−70.7±0.2	−8.1±0.01	77.6±0.4	18.0±0.1	−32.7±0.8	−35.8
1HXW	4	−41.8±0.3	−20.9±0.2	−75.2±0.2	−8.5±0.01	79.4±0.3	19.0±0.1	−36.2±0.7	−30.9
1RD4	5	−7.4±0.2	−4.2±0.1	−53.9±0.2	−6.4±0.01	33.3±0.2	8.8±0.1	−24.6±0.8	−41.3
1DZK	6	−3.3±0.1	−1.6±0.0	−27.5±0.1	−3.9±0.01	13.0±0.1	4.0±0.0	−15.8±0.6	−43.1
1I06	7	−1.3±0.1	−0.6±0.0	−21.4±0.1	−3.6±0.01	7.7±0.1	2.2±0.0	−14.6±0.7	−13.4
1QY1	8	−3.5±0.1	−1.7±0.0	−26.9±0.1	−3.9±0.01	10.8±0.1	3.0±0.0	−15.9±0.7	−22.1
1KZN	9	−38.1±0.4	−18.5±0.2	−63.5±0.2	−6.8±0.02	74.2±0.4	17.8±0.1	−29.4±0.9	−43.0
1LZB	10	−57.3±0.9	−28.9±0.4	−38.5±0.3	−5.3±0.02	78.4±0.9	18.7±0.2	−26.5±0.6	−26.9
1KJL	11	−61.6±0.3	−31.2±0.2	−21.2±0.1	−3.7±0.01	57.7±0.3	13.0±0.1	−20.7±0.6	−18.5
2FQY	12	−65.1±0.3	−32.4±0.1	−34.7±0.1	−4.3±0.01	69.7±0.4	16.6±0.1	−21.2±0.9	−35.3
1S0R	13	42.7±0.6	21.0±0.3	−19.3±0.1	−3.0±0.01	−48.9±0.5	−11.2±0.1	−16.9±0.8	−15.2
1FDQ	14	−93.8±1.0	−45.4±0.5	−41.2±0.2	−5.8±0.01	100.7±0.6	24.5±0.1	−27.3±0.6	−24.0

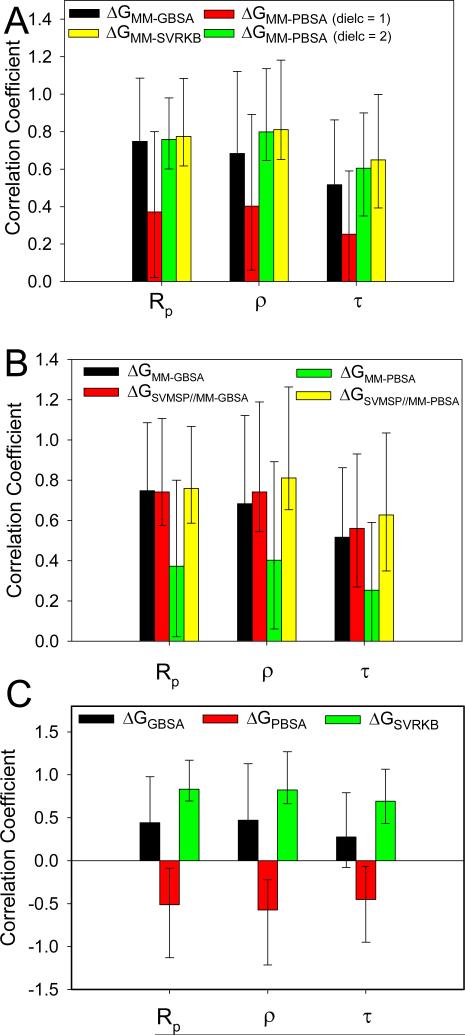
Figure 6. Performance on Pearson's correlation coefficient R_p, Spearman's ρ and Kendall's τ correlation coefficients.

(A) ΔG_MM-GBSA, ΔG_MM-PBSA (dielc = 1), ΔG_MM-PBSA (dielc = 2), and ΔG_MM-SVRKB for multiple MD structures; (B) ΔG_MM-GBSA, ΔG_{SVMSP//MM-GBSA}, ΔG_MM-PBSA and ΔG_{SVMSP//MM-PBSA} for multiple MD structures; and (C) ΔG_GBSA, ΔG_PBSA, and ΔG_SVRKB for single crystal structure.

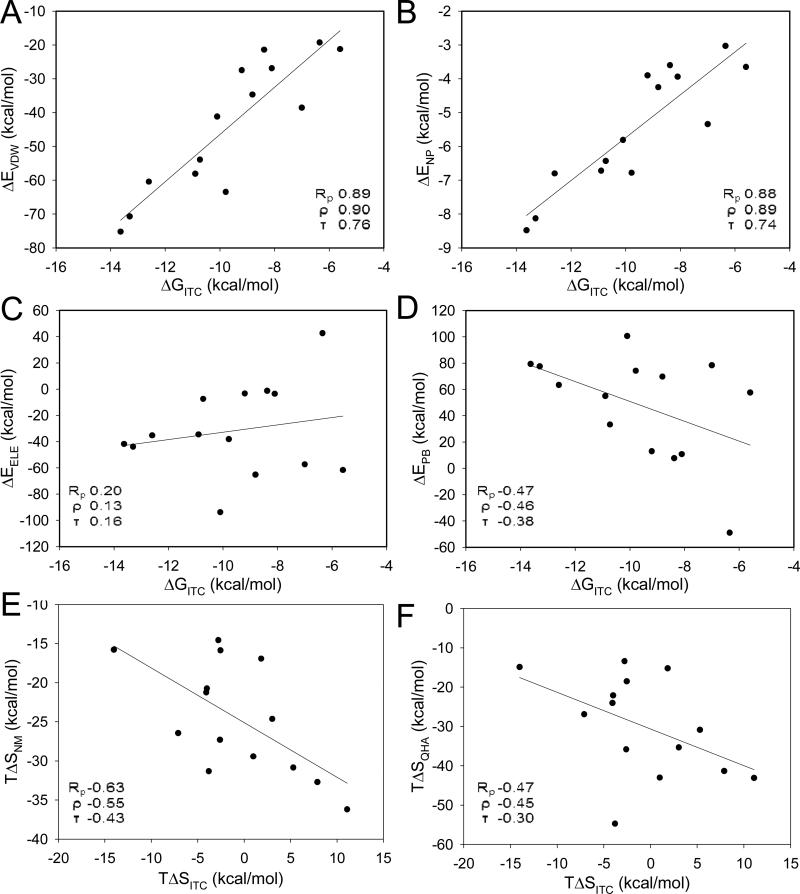
MM-GBSA and MM-PBSA calculations are performed on multiple structures collected from MD simulations. Typically, snapshots are selected at regular intervals. We wondered how MD snapshots can be pre-scored to improve the MM-PBSA or MM-SVRKB results. We had previously developed a scoring approach (SVMSP) to distinguish between native and non native binding modes.²¹ Scoring of MD snapshots with SVMSP is expected to enrich these structures for native-like complexes. SVMSP was used to score all snapshots from MD simulations for each of the 14 targets considered in this work. A total of 500 complexes with the top SVMSP scores were selected for MM-GBSA calculations. The combined SVMSP//MM-GBSA scoring did not improve the predictive abilities of MM-GBSA suggesting that the GB method is less sensitive to the structure used in the calculation (Table 3, Fig. 6B). However, a dramatic boost in performance is observed for SVMSP//MM-PBSA (Table 3, Fig. 6B). In fact, an increase of 0.39, 0.41, and 0.38 is seen for R_p, ρ and τ, respectively. In Set 2, SVMSP//MMPBSA's prediction of the binding affinity trend is as good as MM-PBSA_ADAPT. Components of the MM-PBSA or MM-GBSA calculations are insightful as they provide insight into the free energy of binding (Table 6). But an important question is whether these components correlate with the experimentally-determined thermodynamic parameters provided by ITC. Each component of the MM-GBSA and MM-PBSA calculations is plotted against the ITC free energy. It was interesting, but not completely surprising^{38, 40} that the non-polar components of the binding affinity correlated with the ITC free energy (Table 4 and Fig. 5). The correlation coefficients were R_p = 0.89, ρ = 0.90, τ = 0.76 and R_p = 0.88, ρ = 0.89, τ = 0.74 for the van der Waals energy (ΔE_VDW) and the non-polar component of the solvation free energy (ΔE_NP), respectively. There was no correlation between the electrostatic components of the free energy (ΔE_ELE) and the ITC free energy. There was also no correlation between the reaction field energy calculated by PB (ΔE_PB) and the ITC free energy. This is consistent with previous results that showed that the non-polar component of the free energy was a significantly better predictor of the stability of protein-protein complexes than the electrostatic component.^{38, 40} Finally, there was no correlation between molecular weight of ligand and binding affinity (R_p = −0.51, ρ = −0.65, τ = −0.51).

Table 4.

Correlation Coefficients for Components of Free Energy Calculations

Component	Rp	ρ	τ
Set 1 complexes
ΔEVDW	0.89	0.90	0.76
ΔENP	0.88	0.89	0.74
ΔEELE	0.20	0.13	0.16
ΔEPB	−0.47	−0.46	−0.38
TΔSNM	−0.63	−0.55	−0.43
TΔSQHA	−0.47	−0.45	−0.30
TΔSNMLig	−0.45	−0.10	−0.07
TΔSNMApo	0.02	−0.12	−0.07

Figure 5. Regression plots between experimental free energy (ΔG_ITC) and different component of calculated free energy.

(A) ΔE_VDW; (B) ΔE_NP; (C) ΔE_ELE; (D) ΔE_PB; (E) TΔS_NM; and (F) TΔS_QHA.

The entropy component of the MM-GBSA and MM-PBSA calculations follows a similar trend to the true entropy of binding. The availability of ITC data for each of our systems provides an opportunity to compare computed versus experimental entropy. For MM-PBSA and MM-GBSA, the entropy is typically determined using either normal modes or a quasiharmonic analysis. Fig. 3C shows that these two approaches result in different free energies with overall better agreement for the free energy from the normal mode analysis. The correlations MM-PBSA free energies using normal mode was R_p = 0.37, ρ = 0.40, τ = 0.25, compared with R_p = −0.20, ρ = −0.30, τ = −0.25 for the quasiharmonic analysis. The normal mode and quasiharmonic entropies are compared to the experimental entropy. A plot of TΔS_ITC versus TΔS_NM or TΔS_QHA shows that computed and experimental entropies are anti-correlated with correlation coefficients of (R_p = −0.63; ρ = −0.55; τ = −0.43) and (R_p = −0.47; ρ = −0.45; τ = −0.30), respectively (Fig. 5E and 5F). No change is observed when the entropy change of ligand only (TΔS_NM^Lig), or receptor only (TΔS_NM^Apo) are compared to the ITC entropy (Table 4).

The performance of MM-GBSA and MM-PBSA is compared to GBSA and PBSA, which correspond to calculations performed on a single crystal structure for each of the complexes in Table 1. Correlation coefficients reveal that both GBSA and PBSA perform poorly in rank-ordering complexes when a single crystal structure is used (Fig. 6C). For GBSA all three correlation factors were smaller than 0.5 (R_p = 0.44; ρ = 0.47; τ = 0.27), and for PBSA, predicted and experimental data were anti-correlated (R_p = −0.51; ρ = −0.57; τ = −0.45). SVRKB, on the other hand, performed well consistent with our previous study ²² (R_p = 0.83; ρ = 0.82; τ = 0.69).

DISCUSSION

MM-GBSA and MM-PBSA calculations are applied to a diverse set of 14 ligands bound to 11 different proteins. A unique aspect of this work is that (i) a diverse set of proteins and ligands are used in contrast to most studies that compare ligands bound to the same protein; (ii) all complexes were previously solved by x-ray crystallography and binding was characterized by ITC. The ligands included small organic compounds, cyclic and linear peptides, fragment like small molecules, and carbohydrates. Most free energy calculations did not accurately reproduce the ITC free energy. But there were several cases that were in excellent agreement with ITC: Three complexes for MM-PBSA calculations, and four for MM-GBSA. Overall, MM-PBSA resulted in less deviation from the experimental data than MM-GBSA. But the opposite was observed for rank-ordering. MM-GBSA correlated significantly better with the ITC free energy (R_p = 0.75; ρ = 0.68; τ = 0.52) when compared to MM-PBSA (R_p = 0.37; ρ = 0.40; τ = 0.25). The non-polar terms (ΔG_VDW and ΔG_NP) showed strong correlation with the experimental free energy (R_p = 0.89; ρ = 0.90; τ = 0.76 and R_p = 0.88; ρ = 0.89; τ = 0.74 for ΔG_VDW and ΔG_NP, respectively). An increase in the dielectric constant for the MM-PBSA calculations worsened agreement of the computed and experimental free energies. However, rank-ordering appeared to significantly improve upon increase of the dielectric constant. But close inspection of the components of the free energy reveals that this increase is attributed to the lower contribution of electrostatics as a results of an increase of the dielectric constant. The Coulomb and electrostatic terms are inversely proportional to the dielectric constant and to the square of the dielectric constant, respectively. Less contribution from electrostatics leads to a free energy that is dominated by the non-polar and entropy components resulting to better performance. There was no correlation between the electrostatic components of the MM-GBSA and MM-PBSA free energy and the ITC free energy.

Two models for the entropy were considered, normal mode and quasiharmonic. Normal mode analysis assumes that each structure is at a potential energy minimum. Quasiharmonic analysis is based on a covariance analysis of the atomic fluctuation. Our data showed that the free energies using normal mode analysis correlated significantly better than free energies using quasiharmonic analysis. A possible explanation is that the simulations used in this study may not have been sufficiently long to ensure convergence of quasiharmonic analysis. Neither the normal mode entropy nor the quasiharmonic entropies correlated with the ITC entropy. This is likely due to the fact that the ITC entropy includes both solvation and configurational entropy,⁴¹ while the computed entropy only includes the configurational entropy. The solvation entropies may be indirectly captured by the other terms of the MM-GBSA or MM-PBSA free energy.

Small-molecule binding often induces conformational change to the target protein. This adaptation energy is often ignored in MM-GBSA or MM-PBSA calculations as a single simulation is carried out starting with the complex structure. The structure of the apo protein is extracted from the complex. We studied the effect of this adaptation energy by running a separate simulation for ligand, apo and complex structures. We did this for 6 of the 14 complexes whose apo structure was solved independently by x-ray crystallography. Overall, this resulted in poorer agreement with the ITC data when comparing the absolute values of the free energies. However, the adaptation energy resulted in a significant boost in rank-ordering. The ΔG_PB-ADAPT resulted in a Pearson (Spearman) correlation of 0.95 (0.89) compared with 0.89 (0.83) for ΔG_MM-GBSA and 0.42 (0.14) for ΔG_MM-PBSA. The ΔG_PB-ADAPT showed the best rank-ordering among all methods that were tested in this work.

Typically snapshots for MM-GBSA or MM-PBSA calculations are selected at regular intervals in an MD simulation. We wondered whether different approaches for selecting structures will influence the free energy of binding. We used a recently-developed machine learning-based scoring approach (SVMSP) to pre-score all the snapshots in a trajectory. SVMSP is trained from crystallography and docked protein-decoy structures to classify protein-ligand complexes.²¹ It is therefore expected that the method will enrich MD snapshots for native-like structures. Rank-ordering of snapshots (Table 3) had little influence on the MM-GBSA free energies (Table 3). However, rank-ordering with MM-PBSA calculations improved significantly from R_p = 0.37, ρ = 0.40, τ = 0.25 for snapshots selected at regular intervals to R_p = 0.76, ρ = 0.81, τ = 0.63 for SVMSP-selected snapshots. These results indicate that the Poisson-Boltzmann calculations are more sensitive to the quality of the structure than MM-GBSA.

In sum, MM-GBSA and MM-PBSA methods come short in reliably reproducing the free energy of binding. However, these methods can perform remarkably well for rank-ordering diverse set of compounds. MM-GBSA can perform well by merely using snapshots from an MD simulation of the complex, while MM-PBSA is significantly more sensitive to the structures used. Filtering MD structures with scoring functions to enrich for native-like complexes results in excellent rank-ordering by MM-PBSA. In addition, running separate simulations of the receptor also improves the rank-ordering abilities of MM-PBSA. While previous studies have found that rank-ordering performance for MM-PBSA improves with increasing dielectric constant, we found that this is mainly due to the smaller contributions of electrostatics as a result of increasing the dielectric constant (at ε = 5, for example, the Coulomb energy is reduced by a factor of 1/5 and the PB solvation energy by 1/25). It was remarkable that the non-polar components correlated very well with the free energy. The combination of non-polar and entropy also correlated very well with the free energy, which is why overall correlation improved at higher dielectric constants for MM-PBSA. Finally, the MM-PBSA entropy does not correlation with the ITC entropy.