Moderating the Covariance Between Family Member’s Substance Use Behavior

Abstract

Twin and family studies implicitly assume that the covariation between family members remains constant across differences in age between the members of the family. However, age-specificity in gene expression for shared environmental factors could generate higher correlations between family members who are more similar in age. Cohort effects (cohort × genotype or cohort × common environment) could have the same effects, and both potentially reduce effect sizes estimated in genome-wide association studies where the subjects are heterogeneous in age. In this paper we describe a model in which the covariance between twins and non-twin siblings is moderated as a function of age difference. We describe the details of the model and simulate data using a variety of different parameter values to demonstrate that model fitting returns unbiased parameter estimates. Power analyses are then conducted to estimate the sample sizes required to detect the effects of moderation in a design of twins and siblings. Finally, the model is applied to data on cigarette smoking. We find that (1) the model effectively recovers the simulated parameters, (2) the power is relatively low and therefore requires large sample sizes before small to moderate effect sizes can be found reliably, and (3) the genetic covariance between siblings for smoking behavior decays very rapidly. Result 3 implies that, e.g., genome-wide studies of smoking behavior that use individuals assessed at different ages, or belonging to different birth-year cohorts may have had substantially reduced power to detect effects of genotype on cigarette use. It also implies that significant special twin environmental effects can be explained by age-moderation in some cases. This effect likely contributes to the missing heritability paradox.

Introduction

It has long been observed that family members correlate across a wide range of behavioral and physical traits (Pearson and Lee 1903; Fisher 1918). This correlation may be due to genetic factors, including genetic additivity, dominance, epistasis or epigenetic effects. It may also derive from environmental factors—such as sharing a home, interacting with other family members, or social learning and imitation effects. These explanations, however, implicitly assume the covariance between family members is uniform within a particular type of relative and ignores the possibility that some family members could be systematically more similar, due to age or cohort effects. Should such effects exist, they could also affect correlations among different types of relative. For example, the covariance between DZ twins, which constitutes the majority of family studies, is often substantially higher than the covariance between other first-degree relatives, such as non-twin siblings (Schmitt et al. 2008; Neale and Fulker 1984; Plomin and Daniels 2011) or parent–offspring relationships (Neale and Fulker 1984).

There are several possible explanations for systematic differences in the covariance between family members. In fears and phobias, for example, the parent–child correlation is lower than would be expected under an additive genetic model (Neale and Fulker 1984). One explanation may be that there is negative parent–child cultural transmission, perhaps due to psychosocial processes such as “cultural coercion to the biosocial norm” (Cattell 1963). If there is coercion to the biosocial norm, parents phenotypes may be more extreme than the children’s phenotypes and we observe regression to the mean. In extended family models, this would appear as negative parent–child cultural transmission and it would reduce the magnitude of the parent–offspring correlation relative to the twin–sibling correlation. Another possibility is the influence of genetic dominance, which contributes to sibling similarity, but not to parent–child similarity (Falconer 1989). However, this and other forms of genetic non-additivity such as epistasis are confounded with the effects of the shared environment in standard twin analyses.

In the present article, we focus on the possible effects of age and cohort. Siblings who are more similar in age likely share more environmental stimuli, such as teachers in school, friends, and other social activities. Given that siblings have inherently different ages, it is possible to examine the decay in the familial correlation between family members as a function of age differences in the same way that longitudinal designs would model genetic and environmental innovation and attenuation. Prior research has found that siblings who cohabit longer and more recently are more similar on a range of behavioral phenotypes (Hopper and Mathews 1982; Hopper and Culross 1983; Distel et al. 2011). This increased contact is particularly likely for siblings that are more similar in age. Accordingly, this would suggest that as age differences between siblings increase, the sharing of common environmental stimuli would decrease, effectively reducing the covariance between siblings with larger age differences as siblings with larger age discrepancies will live together for shorter periods of time. This environmental explanation of reduced similarity with greater age difference is plausible, but it is not the only plausible age difference mechanism.

Age-specific genetic effects could decrease the covariance between relatives as the age differences between them increases (Eaves et al. 1978; Tambs et al. 1993). If different genes are expressed at different ages then the larger the age difference between relatives, the lower the probability that two family members will be expressing the same genes. There is ample evidence of age-specific genetic factors from longitudinal twin studies of many traits (the literature here is vast, but see van Beijsterveldt et al. 2013; Boomsma et al. 2002; Briley and Tucker-Drob 2013; Conley et al. 2013; Hewitt et al. 1988; Laceulle et al. 2013; Martino et al. 2013; Nance et al. 1998). These observations are supported by direct observations of differential gene expression at different ages (Brainspan 2001). Furthermore, if genes have a cumulative effect across the lifespan, then the effect of additive genetic covariance on relatives of different ages would decrease as a function of age differences as well (Eaves et al. 1986). Evidence from longitudinal studies has also demonstrated that gene expression varies across the lifespan.

To test these possibilities, we develop a method to estimate the decay in the covariance between siblings as a function of age difference. It is able to quantify the extent to which such decay is due to genetic versus environmental factors, and resolve it against twin-specific environmental sharing not due to their shared birthdate. The method requires only cross-sectional data on twins and siblings who have been measured at different ages. We note that resolution between age and cohort effects is also possible when study measurements are not all made at the same time. For example, if all study participants take a test on their 18th birthday, any decay in relatives’ resemblance as a function of age difference would be due to cohort rather than age effects. Conversely, a longitudinal study of the same individuals at different ages could eliminate cohort effects. In a cross-sectional study where all study measurements are taken in a relatively short period of time (e.g., a 2 week period), age and cohort effects are completely confounded. In practice, measurements in a research study are usually collected over a period of time, which may afford some resolution between age and cohort effects. Here we focus on this latter study design, which is perhaps the most common.

The article has the following structure. First is a technical description of the twin-sibling age-difference moderation model. Second a simulation study demonstrates that parameter estimates are recovered accurately. This is followed by a power analysis to explore the necessary sample sizes for various effect sizes. We then provide a substantive example to demonstrate an empirical example where age differences moderate the covariance between twins and non-twin siblings phenotypic similarity, and conclude with discussion.

Age-Difference Moderation Model

If the similarity between family members decreases as family members become more distant in age, observed correlations between sibling pairs would be heterogeneous and on average downwardly biased. In a study comprising sibling pairs with variable age differences, it is possible to model the decay in the phenotypic correlation as a function of age difference. If there are multiple classes of relative with different degrees of genetic resemblance, such as MZ and DZ twins, it becomes possible to decompose this decay into genetic and environmental components when there are age differences between the relatives. Should resemblance between family members not vary as a function of their age difference, then parameters used to describe the decay should be estimated to be zero, and the variance component parameters would equal those from the corresponding standard twin or family model.

We assume here that phenotypic similarity decays according to an exponential function as the age difference between twins and non-twins siblings increases. This assumption is justified on the basis that the cumulative effect of a linear time series with equally spaced time intervals converges to an exponential function. As we expect the relationship between family members to decay over time (and not accumulate as age differences increase), the exponential function is specified to be negative:

$${\mathrm{e}}^{-\mathrm{\gamma }\mid \mathrm{\Delta }{\text{age}}_{ij}\mid }$$

where γ is the decay parameter to be estimated and |Δage_ij| is the absolute difference between ages of the relative pair ij.

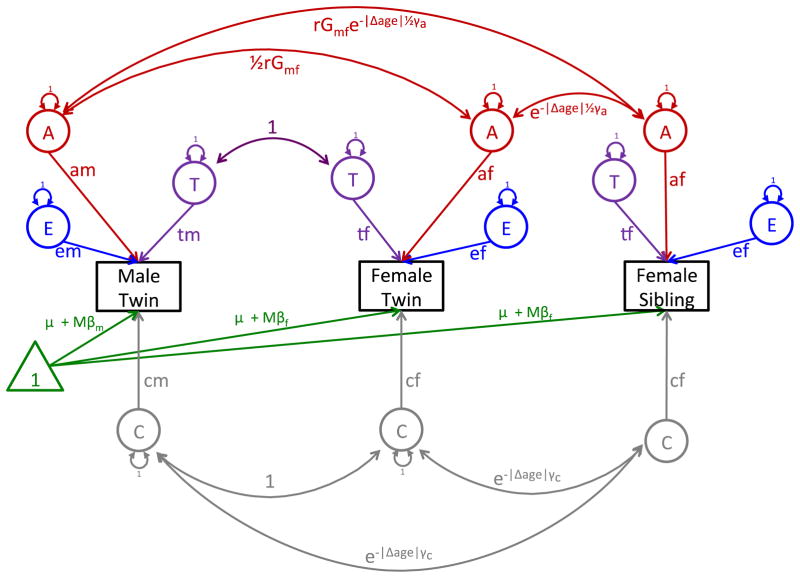
In this article, we restrict our attention to the twin sibling design (Martin and Eaves 1977; Neale and Cardon 1992; Schmitt et al. 2008; Posthuma and Boomsma 2000). Due to its similarity with the classical twin design, the assumptions from the classical twin design apply to the current model. A path diagram for two twins and one sibling is presented in Fig. 1. Extensions to additional siblings (or larger multiple births) follow easily from this diagram. As can be seen in the figure, the phenotypic variance for all family members is decomposed into four sources of variance: additive genetic variance (A), shared environmental variance (C), special twin environment variance (T) and unique environmental variance (E), including measurement error. Accordingly, this model is “just identified” as there are an equal number of estimated parameters as unique pieces of information in the covariance matrix. If all of the parameters are not theoretically justified, they may be dropped, making the model over identified. In either case, the model is identified.

Fig. 1.

Path depiction of the correlation between twins and siblings for one phenotype. The figure presents a simplified path diagram for a pair of opposite sex twins and a non-twin sister. The number of non-twin siblings can be expanded to incorporate multiple siblings

As is the case in the classical twin design the covariance between MZ twins is ${\mathrm{a}}_{\mathrm{s}}^2+{\mathrm{c}}_{\mathrm{s}}^2+{\mathrm{t}}_{\mathrm{s}}^2$, where s indicates the sex of the twins. Analogously, the covariance between same-sex DZ twins is simply $1/2{\mathrm{a}}_{\mathrm{s}}^2+{\mathrm{c}}_{\mathrm{s}}^2+{\mathrm{t}}_{\mathrm{s}}^2$. The expected covariance between opposite-sex DZ twins is 1/2rG_mfa_ma_f + c_mc_f + t_mt_f. The rG_mf parameter allows the genetic covariance between opposite sex twins to be less than the same sex DZ correlation to account for the fact that the opposite-sex twin correlation is often smaller than the same-sex twin correlation.

The covariance for same- and opposite-sex siblings follows directly from the same- and opposite-sex DZ covariance, with the two minor differences. First, because the siblings are not twins, the special twin environment, t_s, does not contribute to the covariation between the sibling and the other twins or siblings in the model. Second, because non-twin siblings are necessarily different ages from their other siblings, the genetic covariation decays as a function of 1/2rG_mfe^{−|Δage|γa} where γ_a is the genetic decay parameter. Similarly, the common environmental covariation between non-twin siblings decay as a function of e^{−|Δage|γc}, where γ_c is the common environmental decay parameter. Because age differences moderate the covariance between the family members, the phenotype is also simultaneously regressed on the respondent’s age to account for the main effect of age on the phenotype.

Simulation

To demonstrate that the model accurately recovers parameters, we simulated data under a variety of conditions. Specifically, data were simulated for five different types of twin families, corresponding with the five possible zygosity groupings with 10,000 families for each family type. Each family was specified to have two twins, two brothers and two sisters. In every case, the twins were simulated to have exactly the same age with a mean of 50 years of age, the brothers had a mean age of 52 and 57, and the sisters had a mean age of 54 and 60 years of age. The standard deviation of all ages was 3 years of age. Given that we are focusing on the absolute age difference between the family members, the fact that the twins are simulated to be younger than the siblings is immaterial. In the absence of age differences between the members of an MZ pair, it seems difficult to understand how decay of additive genetic and common environmental components of variance can be estimated simultaneously. When both additive genetic and common environment variance components are >0, the asymptote for the DZ correlation if only one component can decay will not be zero. Specifically, it will be either half the additive genetic or all the common environment proportion of variance. Only when both components can decay will the asymptote for the DZ correlation at highly disparate ages be zero.

Within these families, data were simulated as a function of 14 parameters: additive genetic, common environmental, special twin environment and unique environmental main effects for males and females, the intercept of the phenotype and main effect of age on the phenotype and, most importantly, genetic and environmental moderation parameters.

Simulation Results

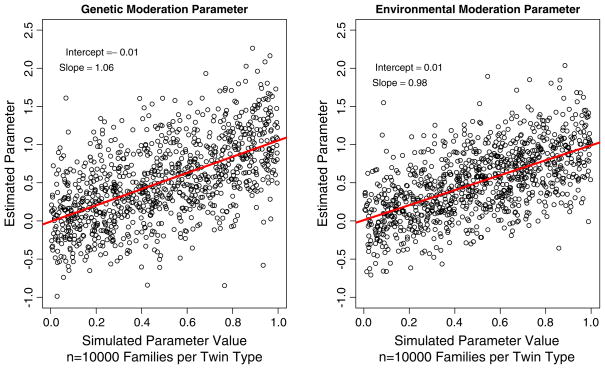
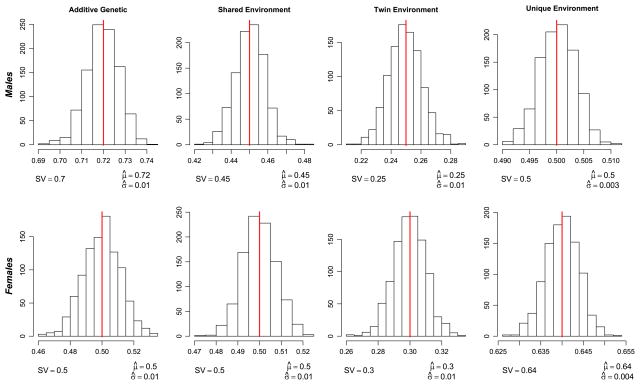
As can be seen in Figs. 2 and 3, the estimated parameter values correspond closely to those used to simulate the data. The distribution of the estimated parameters is centered on the simulated values, indicating that they are unbiased. What is also apparent from the figures is that the variation in the genetic moderation parameter is larger than the variation in the environmental moderation parameter.

Fig. 2.

Simulated and estimated values of the genetic and environmental moderation parameters

Fig. 3.

Histograms of the simulated and estimated values of the additive genetic, common environmental, special twin environment and unique environmental main effects for males and females. The simulated parameter value (SV) is presented as the red line in the graphs and numerically below each histogram. The numerical mean parameter estimate (μ̂) and the standard deviation (σ̂) is presented below each histogram (Color figure online)

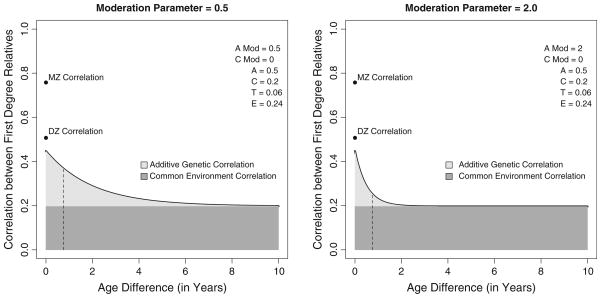
Figure 4 plots two sets of moderation parameters. The left panel presents the results when the genetic moderation parameter is .5 and the common environmental moderation parameter is 0, while the right panel assumes a larger genetic moderation parameter of 2.0. The standardized A, C, T and E parameters are listed in the top right corner of each panel. In both cases the decay in the correlation is entirely a function of age specific differential gene expression, but analogous environmental decay (or simultaneous genetic and environmental decay is entirely possible). Consistent with results of most twin studies, the correlation between the MZ twins is large and the correlation between the DZ twins is smaller though still sizable. The expected correlation between non-twin first-degree relatives is approximately .45 when there is no difference in age. Notably, given that T is included in the model, the DZ correlation is slightly above this line. The dashed vertical line denotes the 9-month age difference, the minimum age difference between non-twin siblings. As can be seen, the decay in the correlation between siblings is relatively rapid. Further, the additive genetic variance, which contributes to the sibling correlation, asymptotes to the common environmental correlation by the time the age difference reaches 10 years.

Fig. 4.

Decay in the correlation between first-degree relatives as a function of age difference for moderate and large values of the genetic decay parameter γ_a

Power Analysis

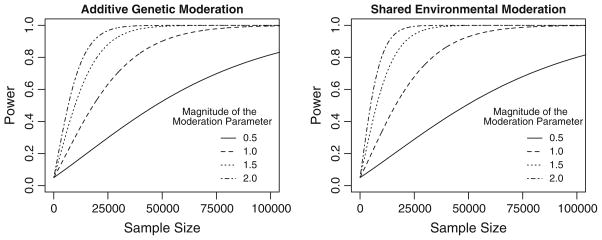
Next, we address is the power to reject the null hypothesis at varying effect sizes. To examine the power for the moderation parameter, the A, C, T and E parameter values were the same as those used in the simulation above. Eight models were then tested where the additive genetic or shared environmental moderation parameters were evaluated at .5, 1.0, 1.5 and 2.0 while the other parameter was fixed to 0. Each model was run 100 times and the mean Chi squared was used in subsequent calculations. As the Chi squared value increases linearly with sample size, these analyses allow us to calculate the power for a given sample size effect size.

As is evident from Fig. 5, the power to reject the null hypothesis for either the environmental or additive genetic moderation parameter is very low, requiring large samples to have sufficient power to reliably detect significant moderation effects. Specifically, if the moderation parameter is .5, to achieve 80 % power, one would need a total sample of approximately 100,000 individuals, i.e., 5,000 families with two twins and two siblings in each of the five zygosity-sex groups. As the effect size gets larger, the required sample size decreases precipitously, to total sample of approximately 30,000 if the genetic moderation parameter is 1.0, 20,000 if the genetic moderation parameter is 1.5 and approximately 15,000 if the genetic moderation parameter is 2.0. The power to detect significant shared environmental moderation is slightly higher, especially with larger effect sizes. For example, a total sample of approximately 10,000 people is required for 80 % power if the common environmental moderation parameter is 2.0. This modest statistical power is because the moderation parameter is identified by a third-order moment of the data (the covariance between age difference and the covariance of the relatives’ phenotypes). It is also consistent with the low power of non-scalar sex limitation parameters in twin studies. Further, the shared environmental coefficients of resemblance are all 1.0, regardless of the twin or sibling type, so the power to detect significant shared environmental moderation is much higher than the power to detect genetic moderation.

Fig. 5.

Power curves for the genetic and environmental moderation parameters at four effect sizes

We ran a series of simulations to test the Type I error rate of the model. Specifically, we simulated 500 datasets with the moderation parameter at zero. We then evaluated the distribution of the test statistic under the null hypothesis of no moderation by fitting models with (1) the moderation parameters fixed to 0; (2) estimating them as free parameters; and (3) comparing their fit using a likelihood ration test. The difference in −2 log-likelihoods very closely followed a Chi square distribution with 1 df. Specifically, of the 500 runs, the difference in −2 log-likelihoods exceeded 2.71 48 times (9.6 %), 3.84 25 times (5.0 %) and 6.63 6 times (1.2 %) consistent with a nominal alpha of .10, .05, and .01, respectively, consistent with a non-significant Kolmogorov–Smirnov test for the departure from the theoretical χ² distribution (D = .02, p = .92).

Demonstration

Respondents

The data for the illustration come from the Virginia 30,000 dataset, which contains a variety of health and lifestyle phenotypes from 14,763 twins and their available family members. Twins were ascertained from either public birth records in the Commonwealth of Virginia or from responses to a letter published in the newsletter of the American Association of Retired Persons (AARP). The twins were not selected for any specific outcome. Questionnaires were mailed to twins. Twins were asked to provide the contact information for other family members, who were subsequently sent a questionnaire. For the current purposes, we restrict the sample to twins and their siblings (Truett et al. 1994; Eaves et al. 1999; Maes 1999).

Phenotype

A self-report lifetime smoking question asked participants to “Write the number which best describes the smoking habits of each of the following individuals during his/her lifetime.” The response options were: (1) never smoked, (2) used to smoke but gave it up, (3) smoked on and off, (4) smoked most of his/her life. This question was asked concerning the respondent themselves and their immediate relatives; only the former are used here.

Results

The model comparison results are presented in Table 1. Notably, for smoking history, all the moderation models fit significantly better than the no moderation model. Because the moderation models are not necessarily nested, we rely on AIC and BIC model fit statistics to compare the moderation models, with the smallest value indicating the best fitting model rather than likelihood ratio tests. As is clear based on the information criteria indices, the A moderation model is consistently the best model according to all of the AIC indices, the df penalty BIC, and sample-size adjusted BIC, but not the BIC.

Table 1.

Model fitting statistics for the moderation models of lifetime smoking history

	Parameters	−2LL	χ2	p	AIC	df Penalty AIC	BIC	df Penalty BIC	Sample-size adjusted BIC
A and C moderation	19	31,491.81	12.27	.002	3,005.81	31,529.81	−92,460.41	31,657.16	31,596.79
A moderation	18	31,493.04	11.04	.001	3,005.04	31,529.04	−92,467.88	31,649.69	31,592.49
C moderation	18	31,497.07	7.01	.008	3,009.07	31,533.07	−92,463.86	31,653.72	31,596.52
No moderation	17	31,504.08	–	–	3,014.08	31,538.08	−92,465.54	31,652.03	31,598.01

Lowest value of each parameter is in bold

N = 6,019

Parameter estimates from each of the four models are presented in Table 2. As can be seen, in all cases the additive genetic variance component is statistically significant and substantively meaningful for both males and females. Accordingly, and unsurprisingly, this suggests that genetic factors contribute substantially to variation in smoking behavior. The shared environmental variance component is also consistently significant for females but for males it is only significant in the C moderation model, a worse fitting model. Thus, it appears that the common environment is more important for females. Furthermore, the unique environmental variance component is highly consistent across all models.

Table 2.

Parameter estimates from the lifetime smoking age difference moderation models

	A and C moderation	A moderation	C moderation	No moderation
Males
Additive genetic	.74 (.63, .84)	.74 (.62, .85)	.66 (.53, .78)	.72 (.58, .83)
Shared environment	.38 (−.01, .52)	.37(−.08, .51)	.43(.15, .58)	.24 (−.19, .42)
Twin environment	.08 (0a, .36)	.03 (−.36, .37)	.24 (0a, .43)	.32 (.08, .46)
Unique environment	.56 (.52, .60)	.56 (.51, .60)	.56 (.53, .61)	.56 (.52, .61)
Females
Additive genetic	.63 (.54, .72)	.65 (.52, .73)	.65 (.54, .74)	.65 (.54, .73)
Shared environment	.53 (.50, .62)	.53 (.41, .61)	.53 (.41, .62)	.45 (.34, .54)
Twin environment	.18 (.00, .36)	.03 (−.37, .37)	−.02 (−.30, .34)	.31 (.15, .41)
Unique environment	.54 (.51, .57)	.54 (.51, .57)	.54 (.51, .57)	.54 (.51, .57)
rGmf	.66 (.51, 1.0)	.64 (.52, 1.0)	.62 (.49, .82)	.65 (.51, 1.0)
Genetic moderation	8.40 (.30, 42.17)	9.48 (1.2, 38.0)
Common environment moderation	.18 (.00, 11.07)	–	8.59 (.8, 18.7)
AgeMales	.19 (.08, .29)	.19 (.08, .29)	.19 (.08, .29)	.19 (.08, .29)
AgeFemales	−.19 (−.28, −.10)	−.19 (−.28, −.10)	−.19 (−.28, −.10)	−.19 (−.28, −.10)
Males
Threshold 1	−.19 (−.25, −.13)	−.19 (−.26, −.12)	−.19 (−.26, −.12)	−.19 (−.26, −.12)
Threshold 2	.93 (.90, .97)	.93 (.89, .97)	.93 (.89, .97)	.93 (.89, .97)
Threshold 3	.27 (.25, .29)	.27 (.25, .29)	.27 (.25, .29)	.27 (.25, .29)
Females
Threshold 1	.10 (.04, .15)	.10 (.04, .15)	.10 (.04, .15)	.10 (.04, .15)
Threshold 2	.62 (.60, .65)	.62 (.60, .65)	.62 (.60, .65)	.62 (.60, .65)
Threshold 3	.31 (.29, .33)	.31 (.29, .33)	.31 (.29, .33)	.31 (.29, .33)

^aBecause the biometrical pathways are sign invariant, the absolute value of lower and upper bounds of the confidence intervals were equal. This indicates that the parameter is not significant, however, the lower bound of the confidence interval cannot be estimated accurately

Beyond the standard variance decomposition depicted above, there are several very interesting comparisons between these models. First, the special twin environment variance component is only significant in the no moderation model, implying that the special twin environment is primarily a function of age similarity in twins rather than something inherently different about the connection between twins, at least for smoking behavior.

Second, the correlation between the genetic factors for males and females (rG_mf) is only significantly different from unity in the C moderation model. This may be due to the fact that the opposite sex sibling correlation is lower than the same sex sibling correlation. Given that there is not very much shared environmental variance for males, the only other model parameter that can generate a reduced opposite sex correlation is the rG_mf parameter.

Finally, the genetic moderation parameters are very large. Importantly, the confidence intervals on these parameters are immense, indicating the low level of precision with which these parameters are estimated. This is entirely consistent with the simulation results that showed a very wide dispersion for the moderation parameters and the power analysis that demonstrated that very large sample sizes are required for adequate power to detect moderation.

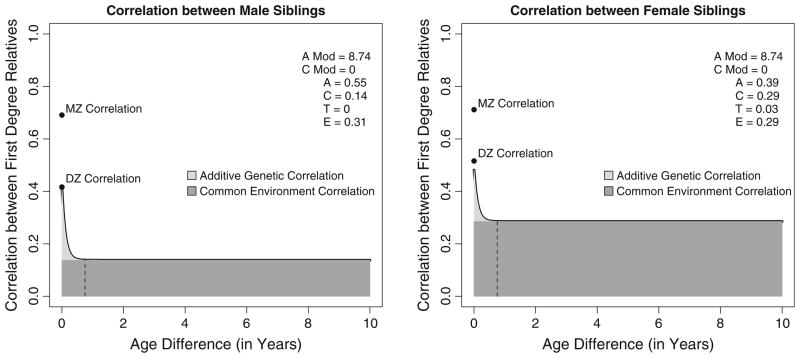
Figure 6 graphs the standardized expected parameters for the A moderation model (the best fitting model based upon the model comparison statistics). The standardized parameters estimates are presented in the top right corner of the figures. As can be seen, the correlation between relatives decays very rapidly, and asymptotes at the correlation due to the common environment. Specifically, the decay in the additive genetic covariance is so rapid that virtually all of the genetic covariance has dissipated by a 9-month age difference, implying that the relationship between siblings (but not twins) is primarily a function of the common environmental correlation. It is important to keep in mind that common environmental correlation is not significant in males, further highlighting the importance of the common environment specifically for females.

Fig. 6.

Graphical depiction of the expected relationship between first-degree relatives

Discussion

Our study of age-related changes in resemblance between twins and non-twin siblings has three important conclusions. First, the simulated parameters are reliably estimated. This demonstrates that the model is identified and that the estimated parameters are unbiased. Second, the power to detect age-difference moderation is fairly low and large sample sizes are required for smaller effect sizes. Further, even with large effect sizes, the precision of the moderation parameter is low. Third, the model can be effectively applied to questions at the heart of behavioral genetics.

This model contributes to our understanding of genetic and environmental transmission, by providing a method for testing genetic and environmental age-difference moderation. As the smoking example illustrates, the genetic factors associated with a phenotype can change across the lifespan. This would be consistent with (and could be validated by) a longitudinal twin study in which the genetic correlation over time is estimated to be less than unity. Thus, if trait-relevant genes are not the same across the lifespan it may be difficult to find specific SNPs or genes that are associated with the phenotype unless individuals are assessed at the same age. This type of effect would undoubtedly contribute to the missing heritability paradox that has plagued the reconciliation between twin studies and Genome Wide Association Studies (GWAS: Maher 2008). We note also that if cohort differences exist (effectively a cohort × genotype interaction) then measuring individuals at the same age may not eliminate the problem that different genetic factors are operating in different individuals over time.

If there is evidence for age-difference moderation of the shared environment contribution to sibling resemblance, several environmental components could be implicated. It may be that sharing friends, acquaintances, school environments or neighborhood factors at critical developmental stages generates greater similarity between relatives of similar than of disparate ages.

While twin and family studies with 20,000–40,000 respondents may seem excessively large, several studies currently exist with approximately this sample size. Specifically, in addition to the Virginia 30,000 that was used for the demonstration in this study, several studies have both twins and siblings, such as the publically available National Longitudinal Study of Adolescent Health (Harris 2013), The Non-shared Environment in Adolescent Development (Neiderhiser et al. 2007), several studies from QIMR Berghofer in Australia (from), and The Netherlands Twin Register (Boomsma et al. 2002) to name a few. While some of these resources are proprietary, there is an abundance of available datasets that can be analyzed with the current method. In addition, the potential to add age difference effects to GCTA analyses, which we plan to describe in another manuscript, further add to its potential utility.

A limitation of the currently available datasets, however, is that there are relatively few siblings. Power to test age difference moderation is enhanced with large age differences between siblings. Thus, the fact that family sizes are smaller than they have been historically implies that data from more families may be needed to estimate the effects and that the likelihood of large age differences is small. Both of these factors will affect the power to detect age-difference moderation. Studies of half-siblings could prove valuable in this context (available in the Add Health data noted above), as they may have greater average difference in age, especially those pairs sharing a father. Importantly, while large sample sizes may seem enormous from twin and family modeling perspective, they are small compared to those required for GWAS studies of complex traits. For instance the most recent GWAS of schizophrenia and educational attainment had over 100,000 observations, though studies of this size are admittedly rare.

Another consideration is that in order to have genetic or environmental age-difference moderation there must be a moderate to high genetic or environmental covariance between relatives. As the genetic or shared environmental variance for the trait is decreases, so does the power to detect decay in it. Thus, if the model implies that the covariance between family members is not a function of shared environmental factors, then shared environmental age-difference moderation would not be empirically or theoretically justified. Note, however, that estimates of genetic and shared environmental variance based on non-twins may have been downwardly biased by age or cohort difference effects (such as adoption studies or half-sibling designs). Modeling these effects is especially important in samples in which a substantial proportion of the relatives are non-twins.

One potential solution to the limited age-range problem is to include parents and children in the moderation analysis. As age difference between parents and children almost invariably exceeds the age difference among siblings, this would greatly enhance the power to test for age difference moderation. A key obstacle in this extension, however, is the treatment of assortative mating. Specifically, the genetic effects of assortative mating may differ according to the age of the offspring, and should be at their maximum at the parental ages at assortment. While this is not necessarily an insurmountable obstacle, further methodological development is necessary to implement such models.