Computational Study of Effects of Tension Imbalance on Phonation in a Three Dimensional Tubular Larynx Model

Summary

Objective

The current study explores the use of a continuum based computational model to investigate the effect of left right tension imbalance on vocal fold vibrations and glottal aerodynamics, as well as its implication on phonation. The study allows us to gain new insights into the underlying physical mechanism of irregularities induced by vocal fold tension imbalance associated with unilateral cricothyroid muscle paralysis.

Method

A three dimensional simulation of glottal flow and vocal fold dynamics in a tubular laryngeal model with tension imbalance was conducted by using a coupled flow-structure interaction computational model. Tension imbalance was modeled by reducing by 20% the Young’s modulus of one of the vocal folds, while holding vocal fold length constant. Effects of tension imbalance on vibratory characteristic of the vocal folds and on the time-varying properties of glottal airflow as well as the aerodynamic energy transfer are comprehensively analyzed.

Results and Conclusions

The analysis demonstrates that the continuum based biomechanical model can provide a good description of phonatory dynamics in tension imbalance conditions. It is found that while 20% tension imbalance does not have noticeable effects on the fundamental frequency, it does lead to a larger glottal flow leakage and asymmetric vibrations of the two vocal folds. A detailed analysis of the energy transfer suggests that the majority of the energy is consumed by the lateral motion of the vocal folds and the net energy transferred to the softer fold is less than the one transferred to the normal fold.

1. Introduction

Tension imbalance is one of the major biomechanical manifestations of unilateral true vocal fold (TVF) paralysis of the cricothyroid muscles. It results from total or partial loss of nerve innervation to one side of the larynx1. Tension imbalance causes asynchronous movements between the two true vocal folds (TVFs) and can lead to breathy and hoarse voice, increased effort with voice production, voice fatigue, decreased loudness, and discomfort with prolonged voice use^2–9. From a biomechanical point of view, the TVFs together with glottal airflow constitute a highly nonlinear self-oscillating system. The pressure-flow relation in the glottis, the stress-strain relation of the TVF tissues, and TVF collision present high nonlinearities¹⁰. Tension imbalance perturbs this nonlinear dynamical system from its neutral state and yields various classic nonlinear dynamic behaviors, such as bifurcation, period-doubling, and chaotic vibration. It has important implications for voice pathology. For example, irregular vibratory patterns of the TVFs in various voice disorders and the corresponding acoustic signals often show sudden jumps to subharmonic regimes and low-dimensional attractors. Bifurcations are also commonly observed in high-speed recording signals of the pathological TVF^{3,5,9, 11–16}.

In the past, pathological studies of phonation were commonly conducted through lumped-element models of the TVF in which the TVF is approximated as arrays of lumped masses connected by springs and dampers^5,13,17–23. Various structural, aerodynamic and acoustic models have been developed and integrated into the lumped element modeling framework for studying dynamics in voice disorders including vocal fold paralysis, polyps, nodules and Parkinson’s diseases²⁴. While this type of model laid the basis for the fundamental theory of nonlinear dynamics of irregular voice production⁴⁶, the shortcomings, such as being restricted to crude statistical quantities, neglecting or simplifying flow viscous effects, and lacking strong physiological correlation between tissue properties and model system parameters, prevent it from providing a comprehensive description of nonlinear behaviors of the laryngeal system.

Recently, with the advances in the field of numerical methods, especially their ability to handle complex flow-structure-interaction problems, continuum-based modeling of phonation has undergone a rapid improvement from initial two-dimensional models to recent three-dimensional models^25–39. By directly solving the partial differential equations of the glottal flow and TVF dynamics, these models are capable of providing an accurate and detailed physical knowledge of flow and TVF behavior as well as their nonlinear interaction processes. Moreover, these models have the potential to provide a relatively complete description of nonlinear dynamic behaviors in voice production. In this way, it is possible to reproduce a wide range of laryngeal pathological conditions to conduct an investigation of the underlying mechanism of various voice disorders.

To advance the state of the art, three dimensional numerical simulations of glottal flow and TVF dynamics in both a normal laryngeal model and an abnormal laryngeal model with tension imbalance were conducted by using our in-house coupled flow-structure interaction computational solver³⁵. The simulations were performed on an idealized tubular-shaped laryngeal model which was designed with a high level of realism with respect to real human laryngeal anatomy³⁵. The dynamics of glottal flow and TVF vibration was investigated in detail for the normal laryngeal model in our previous study. The computational model has been demonstrated to be able to reproduce many of the characteristic features of the glottal flow and TVF dynamics observed in-vivo and in-vitro³⁵. A brief comparison between the normal model and abnormal model in terms of voice quality related statistical quantities and TVF movements was reported as a section in the previous study³⁵. The current paper is a supplemental study to provide a more comprehensive analysis of the effects of tension imbalance on vibratory characteristics of the TVFs, the time-varying properties of the airflow through the glottis, and aerodynamic energy transfer. The analysis demonstrates that the continuum-based biomechanical model can provide a good description of phonatory dynamics in tension imbalance conditions and it allows us to gain new insights into the underlying physical mechanism of irregularities induced by left-right TVF tension imbalance. In the future, such models could be applied to other laryngeal pathological conditions, such as TVF nodules, and coupled with advanced nonlinear dynamic analysis methods to provide complete bifurcation diagrams of nonlinear dynamic behaviors associated with various voice disorders.

2. Computational Modeling and Simulation Setup

The numerical algorithm and simulation set up have been reported in detail in our previous studies^35,37. For the sake of completeness, the current paper describes concisely some salient features of the numerical methods, geometric model, contact model, boundary conditions, and material properties. In the context below, the normal laryngeal model is referred to as the symmetric model and the abnormal larynx model with tension imbalance is referred to as the asymmetric model.

The current study employs an explicitly coupled immersed-boundary-finite-element method based flow-structure interaction solver to model human phonation. The glottal airflow is governed by the 3D, unsteady, viscous, incompressible Navier-Stokes equations, and the TVF dynamics are governed by the Navier equation. The coupling between the flow and solid solver is implemented by tracking the aerodynamic load on the interface mesh as well as its deformed shape and velocity in a Lagrangian fashion.

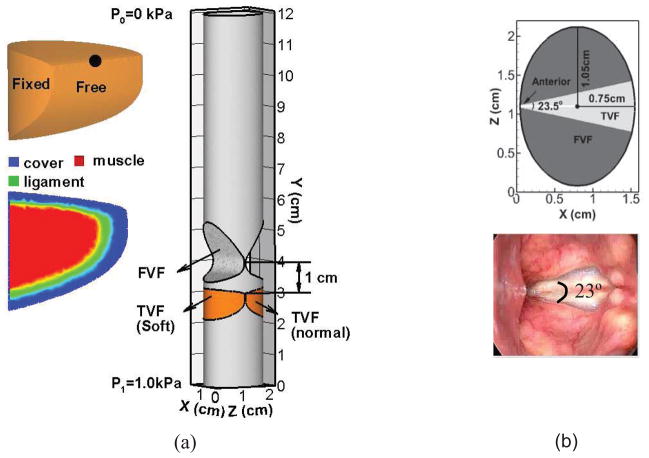
The three-dimensional geometric model of the human larynx is shown in Figure 1(a). The model consists of a 12 cm long elliptical cylinder, a pair of deformable TVFs and a pair of rigid false vocal folds (FVFs). The entire model is immersed in a 1.6 cm × 12 cm × 2.2 cm rectangular computational domain. The cross-section profile of the TVF is generated based on a high resolution laryngeal CT scan of a normal male subject³⁷. The TVF is placed into the elliptical vocal tract with the medial surface 0.01 cm away from the glottal midline, resulting in a 0.02 cm initial gap between the left and right TVFs. The glottal exit is at the plane of y = 3.0 cm. The overall shape and dimensions of the FVF are based on in-vivo measurements⁴⁸. Figure 1(b) is the superior view of the geometrical model of the vocal tract and the laryngoscopic view of the larynx of a human subject. The pair of FVFs is placed in to the elliptical vocal tract with an anterior angle of 23.5°, which is measured from the laryngealscopic superior-to-inferior view of the larynx of the human subject³⁵. The two FVFs are touching at the anterior end, and the gap between them gradually increases toward the posterior end. At the posterior end, the gap between the FVFs is around 0.65 cm. The FVF is located from y = 3.39 cm to y = 5.3 cm. The minimal gap between the FVFs is located at y = 4.0 cm. The distance from the glottal exit to the minimal gap between the FVFs is 1.0 cm.

Figure 1.

(a) The computational domain, geometric model, boundary conditions and three-layer inner structure of the TVF employed in the simulation. (b) Superior view of the geometrical model of the vocal tract and the laryngoscopic view of larynx of a human subject.

The configuration of three inner layers of the TVF is also shown in Figure 1, and it was constructed roughly based on the anatomical data^46,48. The thickness of each layer is assumed to be constant along he anterior-posterior direction. The material of the three layers is assumed to be linear, viscoelastic, and transversally isotropic. The material properties for each layer are reported in Table 1. It should be noted that the TVFs barely vibrate in the longitudinal direction during phonation, and therefore, an in-plane motion constraint is implemented by setting the longitudinal Young’s modulus (E_pz) equal to 10⁴ times the transversal Young’s modulus (E_p) in each layer⁴⁹.

Table 1.

Material properties of the three layers of the vocal folds. ρ is the tissue density, E_p is the transversal Young’s Modulus, ν_p is the in-plane transversal Poisson’s ratio, E_pz is the longitudinal Young’s Modulus, ν_pz is the longitudinal Poisson’s ratio, G_pz is the longitudinal shear modulus, η is the damping coefficient.

	ρ (g /cm3)	Ep (kPa)	νp	Epz (kPa)	νpz	Gpz (kPa)	η (poise)
Cover	1.043	2.041	0.9	20000	0.0	10	2
Ligament	1.043	3.306	0.9	33000	0.0	40	3.5
body	1.043	3.990	0.9	40000	0.0	20	4

In the case of superior laryngeal nerve paralysis, the cricothyroid muscle, which is responsible for stressing the whole TVF, loses its function. That means the initial stress in each layer of the TVF is affected. It has been shown that reducing the Young’s modulus has an equivalent effect as decreasing the initial stress^15,46. Thus, in the current study, tension imbalance is created by reducing 20% of the transverse and longitudinal Young’s moduli of the three inner layers of the left TVF while the material properties of the right TVF are kept the same as the symmetric model. The value of 20% was chosen based on our experience from the previous two dimensional study which shows that irregularities start to develop beyond 20% tension imbalance²³. Prior work suggested that irregularities primarily occur in the case of a significant asymmetry where tension imbalance is usually beyond 50%^15,23. Thus, the current value of 20% is considered a relatively low level of tension imbalance. Nevertheless, it is a good starting point for us to evaluate the application of the developed computer model in studies of pathological conditions. In the future, the model can be extended for simulating higher levels of tension imbalance.

It should be noted that with pathological conditions (such as TVF nodules, carcinomas, or unilateral paralysis/paresis), the medial contact of the two TVFs might be highly asymmetric and the contact location may vary significantly from cycle to cycle⁴⁰. The previous contact model for the normal laryngeal configuration, which fixed the contact location at the center of the larynx, is therefore no longer suitable. To represent the contact in more general contact conditions, a phenomenological, non-linear, spring-based contact force model was implemented and used for the asymmetric model. In this model, each surface vertex of the triangular mesh on one TVF is connected to every surface vertex on the opposite TVF with a non-linear spring. When the two vertexes approach each other and reach a distance smaller than a certain criterion, the spring force is activated and applies a retarding force along the direction of the line joining the two contacting nodes. The non-linear spring force is assumed to increase exponentially with the decrease of the distance between two contacting nodes. This prescription provides a fairly rapid but smooth buildup of contact force and a sufficient magnitude of force to stop the TVFs with a finite gap between them. This gap of about two grid points (0.01 cm or 0.67% of TVF length) is necessary to ensure the minimal resolution for the flow in the gap. While this gap is only about 1/10 of the maximum glottal gap, it nevertheless allows some “leakage” flow even during what would be considered as glottal closure. In the symmetric model in the previous study, a two-grid-point minimum gap was also enforced and it was found that the flow velocity at the glottal exit during glottal closure was able to drop to around 0 m/s. That implies a very small leakage flow rate at the resting gap. Nevertheless, while the data on TVF contact that could be used to develop a more physics-based contact model is lacking, the current model is designed primarily with the objective of being flexible in representing a wide variety of contact conditions, and to enable a robust simulation of phonation. The details about the contact model are also mentioned in the previous study³⁵.

Zero and 1.0 kPa gauge pressure are applied at the exit and inlet, respectively, which yields a typical 1.0 kPa pressure drop across the vocal tract. No-slip and non-penetration boundary conditions are applied on all the walls. A zero displacement boundary condition is imposed on the lateral surfaces of the TVF and a traction boundary condition is applied on the medial surface. The anterior and posterior ends of the TVFs are fixed on the vocal tract wall to mimic the attachment to the arytenoid and thyroid cartilages. The two ends are fixed with an initial glottal width of 0.02 cm. In the previous study, a similar setup was used for the symmetric model, and this gap produced a leakage flow rate of about 10% of the peak flow rate.

The flow solver employs a high resolution, non-uniform 64 × 256 × 128 Cartesian grid for the computational domain. The highest grid density is provided in the intra-glottal and near-supraglottal region (y = 2.0 cm to y = 5.0 cm) with this region discretized by 64 × 134 × 128 grids with uniform distribution in both x and y directions and a non-uniform distribution in the z direction. The minimum glottal gap width is resolved by at least two points in the z direction. The solid-dynamics solver employs 63117 tetrahedral elements to discretize each TVF. Such arrangement of grid resolution is based on the experience with previous 2D and 3D simulations of similar configurations^35,37,39 and is necessary to resolve the relatively thin internal layers of the TVFs.

A small time-step corresponding to 3.5×10⁻⁶ seconds is employed for all the simulations, and this results in about 1200 time-steps per vibration cycle. The simulations are conducted for about 30 cycles which contains about 20 stationary cycles, and each simulation takes about 1200 hours on 128 processors of an Intel 3.0 GHz Quad-Core IBM iDataplex parallel computer.

3. Results and Discussion

3.1. Glottal Waveform

The simulation of the asymmetric model was conducted for over 30 cycles to ensure that a “limit cycle” was reached. Figure 2 shows the temporal variation of glottal flow of the asymmetric model. The plot clearly indicates a pulsatile waveform which reached a stationary, nearly periodic state in about 10 cycles. Small variation in cyclic frequency and amplitude of the waveform suggests that the 20% tension asymmetry between the two TVFs did not generate significant irregularities in the flow. Several essential voice quality-related statistical quantities computed from the waveform of the glottal flow have been reported and compared with the normal laryngeal model in detail in the previous study³⁵. The fundamental frequency in the asymmetric model was 239 Hz, which is a decrease of 1.6% compared to the fundamental frequency of 243 Hz in the symmetric model. Thus, the current level of tension asymmetry did not have a significant effect on the fundamental frequency. The monopole sound strength was measured by the root-mean-square fluctuation of the time-rate of change of the flow²³. This quantity decreased 11.5% from the symmetric model to the asymmetric model, suggesting that the presence of the tension imbalance would require an additional effort to maintain the same sound intensity and might perhaps even increase the threshold pressure for phonation. Moreover, the leakage flow in the asymmetric model increased from 27.43 ml/s in the symmetric model to 51.62 ml/s in the asymmetric model, implying a much larger glottal resting gap in the asymmetric model, which could be the result of the non-synchronous motion of two TVFs.

Figure 2.

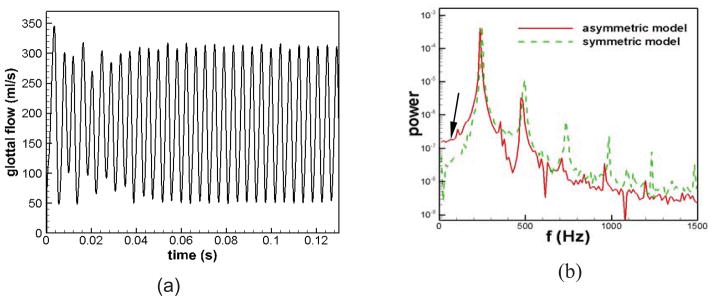
(a) The time history of glottal flow rate in the asymmetric model. (b) The comparison of the frequency spectra of the glottal flow rate during sustained vibration between the asymmetric model and symmetric model.

As described in the previous section, the TVFs were fixed at the two ends with the initial gap of 0.02 cm. The resulting small gap at each end constantly leaks a small amount of flow during the vibration, even when the glottis is fully closed at the center-plane. Interestingly, a significant majority of middle-aged and elderly women have incomplete glottal closure, mainly at the anterior/posterior ends (Södersten et al., 1995; Biever and Bless, 1989). Thus, the current result is not an unreasonable representation of normal phonation in human adults.

To better illustrate the effects of tension imbalance on frequency components, the frequency spectrum of the glottal flow over the sustained vibration stage has been computed and compared with the symmetric model in Figure 2(b). It is clear in Figure 2(b) that both symmetric and asymmetric models are dominated by the fundamental frequency and its harmonics. The energy associated with the fundamental frequency is nearly equal for the two models. However, starting from the third harmonics, there is a roughly one-order of magnitude decrease in the energy of the harmonics from the asymmetric model to the symmetric model. The signal-to-noise ratio (SNR) has been calculated for these two cases, and it decreases from 29.6 in the symmetric model to 27.4 in the asymmetric model. It should be pointed out that the spectrum in Figure 2(b) is only shown till 1500 Hz and the higher frequency noise is not displayed in the figure.

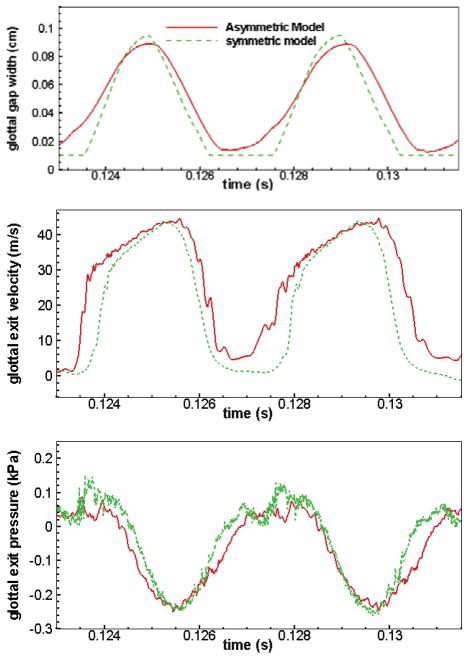
Figure 3 presents the waveform of the glottal gap width, glottal exit velocity, and glottal exit pressure at the mid-coronal plane for both asymmetric and symmetric models. The glottal exit velocity and exit pressure were measured at the point right above the glottis during phonatory vibrations. In general, the symmetric and asymmetric models present similar waveforms of the three quantities. The jet velocity rises quickly during the early opening stage, and then rises more slowly and approaches its maximum value during the late opening stage. The flow then decelerates much more quickly than it accelerated. Both symmetric and asymmetric models have almost the same maximum jet velocity which is around 43 m/s. Both models present a significant phase lag between the maximum values of glottal exit velocity and glottal gap width. This is mainly caused by the air-inertia which delays the buildup of the jet column with respect to the movement of the TVFs⁴⁶, and was also observed in experimental measurements in both excised canine larynges⁴¹ and mechanical scaled-up TVF models⁴². The glottal exit pressure in Figure 3(c) increases or stays near zero as the jet velocity initially increases, until the inflection point where the velocity increases less fast. After that, the glottal exit pressure decreases as the jet velocity continues to increase. When the jet velocity starts to decrease, the glottal exit pressure starts to increase. The glottal exit pressure is below zero during most of the cycle. The maximum and minimum pressures are almost the same for the two models. However, there is also a noticeable difference between the two models when the glottal gap is smallest. While the velocity in the symmetric model is minimum, the velocity in the asymmetric model is always high. This is an indication of a significant increase in the leakage flow rate, caused by a relatively larger glottal gap in the asymmetric model as seen in Figure 3(a). This incomplete glottal closure is caused by the non-synchronous motion of the two TVFs. The incomplete glottal closure in the asymmetric model also results in an earlier opening of the glottis as seen in Figure 3(a).

Figure 3.

Time variation of three important quantities over two successive cycles including: (a) glottal gap width, (b) glottal exit velocity, (c) glottal exit gauge pressure.

3.2. Vocal Fold Deformation

To examine the effects of tension imbalance on TVF vibrations, the displacement histories of two corresponding points on the two TVFs are plotted in Figure 4. These displacements are recorded in both lateral and vertical directions at the superior tip of the mid-coronal plane of the TVF, as shown in Figure 1. The sign of the lateral displacement of the soft (left) TVF is reversed for the sake of comparison with the other fold. Thus, for both TVFs, positive lateral displacement indicates movement away from the centerline whereas a negative value indicates movement towards the centerline.

Figure 4.

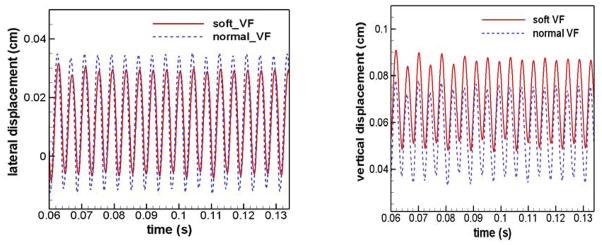
Time history of lateral and vertical displacements of a pair of points on medial surface of two VFs

These plots clearly show that the two TVFs are vibrating at the same fundamental frequency. In the lateral direction, the normal (right) TVF precedes the soft side in phase by 32° and has greater vibration amplitude by 23%, which is found to result in a 0.013 cm shift of the collision plane to the soft side. This is a typical Type I vibration pattern usually associated with relatively small tension imbalance^{7,8,15,23,43,44}. It has been pointed out that for a large tension imbalance, the soft TVF will have much larger vibration amplitudes than the normal fold and the collision plane will shift to the tense side ^8,15. Recently, these two types of distinct vibratory pattern and their dependence on the left-right tension imbalance have been studied by Zhang and Luu⁸ using a combined experimental and computational approach. Our results are in general agreement with their observation that with small left-right tension imbalance, the stiff TVF vibrates at larger amplitudes and constantly leads the soft fold in phase. In the vertical direction, the normal fold still precedes the soft fold in phase and the two TVFs have almost the same vibration amplitude. However, the reduced tension clearly causes a higher equilibrium position on the soft fold and this asymmetric equilibrium position is likely to aggravate the desynchronization of the two TVFs.

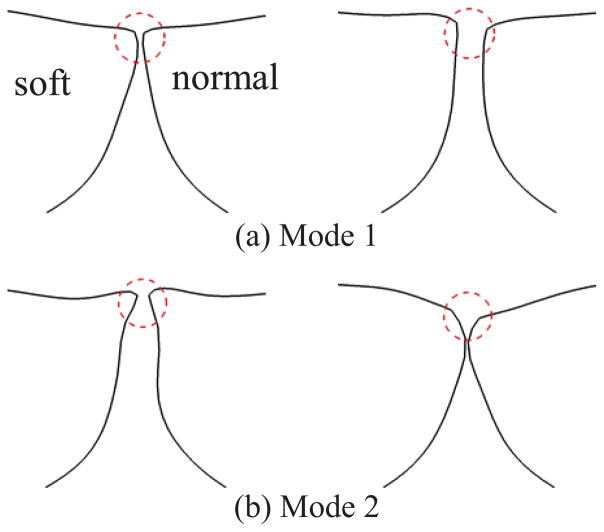
Empirical eigen function analysis was performed to extract the most energetic vibration modes of each TVF. Figure 5 shows the first two principal modes of the two TVFs. It is found that the modal shapes of the two TVFs are nearly identical to each other. The first mode captures the purely lateral motion of the TVFs, which is responsible for generating the monopole source of the sound. The second mode represents the alternating convergent-divergent shape of the glottis and also a clear vertical motion of the superior surface of the TVFs. It should be noted that the shape of these two modes is very similar to those extracted from the symmetric model³⁸.

Figure 5.

Two extreme phases of the most energetic two empirical eigenmodes of VF vibrations at the mid-coronal plane. Circles indicate the position of the glottis.

Although the modal shape does not change with the presence of tension imbalance, the associated energy with each mode in the current asymmetric model is found to be different from the symmetric model. Table 2 lists the energy and its percentage of total energy associated with each empirical eigenmode for each TVF in both symmetric and asymmetric models. In general, the symmetric model presents higher absolute value of energy than the asymmetric model and the normal TVF in the asymmetric model presents higher energy than the soft fold.

Table 2.

Energy percentage of the total energy associated with each empirical eigenmode of each VF in the asymmetric and symmetric models.

	Mode1	Mode2	Total
Soft VF in asymmetric model	4.24 (51%)	3.77 (46%)	8.04 (97%)
Normal VF in asymmetric model	5.61 (57%)	4.03 (41%)	9.64 (98%)
VF in symmetric model	6.03 (52%)	5.24 (46%)	11.27 (98%)

To further illustrate the difference in energy distributions in these cases, the ratio of energy percentage between Mode-1 and Mode-2 are computed. For the symmetric model, this ratio is 1.13 while for the asymmetric model, these ratios are 1.39 and 1.11 for normal and soft folds respectively. It indicates that the normal fold has a stronger lateral motion than the soft TVF in the asymmetric case and the soft fold has a motion pattern that is similar to the fold in the symmetric case. This also might be an early indication of desynchronization of eigenmodes of the two TVFs in the asymmetric model which was also observed with large left-right tension imbalance in other studies⁸. Thus it suggests that the presence of tension imbalance would disrupt the mode entrainment and could lead to biphonation or aphonation.

It should be pointed out that the motion of the VF in this simulation is about one order of magnitude smaller than the real condition. This could be due to several factors. Firstly, the in-plane material property is taken from the past study²⁵ and the material property might be stiff for the current configuration. Secondly, the current model employs a small deformation linear finite element formulation which neglects the effects of geometric and material nonlinearities. This assumption could artificially stiffen the VF. Lastly, the in-plane motion assumption is implemented by using a high longitudinal Young’s modulus, which also increases the stiffness of the VF. The effect of high stiffness is also reflected by the relatively high fundamental frequency in the simulation.

3.3. Aerodynamic Energy Transfer

The current three-dimensional computational model provides the full information of pressure and velocity fields along the TVF surface, and it allows the examination of the aero-elastic energy transfer during TVF oscillation. The effect of tension imbalance on aerodynamic energy transfer on each TVF in the asymmetric model is reported in this section.

In general, the aerodynamic force exerted by the flow on the TVFs can be decomposed into two components: a normal force (flow pressure force) and a tangential viscous force. The work associated with the viscous forces is usually two orders of magnitude smaller than the one associated with the pressure force⁴⁵, and thus is neglected here. The power is computed by multiplying the surface pressure with the normal component of the velocity, and integrating over the entire TVF surface.

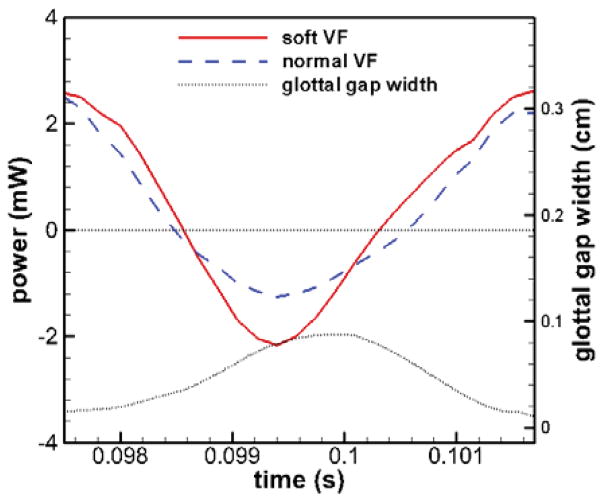
Figure 6 shows the power on each TVF in the asymmetric model over one stationary vibration cycle. The power plot is oscillating between positive and negative values, which correspond to the energy imparted to the solid domain and the energy recovered to the flow domain, respectively. As seen in Figure 6, the negative peak value of power on the soft TVF is greater than the one on the normal TVF and the area under the negative power over one cycle is also larger on the soft TVF; the positive peak value of power and the areas under the positive power over one cycle are almost the same on the two TVFs. In terms of total energy budget, the soft fold gets less energy from the glottal flow and therefore also dissipates less energy. This is associated with the fact that the soft TVF experiences a smaller damping force due to smaller vibration amplitudes. It is interesting to notice that the power curve is generally in phase between the two TVFs, meaning that the energy transfer of the two TVFs are well synchronized even in the presence of the tension imbalance.

Figure 6.

Time history of total power done on two VFs in the asymmetric model by the flow pressure over one stationary cycle. The time history of glottal gap width is also superimposed.

In order to investigate the relationship between energy transfer and glottal vibration, the time history of the glottal gap width is also superimposed in Figure 6. At the phase when the two TVFs are at the location of the minimum gap, the pressure of the transglottal flow pushes them apart and the energy flow rate is at its positive peak. As the glottis further opens, the energy flow rate quickly drops and becomes negative during the second half of the opening phase, indicating that the flow pressure is switching from assisting TVF opening to preventing it. Almost at the same time with the maximum glottal gap, the energy flow rate reaches its negative peak and after that it rapidly rises and becomes positive again. This process indicates that the flow pressure is initially against the closing of the TVFs and later switches to assisting glottis closing. Thus, over the entire cycle, the energy is transferred from the flow to the TVFs during the early opening and late closing phases of the glottis, and transferred back to the flow from the TVFs in the middle of the cycle. Overall, the amount of net energy over one cycle should be positive in order to overcome the damping of the TVF tissues. Along this direction, the net work done on each TVF over one full cycle is calculated and shown in Table 3. The total work is computed by integrating the corresponding power over a certain period of time and has been averaged over all the stationary cycles. The numbers clearly reflect that positive net energy is transferred to the each TVF over a full vibration cycle and the total work done on the soft TVF is smaller than the normal TVF.

Table 3.

Net amount of work and its vertical and lateral components done on each VF over one full cycle (×10−6 J).

	Vertical (Y)	Lateral (Z)	Total
Soft VF	0.06	3.45	3.51
Normal VF	−0.72	4.32	3.60

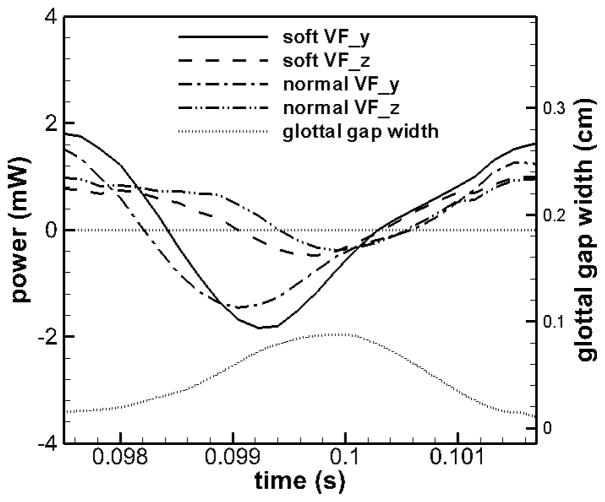
The power can be further decomposed into three individual contributions from longitudinal (X), vertical (Y) and lateral (Z) directions. Each component of the power can be computed as the product of the pressure and surface velocity components along its direction, and each component of total work is the integration of the corresponding power over a certain time period. In the current study, TVFs vibration in the longitudinal (X) direction is four-orders of magnitude smaller than the other two directions and the energy transfer in this direction is therefore neglected. Figure 7 shows the time history of vertical (Y) and lateral (Z) components of power of the two TVFs during one cycle. The history of the glottal gap width is also included in order to provide context.

Figure 7.

Time history of vertical (Y) and lateral (Z) components of power done on two VFs in the asymmetric model over one stationary cycle.

It is noted that the power in the vertical direction varies with much larger amplitudes than the one in the lateral direction. The vertical component changes from −2 mW to 2 mW whereas the lateral component only varies from 0.4 mW to 1 mW. This observation seems to contradict our expectation that more energy should be transferred in the lateral direction wherein the most energetic motion occurs. To further assess this quantity, the corresponding components of the net work done on each TVF over one full cycle is also calculated and shown in Table 3. The quantity has been averaged over all the stationary cycles. Clearly, the vertical component of the total work is at least one order of magnitude smaller than the lateral component on each TVF. Therefore, the majority of the energy is consumed by the lateral motion of TVFs. It is also of interest to notice that the net energy in the vertical direction of the normal TVF is negative over one full cycle, which means that in the vertical direction, energy in the net is transferred from the TVF to the flow. This also implies that the elastic recoil is further helping to push the fluid out of the glottis in the inferior and superior direction. The additional energy should come from the energy exchange between two directions inside the TVF through the elasticity.

4. Conclusion

The focus of the current study is to utilize the developed model to advance the understanding of three-dimensional dynamics of TVF vibrations and glottal flow in a unilateral paralyzed larynx due to cricothyroid muscle paralysis. The simulation reflects a larger glottal leakage in the tension imbalance model, which could be responsible for a “breathy” voice. It is found that with a slight tension imbalance, such as the 20% imbalance employed in the current study, the vibrations of two TVFs are synchronized on the same fundamental frequency; however, the normal TVF precedes the soft fold in phase in both lateral and vertical directions by 32° and it has larger vibratory amplitude in the lateral direction by 23%. The empirical eigen function analysis indicates that at least for the level of imbalance studied here, the complex motion of each TVF can be mainly represented by two principal modes and the modal shape of these modes is nearly identical between the two folds. However, the energy distributions among modes are different between the two folds. The normal TVF has a higher energy ratio between Mode 1 and Mode 2 than the diseased TVF by 25%. This could be an early indication of mode desynchronzation between two folds. The detailed analysis of the energy transfer between the glottal flow and TVF vibrations suggests that the energy flows into the TVFs in the early opening and late closing phases and flows out of the TVFs in the middle of the cycles and the majority of the energy is consumed by the lateral motion of TVFs. The comparison of soft and normal TVFs in the asymmetric model indicates that the net energy transferred to the soft TVF is slightly less than the one transferred to the normal TVF.