Assessment of Traffic-Related Noise in Three Cities in the United States

Abstract

Background

Traffic-related noise is a growing public health concern in developing and developed countries due to increasing vehicle traffic. Epidemiological studies have reported associations between noise exposure and high blood pressure, increased risk of hypertension and heart disease, and stress induced by sleep disturbance and annoyance. These findings motivate the need for regular noise assessments within urban areas. This paper assesses the relationships between traffic and noise in three US cities.

Methods

Noise measurements were conducted in downtown areas in three cities in the United States: Atlanta, Los Angeles, and New York City. For each city, we measured ambient noise levels, and assessed their correlation with simultaneously measured vehicle counts, and with traffic data provided by local Metropolitan Planning Organizations (MPO). Additionally, measured noise levels were compared to noise levels predicted by the Federal Highway Administration’s Traffic Noise Model using (1) simultaneously measured traffic counts or (2) MPO traffic data sources as model input.

Results

We found substantial variations in traffic and noise within and between cities. Total number of vehicle counts explained a substantial amount of variation in measured ambient noise in Atlanta (78%), Los Angeles (58%), and New York City (62%). Modeled noise levels were moderately correlated with measured noise levels when observed traffic counts were used as model input. Weaker correlations were found when MPO traffic data was used as model input.

Conclusions

Ambient noise levels measured in all three cities were correlated with traffic data, highlighting the importance of traffic planning in mitigating noise-related health effects. Model performance was sensitive to the traffic data used as input. Future noise studies that use modeled noise estimates should evaluate traffic data quality and should ideally include other factors, such as local roadway, building, and meteorological characteristics.

1. Introduction

Exposure to road traffic noise is a major public health concern in urban environments. According to the World Health Organization (WHO) community noise guidelines (2009), continuous outdoor noise in residential areas should not exceed 55 dB(A) (16 hours average, day and evening). This threshold, however, is often exceeded in urban residential areas. A recent study conducted in Fulton County, Georgia (Seong, Park et al. 2011) found that 48% of the population is exposed to day time noise levels exceeding 55 dB(A) and 32% of the population is exposed to night time noise levels exceeding 50 dB(A). According to WHO community noise guidelines, approximately 20% of European Union populations are exposed to daytime levels exceeding 65 dB(A) and 30% are exposed to night time levels greater than 55 dB(A). Ambient noise due to increasing vehicle traffic in developing countries also contributes to the environmental degradation of urban areas. Noise assessments conducted in Curitiba, Brazil, identified traffic as the major source of community noise; the average community noise level near roadways was 73.1 dB(A).

Evidence from epidemiological studies supports the association between noise exposure and high blood pressure, increased heart rate, hypertension, ischemic heart disease, stress, sleep disturbance and annoyance, anxiety, and depression (Babisch 2000; Ouis 2002; Ising and Kruppa 2004). Additionally, an experimental study conducted by Ising et al. (1980) found decreased working quality, increased heart/pulse frequency, blood pressure and epinephrine release in subjects exposed to traffic noise compared to unexposed subjects. Moreover, many studies have found dose-response relationships. For example, a linear dose-response relationship between road traffic noise and hypertension was found in people who lived within 100 meters of a highway or major arterial (Bluhm, Berglind et al. 2007). A hospital based case-control study conducted in Berlin found a higher risk of myocardial infarction among subjects who lived on streets with day time average noise levels greater than 70 dB(A) compared to less than 60 dB(A) (Babisch, Beule et al. 2005). Children may be especially vulnerable to the effects of noise. Children exposed to high levels of ambient noise have shown stress symptoms, reductions in learning ability, language development, memory, motivation and concentration (Evans, Lercher et al. 2001).

As the number of vehicles and vehicle miles traveled has increased in urban settings, concern for the adverse health effects associated with transportation-related noise has motivated policy efforts to address noise. In the United States, the Federal Highway Administration (FHWA) established regulation 23 CFR772 in 1973 that requires assessment and abatement of noise in areas affected by highway traffic and construction. The policy encourages state and local governments to prepare their own policies and procedures using a three-part approach to reducing highway traffic noise (i.e., control at the source, effective land use planning, and highway project noise mitigation). For example at the state level, the California Department of Transportation developed a Traffic Noise Analysis Protocol, which requires noise assessment for all highway projects. At the city and county level, San Francisco included a Noise Element in their General Plan to determine and predict the impact of transportation-related noise in urban communities.

Despite documented associations with health effects, and the existence of policies at multiple governmental levels, community noise is rarely systematically and routinely monitored in U.S. cities. Moreover, only a few recent studies in the United States have investigated the health effects of chronic exposure to traffic noise. Seto et al. (2007) developed a GIS-based model to estimate the spatial distribution of surface transportation noise exposure and its relation to annoyance for different neighborhoods in San Francisco. In Georgia, county-wide community noise exposures were estimated by using a 3-dimensional model, Soundplan, which incorporates road traffic data, building geometry, and terrain elevation (Seong, Park et al. 2011).

The primary goal of this paper was to (1) identify the association between automobile and noise in urban areas in the United States, and (2) assess sensitivity of models for predicting noise with traffic data from different sources. This paper represents the first step toward estimating noise exposures for a national cohort of 54,000 African American women in the United States. These assessments were carried out as part of an ongoing longitudinal epidemiological study of the association between noise and air pollution exposure and incident hypertension or diabetes in the Black Women’s Health Study. Our next step will be to estimate noise exposures using Traffic Noise Model (TNM) and to assess the influence of noise on the health outcomes.

2. Materials and Methods

2.1 Noise and Traffic Field Measurements

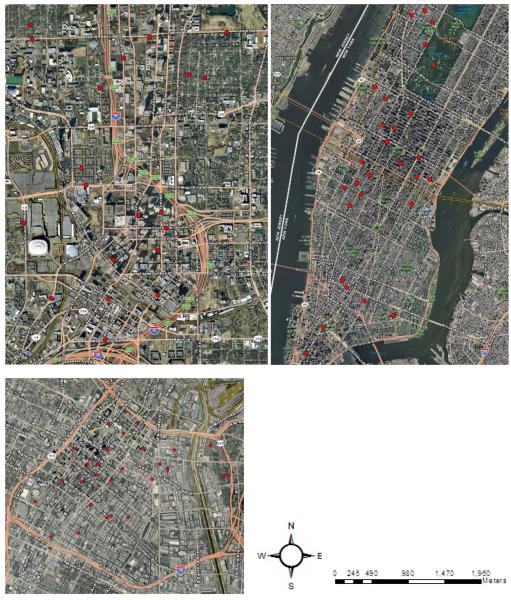
To assess noise levels, we measured 10-minute equivalent continuous sound pressure levels (Leq) in downtown and midtown Atlanta (20 sites), downtown Los Angeles (26 sites) and New York City, Manhattan (26 sites) from November 2011 to January 2012 (72 sites in total) (Figure 1). Measurement locations were selected based on primary land use (residential, commercial, or industrial) and proximity to different classes of roadway representing a diverse set of land use and traffic locations. Noise measurements were collected between the weekday hours of 9AM to 5PM to capture daytime noise when traffic levels are highest as well as when most noise exposures occur. Noise was measured using the 3M SD-200, set for slow-response and A-weighting for a range of 40-100 dB with the field technician standing in the middle of the pedestrian walkway and holding the noise meter with the microphone tilted towards the roadway. Each site was geocoded with a GPS measurement obtained using the Garmin GPSMAP 62s. Unexpected activities and incidents such as building or road construction, noise from parking garages, truck loading, and background noise such as intermittent pink noise, loud music from stores, ambulance and fire trucks passing nearby were noted. In the case of ambulance and fire trucks, we paused and re-started the measurement after they drove away. At each site, simultaneously with the noise measurement, we conducted a 10-minute traffic count. We counted the number of passenger vehicles, medium trucks, and heavy trucks passing along the roadway, as well as the field technician’s estimate of the average speed of the traffic.

Figure 1.

Community noise levels were measured in downtown Atlanta (top left), Manhattan New York (top right), and downtown Los Angeles (bottom left). Red dots represent where noise measurements were conducted.

2.2 Traffic Data from Metropolitan Planning Organizations (MPOs)

In addition to our own field-measured traffic counts, we obtained Annual Average Daily Traffic (AADT) traffic data from the Metropolitan Planning Organizations (MPO) for each of the cities. MPOs are mandated by the FHWA and state agencies to facilitate traffic planning and roadway funding initiatives and are charged with developing transportation plans for their regions. As part of the transportation planning process, MPOs develop travel demand forecast models that include AADT estimates on major roads in the region. From each of the three relevant MPOs we obtained the link files and traffic estimates and used them to assign AADT values to the noise measurement locations. In addition, continuous, hourly traffic counts were collected from the state departments of transportation. These continuous counts were used to compute an average diurnal pattern within the urban areas and this data was used to adjust the MPO AADT values to hour-of-day specific traffic counts for each of our noise monitoring sites.

$$T_{\mathit{ij}}={\mathit{MPO}}_{24{\mathit{hr}}_i}\times \frac{T_j}{T_{24\mathit{hr}}}$$ (1)

Where, T_ij is traffic count on roadway i for specific hour j, MPO_24hri is the 24-hour total traffic count for roadway i, T_j is traffic count of hour j, and T_24hr is daily total traffic.

MPO data supplied by each city was based on different travel demand models. For example, the New York City model was based on the best practices model (BPM) using the BPM covers 28 counties and 3500 transportation analysis zones in NY, NJ and CT and includes roads from minor arterials and above. We used BPM base 2005. The travel demand forecast for the Los Angeles model used by the Los Angeles Department of Transportation and the City Planning Department generates citywide PM peak hour traffic volumes. The model was constructed on the widely-used EMME/2 (see Gan et al., 2012 for detailed description of EMME/2). Estimates were based on the Southern California Association of Governments (1990) regional transportation model (see Los Angeles City Planning, 2013 for details on input data and model structure). The MPO data for Atlanta were generated using the Atlanta Regional Commission (ARC) travel demand model. The model conforms with the U.S. Environmental Protection Agency (EPA) Transportation Conformity Rule and with models based on travel surveys in 2001 and 2002. Consequently, although based on similar modeling approaches, each MPO estimate was derived based on different modeling programs and input data.

2.3 Traffic Noise Model

At each of our 72 measurement sites, we compared our noise measurements with noise levels predicted by the FHWA Traffic Noise Model (TNM), which was developed in 1998 to comply with 23 CFR 772. TNM-based traffic noise analyses are typically conducted for federally-funded highway projects. The model has also been used for city noise assessments (Seto, Holt et al. 2007).

The TNM model with vehicle speed, distance of receptor point from center of the road, ground classification (soft vs. hard ground), and counts of different vehicle types (i.e., passenger cars (V_Auto), medium trucks (V_MT), and heavy trucks (V_HT)) to estimate the hourly equivalent noise level (L_Aeq1h):

$$\begin{array}{cc}\hfill & L_{\mathit{Aeq}1h}=10\times {\mathit{Log}}_{10}\{\left[\frac{V_{\mathit{Auto}}}{1000}\times {10}^{L_{\mathit{Aeq}1h\left(\mathit{Auto}\right)∕10}}\right]\phantom{\}}+\left[\frac{V_{\mathit{MT}}}{1000}\times {10}^{L_{\mathit{Aeq}1h\left(\mathit{MT}\right)∕10}}\right]+[\frac{V_{\mathit{HT}}}{1000}\times \phantom{]}\hfill \\ \hfill & \phantom{[}{10}^{L_{\mathit{Aeq}1h\left(\mathit{HT}\right)∕10}}]\hfill \end{array}$$ (2)

We developed two TNM predictions at each of the 72 sites: (1) using the observed vehicles counted in the field during our noise survey (Leq_{TNM_Obs}) and (2) using vehicle counts from the local MPO (Leq_{TNM_MPO}).

2.4 Data Analysis

2.4.1 Summary Statistics and Linear Regression Models

For each city, we computed means and standard deviations of 10-minute noise measurements, vehicle counts observed at field locations, and noise levels estimated by TNM models. Linear regression models were used to assess (1) the association between (log) traffic counts and the measured noise levels, (2) the association between TNM-predicted noise and the measured noise levels, and (3) the relationship between field-observed traffic counts and MPO traffic counts. Residuals of the linear model comparing TNM-predicted noise with measured noise were plotted in ESRI ArcMap 10.0 to display spatial distribution of over- and under-predicted levels. All statistical analyses were performed in R 2.15.0.

2.4.2 Analysis of Covariance (ANCOVA): testing slopes and intercepts

The analysis of covariance (ANCOVA) with single factor and single covariate was applied to compare the linear relationships derived from the multiple regressions with 10-minute measured noise in Atlanta, Los Angeles and New York. To test the null hypothesis of homogeneous slopes of the regression lines, an interaction term of the categorical predictor (city effect) with the continuous independent variable (log traffic volume) was created to examine how number of vehicles is related to noise level in different cities. A full model with interaction (3) and a reduced model with no interaction (4) were compared to determine whether the regression coefficients were the same for all three cities.

H₀: the effects of traffic volume on noise level does not depend on city (β₁=β₂=β₃)

H_a: the effects of traffic volume on noise level depend on city (at least one of the slopes is different)

3. Results

The measured 10-minute equivalent continuous sound pressure level (Leq) and traffic volumes observed during noise assessments are presented in Table 1. The mean noise levels measured in New York City, Los Angeles, and Atlanta were 69.2, 66.4, and 65.1dBA, respectively.

Table 1.

10 minute average traffic counts and Leq (dBA) measured in major cities in U.S.

City	N	Leq10min	Traffic Counts10min
			Car	Medium Truck	Heavy Truck
Atlanta	20	65.1±7.4	114.6±95	2.1±3	3.0±4.7
Los Angeles	26	66.4±4.6	120.6±84.2	2.8±3.0	4.2±4.3
New York	26	69.2±4.1	167±98.5	5.3±4.5	4.9±4.6

Table 2 compares the average noise levels computed in the three cities: the average 10-minute noise levels measured in the field (Leq_10min, from Table 1), modeled noise levels computed via TNM using traffic counts from field data (Leq_{TNM_Obs}), and modeled noise levels from TNM using MPO traffic (Leq_{TNM_MPO}). Overall, the mean values of TNM-predicted noise levels (both Leq_{TNM_Obs} and Leq_{TNM_MPO}) underestimated the noise levels when compared to field measurements in all three cities, but were consistently ordered in rank (i.e., regardless of whether field-measured or TNM-predicted, Atlanta was ranked the lowest, Los Angeles was ranked second, and New York City was ranked the highest in average noise).

Table2.

New noise levels were computed at sample locations by applying TNM equation and values obtained from TNM-lookup table (Leq_10min = average sound pressure level during 10 minute field measurement, Leq_{TNM_OBS} = observed traffic counts incorporated into TNM model, Leq_{TNM_MPO} = MPO modeled traffic counts incorporated into TNM model.

City	Leq10min	LeqTNM Obs	LeqTNM MPO
Atlanta	65.1±7.4	60.0±8.8	57.1±7.0
Los Angeles	66.4± 4.6	62.3±7.6	60.8±4.0
New York	69.2±4.1	62.7±5.0	67.3±5.7

Results of statistical testing of the difference between slopes of regression lines for the three cities are presented in Table 3. The first ANCOVA Model is a full model with an interaction term. The results demonstrate that traffic is associated with Leq10min, whereas city is not a significant factor in determining noise level. The interaction term between traffic and city was not significant (P=0.114). The slope of the regression lines between traffic and 10-minute Leq was similar for all three cities (Table 4 and Figure 2).

Table 3.

Testing interaction: Analysis of Covariance (ANCOVA) with single factor and single covariate.

MODEL 1 (Dependent Variable: Leq10min)
Predictor	DF	Sum Sq	Mean Sq	F-value	Pr(>F)1
TotalTraffic_log	1	1324.6	1342.6	155.103	<2e-16
City	2	15.5	7.7	0.893	0.414
TotalTraffic_log:City	2	38.9	19.4	2.244	0.114
Residuals	66	571.3	8.7
MODEL 2 (Dependent Variable: Leq10min)
Predictor	DF	Sum Sq	Mean Sq	F-value	Pr(>F)1
TotalTraffic_log	1	1324.6	1342.6	149.6	<2e-16
City	2	15.5	7.7	0.861	0.427
Residuals	68	571.3	8.7
MODEL 3 ANCOVA (MODEL1, MODEL2)
Res.DF	RSS Df	Df	Sum of Sq	F	Pr(>F)1
66	571.32
68	610.2	−2	−38.85	2.244	0.11

Table 4.

Regression Models between traffic (independent variable) and 10-minute Leq (dependent variable) of Atlanta, Los Angeles, and Manhattan.

Atlanta (Leq10min= a+b*TotalTraffic_log)
	Estimate	Std.Error	t-value	Pr(>∣t∣)
intercept	47.00	2.56	18.32	1.25e-12
TotalTraffic_log	10.13	1.31	7.68	6.29e-07
LA(Leq10min=a+b* TotalTraffic_log)
	Estimate	Std.Error	t-value	Pr(>∣t∣)
intercept	53.43	2.32	22.94	< 2e-16
TotalTraffic_log	6.77	1.17	5.77	5.96e-06
NYC (Leq10min= a+b*TotalTraffic_log)
	Estimate	Std.Error	t-value	Pr(>∣t∣)
intercept	49.3	3.0	16.0	1.20e-14
TotalTraffic_log	9.3	1.4	6.5	7.23e-07

Figure 2.

Linear relationship of log_Total traffic and 10- minute Leq. Total traffic is positively related with 10-minute Leq for all three cities.

The second ANCOVA Model was fitted without an interaction term to test significant differences in the slope. Total traffic was still a significantly associated with Leq10min, while the effect of city was not. Model 1 and Model 2 were compared (Table 3) to examine if removing the interaction term significantly affects model fit. Based on the model outcome, there was no significant difference between Models 1 and 2 (P=0.11). Therefore, Model 2 without an interaction term was the most parsimonious model. Findings from model outcomes above were consistent with the regression lines shown in Figure 2 indicating that the total traffic is positively related with 10-minute average Leq for all three cities. The slopes of regression lines for three cities were not significantly different indicating there is no city effect (interaction).

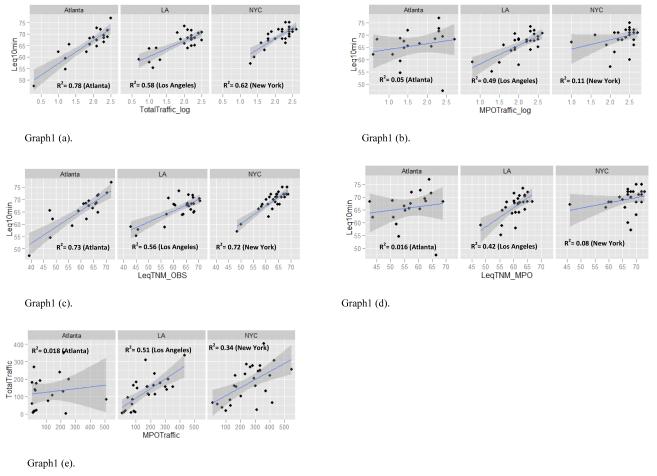
The linear relationship between (log) traffic and measured noise for each city are displayed in Figure 4a-b. Total number of vehicles observed in the field explained a substantial amount of variation in measured noise levels in Atlanta ((R²=0.78), Los Angeles (R²=0.58) and New York City (R²=0.62). MPO traffic counts explained a relatively smaller amount of noise variation in Atlanta (R²=0.06) and New York (R²=0.11), and a moderate amount of noise variation in Los Angeles (R²=0.49).

Figure 4.

Regression Models: (a)10-min Leq vs log _total traffic; (b)10-min Leq vs log _MPO; (c) 10-min Leq vs LeqTNM_OBS; (d) 10-min Leq vs LeqTNM_MPO; (e). Regression model of Total traffic vs MPO

We also evaluated the relationship between 10-minute average noise measurements and TNM-predicted values (Leq_{TNM_Obs} and Leq_{TNM_MPO}) within each city. The TNM-predicted noise levels based on field-observed traffic data (Leq_{TNM_Obs}) explained a large amount of noise variation in all three cities; 73% in Atlanta, 56% in Los Angeles, and 72% in New York (Figure 4c). The amount of variation explained by the MPO TNM model (Leq_{TNM_MPO}) was substantially less: 1.6%, 42% and 8% in Atlanta, Los Angeles, and New York City, respectively (Figure 4d). The higher correlation for Los Angeles may be explained by the better correlation between MPO traffic and observed vehicle counts during our 10-minute survey in that city (Figure 4e).

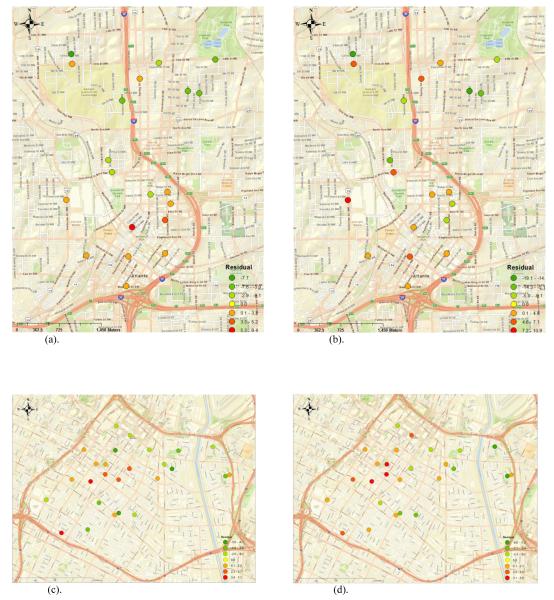
We explored the spatial variation of the residuals for the relationship between TNM-predicted noise levels and measured noise by plotting them over land use maps. In Atlanta, noise levels were generally over-predicted in the downtown area near major roadways and highways. In the midtown area, where land use is more residential, noise levels tended to be under-predicted. No systematic spatial patterns in the residuals were identified for Los Angeles. Overall, noise predictions were higher than the measured noise samples regardless of roadway type or proximity to major highways. Similarly, for New York City, when MPO traffic data was used as input, the TNM tended to over-predict noise levels.

4. Discussion

Our measurements in three cities in the United States revealed considerable variations in noise within and between urban environments. Our results show that noise levels are surprisingly high in all three cities, at or above thresholds associated with adverse health impacts found in other studies (WHO, 2009). This finding suggests the need for more systematic monitoring of noise exposures and potential health impacts in North American cities.

Our sampling of sites was limited, so more complete sampling of streets and citywide noise modeling is necessary to more thoroughly assess differences in population exposures to noise in these three cities. As expected, we found that urban noise is highly correlated with simultaneously measured traffic. Moreover, from our regression models, we found no evidence of differences in the relationship between traffic and noise between cities. This suggests that predictions from noise models that are based on measured traffic data, such as the FHWS’s TNM model, should correlate well with measured noise levels. Indeed, we found this to be true for TNM-predicted noise in all three cities using the field-measured traffic counts. In contrast, measured traffic did not correlate well with the MPO traffic data and we found weaker correlations with TNM-predicted noise levels based on MPO data.

We found that the TNM model tended to under-estimate the average noise levels compared to measured noise levels in each of the three cities, although the maps of residuals suggest that noise may be under or over-predicted depending on land use. However, the measured and modeled rank orderings of mean noise levels were consistent, with Atlanta having the lowest and New York City the highest average noise levels. Because the rankings of TNM-modeled noise levels were consistent with the measured noise levels, TNM models might be appropriate for use in studies whose goal is to estimate the association between noise levels and health outcomes. However, the tendency of TNM models to underestimate noise exposures may lead to underestimates of the size of populations at risk of health impacts from noise.

The reason for TNM’s tendency to underestimate measured noise may be related to a variety of factors. In our study, we only modeled the street being measured. Because sound decay from a linear source is approximately 3 dB per doubling of distance (Harris, 1979), nearby roadways and other sound sources will contribute to noise measured in the field. In most cases, our noise measurements were conducted within 10 m of the primary roadway being measured. Yet, traffic on cross streets and nearby freeways may have contributed to ambient noise measured at our sites. In a recent study of noise in Singapore, the noise-reflecting building façade effect was found to be significant contributor to noise levels (Chew and Lim 1994). In our case, buildings in New York City and Atlanta are generally more compact and higher density than in downtown Los Angles, which resulted in greater TNM underestimates of noise for New York City and Atlanta. In addition, lower correlation between traffic counts and noise levels observed in downtown Los Angeles may have been influenced by streets being wider than the two other cities. With more sophisticated 3-dimensional noise models, such as Soundplan, it is possible to account for reflected sound energy found in urban street canyons. Also, meteorology, which we did not control for in our study, may have an effect on community noise, as it has been documented that under certain atmospheric conditions (e.g., temperature inversions) ambient noise levels may increase (Heimann 2003). Low-speed truck traffic may also contribute to higher measured noise levels in urban environments. The magnitude and spectrum of noise generated from tire-pavement interaction by automobile versus truck are different with varying vehicle speeds. Tire noise becomes a dominant source for trucks once they pass a critical speed of 30 mph, with the sound level increasing approximately 10 to 12 dB(A) per doubling of vehicle speed (Harris 1979).For automobiles, tire/road surface becomes dominant source of noise at both low and high vehicle speeds, whereas the propulsion system (engine, exhaust, cooling system and other auxiliary components in the engine compartment) is the dominant source at low speeds for trucks. On local streets, such as those measured in our study, trucks travel at relatively low speeds, and therefore propulsion noise is an important contributor to ambient noise. Thus propulsion noise may not be fully captured in model, such as TNM that were originally developed for higher-speed freeway planning studies. Also, tire-roadway friction and different pavement types and surface texture can affect noise levels (Wayson, National Cooperative Highway Research Program. et al. 1998).

Our study found that measured sound levels are less correlated with TNM model results based on MPO traffic data than with field-measured traffic. However, MPO data are meant to serve as long term traffic averages for transportation planning activities, and may be the better dataset to use for noise modeling, and for estimating exposures experienced over long periods. MPO data do not account for short-term traffic variations that may arise from road closures, detours, accidents, and such – all of which may have affected our field traffic and noise measurements. If the goal is to estimate long-term exposures and resulting health effects, it may be reasonable to use models based on MPO data, with the caveat that it is assumed that MPOs routinely check their traffic sensors, employ quality assurance protocols to filter out bad data, have robust methods for inferring traffic counts for roads without actual sensor data, and that they conduct validation studies to ensure the overall quality of their reported traffic data.

Our noise measurement methodology may not be applicable to research on chronic health effects, because 10-minute measurement may not represent long-term exposure and the noise samples were not collected systematically within the 9-5 period. Subsequently our results may not reflect the differences in traffic volumes during rush, noon, in-between hours and night time. The relatively high correlations in our short-term measurement and TNM results indicate that the model results are capable of predicting noise levels in downtown areas in major American cities. Our measurement also has relevance to acute exposures to noise. For example, a case-crossover study conducted in Beijing found that exposure duration has been linked to changes in heart rate variability (HRV) with an incremental change in noise (dB) at five-minute interval (Huang et a, 2013).

The travel demand models used in each city are based on demographics, household travel surveys, and economic activities, which are used to apportion household trips from origins to destinations. The more sophisticated models use congestion factors on main roads to begin apportioning traffic to smaller streets. There are three main limitations in these models for the purpose of noise modeling in the United States: (1) there is no accepted best practice model used in all locations, which may result in considerable heterogeneity between cities; (2) the models are often calibrated for the purpose of transportation planning and as such are based on simplified road networks that are topologically inaccurate – meaning the roads are not placed in accurate geographic position or the network is missing many of the smaller links (we found many problems of this kind in Los Angeles); and (3) the models are generally calibrated to predict traffic on major roads and highways and as a result may miss many smaller roads that contribute importantly to noise variation over smaller areas in residential neighborhoods. As a result, differences in MPO data may introduce substantial difference in traffic levels and subsequent noise in different cities.

Moreover, for noise studies seeking to assess health impacts, living on the street versus the garden or court yard side of a building makes a significant difference in noise levels. Although our sampling strategy took into consideration different land use types, our noise samples and models do not capture the differences in noise levels due to building design. This limitation is inherent in most noise studies.

Currently there are no standardized approaches to noise monitoring for chronic health studies in the United States. Thus adopting the European Directive that requires 24-hour measurements of noise levels and the use of specific noise indicators for the assessment of noise-related health effects, could lead to more effective surveillance and tracking of noise and associated health outcomes in the United State. Adoption of this or other similar directives would also require specification of acceptable travel demand and noise models.

5. Conclusion

Based on noise surveys conducted in downtown areas in Atlanta, Los Angeles, and New York, we were able to explain substantial variability in ambient noise by instantaneous traffic counts. The correlation between urban traffic and noise highlights the importance of ongoing traffic monitoring and planning activities to mitigate noise-related health effects. Field measurements and model predictions indicate New York City had the greatest number of vehicles and highest noise levels, followed by Los Angeles and Atlanta. We were best able to predict noise levels at sample locations by applying the TNM model and traffic data gathered from our field study. TNM noise estimates based on MPO traffic data, while not well correlated with our short-term noise measurements, may reflect longer-term noise exposures. Because modeled noise predictions are one of the important tools for noise assessment, and are sensitive to traffic data used as input, future noise studies should evaluate traffic data quality and other factors such as local roadway, building, and meteorological characteristics.

Our study showed that association between traffic and ambient noise levels in three major cities in the United States. The results, however, varied depending on the estimates of traffic use to calibrate noise models. It is likely that noise levels are influenced by other factors such as street width, height and surface material of buildings, presence of sound wall, green space, slope of roadway, tire-pavement interaction, and weather conditions. For future research, these factors need to be addressed explicitly to elucidate the unexplained variability between automobile and ambient noise.

Figure 3.

Analysis of model residuals: (a) Residual of oberved and modeled noise levels in Altanta (TNM model vs observed traffic); (b) Residual of observed and modeled noise levels in Atlanta (TNM model vs MPO traffic);(c) Residual of observed and modeled noise levels in LA (TNM model vs observed traffic); (d) Residual of observed and modeled noise levels in LA (TNM model vs observed traffic); (e) Residual of observed and modeled noise levels in Manhattan (TNM model vs observed traffic); (f) Residual of observed and modeled noise levels in Manhattan (TNM model vs MPO traffic)