Incorporating Prior Biologic Information for High Dimensional Rare Variant Association Studies

Abstract

Background

Given the increasing scale of rare variant association studies, we introduce a method for high-dimensional studies that integrates multiple sources of data as well as allows for multiple region-specific risk indices.

Methods

Our method builds upon the previous Bayesian risk index (BRI) by integrating external biological variant-specific covariates to help guide the selection of associated variants and regions. Our extension also incorporates a second-level of uncertainty as to which regions are associated with the outcome of interest.

Results

Using a set of study-based simulations, we show that our approach leads to an increase in power to detect true associations in comparison to several commonly used alternatives. Additionally, the method provides multi-level inference at the pathway, region and variant levels.

Conclusion

To demonstrate the flexibility of the method to incorporate various types of information and the applicability to a high-dimensional data, we apply our method to a single region within a candidate gene study of second primary breast cancer and to multiple regions within a candidate pathway study of colon cancer.

1. Introduction

Rare variant association studies have gained a tremendous amount of popularity and there has been a concurrent surge in the development of methods to detect associations between rare variants and complex disease outcomes. The majority of these methodological developments center around the idea of collapsing variants within a single region to test the collective frequency or weighted frequency of the variants within the cases and controls [1-3]. While these methods are powerful in detecting associated regions, they do not allow inference at the variant level and there can be a substantial loss in power when the effects of the rare variants are mixed (both risk and protective). Moreover, many methods that aggregate all variants in region without a model selection procedure have a substantial loss of power as the number of null variants increases (holding the number of associated variants constant) and the noise overwhelms the signal. More recent work has expanded upon these basic collapsing methods to formally incorporate uncertainty into the variants that enter the risk index and to account for the direction of effect of the variants [4-7]. There has also been an emergence of methods that focus on testing the hypothesis that there is an increase or decrease in the probability of some of the mutations being found in the affected individuals by computing a test statistic that is based on determining if the mixture distribution of probabilities under the alternative hypothesis has variance. This test on the variance of the mixture distribution bypasses the need to make an assumption on the direction of the effect of each variant [8,9]. As a unified approach, the Bayesian Risk Index (BRI) [5] formally incorporates uncertainty of both the inclusion of variants and the direction of effect via Bayesian model uncertainty (BMU) techniques and it allows for intuitive multi-level inference at the region and variant level. This multi-level inference of BRI provides the practitioner with the ability to pinpoint specific variants that are driving a regional association.

To date, most statistical methods developed for rare variant association studies have focused on demonstrating power in small-scale studies involving a single region. As large-scale chip arrays and sequencing technologies become more efficient and cost effective, the scale of studies involving rare variants has begun to drastically increase with a shift from candidate regions or gene studies to pathway and whole exome studies involving millions of variants. Thus, there is a need of more powerful tools to analyze large-scale rare variant studies involving multiple regions across the genome. To accommodate multiple regions, one possible solution is to perform independent tests across each region using the current collapsing methods. However, this approach leads to uncertainty in determining an appropriate significance threshold accounting for the multiple tests within and across regions and the approach does not borrow strength across regions. Within studies involving common variants, it has been shown that modeling a multivariate genetic profile via Bayesian model uncertainty methods leads to an increase in power to detect true associations over marginal tests [10]. Thus, it may be more appropriate to bypass the assumption of conditional independence of the regions and model the outcome as a function of a multi-regional genetic profile in order to borrow strength across regions. With this in mind, our integrative BRI allows for multiple region specific risk indices within each model. As in BRI, we formally incorporate uncertainty into the variants that are included within the region specific risk index as well as the direction of effect for each variant. However, we also introduce a second level of uncertainty as to which region specific risk indices are included in the model. This second level incorporates prior information and builds upon a recent extension of BMU that integrates external biological covariates into the probability that any variant is associated (iBMU). This approach has been shown to lead to an increase in power and a more efficient model search over other commonly used variable selection techniques (unpublished data). For rare variant analysis, we extend the current BRI method by incorporating external variant-specific covariates into the probability that any variant is included within a risk index in order to gain power in detecting rare variation within large-scale studies.

The remainder of the paper is organized as follows: Section 2 gives a brief review of the Bayesian model uncertainty framework and more specifically the Bayesian risk index. We then describe the extension of BRI to incorporate multiple regions and integrate external biological knowledge denoted as iBRI. In Section 2 we also describe a set of single region and a set of multiple region simulations in which we will use to assess the power of iBRI compared to several alternative methods. Section 3 provides the results of the simulation study as well as results of two applications of iBRI to detecting rare variants within a candidate gene study of second primary breast cancer and a candidate pathway study of colon cancer using the Illumina exome chip. Finally, in Section 4 we end with a discussion of our novel method as well as future directions.

2. Methods

2.1 Bayesian Risk Index Overview

Detailed descriptions of the general BMU framework have been described previously [11,12]. For rare variant analysis in genetic association studies, we assume that for a set of n individuals we have: 1) an n dimensional binary outcome vector Y Y that represents an individual’s disease status, 2) a set of p genotypes within a (n × p) dimensional matrix G Gwhere G_iv = 0, 1, 2, G_iv = 0,1,2 for the number of copies of the minor allele measured for individual i at variant v, and 3) a set of q covariates within a (n × q) dimensional matrix Z Z included in all models. These covariates include variables such as age, sex, and variables used to control for potential confounding by population stratification. Within the BMU framework, we consider all models M_y ∈ MM_γ ∈M, defined by a distinct subset of the p genetic variants and including all q adjustment variables in each model. In particular, each model M_yM_γ is indexed by a p dimensional indicator vector y γ where y_v = 1 γ_v = 1 if variant v is included in model M_yM_γ and y_v = 0 γ_v = 0 if v is not included in model M_γ. Within the Bayesian risk index [5] (BRI) we extend each model in the BMU framework to also indicate the direction of effect for each variant if included so that if γ_v = 1 variant v is included as a risk factor and if γ_v = −1 variant v is included as a protective factor. Then, given any model M_γ , we define a risk index as the collective frequency of the variants in model M_γ that is of the form:

$${\mathbf{X}}_{i\gamma }=\sum _{v=1}^p{\gamma }_v{G}_{\mathit{iv}}.$$

We can then relate the outcome to the risk index based on the logistic regression formula:

$${\mathbf{M}}_{\gamma }:\text{logit}(Y_i=1)={\beta }_0+\beta {\mathbf{Z}}_i+{\beta }_{\gamma }{\mathbf{X}}_{\mathbf{i}\gamma }.$$

Within this model specification we note that for each risk index, X_γ, we have a single effect, β_γ, for the group of variants included in the model which we will refer to as the rare variable load.

2.2 Multiple Regions within BRI

As described in Quintana et al., the BRI framework is based on modeling the relationship of the outcome variable and a single risk index that is formed by looking at the collective frequency of a subset of variants. This framework works best when the total number of variants of interest is relatively small and within a single region. To extend this approach, we assume that we have genotype data on a set of p genetic variants that belong to a set of p_R regions and we wish to model the outcome variable using multi-regional genetic profile. In particular, for each model M_γ, we wish to incorporate a risk index for each region R_j defined as:

$${\mathbf{X}}_{{\mathit{iR}}_j\gamma }=\sum _{v\in R_j}{\gamma }_v{G}_{\mathit{iv}}.$$

We then relate the outcome to the risk indices for each region based on the logistic regression formula:

$${\mathbf{M}}_{\gamma }:\text{logit}(Y_i=1)={\beta }_0+\beta {\mathbf{Z}}_i+\sum _{j=1}^{p_R}{\beta }_{{\mathbf{R}}_{\mathrm{j}}\gamma }{\mathbf{X}}_{{\mathit{iR}}_j\gamma }.$$

Here, β_Rjγ is the model-specific rare variant load for region R_j. We note that when γ_v = 0 for all variants in region R_j, the region-specific risk index is not included in our model. Thus, our extension of BRI for multiple regions introduces a second level of uncertainty on the regions associated with the outcome of interest as well as the variants included in each region-specific risk index.

2.3 Integrative Bayesian Risk Index

In addition, we wish to extend the current BRI framework to integrate external variant-specific biological information. We denote our integrative extension as iBRI. In particular, we integrate a set of c variant-specific covariates specified within a (p × c) dimensional covariate matrix W into the estimation of marginal inclusion probabilities by introducing a second-stage regression on the probability that any variant is associated. Specifically, we define the probability that any variant is associated as a function of the variant-specific covariates using a probit model:

$$\text{probit}\left(p\right({\gamma }_v\ne 0\mid {\alpha }_0,\alpha \left)\right)={\alpha }_0+\alpha {\mathbf{W}}_v.$$

Here, α is a c-dimensional vector of regression coefficients quantifying the increase or decrease in probability of association of each variant given the variant-specific covariate and α₀ specifies a baseline probability of association common to all variants. Similar to [10], we define the baseline probability to incorporate an implicit multiplicity correction in that the prior probability of at least one variant being associated remains constant as the total number of variants of interest increase. That is, α₀ = Φ⁻¹(2^−1/p) where Φ⁻¹() is the inverse of the normal cdf.

2.4 Posterior Multi-level Inference

Given any model M_γ ∈M, we can quantify the evidence that the data supports the model via posterior model probabilities defined as:

$$p({\mathbf{M}}_{\gamma }\mid \mathbf{Y})=\frac{p(\mathbf{Y}\mid {\mathbf{M}}_{\gamma })p\left({\mathbf{M}}_{\gamma }\right)}{\sum _{{\mathbf{M}}_{\gamma }\in \mathbf{M}}p(\mathbf{Y}\mid {\mathbf{M}}_{\gamma })p\left({\mathbf{M}}_{\gamma }\right)};$$

where p(Y |M_γ ) is the marginal likelihood of each model after integrating out model specific parameters, θ_γ, and p(M_γ) is the prior probability of model M_γ. Wilson et al. [10] provides a detailed description of how to approximate the marginal likelihood and specify the prior model probability to incorporate an implicit multiplicity correction. This specification allows the prior probability at baseline of at least one variant being associated to remain constant as the total number of variants of interest increase.

We can use the posterior model probabilities to provide intuitive multi-level inference for any predefined set of the predictor variables of interest. In particular, for some set of variants,v ∈S, we can quantify the evidence that at least one variant within the set is associated via set specific posterior probabilities:

$$p({\Gamma }_s=1\mid Y)=\sum _{{\mathbf{M}}_{\gamma }\in \mathbf{M}:{\Gamma }_s=1}p({\mathbf{M}}_{\gamma }\mid \mathbf{Y});$$

where, Γ_S = 1 if at least one variant within set Sis in model M_γ. Thus, the posterior probability for any set is simply the sum of the posterior model probabilities for every model that includes at least one variant within the set. In genome-wide rare variant studies, some examples of multi-level quantities of interest are: 1) the genome-wide global posterior probability that at least one variant is associated (calculated as the sum of the posterior model probabilities of all of the non-null models); 2) the gene-level posterior probability that at least one variant is associated within a gene (calculated as the sum of the posterior model probabilities of all of the models that include a variant within a specific gene); and 3) marginal posterior probabilities that any particular variant, v, is associated (calculated as the sum of the posterior model probabilities of all models that include variant v). Finally, given any multi-level posterior probability, p(Γ_S = 1| Y), we can also calculate the multi-level Bayes factors (BF) as the posterior odds that at least one variant within the set is associated divided by the prior odds:

$$\mathrm{BF}[{\Gamma }_s=1:{\Gamma }_s=0]=\frac{p({\Gamma }_s=1\mid Y)}{p({\Gamma }_s=0\mid Y)}÷\frac{p({\Gamma }_s=1)}{p({\Gamma }_s=0)}.$$

2.5 Posterior Computation

To compute posterior model probabilities and estimate the regression coefficients of the second-stage model on the marginal inclusion probabilities, we iterate between a Metropolis Hastings (MH) algorithm to sample models M_γ ∈M and a Gibbs sampling algorithm to sample the second-stage regression coefficients α. Within the MH algorithm, new models are proposed based on randomly selecting one variant and changing its status within the current model. Within the Gibbs algorithm, full conditionals are calculated to sample α given the currently sampled model. By iterating between the MH and Gibbs algorithms, we can obtain a sample of models from the model space as well as a sample from the posterior distribution of α which is used to approximate the posterior model probabilities as well as the multi-level posterior summaries. In particular, the posterior model probabilities are renormalized over the sum of sampled models and the prior model probabilities, p(M_γ), are approximated by using the Monte Carlo estimates of the inclusion probabilities, p(γ_v ≠ 0), given the sampled values of α. The sampling algorithms and calculation of all of the posterior summaries are available in the Bayesian Variant Selection (BVS) R package on CRAN [13].

2.6 Simulation Study

We wish to assess the power of iBRI compared to several commonly used alternatives on a set of single region simulations as well as a set of multiple region simulations. In particular, we compare our method to the original non-integrative BRI of Quintana et al. [5] , the weighted sum statistic of Madsen and Browning [3], the C-alpha method of Neale et al. [8], and the comprehensive step-up approach of Hoffmann et al. [4] within the single and multiple regions. For the simulations involving multiple regions, we compute independent tests of each region under the BRI, weighted sum, C-alpha and comprehensive step-up approaches.

Within our simulation study, we created a set of 1000 simulations that were comprised of a single region of variants based on the WECARE Study (described in Section 3.2). Each single region simulation is based on the available genetic data of 134 rare variants for 1912 individuals within BRCA1 as part of the WECARE Study. We also created a set of 1000 multiple region simulations. Each multiple region simulation is based on exome-array data from The Kentucky Colorectal Cancer Study (KY - described in Section 3.3) including 114 genes within the DNA repair pathway and comprised of 473 rare variants for 1,356 individuals. The 114 genes play a role within 10 unique DNA repair sub-pathways. For each simulation within both the single and multiple region simulation sets we:

1. Define variant-specific covariates. For the single region simulations, variant-specific covariates are defined within a (134 × 4) dimensional matrix W indicating the effect type of each variant (Intervening Sequence (IVS), Synonymous, Missense, Truncation). For the multiple region simulations, variant-specific covariates are defined within a (473 x 10) dimensional matrix W indicating the DNA repair sub-pathway that each variant is involved in.

2. Randomly select one of these variant-specific covariates and sample an α within {0,1,2,3} for that covariate (all of the other covariates are assumed to have an α-level of 0). Marginal probabilities of association are then calculated for each rare variant based on the assigned α-levels.

3. Select between 0:10 causal rare variants based on the marginal probabilities.

4. Randomly select a log(OR) for all causal rare variants within the simulation within {.5,1,1.5,2,2.5}.

5. Simulate each individual’s case/control status based on the selected causal variants and log(OR).

We note that when the α-level for the associated variant-specific covariate is selected to be 0, the casual variants within the simulation are independent from all variant-specific covariates and the simulation is referred to as a non-informative simulation. When the α-level for the associated variant-specific covariate is greater than 0, we refer to the simulation as informative.

3. Results

3.1 Simulation Results

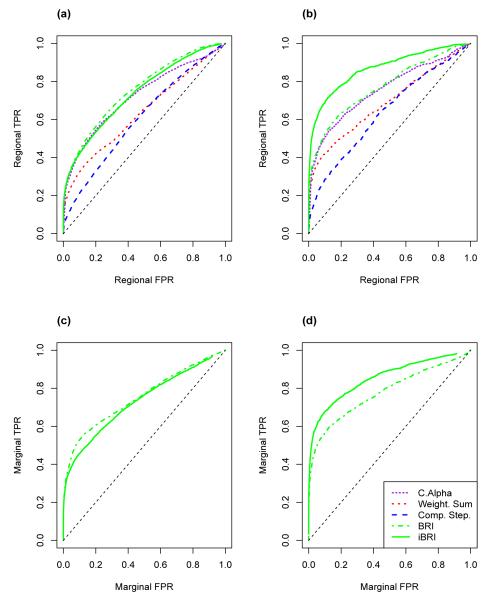
We ran the integrative BRI (iBRI) and rare variant alternative analyses on the set of 1000 single region WECARE Study-based simulations as well as the set of 1000 multiple region KY study-based simulations. In particular, we compare the power to detect regional associations of the rare variants using iBRI with BRI, the weighted sum approach, c-alpha, and the comprehensive step-up approach. We also compare the power to detect marginal associations of the rare variants within the simulated data under iBRI and BRI. We plot regional and marginal ROC curves for each method for the single region WECARE Study-based simulations and the multiple region KY study-based simulations in Figure 1 and 2 respectively. Specifically, in plots a) and b) of both Figure 1 and 2 the regional true positive rate (TPR) is plotted against the regional false positive rate (FPR) as we vary the regional BF for the iBRI and BRI approaches and the regional p-value for the weighted sum, c-alpha and comprehensive step-up approaches. In plot a) we calculate regional TPR and FPR within all non-informative simulations and in plot b) we calculate the same quantities within all informative simulations.

Figure 1. ROC Curves for Single Region WECARE Study-Based Simulations.

In plots a) and b) regional false positive rates are plotted against regional true positive rates as the regional BF threshold varies for iBRI and BRI and as the regional p-value thresholds vary for the weighted sum, c-alpha, and comprehensive step-up approaches. In plots c) and d) marginal false positive rates are plotted against marginal true positive rates as the marginal BF threshold varies for iBRI and BRI. Plots a) and c) are across all non-informative simulations and plots b) and d) are across all informative simulations.

Figure 2. ROC Curves for Multiple Region Exome Study-Based Simulations.

In plots a) and b) regional false positive rates are plotted against regional true positive rates as the regional BF threshold varies for iBRI and BRI and as the regional p-value thresholds vary for the weighted sum, c-alpha, and comprehensive step-up approaches. In plots c) and d) marginal false positive rates are plotted against marginal true positive rates as the marginal BF threshold varies for iBRI and BRI. Plots a) and c) are across all non-informative simulations and plots b) and d) are across all informative simulations.

Within regions that demonstrate strong evidence of an association amongst the rare variants, we compare the power to pinpoint which of the rare variants are most likely driving the regional associations. In particular, in plots c) and d) of both Figure 1 and 2, the marginal TPR is plotted against the marginal FPR as the marginal BF threshold varies under the iBRI and BRI approaches. In plot c) we calculate the marginal TPR and FPR within all non-informative simulations and in plot d) we calculate the same quantities within all informative simulations.

Within Figures 1 and 2 we see that iBRI and BRI have slightly higher power to detect regional associations over the alternative methods within our single and multiple region simulations. Also, when the variant-specific covariates are truly informative with regards to the casual variants, iBRI has an increase in power to detect associated regions over the alternatives (Figures 1 and 2 plot b) and has an increase in power to detect associated variants over the basic BRI (Figures 1 and 2 plot d). This potential increase does not come with a corresponding drastic loss in power to detect associated regions and variants of iBRI when the variant-specific covariates are truly uninformative (Figures 1 and 2 plots a and c).

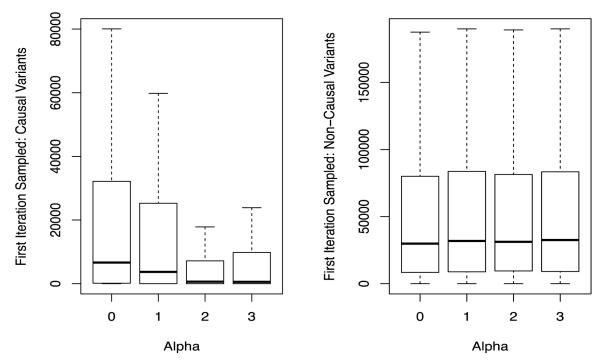
Given the tremendous size of the model space when we are analyzing multiple regions simultaneously with iBRI, we also assess the degree to which the integration of informative variant-specific covariates can influence the speed of convergence of the model search algorithm. In particular in Figure 3, we plot the number of iteration until a truly causal variant (plot a) and non-causal variant (plot b) is sampled as a function of the known simulated value of α level. As the variant-specific covariates become more informative there is a decrease in the mean number of iterations needed for a causal variant to be sampled. Additionally, there is not an increase in the mean number of iterations needed to propose other, non-causal variants. Thus, the integration of external biological covariates with iBRI leads to a more efficient model search algorithm when these covariates are truly informative with regard to the causal variants.

Figure 3. Sampling Causal and Non-Causal Predictors in Multiple Region Exome Study-Based Simulations.

We plot the number of iterations under iBMU until the first acceptance of the causal (plot a) and non-causal (plot b) variants as a function of the known simulated value of α.

3.2 BRCA1 Results

The WECARE (Women’s Environmental Cancer and Radiation Epidemiology) Study is a population-based case-control study designed to investigate genetic risk factors of second primary breast cancer. For a more detailed description of the study see [14]. The study includes 640 non-Hispanic women with contralateral breast cancer (cases) and 1,272 women with unilateral breast cancer (controls) individually matched based on age at and year of primary diagnosis, race, and reporting registry. For all participants, the complete coding sequences of BRCA1 (5,589 bp split into 22 coding exons) and BRCA2 (10,254bp and 26 coding exons) were screened for variations by denaturing high- performance liquid chromatography, using leukocyte genomic DNA as a template, identifying a large number of both common and rare variants [15-17]. To demonstrate the use of iBRI within a single region of a candidate pathway study, we analyze all self-identified white individuals with a logistic regression adjusted by age to investigate a subset of 134 rare BRCA1 variants (MAF between .0003 and .05) and integrate variant-specific biological covariates of whether or not a variant is known as being deleterious and the effect type of each variant (IVS, Synonymous, Missense, Truncation) into the analysis to help guide variant selection. Thus, for the WECARE Study analysis, W is a (134 × 5) dimensional matrix.

By using our novel iBRI approach within BRCA1 and integrating external variant-specific biological covariates of whether a variant is known as deleterious and the effect type each variant, we find a regional BF of 4.7e+10 giving extremely strong evidence that at least one variant within BRCA1 is associated with second primary breast cancer. Using the non-integrative BRI we find a modest regional BF of 29.3. Given the extremely strong evidence of an association within BRCA1, we are interested in pinpointing the variants most likely driving the association. In Table 1, we provide information on the top 10 variants found using iBRI. In particular, variants are organized based on their effect type and each effect type is ordered based on the effect BF giving the evidence that at least one variant with the corresponding effect type is associated. For each variant, we also report: 1) the exon the variant is located in, 2) if a variant is known deleterious, 3) the count of cases and controls that have the variant, 4) the marginal BF under iBRI, and 5) the marginal BF under BRI. The variants with identified as either a truncation or missense effect are most likely associated with second primary breast cancer. By integrating data on each variants’ effect type and if a variant is known as deleterious, we find that the variants with a truncation or missense effect, as well as variants that are known as deleterious, have a great increase in marginal BF’s using iBRI over the non-integrative BRI. This is reflected in an elevated estimate for the α corresponding to the “deleterious” covariate of 2.39 (95% Credible Interval (CI) of 1.09 to 3.61) and for the α corresponding to the “truncation” covariate of 0.55 (95% CI of −0.77 to 1.88). In contrast, we do not see a dramatic increase in evidence for the two variants defined as synonymous or IVS effect type and are not known deleterious variants. We also note that marginal BF’s under the iBRI and BRI for variants V52, V3, V112 and V106 are slightly different although the data for each is identical (counts in cases and controls and predictor-level covariates). In part, this reflects the uncertainty in the estimation of each BF. In addition, this also reflects that each marginal BF is calculated conditional upon all other markers in the analysis. Thus, if two variants are correlated or found on the same individual it is unlikely that they will co-occur within the same top model since the added information from the additional variant is reduced. This will cause a dilution in the marginal BF of the less likely marker driving the association.

Table 1. BRCA1: Top Variants.

Table of the top 10 variants found using iBRI. Variants are organized based on the effect type of each variant. Effect type BF’s are reported under each effect. For each variant we report: 1) The exon of the variant, 2) if the variant is a known deleterious variant, 3) the number of cases and controls that the variant is found in, 4) the marginal BF of the variant under iBRI, and 5) the marginal BF of the variant under BRI.

Effect	Variant	Exon	Deleterious	Cases/ Controls	iBRI	BRI
Truncation (BF=7.4e+08)	V2	2	Yes	9/4	3667.3	42.4
	V122	11	Yes	3/0	1927.0	32.1
	V52	11	Yes	2/0	692.5	13.5
	V3	2	Yes	2/0	688.7	13.9
	V112	11	Yes	2/0	683.7	12.8
	V106	11	Yes	2/0	662.4	13.3
Missense (BF=4.1e+03)	V13	5	Yes	8/2	15690.9	124.4
	V8	3	Yes	2/0	413.9	13.3
IVS (BF=7.0)	V137	12	No	2/0	26.3	13.0
Synonymous (BF=1.0)	V7	3	No	2/0	5.1	9.7

3.3 Exome Analysis of DNA Repair Pathway Results

The Kentucky Colorectal Cancer Study (KY) was initiated in July 2003 through the University of Kentucky Cancer Center[18]. A web based reporting system implemented by Kentucky Cancer Registry in 2003 has facilitated rapid report of cases state wide, with approximately 76.8% cases reported to the registry within 6 months of diagnosis. Cases (>21yrs) diagnosed with histologically confirmed colon cancer and entered into the registry within 6 months of their diagnoses are invited to join the study. Unrelated controls are recruited through random digit dialing and are frequency matched the to the cases by age (±5 years), gender, and race. Exclusions from the study are those individuals who have been diagnosed with colon cancer because of known hereditary forms of colon cancer or polyposis such as Familial Adenomatous Polyposis (FAP), Hereditary Non-Polyposis Colorectal Cancer (HNPCC), Peutz-Jeghers, and Cowden disease. Currently there are more than 1,040 incident population-based cases of colorectal cancer and 1,750 population-based controls fully recruited, with comprehensive epidemiologic data, pathology data, and DNA from cases and controls. 338 cases with positive family history, as defined as having a 1^st or 2^nd degree relative with colon cancer, and 1018 controls with negative family history from the KLY study were genotyped using the Illimina Infinium HumanExome array (genome.sph.umich.edu/wiki/Exome_Chip_Design). The array was constructed from exome sequencing 10,789 exomes, thus capturing 60% of non-synonymous SNPs with an allele frequency of 1/7000, 80% of SNPs with an allele frequency of 1/5000 and >99% of SNPs with an allele frequency of 1/1000. While the overall array includes 65,613 rare (MAF < 0.01) variants across 15,010 gene regions, to demonstrate the use of iBRI within multiple regions of a candidate pathway study, we investigate a subset of 473 rare variants (MAF between .0007 and .01) in 151 DNA repair pathway genes (114 with observed variants see Supplemental Table 1 for more details). The first-stage model includes sex, age and the first four principle components from an investigation of population structure. We integrate a variant-specific biological covariates that indicate the specific DNA repair pathway that the variant is involved in into the analysis to help guide variant selection. For the KY exome analysis, W is a 473 × 10 matrix. See Supplemental Table 1 for variant, gene and subpathway details.

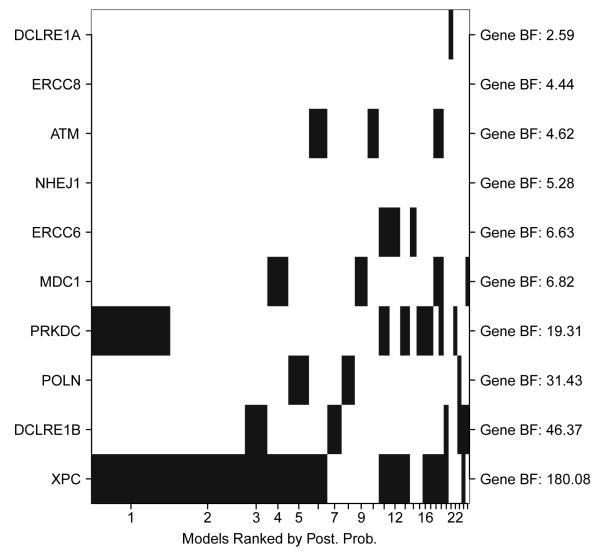
Using our novel iBRI approach within the 114 unique gene regions of the DNA repair pathway we find a global BF of 13.0 giving strong evidence that at least one variant within the entire analysis is associated. This global summary is not available using the other approaches of testing each region individually using the current collapsing methods of BRI, C-alpha, comprehensive step-up, and weighted sum. Given strong evidence of a global association within the study, we are interested in pinpointing the likely regions (or genes) that are driving the association. With this in mind, Figure 4 plots the inclusion of the top 10 regions found using iBRI within the top 25 models. On the x-axis we order the top regions based on the regional BFs (reported on the right margin) and on the y-axis we have the top models found ordered based on posterior model probabilities. Each column represents the inclusions/ exclusions of the top 10 regions (a region is defined as being included in a model if at least one variant within the region is included in the model) within the respective model and the width of each column is proportional to the posterior model probability of the top model. We can see in Figure 4 that the top model includes at least one variant within gene XPC and gene PRKDC. In fact, many of the top models include at least one variant within multiple regions. Thus, it is likely that modeling the outcome as a multi-regional genetic profile will give us added power over testing each region individually. Table 2 reports more information on the top 10 genes found using the iBRI approach. Within the table, the genes are organized based on the specific DNA repair pathway that the gene is involved in and pathway BF that quantify the evidence that at least one variant within the specific DNA repair pathway is associated are reported under each pathway. Next to each gene we report: 1) the gene BF found using iBRI, 2) the most likely associated variant within the gene determined based on marginal BF, 3) the gene p-values for C-alpha, weighted sum, and comp. step., and 4) the gene BF under BRI. Within Table 2 we can see that four specific DNA repair pathways have strong evidence of an association with colon cancer: 1) Nucleotide excision repair (NER), 2) non-homologous end joining (NHEJ), 3) Cross-link repair (XLR), and 4) Ataxia telangiectasia mutated (ATM). The most likely DNA repair pathway associated with colon cancer is NER with a pathway BF of 30.8 and a corresponding α of 0.31 (95% CI of −1.81 to 1.86). Within NER, genes XPN, ERCC6, and ERCC8 have strong evidence of an association. These genes have also been detected as being associated with colon cancer in an independent data set. However, both ERCC6 and ERCC8 would not have been detected using the non-integrative alternative methods.

Figure 4. Top Model Inclusions for Top Regions in DNA repair pathway.

We plot the top regions (or genes) included in the top 25 models found under the iBRI approach. The inclusion/exclusion of the top 10 regions are plotted in the rows and the rows are ordered based on each regional BF (reported on the right axis). The regions included/ excluded within each of the top 25 models are plotted in the columns. These columns have width proportional to and are ordered based on the posterior probability of the corresponding model.

Table 2. DNA Repair Pathway: Top Regions.

Table of the top 10 genes found using iBRI. Genes are organized based on the DNA repair pathway that the genes are involved in. Pathway BF’s are reported under each pathway. For each gene we report 1) the gene BF under iBRI, 2) the most likely associated variant within the gene determined based on marginal BF’s, 3) the gene p-value under C-alpha, weighted sum, comp. step., and 4) the gene BF under the independent gene tests of BRI. Highlighted genes have been detected in an independent study.

Pathway	Gene	iBRI	Likely Assoc. Variant	C-Alpha	Weight. Sum.	Comp. Step.	BRI
NER (BF=30.8)	XPC	180.1	exm292542	0.006	0.164	0.588	7.2
	ERCC6	6.6	exm824160	0.374	0.337	0.78	1.0
	ERCC8	4.4	exm456709	0.386	0.032	0.077	1.5
NHEJ (BF=11.0)	PRKDC	19.3	exm699583	0.084	0.079	0.083	1.6
	NHEJ1	5.3	exm267278	0.404	0.120	0.327	1.1
XLR (BF=9.7)	DCLRE1B	46.4	exm85671	0.079	0.020	0.012	7.3
	POLN	31.4	exm382361	0.089	0.024	0.017	4.8
	DCLRE1A	2.6	exm857026	0.666	0.405	0.780	0.6
ATM (BF=2.2)	MDC1	6.8	exm528405	0.359	0.100	0.113	2.0
	ATM	4.6	exm953816	0.37	0.174	0.274	1.7

4. Discussion

The original Bayesian risk index (BRI) has many potential advantages over alternative rare variant approaches. The approach selects a subset of variants to include in the risk index, allows for both risk and protective variants to contribute, and formally incorporates the uncertainly in that selection. This allows for increased power when the number of causal variants is small in proportion to the overall number of variants evaluated and avoids dilution of power if both risk and protective variants are present. Additionally, the BRI allows for formal inference via Bayes factors for both regional association and for the contribution of any specific variant. For the integrated Bayesian risk index (iBRI) presented here, we make two important extensions. First, within a single regression analysis model, we include a multi-regional profile consisting of a risk index for each region. Second, we allow for prior information to guide the inclusion of each region and the inclusion of which variants within each regional risk index.

As genetic association studies move forward to acquire numerous rare variants across the genome using array or sequencing technologies, the ability to model multiple regions will be crucial for combined analyses. A regression framework allows this to be accomplished by simply expanding the linear predictor to include a sum over all region specific risk indexes. Such extension is not easily implemented with some alternative approaches, such as C-alpha [8], in which the analysis is either on a specific region independently or across numerous regions in aggregate. However, even though such an extension is conceptually straightforward in regression, implementation to numerous regions quickly leads to limitations in the number of regions that can be feasibly evaluated. Conventional model selection procedures could be employed on a set of regional risk indexes, but this would require preconstructing the indexes and a loss of the ability to have variant selection within each regions. Furthermore, since uncertainty in the final model determination is not incorporated in many of these approaches, problems can arise with hypothesis testing, such as an increase in type I error for forward-selection algorithms.

Bayesian model uncertainty approaches offer a solution that allows for the uncertainty in the model search to be propagated up from selection of variants within each region to selection of regions across all variants evaluated. In addition, formal and valid inference can be accomplished via Bayes factors. Specifically in terms of formal inference, iBRI allows for multi-level inference at the global, regional and marginal levels. This intuitive multi-level inference provides a practitioner with the ability to not only assess the global impact of rare variation, but to also to pinpoint the association within pathways, genes, and specific variants within these regions. Thus, with limited resources for follow-up studies, the practitioner can focus more attention on smaller regions surrounding specific variants rather than entire regions. Conversely, inference on higher-level combinations allows for subtle effects from variants, regions and genes to guide broad conclusions regarding pathways and their potential aggregate effect. In the analysis of the DNA repair pathway, a single Bayes factor of 30.8 indicates an noteworthy association for the NER pathway in aggregate (Table 2) – formally summarizing the overall evidence from three genes with elevated Bayes factors greater than 3 (XPC, ERCC6, and ERCC8) and seven genes with nominal Bayes factors (DDB2, ERCC2, ERCC3, ERCC4, ERCC5, RAD23A, XAB2).

Another key feature of the iBRI approach is the integration of prior biological information. Due to the difficulty for marginal rare variant analysis and rare variant load tests to indicate specific variants, many investigators are simply filtering variants based on biofeatures and annotation. Unfortunately, these often reduce to ad hoc deterministic decisions based largely on the whim of the investigator. The inclusion of prior covariates in a second-stage probit regression on the probability of inclusion of any variant allows the investigator to focus on characterizing the variants, using information such as functional prediction scores or pathway level information (PolyPhen-2 [20], SIFT [19], MutationTaster [22], LRT [21], PANTHER [23], PhD-SNP [24], SNPs3D [25], PMut [26], SNAP [27], MutPred [28] and SNPs&GO [29]). Moreover, these prior covariates simply define an exchangeable class of variants and do not predetermine the weight or importance of the information a priori [30-33]. The impact on probability of inclusion is estimated from the data. This is clearly seen in the WECARE Study example for BRCA1 (Table 1). A priori, variants’ biological effects were determined as either truncation, missense, IVS, or synonymous. Upon analysis, since numerous truncation variants demonstrate evidence for association, those truncation variants with more modest numbers were deemed more noteworthy. For example, based simply upon the case-control comparison (2 cases vs. 0 controls), variants V52, V3, V112, and V106 have Bayes factors of ~13 from the BRI analysis. Rather, than offering post-hoc additional justification of that these variants are of interest because they are simply truncation variants, the iBRI formally incorporates that information, estimates its impact, and elevates the Bayes factor for these variants to over 600. Additionally, since the impact of prior information is estimated from the data, if that information is non-informative, our simulation results indicate that there is no increase in the detection of false positives (Figures 1 and 2). Conversely, as the prior information becomes more informative in terms of specificity and sensitivity in identifying the true causal variants, the estimated α’s increase and performance is improved.

The BRI and iBRI methods do come with an added computational cost of running a MH algorithm to sample models from the high-dimensional model space as well as a Gibbs algorithm to sample posterior estimates of the effects of the variant-specific external biological covariates, α in the case of iBRI. The computational complexity of running one iteration of the MH algorithm corresponds to the computational cost of estimating model specific parameters and the marginal likelihoods for each unique model sampled. This scales linearly with the sample size n and cubically with respect to the number of model specific parameters being estimated. Thus, an increase in sample size will not cause a significant increase in computation time of the MH algorithm. However, as the number of region-specific risk indices being incorporated within any given model increases the computation time of the algorithm will increase substantially. The computational complexity of one iteration of the Gibbs algorithm under the iBRI approach scales linearly with respect to the number of variant-specific external covariates, c, and the total number of variants under consideration, p. Therefore, as we increase these parameters we will not see a significant increase in computation time per iteration of the Gibbs sampling algorithm. With regards to the added computational complexity of iBRI for analyzing multiple regions vs. modeling a single region, the analysis of 1 gene region for the WECARE study took approximately 3 hours for 100K iterations on a 2.3 Ghz CPU whereas the analysis of 114 gene regions for the KY data took approximately 6 hours for the same number of iterations on the same machine. Thus, we see that the computation time to run iBRI on a study involving multiple regions doubles with respect to running the same approach on a single region; most likely demonstrating the added computational complexity of estimating effects of multiple risk indices for each unique model. With regards to the added computational complexity of the Gibbs sampling algorithm needed for the iBRI approach versus the BRI approach, the analysis of 134 rare variants within the WECARE study took approximately 2.5 hours for 100K iterations of the MH algorithm under the BRI approach compared to the 3 hours for 100K iterations of the Gibbs/MH algorithm under the iBRI approach. This increase in .5 hours to run the iBRI approach compared to the BRI approach on the WECARE study demonstrates the added computational time required to perform the Gibbs algorithm of iBRI.

These examples give the user a good idea of the computational complexity of the BRI and iBRI approaches for a set number of iterations of the Gibbs/MH algorithms. However, it needs to be noted that as the total number of variants of interest increases the total number of iterations of the algorithms needed for convergence of posterior quantities will also increase. Currently, we suggest doing two independent runs of the search algorithms and comparing the global and marginal posterior quantities computed under a set number of iterations of each independent run to determine if the algorithm has converged. While we have shown that the integration of external variant-specific covariates into the probability that each variant is associated can increase the efficiency of the model search algorithm (Figure 3) when the covariates are truly informative with regards to the causal variants, it is of future interest to investigate alternative algorithms and computational techniques to allow for whole-genome analysis. Also, as the number of variant-specific covariates increases, there is the potential for an additional level of uncertainty into which variant-specific covariates should be used to inform the variant and region selection.

In conclusion, the iBRI method is a powerful and flexible regression framework that allows for the investigation of rare variants across numerous regions and the integration of prior biological annotation and functional information. In addition, adjustment variables, such as principle components for population structure, can be included as well as an extension to non-dichotomous outcome traits such as quantitative or survival traits.