Diffusion-controlled reaction rates for two active sites on a sphere

Abstract

Background

The diffusion-limited reaction rate of a uniform spherical reactant is generalized to anisotropic reactivity. Previous work has shown that the protein model of a uniform sphere is unsatisfactory in many cases. Competition of ligands binding to two active sites, on a spherical enzyme or cell is studied analytically.

Results

The reaction rate constant is given for two sites at opposite ends of the species of interest. This is compared with twice the reaction rate for a single site. It is found that the competition between sites lowers the reaction rate over what is expected for two sites individually. Competition between sites does not show up, until the site half angle is greater than 30 degrees.

Conclusions

Competition between sites is negligible until the site size becomes large. The competitive effect grows as theta becomes large. The maximum effect is given for theta = pi/2.

Background

The purpose of this article is to generalize the Smoluchowski [1] calculation of the steady state bimolecular rate constant, 4πDR, to anisotropic reactivity. This was necessary because previous work [2,3], has shown that diffusion-controlled protein-ligand binding is not modeled successfully by a uniformly reactive protein for some cases. As a consequence of this, more realistic models of proteins were created. Previously this was done by having one reactive site on a spherical molecule or cell [4-6]. Berg and Purcell considered many sites on a sphere [7]. This paper considers two axially symmetric sites on opposite ends of a sphere reacting with small molecules. See Figure 1. This might be used to model a protein-ligand reaction: such as the diffusion-controlled reaction of acetylcholine with the active sites of tetrameric mouse acetylcholinesterase [8].

Figure 1.

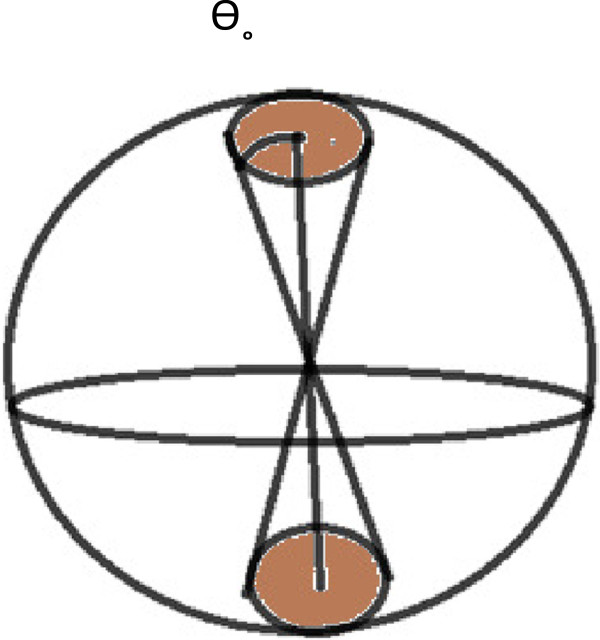
A non-reactive sphere with two reactive spherical caps of half angle θ _° at each end.

Methods

We want to solve

$$\begin{array}{l}{\partial }^2\mathit{c}\left(\mathit{r},\mathrm{\theta }\right)/\partial {\mathit{r}}^2+\left(2/\mathit{r}\right)\partial \mathit{c}\left(\mathit{r},\mathrm{\theta }\right)/\partial \mathit{r}\\ +1/{\mathit{r}}^2\left(1/\mathit{\text{sin}}\mathrm{\theta }\right)\partial /\partial \mathrm{\theta }\left(\mathit{\text{sin}}\mathrm{\theta }\partial \mathit{c}\left(\mathit{r},\mathrm{\theta }\right)/\partial \mathrm{\theta }\right)\\ =0\end{array}$$ (1)

where c(r, θ) gives the ligand concentration. Figure 1 shows that there is symmetry between the two active sites. As a consequence of this, the net flux normal to the equatorial plane vanishes for all r. This reduces the two site problem to a one site problem, where now θ varies from 0 to π/2. Mathematically this says

$$\partial \mathit{c}\left(\mathit{r},\mathrm{\theta }\right)/\partial \mathrm{\theta }=0\mathrm{\theta }=\mathit{\pi }/2$$ (2)

We also have

$${\mathit{c}}_{{}_{°}}={\text{lim}}_{\mathit{r}\to \infty }\mathit{c}\left(\mathit{r},\mathrm{\theta }\right)$$ (3)

where c˳ is the bulk concentration of ligand. The reactive boundary conditions are given by

$$\mathit{c}\left(\mathrm{R},\mathrm{\theta }\right)=00\le \mathrm{\theta }\le {\mathrm{\theta }}_{\circ }$$ (4)

and

$$\partial \mathit{c}\left(\mathit{r},\mathrm{\theta }\right)/\partial \mathit{r}|{}_{\mathit{r}=\mathit{R}}=0{\mathrm{\theta }}_{°}\le \mathrm{\theta }\le \mathit{\pi }/2$$ (5)

As done previously [6,9], equation (4) is replaced by the constant flux boundary condition

$$\partial \mathit{c}\left(\mathit{r},\mathrm{\theta }\right)/\partial \mathit{r}|{}_{\mathit{r}=\mathit{R}}=\mathrm{Q}0\le \mathrm{\theta }\le {\mathrm{\theta }}_{\circ }$$ (6)

where Q is evaluated, by requiring the average concentration of ligand to vanish over the active site. (see ref. [6], equation 8, κ → ∞)

$${\displaystyle {\int }_0^{\mathrm{\theta }˳}\mathit{c}\left(\mathit{R},\mathrm{\theta }\right)\mathit{\text{sin}}}\mathrm{\theta }\mathit{d}\mathrm{\theta }=0$$ (7)

The diffusion limited rate constant for the two site problem is

$${\mathrm{k}}_{\mathrm{DC}}=\frac{2\mathit{\pi }{\mathit{R}}^2\mathit{D}}{{\mathit{c}}_{\circ }}{\displaystyle {\int }_0^{{\mathrm{\theta }}_{\circ }}\frac{\partial \mathit{c}}{\partial \mathit{r}}}|{}_{\mathrm{r}=\mathrm{R}}\text{sin}\mathrm{\theta }\mathit{d}\mathrm{\theta }$$ (8)

Where D is the diffusion coefficient of the ligands and R is the radius of the sphere. The accuracy of the constant flux boundary condition may be seen, for small θ˳ (e.g. small binding sites), by considering a reactive disk in an insulating plane. For this problem, the exact solution is known [6]. It is k_DC = 4 Da, where a = the disk radius. The constant flux method yields [6] k_DC = 3.7 Da. Thus the constant flux boundary condition is accurate for small reactive sites.

The solution of equation (1) is given by

$$\mathit{c}\left(\mathit{r},\mathrm{\theta }\right)=\mathit{\alpha }+{\displaystyle {\sum }_{\mathit{m}}^{\infty }{\mathit{a}}_{\mathit{m}}{\mathit{f}}_{\mathit{m}}\left(\mathit{r}\right){\mathit{P}}_{\mathit{m}}\left(\text{cos}\mathrm{\theta }\right)}$$ (9)

where the P _m (x) are Legendre polynomials of order m. Application of the boundary condition given by equation (2) yields

$$\mathit{c}\left(\mathit{r},\mathrm{\theta }\right)=\mathit{\alpha }+{\displaystyle {\sum }_{\mathit{m}}^{\infty }{\mathit{\alpha }}_{2\mathit{m}}{\mathit{f}}_{2\mathit{m}}\left(\mathit{r}\right){\mathit{P}}_{2\mathit{m}}\left(\text{cos}\mathrm{\theta }\right)}$$ (10)

Equation (3) is satisfied with α = c˳ and with the radial functions

$${\mathit{f}}_{2\mathit{m}}\left(\mathit{r}\right)=1/{\mathit{r}}^{2\mathit{m}+1}$$ (11)

The coefficients a_2m in equation (10) are found using equations (5) and (6). Details, parallel a previous derivation [6].

Results and discussion

In this section we present the results and discuss how the method represents a step forward in the field of diffusion-controlled kinetics and biophysics in general.

The results are given by the solution of the model in the preceding section, and by comparing it to twice the rate limited constant for the one site problem [6]. The difference between the two problems, gives a measure of competition between the two sites for reaction with ligands.

The diffusion limited rate constant for the two site problem is

$$\mathrm{k}2={\mathrm{k}}_{\mathrm{DC}}/4\mathrm{\pi }\mathrm{DR}$$ (12)

where 4πDR is the rate constant for a uniformly reacting sphere. The reciprocal of our rate constant is

$$\begin{array}{l}1/\mathrm{k}2=1+\frac{1}{4{\left(1-\text{cos}\mathrm{\theta }\circ \right)}^2}{\sum }_{\mathit{m}=1}^{\infty }\\ {\displaystyle \left({\left({\mathit{P}}_{2\mathit{m}-1}\left(\text{cos}\mathrm{\theta }\circ \right)-{\mathit{P}}_{2\mathit{m}+1}\left(\text{cos}\mathrm{\theta }\circ \right)\right)}^2/\left(\mathit{m}+\frac{1}{2}\right)(2\mathit{m}+\frac{1}{2}\right)}\end{array}$$ (13)

The reciprocal of the rate constant for one site is given by

$$\begin{array}{l}1/\mathrm{k}1=1+\frac{1}{2{\left(1-\text{cos}\mathrm{\theta }\circ \right)}^2}{\sum }_{\mathit{m}=1}^{\infty }\\ {\displaystyle \left({\left({\mathit{P}}_{\mathit{m}-1}\left(\text{cos}\mathrm{\theta }\circ \right)-{\mathit{P}}_{\mathit{m}+1}\left(\text{cos}\mathrm{\theta }\circ \right)\right)}^2/\left(\mathit{m}+\frac{1}{2}\right)(\mathit{m}+1\right)}\end{array}$$ (14)

Figure 2 shows plots of k2 (θ˳) (the rate constant for 2 sites), twok1 (θ˳) (twice the rate constant for 1 site) and k1 (θ˳) (the rate constant for one site [6]) versus θ_°. For small θ˳, the two site rate constant and 2 × the single site rate constant are in agreement with each other, as would be expected(both behaving as two active sites on a large sphere). As θ˳ grows above 30 degrees, the curves grow apart. The two site curve, being less than 2 × the one site curve.

Figure 2.

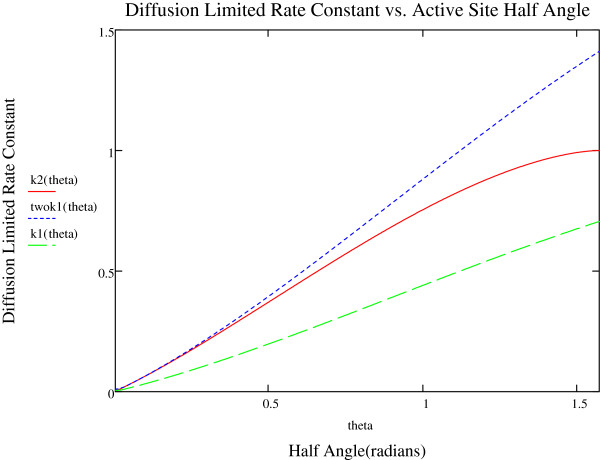
Plot showing the variation of the diffusion-limited rate constant with half-angle theta for 3 different cases.

The difference between the curves is a measure of the competition between the two sites. The competition effect does not show up till around 30 degrees. For $\mathrm{\theta }\circ =\frac{\mathit{\pi }}{2},\mathrm{k}2=1$, which is the exact result. Thus, the constant flux boundary condition, is good for large θ˳.

This paper represents progress in the field, by presenting a new model for the interpretation of experimental data. This is for macromolecule-ligand binding reactions that fall in the diffusion-controlled regime. Previously, only one site models were available for modeling proteins. Proteins with multiple binding sites can now be studied.

Conclusions

The analytical expression for the diffusion-limited rate constant to two active sites on a sphere has been given. The result was used to study the competitive effects between the two sites. The effect doesn’t show up until the site half-angles is greater than 30 degrees. The competitive effect grows until its maximum value is reached at θ˳ = π/2.

Competing interests

There are no competing interests for this paper.

Acknowledgements

I would like to thank Attila Szabo, of the NIH, for suggesting this problem.