BlockClust: efficient clustering and classification of non-coding RNAs from short read RNA-seq profiles

Abstract

Summary: Non-coding RNAs (ncRNAs) play a vital role in many cellular processes such as RNA splicing, translation, gene regulation. However the vast majority of ncRNAs still have no functional annotation. One prominent approach for putative function assignment is clustering of transcripts according to sequence and secondary structure. However sequence information is changed by post-transcriptional modifications, and secondary structure is only a proxy for the true 3D conformation of the RNA polymer. A different type of information that does not suffer from these issues and that can be used for the detection of RNA classes, is the pattern of processing and its traces in small RNA-seq reads data. Here we introduce BlockClust, an efficient approach to detect transcripts with similar processing patterns. We propose a novel way to encode expression profiles in compact discrete structures, which can then be processed using fast graph-kernel techniques. We perform both unsupervised clustering and develop family specific discriminative models; finally we show how the proposed approach is scalable, accurate and robust across different organisms, tissues and cell lines.

Availability: The whole BlockClust galaxy workflow including all tool dependencies is available at http://toolshed.g2.bx.psu.edu/view/rnateam/blockclust_workflow.

Contact: backofen@informatik.uni-freiburg.de; costa@informatik.uni-freiburg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Genome-wide sequencing revealed that DNA is pervasively transcribed, with the majority of the DNA encoding for non-coding RNAs (ncRNAs) (Jacquier, 2009). ncRNAs are important parts of cellular regulation that were long ignored but have received an increasing level of attention over the past decade. There have been reports of up to 450 000 predicted ncRNAs in the human genome alone (Rederstorff et al., 2010), the vast majority of them having no functional annotation. While the exact numbers, and even the magnitude, of regulators and interactions are of course a matter of discussion, they reflect the current challenge for the analysis of whole-transcriptome data.

Comparatively assigning a putative function to ncRNAs requires the detection of RNA families or classes with a common function. RNA families contain sequences that are related via evolution, whereas the members of RNA classes are defined only by a common function without evolutionary relationship, with miRNAs and snoRNAs being well-known examples. RFAM (Burge et al., 2013) is the largest known collection of known RNA families. However, only a minor part of the transcriptome is covered by those examples. For that reason, Will et al. (2007) and Torarinsson et al. (2007) introduced clustering of transcripts according to sequence and structure as a mean to assign functions. This is now used as a standard tool for the detection and analysis of ncRNA in genomic and metagenomic data [see e.g. Parker et al. (2011), Saito et al. (2011), Weinberg et al. (2009) or Shi et al. (2009)].

There are, however, several caveats if one relies only on the genomic sequence and its predicted secondary structure. First, the genomic sequence is often changed by post-transcriptional modifications. The database of RNA modification pathways [MODOMICS, see Machnicka et al. (2013)] lists 144 types of modifications, from methylation of RNA bases to editing events like C-to-U or A-to-I editing [see e.g. Su and Randau (2011) or Nishikura (2010)]. Second, the reliability of the classification depends on the quality of secondary-structure prediction, which is often low [see e.g. Mathews et al. (2004)]. The reason is not only that the energy model for secondary structure is incomplete, but RNA modifications and the influence of RNA-binding proteins also add layers of complexity. In the case of transcriptome data, an additional problem is that often the full transcript is not seen in the deep sequencing. This implies that one has to perform local secondary-structure prediction, which is an even harder task (Lange et al., 2012). Third, relying on structure is optimal for structured ncRNA, but would miss many long ncRNAs that often do not have a conserved structure [for a review, see e.g. Rinn and Chang (2012)].

There is, however, a similarity other than the genomic sequence and its predicted secondary structure that can be used for the detection of RNA classes, namely the pattern of processing and its traces in small RNA-seq reads data (Findeiss et al., 2011). The reason is simply that these processing patterns depend on the functional molecule and its 3D-structure, and thus should carry information not only about the structure of the polymer but also about all modifications and processing of the RNA molecule. This is well understood for prominent examples like miRNA, where most pre-miRNA have a hairpin structure with a 2-nt 3′ overhang that are processed into a double-stranded RNA consisting of the miRNA and its complement miRNA* [see e.g. Gan et al. (2008), for alternative processing modes see e.g. Ando et al. (2011)]. Computational approaches for finding new miRNAs in deep sequencing data such as miRDeep rely on the detection of traces of this process (Friedlander et al., 2008).

It has now become clear that this is not limited to miRNA. Instead, class specific slicing of widely expressed ncRNAs (but no mRNAs) into smaller RNAs is a widespread regulatory mechanism (Li et al., 2012). Examples are tRNA, where there are several species of tRNA-derived fragments such as tRNA halves, 5′ tRF, 3′ U tRF or 3′ CCA tRF are known (Gebetsberger and Polacek, 2013). Similarly, snoRNA-derived (sdRNAs) fragments are specific for the snoRNA class and the size and position distribution of the sdRNAs are conserved across species (Taft et al., 2009).

In this article, we introduce BlockClust, an efficient approach to detect transcripts with similar processing patterns. We propose a novel way to encode expression profiles in compact discrete structures, which can then be processed using fast graph-kernel techniques.

Note that in this work we do not deal with long RNA sequences such as messenger RNAs which require to deal with exon boundaries or with extreme variability in length and expression levels, rather we consider the transcripts that are retrieved from small RNA-seq protocols and we therefore optimize BlockClust to process transcripts characteristic of small ncRNAs of length 50–200 nt.

We perform both unsupervised clustering and develop ncRNA family specific discriminative models; finally we show how the proposed approach is scalable, accurate and robust across different organisms or experimental protocols.

2 MATERIALS AND METHODS

The core idea of the BlockClust method is to characterize transcribed loci using the expression profiles obtained from deep sequencing experimental protocols. To do so, we extract characteristic attributes from the expression profiles, such as the entropy of the read length or the normalized read expression. We then encode the sequence of several of these attributes in compact discrete structures, which we then process using fast graph-kernel techniques.

More specifically, in order to achieve high computational efficiency, we do not use alignment-based techniques as done e.g. in deepBlockAlign (Langenberger et al., 2012), and we do not resort to a set of handcrafted measurements or features to describe the entire profile as done e.g. in DARIO (Fasold et al., 2011). Instead in BlockClust we partition the reads of an expression profile in a sequence of blocks. We then discretize the statistics of the reads distribution in each block and we encode the result in a discrete data structure. Such representations can be processed by high-performance machine-learning techniques such as kernelized Support Vector Machines (Joachims, 1999) to build classification models or by Locality Sensitive Hashing techniques (Heyne et al., 2012) to obtain fast clustering approaches.

In summary, the two key components in BlockClust are: (i) the expression profile encoding with discretized attributes, and (ii) the combinatorial feature generation from the sequence of attributes.

2.1 Expression profiles encoding

With the term expression profile we denote the set of assembled read sequences relative to a given transcript. In order to extract these profiles, read sequences from the deep sequencing experiments are aligned (or mapped) against their corresponding reference genome in order to get the chromosomal coordinates (note that BlockClust can in principle work on reads that are mapped to assembled transcripts, when there is no reference genome). The information about mapped reads is generally stored using the Sequence Alignment/Map (SAM) format or a compressed binary version of the SAM format (BAM). BAM files can be converted to a six-column Browser Extensible Data (BED) file of tags (a tag is a unique read sequence in a deep-sequencing library). The BED format provides information on the normalized expression of each tag, i.e. the ratio of the read count per tag to the number of mappings on the reference genome. Considering tags instead of reads allows a high loss-less compression of the original data. In BlockClust we further represent this information by (i) grouping tags into ‘blocks’ and sequences of blocks into ‘block groups’, (ii) extracting several statistics from the read signal within each block and globally over the whole block group and (iii) discretizing these statistics. In this way we can represent hundreds of thousands of reads over regions spanning hundreds of nucleotides with few bytes. More in details, the expression-profile-encoding phase is composed of the following steps: (i) conversion of BAM file to BED file of normalized tag expressions, (ii) block and block groups extraction, (iii) statistics extraction for each block and block group, (iv) discretization of the statistics, (v) graph encoding of the block group and of the associated discretized statistics. The novel contribution of this work lies in the details of phases 3 and 5.

2.1.1 Blocks and block groups

In order to enhance computational performance, we compress expression profiles by grouping reads into blocks. Because of biological noise and sequencing errors, the read positions do not respect any exact boundary notion, and one cannot therefore assume that blocks should be non-overlapping. For this reason we use the blockbuster tool (Langenberger et al., 2009) to identify blocks. The idea is to perform peak detection on the signal obtained by counting the number of reads per nucleotide. This signal, spanning adjacent loci, is then modeled with a mixture of Gaussians. An iterative greedy procedure is then used to collect reads that belong to the same block, starting from the largest Gaussian component, and removing them in successive iterations. The tool further assembles a sequence of adjacent blocks into a block group if the blocks are either overlapping or are at a distance smaller than a user-defined threshold. Finally, in BlockClust we assume that a gene can span at most a single block group.

2.1.2 Blocks and block groups attributes

To identify patterns in expression profiles we partition the reads into blocks and block groups and then describe each block and the entire group of blocks with a set of statistics and measures. Note that it is not possible to characterize different ncRNA families using only simple statistics on the overall distribution of reads. To increase the discriminative power we therefore consider the exact sequence of blocks, making use of attributes relative to each individual block and relative to the relations between adjacent blocks. More precisely we define three types of descriptive attributes: (i) block group attributes, (ii) individual block attributes and (iii) block edge attributes, i.e. measures about the relation between two adjacent blocks in a block group. The block group attributes are: entropy of read starts, entropy of read ends, entropy of read lengths, median of normalized read expressions and normalized read expression levels in first quantile. The block attributes are: number of multi-mapped reads, entropy of read lengths, entropy of read expressions, minimum read length and block length. The block edge attributes are: contiguity and difference in median read expressions. The entropy of read starts is defined as $-\sum _i{q}_i{\log }_2{q}_i$, where q_i is the fraction of reads in a given block group starting at position i. The other entropies are defined correspondingly. The overall expression is defined as the sum over all tag expressions per block. The block contiguity is defined as the overlap fraction or the fractional distance between two consecutive blocks. For more details see Supplementary Material Section S.4.

2.1.3 Attribute discretization

To identify patterns in large collections of sequences of blocks we propose to discretize the attributes, treating the resulting intervals as nominal values. This achieves the combined result of reducing data storage requirements and it allows us to use powerful machine-learning techniques that work on discrete data structures. Discretization methods can be divided into those that choose the intervals taking the class information into account and those that are class-blind. As we seek an approach that is ultimately capable of novel discoveries, we opt for the latter. Between the two main class-blind approaches, the equal-width and the equal-frequency discretization, we observe that the first method can yield empty intervals and lose a large amount of information. We chose therefore the equal-frequency algorithm, which sorts all values and then divides the range into a user-defined number of intervals so that every interval contains the same number of values (note that special care must be taken to treat identical values, which can potentially spread over several intervals. We adjust the procedure so that duplicate values belong to a single interval).

2.1.4 Graph encoding

Since the number of blocks is variable we cannot use a simple vector or matrix encoding of the attributes. Instead we encode the sequence of blocks with attributes as a graph with discrete labels. We adopt an encoding similar in spirit to the one used in Kundu et al. (2013). In BlockClust we encode a single non-protein-coding gene with a graph made of two disconnected components: in the first one we represent the overall block group information, while the second one is used to represent the sequence of individual blocks and their relationships. The first component is modeled as a position specific sequence of discretized attributes, that is, each block group attribute type appears consistently at the same position in the modeling sequence (see Figure 1 at the top of the Graph Encoding box). The second component is modeled as a sequence of vertices, each representing a single block, called the backbone sequence. The discretized block attributes are represented as a position-specific sequence and this sequence is connected to the correspondent block vertex. Two blocks that appear subsequently in the assembled transcript are encoded as adjacent vertices. The block edge attributes between two adjacent blocks with starting coordinates i and j respectively, with i < j, are appended at the end of the attributes for the block with starting coordinates i. Note that in practice we collapse the vertex representing the block together with the vertex representing the first attribute. The final structure for the second component is therefore a sort of ‘comb’-shaped graph as shown in Figure 1. Note that the order of the attributes affects the discriminative capacity of the encoding and it therefore needs to be optimized (see Section S.4 in Supplementary Material).

Fig. 1.

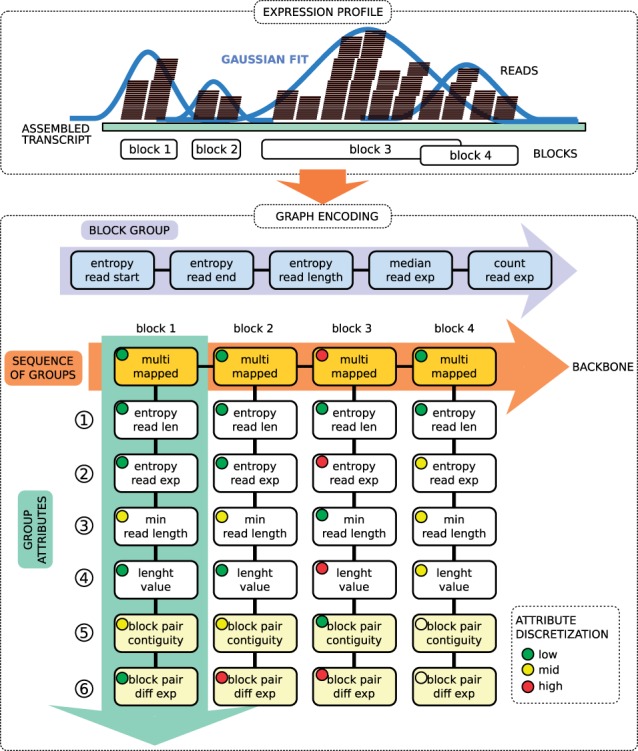
Read profile encoding. (Top) Read profile, and successive partition of reads in blocks (blockbuster). (Bottom) The block partitioned reads are encoded as a graph with two disconnected components: (i) BLOCK GROUP: which contains statistics and attributes of the global distribution of reads; (ii) SEQUENCE OF BLOCKS: which encodes a list of attributes for each individual block. The backbone is the sequence of the most discriminate type of block attribute. The discretized value of each attribute is depicted by a color-coded circle in the corresponding box

The reason for this type of more complex modeling, as compared to a simple sequential encoding, becomes clearer in the next section, where we introduce how the actual features are extracted in a combinatorial way from the graph encoding.

2.2 Combinatorial feature generation

In BlockClust we do not employ alignment-based techniques to compare block groups, as we would incur in high computational costs. Instead given the graph encoding of a block group we extract an explicit feature representation that can be processed more efficiently. The type of features considered are those developed for a recently proposed graph kernel called Neighborhood Subgraph Pairwise Distance Kernel (NSPDK) (Costa and Grave, 2010) and used for the efficient clustering of ncRNA molecular graphs in Heyne et al. (2012).

NSPDK is a fast graph kernel based on exact matching between pairs of small subgraphs. One can view the similarity notion expressed by NSPDK as a generalization of the k-mer substring kernel for strings (with gaps) to the case of graphs. The idea is to decompose a graph into a set of smaller fragments and express the similarity between two graphs as the fraction of common fragments. In NSPDK the fragments are pairs of neighborhood subgraphs for a small radius (parametrized by the maximum allowed radius R) at increasing distances (parametrized by the maximum allowed distance D). Intuitively the radius parameter controls the complexity of the features, while the distance parameter controls the range of locality for the non-linear interactions. A neighborhood graph is a subgraph specified by a root vertex v and a radius R, consisting of all vertices that are at a distance (the distance between two vertices v and u on a graph is defined as the number of edges in the shortest path between v and u) not greater than D from v. All pairs of neighborhood subgraphs can be efficiently enumerated in near linear time and hashing techniques can be used to extract quasi-canonical identifiers from these pairs (see Supplementary Material Section S.1 for a formal introduction and additional details). As shown in Heyne et al. (2012) we can use these identifiers to build feature indices and represent graphs as vectors in a very high-dimensional vector space. Differently from what is done in Costa and Grave (2010) and Heyne et al. (2012) here we make use of the notion of viewpoint [first introduced in Frasconi et al. (2012)]. A viewpoint is an additional information that is placed on specific vertices in the graph encoding. The intended effect is to constrain the feature-generation mechanism in such a way that at least one of the two subgraph root is a viewpoint. In this way we can choose which specific vertices are more relevant in a given domain. In our case we place viewpoints on the backbone, i.e. the chain of vertices representing the blocks. In this way we generate features that at the same time (i) take into account an incremental amount of attributes, but (ii) that work on a much smaller subset of the exponentially large set of possible combinations. Since the sequential order in which we encode the attributes determines the combinations generated, we need to determine the optimal order (see Section 3.1.3 for further details on the parameters optimization step). The features obtained following the NSPDK approach contain pairs, triplets and higher order combinations of the original attributes. Having these complex features allow linear models to express complex classification decisions that are non-linear with respect to the original sequential information. Figure 2 depicts how the features are generated with a given radius and distance. The technique that we present here allows therefore to combine the benefits of large-scale efficiency provided by linear methods and locality sensitive hashing with accurate non-linear modeling.

Fig. 2.

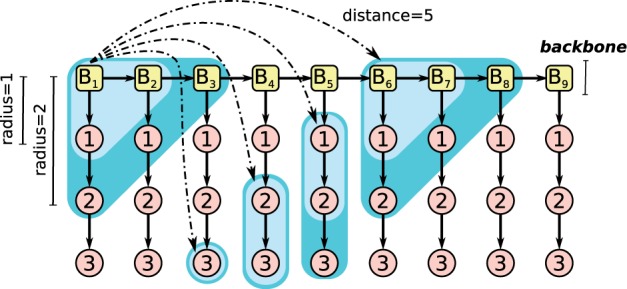
Combinatorial features. Given a directed graph, the NSPDK approach constructs a large number of features taking only specific subgraphs into account. The procedure is parametrized by the maximum radius R and the maximum distance D. Each vertex is considered in turn as a root. A neighborhood graph of radius r = 1, … , R is extracted around each root. All possible pairs of neighborhood graphs of the same size r are considered, provided that their respective roots are exactly at distance d = 1 … D. Viewpoints are used to constrain at least one of the roots to be on the backbone. The graph shows a specific case of combinatorial feature construction with r = 1, 2 and d = 5 with the viewpoint in v = B₁

2.3 ncRNA expression profile clustering

The similarity notion of NSPDK can be used directly by clustering algorithms that make use of pairwise similarity or distance information. More specifically the similarity between two expression profiles is equivalently defined as the dot product of the corresponding high-dimensional vector representations. Note that in large-scale settings, when a quadratic complexity in space or time is unfeasible, we can avoid to materialize the pairwise similarity matrix and resort instead to more efficient locality sensitive hashing techniques (see Supplementary Material Section S.2 for details) as introduced in Heyne et al. (2012). This technique allows us to extract the approximate nearest neighbors in linear time complexity.

As a clustering algorithm BlockClust uses the Markov Cluster Process (MCL) algorithm (Enright et al., 2002). Given a weighted nearest neighbor graph G between the instances to be clustered, the MCL algorithm applies a parametrized algebraic process to the matrix of random walks on G. The underlying idea is to characterize clusters as subgraphs such that a random walk on the graph will infrequently go from one subgraph to another. The MCL was chosen as it produces balanced non-hierarchical clusters and it does neither need seeding information nor a user-defined number of clusters. Moreover it can be employed in large-scale settings as it can work with sparse graph/matrix implementations. In our application setting, the inflation parameter, which affects the cluster granularity, was selected to retain relatively small clusters.

2.4 ncRNA expression profile classification

In addition to unsupervised clustering, BlockClust provides a supervised classification mode. Given a set of expression profiles for a known ncRNA family or class and a set of negative examples, i.e. expression profiles of ncRNAs with a different or unknown function, BlockClust can efficiently build a discriminative linear binary classifier. As in the unsupervised clustering mode, we first extract explicit high-dimensional vector representations from the expression profile encodings. Subsequently BlockClust uses fast and scalable linear techniques such as Stochastic Gradient Descent Support Vector Machines (Bottou, 2010) to induce a discriminative model. Note that even if we use linear models to allow scaling to genome wide data settings, the resulting classifier is in fact non-linear in the original attribute space.

The resulting models are precise and surprisingly robust: a model for the identification of tRNA genes can be trained on human data with reads extracted under a specific experimental protocol (say Illumina GAII) and it can be used to reliably annotate expression profiles across diverse organisms (e.g. fly or plants), from data produced by different experimental protocols (see Section 3.2).

3 RESULTS AND DISCUSSION

In order to evaluate the BlockClust approach we formulate and analyze the following questions.

• Q1: Is the BlockClust encoding of expression profiles informative enough to be used in clustering procedures to detect specific ncRNA classes?
• Q2: Is the BlockClust encoding of expression profiles robust across different sequencing platforms, organisms, tissues, cell lines?
• Q3: Can BlockClust be used for the annotation of known ncRNAs classes?
• Q4: How does BlockClust compare to other tools for clustering or classification of expression profiles?

3.1 Q1: clustering ncRNAs with encoded expression profiles

3.1.1 Performance measures

Given the graph encoding of two expression profiles, BlockClust can compute a similarity score between the corresponding high-dimensional feature representations. Formally, given two expression profiles a and b, if x_a and x_b are the corresponding vector representations, then their (cosine) similarity is defined as $S(a,b)=\frac{\langle x_a,x_b\rangle }{\sqrt{\langle x_a,x_a\rangle \langle x_b,x_b\rangle }}.$ To assess the quality of this similarity notion, we measure the grouping tendency for profiles of functionally identical RNAs. As a measure we chose the Area Under the Curve for the Receiver Operating Characteristic (AUC ROC), which is defined as the integral of the fraction of true positives out of the total actual positives with respect to the fraction of false positives out of the total actual negatives at various threshold settings. More precisely, given a profile a we sort all other profiles by decreasing similarities with respect to a. Ideally, we expect the neighboring instances to share the same ncRNA class, i.e. we expect the same class to appear preferentially at the beginning of the sorted list. We consider the class of profile a as the positive class and all other classes as the negative class. Given this assignment we can compute the AUC ROC as if a was a classifier. The overall performance is then computed as the average AUC ROC over all instances. As a general rule of thumb, AUC ROC values >0.9 are excellent, ∼0.8–0.9 are indicative of good performance, 0.7–0.8 indicate a somewhat sufficient quality, while 0.5 is the baseline for pure random performance.

Since the similarity score can be used for clustering purposes we also need a performance measure for the final cluster quality. We do not resort to measures such as the adjusted Rand index or the F1 score since we expect the same ncRNA class to be partitioned in several highly similar sub-groups, a situation that would be penalized by such measures. We therefore score the cluster purity via the average precision per cluster, defined as the fraction of instances belonging to the majority class present in each cluster.

3.1.2 Datasets

We used NGS data generated by Illumina sequencing of human embryoid body (EB) and embryonic stem cells (hESC) (Morin et al., 2008), H1 cell line (H1) and IMR90 cell line (Bernstein et al., 2010), referred to as Development Data in the following. In order to evaluate robustness of BlockClust we used a comprehensive collection of datasets (see Supplementary Table S1), which we refer to as Benchmark Data, that comprises 32 samples, out of which 13 from human, seven from mouse, five from fly (Drosophila melanogaster), two from chimp, two from worm (Caenorhabditis elegans) and three samples from plant (Arabidopsis Thaliana). The sequencing machines were: Illumina GAII, Illumina GAIIx, Illumina GA, Illumina HiSeq 2K. Cell types, tissues and organisms include human and chimp brain tissues, human skin, embryos of worm, head and body of fly, testis and uterus of mouse and leaves and seeds of plant. Cell lines range from the H1 cell line to breast cancer cell line MCF-7 from human, from S2 to KC cells for the fly.

3.1.3 Parameters optimization

The BlockClust system configuration comprises several parametric choices for each phase: (i) block identification, (ii) graph encoding and (iii) clustering or classification (see Table 1). For the blockbuster module used in phase (i) we need to specify the desired grain resolution in terms of cluster distance and standard deviation; in (ii) for the attribute construction phase we need to specify the discretization resolution and for the feature construction phase the complexity of the features via the maximal radius and distance needs to be set; finally in the clustering phase (iii) we need to specify the desired grain resolution for the clusters via the inflation and pre-inflation parameters and the regularization trade-off in the classification phase.

Table 1.

Parameter optimization

Component	Parameter	Interval	Step	Optimum
blockbuster	Cluster distance	20–100	10	40
blockbuster	Scale of standard deviation	0.2–0.8	0.1	0.5
Encoding	Discretization bins	3, 5, 7	2	3
NSPDK	Radius R	1, 3, 5, 7	2	5
MCL	Inflation	1–30	0.3	20
MCL	Pre-inflation	1–30	0.3	20

Overview of the parameters value ranges, search step size and the selected optimal values. Note that D is set as a function of R: D = 2 × R + 1.

We optimized all parameters using a 35/35/30%-dataset split of Development Data into train/validation/test set, respectively. In the remainder of the article all performance measures are reported on the test set, while the quality of the parametric choices are evaluated on the validation set. Note that the parameters are not optimized on each ncRNA class separately.

One initial difficulty to overcame is represented by the circular notion that (i) we would like to partition the dataset without splitting the profiles that belong to a unique ncRNA, but at the same time and (ii) we need to have a parametric method to identify the extent of the underlying ncRNAs and the parameters have to be determined on a valid dataset partition. We therefore break the circularity by employing the conservative and non-informed notion of read stretches, defined as a series of sorted reads separated by a maximum distance d. With the exception of a few ribosomal RNAs, most of the classic short ncRNAs are not longer than 500 nt. Finally, we set d to 500 and partition the set of the resulting read stretches in train, validation and test sets.

In order to evaluate the quality of the pre-processing step, i.e. the extraction of blocks and block groups, we measured the fraction of retrieved annotations. An annotation is considered retrieved if there is a reciprocal overlap of at least 70% between the annotation and the block group. All the transcripts failing this criteria and which are also not in the length range of 50–200 nt were discarded. For further details on the parameter optimization phase refer to Supplementary Section S.3.

3.1.4 Performance results

In Table 2 we report for each ncRNA class the average AUC and the overall weighted mean on all classes averaged over 10 random test splits of Development Data. In our sample we observed seven ncRNA classes, namely: miRNAs, tRNAs and C/D-box snoRNAs (which contribute to the majority of the profiles) and rRNAs, snRNAs, Y_RNAs and HACA-box snoRNAs. Overall, we observed good average performance results (AUC ROC ≈ 0.8). Best results were with miRNA (AUC ROC ≈ 0.9), H/ACA-box snoRNA (AUC ROC ≈ 0.9) and rRNA (AUC ROC ≈ 0.85), good results were obtained with tRNA (AUC ROC ≈ 0.75) and C/D-box snoRNAs, while snRNA and YRNA performed poorly (AUC ROC ≈ 0.6). These last ones are also the least represented having only ∼10 instances each.

Table 2.

Clustering performance of BlockClust averaged over 10 random test splits of Development Data

ncRNA class	Number of transcripts	AUC	Number of clusters	Precision
miRNA	168	0.896	10	0.855
tRNA	173	0.741	17	0.837
C/D-box snoRNA	78	0.731	7	0.683
H/ACA-box snoRNA	4	0.838	0	0
rRNA	20	0.872	2	0.956
snRNA	7	0.637	0	0
Y_RNA	8	0.685	0	0
Weighted average	458	0.805	36	0.813

AUC ROC was measured from the expression profile similarities and precision from the clusters generated by the MCL algorithm. Note that due to the very low number of transcripts for the classes H/ACA-box snoRNAs, snRNAs and Y_RNAs we could not retrieve any significant clusters.

In Table 2 we report also details on the precision clustering performance for the four ncRNA classes with the largest number of instances: tRNA, miRNA, rRNA and C/D-box snoRNA. We used the MCL-clustering algorithm with inflation parameter set to 20 to capture also small clusters. The clusters obtained for tRNA, miRNA and rRNA are quite consistent, containing <20% extraneous material on average, while for C/D-box snoRNAs the precision is ≈68%. For the remaining three classes with low number of instances, MCL could not identify any cluster.

3.2 Q2: robustness and range of applicability

A desirable property for a parametric computational approach is to require little to no parameter re-configuration when the data changes in ways that are marginal with respect to task at hand. In our case we would like the parametrization of BlockClust to be insensitive to the sequencing machine type and to factors like the cell line, tissue and organism. In order to evaluate the extent of BlockClust robustness we applied BlockClust on Benchmark Data.

Supplementary Table S4 shows that the clustering performance measured via the AUC ROC is good and consistent with the performance measured on the Benchmark Data. This result tells us that the parameters for blockbuster and the encoding parameters (such as the type of attributes and their discretization levels, and the values for the maximum radius and the maximum distance in NSPDK) are indeed insensitive to the variation of sequencing machine or organism.

3.3 Q3: annotation of known ncRNAs with encoded expression profiles

BlockClust can be used to extract expression-profile models for each ncRNA class and thus provides a way to automatically classify and annotate unknown deep sequencing data into known ncRNA functions. Our models have linear complexity, are extremely efficient and can be used to scan genomes and meta-genomes, achieving a speed of 2–4 million reads per minute on standard hardware (Intel Core i3-2100 at 3.10 GHz) if we start from BED files as input and exclude the genome mapping phase. We tested the robustness and accuracy of these models on the major ncRNA classes: miRNAs, tRNAs and C/D-box snoRNAs. Table 3 shows results for supervised classification task averaged over 10 random test splits of Development Data. In Supplementary Table S5 we report very good results across a variety of conditions present in Benchmark Data. The classifiers that we build exhibit the same robustness that was found for the clustering task in Section 3.2. That is, models trained on the processing traces of ncRNAs in human, can be used without any re-calibration to identify the same type of ncRNA class in distant organisms such as worm, fly and plant, irrespective of changes in the sequencing machine type or the cell line or tissue. These models maintain generally a high precision (≈0.9) for tRNAs and miRNAs while they suffer from a more severe drop in recall (≈0.8 for miRNA and 0.65 for tRNA). In the case of C/D-box snoRNAs results are more variable and exhibit in general quite poor recall rates.

Table 3.

Classification performance of BlockClust averaged over 10 random test splits of Development Data

ncRNA class	Number of transcripts	PPV	Recall
miRNA	168	0.901	0.886
tRNA	173	0.899	0.796
C/D-box snoRNA	78	0.870	0.474

3.4 Q4: Performance comparison

Other approaches known in literature that can process expression profiles derived from deep sequencing data are deepBlockAlign (Langenberger et al., 2012) and DARIO (Fasold et al., 2011).

3.4.1 Clustering performance comparison

Since currently there are no available tools that can cluster expression profiles, we compare against deepBlockAlign even though this tool aims at solving a different problem. deepBlockAlign is a tool to align expression profiles which also uses blockbuster to generate block groups. deepBlockAlign uses a variant of the Sankoff algorithm to obtain an optimal alignment and computes a corresponding pairwise similarity score between expression profiles. Finally these similarities can be used to cluster expression profiles.

We applied both tools to the Benchmark Data. We evaluated both the quality of the similarity notion generated by the tools as well as the quality of the clusters that can be obtained under the respective similarities. In Table 4 we report the average AUC ROC for each individual ncRNA class. The class specific and weighted-averaged ROC scores indicates that BlockClust is highly competitive.

Table 4.

Metric performance: BlockClust versus deepBlockAlign

ncRNA class	Number of instances	BlockClust	deepBlockAlign
		AUC ROC	AUC ROC
miRNA	3869	0.925	0.714
tRNA	4988	0.795	0.701
C/D-box snoRNA	731	0.762	0.615
H/ACA-box snoRNA	142	0.859	0.720
rRNA	770	0.873	0.759
snRNA	240	0.698	0.610
YRNA	244	0.694	0.656
Weighted average	11061	0.839	0.700

Comparison on Benchmark Data. The AUC ROC results across different species, tissues and cell lines are averaged with weight proportional to the number of instances per class.

An additional advantage of BlockClust is its computational complexity and wall clock runtime. Since deepBlockAlign is designed with the purpose of actually generating the alignments of the read profiles, it has a quadratic complexity in the number of profiles. BlockClust on the other hand, is designed to solve the clustering problem and, by exploiting the hashed approximate nearest neighbors query technique, it can achieve a quasi-linear runtime. Moreover, deepBlockAlign uses computationally expensive algorithms like Needleman–Wunsch (O(m²)) for block alignment with $m\in 15\dots 30$ nucleotides, and a variant of the Sankoff algorithm for block group alignment (O(n⁶)), where $n\in 1\dots 5$ is the number of blocks. In contrast BlockClust uses explicit graph kernels with a linear complexity (O(n)) since it performs a simple dot product and a preprocessing attribute extraction phase that runs in O(m). Not surprisingly, given the different problems that are solved, BlockClust achieves a speedup of 60-fold, with a wall clock runtime of 50 s as compared to 58 min for deepBlockAlign on a dataset of ≈600 profiles.

In addition, we evaluated the quality of the clusters that can be obtained using the deepBlockAlign similarity score. As we have done with BlockClust, we applied the MCL algorithm to the neighborhood graph obtained with the deepBlockAlign similarity score. We then compared the resulting clusters obtained varying the inflation and the pre-inflation parameters of MCL. In Figure 3 we report the median cluster precision versus the resulting number of clusters for different MCL parameter settings. We observe that BlockClust tends to produce larger clusters with a higher precision on average than deepBlockAlign.

Fig. 3.

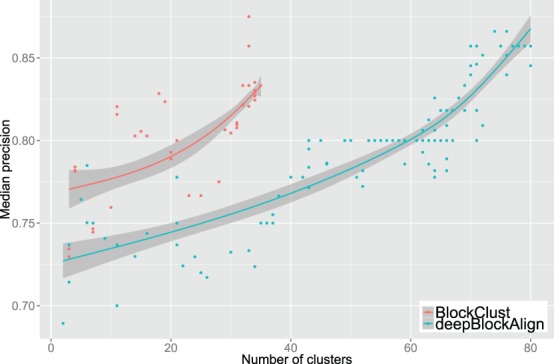
Clustering performance: BlockClust versus deepBlockAlign. Comparison of median precision with respect to number of clusters on the GSM450239 dataset when the MCL clustering algorithm uses the expression profile similarity scores produced by BlockClust (red) or by deepBlockAlign (blue)

As a final remark, note that deepBlockAlign was developed and optimized to identify similar processing patterns, even for different RNAs (e.g. between miRNA and some tRNAs) and it therefore might give suboptimal results when used to cluster the ncRNAs into the families of their primary function.

3.4.2 Classification performance comparison

The DARIO tool is used in a supervised setting to classify expression profiles into known ncRNA classes. The tool also uses blockbuster in a pre-processing phase to identify block groups. Given a block group DARIO extracts a set of attributes without any need for discretization. Random forests are then employed as the underlying predictive system. Note that, differently from BlockClust, DARIO does not explicitly take the sequential arrangement of the blocks into account.

In Table 5 we report the classification performance for both tools: clearly, for all three classes BlockClust has better precision than DARIO. BlockClust shows higher recall for miRNAs where as DARIOs recall is higher for remaining two classes.

Table 5.

Classification performance: BlockClust versus DARIO

	miRNA		tRNA		snoRNA C/D-box
	PPV	Recall	PPV	Recall	PPV	Recall
BlockClust	0.88	0.89	0.95	0.80	0.74	0.39
DARIO	0.85	0.81	0.92	0.88	0.46	0.52

Comparison on the GSM769510 dataset.

Since DARIO cannot be run as a standalone tool, and it is accessible only via a web interface, we could not reliably compare the respective run times.

3.5 Analysis of known ncRNA clusters

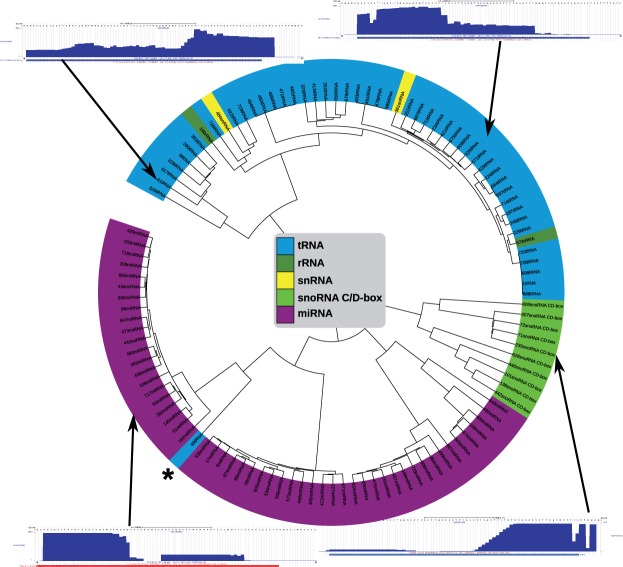
To validate our approach, we clustered all block groups from the data set GSM768988. The MCL clustering produced several small clusters. We analyzed the clusters from each ncRNA class that achieved the highest precision. In Figure 4, we show the dendrogram together with representative read profiles for the selected clusters.

Fig. 4.

Dendrogram of clusters with highest precision. One representative read profile for miRNAs and snoRNAs, and two for tRNAs are shown. The horizontal bar under each profile represents the annotation of the corresponding ncRNA

For tRNAs, we see very different profiles composed of a mixture of tRNA halves and 5′- or 3′-derived fragments. This can already be seen in the two examples shown in Figure 4. The left profile corresponds to a tRNA having mainly 3′-derived fragments, whereas 5′-derived fragments dominate the right profile. MicroRNAs exhibit the typical block-like structure, either with only one solid block for the miRNA, or with two blocks for miRNA and miRNA* [see Fasold et al. (2011) for more details and illustrations].

When examining snoRNAs, we found an even more interesting processing pattern with a step-wise extension. For that reason, we investigate the snoRNA cluster in more detail. The cluster with the highest precision contains only C/D-box snoRNAs. According to the literature (Taft et al., 2009), snoRNA-derived fragments from C/D-box snoRNAs are predominantly stemming from the 5′-end. Thus, according to the literature, the profiles for the snoRNAs shown in Figure 5 should be prototypical examples. However, to our surprise, our C/D-box snoRNA cluster contained mostly 3′-derived fragments with quite some variation in length.

Fig. 5.

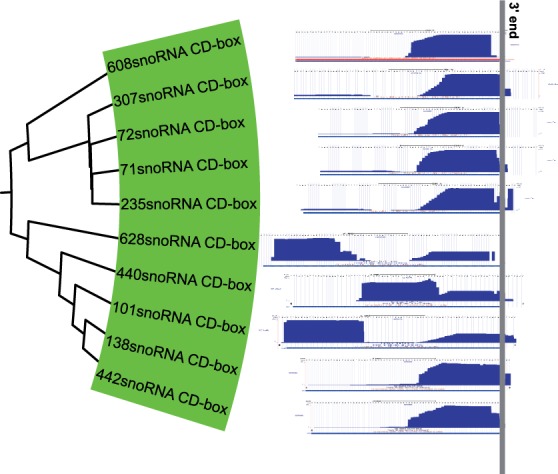
Read profiles of the snoRNA cluster. All profiles are having the same scale with respect to the genomic sequence. Furthermore, they are aligned at the 3′-end of the annotated transcript

Finally, we examined the tRNA that was clustered together with the miRNAs (marked with a star in Figure 4). When analyzing the read profile of this tRNA we could only find very precisely cut 5′-derived fragments (see Figure 6). It is very conceivable that this tRNA might actually be processed by Dicer and/or is associated with the Argonaute complex. First, the 5′-derived fragment has a length of ≈26 nt, which is compatible with the possible lengths for miRNAs. Second, it is known that 5′-tRFs are likely to be processed by Dicer (Gebetsberger and Polacek, 2013). A miRNA-like function has been investigated in detail by Maute et al. (2013). Finally, it has been shown that only the 5′-derived fragments but not the 3′-derived ones are inhibiting translation and are associated with the Argonaute complex (Ivanov et al., 2011).

Fig. 6.

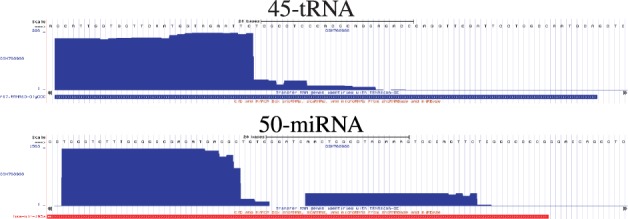
Read profiles of a tRNA clustered within miRNAs and a close-by miRNA. The horizontal bar under each profile represents the annotation of the corresponding ncRNA

4 CONCLUSION

We have introduced BlockClust, an efficient approach to detect transcript with similar processing patterns. The procedure that we have proposed is stable with respect to changes in sequencing machines, cell lines and organisms and can be used to reliably cluster and annotate sequencing output at increasing depths. Differently from other methods, in BlockClust we encode expression profiles with discrete structures that can be processed efficiently and, at the same time, can retain most of the information content of the profiles.

In future work we will present the application of BlockClust to large deep sequencing datasets to discover novel classes of functional ncRNAs.

BlockClust, including all tool dependencies, is available at the Galaxy tool shed (Goecks et al., 2010), and can easily be installed and used via a web interface.

Funding: German Research Foundation (DFG-grant SFB 992/1 and BA 2168/3-1 to R.B.).

Conflict of Interest: none declared.