Detecting independent and recurrent copy number aberrations using interval graphs

Abstract

Motivation: Somatic copy number aberrations (SCNAs) are frequent in cancer genomes, but many of these are random, passenger events. A common strategy to distinguish functional aberrations from passengers is to identify those aberrations that are recurrent across multiple samples. However, the extensive variability in the length and position of SCNAs makes the problem of identifying recurrent aberrations notoriously difficult.

Results: We introduce a combinatorial approach to the problem of identifying independent and recurrent SCNAs, focusing on the key challenging of separating the overlaps in aberrations across individuals into independent events. We derive independent and recurrent SCNAs as maximal cliques in an interval graph constructed from overlaps between aberrations. We efficiently enumerate all such cliques, and derive a dynamic programming algorithm to find an optimal selection of non-overlapping cliques, resulting in a very fast algorithm, which we call RAIG (Recurrent Aberrations from Interval Graphs). We show that RAIG outperforms other methods on simulated data and also performs well on data from three cancer types from The Cancer Genome Atlas (TCGA). In contrast to existing approaches that employ various heuristics to select independent aberrations, RAIG optimizes a well-defined objective function. We show that this allows RAIG to identify rare aberrations that are likely functional, but are obscured by overlaps with larger passenger aberrations.

Availability: http://compbio.cs.brown.edu/software.

Contact: braphael@brown.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Copy number aberrations (CNAs) are gains and losses of large segments of the genome—ranging in size from a few kilobases to whole chromosomes. Somatic CNAs (SCNAs) that occur during the lifetime of an individual are a major contributor to cancer development, particularly for solid tumors (Cancer Genome Atlas Research Network, 2013; McLendon et al., 2008; The Cancer Genome Atlas Network, 2012; Zack et al., 2013).

In the last decade, technologies with increasing resolution have been introduced to measure CNAs. Cytogenetic techniques such as comparative genomic hybridization were replaced by higher resolution array-comparative genomic hybridization (aCGH) and SNP genotyping arrays, and most recently these are being supplanted by high-throughput sequencing platforms. The latter identify CNAs as deviations from the expected number of reads aligned to an interval of the reference genome (Chiang et al., 2008; Xi et al., 2010), and depending on the sequencing depth and technology, can measure CNAs to single-nucleotide resolution. In parallel with the technological developments, numerous computational methods have been developed to identify CNAs in single samples (Chiang et al., 2008; Hupé et al., 2004; Olshen et al., 2004).

A key challenge in applying these technologies to cancer genomes is that most SCNAs measured in tumor samples are random, passenger events that do not contribute to the cancer phenotype. A common strategy to distinguish functional, driver aberrations from such random, passenger events is to identify recurrent aberrations shared by multiple samples (Rueda and Diaz-Uriarte, 2010). However, this is a notoriously difficult problem because SCNAs vary widely in length and position across different samples. For example, a tumor-suppressor gene might be deleted by a small focal aberration in one sample, while in another sample the same gene is deleted by a whole chromosome loss. The varying size and starting/ending positions of aberrations across samples create a complex pattern of overlapping aberrations. This makes it difficult to determine which gene or genomic locus (if any) is the target of the aberration, a necessary prerequisite for any statistical test of recurrence.

Early methods for finding recurrent SCNAs used the straightforward approach of finding the minimum common region of aberrations across samples (Aguirre et al., 2004). Subsequently, numerous methods with more complex models were introduced (Ben-Dor et al., 2007; Beroukhim et al., 2007; Diskin et al., 2006; Magi et al., 2011; Mermel et al., 2011; Morganella et al., 2011; Niida et al., 2012; Sanchez-Garcia et al., 2010; Walter et al., 2011). While these methods differ in important details, they all use variations of two basic steps: (i) compute a score at each genomic locus (typically a probe in microarray datasets) indicating the recurrence; (ii) examine correlations between recurrences scores of nearby loci to separate the true target region from other close, high-scoring regions. In addition, some approaches also compute the statistical significance of the resulting predictions, using either a fixed distribution or a permutation test that preserves the lengths of SCNAs.

A major challenge in detecting recurrent SCNAs is that closely located driver aberrations lead to correlations between the recurrence scores. For example, Figure 1 shows SCNAs in 20 samples. The number of samples with an aberration at each locus gives a recurrence score across the genome. However, these peaks are correlated: e.g. the fifth peak results largely from intervals shared with the fourth and third peaks. Methods that predict recurrent SCNAs must address the problem of how to separate peaks, or high scoring regions, into independent copy number events. One of the most-widely used methods, GISTIC (Beroukhim et al., 2007), introduced a greedy procedure that removes the aberrations contributing to the highest peak, and then rescores the remaining SCNAs, continuing this iterative procedure until no more significant peaks are found. While GISTIC has been very successful in identifying recurrent SCNAs, the greedy nature of the peel-off procedure reduces the sensitivity to discover real secondary driver events if they are close to another primary driver event.

Fig. 1.

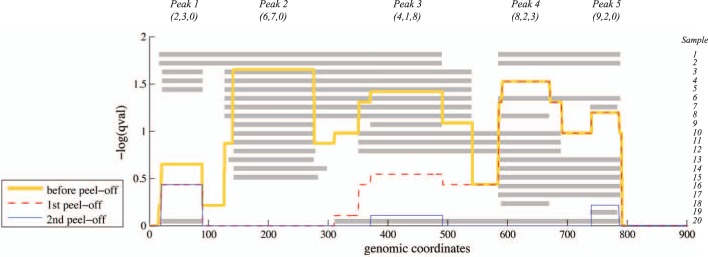
SCNAs in 20 samples with an interleaved pattern of overlapping intervals and three recurrent aberrations (Peaks 2, 3 and 4). Gray rectangles represent locations of SCNAs in each sample. The aberration score (e.g. G-score or q-value from GISTIC) is shown in yellow and has five distinct peaks. Greedy algorithms such as GISTIC/GISTIC2 select the highest scoring Peak 2 and then peel off the constituent intervals leaving Peak 4 as the next highest score (red line). Blue line indicates the distribution of score after selecting Peak 4 in the second peel off. Peak 3 is not identified, although there are four intervals starting immediately before Peak 3 (left intervals), eight intervals ending immediately after Peak 3 (right intervals), and one interval satisfying both conditions (unique intervals). Numbers under each peak name indicate the number of (left, unique, right) intervals for that peak, which we use for scoring in RAIG (Section 2). Note that each peak corresponds to a maximal clique in the interval graph representation (Fig. 2)

JISTIC (Sanchez-Garcia et al., 2010) and GISTIC2 (Mermel et al., 2011) proposed alternative peel-off procedures with better performance. GISTIC2 uses an arbitrated peel-off procedure that rescores secondary peaks by assigning weights to intervals in proportion to the number of peaks in which they contribute (Fig. 1). While this approach considers the correlations between high-scoring peaks, these correlations are considered in an iterative manner: there is no attempt to globally maximize an objective function. We observed that the peel-off procedure could fail to detect high-scoring recurrent regions that were composed of numerous intervals that are shared with other recurrent regions, e.g. peak 3 in Figure 1. The continued development of peel-off procedures emphasizes the difficulty in identifying recurrent SCNAs, particularly secondary aberrations that are nested within larger aberrations. Indeed, the overlap between the predictions from different methods is generally fairly small (Yuan et al., 2012). Moreover, the peel-off procedures implemented in GISTIC, GISTIC2, JISTIC and related methods were originally developed for microarray data and rely on markers (probes) to define either boundaries or weights of peaks. This complicates the application of these approaches to high-throughput sequencing datasets.

At the same time, existing methods for identifying SCNAs do not address the challenges of rare SCNAs that may not be statistically significant on their own. Recent cancer genome sequencing studies have shown that a relatively small number of genes are mutated at high frequency in a cohort of cancer patients with many genes mutated at lower frequencies (Garraway and Lander, 2013). This ‘long tail’ phenomenon implies that rare mutations/aberrations cannot be discarded and require further scrutiny. A promising approach to address this long tail is to analyze combinations of mutations/aberrations in various signaling and regulatory pathways (Ciriello et al., 2012; Leiserson et al., 2013; Vandin et al., 2011, 2012). While rare somatic mutations may be directly incorporated in pathway analyses, there is no corresponding approach to identify rare SCNAs: most approaches focus on the problem of identifying SCNAs that are individually significant.

To address the limitations of current approaches in detecting rare and secondary aberrations, we were motivated to develop a new approach that identifies both recurrent and independent SCNAs by optimizing a score that considers the composition and the correlation between all SCNAs on a chromosome across a set of samples. We introduce RAIG (Recurrent Aberrations from Interval Graphs), an algorithm to detect independent and recurrent SCNAs by selecting an optimal subset of maximal cliques in an interval graph. In contrast to existing approaches that deconvolve the recurrence score, RAIG analyzes the combinatorial structure of the underlying intervals, and thus explicitly models the dependencies between the values of the recurrence score. RAIG uses a dynamic programming algorithm to optimize a rigorous objective function for the selection of recurrent aberrations. Moreover, RAIG is very efficient, as maximal cliques in an interval graph can be efficiently enumerated. We show that our RAIG algorithm performs very well on both simulated data and data from several cancer types from The Cancer Genome Atlas (TCGA). In particular, RAIG has higher sensitivity in detecting rare SCNAs and secondary aberrations that are missed by iterative peel-off procedures, while also retaining high specificity. RAIG is simple and fast, and readily adaptable for high-throughput sequencing data.

2 METHODS

2.1 Interval graph representation of SCNAs

As in most methods for analyzing recurrent SCNAs, we begin with a collection of segmented copy number profiles from a set of individuals. Thus, we assume that the copy number data from each individual has been parsed into a collection of putative deletion and amplification intervals, using one of the many algorithms to segment copy number data into intervals of equal copy number (e.g. Chiang et al., 2008; Hupé et al., 2004; Olshen et al., 2004). Because we analyze interval data, rather than probe data, our approach is readily applicable to microarray or high-throughput sequencing approaches for measuring copy number.

The first step in determining recurrent SCNAs is to find regions of common intersection between intervals across a subset of samples (Fig. 2A). Here, we introduce a general approach to finding common intersections. We model the intersections between segmented copy number profiles using an interval graph G. For a chromosome arm $\mathcal{A}$, let G = (V,E) be a graph where each vertex $v\in V$ corresponds to an interval in a sample and each edge $e=(u,v)\in E$ joins intervals that intersect (Fig. 2B). Interval graphs are a special class of graphs and a number of important optimization problems, that are generally NP-hard, can be solved efficiently on interval graphs (Golumbic, 2004), a fact we will exploit in our algorithm below. Although interval graphs have been used many times in bioinformatics since Benzer’s experiments in bacterial genes in the 1950s (Benzer, 1959), to our knowledge they have not been used to model the problem of finding recurrent SCNAs.

Fig. 2.

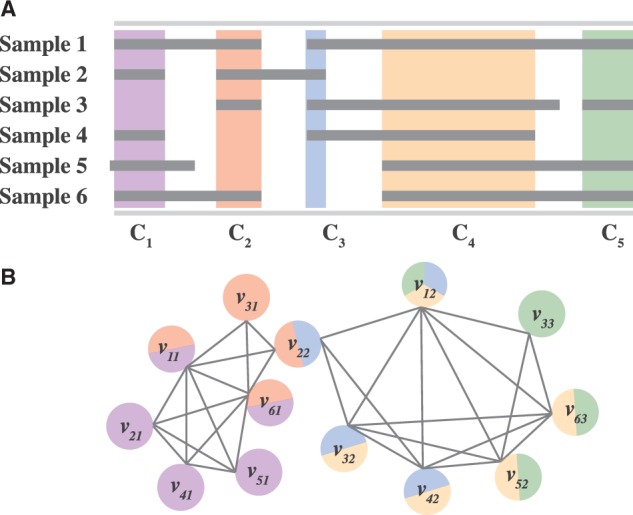
(A) SCNAs (gray rectangles) in different samples with regions of common intersections C₁,C₂, … ,C₅ highlighted in different colors. (B) The interval graph formed from SCNAs in (A). Each vertex v_ij represents the j-th aberration in sample i. Two vertices are connected with an edge if their corresponding aberrations intersect. Vertices are colored according to the common intersections in which the aberration is involved

A set of intervals containing a common region of intersection corresponds to a clique in the interval graph G; i.e. a set of vertices with edges between each pair, also known as a complete subgraph. Similarly, the maximal set of intervals sharing a common intersection that cannot be extended by adding an additional sample corresponds to a maximal clique, a clique that cannot be extended with an additional vertex. Finding all maximal cliques in general graphs is an NP-hard problem (even finding a maximum clique in general is NP-complete), but one can enumerate all maximal cliques in an interval graph in polynomial time (Habib et al., 2000).

For each chromosome arm, we construct two separate interval graphs: one for amplifications and one for deletions. We compute all maximal cliques and order them according to their genomic location $C=(C_1,C_2,\dots ,C_m)$. This ordering can be easily obtained by sorting all interval endpoints, and scanning their common regions using a sweep line algorithm from left to right [For instance see Habib et al. (2000).] Similar to GISTIC2 (Mermel et al., 2011), we also define a gene-level version of overlaps for deletions. That is, different portions of a gene may be deleted in different individuals. We consider all such events as deletions of the gene and thus we consider two deletion intervals u and v as overlapping if at least one endpoint of u and one endpoint of v are located within the same gene.

2.2 From maximal cliques to independent and recurrent SCNAs

Each maximal clique C_k represents an aberration that is common to multiple individuals, and corresponds to a peak in the recurrence score plot (cf. Fig. 1). However, only a subset of these maximal cliques are likely to be interesting SCNAs. For example, a single erroneous interval in only one individual could create two maximal cliques from what should be considered a single recurrent aberration. Figure 2 shows such an example, where maximal clique C₅ is determined by a single interval v₃₃ in sample 3. If this interval was deemed to be experimental error rather than true SCNA and removed, then clique C₅ would disappear. Similarly, clique C₃ is determined by a single interval v₂₂ in sample 2. If the endpoint of this interval was shifted slightly to the right (e.g. if the segmentation was slightly off), then clique C₃ would disappear. If both errors occurred and C₅ and C₄ were removed, then C₄ corresponds to the single common region of SCNA in most samples.

Thus, in addition to considering maximal cliques, we should also analyze maximal cliques that result after the removal, or shifting of endpoints, of a small number of erroneous intervals. Because the removal of intervals, or shifting of interval endpoints, affects neighboring cliques on the genome, we consider blocks of consecutive cliques. We propose an algorithm that finds an optimal partition of maximal cliques into blocks according to both the number of intervals that contribute to each maximal clique and the dependencies between these contributions.

2.3 Algorithm

Our RAIG algorithm examines maximal cliques, or small blocks of consecutive maximal cliques in C, as potential recurrent SCNAs. We define a block B_ij as an ordered list (C_i,C_i+1, … ,C_j) of consecutive maximal cliques. Below, we define the score for each block. Our goal is to select a collection of non-overlapping blocks whose total score (i.e. the sum of the scores of each block in the collection) is maximized under the constraints that the size of the blocks is not too large and the score of each block in the collection is above a threshold. In the following sections, we formally define our scoring scheme and optimization problem. Then we present an efficient algorithm to solve the problem.

2.3.1 Scoring blocks

Let $C=(C_1,C_2,\dots ,C_m)$ be the ordering of all maximal cliques such that for every interval v, the maximal cliques containing v are in consecutive order. Given the ordering C, for every clique C_k, let c_k be a coordinate such that c_k belongs to all the intervals in C_k but does not belong to any interval which is not in C_k. Note that because of the definition of maximal cliques, for every k, such c_k always exists and we have c₁ < c₂ < ⋯ < c_m.

For a given interval v, let a_v be its left endpoint and let b_v be its right endpoint, respectively. We refer to a_v and b_v as the boundary endpoints of the interval. Given a maximal clique C_k, we define $\mathcal{L}(C_k)=\{v|c_{k-1}<a_v\le c_k\}$ and $\mathcal{R}(C_k)=\{v|c_k\le b_v<c_{k+1}\}$. In other words, $\mathcal{L}(C_k)$ is the set of intervals whose left endpoints are located before c_k but after c_k−1, while $\mathcal{R}(C_k)$ is the set of intervals whose right endpoints are located after c_k but before c_k+1. The sets $\mathcal{L}(C_k)$ and $\mathcal{R}(C_k)$ are the intervals that make a contribution uniquely to clique C_k. Note that $\mathcal{L}(C_k)\cap \mathcal{R}(C_k)$ is the set of intervals that are unique to C_k.

Analogously, given a block B_i,j (i.e. consecutive cliques C_i, … ,C_j), we define $\mathcal{L}(B_{i,j})=\{v|c_{i-1}<a_v\le c_i\text{and}{c}_j\le b_v\}$ to be the set of intervals whose left endpoint are located between C_i−1 and C_i, and similarly $\mathcal{R}(B_{i,j})=\{v|c_j\le b_v<c_{j+1}\text{and}{a}_v\le c_i\}$ to be the set of intervals whose right endpoints are located between C_j and C_j+1. To define a score W(B_i,j) for the block B_i,j, we suppose that the block resulted from a single recurrent SCNA, defined by a single maximal clique C_p, called the pivot, within the block B_i,j (i.e. i ≤ p ≤ j), and nearby cliques created by erroneous intervals/endpoints in some samples. Thus, to score the block B_i,j with pivot C_p, we count all the intervals that cross the pivot C_p, whose left endpoints are located after c_i−1 but before c_i (for all i ≤ p, where c_i is the left boundary of the block), together with those intervals whose right endpoints are located after c_j but before c_j+1 (for all j ≥ p, where c_j is the right boundary of B_i,j) (Fig. 3A). Our score W(B_i,j) for the block W(B_i,j) is the number of such pairs of left and right endpoints, maximized over all possible pivot cliques. Formally, we define:

$$W(B_{i,j})=\underset{p:[i,j]}{\max }2\times \min (|{\displaystyle \underset{s:[i,p]}{\cup }\mathcal{L}}(B_{s,p})|,|{\displaystyle \underset{e:[p,j]}{\cup }\mathcal{R}}(B_{p,e})|).$$ (1)

Fig. 3.

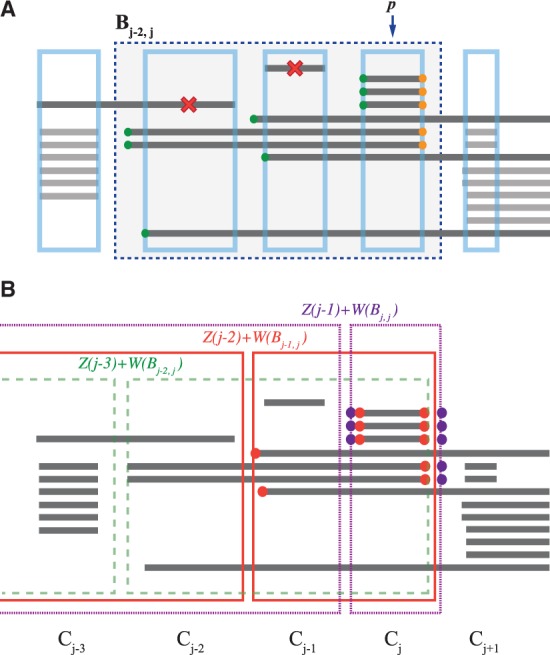
(A) The computation of the weight $W(B_{j-2,j})$ for block B_j−2,j (blue dashed rectangle) with pivot clique p = j. Intervals that do not cross C_p (indicated by red cross) are considered noise, and ignored. The score for the block $W(B_{j-2,j})$ is calculated from the left endpoints (green) and right endpoints (orange) of the remaining intervals. (B) Example of recurrence Z(j) to compute optimal collection of non-overlapping blocks terminating at the maximal clique j. Dashed green, solid red and dotted purple rectangles represent the possible selections of blocks $B_{j-2,j},B_{j-1,j}$ and B_j,j, respectively, with the corresponding terminal clique from the previous step of the recurrence. Scores $W(B_{j-1,j})$ and $W(B_{j,j})$ are computed using endpoints indicated by red and purple circles, respectively. In this case, $W(B_{j,j})$ is the optimal selection

We count pairs of boundary endpoints because intervals that are unique to B_i,j are elements of both $\mathcal{L}(B_{i,j})$ and $\mathcal{R}(B_{i,j})$, and also to avoid asymmetry where the number of left and right endpoints differs drastically.

2.3.2 Finding an optimal block partition

In this section, we formally define the problem of finding an optimal selection of non-overlapping blocks and present an efficient algorithm to solve the problem. Each selected block defines a target region of an independent SCNA.

Let P denote a selection of non-overlapping blocks B_i,j according to the ordering C. Each such selection P corresponds to a collection of independent SCNAs. Our goals is to identify not only recurrent aberrations in many samples (primary events), but also rare, secondary aberrations that might be obscured by complex and overlapping segments with primary events. Thus, we comprehensively consider all potential selections of non-overlapping blocks. We score the selection as the sum of the scores of each of the blocks in P whose score is above a minimum threshold δ.

$$\mathcal{W}(P)={\displaystyle \sum _{B_{i,j}\in P,W(B_{i,j})\ge \delta }W}(B_{i,j}),$$ (2)

where W(B_i,j) is the score of a block B_i,j in the selection. The parameter δ is used to reduce the possibility of over-partitioning that could result from individual cliques with low scores preventing the creation of larger blocks.

We aim to solve the following problem.

Problem 1 —

Given an interval graph G with maximal cliques $C=(C_1,\dots ,C_m)$, a minimum block score δ, and a maximum block size r ≤ m, find a selection $P^{*}$ of non-overlapping blocks such that for each block $B_{i,j}\in P^{*}$

1. The score W(B_i,j) ≥ δ;

2. The block size j −i + 1 ≤ r;

and such that the score $\mathcal{W}(P^{*})$ is maximized over all such selections.

We solve this problem using dynamic programming. Let Z(j) be the highest scoring selection of non-overlapping cliques from C₁, … ,C_j. Then we have the following recurrence:

$$Z(j)=\{\begin{array}{l}{\max }_i\left(Z(i-1)+W(B_{i,j})\right)\text{if}W(B_{i,j})\ge \delta ,\hfill \\ Z(j-1),\text{otherwise},\hfill \end{array}$$ (3)

where i = j − r + 1, … ,j. We also have the initial condition Z(0) = 0.

The recurrence derives the best selection of non-overlapping blocks in the first j maximal cliques of the ordering C, using the optimal solution of the first j − 1 cliques. Since we take multiple consecutive cliques into consideration, we have to consider an indicator i of the starting clique of the block ending at j, where j − r + 1 ≤ i ≤ j. Then we can get the best selection of the first i cliques by calculating the score for all possible i, which is the score Z(i − 1) of the best selection prior to i, plus the score W(B_i,j) of the block from i to j (Fig. 3B). Note that our algorithm is very fast; knowing the ordering C₁, … , C_m of the maximal cliques and scores W(B_i,j) of every block B_i,j in advance, the dynamic programming step takes only O(mr), where r is the bound on the block size. Computing the ordering C₁, … , C_m of the maximal cliques requires $O(m\log m)$ by employing a sorting procedure and a simple line sweep algorithm. Note that m, the number of maximal cliques, is bounded by the total number of intervals in all samples. Finally, computing the scores of all blocks B_i,j with their sizes bounded by r takes O(mr²). Thus the total running time of our method is $O(m\log m+m{r}^2)$.

2.4 Defining the target regions of aberrations and assessing significance

The final tasks in the identification of recurrent SCNAs are: (i) to determine the target region, or genomic location, of the aberration; (ii) to identify the statistical significance of the aberration. For a given block W(B_i,j) in the optimal selection $P^{*}$, a natural choice of target region is the minimal common region (MCR) (Aguirre et al., 2004), or the smallest region contained in the intersection of all intervals that contributed to the score of the block W(B_i,j). However, the MCR is often too restrictive, as it is sensitive to the location of one or a small number of intervals; e.g. a small, erroneous interval in one sample could produce a very small MCR. Thus, we define a less restrictive target region by removing t pairs of left and right boundary endpoints. Formally, for a block B_i,j with pivot C_p, let $\stackrel{\sim }{\mathcal{L}}(B_{i,j})$ be the descending ordered list of the positions of all left endpoints in the set $\mathcal{L}(B_{i,j})$, and let $\stackrel{\sim }{\mathcal{R}}(B_{i,j})$ be the ascending ordering list of the position of all right endpoints in the set $\mathcal{R}(B_{i,j})$. The MCR of the block B_i,j is the first element of $\stackrel{\sim }{\mathcal{L}}(B_{i,j})$ and the first element of $\stackrel{\sim }{\mathcal{R}}(B_{i,j})$. For a given value t, we choose the region between the (t + 1)-th element of $\stackrel{\sim }{\mathcal{L}}(B_{i,j})$ and the (t + 1)-th element of $\stackrel{\sim }{\mathcal{R}}(B_{i,j})$.

Finally, similar to other approaches (Beroukhim et al., 2007; Diskin et al., 2006; Sanchez-Garcia et al., 2010; Walter et al., 2011), we assess the statistical significance of our predictions using a permutation test. We used the cycle shift permutation from DiNAMIC (Walter et al., 2011) that preserves the number and length of SCNAs in each sample, while permuting their positions. The cycle shift permutation also preserves any positional correlations between aberrations within a sample. We performed the cycle shift permutation on all samples to define a permuted collection of intervals R. Then for a predicted region B_i,j, we define the permutational P-value as

$$p(B_{i,j})=\frac{\#R\text{such that}{\max }_{B\in P_R^{*}}W(B)\ge W(B_{i,j})}{\text{total number of permutations}}.$$ (4)

Note that this P-value is conservative as we compare the observed score to the maximum score of block in the permuted data. Finally, we compute a q-value using the Benjamini–Hochberg method.

3 RESULTS

3.1 Simulated datasets

We first compared RAIG with four other approaches: GAIA (Morganella et al., 2011), JISTIC (Sanchez-Garcia et al., 2010), GISTIC (Beroukhim et al., 2007) and GISTIC2 (Mermel et al., 2011) on simulated data. We used simulated data from Morganella et al. (2011) that offers three SCNA scenarios and two different noise models of increasing complexity that model both uncertainty in the amplitude and the position of SCNAs (both amplifications and deletions) in samples. A description of the parameters of these simulations is in the Supplementary Material. For each Scenario, we simulated a chromosome of 1000 probes considering SCNA widths of 100, 200 and 400, and intensity noises 0, 0.25, 0.5, 0.75 and 1. To take the amount of overlap with the true SCNA into consideration, we count a prediction as correct if the predicted SCNA has 30% reciprocal overlap with the true SCNA. As we varied the parameters of each method, we computed the precision as the fraction of predictions that are correct and the recall as the fraction of true SCNAs that are predicted. Supplementary Table S2.1 gives the parameter settings for each method.

All methods performed very well (≈90% recall and precision) on the first noise model for all three scenarios (Supplementary Fig. S1). On the second noise model, RAIG was the top performer across all three Scenarios achieving 99.2% recall and 98.2% precision in Scenario I, 87.9% recall and 99.8% precision in Scenario II (Supplementary Fig. S1), and 88.9% recall and 99.3% precision in Scenario III (Fig. 4A). In comparison, other methods cannot achieve such high recall and precision based on 30% reciprocal overlap with the true SCNA. JISTIC performed better than the other three methods, achieving 87.2% recall and 85.3% precision in Scenario III (Fig. 4A), but was still below RAIG.

Fig. 4.

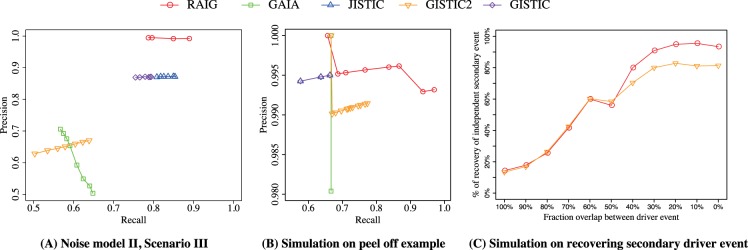
(A and B) Precision–recall curves for five methods on simulated data. Each point represents the precision and recall at a different prediction threshold: q-value of each method. (A) Second noise model of the third scenario from (Morganella et al., 2011). (B) Simulated dataset of peel-off example: e.g. Peaks 2, 3, and 4 in Figure 1. (C) Comparison of RAIG and GISTIC2 in recovering an independent secondary driver event as a function of the fraction of intervals shared by the primary and driver event, a simulation described in Mermel et al. (2011)

Other measures of performance are the sensitivity, defined as the fraction of genomic locations covered by true SCNAs that overlap predictions, and the specificity, defined as the fraction of genomic locations covered by predictions that overlap true SCNAs. Unlike recall and precision, these measures do not consider the number of predictions, and thus a method that fragments SCNAs into many smaller predictions can perform well on sensitivity and specificity. On the more complicated second noise model, RAIG has better sensitivity than other methods and also achieves high specificity: 99.3%, 97.8% and 97.6% in Scenarios I, II and III, respectively (Supplementary Fig. S1).

To compare each method’s ability to identify overlapping secondary aberrations, we used two additional simulations. First, we generated a third simulated dataset consisting of three overlapping SCNAs, analogous to peaks 2, 3 and 4 in Figure 1. In this simulation, a simulated chromosome contains three recurrent aberrations of length 200 probes across 25 samples. The three aberrations are at the median position of the chromosome to minimize edge effects and with a fixed distance 25 probes between them. We introduced normally distributed amplitude noise (σ = 0.25) and spatial noise obtained by resizing and shifting the middle aberration as in Morganella et al. (2011). Finally, we simulated 100 chromosomes for this dataset and examine its precision and recall for different approaches.

Requiring a minimum of 30% reciprocal overlap between true and predicted aberrations, we found that RAIG outperformed all other methods (Fig. 4B). In particular, RAIG obtained 97% recall and 99% precision. In comparison, GISTIC, JISTIC and GAIA all obtained a recall of 66.7% in its favorable case, with 100% precision. The reason for the low recall is because these methods detected the outer two SCNAs, but could not detect the middle SCNA, due to their use of iterative/greedy peel-off procedures. The arbitrated peel-off procedure used in GISTIC2 performed better (recall of 77.3% and 99.1% precision) since it gave more weight to the middle aberration, but its performance was still significantly below RAIG.

Finally, we generated a simulated dataset using that same approach that was used in the GISTIC2 publication (Mermel et al., 2011) to demonstrate the superiority of the GISTIC2 arbitrated peel-off procedure over the earlier greedy peel-off procedure used in GISTIC. In this simulation, we follow the steps in the GISTIC2 publication (Mermel et al., 2011) to generate simulated chromosomes in 500 samples, including a primary driver event, a secondary driver event and passenger events presenting in 10%, 5% and 85% of samples. Each passenger event is chosen randomly from the collection of 4508 cancer samples from Pan-cancer dataset (Weinstein et al., 2013) and placed on the chromosome with uniform midpoint. We considered recently discovered Pan-cancer driver events (Zack et al., 2013) as the known driver events for generating lengths and amplitude of driver SCNAs. We considered different overlaps between the primary and secondary driver events from 100% (complete dependence where all intervals contain both aberrations) to 0% (complete independence where no intervals contain both aberrations). For each overlap fraction, we created 1000 simulated datasets, each with 500 samples, and examined its percentage recovery of the secondary driver event. When the overlap between primary and secondary driver events is low (<50%), RAIG has a clear advantage over GISTIC2 in recovering more secondary driver events than GISTIC2 (Fig. 4C). In the more difficult case where the overlap between primary and secondary and driver events is high (>50%), RAIG and GISTIC2 recover similarly low proportions of secondary events.

3.2 Cancer datasets

We compared RAIG with other approaches on three recent cancer datasets from TCGA: 563 Glioblastoma Multiforme (GBM) samples, 490 Kidney Renal Clear Cell Carcinoma (KIRC) samples and 847 Breast Invasive Carcinoma (BRCA) samples. We downloaded segmented copy number data from Broad Institute’s Genome Data Analysis Center (GDAC). We considered only focal events by setting a cutoff to distinguish broad from focal events, i.e. only considering SCNAs whose lengths are <90% of chromosome arm. We compared the recurrent regions identified by three different methods: GISTIC2, GAIA and RAIG, running each of the first four methods with their default settings and selecting predictions with q-value < 0.5. For the parameters of each method, please see Supplementary Table S2.1.

Overall, we find that while RAIG and GISTIC2 predict approximately the same number of SCNAs, the SCNAs predicted by GISTIC2 are >10–20-fold larger (Table 1). We observe a fair amount of overlap between the predictions from different methods, and also many predictions that were unique to a single method or pairs of methods (Fig. 5, Supplementary Fig. S2). Since the driver aberrations in these samples are not known, to compare the performance of the methods we also examined the fraction of each predicted SCNA that overlaps genes from the Sanger Institute Cancer Gene Census (Forbes et al., 2011), a list of known cancer genes. Because the SCNAs predicted by RAIG are smaller than other methods, we find fewer census genes. However, a significantly larger fraction of RAIG’s predictions overlap census genes, suggesting that RAIG has high specificity. Moreover, many of the additional census genes found by GISTIC2 and GAIA are in large SCNAs that contain many genes—both census genes and non-census genes. We further detail these results in the following sections.

Table 1.

SCNA predictions by RAIG, GISTIC2 and GAIA on GBM, KIRC and BRCA datasets

Datasets	GBM			KIRC			BRCA
Methods	RAIG	GISTIC2	GAIA	RAIG	GISTIC2	GAIA	RAIG	GISTIC2	GAIA
No. of predictions (amp/del)	71/50	70/51	44/160	12/24	9/17	20/35	47/41	62/51	114/132
Avg. size of regions (kb)	146.43	3297.72	803.00	1998.66	30331.24	4367.74	417.27	5713.15	2965.26
No. of census genes	25	78	50	22	102	42	19	89	125
No. of census genes/Mb	1.41	0.19	0.30	0.31	0.12	0.17	0.52	0.14	0.17
Pct. of census gene overlap	32.6	1.9	3.7	5.02	1.5	1.8	50.3	1.9	2.1

Supplementary Figure S3 gives histograms of the sizes of predicted region. Pct. of census gene overlap gives the percentage of the total predicted SCNAs that are covered by genes from Sanger’s Cancer Gene Census.

Fig. 5.

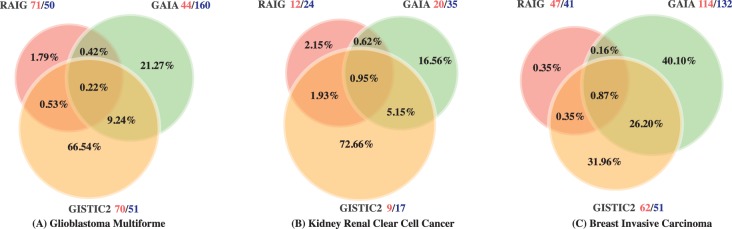
Intersections between genomic positions predicted to be recurrent SCNAs by GAIA, GISTIC2 and RAIG in (A) GBM, (B) KIRC and (C) BRCA datasets. Percentages are according to the union of genomic positions predicted by all methods. Red and blue numbers next to names of methods indicate the number of amplifications and deletions, respectively

3.2.1 GBM

RAIG detected 71 recurrent amplifications and 50 recurrent deletions, compared with 70 amplifications and 50 deletions for GISTIC2 and 44 amplifications and 160 deletions for GAIA. Comparison of the predictions revealed 24 regions reported by all three methods (Fig. 5A, Supplementary Fig. S2A, Supplementary Table S1.1). Most of these shared regions contain well-known cancer genes and are highly consistent with the previous studies (Beroukhim et al., 2007; McLendon et al., 2008), including amplifications in PDGFRA, MET, CDK6, MYCN, SOX2, MDM4, MDM2 and CDK4; amplifications close to EGFR; and deletions in NF1, CDKN2A, CDKN2C and PTEN.

RAIG, GISTIC2 and GAIA predictions included 25, 78 and 50 census genes, respectively. However, the increase in number of census genes for GISTIC2 and GAIA comes with a cost: GISTIC2 and GAIA predictions are longer on average than RAIG predictions and GAIA makes many more predictions (Table 1). Thus, we computed the number of census genes identified per Mb in predicted regions and found that RAIG predictions were significantly enriched for census genes: including nearly 1.41 genes/Mb compared with 0.19/Mb for GISTIC2 and 0.3/Mb for GAIA. Seen another way, the percentage of prediction covered by a census gene is significantly greater for RAIG (32.6%) compared with the other methods (1.9% and 3.7%). Supplementary Figure S4A compares the lengths of RAIG and GISTIC2 predictions containing several well-known genes including PTEN, CDKN2A and MDM4. Overall, we find that RAIG makes smaller predictions that are more focused on the known target genes of the aberrations compared with GISTIC2 and GAIA.

We also found that several of the predictions that are unique to RAIG contain genes with reported associations to cancer, although not in the Cancer Gene Census. One example is a focal deletion of RSU1, a suppressor of RAS. RAS loss of function plays a key role in GBM (Tsuda et al., 1995). RSU1 deletions are rare (found in only 10 of the 563 samples) and these deletions accumulate at C-terminus of RSU1 (Supplementary Fig. S5). Another rare aberration unique to RAIG is an amplification of VEGFA (found in only 18 of the 563 samples), a signature gene of the ‘mesenchymal’ GBM subtype that was more highly expressed in one of signaling patterns in GBM (Brennan et al., 2009).

3.2.2 KIRC

RAIG predicted 12 recurrent amplifications and 24 recurrent deletions (using gene-level overlap scoring for deletions), compared with 9 amplifications and 17 deletions for GISTIC2 and 20 amplification and 35 deletions for GAIA. Comparison of the predictions revealed six regions reported by all three methods (Fig. 5B, Supplementary Fig. S2B, Supplementary Table S1.2). Most of these shared regions contain well-known cancer genes and are highly consistent with the previous studies (Cancer Genome Atlas Research Network, 2013). These include deletions of tumor–supressor genes CDKN2A at 9p21, PIK3CA at 3q26, RUNX3 at 1p36 (Beroukhim et al., 2009), chromatin remodeling gene ARID1A at 1p36.11, and PTPRD at 9p23. ARID1A was recently reported to be a new prognostic marker in KIRC (Lichner et al., 2013). However, while GISTIC2 predicts a large 31.2 Mb deletion at 1p36.33-p35.2 that includes ARID1A and 7 other census genes, RAIG predicts a more specific 2.24 Mb deletion containing only ARID1A (Fig. 6A). A similar example is amplification of MDM4, which is contained in a large 88.2 Mb amplification predicted by GISTIC2, but a 1.18 Mb amplification in RAIG (Fig. 6B).

Fig. 6.

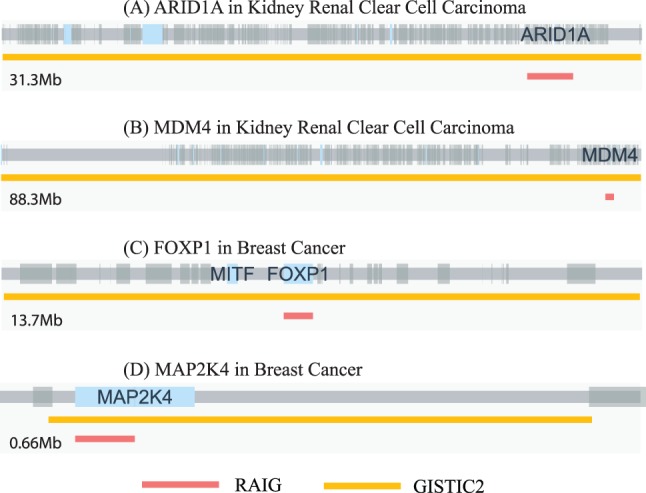
Predicted aberrations for RAIG (red) and GISTIC2 (orange) containing several known cancer genes. Gray bar indicates genome with large gray and blue boxes indicating genes and census genes, respectively. Supplementary Figure S4 shows all cancer census genes common to both methods

Some of the recurrent regions identified by at least two methods have been reported in previous studies, e.g deletions in NEGR1 at 1p31, NRXN3 at 14q24 and PTEN at 10q23 (Cancer Genome Atlas Research Network, 2013) identified by RAIG and GISTIC2. Two well-known arm-level SCNAs in KIRC are amplification of 5q and deletion on 3p. RAIG refined these arm-level events into several independent SCNAs including aberrations containing GBE1, PTPRG, CADM2 and ROBO1/2 on 3p. The latter three genes have previously reported roles in cancer. However, these smaller aberrations were not significant, likely due to the whole arm aberrations that lead to a relatively flat permutational distribution using the cycle-shift permutation. While these rare aberrations were not statistically significant on their own, they can be analyzed in combination with other mutations/aberrations using pathway and network analyses (Ciriello et al., 2012; Leiserson et al., 2013; Vandin et al., 2011, 2012).

3.2.3 BRCA

RAIG detects 47 amplifications and 41 deletions (using gene-level overlap scoring for deletions) compared with 62 amplifications and 51 deletions for GISTIC2 and 114 amplifications and 132 deletions for GAIA (Fig. 5C, Supplementary Fig. S2C, Supplementary Table S1.3). Altogether, there are 28 regions common to the three methods (Supplementary Fig. S2C). These regions include previously reported recurrent SCNAs (The Cancer Genome Atlas Network, 2012) such as: focal amplification of regions containing CCND1, ERBB2, MYC, MDM4 and ZNF703; amplified regions near ZNF217, GATA3 and FOXA1; and focal deletion of regions containing FOXP1, CSMD1, RB1, PTEN, CDKN2A, PTPRD, MAP2K4 and MLL3. Moreover, RAIG and GISTIC2 identified an amplified region containing ESR1; activating mutations in ESR1 were recently reported to be a key mechanism in breast cancer (Robinson et al., 2013).

We observe a similar result as in the GBM dataset. While GISTIC2 and GAIA predictions contain more census genes, their predictions are larger. The result is that RAIG has ≥3-fold census genes/Mb than the other methods (Table 1). Seen another way, the percentage of prediction covered by a census gene is significantly greater for RAIG (50.3%) compared with the other methods (1.9% and 2.1%). For example, GISTIC2 predicts a 13.6 Mb deletion with census genes FOXP1 and MITF, while RAIG predicts a specific deletion with the size 0.62 Mb containing only FOXP1 (Fig. 6C). A similar example is deletion of MAP2K4, which is contained in a relatively large 0.56 Mb deletion in GISTIC2 output but a 0.06 Mb deletion in RAIG (Fig. 6D).

RAIG identified some important regions listed as follows which are not identified by the other methods. A notable example is a rare deletion of RUNX1 (Fig. 7) in 33 samples (|L(C)| = 16 and |R(C)| = 21). Deletion of RUNX1 is consistent with previous reports of inactivating mutations in RUNX1 in breast cancer (Banerji et al., 2012).

Fig. 7.

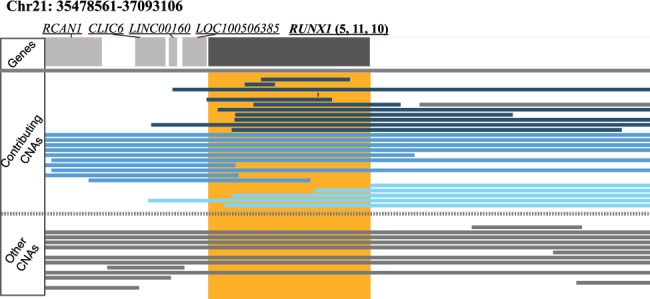
Rare deletion identified by RAIG in RUNX1 in BRCA. Genes are dark gray rectangles at top while RAIG prediction is orange rectangle. Contributing SCNAs are those interval that contribute to the score W for the recurrent region (maximal clique), while other SCNAs are intervals that do not contribute score. There are 5 left, 11 unique and 10 right intervals indicated by light blue, dark blue and cyan in the CNA panel, respectively, that contribute to the RUNX1 score, i.e. $\mathcal{L}(B)=16$ and $\mathcal{R}(B)=21$

4 DISCUSSION

We introduce RAIG, an algorithm to find independent and recurrent SCNAs. We demonstrate that RAIG performs well compared with the existing methods on synthetic and real datasets. On simulated datasets, RAIG achieved the highest precision and recall, and also made smaller, more focused predictions. On real datasets, RAIG predicted independent and recurrent SCNAs in a significantly smaller fraction of the genome than the widely used GISTIC2 algorithm and the GAIA algorithm. Overall, the overlap between different methods is modest, demonstrating the difficulty in identifying recurrent SCNAs. RAIG showed the highest enrichment of known cancer genes from The Cancer Gene Census, suggesting that RAIG has high specificity. While it is difficult to estimate the sensitivity of each method on real data, we found that a number of the genes that were unique to RAIG are known cancer genes. Finally, the efficient clique enumeration and optimization steps make RAIG perform more than thousand times faster than other methods, although total running times are influenced by the type of nature of the statistical test that is performed (Supplementary Table S2.2).

At the same time, RAIG does miss some SCNAs that likely contain important cancer genes. In examining these cases, we found that the majority had relatively few boundary endpoints that surround the maximal clique containing these genes. However, the amplitude of the SCNAs in these samples was very high. One example is FGFR1 in BRCA, where the average frequency and amplitude are 0.12 and 0.98, respectively. We found that other intervals (with lower amplitude) obscure the high-amplitude intervals containing FGFR1. GISTIC2 use copy number amplitude in addition to number of samples for its recurrence score. Further improvements to RAIG may be obtained by running with higher amplitude thresholds, or by incorporating amplitude into the objective function optimized by RAIG; e.g. by creating a weighted score for intervals according to their amplitude. To test the former hypotheses, we ran RAIG on the BRCA dataset using only intervals whose amplitude was >0.5. RAIG returned a region on 8p containing FGFR1 and two other genes.

Since RAIG considers all possible partitions of the data, it is able to detect rare SCNAs and secondary events that are obscured by complex, overlapping rearrangements and missed by iterative peel-off procedures used in all existing methods. Although such rare aberrations are not statistically significant on their own, one of the outcomes from recent cancer sequencing studies is the demonstration of extensive mutational heterogeneity in cancer with driver mutations distributed over a large number of genes (Vogelstein et al., 2013). Thus, obtaining a comprehensive view of the mutations that drive cancer requires the analysis of combinations of rare and common mutations in pathways and interaction networks (Cerami et al., 2010; Ciriello et al., 2012; Leiserson et al., 2013; Vandin et al., 2011, 2012; Vaske et al., 2010).