Abstract
Motivation: De novo assemblies of genomes remain one of the most challenging applications in next-generation sequencing. Usually, their results are incomplete and fragmented into hundreds of contigs. Repeats in genomes and sequencing errors are the main reasons for these complications. With the rapidly growing number of sequenced genomes, it is now feasible to improve assemblies by guiding them with genomes from related species.
Results: Here we introduce AlignGraph, an algorithm for extending and joining de novo-assembled contigs or scaffolds guided by closely related reference genomes. It aligns paired-end (PE) reads and preassembled contigs or scaffolds to a close reference. From the obtained alignments, it builds a novel data structure, called the PE multipositional de Bruijn graph. The incorporated positional information from the alignments and PE reads allows us to extend the initial assemblies, while avoiding incorrect extensions and early terminations. In our performance tests, AlignGraph was able to substantially improve the contigs and scaffolds from several assemblers. For instance, 28.7–62.3% of the contigs of Arabidopsis thaliana and human could be extended, resulting in improvements of common assembly metrics, such as an increase of the N50 of the extendable contigs by 89.9–94.5% and 80.3–165.8%, respectively. In another test, AlignGraph was able to improve the assembly of a published genome (Arabidopsis strain Landsberg) by increasing the N50 of its extendable scaffolds by 86.6%. These results demonstrate AlignGraph’s efficiency in improving genome assemblies by taking advantage of closely related references.
Availability and implementation: The AlignGraph software can be downloaded for free from this site: https://github.com/baoe/AlignGraph.
Contact: thomas.girke@ucr.edu
1 INTRODUCTION
Recent advances in next-generation sequencing (NGS) have made it possible to sequence new genomes at a fraction of the time and cost required only a few years ago. These improvements now allow experimental scientists to integrate genome sequencing approaches into their daily research. In the absence of a close reference genome, whole-genome shotgun NGS sequencing is the most common approach where a de novo assembly algorithm is used to join reads into longer continuous contigs and scaffolds. Most NGS de novo assemblers create a string or de Bruijn graph representing the connections among the reads and output the paths in the graph as assembled contigs. Examples of these algorithms include Edena (Hernandez et al., 2008), Velvet (Zerbino and Birney, 2008), ABySS (Simpson et al., 2009), ALLPATHS-LG (Gnerre et al., 2011), SOAPdenovo (Li et al., 2010; Luo et al., 2012), MaSuRCA (Zimin et al., 2013), CABOG (Miller et al., 2008), Euler-USR (Chaisson et al., 2009) and IDBA (Peng et al., 2010). This de novo assembly approach fundamentally differs from alignment-based resequencing approaches, where the NGS reads are not assembled but aligned against a similar reference genome using a variant tolerant short read aligner and structural variant detection algorithms (Ossowski et al., 2008; Zeitouni et al., 2010). Large parts of the sequence of the target genome can then be reconstructed from the mismatches, indels and rearrangements observed in the alignment results. De novo assemblies tend to be computationally more challenging than alignment-based approaches. Additional limitations include (i) the assembly results are often fragmented into large numbers of contigs, (ii) the genome covered by the assembled contigs/scaffolds is commonly incomplete and (iii) the frequency of falsely assembled contigs can be high because of chimeric joins. The most important reasons for these complications are usually sequencing errors, repeat sequences in the target genome, non-uniform sequencing depth and limited read length of NGS data. These error sources result in false-positive, incomplete and branched paths in the assembly graph, and thus greatly limit the lengths and completeness of the final contigs (Chaisson and Pevzner, 2008; Peng et al., 2010; Zerbino and Birney, 2008). Combining both de novo assembly and alignment-based approaches presents a powerful alternative when a closely related reference genome sequence is available, but its genetic differences relative to the target genome are too pronounced to resolve them with an alignment approach alone (Phillippy et al., 2008; Schatz et al., 2013; Schneeberger et al., 2011). In this case, one can first assemble the reads into contigs and then align them together with the reads to the reference. The much longer contigs facilitate the identification of complex rearrangements, whereas the read alignments are useful for detecting smaller variations in regions that are not covered by contigs. Because of the rapidly increasing number of reference genomes becoming available for most organism groups, this reference-assisted assembly approach will soon become the default option for many genome sequencing projects. Compared with de novo assemblies, reference-assisted assemblies have many advantages. First, the alignments of the contigs and reads against the close reference provide valuable proximity information that can be used to extend contigs with additional reads and to join contigs even if they overlap only by a few nucleotides. Second, the proximity information in the alignment can also be used to orient and order contigs along the reference to build a scaffold map of the entire assembly. Third, the alignment map can be used to evaluate the quality of contigs and pinpoint potential misassemblies.
Previous studies on reference-assisted assemblies include the AMOScmp software (Pop et al., 2004a), an add-on tool for the ARACHNE assembler (Gnerre et al., 2009) and custom workflows largely based on existing assembly software (e.g. Schneeberger et al., 2011). The first two were designed primarily for Sanger reads, whereas the latter has been used for NGS genome assembly. Downstream of the primary assembly, scaffolding algorithms, such as RACA (Kim et al., 2013), can be used to order and orient preassembled contigs to a connection map by incorporating additional sequence information from mate pair or PE reads and/or from closely related genomes (Boetzer et al., 2011; Dayarian et al., 2010; Gao et al., 2011; Gritsenko et al., 2012; Pop et al., 2004b; Salmela et al., 2011). The resulting scaffolds often contain gaps, which are unresolved sequence areas between the original contigs. Dedicated gap-filling algorithms can be used to partially fill these gaps (Boetzer and Pirovano, 2012; Luo et al., 2012; Tsai et al., 2010). More recently, components of reference-based strategies have also been incorporated into some of the de novo assembly suites themselves such as the cheat mode option of ALLPATHS-LG (Gnerre et al., 2011) and IDBA-hybrid (unpublished).
This study proposes a novel algorithm, called AlignGraph, for improving the lengths and completeness of contigs or scaffolds by reassembling them with help provided by a reference genome of a closely related organism. In contrast to existing reference-assisted methods, AlignGraph is a secondary assembly algorithm that loads the alignment information of PE reads and preassembled contigs/scaffolds against the reference into a novel assembly graph, called the PE multipositional de Bruijn graph, that we specifically designed for facilitating secondary assemblies. By traversing this graph, the contigs or scaffolds of the primary assembly can be extended and joined. AlignGraph differs from most scaffolding algorithms by extending contigs exclusively with resolved rather than unresolved bases (Ns) and by acting either upstream and/or downstream of them.
AlignGraph’s functionalities are unique by solving several challenges in improving assembly results. As a de Bruijn graph-based method, it solves limitations typical for many heuristic extension methods that are often used in the de novo assembly area (Dohm et al., 2007; Jeck et al., 2007; Warren et al., 2007). For instance, if there are multiple solutions for how to extend a contig, then finding the correct one can be challenging with most heuristic methods. Those ambiguous solutions, which correspond to branched paths in the de Bruijn graph, are usually caused by repetitive sequences in genomes and frequently lead to early terminations of the contig extension process. The de Bruijn graph method is often more efficient than heuristic methods in finding the correct solution here because the contextual information, required for resolving these ambiguities, is maintained in the graph (Chaisson and Pevzner, 2008; Zerbino and Birney, 2008). This issue is not as pronounced in assemblies with much longer Sanger reads, as those are more likely to span non-repetitive regions with repetitive regions in between (Gnerre et al., 2009). Thus, it is particularly important to address this problem in assemblies with short reads. In comparison with the conventional de Bruijn graph, our PE multipositional de Bruijn graph has several additional advantages. First, many branched paths can be eliminated directly in the graph with the help of the additional PE read and alignment information. This simplifies the identification of correct paths. Second, many false-positive paths, caused by sequencing errors, can be eliminated by correcting erroneous reads with correct reads that align to the same position in the reference genome. Third, guided by the alignment information to the reference genome, the PE multipositional de Bruijn graph is less affected by regionally low read coverage that often gives rise to incomplete paths in the conventional de Bruijn graph. As a result, many incorrect extensions and early terminations can be avoided.
2 METHODS
2.1 AlignGraph algorithm
This section describes the AlignGraph algorithm. Its workflow can be divided into the following three major steps. Figure 1B illustrates these steps with an example.
Alignment maps. The PE reads are aligned against both the preassembled contigs and the close reference genome; the contigs are aligned against the reference.
Contig reassembly. The alignment mapping results are used to construct a positional variant of the de Bruijn graph, called the PE multipositional de Bruijn graph.
Graph traversal. The resulting graph is edited and traversed to obtain extended contigs.
Throughout the text, the source genome of the PE reads and the preassembled contigs is referred to as the target genome, whereas the genome of the closely related species for guiding the contig improvement steps is referred to as the reference genome. For simplicity, the following description of AlignGraph refers mostly to contigs, but it also applies to scaffolds containing a limited amount gaps.
Fig. 1.
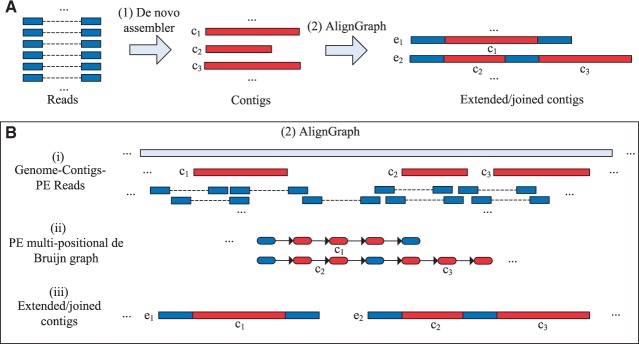
Overview of the AlignGraph algorithm. The outline on the top (A) shows AlignGraph in the context of common genome assembly workflows, and the one on the bottom (B) illustrates its three main processing steps. (A) In Step 1, the PE reads from a target genome are assembled by a de novo assembler into contigs (here and c3). Subsequently (Step 2), the contigs can be extended (blue) and joined by AlignGraph (e1 and e2). (B) The workflow of AlignGraph consists of three main steps. (i) The PE reads are aligned to the reference genome and to the contigs, and the contigs are also aligned to the reference genome. (ii) The PE multipositional de Bruijn graph is built from the alignment results, where the red and blue subpaths correspond to the aligned contigs and sequences from PE reads, respectively. (iii) The extended and/or joined contigs (here e1 and e2) are generated by traversing the graph
Prerequisites
Before the above steps, the user is expected to generate genomic PE reads for the target genome of interest and to assemble them with a de novo NGS genome assembler. Because most genome assemblers perform better with PE than single-end data, AlignGraph also depends on this sequence type. A major advantage of AlignGraph is its design to work with most genome assemblers, but the quality of the initial de novo assembled contigs is expected to impact the final results (see Section 3.2). For optimal results, it is also important to follow the recommendations of the chosen de novo assembler with respect to insert length of the sequencing library, minimum coverage of the target genome with PE reads and other recommendations. If scaffolds are inputted, it is usually beneficial to fill them with a gap-filling algorithm before processing them with AlignGraph (e.g. Boetzer and Pirovano, 2012). Another requirement for AlignGraph is the availability of a closely related reference genome sequence. Nearly complete reference genomes of high quality will yield the best results, but partially sequenced genomes can be used as well.
(i) Alignment maps
In the initial preprocessing step of AlignGraph, the PE reads, used for the de novo assembly in the Prerequisite section, are aligned to the contigs and to the reference genome, and the contigs are also aligned to the reference genome. Aligning the reads to the contigs simplifies their alignments to the reference by guiding them with the much longer contigs as backbone (see below). Generating reliable alignments among the PE reads and the contigs is relatively straightforward because both are from the same genetic background, thus requiring a low level of variant tolerance in the alignments. Aligning the contigs to the reference genome demands a higher level of variant tolerance. However, because of the relatively large length of the contigs, their alignments to the reference can also be generated reliably, as long as the evolutionary distance between the target and reference genome is not too large. The current implementation of AlignGraph uses Bowtie2 and BLAT for these two alignment steps, respectively (Kent, 2002; Langmead and Salzberg, 2012). In contrast to this, aligning the relatively short PE reads to the reference genome is a more challenging task owing to the difficulty of generating reliable short alignments containing larger numbers of mismatches and gaps. This problem does not apply to the reads aligning to the contigs because their alignment positions to the reference genome can be inferred from the more robust contig alignments. For the PE read to reference genome alignment, it is important to choose a highly variant tolerant short read aligner that is able to reliably align most of the short reads to their true source locations in the reference genome while minimizing the number of false-positive read placements. Clearly, the latter would negatively impact the precision performance of AlignGraph by leading to chimeric joins in the downstream contig extension steps. Although a wide range of short read aligners has been developed over the past years (Li and Homer, 2010), none of them has been specifically designed or optimized for aligning short reads against reference genomes with sequence differences more pronounced than those observed among genomes within the same species. To minimize the above challenges, we have chosen for this critical step the highly tunable Bowtie2 aligner with parameter settings that we optimized for aligning PE reads from a target genome to a reference genome sharing variable degrees of sequence similarity. The use of PE read alignments in this step is also important because the additional sequence information, provided by the second read in a PE, increases the specificity of the alignment process compared with single-end reads, and thus reduces the number of false read placements. To account for rearrangements among the two genomes, we use for the alignments of the PE reads against the reference genome more relaxed insert length variation settings than in the alignments against the contigs.
(ii) Contig reassembly with PE multipositional de Bruijn graph
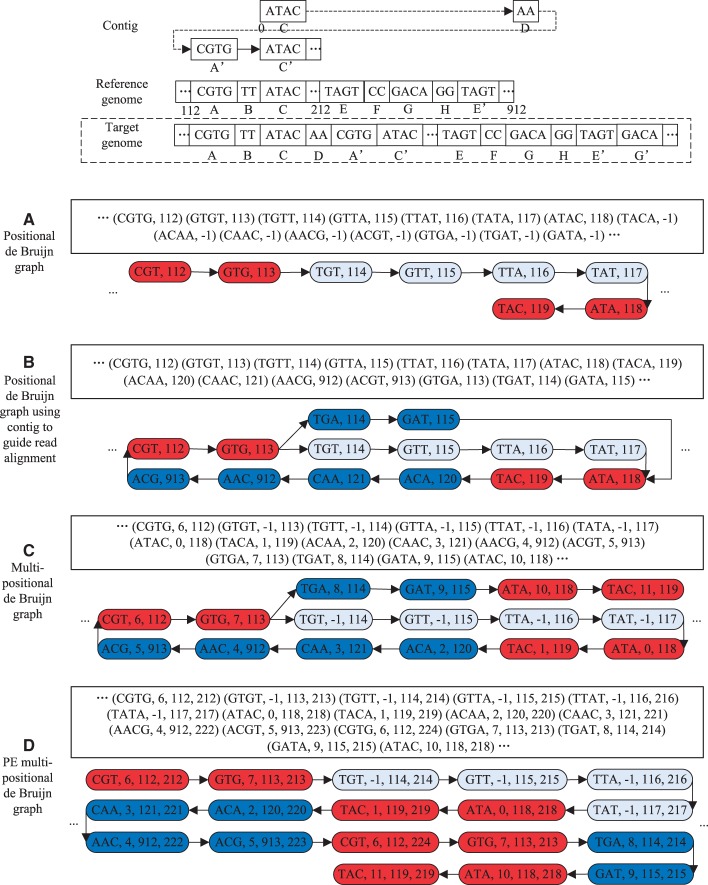
The core functionality of AlignGraph is the extension of the contigs by reassembling them using the alignment results obtained in the previous step. To achieve this efficiently, we build from the alignment maps a variant of the de Bruijn graph, here called the PE multipositional de Bruijn graph. This method combines the PE de Bruijn graph (Medvedev et al., 2011) and the positional de Bruijn graph (Ronen et al., 2012), where we incorporate both PE read information and alignment positions into the graph (Pevzner et al., 2001). The former was designed to generate more complete contigs in de novo assemblies and the latter to correct contig errors in secondary assemblies. Our approach solves several problems in improving assembly results that we briefly discussed in Section 1 (see also Table 1). The following describes our modified de Bruijn graph in more details, where we first introduce important concepts of conventional de Bruijn graph-based assembly methods.
Table 1.
Problems the PE multipositional de Bruijn graph solves in comparison with the conventional de Bruijn graph
| Problem | Consequence | Solution |
|---|---|---|
| Repeat sequences | Branched paths | Distinguishes paths for repetitive regions by incorporating PE read and alignment position information |
| Sequencing errors | False-positive paths | Corrects paths from erroneous reads with correct reads aligned to the same position |
| Low sequencing depth | Incomplete paths | Builds paths from reads in low coverage areas supported by reference |
Background
The most widely used method for genome assemblies from short reads is the de Bruijn graph method (Pevzner et al., 2001). A de Bruijn graph is a directed graph: two connected nodes represent k + 1 bases, where the first node represents the first k bases, and the second node the second k bases (called k-mer). To construct a de Bruijn graph, connected nodes are constructed from each read of length l, and two nodes from different reads are joined if they share the same k-mers. In theory, the graph contains a walk representing the full sequence of the genome if traversed properly. However, this walk is hard to obtain in practice because of false-positive, incomplete and branched connections in the graph that are caused by errors in the reads and repeats in the genome. The false-positive and incomplete paths are due to false-positive k-mers with sequencing errors and missing k-mers from regions of low sequencing depth, respectively. The branched paths are caused by joins of k-mers from repetitive regions. Several variations of the de Bruijn graph have been proposed to solve these limitations, especially the branched paths, while preserving all of its genome information (Medvedev et al., 2011; Peng et al., 2010; Ronen et al., 2012). The PE de Bruijn graph (Medvedev et al., 2011) is built from PE reads, where each k-mer contains k bases from the left pair plus its corresponding k bases from the right pair. In contrast to this, the positional de Bruijn graph (Ronen et al., 2012) incorporates read alignment information by including in each k-mer the k bases plus its alignment position. With the additional information assigned to the k-mers, k-mers from repetitive regions can often be distinguished, and thus the number of branches in the graph can be reduced. In addition, because the positional de Bruijn graph is built from read alignments, false-positive and incomplete paths can be largely avoided. We emphasize that the PE de Bruijn graph requires the left pair forward-strand read and the right pair reverse-strand read or vice versa, but it is difficult to know their orientation. This problem can be resolved if the PE de Bruijn graph is built from aligned reads, where their orientation can be obtained from the alignments.
PE multipositional de Bruijn graph
We derive the PE multipositional de Bruijn graph as a combination of the PE de Bruijn graph and the positional de Bruijn graph. Each k-mer of the PE multipositional de Bruijn graph is composed of three left/right element pairs: the k bases of each the left and the right read pair (called left or right k bases), the alignment position of each the left and the right k bases to the contigs and the alignment position of each the left and the right k bases to the reference genome. Two k-mers can be joined if they have similar k bases and close alignment positions within the constraints defined in the formulas below. Formally, let s be the k bases from the left read pair and the corresponding k bases from the right read pair, then the k-mer of PE multipositional de Bruijn graph is a 6 tuple (, ), where c is the alignment position of s to the contigs, g is the alignment position of s to the reference genome, is the alignment position of to the contigs and is the alignment position of to the reference genome. Two k-mers () and () can be joined if constrains (1)–(6) are met:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where δ and ε are small numbers with the default values 5 and 25, respectively, and D is the variability of the insert length I of the PE reads. The variability D is equal to , where Iu and Il are the upper and lower limits of I, respectively. The variables in the above formulas are explained below.
δ: To join two k-mers and tolerate sequencing errors, we allow a small number of mismatches δ between si and sj and between and in (1) and (2), respectively.
ε: We allow a small shift ε between each pair of alignment positions in (3)–(6) because the same k bases si and sj (or and ) from different reads may align to different but close positions in the contigs or genome, as discussed in Ronen et al. (2012).
2D: We allow a shift of and ’s alignment positions to the contigs in (5) and to the reference genome in (6). The maximum and minimum alignment distances between a read pair are and , respectively, where l is the read length, assuming the same read length for both members in a pair. Thus, the maximum alignment distance of two right reads with left reads aligned at the same position is . This distance is equal to the distance between any two k-mers from the same position in the right read pairs, so the maximum distance between and will be .
−1: si and sj (or and ) can be joined if one or both of them are aligned directly to the reference genome rather than guided by the de novo contigs. In those cases, we assign −1 as alignment position to the contigs. This is important because we allow contig extensions only if the alignable and unalignable bases to contigs can be joined.
It is important to guarantee that each k-mer corresponding to an insertion of a read alignment has a position in the reference genome. To achieve this, we append the inserted k-mer to the end of the genome sequence. In our implementation of the PE multipositional de Bruijn graph, we first iteratively load sections of the reference genome into memory. Then we perform the following operation. We test for each k-mer in each aligned read at genome position g, whether there is already a k-mer at g and whether the new k-mer can be joined with it. If so then we join the two k-mers; otherwise, we attach the new k-mer to position g. The connection between two k-mers is recorded by using pointers, and the read coverage for each k-mer is stored along with it. Figure 2 illustrates the main advantages of the PE multipositional de Bruijn graph compared with the positional de Bruijn graph with several examples (see also Table 1). This includes the contig-guided PE read alignment against the reference genome resulting in a larger number of alignable reads, and thus a more complete de Bruijn graph (Fig. 2B), as well as the reduction of branched paths in the graph by distinguishing reads from different repetitive regions (Fig. 2C and D). For space reasons, the advantages over the conventional de Bruijn graph in reducing false-positive and incomplete paths are not shown. The PE multipositional de Bruijn graph can converge to the positional de Bruijn graph by relaxing the above constraints (2), (3), (5) and (6). In our tests, the former shows usually an up to 5% better performance than the latter with respect to several sensitivity measures (see below for definitions). This improvement is considerable because the number of branches that are only resolvable by the PE multipositional de Bruijn graph is usually not large.
Fig. 2.
Advantages of the PE multipositional de Bruijn graph compared with the positional de Bruijn graph. In the target genome given on the top, A and and and and are repetitive regions. Each PE read of length 2 × 4 bp is sequenced with one pair from region and the other from the corresponding position of region (the pair from is omitted for simplicity). In comparison with the target genome, the reference genome has a repeat-free region ABC similar to and a region similar to . The reads from region are assembled with a de novo assembler into a contig starting from , but regions A and B are not assembled because of low sequencing depth, repeats or other problems. When aligning the contig to the reference genome, the repetitive regions C and are both aligned to C in the reference genome, and the insertion D is assigned to the end of the reference. In (A) reads are aligned directly to the reference genome to build the initial positional de Bruijn graph, and in (B–D) the reads are aligned to the preassembled contigs and then aligned to the reference to build first the extended positional de Bruijn graph and then the PE multipositional de Bruijn graph. (A) The initial positional de Bruijn graph is built here with 3-mers. Some reads cannot be aligned to the reference genome because of sequence differences in the target genome, as indicated here by 3-mers with −1 as alignment position. The repetitive regions A and (or C and ) are collapsed into one path in red in the graph. (B) The initial positional de Bruijn graph is constructed with help from the read-to-contig alignment information. The read-to-reference genome alignment information yields a more complete positional de Bruijn graph, but the repetitive regions A and (or C and ) are still collapsed resulting in branch points. (C) An extended positional de Bruijn graph is built by incorporating into each 3-mer the read alignment position to the contig. As a result of this operation, the repetitive regions C and can be distinguished into two paths, where the 3-mers have different alignment positions in the contig, but A and are still collapsed. (D) The PE multipositional de Bruijn graph is constructed by incorporating into each 3-mer their PE read alignment positions to the reference genome (the right three bases and their alignment position to the contig is omitted here). With this information the repeats A and can be distinguished into two paths, as the 3-mers have different PE alignment positions in the reference genome. The final graph contains only one single path allowing to output an extended contig corresponding to the region in the target genome
(iii) Graph traversal returns extended contigs
To remove errors, the de Bruijn graph needs to be edited before its traversal. The three major types of errors are tips, bubbles and erroneous connections (Chaisson and Pevzner, 2008; Peng et al., 2010; Zerbino and Birney, 2008). Most of them are caused by errors in the reads. A tip is a short path with a dead end, whereas a bubble consists of two short paths sharing the same start and end nodes. Most of the tips and bubbles can be corrected by joining k-mers with mismatches. The remaining errors can be removed by applying a coverage cut-off filter similar to the strategies used by most de novo assemblers. Because of the additional information encoded in the modified de Bruijn graph, one can use here a relatively small coverage threshold. After these error removal steps, the PE multipositional de Bruijn graph is traversed, using a breadth-first strategy, to generate the final contigs. Each traversal stops at a branch position and an extended contig is returned. After returning the extended contigs, the remaining unextended contigs (identical with initial de novo contigs) are provided to the user in a separate file. Finally, contigs with sufficient PE read connections and a path between them can be joined. Occasionally, those connections can be missed by the above filtering step because of too low read coverage in local areas of the connecting path.
2.2 Software implementation
AlignGraph is implemented in C++ for Linux operating systems. Its required input includes the PE reads, the preassembled de novo contigs and the reference genome. Its output includes the extended contigs as well as the remaining non-extended contigs. AlignGraph runs the alignment steps with BLAT and Bowtie2 automatically, but both need to be installed on the system. AlignGraph’s run time is currently 23–57 min per million aligned reads. In the performance tests of this study, the memory usage was 36–50 GB, and it stays <100 GB even for entire mammalian genomes. These requirements are more moderate than those of most de novo assemblers (Luo et al., 2012).
3 EVALUATION
3.1 Experimental design
Background
To evaluate AlignGraph’s efficiency in improving genome assemblies, we performed a series of systematic performance tests. For this, we downloaded publicly available assemblies and/or assembled genomic PE read sets from organisms of variable genome complexity with seven widely used de novo assemblers, extended the resulting contigs with AlignGraph, and then evaluated the improvements with a set of standard metrics for comparing assembly results (Table 2). In these tests, it was important to choose the NGS read samples from organisms where the genome sequence of both the target genome and a close reference genome are known. This way one can evaluate the completeness and correctness of the results against a true result rather than one that is unknown or only partially known. To also assure the improvements obtained by AlignGraph are not simply the result of insufficient optimizations of the upstream de novo assembly, we included preassembled contig and scaffold sets that are widely accepted by the community as benchmark datasets for evaluating assembly software. Today’s requirements for assembling genomes from NGS were met by choosing read samples with ≥75 bp and PE read information. In total, we performed assembly tests on the following three sample sets.
Table 2.
Performance evaluation of AlignGraph
| Upstream assembler | Contig set | N Contigs4 | N505 | N covered bases6 | Average length7 | Maximum length8 | MPMB9 | Average identity10 (%) |
|---|---|---|---|---|---|---|---|---|
| (a) Contigs of A.thaliana genome | ||||||||
| Velvet | All1 | 30 037 | 3515 | 82 844 417 | 2668 | 27 792 | 22.2 | 95.2 |
| Extendable2 | 8615 | 4148 | 28 007 451 | 3262 | 27 398 | 0.3 | 97.6 | |
| Extendable + AlignGraph3 | 5751 | 7876 | 32 467 110 | 5521 | 49 768 | 1.6 | 94.8 | |
| ABySS | All | 30 972 | 2559 | 69 432 667 | 2206 | 29 760 | 13.4 | 97.2 |
| Extendable | 11 693 | 2820 | 28 885 212 | 2454 | 16 343 | 0.5 | 98.7 | |
| Extendable + AlignGraph | 8427 | 5484 | 35 859 786 | 4151 | 25 321 | 1.1 | 95.8 | |
| (b) Contigs of human chromosome 14 | ||||||||
| ALLPATHS-LG | All | 4383 | 38 590 | 83 849 397 | 19 201 | 240 764 | 0.3 | 98.9 |
| Extendable | 1674 | 39 851 | 35 746 095 | 20 806 | 200 495 | 0.1 | 98.9 | |
| Extendable + AlignGraph | 785 | 71 847 | 36 441 001 | 45 358 | 305 880 | 0.0 | 97.5 | |
| ALLPATHS-LGc | All | 3856 | 43 856 | 83 860 939 | 21 818 | 275 446 | 0.2 | 99.3 |
| Extendable | 1296 | 45 719 | 31 457 201 | 24 346 | 275 446 | 0.1 | 99.5 | |
| Extendable + AlignGraph | 608 | 86 613 | 34 614 465 | 54 406 | 294 615 | 0.0 | 96.9 | |
| SOAPdenovo | All | 10 865 | 16 855 | 80 135 941 | 7623 | 147 494 | 5.9 | 94.9 |
| Extendable | 5613 | 17 412 | 45 246 077 | 8223 | 141 981 | 0.9 | 96.4 | |
| Extendable + AlignGraph | 3469 | 32 881 | 52 861 640 | 15 271 | 219 841 | 0.5 | 95.0 | |
| MaSuRCA | All | 19 034 | 5767 | 75 497 302 | 3802 | 53 837 | 13.9 | 98.9 |
| Extendable | 9241 | 6047 | 38 842 517 | 4199 | 51 249 | 0.2 | 99.2 | |
| Extendable + AlignGraph | 5665 | 11 590 | 43 930 184 | 7666 | 66 758 | 0.4 | 98.1 | |
| CABOG | All | 3118 | 46 523 | 84 989 190 | 27 401 | 296 888 | 0.3 | 97.3 |
| Extendable | 1692 | 45 669 | 46 499 763 | 27 089 | 296 888 | 0.0 | 98.7 | |
| Extendable + AlignGraph | 701 | 101 907 | 50 527 605 | 70 362 | 443 952 | 0.1 | 97.6 | |
| Bambus2 | All | 11 219 | 8378 | 64 011 072 | 5764 | 449 449 | 3.1 | 89.9 |
| Extendable | 6995 | 7521 | 37 857 989 | 5439 | 62 798 | 0.3 | 97.6 | |
| Extendable + AlignGraph | 2722 | 19 989 | 39 147 357 | 14 176 | 86 154 | 0.5 | 96.5 | |
| (c) Scaffolds of human chromosome 14 | ||||||||
| SOAPdenovo | All | 3902 | 391 693 | 85 417 248 | 24 397 | 1 852 152 | 1.0 | 82.9 |
| Extendable | 901 | 387 309 | 40 296 035 | 47 526 | 1 019 659 | 0.1 | 84.5 | |
| Extendable + AlignGraph | 767 | 544 209 | 47 823 279 | 63 525 | 2 246 638 | 0.1 | 81.0 | |
| MaSuRCA | All | 721 | 580 822 | 65 433 305 | 63 876 | 2 943 966 | 1.3 | 57.2 |
| Extendable | 101 | 289 703 | 5 554 781 | 52 820 | 1 516 804 | 0.0 | 81.9 | |
| Extendable + AlignGraph | 78 | 316 946 | 6 986 224 | 86 552 | 1 573 741 | 0.0 | 83.4 | |
| CABOG | All | 471 | 387 876 | 81 163 688 | 176 590 | 1 944 475 | 0.1 | 91.9 |
| Extendable | 146 | 358 688 | 29 372 033 | 200 539 | 1 905 529 | 0.0 | 98.2 | |
| Extendable + AlignGraph | 67 | 906 407 | 33 708 925 | 481 712 | 2 051 503 | 0.0 | 94.1 | |
| Bambus2 | All | 569 | 319 334 | 64 378 693 | 116 582 | 1 477 847 | 0.1 | 77.4 |
| Extendable | 66 | 272 436 | 6 949 338 | 119 858 | 641 463 | 0.0 | 92.0 | |
| Extendable + AlignGraph | 80 | 377 905 | 8 963 132 | 114 852 | 812 353 | 0.1 | 85.4 | |
(a) Genomic PE reads from A.thaliana were assembled with Velvet and ABySS. The resulting contigs were extended with AlignGraph using as reference the genome sequence from A.lyrata. (b–c) The subsequent panels contain assembly results for the human chromosome 14 sample from the GAGE project where the chimpanzee genome served as reference. (b) Contig assembly results are given for the de novo assemblers ALLPATHS-LG, ALLPATHS-LGc (in cheat mode), SOAPdenovo, MaSuRCA, CABOG and Bambus2. (c) Scaffolded assembly results are given for SOAPdenovo, MaSuRCA, CABOG and Bambus2. The results are organized row-wise as follows: the number of initial contigs obtained by each de novo assembler1, the ‘extendable' subset of the initial contigs that AlignGraph was able to improve2, and the extension results obtained with AlignGraph3. The additional columns give the number of contigs4, N50 values5, the number of covered bases6, the average7, and maximum8 length of the contigs, the number of misassemblies per million base pairs (MPMB)9, and the average identity among the true contigs and the target genome10. More details on these performance criteria are provided in Section 3.1.5.
3.1.1 Arabidopsis thaliana sample
The first sample set was from the model organism Arabidopsis thaliana, which is a flowering plant with a compact genome of 130 Mb in size. The PE read set chosen for this test is from a genomic Illumina NGS library with a read length of 2 × 75 bp. As de novo assemblers, we included in this test Velvet and ABySS, which we chose here as software representatives performing well on single library data and because of their good sensitivity and precision performance (Lin et al., 2011). The VelvetOptimiser tool was used to optimize the parameter settings for the Velvet assembly. ABySS was run with the same k-mer length as Velvet, whereas the remaining parameters were set to their defaults. To extend the preassembled contigs with AlignGraph, we used the publicly available genome sequence from the related Arabidopsis lyrata species as reference [Table 2(a)]. The latter was chosen because it constitutes a more challenging reference genome for testing AlignGraph’s performance in improving genome assemblies than the references used in the other tests below. This is the case for the following reasons (Hu et al., 2011): A.lyrata and A.thaliana diverged >10 million years ago; their genomes differ by many regional rearrangements; the sequence similarity in the common regions of their genomes is only 80%; and the A.lyrata genome sequence is still incomplete and fragmented into many scaffolds.
3.1.2 Human sample from Genome Assembly Gold-standard Evaluations
The second sample set is from the community project GAGE (Genome Assembly Gold-standard Evaluations), from which we selected the sample for the human chromosome 14 (Salzberg et al., 2012). Its Illumina sequences consist of PE reads with a length of 76–101 bp from three different libraries. We downloaded the preassembled contig sets provided by the GAGE project for the five assemblers that ranked highest in the benchmark tests by Salzberg et al. (2012) in assemblies from multiple genome libraries with variable insert lengths. Those included ALLPATHS-LG, SOAPdenovo, MaSuRCA, CABOG and Bambus2. As reference sequence for guiding AlignGraph, we used the chimpanzee genome. For ALLPATH-LG in its cheat mode, we reassembled the contigs ourselves because this assembler exhibits a better sensitivity and precision performance when providing a closely related reference genome. Here it was important to compare the performance of ALLPATHS-LG with AlignGraph when both are guided by the same reference genome.
In addition to contigs, we evaluated AlignGraph’s performance in improving the scaffold sets provided by the GAGE project for the same human sample set. Before their reassembly with AlignGraph, we reduced the number of unresolved sequence regions (gaps filled with ambiguous N bases) in the scaffolds by applying the GapFiller algorithm, which is currently one of the most efficient gap-filling methods (Boetzer and Pirovano, 2012).
To also evaluate the influence of the similarity shared among the reference and target genomes on AlignGraph’s performance, we included tests with four reference genomes of variable similarity to the human genome. The reference genomes chosen for this test were from gorilla, orangutan, gibbon and macaque. The genome sequence from gibbon was the only one that is still incomplete containing scaffolds rather than fully assembled chromosomes.
3.1.3 Published genome
In addition to the tests above, we were interested in evaluating to what extent AlignGraph can improve the genome sequence generated with another reference assisted assembly approach. For this test, we chose the published genome sequence from Landsberg erecta (Ler-1; Schneeberger et al., 2011). The latter is a strain of A.thaliana, which is too diverged from the known references to resolve its genome sequence with a simple resequencing approach. Thus, Schneeberger et al. (2011) assembled its genome with a reference-assisted pipeline approach that included ALLPATHS-LG and several refinement steps.
3.1.4 Data sources
The genome sequences used in the above tests were downloaded from the following community sites: A.thaliana from TAIR, A.lyrata from JGI, Landsberg erecta from 1001 Genomes and human and other primates from Ensembl. From the GAGE site, we downloaded the PE read sets and the preassembled contigs and scaffolds for the human chromosome 14 sample (Salzberg et al., 2012). The PE read sets from A.thaliana and Landsberg erecta were downloaded from NCBI’s Sequence Read Archive and the 1001 Genome site, respectively. The A.thaliana read set contained 32 million 2 × 75 bp PE reads (accession: SRR073127), the human read set contained 62 million 2 × 76–101 bp PE reads and the Ler-1 read set contained 73 million 2 × 40–101 bp PE reads.
3.1.5 Performance measurements
Most of the performance measures used by this study are adapted from the GAGE project (Salzberg et al., 2012). To evaluate the completeness of the contigs, we aligned them to the target genome with BLAT. If a contig could not be aligned as a single global alignment, it was split according to the local alignment results into the smallest possible number of subcontigs. The resulting contigs are called true contigs. The precision measures include the number of misassemblies per million base pairs (MPMB) and the average identity between contigs and target genome. Misassemblies caused by misjoin errors result in chimeric contigs. Their number can be calculated as the number of splits necessary to obtain the true contigs. Thus, MPMB 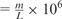 , where m is the numbers of misassemblies, and L is the cumulative length of the contigs. The average identity between true contigs and the target genome is calculated as
, where m is the numbers of misassemblies, and L is the cumulative length of the contigs. The average identity between true contigs and the target genome is calculated as 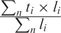 where ti is the identity for contig i, and li is the length of contig i (0 <i≤n). In this formula, the identity ti of the true contigs i is calculated as the number of aligned bases over the length of the alignment. The sensitivity measures include the N50 value and the number of covered bases. The former is the contig size at 50% of the total number of contig bases, and the latter is the total number of genome bases covered by the contigs. Two additional measures are the average length and maximum length of the true contigs. In all tests, we considered only contigs with a length of at least 1000 bp but used the entire set (including the shorter ones) in AlignGraph’s extension steps.
where ti is the identity for contig i, and li is the length of contig i (0 <i≤n). In this formula, the identity ti of the true contigs i is calculated as the number of aligned bases over the length of the alignment. The sensitivity measures include the N50 value and the number of covered bases. The former is the contig size at 50% of the total number of contig bases, and the latter is the total number of genome bases covered by the contigs. Two additional measures are the average length and maximum length of the true contigs. In all tests, we considered only contigs with a length of at least 1000 bp but used the entire set (including the shorter ones) in AlignGraph’s extension steps.
3.2 Results
3.2.1 Extension of A.thaliana contigs
The performance test results for the A.thaliana dataset are given in Table 2(a). In comparison with the initial contig sets assembled by Velvet or ABySS, AlignGraph extends 28.7–37.8% of them when guided by the A.lyrata genome as reference. The resulting set of extended contigs contains 27.9–33.2% less sequences because AlignGraph has joined many of the initial contigs. This leads to improvements of the N50, the number of covered bases, average contig length and maximum contig length for the extendable contig set by 89.9–94.5%, 15.9–24.1%, 69.3–69.2% and 54.9–81.6%, respectively. These improvements are accompanied only by minor increases of MPMB errors. The MPMB values of the extendable and extended contigs are usually much lower than for the complete set because of their pre-filtered nature that improves their quality. As expected the average identity also drops slightly (2.8–2.9%) because with increased length of the assembled sequences, internal sequence variations accumulate and complicate the alignment of the extended contigs against the target genome. A similar trend can be seen in the results below for the much longer scaffolds where the average identity is always lower for all of the tested assemblers [Table 2(c)]. For all three sample sets (Sections 3.2.1–3.2.4), the AlignGraph results contain a comparable number of sequence variations to the target genomes as the results of de novo assemblers (data not shown). This indicates a high sequence quality of the reassembled contigs.
3.2.2 Extension of human contigs and scaffolds from GAGE
The test results for the human chromosome 14 contigs are given in Table 2(b). Of the contigs assembled by ALLPATHS-LG, 38.2% can be extended and the extension result contains 53.1% less contigs because of the joins generated by AlignGraph. These improvements are more pronounced than in the above experiment with A.lyrata as reference because the genomes of human and chimpanzee share a much higher sequence similarity than the genomes of A.thaliana and A.lyrata. The N50, the number of covered bases, average contig length and maximum contig length for the extendable contig set consistently improve by 80.3, 1.9, 118.0 and 52.6%, respectively. Similar results could be obtained with the other de novo assemblers SOAPdenovo, MaSuRCA, CABOG and Bambus2. After AlignGraph processing, their extendable contigs improved for the same four evaluation metrics by 88.8–165.8, 3.4–16.8, 82.6–160.6 and 30.3–54.8%, respectively. If ALLPATHS-LG is run in its cheat mode by guiding it with the same reference genome as AlignGraph, then both the sensitivity and precision measures of the ALLPATHS-LGc contigs improve compared with the assembly without a reference. Nevertheless, AlignGraph is still able to extend 33.6% of the ALLPATHS-LGc contigs, and the extension results contain 53.1% less contigs, whereas the four evaluation metrics improve by 89.4, 10.0, 123.5 and 7.0%, respectively. These improvements indicate that the reference-assisted approach used by AlignGraph is more efficient than the one from ALLPATHS-LG in its cheat mode at the contig assembly stage.
AlignGraph’s performance results on the scaffolds from the same human chromosome 14 dataset are given in Table 2(c). The scaffold sets from SOAPdenovo, MaSuRCA, CABOG and Bambus2 contain much smaller numbers of sequences than their corresponding contig sets. Nevertheless, AlignGraph is able to extend 11.6–31.0% of them and improve the N50 value and the number of covered bases by 9.4–152.7 and 14.8–29.0%, respectively. The extension results for the scaffold set of Bambus2 contain a slightly larger number of sequences (14) than the extendable set. The reason for this is that many of them are short, and AlignGraph extends them often to scaffolds with a length above the 1000 bp requirement, thus increasing the number of reported scaffolds (see Section 3.1.5). This trend also explains the slightly lower average length of the extended scaffold set from Bambus2.
3.2.3 Influence of similarity of reference genome
To assess AlignGraph’s performance with reference genomes of variable similarity to the target genome, we post-processed the de novo assemblies of the human dataset with AlignGraph using as reference the genome sequences from five different primates. The columns in Table 3 list these organisms according to their evolutionary distances to the human genome (increasing from left to right). To avoid confusions, exact sequence similarity values to the human genome are not provided because there are many possibilities to calculate them, which can lead to different results. As expected, the performance measures degrade with the evolutionary distance between the target and reference genomes. Although the first four reference genomes show respectable improvements, the macaque genome seems to be too diverged from human to achieve any major improvements. However, this performance drop is mainly due to the difficulty of aligning short reads to a highly diverged reference. Future improvements in NGS read length and alignment algorithms are likely to enhance AlignGraph’s performance in this regard.
Table 3.
Performance with reference genomes of variable similarity
| Percentage of | Chimpanzee | Gorilla | Orangutan | Gibbon | Macaque |
|---|---|---|---|---|---|
| Aligned readsa | 94.5% | 91.6% | 88.9% | 49.9% | 24.9% |
| Extendable contigsb | 51.0% | 36.4% | 24.9% | 6.7% | — |
| Improved N50c | 109.9% | 84.0% | 73.2% | 65.3% | — |
The tests were performed on the human chromosome 14 sample where the listed primate genomes served as reference. The results include the percentage values of aalignable reads, bExtendable contigs relative to the initial set cImprovements of the N50 values relative to the extendable contigs. Because of space limitations, the latter two rows contain averaged percentage values for the five assemblers ALLPATHS-LG, SOAPdenovo, MaSuRCA, CABOG and Bambus2.
3.2.4 Improvements to published genome
The test results for the published Landsberg erecta genome are shown in Table 4. The initial scaffold set used in this test consisted of 1676 sequences. AlignGraph extended 27.6% of these scaffolds, whereas the extended set contains 20.3% fewer scaffolds. In addition, AlignGraph improves the N50 value, the number of covered bases, the average contig length and maximum length values for the extendable scaffolds by 86.6, 8.1, 35.7 and 8.1%, respectively. These improvements demonstrate AlignGraph’s usefulness in improving published genome sequences, even for those that have been carefully curated by their authors.
Table 4.
Improvements to published genome
| Contig set | N contigs | N50 | N total basesa | Average length | Maximum length |
|---|---|---|---|---|---|
| All | 1676 | 341 653 | 112 578 343 | 67 170 | 2 930 180 |
| Extendable | 462 | 448 682 | 57 574 961 | 124 621 | 2 930 180 |
| Extendable + AlignGraph | 368 | 837 458 | 62 216 675 | 169 067 | 3 168 537 |
The published scaffolds from Landsberg erecta were extended with AlignGraph using the A.thaliana genome as reference. The rows and columns are arranged the same way as in Table 2, but several columns are missing here because it is not possible to compute the corresponding performance measures in a meaningful manner without having access to a ‘true’ target genome sequence. aIn addition, we report here the total number of bases in the contigs.
In summary, the above performance tests demonstrate AlignGraph’s efficiency in improving the results of a variety of de novo assemblers and species with variable genome complexity by taking advantage of closely related reference genomes.
4 CONCLUSIONS AND FUTURE WORK
This study introduces a novel de Bruijn graph-based algorithm for improving de novo genome assemblies guided by sequence information from a closely related species. The chosen PE multipositional de Bruijn graph approach provides an elegant and efficient solution to this problem. Our performance results demonstrate that the implemented AlignGraph software is able to improve the results of a wide range of de novo assemblers for complex genomes even with relatively diverse and suboptimal guide sequences as reference. Moreover, our results demonstrate AlignGraph’s usefulness for improving unfinished genome assemblies. Another advantage is that AlignGraph can be used in combination with most existing de novo assemblers. In the future, we will expand AlignGraph in the following areas: (i) we will provide support for additional variant-aware alignment tools for both PE read and contig data, such as GSNAP and GMAP, respectively, (ii) de novo assembly functionality will be added to AlignGraph to further optimize assemblies at many stages of the reference-assisted workflow, (iii) utilities will be incorporated for detecting and resolving misassemblies either in the initial contigs or in the extensions and (iv) the processing of scaffolds with large gaps will be improved.
ACKNOWLEDGEMENT
The authors acknowledge the support of the core facilities at the Institute for Integrative Genome Biology (IIGB) at University of California (UC), Riverside.
Funding: The USDA National Institute for Food and Agriculture (NIFA-2010-65106-20675 to T.G.) and the National Science Foundation (ABI-0957099 to T.G., IOB-0420152 to T.G., MCB-1021969 to T.G. and DBI-1262107 to T.J.).
Conflict of interest: none declared.
REFERENCES
- Boetzer M, Pirovano W. Toward almost closed genomes with gapfiller. Genome Biol. 2012;13:R56. doi: 10.1186/gb-2012-13-6-r56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boetzer M, et al. Scaffolding pre-assembled contigs using sspace. Bioinformatics. 2011;27:578–579. doi: 10.1093/bioinformatics/btq683. [DOI] [PubMed] [Google Scholar]
- Chaisson MJ, Pevzner PA. Short read fragment assembly of bacterial genomes. Genome Res. 2008;18:324–330. doi: 10.1101/gr.7088808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaisson MJ, et al. De novo fragment assembly with short mate-paired reads: does the read length matter? Genome Res. 2009;19:336–346. doi: 10.1101/gr.079053.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayarian A, et al. Sopra: scaffolding algorithm for paired reads via statistical optimization. BMC Bioinformatics. 2010;11:345. doi: 10.1186/1471-2105-11-345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dohm JC, et al. Sharcgs, a fast and highly accurate short-read assembly algorithm for de novo genomic sequencing. Genome Res. 2007;17:1697–1706. doi: 10.1101/gr.6435207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao S, et al. Opera: reconstructing optimal genomic scaffolds with high-throughput paired-end sequences. J. Comput. Biol. 2011;18:1681–1691. doi: 10.1089/cmb.2011.0170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gnerre S, et al. Assisted assembly: how to improve a de novo genome assembly by using related species. Genome Biol. 2009;10:R88. doi: 10.1186/gb-2009-10-8-r88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gnerre S, et al. High-quality draft assemblies of mammalian genomes from massively parallel sequence data. Proc. Natl Acad. Sci. USA. 2011;108:1513–1518. doi: 10.1073/pnas.1017351108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gritsenko AA, et al. Grass: a generic algorithm for scaffolding next-generation sequencing assemblies. Bioinformatics. 2012;28:1429–1437. doi: 10.1093/bioinformatics/bts175. [DOI] [PubMed] [Google Scholar]
- Hernandez D, et al. De novo bacterial genome sequencing: millions of very short reads assembled on a desktop computer. Genome Res. 2008;18:802–809. doi: 10.1101/gr.072033.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu TT, et al. The Arabidopsis lyrata genome sequence and the basis of rapid genome size change. Nat. Genet. 2011;43:476–481. doi: 10.1038/ng.807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeck WR, et al. Extending assembly of short DNA sequences to handle error. Bioinformatics. 2007;23:2942–2944. doi: 10.1093/bioinformatics/btm451. [DOI] [PubMed] [Google Scholar]
- Kent W. Blatthe blast-like alignment tool. Genome Res. 2002;12:656–664. doi: 10.1101/gr.229202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, et al. Reference-assisted chromosome assembly. Proc. Natl Acad. Sci. USA. 2013;110:1785–1790. doi: 10.1073/pnas.1220349110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, Salzberg SL. Fast gapped-read alignment with bowtie 2. Nat. Methods. 2012;9:357–359. doi: 10.1038/nmeth.1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Homer N. A survey of sequence alignment algorithms for next-generation sequencing. Brief. Bioinform. 2010;11:473–483. doi: 10.1093/bib/bbq015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, et al. De novo assembly of human genomes with massively parallel short read sequencing. Genome Res. 2010;20:265–272. doi: 10.1101/gr.097261.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y, et al. Comparative studies of de novo assembly tools for next-generation sequencing technologies. Bioinformatics. 2011;27:2031–2037. doi: 10.1093/bioinformatics/btr319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo R, et al. Soapdenovo2: an empirically improved memory-efficient short-read de novo assembler. Gigascience. 2012;1:18. doi: 10.1186/2047-217X-1-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medvedev P, et al. Paired de bruijn graphs: a novel approach for incorporating mate pair information into genome assemblers. J. Comput. Biol. 2011;18:1625–1634. doi: 10.1089/cmb.2011.0151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JR, et al. Aggressive assembly of pyrosequencing reads with mates. Bioinformatics. 2008;24:2818–2824. doi: 10.1093/bioinformatics/btn548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ossowski S, et al. Sequencing of natural strains of Arabidopsis thaliana with short reads. Genome Res. 2008;18:2024–2033. doi: 10.1101/gr.080200.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y, et al. Research in Computational Molecular Biology. Berlin Heidelberg: Springer; 2010. Idba–a practical iterative de bruijn graph de novo assembler; pp. 426–440. [Google Scholar]
- Pevzner P, et al. An eulerian path approach to dna fragment assembly. Proc. Natl Acad. Sci. USA. 2001;98:9748. doi: 10.1073/pnas.171285098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillippy AM, et al. Genome assembly forensics: finding the elusive mis-assembly. Genome Biol. 2008;9:R55. doi: 10.1186/gb-2008-9-3-r55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pop M, et al. Comparative genome assembly. Brief. Bioinform. 2004a;5:237–248. doi: 10.1093/bib/5.3.237. [DOI] [PubMed] [Google Scholar]
- Pop M, et al. Hierarchical scaffolding with bambus. Genome Res. 2004b;14:149–159. doi: 10.1101/gr.1536204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronen R, et al. Sequel: improving the accuracy of genome assemblies. Bioinformatics. 2012;28:i188–i196. doi: 10.1093/bioinformatics/bts219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salmela L, et al. Fast scaffolding with small independent mixed integer programs. Bioinformatics. 2011;27:3259–3265. doi: 10.1093/bioinformatics/btr562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salzberg SL, et al. Gage: a critical evaluation of genome assemblies and assembly algorithms. Genome Res. 2012;22:557–567. doi: 10.1101/gr.131383.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schatz MC, et al. Hawkeye and AMOS: visualizing and assessing the quality of genome assemblies. Brief. Bioinform. 2013;14:213–224. doi: 10.1093/bib/bbr074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneeberger K, et al. Reference-guided assembly of four diverse Arabidopsis thaliana genomes. Proc. Natl Acad. Sci. USA. 2011;108:10249–10254. doi: 10.1073/pnas.1107739108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson J, et al. Abyss: a parallel assembler for short read sequence data. Genome Res. 2009;19:1117–1123. doi: 10.1101/gr.089532.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai IJ, et al. Method improving draft assemblies by iterative mapping and assembly of short reads to eliminate gaps. Genome Biol. 2010;11:R41. doi: 10.1186/gb-2010-11-4-r41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren RL, et al. Assembling millions of short DNA sequences using ssake. Bioinformatics. 2007;23:500–501. doi: 10.1093/bioinformatics/btl629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeitouni B, et al. SVDetect: a tool to identify genomic structural variations from paired-end and mate-pair sequencing data. Bioinformatics. 2010;26:1895–1896. doi: 10.1093/bioinformatics/btq293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerbino D, Birney E. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Res. 2008;18:821–829. doi: 10.1101/gr.074492.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimin AV, et al. The masurca genome assembler. Bioinformatics. 2013;29:2669–2677. doi: 10.1093/bioinformatics/btt476. [DOI] [PMC free article] [PubMed] [Google Scholar]