Biaxial Response of Ovine Spinal Cord Dura Mater

Abstract

The dura mater performs a major functional role in the stability and mechanical response of the spinal cord complex. Computational techniques investigating the etiology of spinal cord injury require an accurate mechanical description of the dura mater. Previous studies investigating the mechanical response of the dura mater have reported conflicting results regarding the anisotropic stiffness of the dura in the longitudinal and circumferential direction. The aim of this study was to investigate the biaxial response of the dura mater in order to establish the tissue level mechanical behavior under physiological loading scenarios. To this end, square sections of the dura were tested in a custom biaxial setup under a comprehensive uniaxial and biaxial loading protocol. The resultant data were fit via a transversely isotropic continuum model and an anisotropic continuum constitutive model. The transversely isotropic formulation failed to accurately predict the dura mater’s uniaxial behavior. The anisotropic formulation accurately predicted the uniaxial response in both longitudinal and circumferential directions. Significantly higher stiffness (p < 0.0001) was observed in the circumferential direction as compared to the longitudinal direction. Further, the longitudinal direction displayed a significantly lower degree of nonlinearity (p < 0.045) and significantly higher degree of collagen fiber dispersion (p < 0.032) as compared to the circumferential direction. Results indicate that the dura mater has differential mechanical response in the longitudinal and circumferential directions and future studies should utilize an anisotropic two fiber family continuum model to accurately describe dura mater mechanics.

Introduction

The dura mater plays a major functional role in the spinal cord-meningeal complex (SCM). Being the strongest structure of the meninges, it helps in sustaining the flow and pressure of the cerebral spinal fluid (CSF) and protects the spinal cord from external mechanical loading. Loss of integrity of the dura can result in subdural and epidural hematomas. Accidental damage of the dura during procedures such as lumbar puncture and epidural anesthesia can potentially result in post-dural-puncture headaches (PDPH).

Studies investigating the mechanical response of the spinal cord structure due to traumatic injurious loading to the spine, as well as the aforementioned maladies, require an accurate description of the mechanical behavior of the intact dura. Further, these material models are required for researchers using computational tools (such as the finite element method) and experimentalists that are developing physical surrogate models of the spinal cord (Kroeker et al., 2009). Accordingly, multiple studies have examined the mechanical response of the dura mater. Uniaxial tensile testing of longitudinal and circumferential dura samples from both human and bovine subjects revealed higher stiffness in the longitudinal direction as compared to the circumferential direction (Runza et al., 1999). Similar results were observed by Maikos et al. (2009) with data obtained from rat spinal dura samples. Both studies used histological techniques to observe the collagen orientation and found architectural evidence supporting these anisotropic results. Based on these data, it has been generally accepted that collagen fibers within the dura are preferentially aligned in the longitudinal direction and interspersed with thick elastic fibers. However, more recent studies examining the elastic and viscoelastic behavior of the dura mater in the longitudinal and circumferential directions have reported higher stiffness in the circumferential direction as compared to the longitudinal direction (Persson et al., 2010; Wilcox et al., 2003). Further, histological studies have reported that the dural collagen fibers are not preferentially aligned in the longitudinal direction and that a substantial subset of the total collagen fiber content has been observed to be oriented in the circumferential direction (Fink and Walker, 1989; Reina et al., 1997). Consequently, significant controversy exists as to the true mechanical and ultrastructural relationship of the spinal dura mater.

Physiologically, one might expect that significant loading can occur simultaneously in both the longitudinal and circumferential directions. Radial pressure from the pulsatile flow of the cerebrospinal fluid produces circumferential stresses/strains, and flexural movement of the head/spine can produce tensile loads to the dura in the longitudinal direction. Hence, it is imperative that the dura be mechanically tested in both these directions simultaneously, similar to cardiovascular tissues, such that the interaction of these biaxial stresses can be fully appreciated with respect to the overall dural mechanical behavior.

Thus, in order to provide further insight on dura mechanical behavior under physiological loading conditions, the present study investigated the planar mechanical properties of the ovine cervical dura mater by simultaneously (biaxially) testing the dura in the longitudinal and circumferential directions. Further, we quantified the divergent longitudinal and circumferential mechanical response of the dura mater by modifying a previously established two-fiber family strain energy density function that was originally derived to model vascular tissue (Gasser et al., 2006).

Methods

Specimen Preparation

Four ovine cervical spines were obtained from subjects euthanized for reasons unrelated to this study. Ovine specimens were chosen to ensure continuity with our current efforts in developing computational and experimental models of the ovine SCM. Laminectomies were performed for cervical levels C1-C6 to gain access to the spinal cord complex. Careful dissection of the nerve root connections allowed for the intact removal of the SCM from the associated hard tissue. The dura was detached from the spinal cord after careful resection of the denticulate ligaments. The dural specimens were cut into squares of approximately 25×25mm. A small notch, indicating the longitudinal direction, at the periphery of each sample was introduced to ensure that the correct orientation was maintained during the entire preparation and testing period. Specimens were visually evaluated for mechanical integrity and macroscopic abnormalities before being mechanically tested. Three specimens were obtained from each spine, resulting in a total sample size of 12. The thickness of the dura samples (0.35mm±0.09) was measured post hoc to account for saline absorption and tissue swelling during testing [Figure 1A]. Digital images (3 images/specimen, E520 Evolt 10MP Digital SLR, Olympus, Center Valley, PA) of dural cross-sections were obtained with a microscope (Fisher Scientific, Waltham, MA) and the resultant images processed with ImageJ (NIH, Bethesda, MD) to quantify the mean cross-sectional area, which was used in subsequent stress calculations.

Figure 1.

A) Thickness of dura samples measured post hoc at five locations within the vicinity of the stain markers. B) Dura sample ready to be tested in a custom biaxial test setup.

Mechanical Testing

A custom biaxial testing device developed by our group was used for mechanically evaluating the dural specimens (McGilvray et al., 2010). The specimens were mounted to the device in a trampoline-like fashion by tying two braided fishing lines (50lb capacity) per side with a surgeon’s knot. The other termini of the lines were attached to the actuating mechanisms [Figure 1B]. The specimen was tested while completely immersed in PBS at room temperature. Local strains were measured by video-tracking of 9 ink dots placed onto the epidural surface. The system produced a resolution of 2.5µm/pixel (1024×768) and video was collected at 15Hz. Load data were recorded in the two orthogonal directions with the use of two 10lb capacity load cells (Model 31, Sensotec, Honeywell, Columbus, Ohio) at 100Hz. The ratio of relative elongation in each direction was kept constant (λ_l / λ_c : λ_c / λ_l), where λ_l represents the stretch ratio in the longitudinal direction and λ_c represents the stretch ratio in the circumferential direction. Each dural specimen was subjected to three biaxial loading protocols (1:1, 2:1 and 1:2) and two uniaxial loading protocols (Sacks and Chuong, 1993). The biaxial data were utilized for determining the coefficients of the specified strain energy functions (as outlined below), whereas the uniaxial tests provided an independent data set for experimental comparison to the model’s subsequent predictions using these optimized coefficients. A reference state was established by loading specimens to 0.5N in both directions. The order of the tests was randomized to minimize order effects. Each loading condition was applied for 10 cycles and load-deformation data were collected on the last cycle. The Lagrangian stress (T) was calculated by dividing the measured force (P) response by the undeformed cross-sectional area (product of thickness and width normal to the applied loading direction). The Lagrangian stress was transformed to the Cauchy stress (t) by:

$$\mathit{t}=F_{ij}T$$ (1)

where F_ij represents the in-plane deformation gradient, computed from the average displacement between three pairs of optical markers in the longitudinal and circumferential directions. The out-of-plane stretch ratio (λ₃) was obtained by:

$${\lambda }_3=\frac{J}{{\lambda }_l{\lambda }_c}$$ (2)

where λ_l and λ_c represent the in-plane (longitudinal and circumferential) stretch ratios. Assuming incompressibility, the determinant of the deformation gradient tensor (J) was set to unity (Gasser et al., 2006; Holzapfel et al., 2002). The resultant Cauchy stresses and principal stretch ratios were used for constitutive modeling and data fitting.

Constitutive Modeling

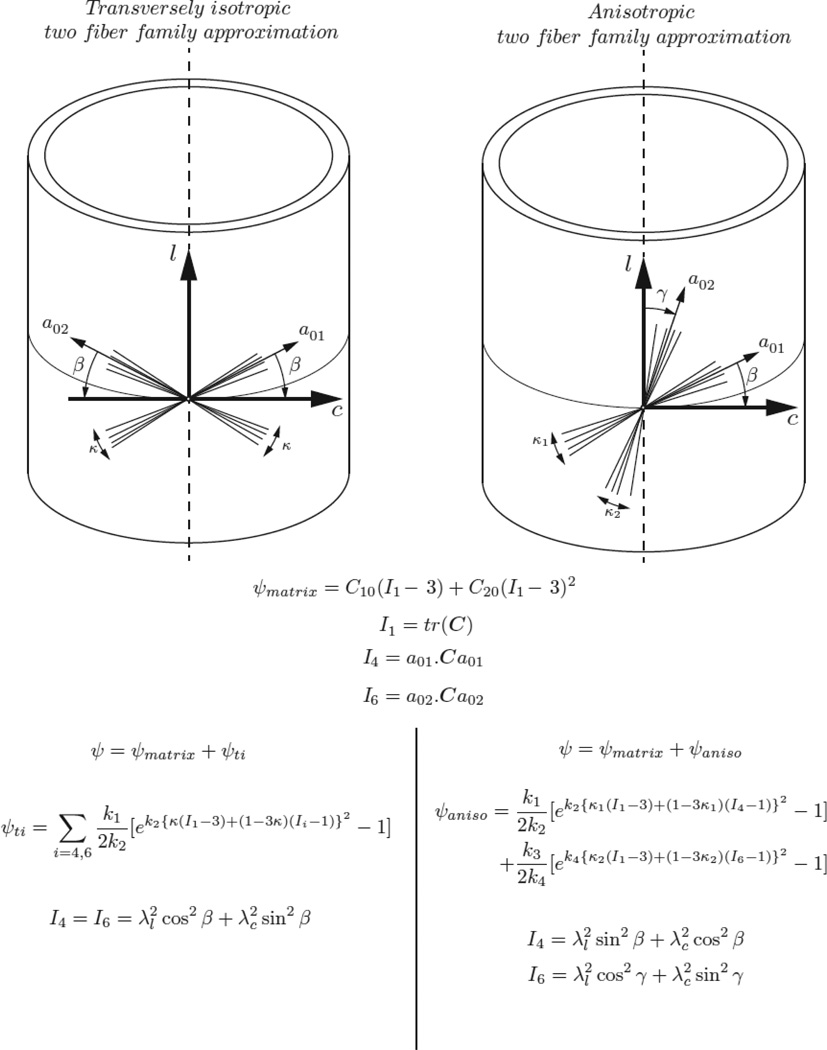
As a first attempt to model the dura using a continuum description for a fiber-reinforced composite, a transversely isotropic two fiber family strain energy function first proposed by Gasser et al. (Gasser et al., 2006) was used to describe the observed biaxial behavior. This formulation assumes identical mechanical behavior (specifically, stiffness and nonlinearity) between the two fiber families. The total strain energy density (W) for the transversely isotropic Gasser model (TI_G) is calculated from the following formulation:

$$W=C_{10}(I_1-3)+C_{20}{(I_1-3)}^2+\sum _{i=4,6}\frac{k_1}{2k_2}[e^{k_2{\{\kappa (I_1-3)+(1-3\kappa )(I_i-1)\}}^2}-1]$$ (3)

where, the isotropic ground substance is modeled as a Yeoh hyperelastic polynomial material model (first two terms in equation 3). The coefficients C₁₀ and C₂₀ represent twice the initial shear modulus and the nonlinearity, respectively, and I₁ is the first strain invariant of the right Cauchy-Green deformation tensor. The two families of fibers in the dura mater (final series in equation 4) were modeled via an exponential three-term strain energy density function where k₁ is a material parameter with dimensions of stress representing the overall stiffness, k₂ is a dimensionless parameter describing the nonlinearity of the collagen fiber behavior, and κ describing the degree of fiber dispersion. I₄ and I₆ represent the fourth and sixth anisotropic strain invariants that describe the orientation of each fiber family (by use of the β angle) with respect to the circumferential axis:

$$I_4=I_6={\lambda }_l^2{\text{cos}}^2\beta +{\lambda }_c^2{\text{sin}}^2\beta$$ (4)

Based on the aforementioned studies reporting divergent behavior in the longitudinal and circumferential directions of the dura (Maikos et al., 2008; Runza et al., 1999; Wilcox et al., 2003), a more general anisotropic formulation of Equation 3 was fit to the biaxial data. This formulation provided two pairs of parameters for each of the fiber directions: k₁ and k₂ for describing the stiffness and nonlinearity, respectively, in the longitudinal direction; k₃ and k₄ for describing the stiffness and nonlinearity, respectively, in the circumferential direction. Further, each family of fibers was associated with an independent degree of fiber dispersion (κ₁ and κ₂). Thus, this anisotropic Gasser model (ANISO_G) variant of Equation 3 resulted in an eightparameter strain energy density function:

$$W=C_{10}(I_1-3)+C_{20}{(I_1-3)}^2+\frac{k_1}{2k_2}[e^{k_2{\{{\kappa }_1(I_1-3)+(1-3{\kappa }_1)(I_4-1)\}}^2}-1]+\frac{k_3}{2k_4}[e^{k_4{\{{\kappa }_2(I_1-3)+(1-3{\kappa }_2)(I_6-1)\}}^2}-1]$$ (5)

A visual description of the two formulations and their associated strain energy and invariant equations are provided in Figure 2. The theoretical Cauchy stress was obtained by differentiating the total strain energy density by the right-Cauchy-Green deformation tensor (C) (Ayturk et al., 2012; Holzapfel, 2000; Holzapfel and Ogden, 2009). All fitting was performed with the lsqcurvefit function in MATLAB (Version 2013a, MathWorks, Natick, MA) via minimization of the sum of squared errors in the predicted stresses. Significant differences in the resultant mean fitted parameters for each of the fiber families were compared using the Wilcoxon-Mann-Whitney rank-sum test, with the significance level set at p<0.05 (ranksum , MATLAB 2013a, MathWorks, Natick, MA). Fit and prediction performance was evaluated via determination of the root mean squared error (RMSE).

Figure 2.

Fiber family orientation and associated strain energy descriptions for the transversely isotropic (TI_G) and anisotropic (ANISO_G) two fiber family approximations. The same strain energy function was used to describe the isotropic ground substance for both models. Here, l represents the longitudinal direction and c represents the circumferential direction

Results

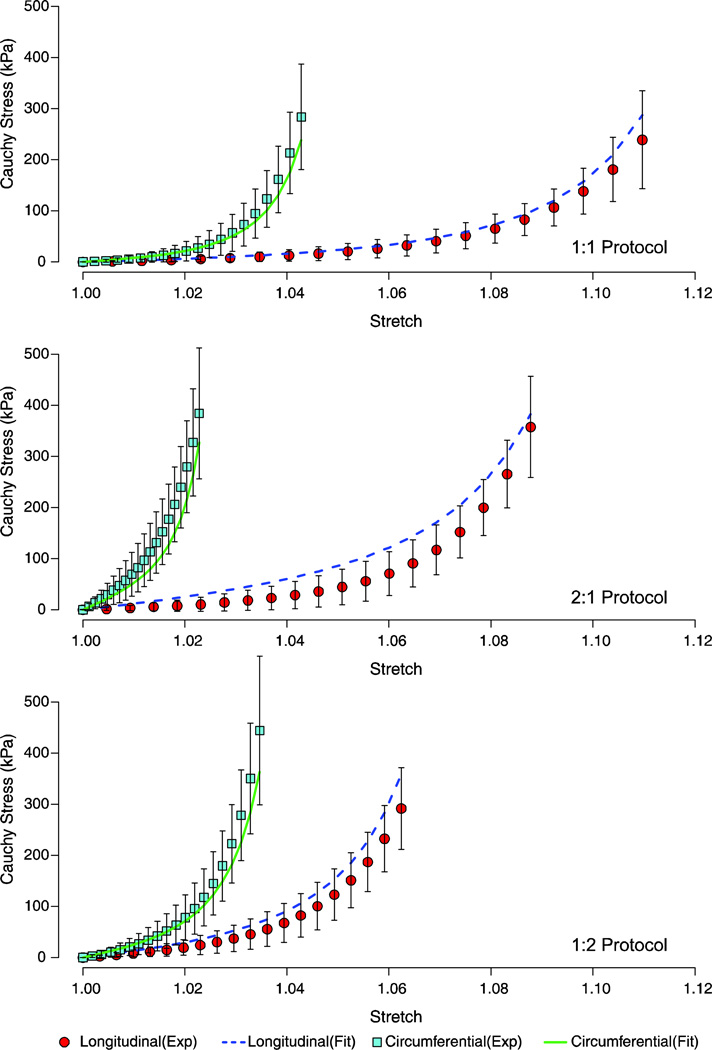
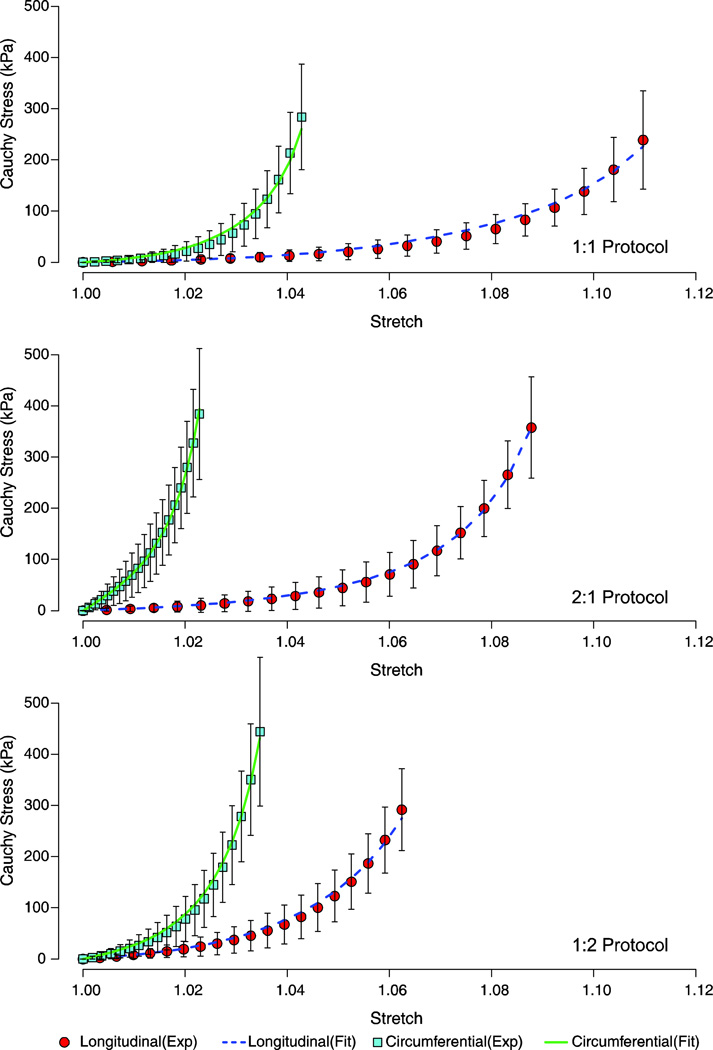
Nonlinear responses were observed for both the longitudinal and circumferential directions when subjected to a biaxial testing regime (1:1, 2:1, and 1:2 protocols). The transversely isotropic Gasser (TI_G) model (equation 3) produced mean biaxial data fits with a root mean squared error (RMSE) for all predictions for each the biaxial protocols (1:1, 2:1, and 1:2) below 43.97kPa [Figure 3]. The anisotropic Gasser (ANISO_G) model (equation 5) resulted in a closer fit to the biaxial protocols as compared to the TI_G model fits, with RMSE values for each of the fitted longitudinal and circumferential responses below 8.68kPa [Figure 4].

Figure 3.

Fitted stress-stretch response of the biaxial protocols (1:1, 2:1, and 1:2) based on the transversely Gasser model (Equation 3). The mean experimental data are shown with one standard deviation error bars.

Figure 4.

Fitted stress-stretch response of the biaxial protocols (1:1, 2:1, and 1:2) based on the anisotropic Gasser model (Equation 5). The mean experimental data are shown with one standard deviation error bars.

The mean fitted coefficients for the TI_G model are provided in Table 1 and the mean fitted coefficients for ANISO_G model are presented in Table 2. The ANISO_G model predicted higher values for the coefficients associated with the matrix ground substance (C₁₀ , C₂₀) as compared to the TI_G model (p < 0.001). For the ANISO_G model, the longitudinal and circumferential directions yielded significant differences (p < 0.0001) with respect to the fitted coefficients that represent the overall stiffness (k₁ and k₃, Table 2), with higher k₁ values than k₃ values. Significant differences (p = 0.045) were also found between the coefficients that represent the nonlinearity of the collagen fibers (k₂ and k₄, Table 2), with k₂ (circumferential direction) values being substantially higher than the fitted values for k₄ (longitudinal direction). The degree of fiber dispersion (κ) in the TI_G model was predicted to be 0.11 and the angle between the two fibers directions (2* β ; Figure 2) was found to be 86.8°. For the ANISO_G model, statistical differences were found between the degree of fiber dispersion parameters (κ₁ (0.11±0.09) and κ₂ (0.15 ± 0.08), p = 0.032) for the two fiber families, with fiber dispersion higher in the longitudinal direction as compared to the circumferential direction. The anisotropic fit also predicted the average orientation of the two fiber families (β and γ in Figure 2) wherein, one fiber family (a₀₁) was found to be oriented at 4.8° (β) with respect to the circumferential axis and the other fiber family was oriented 40.7° (γ) with respect to the longitudinal axis [Figure 2].

Table 1.

Fitted coefficients for the TI_G model, data represent mean (SD) values. C₁₀, C₂₀, k₁ are in MPa, β is in degrees and k₂ and κ are unit less.

Matrix		Circumferential and longitudinal fibers
C10	C20	k1	k2	κ	β
0.004 (0.01)	0.24 (0.676)	0.62 (0.45)	326.8 (307.4)	0.11 (0.08)	43.4 (9.1)

Table 2.

Fitted coefficients for the ANISO_G model, data represent mean (SD) values. C₁₀, C₂₀, k₁ and k₃ are in MPa, β and γ are in degrees and k₂,k₄,κ₁ and κ₂ are dimensionless. ^∥, ^* and ^# indicate statistical significance. Specifically, these significance values compare the stiffness (k₁, k₃), nonlinear response (k₂, k₄), and the mean fiber orientation (β,γ) associated with the two fiber families of the ANUSO_G model.

Matrix		Circumferential fibers				Longitudinal fibers
C10	C20	k1 ∥	k2 #	κ1 *	β	k3 ∥	k4 #	κ2 *	γ
0.055 (0.03)	3.29 (4.05)	1.13 (1.5)	888.4 (1417)	0.11 (0.09)	4.88 (7.4)	0.32 (0.27)	277 (273)	0.15 (0.08)	40.8 (30.5)

^∥corresponds to p < 0.0001,

^#corresponds to p = 0.045 and

^*corresponds to p = 0.032

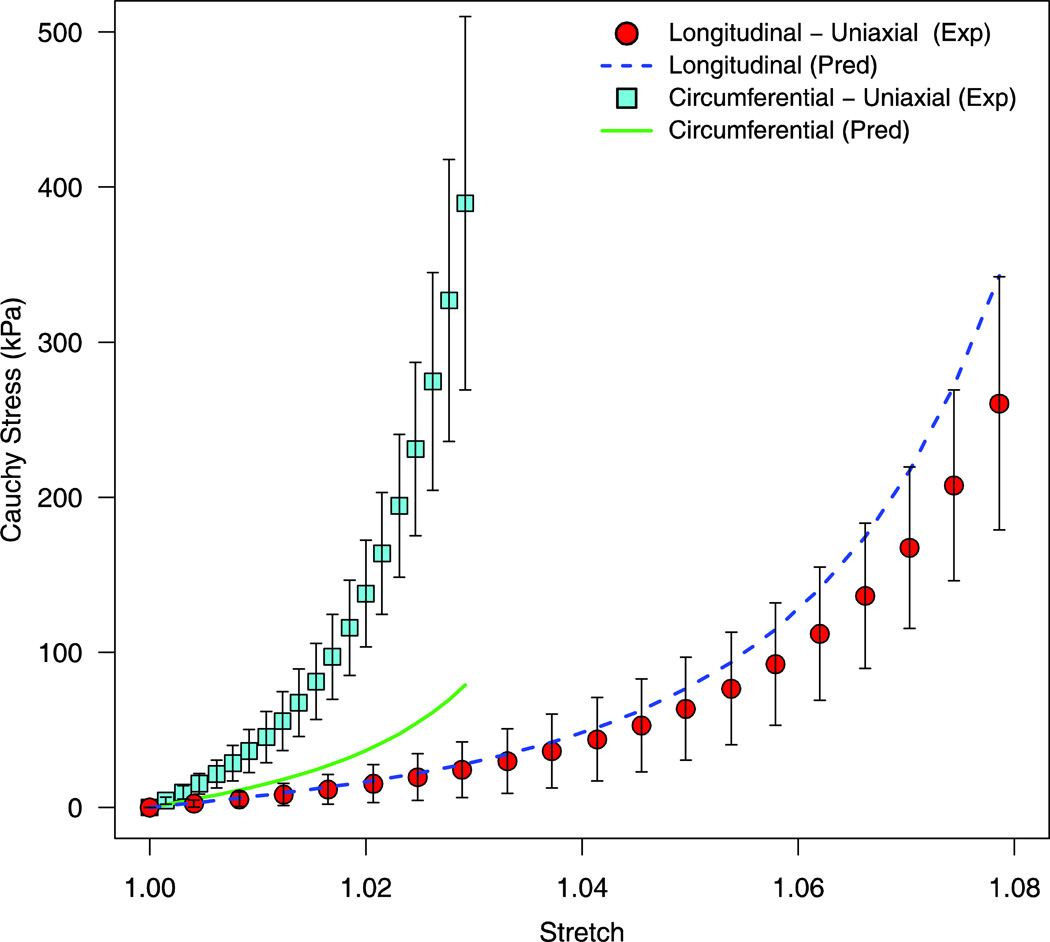
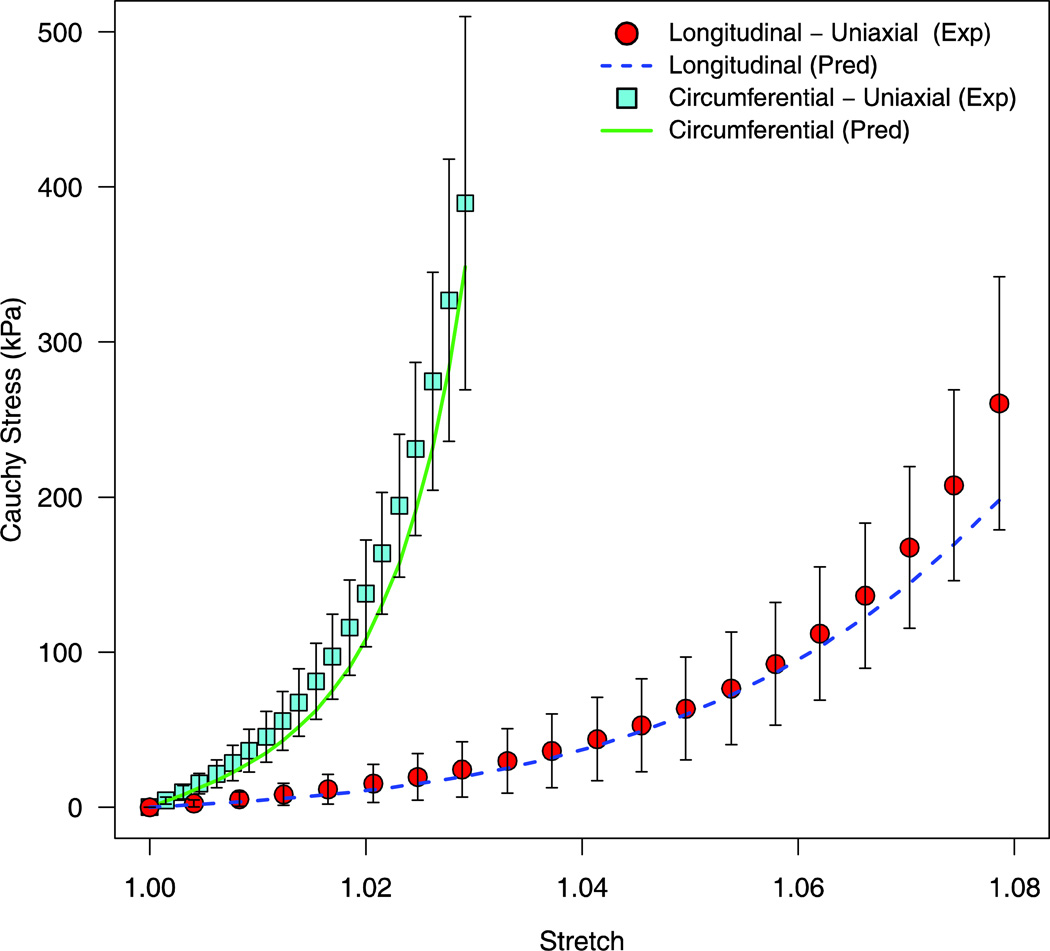
The predictive capability of the two Gasser models was evaluated by predicting the uniaxial stress response from the longitudinal and circumferential uniaxial protocols. The TI_G model failed to accurately predict this uniaxial behavior, with an RMSE of 123.9kPa for the circumferential uniaxial protocol (experimental variability = 44.5kPa) and an RMSE of 28.9kPa for the longitudinal uniaxial protocol (experimental variability = 35.1kPa) [Figure 5]. The ANISO_G model was better able to predict the uniaxial protocols as compared to the TI_G model, with a RMSE of 25.1kPa for the circumferential uniaxial protocol and 17.8kPa for the longitudinal uniaxial protocol [Figure 6].

Figure 5.

Predicted stress-stretch response of the uniaxial loading protocols via the fitted coefficients of the TI_G model (Equation 3). The corresponding mean experimental data are shown with one standard deviation error bars.

Figure 6.

Predicted stress-stretch response of the uniaxial loading protocols via the fitted coefficients of the ANISO_G model (Equation 5). The corresponding mean experimental data are shown with one standard deviation error bars.

Discussion

This study investigated the longitudinal and circumferential mechanical response of the ovine spinal dura mater using a biaxial testing protocol. These data served as inputs for fitting to constitutive continuum models. Studies investigating the mechanical response of the dura generally report the stiffness in the longitudinal and circumferential directions via a uniaxial loading protocol performed on prepared (ex: dog bone-shaped) specimens (Persson et al., 2010; Runza et al., 1999). It has previously been reported that stiffness of the dura in the circumferential direction is much higher as compared to the longitudinal direction (Persson et al., 2010; Wilcox et al., 2003). It was observed in this study that k₁ (the overall circumferential stiffness) was significantly higher than k₃ (the overall longitudinal stiffness), which is in agreement with these previous studies. However, it is important to note than other studies have reached different conclusions regarding the stiffness of the dura in the longitudinal and circumferential directions. Runza et al. 1998 and Maikos et al. 2008 reported higher stiffness in the longitudinal direction as compared to the circumferential direction using both human and animal specimens. This disparity may be attributed to the varying maximal strains attained in these studies. For the biaxial protocol employed in the current study, dura specimens were not loaded to their maximum possible (non-failure) strain in the longitudinal direction. Previous uniaxial studies have reported higher stiffness in the longitudinal direction as compared to the circumferential direction when the stiffness was calculated at 90% of the maximum strain value (Persson et al., 2010; Runza et al., 1999). Quantitatively, the stiffness values obtained in this study (longitudinal: 1.13 ± 1.5 MPa, circumferential: 0.32 ± 0.27 MPa, Table 2) were comparable to values reported previously for rat dura in the longitudinal direction (1.20 ± 0.79 MPa) (Maikos et al., 2008).

This study also found significant differences in the k₂ and k₄ fitted coefficients that represent the nonlinearity of the loading behavior, with higher nonlinearity observed in the circumferential direction as compared to the longitudinal direction (k₂ > k₄). This was predominantly due to the extended and gradual toe region observed in the longitudinal stress-strain response. Physiologically, this can be correlated to the relatively low deformations that the spinal cord is subjected to during activities of daily living (i.e. during flexion, extension, lateral bending of the cervical spine). This necessitates that the dura remain relatively compliant in the longitudinal direction so as to induce minimal stress to the underlying spinal cord complex. Conversely, higher nonlinearity in the circumferential direction can be attributed to the dura mater’s role in maintaining the pulsatile flow of the cerebrospinal fluid by efficiently constraining the dura’s diametric dimension, and, therefore, preserving the fluid pressure. Microstructurally, the greater toe region observed in the longitudinal direction may potentially be due to a higher degree of crimp in the longitudinally-aligned collagen fibers as compared to fibers aligned in the circumferential direction. A previous study found higher crimping of collagen fibers in the longitudinal direction as compared to the circumferential direction via histological staining, however, no statistical significance was reported (Persson et al., 2010).

Circumferential fibers were found to be oriented at an angle of 4.8° with respect to the horizontal axis with an associated degree of fiber dispersion of 0.11. Longitudinal fibers were found to have a higher level of fiber dispersion (κ₂ = 0.15) and were oriented at an angle of 50.3° with respect to the horizontal axis. These results compare well with previously published values for collagen fiber orientation in bovine dura mater. Persson et al. reported that collagen fibers were aligned at an angle of 48° with respect to the horizontal axis from histological sections in the longitudinal-circumferential plane (Persson et al., 2010). The fiber dispersion data reported herein indicate that collagen fibers in the circumferential direction were more preferentially aligned as compared to collagen fibers in the longitudinal direction (κ₁ < κ₂). The higher degree of fiber dispersion in the longitudinal direction could potentially delay the recruitment of individual collagen fiber strands during loading, resulting in the longer and gradual toe region observed in this direction [Figure 6].

The TI_G phenomenological model employed in this study was developed specifically for arterial wall mechanics. This model was optimized based on the assumption that the two fiber families in arteries differ only in terms of their preferred orientation and no mechanical divergence was anticipated for these families. Consequently, this model has been shown to work quite well for arterial and venous tissues (Gasser et al., 2006; McGilvray et al., 2010). To address the controversy surrounding dura mater fiber orientation, the current study generalized this original model by assigning separate pairs of material parameters for the longitudinal (k₁, k₂) and circumferential (k₃, k₄) directions as well as prescribing distinct coefficients for the fiber orientation and degree of fiber dispersion (β and γ, κ₁ and κ₂) in these two directions. The results presented in this study demonstrated that this anisotropic model was able to delineate the divergent mechanical behavior of the two fiber families, and thus provided a continuum representation of the dura’s ultrastructural arrangement. Finally, in regards to the matrix ground substance, the ANISO_G model predicted higher values for C₁₀ and C₂₀ as compared to the TI_G model indicating a higher contribution of the matrix ground substance to the overall stiffness and nonlinear mechanical response of the dura mater when modeled as an anisotropic material.

Certain limitations in this study need to be addressed. The fitted parameters in this study were associated with a high degree of variance, which necessitated the use of a non-parametric statistical measure. Previous studies investigating the mechanical behavior of biological tissue via constitutive modeling have also reported a high degree of variance in their fitted parameters (Ayturk et al., 2012; Guerin and Elliott, 2007; Vande Geest et al., 2006). However, the ability of our fitted parameters to accurately predict the dura’s uniaxial behavior demonstrates the robust nature of the data and somewhat mitigates this limitation. Planar biaxial testing of biological soft tissues rests on the assumption of incompressibility. Further, biaxial testing cannot provide a complete three-dimensional mechanical description of the material tested since most continuum models do not explicitly include shear contributions (Holzapfel and Ogden, 2009). This limitation also applies to the continuum model employed in the current study. The biaxial protocol used in current study did not include a 3:1 (λ_l / λ_c : λ_c / λ_l) test, which might be needed to more comprehensively characterize the longitudinal stiffness of dural tissue within the upper extrema of the linear stress-strain region. However, it is unclear as to the magnitude and extent of longitudinal strains that the dura experiences during activities of daily living. In addition, the dynamic nature of spinal cord injuries necessitates comprehensive viscoelastic characterization of tissues in the spinal cord complex, which includes the dura mater. Temporally dependent behavior was not examined in the current study. Finally, the TI_G model has been mathematically proven to be a strictly convex function. However, the anisotropic version used in this study has not yet been proven to be strictly convex. The use of unconstrained optimization procedures for determination of material coefficients do not guarantee convexity, even with use of a strictly convex function (Holzapfel and Ogden, 2009). Thus, reasonable restrictions must be provided to the values of these material constants. Failure in providing these restrictions can lead to non-unique solutions (Fung, 1981). We emphasize that validation of the fitted parameters obtained from iterative optimization procedures should be performed by examining their predictive capability, as employed in this study.

To conclude, this study employed a biaxial testing protocol combined with a constitutive continuum model to elucidate the divergent mechanical response of the dura mater in the longitudinal and circumferential directions. Significantly higher stiffness was observed for the circumferential direction and a significantly higher degree of nonlinearity (longer toe region) was observed in the longitudinal direction.