Abstract
Oxidizing two native methionine residues predominantly populates the denatured state of monomeric λ repressor (MetO-λLS) under nondenaturing conditions. NMR was used to characterize the secondary structure and dynamics of MetO-λLS in standard phosphate buffer. 13Cα and 1Hα chemical shift indices reveal a region of significant helicity between residues 9 and 29. This helical content is further supported by the observation of medium-range amide NOEs. The remaining residues do not exhibit significant helicity as determined by NMR. We determined 15N relaxation parameters for 64 of 85 residues at 600 and 800 MHz. There are two distinct regions of reduced flexibility, residues 8–32 in the N-terminal third and residues 50–83 in the C-terminal third. The middle third, residues 33–50, has greater flexibility. We have analyzed the amplitude of the backbone motions in terms of the physical properties of the amino acids and conclude that conformational restriction of the backbone MetO-λLS is due to nascent helix formation in the region corresponding to native helix 1. The bulkiness of amino acid residues in the C-terminal third leads to the potential for hydrophobic interactions, which is suggested by chemical exchange detected by the difference in spectral density J(0) at the two static magnetic fields. The more flexible middle region is the result of a predominance of small side chains in this region.
Protein folding, while an essential process in biology, is not well-understood in detail. It is known, however, that the nature of the denatured state is a critical aspect in the mechanism of protein folding, because it affects the thermodynamics and kinetics of folding (1). Since most natural proteins are stable, to study the denatured state, it is necessary to find a way to populate it. The most relevant denatured state model would be one that exists under physiological conditions that favor the native state because this denatured state is the starting point for folding.
To understand the forces that drive the folding of monomeric λ repressor, we developed a model of the denatured state under nondenaturing conditions by oxidizing its two methionines. We call our model MetO-λLS1 (2). The circular dichroism spectrum of the predominantly unfolded MetO-λLS indicates that it possesses significant helicity under native-like conditions, but circular dichroism provides information about only the average secondary structure of all residues. To determine whether specific regions of the molecule are more likely to be helical than others, it is necessary to use a technique that provides residue-specific information, such as NMR.
NMR relaxation experiments can quantify the flexibility of a protein on a residue-by-residue basis. 15N backbone dynamics have been used to study the denatured states of staphylococcal nuclease (3), the SH3 domain of drk (4), the D2 domain of annexin I (5), apomyoglobin (6), fibronectin type III (7), reduced hen lysozyme (8), and protein G (9). The dynamics of the most highly denatured of these proteins, protein G and the fibronectin type III domain, are relatively uniform over the entire molecule, indicating a high degree of flexibility. The proteins studied under more native-like conditions, staphylococcal nuclease, apomyoglobin, and the D2 domain of annexin I, exhibit more variability in the relaxation parameters and have regions of reduced flexibility. The interpretation of these results is varied. One group correlates the reduced flexibility with secondary structure (5), while another hypothesizes that rigidity is due to hydrophobic interactions (10). A third group combines these ideas by hypothesizing that secondary structure formation is the result of hydrophobic interactions (11). In summary, there is not yet a good molecular explanation for regions of reduced flexibility in denatured proteins.
In this study, we used NMR to characterize the structural and dynamic properties of the MetO-λLS form of monomeric λ repressor under nondenaturing conditions. We first assigned the backbone resonances and then used these data, in combination with other NMR experiments, to assess the structural properties and backbone dynamics of this denatured state model.
EXPERIMENTAL PROCEDURES
Overexpression and Protein Purification
The variant of monomeric λ repressor used in this study, λLS, consists of residues 1–85 with the following substitutions: G46A, G48A, I54K, I56K, and S77A. λLS was overexpressed in BL21(DE3) cells (Stratagene) from the gene under the T7 promoter in the pET9a vector from Novagen. For 15N-labeled protein, the bacteria were grown in M9 minimal medium (6 g/L Na2HPO4, 3 g/L KH2PO4, 0.5 g/L NaCl, 1 mM MgSO4, 0.1 mM CaCl2, and 2 g/L glucose) supplemented with 1 g/L 15NH4Cl either with or without 1% 15N BioExpress from Cambridge Isotope Labs. For 15N- and 13C-labeled protein, the bacteria were grown in M9 minimal medium (6 g/L Na2HPO4, 3 g/L KH2PO4, 0.5 g/L NaCl, 1 mM MgSO4, and 0.1 mM CaCl2) supplemented with 1 g/L 15NH4-Cl and 2 g/L [13C]glucose from Cambridge Isotope Labs. Expression was induced at an OD of 0.4–0.6 by addition of IPTG to a concentration of 0.4 mM. The cells were incubated at 37 °C for a further 3–4 h before being harvested by centrifugation and resuspended in lysis buffer [50 mM Tris-HCl and 10 mM EDTA (pH 8.0)].
λ1–85 variants were purified by a modified version of an earlier protocol (12). Cell lysates were generated in a French pressure cell at 12 000 lb/in.2 The lysates were run through a DEAE Sephacel column (Amersham Biosciences) to remove cell debris and other proteins. The flow-through was collected and applied directly to an Affigel Blue (Bio-Rad) column that was run in phosphate buffer at pH 7. The protein was eluted from the column in 300 mM KCl. The eluted fraction was dialyzed against degassed distilled H2O overnight and then lyophilized. (Degassed water was used to minimize methionine oxidation during purification.) The lyophilized protein was redissolved in deionized H2O and further purified by size-exclusion chromatography on a Sephadex G-50 column (Amersham Biosciences). The final purity of each protein was checked by reverse-phase HPLC and electrospray mass spectrometry. For each protein, the MS-determined mass was within 1 amu of the expected mass, further confirming the proper amino acid substitutions. Both HPLC and mass spectrometry indicated no significant oxidation of the methionine residues. All protein concentrations were determined using the method of Edelhoch (13).
Protein Oxidation
Methionine oxidation was carried out as follows. Lyophilized protein was hydrated in deionized water to a concentration of 1 mg/mL. To the protein solution were added ~20 µL of 0.1 M perchloric acid per milliliter to bring the pH below 3 and 30% hydrogen peroxide to a final concentration of 0.05%. This solution was incubated on the bench for 45 min before a spin column was used for buffer exchange into the sample buffer [20 mM phosphate and 100 mM NaCl (pH 6)]. Oxidation of methionine to sulfoxide was checked by reverse-phase HPLC and electrospray mass spectrometry.
NMR Spectroscopy
All three-dimensional NMR spectra were recorded at 25 °C on a Varian Unity 800 spectrometer with a triple-resonance z-shielded gradient cryoprobe on samples at concentrations of 0.2–0.4 mM in 20 mM sodium phosphate buffer (pH 6). Two-dimensional gradient-enhanced sensitivity-enhanced 1H–15N HSQC experiments (14) were conducted with a spectral width in the 1H dimension of 7000 Hz and 1024 complex points and a spectral width in the 15N dimension of 1500 Hz and 128 complex points. Denatured state resonance assignments were made by using a suite of triple-resonance experiments, including HNCO (15), (HCA)CO(CA)NH (16), HNCACB (17), and HN(CO)-CACB (18). In all of the three-dimensional NMR spectra of the native state, the spectral width in the 1H dimension was 8000 Hz with 1024 complex points. The spectral width in the 15N dimension was 1500 Hz with 34 or 37 complex points. The spectral width in the 13C dimension was 3000 Hz with 40 complex points for the HNCO experiments. The spectral width was 10 000 Hz with 70 complex points for the HNCACB and HN(CO)CACB experiments. All NMR spectra were processed using NMRPipe (19). Three-dimensional spectra were analyzed using NMRView (20) or CARA (21) (CARA can be downloaded free from www.nmr.ch).
NOESY-HSQC
NOESY spectroscopy of MetO-λLS was performed using a 200 ms mixing time. This mixing time is long compared to the times used for native proteins. The danger in using long mixing times in native proteins is that there may be signals from spin diffusion rather than real NOEs. Spin diffusion is not a large problem in denatured proteins, which allows for the use of longer mixing times to obtain more intense NOEs (22).
Relaxation Measurements
All NMR spin relaxation measurements were performed on a single sample at a protein concentration of 0.2 mM in 20 mM sodium phosphate buffer at pH 6.0 with 10% 2H2O. The data were obtained using proton-detected, sensitivity- and gradient-enhanced inversion-recovery and CPMG pulse sequences for R1 and R2, respectively (23), on Varian INOVA 600 MHz and Varian INOVA 800 MHz instruments at the Duke University NMR Center. Spectra at 600 MHz were collected as 1024 × 64 complex points with 32 transients and spectral widths of 8000 and 1350 Hz in the 1H and 15N dimensions, respectively. Spectra at 800 MHz were collected as 1024 × 64 complex points with 32 transients and spectral widths of 10 000 and 1800 Hz in the 1H and 15N dimensions, respectively. The longitudinal relaxation rates, R1, were determined using inversion–recovery delays of 10, 40, 80, 100, 150, 230, 430, 630, and 840 ms at 600 and 800 MHz. The transverse relaxation rates, R2, were determined with CPMG delays of 10, 30, 50, 70, 90, 110, 150, and 170 ms at 600 MHz and 10, 30, 50, 70, 90, 110, 130, and 150 ms at 800 MHz. {1H}−15N heteronuclear NOEs were determined using spectra collected with a 3 s saturation period and a 2 s recycle delay or no saturation and a 5 s recycle delay at 600 and 800 MHz. Spectra were processed using NMRPipe; peak intensities were determined using Sparky (T. D. Goddard and D. G. Kneller, SPARKY 3, University of California, San Francisco), and relaxation rates were determined by a fitting to a two-parameter single-exponential decay equation. Errors in relaxation parameters are from the fits by Sparky.
Reduced Spectral Density Function Mapping
The measured relaxation parameters are related to the spectral density function of the amide bond vector by the following equations (24):
| (1) |
| (2) |
| (3) |
where d = (µ0hγHγN)/(8π2rNH3), , ωH and ωN are the Larmor frequencies of the 1H and 15N nuclei, respectively, µ0 is the permeability of free space, γH and γN are the gyromagnetic ratios of 1H and 15N, respectively, h is Planck’s constant, Δσ is the chemical shift tensor, and rNH is the length of the amide bond vector. The values used for Δσ and rNH are −170 ppm and 1.02 Å, respectively.
The relaxation parameters were analyzed using reduced spectral density function mapping to determine spectral density values at three frequencies (25). Assuming that J(ω) is effectively constant when ω ≈ ωH on the basis of Method 1 of Farrow et al. (25), eqs 1–3 are modified so that J(ωH), J(ωH – ωN), and J(ωH + ωN) are replaced by J(0.87ωH) and rewritten as follows:
| (4) |
| (5) |
| (6) |
These equations relate the observed relaxation parameters to the spectral density function at three frequencies based on the following equations:
| (7) |
| (8) |
| (9) |
where R1 = 1/T1 and R2 = 1/T2.
The value of J(0.87ωH) was calculated using eq 7 and the values of NOE and T1. Values of J(ωN) and J(0) were calculated using eqs 8 and 9, repectively.
Lipari—Szabo Model-Free Analysis
The original model-free formalism from Lipari and Szabo (26, 27) was used to determine τe and S2 using the relxn2.2 program (28) written by A. Lee according to the following equation:
| (10) |
where 1/τ = 1/τm + 1/τe, τm is the global correlation time, and τe is a fast internal motion time. The values used for Δσ and rNH are −170 ppm and 1.02 Å, respectively.
Physical and Chemical Parameters of Primary Structure
The per-residue AABUF and bulkiness using the values of Rose et al. (29) and Zimmerman et al. (30) were calculated utilizing the Expasy website, with a seven-residue moving-average window.
RESULTS
Backbone Assignments
Standard multidimensional NMR experiments were used to assign the backbone atoms of MetO-λLS under native conditions. These experiments included HNCO, HNCACB, and HN(CO)CACB. The experiments detecting 13Cα and 13Cβ were used to make some sequential assignments. Unfortunately, the chemical shift degeneracy of the Cα and Cβ nuclei and the repeats in the sequence make it difficult to distinguish between residues of the same type. To overcome this problem, we exploited the chemical shift dispersion in the 13CO atom by using the (HCA)CO(CA)NH experiment (16). In combination with the HNCO experiment, this pulse sequence allows sequential assignments to be made through the 13CO atoms. We obtained sequential assignments for 73 of 83 non-proline residues in MetO-λLS. The assigned 1H–15N HSQC spectrum of MetO-λLS is shown in Figure 1. The chemical shifts for the backbone nuclei in MetO-λLS are listed in the Supporting Information.
Figure 1.
1H–15N HSQC spectrum (800 MHz) of MetO-λLS in 20 mM phosphate buffer at pH 6 and 25 °C.
Deviation from Random Coil Chemical Shifts
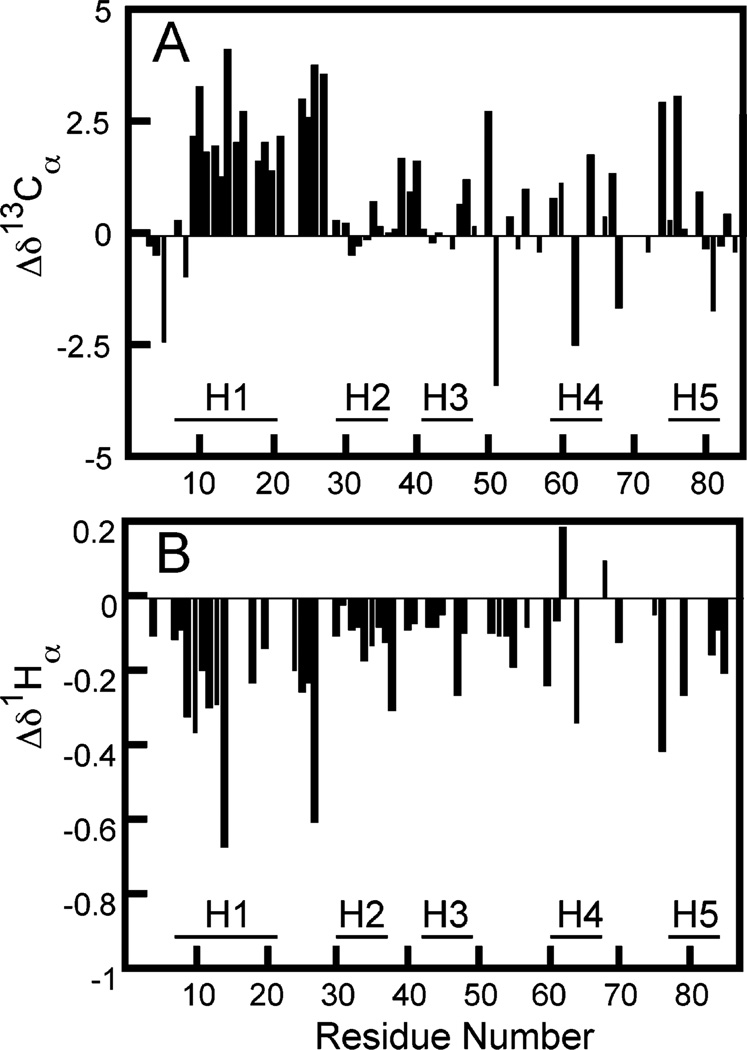
Chemical shift indices provide an indication of nascent helicity in the denatured state. There are four nuclei that can be used for chemical shift deviation calculations: 13Cα, 13Cβ, 13CO, and 1Hα (31). A systematic study of the correlation between chemical shift index and secondary structure shows that the best statistical correlation is provided by the random coil values of Schwarzinger et al. (32). Shown in Figure 2 are the chemical shift index values versus residue number for 13Cα and 1Hα atoms in MetO-λLS determined using sequence-corrected random coil values from Schwarzinger et al. (33).
Figure 2.
Difference between chemical shifts for (A) 13Cα and (B) 1Hα in MetO-λLS and sequence-corrected random coil chemical shifts from Schwarzinger et al. (33). The bars indicate the position of helices in the native state.
Short-Range and Medium-Range Amide NOEs from NOE-SY-HSQC
In general, there are fewer NOEs detected in denatured proteins than in native globular proteins. Forty-four assignable short-range and medium-range amide NOEs are detected in MetO-λLS using a three-dimensional NOESY-HSQC experiment. None of these NOEs are from amide 1H resonances more than five residues apart. A summary of the medium-range NOEs is shown in Table 1, and the short-range NOEs are shown in Figure 3.
Table 1.
Medium-Range HN–HN NOEs from Three-Dimensional NOESY-HSQC Spectra
| atom 1 | atom 2 | range | atom 1 | atom 2 | range |
|---|---|---|---|---|---|
| Gln 11 | Thr 8 | 3 | Val 73 | Ile 68 | 5 |
| Lys 26 | Tyr 22 | 4 | Ile 68 | Ser 72 | 4 |
| Leu 31 | Asn 27 | 4 | Ile 80 | Ala 77 | 3 |
| Phe 51 | Val 47 | 4 | Ile 84 | Ile 80 | 4 |
| Lys 67 | Leu 64 | 3 |
Figure 3.
Short-range HN–HN and HN–Hα NOEs in MetO-λLS observed in a NOESY-HSQ spectrum obtained with a mixing time of 200 ms.
Typically, two kinds of short-range NOEs identify secondary structure in denatured proteins. The dNN(i, i + 1) NOEs are more prevalent in helical conformations. The dNα(i, i + 1) NOEs are more prevalent in extended conformations (34). The slightly longer-range dNN(i, i + 2) NOEs are commonly found in α- and 310-helices (34). Although the total number of NOEs is small for MetO-λLS, there are several indicative of helical structure in the region corresponding to helix 1 in the native state. There are many dNN(i, i + 1) and dNN(i, i + 2) NOEs in the region between residues 8 and 33. A few medium-range NOEs are clustered in regions corresponding to helices 1, 4, and 5 in the native state. However, only the region corresponding to helix 1 exhibits a consistent stretch of short-range NOEs.
15N Relaxation
The 15N relaxation parameters, R1, R2, and heteronuclear NOE ({1H}−15N NOE), were quantified for 64 of 85 residues in MetO-λLS at static magnetic fields of 600 and 800 MHz. The other residues either are prolines, are unassigned, or have intensities too low to obtain reasonable fits. These relaxation data are shown in Figure 4. A table of these values is provided in the Supporting Information.
Figure 4.
Relaxation parameters from 600 (●) and 800 MHz (○) vs residue number for MetO-λLS in 20 mM phosphate buffer at pH 6 and 25 °C: (A) 15N longitudinal relaxation rate, R1, (B) 15N transverse relaxation rate, R2, and (C) heteronuclear NOEs with a proton saturation period of 3 s.
R1 is relatively uniform across the sequence of the protein, except for small decreases at the N- and C-termini. There is more variation of R2 over the sequence. The R2 is small, around 3–4 s−1 at 600 MHz, at the termini and between residues 32 and 48. Above average values are observed between residues 8–32 and 50–82. Most of the {1H}−15N NOE values are less than 0.5, which is typical of denatured proteins. The pattern of the {1H}−15N NOEs follows that of R2, with the lowest values at the termini, a low region in the middle, and two regions of above average values. Although R1 and heteronuclear NOEs are both sensitive to high-frequency motions, it appears that R1 is less sensitive because the R1 values are not low in the middle of the molecule where the heteronuclear NOEs are low.
The values of R2 can be increased by conformational exchange due to self-association (35). The R2 value at 600 MHz was estimated for five protein concentrations ranging from 0.05 to 0.4 mM in determining the contribution to R2 from self-association. For most residues, the contribution to R2 from Rex is less than 1 s−1 at a protein concentration of 0.2 mM, which is within error. For the residues whose R2 values are most sensitive to self-association, the maximum amount of Rex from this source is 2.7 s−1 at a protein concentration of 0.2 mM.
Spectral Density Mapping
Spectral density mapping, developed by several groups, allows a description of the spectral density function to be generated using 15N relaxation data (36–38). The reduced spectral density mapping method formulated by Farrow et al. uses R1, R2, and NOE values to calculate values of the spectral density at three frequencies: J(0), J(ωN), and J(0.87ωH) for each static magnetic field (see Experimental Procedures) (25). Using this approach and data collected at two static magnetic fields, we calculated values of the spectral density for 64 residues at five frequencies: 0, 60, 80, 522, and 696 MHz. Histograms of the spectral densities at J(0), J(ωN), and J(ω0.87H) are shown in Figure 5.
Figure 5.
Calculated values of the spectral density function at J(ω0.87H), J(ωN), and J(0) for MetO-λLS from relaxation data at 600 (●) and 800 MHz (○) corresponding to J(696), J(522), J(80), J(60), and J(0).
There is little variation in J(ωN), except at the termini where the values are diminished, which is shown in Figure 5B. J(0.87ωH) exhibits more variation with larger values at the termini and in the middle of the molecule, which is shown in Figure 5A. The relative increase in fast motions (~200 ps) indicated by larger values of J(0.87ωH) at the termini is typical of native and denatured proteins. In the middle of the protein, there is an increase in the contribution of fast motions to the spectral density function (panel A) without a concomitant decrease in the contribution of intermediate timescale motions (panel B).
The spectral density at zero frequency, J(0), applies to motions equal to and slower than the global correlation time, τc. The value of J(0) is the only spectral density for which there is a contribution from R2. Motions slower than the correlation time increase the value of R2 by contributing to chemical exchange (Rex). This elevation in R2 will lead to an artifactual increase in J(0). The values of J(0) calculated from relaxation data at 600 and 800 MHz are shown in Figure 5C. J(0) is smaller at the termini and in the middle of the protein due to the increase in the magnitude of faster motions in these regions indicated by the increases in J(0.87ωH). The higher values of J(0) indicate the regions where there is reduced flexibility in MetO-λLS. For some residues, the value of J(0) is larger at 800 MHz than at 600 MHz. This increase is probably due to contributions from chemical exchange. The contribution to relaxation (Rex) is discussed further in the next section.
Model-Free Analysis
While reduced spectral density mapping allows probabilities of motions at particular time scales to be determined, it does not provide a molecular interpretation of those motions. The original model-free formalism developed by Lipari and Szabo assumes that the molecule undergoes slow isotropic tumbling at the global correlation time with faster, spatially restricted internal motions at a time τe (26, 27). The order parameter, S2, describes the fraction of motion that can be attributed to isotropic tumbling and ranges between 0 and 1, where 1 represents a totally rigid N–H bond.
A global correlation time is required to apply the standard model-free analysis to relaxation data. However, the tumbling of a partially folded or unfolded molecule may not be described well by a single correlation time (3). One solution that we applied to this problem is to treat each residue as a separate dynamic segment and to fit a separate correlation time to each residue (3). The parameters determined using the model-free equations to fit for S2, τe, and a τm for each residue are shown in Figure 6. The average τm determined by this method is 6.7 ns with a standard deviation of 2.7 ns. This model has an average χ2 normalized for the number of parameters that is lower than those of other models discussed below and therefore seems to be the best model describing the relaxation of most residues in MetO-λLS. However, six residues (47, 51, 59, 72, 74, and 81) have anomalously high τm values which are better fit to a model that includes Rex as a fitting parameter.
Figure 6.
Model-free parameters for MetO-λLS derived from 15N relaxation measurements at 600 and 800 MHz using the model fitting S2, τe, and τm.
The model in which S2, τe, and a τm were fitted did not provide information about the contribution to relaxation from chemical exchange. To apply the standard model-free analysis to relaxation data for MetO-λLS, and obtain values for Rex, an estimate for the global correlation time was required. A τm can be fit using a global model-free fit to all the relaxation data, which accounts for the effect of fast internal motions (39). This method yielded a τm value of 6.9 ns. Anisotropic motion could distort the value of τm determined by this method (28); however, it is likely that conformational averaging in MetO-λLS leads to isotropic tumbling (3). In a similar approach, Tjandra and Bax removed residues with internal motions that led to low NOEs (40). A NOE cutoff of 0.6, which includes only residues 9, 11–21, and 84, also gave a τm value of 6.9 ns. This value is well within experimental error of the average obtained from the individual τm values obtained from the fit described above.
The correlation time of a native globular protein is often determined by using the ratio of T1 to T2 values (41). Using this procedure, the τm is 5.3 ns from the 800 MHz data and 5.0 ns from the 600 MHz data. This method does not account for internal motions that affect the values of T1 and T2 (28). The τm value from the T1/T2 ratio is probably an underestimate because it ignores fast internal motions in the protein and the most reasonable correlation time is the one from global fitting of the relaxation parameters to the model-free equations.
In summary, we used a global correlation time, τm, of 6.9 ns to fit the relaxation data from both static magnetic fields to two additional models that include Rex: (1) S2 and Rex and (2) S2, τe, and Rex. Of the two models, the χ2 for the model fitting three parameters, S2, τe, and Rex, was the lowest. These model-free parameters versus residue number are shown in Figure 7. The majority of the order parameters are below 0.8, which is consistent with a denatured protein. The pattern of order parameters is the same for both the model that fits a τm for each residue and the model that uses a global correlation time. The pattern supports the conclusions from reduced spectral density mapping. Both types of analyses show two regions of reduced flexibility, between residues 8 and 31 and between residues 50 and 82, with increased flexibility at the termini, and between residues 32 and 49.
Figure 7.
Model-free parameters for MetO-λLS derived from 15N relaxation measurements at 600 and 800 MHz using the model fitting S2, τe, and Rex.
Lipari—Szabo Mapping
Analysis of spectral density functions without the need to fit model-free parameters is accomplished using the graphical Lipari–Szabo mapping developed by Andrec et al. (42). In this analysis, J(ω0.87H) versus J(ωN) is plotted for each residue. A theoretical curve for rigid tumbling is shown as a line with correlation times indicated. The relative distance between a residue and the point for rigid tumbling is indicative of the order parameter, S2. This analysis, shown in Figure 8, supports the finding that the middle of the molecule is much more flexible than the regions between residues 8–32 and 50–82 because residues 33–49, which are colored green, are farther from the rigid tumbling line at 6.9 ns. The three types of analysis used for the relaxation data, reduced spectral density mapping, model-free analysis, and Lipari–Szabo mapping, all indicate that the residues in the middle third of MetO-λLS are the most flexible with reduced flexibility in the N-terminal and C-terminal thirds.
Figure 8.
Lipari-Szabo maps for the analysis of MetO-λLS backbone dynamics using the method described by Andrec et al. (42) at (A) 600 and (B) 800 MHz. The points on the maps correspond to residues in the protein and have been colored according to their position in the primary structure, shown in the legend.
DISCUSSION
Backbone Flexibility Correlates with Amino Acid Composition
The amplitudes of the order parameters from Lipari–Szabo model-free analysis correlate surprisingly well with the size of the amino acids in MetO-λLS. Side chain bulkiness, defined by Zimmerman et al. as the ratio of the side chain volume to length, is plotted versus residue number in Figure 9A (30). The order parameter correlates with this property with a correlation coefficient of 0.52 and a p value of 1.9 × 10−5, shown in Figure 9B. There is a precedent for correlation of motional parameters in denatured proteins with physical properties of amino acids. A parameter called “average area buried upon folding” (AABUF) developed by Rose et al. (29) correlates well with dynamic properties in the denatured state of apomyoglobin at pH 2.3 (10). This correlation persists even when apomyoglobin is denatured in 8 M urea at pH 2.3 (43). The authors concluded that local hydrophobic interactions persist even in 8 M urea because the regions of rigidity correspond to regions where AABUF is high. The amplitudes of the order parameters in MetO- λLS also correlate well with AABUF (shown in Figure 9C), with a correlation coefficient of 0.56 and a p value of 3 × 10−6 (shown in Figure 9D).
Figure 9.
Physicochemical characteristics of the amino acid sequence of λLS calculated over a seven-residue moving average window: (A) bulkiness of the side chain (30) and (B) average area buried upon folding (29). Linear correlations between physicochemical characteristics of the amino acid sequence of λLS, (C) bulkiness (30) and (D) average area buried upon folding (29), and the order parameters of MetO-λLS from the model fitting S2, τe, and Rex.
Three Regions with Distinct Structural and Dynamic Properties
The source of the correlation between dynamic properties and the size of the side chain is different for three different regions in MetO-λLS. Chemical shift and NOE data indicate that the N-terminal region between residues 8 and 32 has significant nascent helicity and therefore has less backbone flexibility. The region in the middle of the protein between residues 33 and 50 is more flexible due to a predominance of small side chains leading to lower excluded volume restrictions on backbone motion. The C-terminal region between residues 50 and 83 is less flexible but does not seem to have significant secondary structure.
The chemical shifts and NOEs provide a consistent picture of regions of high helicity in this denatured ensemble. The chemical shift indices for 13Cα and 1Hα lead us to conclude that residues in the helix 1 region of the native state have a distribution of ϕ and ψ values biased toward α-helical secondary structure in MetO-λLS. This conclusion is also consistent with the NOE data because the majority of the assigned NOEs are also observed in the same region. Additional evidence of nascent helical structure in helix 1 comes from previous studies of a peptide model of helix 1 of λ repressor, which exhibited 40% helicity by CD and demonstrated many dNN(i, i + 1) and dNα(i, i + 3) NOEs that are indicative of helix formation (44). For the rest of the molecule, the lack of consistent stretches of helical chemical shifts and NOEs suggest that the backbone conformation is not strongly biased to the helical region of ϕ–ψ space.
The middle region of MetO-λLS, consisting of residues 33–50, exhibits a greater than average flexibility and consists of smaller amino acids. Regions with bulkier side chains are expected to have more steric hindrance, thereby limiting side chain flexibility more than smaller side chains. Regions of apomyoglobin at pH 2.3 with higher flexibility contain a number of Gly and Ala residues (43). The authors hypothesized that regions of polypeptides with small amino acids might act as “molecular hinges” that allow regions of nascent secondary structure to more easily come together (43).
The hinge in unfolded λ repressor near helix 3 may be an indirect consequence of the sequence requirements of protein function. Full-length bacteriophage λ repressor protein binds to DNA as a dimer and represses transcription. The helix–turn-helix motif that binds to DNA consists of helices 2 and 3. The residues that make the closest contact with the DNA are residues 45–50. In the wild-type sequence, this stretch of residues consists of one Ser, one Val, two Gly’s, one Ala, and one Leu. Since the N-terminal part of helix 3 fits furthest into the major groove of B-form operator DNA, small residues are required to make a good contact with the DNA (45). The presence of these small side chains leads to backbone flexibility in this region. Despite the fact that the variant used in the backbone dynamic studies of the denatured state has two Gly residues substituted with Ala in helix 3, it is still the region with the most flexibility.
Previous protein folding calculations using the diffusion-collision model have suggested that helices 1 and 4 form early in the folding pathway (46). The sequence of helix 4 is predicted by AGADIR (47) to have a high intrinsic helicity (in the absence of tertiary interactions) of 49%. However, there seems to be little nascent helicity in this region of MetO-λLS based on chemical shift indices and amide NOEs. The substitutions made in this variant are outside of this region so would not perturb the intrinsic helicity.
There are three types of evidence of conformational exchange in the C-terminal region of MetO-λLS. The difference between the J(0) spectral density function calculated at the two static magnetic fields for many residues in this region (bottom panel of Figure 5), higher-than-average order parameters, and according to one of the fitting models significant Rex values (top panel of Figure 7) indicate conformational exchange. To contribute to Rex, this conformational exchange must be relatively slow (micro- to milliseconds), suggesting that there is a barrier between two significantly populated (>5%) subensembles whose C-terminal conformations differ. This raises the question of the nature of the conformational exchange between these two subensembles. One possibility is a non-native hydrophobic collapse in this region, which has a number of hydrophobic residues. This might explain the lack of significant helical structure, despite the predicted high helical propensity of the sequence. Such a hydrophobic collapse might disfavor helix formation and is expected to be even greater in the wild-type protein, which has more hydrophobic resides (Ile and Ala) at positions 54 and 56 and unoxidized methionines (48).
Conformational Restriction Favors Protein Folding
The dynamics of proteins that are highly denatured, such as protein G in 7.4 M urea and the SH3 domain of drk in 2 M GdnCl, are relatively uniform over the entire molecule and indicate a high degree of flexibility. On the other hand, studies of proteins under more physiological conditions have shown that these polypeptides often contain regions of the molecule that are more rigid than others. These studies have interpreted the restricted flexibility as resulting from nascent helicity (5), hydrophobic interactions (10), or secondary structure formation due to hydrophobic interactions (11). Our results suggest that the sources of regions of conformational restriction in the denatured state of monomeric λ repressor populated under nondenaturing conditions are nascent helicity and a possible non-native hydrophobic interaction.
The size of conformational space for a denatured protein is critical to the our understanding of protein folding (49). The reduction of conformational space in unfolded proteins by restrictions imposed solely from steric hindrance and hydrogen bond satisfaction was found by Fitzkee and Rose to be 9 orders of magnitude (50). The addition of side chains would further restrict conformational space (51). Hence, conformational restriction seen in the backbone dynamics of unfolded proteins presumably comes from three sources: backbone sterics, solvation, and side chain sterics.
Protein folding is the result of a combination of opposing forces. Favorable forces include hydrogen bonding, electrostatics and van der Waals contacts in the protein, and the gain of entropy of the solvent. The main unfavorable force opposing folding is the loss of conformational entropy of the protein (52). In the native state, amino acid side chains are relatively restricted compared to the denatured state. The steric hindrance of bulky side chains leads to reduced flexibility and reduced backbone entropy. Even a small bias toward local structure, reflected in reduced backbone entropy, significantly reduces the conformational entropy of the denatured state. Therefore, the net loss of total entropy upon folding would decrease, making protein folding more favorable (53).
The evidence presented here suggests that, in the denatured state under native conditions, there is conformational restriction in the N- and C-terminal thirds of the monomeric λ repressor. In the N-terminal third, this restrictions lead to nativelike helix formation, which favors folding. In the C-terminal third, the NMR data suggest the absence of helicity despite an intrinsically helical sequence. This observation suggests that the conformational restriction in the region is due to non-native interactions. Whatever the source of conformational restriction, this too is expected to favor the native state by reducing the conformational entropy of the denatured state ensemble.
Supplementary Material
ACKNOWLEDGMENT
We are grateful to Drew Lee and Art Palmer for helpful discussions about model-free analysis. We acknowledge Gary Pielak and Matthias Buck for comments on the manuscript. We thank Ron Venters for invaluable help with all NMR experiments. We also thank members of the Oas lab. We thank an anonymous reviewer for insightful comments that greatly improved the manuscript.
Footnotes
This work was supported by a grant from the National Institutes of Health (GM45322 to T.G.O.).
Abbreviations: AABUF, average area buried upon folding; CD, circular dichroism; {1H}−15N NOE, heteronuclear NOE; HSQC, heteronuclear single-quantum coherence; λLS, residues 1–85 of repressor λ with G46A, G48A, I54K, A56K, and S77A substitutions; MetO-λLS, λLS with oxidation of Met 40 and Met 42; NOE, nuclear Overhauser effect; NOESY, nuclear Overhauser effect spectroscopy; R1, longitudinal relaxation rate; R2, transverse relaxation rate; Rex, relaxation from chemical exchange.
SUPPORTING INFORMATION AVAILABLE
A table of chemical shifts of the backbone atoms of MetO-λLS and a table of relaxation data (R1, R2, and {1H}−15N NOE) for the 15N atoms at 800 and 600 MHz. This material is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Shortle D. The denatured state (the other half of the folding equation) and its role in protein stability. FASEB J. 1996;10:27–34. doi: 10.1096/fasebj.10.1.8566543. [DOI] [PubMed] [Google Scholar]
- 2.Chugha P, Sage HJ, Oas TG. Methionine oxidation of monomeric λ repressor: The denatured state ensemble under nondenaturing conditions. Protein Sci. 2006;15:533–542. doi: 10.1110/ps.051856406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alexandrescu AT, Shortle D. Backbone dynamics of a highly disordered 131 residue fragment of staphylococcal nuclease. J. Mol. Biol. 1994;242:527–546. doi: 10.1006/jmbi.1994.1598. [DOI] [PubMed] [Google Scholar]
- 4.Farrow NA, Zhang O, Forman-Kay JD, Kay LE. Comparison of the backbone dynamics of a folded and an unfolded SH3 domain existing in equilibrium in aqueous buffer. Biochemistry. 1995;34:868–878. doi: 10.1021/bi00003a021. [DOI] [PubMed] [Google Scholar]
- 5.Ochsenbein F, Guerois R, Neumann JM, Sanson A, Guittet E, van Heijenoort C. 15N NMR relaxation as a probe for helical intrinsic propensity: The case of the unfolded D2 domain of annexin I. J. Biomol. NMR. 2001;19:3–18. doi: 10.1023/a:1008390606077. [DOI] [PubMed] [Google Scholar]
- 6.Eliezer D, Chung J, Dyson HJ, Wright PE. Native and non-native secondary structure and dynamics in the pH 4 intermediate of apomyoglobin. Biochemistry. 2000;39:2894–2901. doi: 10.1021/bi992545f. [DOI] [PubMed] [Google Scholar]
- 7.Meekhof AE, Freund SM. Probing residual structure and backbone dynamics on the milli- to picosecond timescale in a urea-denatured fibronectin type III domain. J. Mol. Biol. 1999;286:579–592. doi: 10.1006/jmbi.1998.2479. [DOI] [PubMed] [Google Scholar]
- 8.Klein-Seetharaman J, Oikawa M, Grimshaw SB, Wirmer J, Duchardt E, Ueda T, Imoto T, Smith LJ, Dobson CM, Schwalbe H. Long-range interactions within a nonnative protein. Science. 2002;295:1719–1722. doi: 10.1126/science.1067680. [DOI] [PubMed] [Google Scholar]
- 9.Sari N, Alexander P, Bryan PN, Orban J. Structure and dynamics of an acid-denatured protein G mutant. Biochemistry. 2000;39:965–977. doi: 10.1021/bi9920230. [DOI] [PubMed] [Google Scholar]
- 10.Yao J, Chung J, Eliezer D, Wright PE, Dyson HJ. NMR structural and dynamic characterization of the acid-unfolded state of apomyoglobin provides insights into the early events in protein folding. Biochemistry. 2001;40:3561–3571. doi: 10.1021/bi002776i. [DOI] [PubMed] [Google Scholar]
- 11.Alexandrescu AT, Abeygunawardana C, Shortle D. Structure and dynamics of a denatured 131-residue fragment of staphylococcal nuclease: A heteronuclear NMR study. Biochemistry. 1994;33:1063–1072. doi: 10.1021/bi00171a004. [DOI] [PubMed] [Google Scholar]
- 12.Burton RE, Huang GS, Daugherty MA, Fullbright PW, Oas TG. Microsecond protein folding through a compact transition state. J. Mol. Biol. 1996;263:311–322. doi: 10.1006/jmbi.1996.0577. [DOI] [PubMed] [Google Scholar]
- 13.Edelhoch H. Spectroscopic determination of tryptophan and tyrosine in proteins. Biochemistry. 1967;6:1948–1954. doi: 10.1021/bi00859a010. [DOI] [PubMed] [Google Scholar]
- 14.Kay LE, Keifer P, Saarinen T. Pure absorption gradient enhanced heteronuclear single quantum correlation spectroscopy with improved sensitivity. J. Am. Chem. Soc. 1992;114:10663–10665. [Google Scholar]
- 15.Grzesiek S, Bax A. Improved 3D triple-resonance NMR techniques applied to a 31-kDa protein. J. Magn. Reson. 1992;96:432–440. [Google Scholar]
- 16.Lohr F, Ruterjans H. A new triple-resonance experiment for the sequential assignment of backbone resonances in proteins. J. Biomol. NMR. 1995;6:189–197. doi: 10.1007/BF00211783. [DOI] [PubMed] [Google Scholar]
- 17.Wittekind M, Mueller L. HNCACB, a high-sensitivity 3D NMR experiment to correlate amide-proton and nitrogen resonances with the α-carbon and β-carbon resonances in proteins. J. Magn. ResonSer. B. 1993;101:201–205. [Google Scholar]
- 18.Yamazaki T, Lee W, Arrowsmith CH, Muhandiram DR, Kay LE. A suite of triple-resonance NMR experiments for the backbone assignment of N-15, C-13, H-2 labeled proteins with high-sensitivity. J. Am. Chem. Soc. 1994;116:11655–11666. [Google Scholar]
- 19.Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. NMRPipe: A multidimensional spectral processing system based on unix pipes. J. Biomol. NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 20.Johnson BA, Blevins RA. NMRView: A computer-program for the visualization and analysis of NMR data. J. Biomol. NMR. 1994;4:603–614. doi: 10.1007/BF00404272. [DOI] [PubMed] [Google Scholar]
- 21.Keller R. CARA. Zurich: Swiss Federal Institute of Technology; 2004. [Google Scholar]
- 22.Zhang O, Forman-Kay JD. NMR studies of unfolded states of an SH3 domain in aqueous solution and denaturing conditions. Biochemistry. 1997;36:3959–3970. doi: 10.1021/bi9627626. [DOI] [PubMed] [Google Scholar]
- 23.Farrow NA, Muhandiram R, Singer AU, Pascal SM, Kay CM, Gish G, Shoelson SE, Pawson T, Forman-Kay JD, Kay LE. Backbone dynamics of a free and phosphopeptide-complexed src homology 2 domain studied by 15N NMR relaxation. Biochemistry. 1994;33:5984–6003. doi: 10.1021/bi00185a040. [DOI] [PubMed] [Google Scholar]
- 24.Abragam A. Principles of nuclear magnetism. Oxford, U.K: Clarendon Press; 1961. [Google Scholar]
- 25.Farrow NA, Zhang O, Szabo A, Torchia DA, Kay LE. Spectral density function mapping using 15N relaxation data exclusively. J. Biomol. NMR. 1995;6:153–162. doi: 10.1007/BF00211779. [DOI] [PubMed] [Google Scholar]
- 26.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 27.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982;104:4559–4570. [Google Scholar]
- 28.Lee AL, Wand AJ. Assessing potential bias in the determination of rotational correlation times of proteins by NMR relaxation. J. Biomol. NMR. 1999;13:101–112. doi: 10.1023/a:1008304220445. [DOI] [PubMed] [Google Scholar]
- 29.Rose GD, Geselowitz AR, Lesser GJ, Lee RH, Zehfus MH. Hydrophobicity of amino acid residues in globular proteins. Science. 1985;229:834–838. doi: 10.1126/science.4023714. [DOI] [PubMed] [Google Scholar]
- 30.Zimmerman JM, Eliezer N, Simha R. The characterization of amino acid sequences in proteins by statistical methods. J. Theor. Biol. 1968;21:170–201. doi: 10.1016/0022-5193(68)90069-6. [DOI] [PubMed] [Google Scholar]
- 31.Wishart DS, Sykes BD. Chemical shifts as a tool for structure determination. Methods Enzymol. 1994;239:363–392. doi: 10.1016/s0076-6879(94)39014-2. [DOI] [PubMed] [Google Scholar]
- 32.Mielke SP, Krishnan VV. An evaluation of chemical shift index-based secondary structure determination in proteins: Influence of random coil chemical shifts. J. Biomol. NMR. 2004;30:143–153. doi: 10.1023/b:jnmr.0000048940.51331.49. [DOI] [PubMed] [Google Scholar]
- 33.Schwarzinger S, Kroon GJ, Foss TR, Chung J, Wright PE, Dyson HJ. Sequence-dependent correction of random coil NMR chemical shifts. J. Am. Chem. Soc. 2001;123:2970–2978. doi: 10.1021/ja003760i. [DOI] [PubMed] [Google Scholar]
- 34.Wagner G, Neuhaus D, Worgotter E, Vasak M, Kagi JH, Wuthrich K. Nuclear magnetic resonance identification of “Half-turn” and 310-helix secondary structure in rabbit liver metallothionein-2. J. Mol. Biol. 1986;187:131–135. doi: 10.1016/0022-2836(86)90413-4. [DOI] [PubMed] [Google Scholar]
- 35.Ye K, Wang J. Self-association reaction of denatured staphylococcal nuclease fragments characterized by heteronuclear NMR. J. Mol. Biol. 2001;307:309–322. doi: 10.1006/jmbi.2000.4449. [DOI] [PubMed] [Google Scholar]
- 36.Ishima R, Iwahara J, Yokoyama S, Nagayama K. Gaussian spectral-density function for protein internal motions. J. Magn. ResonSer. B. 1996;111:281–284. doi: 10.1006/jmrb.1996.0094. [DOI] [PubMed] [Google Scholar]
- 37.Peng JW, Wagner G. Mapping of the spectral densities of N-H bond motions in eglin c using heteronuclear relaxation experiments. Biochemistry. 1992;31:8571–8586. doi: 10.1021/bi00151a027. [DOI] [PubMed] [Google Scholar]
- 38.Peng JW, Wagner G. Frequency spectrum of NH bonds in eglin c from spectral density mapping at multiple fields. Biochemistry. 1995;34:16733–16752. doi: 10.1021/bi00051a023. [DOI] [PubMed] [Google Scholar]
- 39.Dellwo MJ, Wand AJ. Model-independent and model-dependent analysis of the global and internal dynamics of cyclosporine-A. J. Am. Chem. Soc. 1989;111:4571–4578. [Google Scholar]
- 40.Tjandra N, Feller SE, Pastor RW, Bax A. Rotational diffusion anisotropy of human ubiquitin from N-15 NMR relaxation. J. Am. Chem. Soc. 1995;117:12562–12566. [Google Scholar]
- 41.Kay LE, Torchia DA, Bax A. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: Application to staphylococcal nuclease. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- 42.Andrec M, Montelione GT, Levy RM. Lipari-Szabo mapping: A graphical approach to Lipari-Szabo analysis of NMR relaxation data using reduced spectral density mapping. J. Biomol. NMR. 2000;18:83–100. doi: 10.1023/a:1008302101116. [DOI] [PubMed] [Google Scholar]
- 43.Schwarzinger S, Wright PE, Dyson HJ. Molecular hinges in protein folding: The urea-denatured state of apomyo-globin. Biochemistry. 2002;41:12681–12686. doi: 10.1021/bi020381o. [DOI] [PubMed] [Google Scholar]
- 44.Marqusee S, Sauer RT. Contributions of a hydrogen bond/salt bridge network to the stability of secondary and tertiary structure in λ repressor. Protein Sci. 1994;3:2217–2225. doi: 10.1002/pro.5560031207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pabo CO, Lewis M. The operator-binding domain of λ repressor: Structure and DNA recognition. Nature. 1982;298:443–447. doi: 10.1038/298443a0. [DOI] [PubMed] [Google Scholar]
- 46.Burton RE, Myers JK, Oas TG. Protein folding dynamics: Quantitative comparison between theory and experiment. Biochemistry. 1998;37:5337–5343. doi: 10.1021/bi980245c. [DOI] [PubMed] [Google Scholar]
- 47.Munoz V, Serrano L. Elucidating the folding problem of helical peptides using empirical parameters. Nat. Struct. Biol. 1994;1:399–409. doi: 10.1038/nsb0694-399. [DOI] [PubMed] [Google Scholar]
- 48.Black SD, Mould DR. Development of hydrophobicity parameters to analyze proteins which bear posttranslational or cotranslational modifications. Anal. Biochem. 1991;193:72–82. doi: 10.1016/0003-2697(91)90045-u. [DOI] [PubMed] [Google Scholar]
- 49.Srinivasan R, Rose GD. Methinks it is like a folding curve. Biophys. Chem. 2002;101:167–171. doi: 10.1016/s0301-4622(02)00147-3. [DOI] [PubMed] [Google Scholar]
- 50.Fitzkee NC, Rose GD. Sterics and solvation winnow accessible conformational space for unfolded proteins. J. Mol. Biol. 2005;353:873–887. doi: 10.1016/j.jmb.2005.08.062. [DOI] [PubMed] [Google Scholar]
- 51.Bromberg S, Dill KA. Side-chain entropy and packing in proteins. Protein Sci. 1994;3:997–1009. doi: 10.1002/pro.5560030702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Creighton TE. Proteins: Structures and molecular properties. 2nd ed. New York: W. H. Freemen and Co; 1993. [Google Scholar]
- 53.Chellgren BW, Creamer TP. Side-chain entropy effects on protein secondary structure formation. Proteins. 2006;62:411–420. doi: 10.1002/prot.20766. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.