Rhythmic Bursting in the Pre-Bötzinger Complex: Mechanisms and Models

Abstract

The pre-Bötzinger complex (pre-BötC), a neural structure involved in respiratory rhythm generation, can generate rhythmic bursting activity in vitro that persists after blockade of synaptic inhibition. Experimental studies have identified two mechanisms potentially involved in this activity: one based on the persistent sodium current (I_NaP) and the other involving calcium (I_Ca) and/or calcium-activated nonspecific cation (I_CAN) currents. In this modeling study, we investigated bursting generated in single neurons and excitatory neural populations with randomly distributed conductances of I_NaP and I_Ca. We analyzed the possible roles of these currents, the Na⁺/K⁺ pump, synaptic mechanisms, and network interactions in rhythmic bursting generated under different conditions. We show that a population of synaptically coupled excitatory neurons with randomly distributed I_NaP- and/or I_CAN-mediated burst generating mechanisms can operate in different oscillatory regimes with bursting dependent on either current or independent of both. The existence of multiple oscillatory regimes and their state dependence may explain rhythmic activities observed in the pre-BötC under different conditions.

1 INTRODUCTION

The pre-Bötzinger complex (pre-BötC), a medullary neural structure critically involved in respiratory rhythm generation in mammals, can in vitro generate synchronized neural oscillations that persist after pharmacological blockade of synaptic inhibition (Ramirez et al., 1996; Rekling and Feldman, 1998; Smith et al., 1991). Despite many years of intensive investigations, the neural mechanisms underlying these oscillations remain largely unknown.

Butera et al. (1999a,b) suggested that population bursting observed in the pre-BötC in vitro arises from the persistent (slowly inactivating) sodium current (I_NaP) in pre-BötC neurons and the excitatory synaptic interactions between these neurons. The presence of I_NaP in pre-BötC was confirmed (Del Negro et al., 2002a; Koizumi and Smith, 2008; Rybak et al., 2003a), and the pre-BötC rhythmic activity in medullary slices in vitro from neonatal rats could be abolished by the I_NaP blocker riluzole (Koizumi and Smith, 2008; Rybak et al., 2003b).

Alternatively, Thoby-Brisson and Ramirez (2001), using medullary slices from P6-P13 mice containing the pre-BötC, found two distinct types of intrinsically bursting cells whose bursting was, respectively, sensitive and insensitive to the calcium current blocker Cd²⁺. Later, Peña et al. (2004) found that the Cd²⁺-sensitive bursters were riluzole insensitive, whereas most of the Cd²⁺-insensitive ones were riluzole sensitive. Furthermore, rhythmic activity in the Cd²⁺-sensitive bursters could be blocked by flufenamic acid (FFA), a pharmacological blocker of the calcium-activated nonspecific cation current (I_CAN) (Del Negro et al., 2005), suggesting that both I_Ca and I_CAN are involved in bursting generated in the pre-BötC. Further studies of the possible role of I_CAN and the metabotropic mechanisms involved in its activation (Beltran-Parrazal et al., 2012; Ben-Mabrouk et al., 2012; Krey et al., 2010; Pace and Del Negro, 2008; Pace et al., 2007; Rubin et al., 2009) produced inconsistent results. As a result, the involvement and specific roles of these and other possible sodium and calcium mechanisms in the bursting activity observed in the pre-BötC remain unresolved and require further investigation.

In this modeling study, we consider the intrinsic Na⁺- and Ca²⁺-dependent bursting generated in single cells and heterogeneous populations of synaptically coupled excitatory neurons with conductances of I_NaP and I_Ca randomly distributed across neurons in the populations. We study the possible roles of synaptic interactions, ionotropic and metabotropic synaptic mechanisms, intracellular Ca²⁺ release, and the Na⁺/K⁺ pump in the cellular and network rhythmic bursting. We show that heterogeneous populations of excitatory neurons can generate rhythmic bursting dependent on I_NaP and/or I_CAN, or independent of both, and that the involvement of each mechanism may depend on the neuronal excitation, strength of synaptic interactions, and expression of particular ionic channels. We suggest that the rhythmic bursting activity discovered in the pre-BötC in vitro is state dependent, and hence, depending on the state, the pre-BötC can operate in multiple oscillatory regimes involving different I_NaP- and/or I_CAN-dependent mechanisms. We also support the previous suggestion that the electrogenic Na⁺/K⁺ pump can play an important role in the generation ofthis rhythmic bursting by performing the burst termination function in multiple regimes of oscillations. The results of this theoretical modeling study provide important insights into various rhythmic activities observed in the pre-BötC and possibly other brainstem and spinal cord circuits.

2 METHODS

In this study, we used the computational models of single neurons and neuron populations with excitatory synaptic interactions developed and fully described by Jasinski et al. (2013). Specifically, the models of single neurons were developed in the Hodgkin–Huxley style. Formal descriptions of ionic channel kinetics and other cellular biophysical mechanisms in these models were derived from our previous models (Rybak et al., 2003a,b, 2007; Smith et al., 2007) and other recent models (Rubin et al., 2009; Toporikova and Butera, 2011).

The simulated populations contained N=50 neurons with all-to-all fast glutamatergic-like excitatory synaptic interconnections. The heterogeneity of neurons within the population was provided by the uniformly distributed maximal conductances of leakage, persistent sodium, and calcium channels. The weights of synaptic interactions were also distributed (using a normal distribution).

The initial conditions for membrane potentials, intracellular calcium and sodium concentrations, and channel gating variables were chosen using a uniform distribution within the physiologically realistic ranges of values for each variable, and a settling period of 10–20 s was allowed in each simulation to make sure that the results are independent of initial conditions. Most simulations were repeated 10–20 times and demonstrated qualitatively similar behavior for all values of distributed parameters and initial conditions.

The full mathematical descriptions used the model and all simulation details can be found in our previous paper (Jasinski et al., 2013). All simulations were performed using custom written C software for a Linux-based operating system that ran locally on a 6-core workstation in the laboratory or remotely on the high-performance parallel cluster Biowulf at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov).

3 RESULTS

3.1 The Intrinsic Na⁺ and Ca²⁺-Dependent Mechanisms for Single-Neuron Bursting

3.1.1 Bursting Mechanisms Involving Persistent (Slowly Inactivating) Sodium Current (I_NaP)

The presence of persistent (i.e., noninactivating) sodium current is not sufficient for a neuron to generate intrinsic bursting, there should be an additional burst-terminating mechanism. In the classical model of an I_NaP-dependent bursting neuron proposed by Butera et al. (1999a, Model 1), burst termination was based on the slow inactivation of the persistent sodium channels themselves. The other proposed burst-terminating mechanisms were based on the slowly activating, voltage-dependent (e.g., Butera et al., 1999a, Model 2) or calcium-dependent (e.g., El Manira et al., 1994; Ryczko et al., 2010) potassium currents. In our previous (Jasinski et al., 2013) and present studies, we have suggested and investigated the possible involvement of a mechanism based on the activity-dependent accumulation of sodium ions within the cell ([Na⁺]_in), and subsequent activation of the electrogenic Na⁺/K⁺ pump (I_Pump) removing the intracellularly accumulated sodium ions.

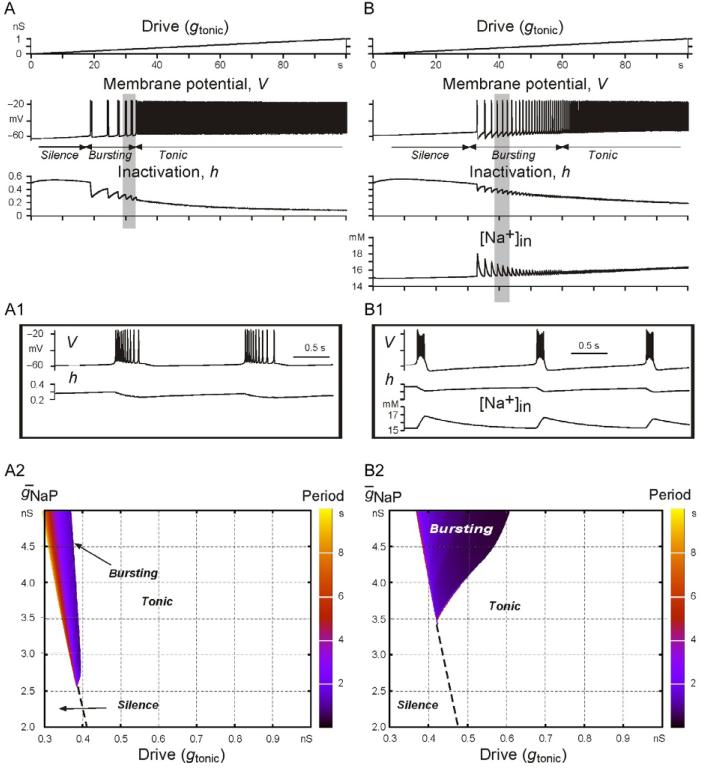
Figure 1 illustrates the possible effects of I_Pump on I_NaP-dependent bursting. Two single-neuron models exhibiting I_NaP-dependent bursting were studied (see model details and descriptions in Jasinski et al., 2013). The first model (Fig. 1A,A1,A2) was qualitatively similar to the classical Butera model (Butera et al., 1999a, Model 1) but with parameter values drawn from previous experimental measurements (Rybak et al., 2003a). Burst termination in this model was based only on the slow inactivation of I_NaP (defined by the inactivation variable h, see Fig. 1A,A1,A2), and the slow recovery from inactivation controls the membrane potential trajectory during the interburst interval defining the onset of the next burst. In the second model (Fig. 1B,B1,B2), in addition to the slowly inactivating I_NaP (as in the first model), we incorporated the burst-terminating mechanism based on the intracellular accumulation of sodium ([Na⁺]_in) followed by [Na⁺]_in-dependent activation of the Na⁺/K⁺ pump and its associated current (I_Pump). This Na⁺/K⁺ pump-based mechanism was not only involved in burst termination but also in membrane potential recovery during the interburst interval.

FIGURE 1.

Simulation of I_NaP-dependent bursting using two single-neuron models with different burst-terminating mechanisms. In the first model (A), burst termination was based on the slow inactivation of the persistent sodium channels. In the second model (B), there were two burst-terminating mechanisms: one based on the slow inactivation of I_NaP (as in the first model) and the other based on intracellular Na⁺ accumulation and subsequent activation of the electrogenic Na⁺/K⁺ pump. Panels A and B show the neuron response (changes in the membrane potential) to the slow ramp increase of input synaptic drive (shown at the top) and the dynamic changes in the relevant variables (h and [Na⁺]_in). Insets A1 and B1 (from A and B panels, respectively, highlighted by gray) show the shape of the generated bursts and the changes in the relevant variables. Panels A2 and B2 show regions of silence, bursting, and tonic activity in the 2D space ḡ_NaPḡ_tonic for the corresponding models presented in A and B, respectively. The bursting period in each plot is indicated by color/gray level scale bar on the right of each diagram. See text for details.

These models were comparatively investigated with respect to their response to tonic excitatory drive (g_tonic) that was elevated slowly from 0 to 1 nS to sweep a range of baseline membrane potentials (see Fig. 1A,B and the corresponding insets A1,B1). In each model, the neuron started rhythmic bursting when the drive exceeded some model-specific threshold (Fig. 1A,B), and the frequency of this bursting increased (bursting period decreased) with increasing g_tonic. Then, when the drive exceeded another model-specific threshold, the neuron switched from rhythmic bursting to tonic spiking.

Figure 1A2,B2 shows, respectively, the bursting regions for each model represented in the 2D space of parameters ḡ_NaP,g_tonic, where ḡ_NaP is the maximal conductance of I_NaP. This figure shows that the model with the Na⁺/K⁺ pump involved in burst termination has a significantly wider area of bursting in the above parameter space than the classical model with burst termination based on the voltage-dependent I_NaP inactivation alone.

The other interesting difference between the models is the dependence of burst frequency on ḡ_NaP. Specifically, when ḡ_NaP is decreasing (at a constant g_tonic) to simulate the effect of I_NaP blockers (i.e., when we move vertically downward within bursting areas in Fig. 1A2, the burst frequency is decreasing in the first model but remaining almost constant in the second model; Fig. 1B2). There is also an interesting issue concerning the different effects of I_NaP suppression used to simulate thepossible effects of riluzole, that is, a decrease in g _NaP at a constant excitatory drive that would correspond to a vertical downward shift from bursting regions in each 2D plot in Fig. 1A2,B2. One can see that in the first model (see Fig. 1A2), this ḡ_NaP reduction can only cause a switch from bursting to silence, whereas in the second model containing the Na⁺/K⁺ pump (Fig. 1B2), the result depends on the drive. At low drive, this I_NaP suppression also produces a switch from bursting to silence, but at higher drive, it causes a switch from bursting to tonic spiking in the majority of the bursting region.

3.1.2 Bursting Involving Calcium (I_Ca) and Calcium-Activated Nonspecific Cation (I_CAN) Currents

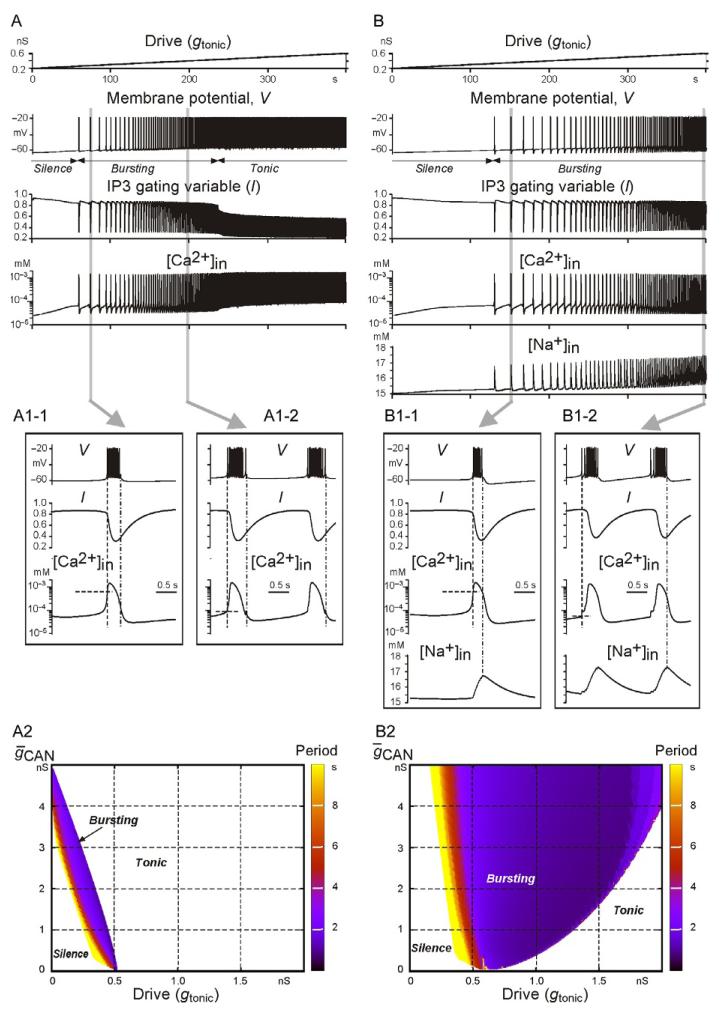
This part of our study was motivated by several recent experimental and modeling studies (Crowder et al., 2007; Dunmyre et al., 2011; Krey et al., 2010; Pace and Del Negro, 2008; Pace et al., 2007; Toporikova and Butera, 2011) and focused on simulation of an I_CAN-dependent bursting mechanism (see model details and descriptions in Jasinski et al., 2013). In the two models considered, I_CAN was activated by intracellular Ca²⁺ accumulation ([Ca²⁺]_in) whose accumulation was provided by the inositol triphosphate (IP₃)-dependent Ca²⁺ release from intracellular stores.This process in our models critically depended on Ca²⁺ influx through voltage-gated calcium current (I_Ca) which provided an initial [Ca²⁺]_in accumulation, which then induced a nonlinear positive feedback mechanism known as Ca²⁺-induced Ca²⁺ release (CICR). Both the input synaptic activation (provided by synaptic drive) and the [Ca²⁺]_in-dependent activation of I_CAN contributed to the initial membrane depolarization (burst onset), and their contributions depended on the input synaptic activation. Two burst-terminating mechanisms were considered. One mechanism involved Ca²⁺-dependent inactivation of the IP₃ receptor (regulated by the gating variable l, see Fig. 2), leading to the reduction of intracellular Ca²⁺ and deactivation of I_CAN (see details in Jasinski et al., 2013; Toporikova and Butera, 2011). The second mechanism was based on the activity-dependent accumulation of [Na⁺]_in followed by the [Na⁺]_in-activated I_Pump, that is, the same Na⁺/K⁺-based mechanism as in the second I_NaP-based models described above. However, in contrast to the I_NaP-based models, the slow accumulation of [Na⁺]_in in these models was mainly provided by I_CAN instead of I_NaP.

FIGURE 2.

Simulation of an I_Ca- and I_CAN-dependent bursting using two single-neuron models with different burst-terminating mechanisms. In the first model (A), burst termination was based on the Ca²⁺-dependent IP₃ receptor inactivation (see the traces for IP₃ receptor gating variable l and [Ca²⁺]_in). In the second model (B), there were two burst-terminatingmechanisms: one based on the Ca²⁺-dependent IP₃ receptor inactivation (as in the first model) and the other based on intracellular Na⁺ accumulation (see [Na⁺]_in traces) and subsequent activation of the Na⁺/K⁺ pump. Each column shows the neuron response to the slow ramp increase of input excitatory synaptic drive (shown at the top). Insets A1-1 and A1-2, and B1-1 and B1-2 (from A and B traces, respectively, highlighted by gray) show the shape of generated bursts and the changes in relevant variables. Panels A2 and B2 show regions of silence, bursting, and tonic activity in the 2D space ḡ_CAN,g_tonic for the models shown in panels A and B, respectively. The bursting period in each plot is indicated by a color/gray level scale bar on the right of each diagram. See text for details.

Two distinct models were considered (see also Jasinski et al., 2013): one with burst termination based entirely on the Ca²⁺-dependent inactivation of the IP₃ receptor without the Na⁺/K⁺ pump involved (see Fig. 2A,A1-1,A1-2,A2) and the other with both mechanisms (based on Ca²⁺-dependent IP₃ receptor inactivation and Na⁺/K⁺ pump activation) contributing to burst termination (Fig. 2B,B1-1, B1-2,B2). Figure 2A,B shows the response of each model to g_tonic, slowly increasing from 0.2 to 0.6 nS. Similar to the I_NaP-based models described above, both of these models showed a progression over the three regimes of silence, bursting, and tonic spiking as drive was increased, and the burst frequency was increasing in the bursting regime with increasing g_tonic.

The insets in panels A1-1 and B1-1 show burst details in each model at relatively low values of drive, whereas the insets in panels A1-2 and B1-2 show burst details in these models at higher values of drive. At low drives, the initial rising of [Ca²⁺]_in through I_Ca and the CICR mechanism precedes membrane depolarization and burst onset (indicated by the vertical dashed line). This accumulated [Ca²⁺]_in activates I_CAN, which in turn produces the membrane depolarization and burst onset. In contrast, at higher drives, the initial membrane depolarization is provided by the dynamics of synaptic input (i.e., drive) and I_Pump (decreasing during the preceding interburst interval), and hence the onset of the burst (indicated by the dashed line) precedes the [Ca²⁺]_in-dependent I_CAN activation. This can also explain a clear difference in the intraburst spike pattern between the corresponding bursts (a decrementing spike frequency at lower drives vs. an initial ramp increase in spike frequency within the burst at higher drives; see panels A1-1 and B1-1 vs. panels A1-2 and B1-2). Although I_CAN does not play a leading role in burst initiation at higher drives, it contributes to the above patterning of intraburst spikes (the initial ramp in spike frequency) in both models. In addition, I_CAN is critical for burst termination in both models, as described below.

The insets in Fig. 2 also demonstrate the differences between the two models in burst termination. In the first model (panels A1-1 and A1-2), burst termination (controlled by IP₃ receptor inactivation defined by variable l, see Jasinski et al., 2013) occurs when [Ca²⁺]_in drops below the threshold for I_CAN activation (indicated by the dot-dashed line). In the second model (panels B1-1 and B1-2), burst termination is mostly provided by the I_CAN-dependent intracellular accumulation of [Na⁺]_in followed by [Na⁺]_in-dependent activation of the Na⁺/K⁺ pump (see the vertical dot-dashed line, showing that bursts are terminated not when [Ca²⁺]_in drops below the half-activation concentration for I_CAN, as in panels A1-1 and A1-2, but when [Na⁺]_in reaches its maximum).

Figure 2A2 and B2 shows maps of the bursting regions for the two models in the 2D space of ḡ_CAN,g_tonic where ḡ_CAN is the maximal conductance of I_CAN. The most important difference between these two models is that the second model has a significantly wider region of bursting in the (ḡ_CAN,g_tonic) plane. The mainconclusion here is that the Na⁺/K⁺ pump-dependent burst-terminating mechanism greatly increases the area of the bursting region in the parameter space. The other interesting difference between the models concerns the different effects of I_CAN suppression simulating the possible effect of FFA (implemented as a decrease in ḡ_CAN at a constant drive, that is, a vertical downward shift from the bursting regions in each 2D plot). In the first model, this g _CAN reduction would only cause a switch from bursting to silence, whereas in the second model the result depends on the drive. At low drive, this I_CAN suppression would also produce a switch to silence, but at higher drive (roughly to the right of 0.6, i.e., in the majority of the bursting region) it would cause a switch from bursting to tonic spiking.

3.2 Modeling a Heterogeneous Neural Population with Randomly Distributed ḡ_NaP,ḡ_Ca, and g_L

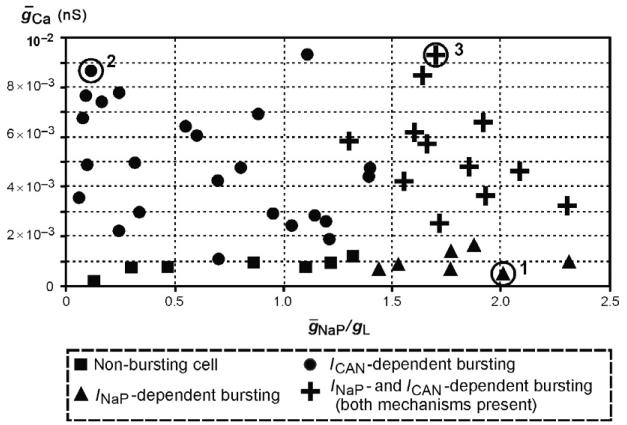
Experimental studies in neonatal/juvenile mouse in vitro slice preparations have demonstrated that I_NaP- and I_Ca/I_CAN-mediated mechanisms may coexist in the pre-BötC (e.g., Peña et al., 2004). In this connection, we wanted to investigate how the above different intrinsic mechanisms can operate together within a heterogeneous population of neurons with mutual excitatory synaptic interactions. A population of 50 excitatory neurons was considered, in which the maximal conductances for persistent sodium (ḡ_NaP), leakage (g_L), and calcium (ḡ_Ca) currents in each neuron were randomly selected from their physiological ranges (ḡ_NaP ∈ [0,5] nS, g_L ∈ [2,3] nS, and ḡ_ca ∈ [0,0.01] nS; see details in Jasinski et al., 2013). The result of particular parameter distributions is shown in Fig. 3. In this figure, each of 50 neurons is represented by a symbol in the 2D space of (ḡ_Ca,ḡ_NaP,g_L). The intrinsic bursting properties of each neuron in the population depended on the particular values of these parameters assigned from their random distributions. The ratio ḡ_NaP/g_L effectively defined the essential biophysical conditions for I_NaP-dependent bursting (Butera et al., 1999a; Purvis et al., 2007), whereas the Ca²⁺-dependent mechanisms activating I_CAN were linked in our model to ḡ_Ca.

FIGURE 3.

Bursting properties of neurons within a 50-neuron population with randomly distributed ḡ_NaP, g_L, and ḡ_Ca. Synaptic interactions between all neurons were set to zero (uncoupled case). The maximal conductance of persistent sodium, leakage, and calcium currents were uniformly distributed within the following ranges: ḡ_NaP ∈ [0.0.01] nS, g_L [2,3]nS, and ḡ_Ca ∈ [0.0.01] nS (see Jasinski et al., 2013). Each neuron is represented by a symbol (triangle, filled circle, cross, or square) in the 2D space of ḡ_Caḡ_NaPḡ_L located in accordance with the particular values of these parameters in this neuron assigned from the random distributions. Symbols indicate the types of bursting expressed in each neuron in the uncoupled case. Key is shown at the bottom. One representative neuron of each bursting type, indicated by the circles around the corresponding symbol and the numbers 1, 2, or 3, respectively, was used for description of its firing under different conditions shown in the following Figs. 4 and 5. See text for details.

To test the ability of each neuron in the population to generate intrinsic bursting activity, we removed all synaptic interactions between the neurons (by setting all weights of synaptic interactions between the neurons w_ji = 0) and then tested the response of each neuron to slow ramp increases of excitatory drive (as we did for the single-neuron models described above). In order to identify the bursting mechanism involved in each neuron tested, we repeated this process under conditions when either ḡ_NaP = 0 or ḡ_CAN = 0 or both ḡ_NaP = ḡ_CAN = 0.

In Fig. 3, all neurons exhibiting an I -dependent bursting (i.e., those whose bursting persisted at some level of drive at ḡ_CAN = 0, but was abolished at ḡ_NaP = 0) are represented by triangles, which are mostly located in the area corresponding to the relatively high values of ḡ_NaP/g_L and lower values of ḡ_Ca. The neurons whose bursting was dependent on I_CAN are represented by the filled circles. The bursting in these neurons persisted at ḡ_NaP = 0 but could be abolished if ḡ_CAN = 0; these neurons are located in the area corresponding to the higher values of ḡ_Ca and relatively lower values of ḡ_NaP/g_L. The neurons represented by crosses could express bursting based on any of the above mechanisms, that is, their bursting could be abolished only if ḡ_NaP = ḡ_CAN 0. It located is not surprising that these neurons are in the area corresponding to the higher values of both ḡ_Ca and ḡ_NaP/g_L. Finally, the neurons unable to express bursting under any condition are represented by squares and located in the area corresponding to the lower values of both ḡ_Ca and ḡ_NaP/g_L.

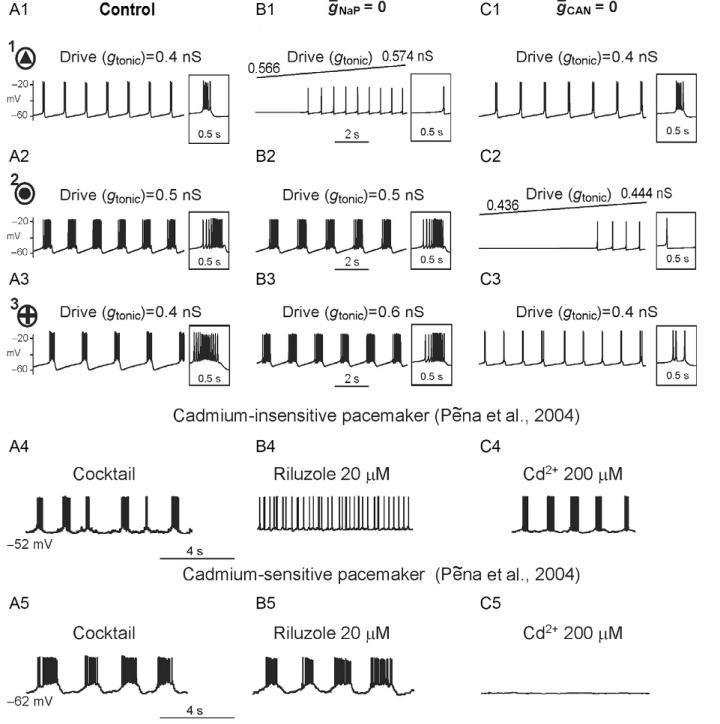
Figure 4, panels A1–C1, A2–C2, and A3–C3, shows the behavior of one representative neuron of each type (indicated in Fig. 3 by the circles around the corresponding symbol and the numbers 1, 2, and 3, respectively) under control conditions (A1, A2, and A3, respectively), and after assigning ḡ_NaP 0 (B1, B2, and B3, respectively) or ḡ_CAN = 0 (C1, C2, and C3, respectively). Specifically,neuron 1 (Figs. 3 and 4A1) with the I_NaP-dependent bursting mechanism did not express bursting when ḡ_NaP = 0 (Fig. 4B1), but maintained bursting activity at ḡ_CAN 0 (Fig. 4C1). Neuron 2 (Figs. 3 and 4A2) with the I_CAN-dependent bursting mechanism did not express bursting at ḡ_CAN = 0 (Fig. 4B2), but maintained bursting activity at ḡ_NaP = 0 (Fig. 4C2). Neuron 3 (Figs. 3 and 4A3) with both bursting mechanisms expressed bursting if either ḡ_CAN 0 (Fig. 4B3) or ḡ_NaP 0 (Fig. 4C2) which could be blocked only if ḡ_NaP = ḡ_CAN = 0 (not shown). As in Section 1, both riluzole-sensitive and Cd²⁺-sensitive pacemaker neurons have been identified in the pre-BötC in vitro (Peña et al., 2004). In this connection, we suggest that neuron 1 simulates the riluzole-sensitive, cadmium-insensitive pacemaker neuron (Fig. 4A4–C4), whereas neuron 2 may simulate the cadmium-sensitive pacemaker (Fig. 4A5–C5).

FIGURE 4.

Firing behavior of the uncoupled representative neurons with different values of ḡ_NaP, ḡ_Ca, and g_L. A1–C1, A2–C2, and A3–C3 show the behavior of one representative neuron of each type (indicated in Fig. 3 by the circles around the corresponding symbol and the numbers 1, 2, and 3, respectively) under control conditions (A1, A2, and A3, respectively), and after blocking I_NaP (ḡ_NaP = 0 in B1, B2, and B3, respectively) or I_CAN (ḡ_CAN 0 in C1, C2, and C3, respectively). Specifically, neuron 1 (A1–C1, also see Fig. 3) with the I_NaP-dependent bursting mechanism did not express bursting when ḡ_NaP = 0 (B1) (exhibiting a switch to tonic spiking with an increase in excitatory drive), but maintained bursting activity at ḡ_CAN 0 (C1). Neuron 2 (A2–C2, also see Fig. 3) with the I_CAN-dependent bursting mechanism = did not express bursting when ḡ_CAN = 0 (C2), but maintained bursting activity at ḡ_NaP 0 (B2). Neuron 3 (A3–C3, also see Fig. 3) with both bursting mechanisms; this neuron= expressed bursting when either ḡ_CAN = 0 (B3) or ḡ_NaP = 0 (C3) which could be blocked only if ḡ_NaP = ḡ_CAN = 0 (not shown). A4–C4 show an isolated riluzole-sensitive, cadmiuminsensitive intrinsically bursting “pacemaker” neuron recorded in the pre-BötC in vitro after pharmacologically blocking excitatory and inhibitory synaptic transmission (Cocktail, A4), and after application of riluzole (B4) and Cd²⁺ (C4). A5–C5 show an isolated riluzole-insensitive, cadmium-sensitive intrinsic burster before (Cocktail, A4) and after application of riluzole (B5) and Cd²⁺ (C5) (also from Peña et al. (2004); fig. 3). See text for details.

3.3 Behavior of the Fully Interconnected Network

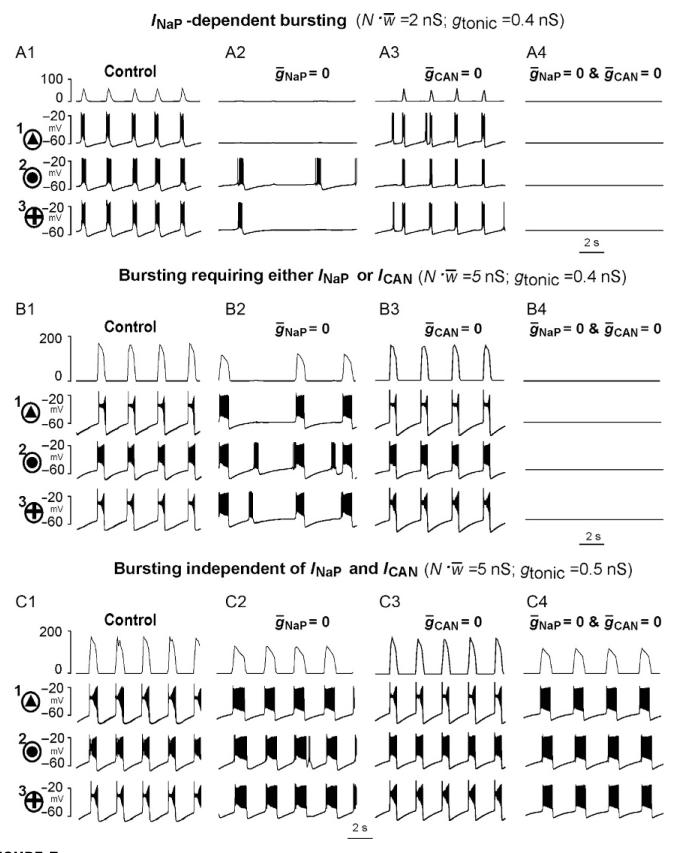
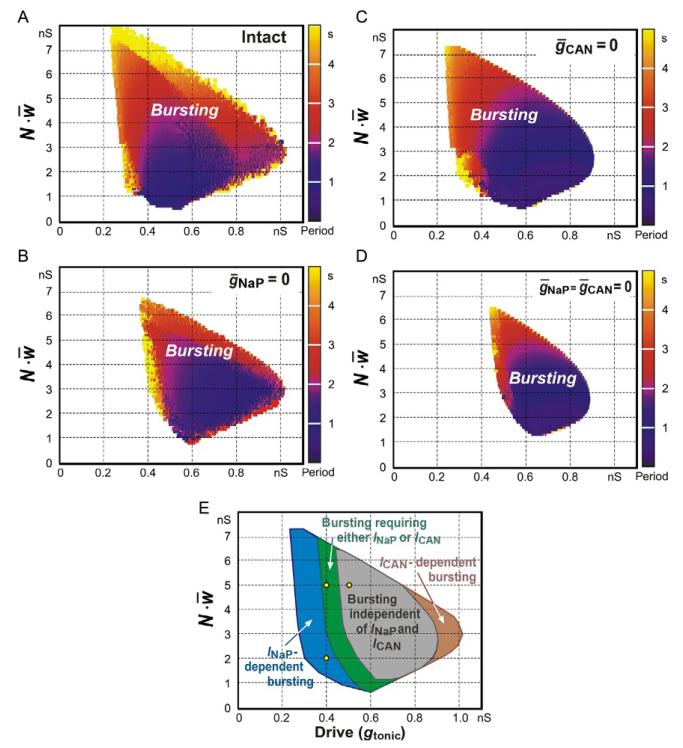
With mutually excitatory synaptic interactions, the neural populations with distributed parameters (e.g., as shown in Fig. 3) were able to generate synchronized rhythmic bursting activity. We studied the activity of the population with parameters distributed as in Fig. 3 with all-to-all excitatory connections with the average synaptic weight w̄ (w̄ ∈ [0,0.2]nS) (see also Jasinski et al., 2013). Figure 5 shows the integrated population activity (upper trace in each panel) and the traces of the membrane potential of the three neurons identified in Figs. 3 and 4 as neurons 1, 2, and 3, under control conditions (panels A1–C1) and after simulated blockade of I_NaP (ḡ_NaP = 0; Fig. 5A2–C2) or I_CAN (ḡ_CAN 0; Fig. 5A3–C3) or both currents (ḡ_NaP = 0 and ḡ_CAN = 0; Fig. 5A4–C4). Figure 6 =A–D shows the bursting regions in the plane of (g_tonic, N.w̄, N = 50) corresponding g = to the intact network (panel A) and when either _NaP = 0 (panel B) or ḡ_CAN = 0 (panel C) or both (ḡ_NaP ḡ_CAN 0, panel D). The diagram in panel E summarizes the results shown in panels = B-D. =

FIGURE 5.

Rhythmic bursting activity generated by the 50-neuron population with mutual excitatory synaptic interconnections. Each panel shows the integrated population activity represented by the average histogram of neuronal activities (upper trace, y-axis represents an average histogram of population activity in spikes/(neurons), bin size 20 ms) and the membrane potential traces of three neurons, indicated in Figs. 3 and 4 as = the neurons 1, 2, and 3, respectively. The top row (A1–A4) represents I_NaP-dependent bursting that occurs in the population at relatively low both neuronal interactions N.w̄ = 2 nS and drive (_tonic 0.4 nS). The middle row (B1–B4) population = illustrates bursting requiring either I_NaP or I_CAN that occurs with increased neuronal interactions Nw̄ = 5 nS at the same level ofdrive (g_tonic = 0.4 nS). The bottom row (C1–C4) shows population bursting independent of I_NaP and I_CAN that exists at a higher level of interactions N w̄ = 5nS and higher drive (g_tonic = 0.5 nS). The first (left) column (A1–C1) shows the population = activity and activities of the identified neurons 1, 2, and 3 under control conditions; the second column (A2–C2) shows the simulated effects of I_NaP blockade ḡ_NaP 0 on the population and single-neuron bursting in the three cases of drive and neuronal interactions described above; the third column (A3–C3) shows the simulated effects of I_CAN blockade ḡ_CAN 0 on the population and single-neuron bursting for the same three cases; the fourth (right) = column (A4–C4) shows the simulated effects of the blockade of both I_NaP and I_CAN (ḡ_NaP = 0 and ḡ_CAN 0). See text for details.

FIGURE 6.

Population bursting in the 2D parameter space (g_tonic, Nw̄) for the intact network (A) and when ḡ_NaP = 0 (B), or ḡ_CAN = 0 (C), or ḡ_NaP = ḡ_CAN = 0 (D). The bursting period in A–D is represented by color/gray level scale bar on the right of each diagram. The results are summarized in E, where bursting involving different mechanisms is distinguished by color/ gray areas. The region for I_NaP-dependent population bursting specified in panel E is not present in B and D; the region in panel E in which population bursting can be based on either I_NaP or I_CAN is not present in D; the region in panel E in which population bursting may exist without both of these currents corresponds to the bursting region shown in D; the very right region in E represents an unstable I_Ca- and I_CAN-dependent bursting. All diagrams (A-E) are built for a single simulated population (based on a particular distribution of parameters shown in Fig. 3)—the same that was used for obtaining results shown in Figs. 4 and 5. Simulations of other populations (resulting from the reinitialization of the randomized parameters within the same ranges and distributions) resulted in qualitatively similardiagrams without significant shifting of borders between the bursting areas or other critical differences. Statistical analysis and averaging data from multiple simulations with parameter reinitialization were not performed. The three points in E correspond to the three regimes shown in Fig. 5, panels A1–A3, B1–B3, and C1–C3, respectively. See text for details.

Our simulations showed that when both the external excitatory drive and the total network input to each neuron were relatively weak (e.g., g_tonic = 0.4 nS; N w̄ 2nS, as in Fig. 5A1–A4, which corresponds to the point (0.4, 2)nS indicated in Fig.=6E by the small circle), the network generated I_NaP-dependent population bursting that could be abolished by setting ḡ_NaP = 0 (Fig. 5A2) despite the presence of unsynchronized rhythmic bursting in a few neurons (e.g., neurons 2 and 3). This type of bursting corresponds to the I_NaP-dependent bursting region in Fig. 6E.

An increase in the total network excitatory synaptic input to each neuron at the same g_tonic (e.g., from N.w̄ = 2–5 nS, simulating an increase in the number of neurons in population; see Fig. 5B1-B4, which corresponds to the point (0.4, 5)nS (indicated in Fig. 6E by another small circle)), allowed the population to maintain (I_CAN-dependent) population bursting at ḡ_NaP 0 (Fig. 5B2): this bursting could be abolished only if both ḡ_NaP = 0 (Fig. 5B4). ing = The same type of burst-could be obtained by increasing drive (e.g., g_tonic 0.5 nS) while keeping a low level of excitatory synaptic interactions within the = network (Nw̄ = 2nS, not shown). This type of bursting, requiring the presence of either I_NaP or I_CAN, corresponds to a special region indicated in Fig. 6E.

A further increase in excitatory drive, for example, by setting g_tonic 0.5 nS at N.w̄ = 5 nS as in Fig. 5C1–C4 (corresponding to the point (0.5, 5)nS indicated = in Fig. 6E by the third small circle), allowed for population bursting independent of both I_NaP and I_CAN (see Figs. 5C4 and 6D and the corresponding region in Fig. 6E). In this case, relatively strong excitatory synaptic interactions within the population provided burst initiation and then its termination via [Na⁺]_in accumulation and Na⁺/K⁺ pump activation. Note that setting ḡ_CAN = 0 to simulate the suppression of only I_CAN could not stop population bursting in the above three cases (see Fig. 5A3–C3). An unstable, irregular I_CAN-dependent bursting could only exist at very high drive values with a moderate level of N.w̄ (see Fig. 6B and very right bursting region in Fig. 6E), and the biological plausibility of this bursting is questionable, although this maybe a region characterized by generation of I_Ca/I_CAN-dependent, low-frequency, high amplitude sigh-like busting (Jasinski et al., 2013).

4 DISCUSSION

4.1 I_NaP-Dependent Bursting

It should be clearly understood that a truly persistent (noninactivating) I_NaP cannot produce rhythmic bursting at cellular or network levels by itself without additional mechanism(s) providing burst termination. In the classical model of Butera et al. (1999a, Model 1) and in many later models (e.g., Dunmyre et al., 2011; Rybak et al., 2003b; Toporikova and Butera, 2011), burst termination was based on the slow voltage-dependent inactivation of I_NaP conductance. This mathematically elegant idea, however, has not received experimental support, since the slow I_NaP inactivation has not yet been characterized in detail in pre-BötC excitatory neurons. Moreover, modeling studies have shown that the I_NaP-dependent bursting based on the slow voltage-dependent inactivation of I_NaP exists in a limited range of neuronal excitability or input excitatory drive, at least at the single-neuron level (Butera et al., 1999a, see also Fig. 1A2), although the dynamic range is extended inheterogeneous excitatory networks (Butera et al., 1999b; Purvis et al., 2007). Even if the slow voltage-dependent inactivation of I_NaP exists, it is unlikely that it could represent the only mechanism for burst termination; other voltage-dependent, or [Ca²⁺]_in-dependent, or [Na⁺]_in-dependent mechanisms could be involved or critically contribute to burst termination.

Several proposals have been made concerning other potential burst-terminating mechanisms, including mechanisms based on (a) slowly activating voltage-dependent potassium current (e.g., Butera et al., 1999a, Model 2) or Ca²⁺-activated potassium current (suggesting [Ca²⁺]_in accumulation during bursts via high voltage-activated calcium currents, e.g., Bevan and Wilson, 1999; El Manira et al., 1994; Ryczko et al., 2010), (b) Na⁺-activated potassium currents (e.g., Krey et al., 2010; Wallen et al., 2007; Yuan et al., 2003), and (c) activation of the Na⁺/K⁺ electrogenic pump (e.g., Ballerini et al., 1997; Darbon et al., 2003; Del Negro et al., 2009; Krey et al., 2010). The two latter mechanisms suggest an important role of [Na⁺]_in accumulation during bursts. However, slowly activating potassium channels have not been characterized so far in the mammalian brainstem/spinal cord, and Ca²⁺-activated potassium channels have been found unnecessary for rhythm generation in vitro in pre-BötC (Onimaru et al., 2003; Zavala-Tecuapetla et al., 2008). Hence, the [Na⁺]_in-dependent burst-terminating mechanisms, such as those involving activation of the Na⁺/K⁺ pump, currently look most plausible, which is supported by experimental studies of Krey et al. (2010).

In this study, we compared single-neuron models capable of generating I_NaP-dependent bursting that differed by the operating burst-terminating mechanisms. In the first model, burst termination was based on the slow inactivation of I_NaP (Fig. 1A,A1,A2), as in the original Butera et al. (1999a) model (Model 1). In the second model, burst termination was provided by both the slow inactivation of I_NaP (as in the first model) and the Na⁺/K⁺ pump activated by [Na⁺]_in accumulating during bursts (Fig. 1B,B1,B2). We found that the contribution of the Na⁺/K⁺ pump to the I_NaP-based bursting as a part of the burst-terminating mechanism significantly increases the range of neuronal excitability (external drive) over which I_NaP-bursting exists (Fig. 1A2,B2).

An additional point of difference between the first model of the Butera et al. (1999a) type and the second model incorporating the Na⁺/K⁺ pump is that the latter has a significantly wider area of bursting in which a reduction in ḡ_NaP at constant g_tonic can produce a switch from bursting to tonic spiking (see in Fig. 1B2), which can explain how riluzole-sensitive intrinsic bursters can become tonically spikingafter application of riluzole (see Fig. 4B4 and Peña et al., 2004). This feature is incompatible with the first model in which burst termination is based only on I_NaP inactivation (Fig. 1A2).

4.2 I_CAN-Dependent Bursting

The essential role of I_CAN in rhythm generation in the pre-BötC in vitro has been suggested as a plausible alternative to I_NaP-dependent mechanisms. Specifically, a metabotropic mechanism has been hypothesized suggesting that synaptically activated metabotropic glutamate receptors (mGluRs) explicitly trigger an IP₃-mediated intracellular Ca²⁺ release, which in turn activates I_CAN (Pace and Del Negro, 2008; Pace et al., 2007).

An important issue in this hypothesized mechanism concerns the onset of bursting, that is, the initial membrane depolarization that initiates spiking. Do synaptically activated mGluRs directly evoke an IP -dependent intracellular Ca² release leading to [Ca²⁺]_in accumulation which in turn activates I_CAN providing membrane depolarization initiating the burst (metabotropic burst-initiating mechanism), or does the synaptic activation by ionotropic mechanisms explicitly cause a necessary membrane depolarization, which evokes an IP -dependent intracellular Ca² release that activates I_CAN?

In the former case (metabotropic burst-initiating mechanism), we should expect a critical role of metabotropic glutamate receptor activation, which is not supported by recent studies showing that bursting in the pre-BötC network persists following the blockade of group I mGluRs (Ben-Mabrouk et al., 2012). In this case, we should also expect dynamic (phasic) changes of IP₃ production within a time scale comparable with the temporal characteristics of bursting. Although it has been shown that a transient stimulation of glutamate receptors could induce calcium-activated currents (e.g., Anwyl, 1999; Berridge, 1998), this effect occurs on a time scale of hundreds of milliseconds or slower, which is not compatible with the temporal characteristics of burst initiation considered here. Therefore, the dynamic IP₃ changes per se probably do not play a major/critical role here and may be ignored. The IP₃ changes, however, may be important in slower processes, for example, they can mediate the effects of neuromodulators.

In the latter case (ionotropic burst-initiating mechanism), the synaptically evoked membrane depolarization by glutamate receptor activation can activate voltagegated calcium currents providing an initial accumulation of [Ca²⁺]_in. The latter can initiate the IP₃-dependent CICR mechanism (Berridge, 1998). For this reason, the latter mechanism does not necessarily require changes in the IP₃ concentration. In this connection, Pace and Del Negro (2008) have confirmed a critical involvement of both the influx of calcium through voltage-gated calcium channels and the CICR-based mechanism in the activation of I_CAN in pre-BötC bursting at the single-neuron level. Here, it is worthy to recall that the idea of an important role of I_CAN in the pre-BötC bursting was earlier proposed by Peña et al. (2004), who demonstrated that rhythmic activity in the Cd²⁺-sensitive intrinsic bursters could be blocked by the I_CAN blocker FFA, and that a combined application of riluzole and FFA abolished rhythmic bursting in the pre-BötC. Later Pace et al. (2007) reported that evenapplication of FFA alone (without riluzole) could stop the rhythm in the slice, hence suggesting that I_CAN alone (i.e., without I_NaP) could be sufficient for bursting in the pre-BötC. However, the possible nonspecific effects of FFA at the concentration used (300 μM) do not warrant this conclusion, especially since FFA at such a high concentration has also been shown to affect sodium channels, by reducing sodium current availability and slowing down sodium channel inactivation (Yau et al., 2010). Moreover, Beltran-Parrazal et al. (2012) have recently reported that IP₃-dependent Ca²⁺ release from internal stores does not really contribute to rhythm generation in the pre-BötC.

Yet, the important finding of Peña et al. (2004) was that Ca²⁺ influx through voltage-gated calcium channels was actually necessary for I_CAN-dependent bursting, since the latter could be abolished by the calcium current blocker Cd²⁺. This allows the suggestion that the [Ca²⁺]_in necessary for I_CAN activation is actually provided by voltage-gated calcium currents. The plausibility of this suggestion has been demonstrated with our model, in which I_CAN-dependent bursting can be abolished in both cases, when either ḡ_CAN = 0 or ḡ_Ca = 0, which is consistent with the results of both Peña et al. (2004) and Pace and Del Negro (2008).

4.3 State/Preparation Dependence of I_NaP- and I_CAN-Dependent Bursting

Despite the decades of intensive investigations, the neural mechanisms responsible for rhythmic bursting in the pre-BötC in vitro are still debated in the literature. The wide spectrum of opinions (explicitly or implicitly supported by some experimental data) ranges from the suggestion of a critical role of I_NaP in pre-BötC bursting (Butera et al., 1999a; Del Negro et al., 2002a; Koizumi and Smith, 2008; Rybak et al., 2003b) to the principal rejection of the role of this current (Del Negro et al., 2002b, 2005) and from the suggestion of critical involvement of I_CAN synaptically activated via ionotropic or metabotropic (or both) mechanisms (Crowder et al., 2007; Krey et al., 2010; Pace and Del Negro, 2008; Pace et al., 2007) to the experimentally justified critiques of this idea (Beltran-Parrazal et al., 2012; Ben-Mabrouk et al., 2012). In this modeling study, we addressed these seemingly conflicting concepts and data and attempted to integrate them and investigate them in a common computational framework. In contrast to previous computational models investigating the possible roles of I_NaP- and I_CAN-dependent bursting mechanisms, in which these currents were included together in the same model of single pre-BötC neurons (Dunmyre et al., 2011; Rubin et al., 2009; Toporikova and Butera, 2011), we principally considered models of heterogeneous neural populations, in which key neuronal biophysical properties defining these bursting mechanisms were randomly distributed across neurons of the population. Therefore, after the initial random distribution of persistent sodium, calcium, and leak conductances, the entire neural population contained subpopulations of neurons whose intrinsic bursting activity (when synaptically uncoupled) critically depended on either I_NaP, or I_CAN, or both of these currents, or could not be evoked at all (Figs. 3 and 4), which is consistent with theexisting experimental data (e.g., Peña et al., 2004; see Fig. 4A4–C4 and A5–C5; Thoby-Brisson and Ramirez, 2001).

In the coupled case, we have shown that depending on the level of neuronal excitation in the network (defined by external tonic excitatory drive to all neurons) and the strength of synaptic interactions within the population (defined by the size of the network and weights of synaptic interactions), the population can generate bursting activity that critically depends on I_NaP, or on either I_NaP or I_CAN, or be independent of both of these currents (Figs. 5 and 6, and specifically Fig. 6E). We consider this as an important result of our study that may resolve the long-standing debate about which of the intrinsic mechanisms proposed from different studies and preparations, I_NaP or I_CAN dependent, is necessary and which is not necessary for rhythm generation in the pre-BötC in vitro.

In this regard, the conclusion from our simulations is that the necessity of these currents for the generation of this rhythmic activity is not absolute but depends on many factors, including the neuronal excitability, network size (number of neurons), and strength of excitatory synaptic interactions. The necessity of I_NaP and I_CAN for rhythm generation in the pre-BötC in vitro may also depend on the experimental preparation, animal type (rat or mouse) and age (reflecting developmental differences in expression of neuronal ionic channels), thickness of the slices used (reflecting numbers of interacting neurons and their synaptic connections as well as sources of tonic excitation), and experimental conditions, such as the metabolic state and extracellular ionic concentrations. Specifically, our simulations give an example of how an increase in the population size or interactions (i.e., an increase in N.w̄) at a relatively constant excitability (g_tonic) can cause a transition from an I_NaP-dependent bursting (abolished at ḡ_NaP = 0, simulating the effect of riluzole; Fig. 5A2,A4) to a bursting activity involving neuronal and excitatory synaptic mechanisms, which can be abolished only if both of the currents are blocked (Fig. 5B2-B4, see also a corresponding representation in Fig. 6E). A similar transition can also be produced by an increase in neuronal excitation (g_tonic) while holding total synaptic weight constant (see Fig. 6E). Moreover, our simulations have shown that at high g_tonic, population bursting can be generated even if both I_NaP and I_CAN are blocked (see Fig. 6E). In our opinion, this modeling result is consistent with, and may provide an explanation for, the experimental findings of Del Negro et al. (2005), who showed that after rhythmic bursting in the pre-BötC was blocked by both FFA and riluzole it could be restored by substance-P, a neuromodulator that can produce strong neuronal excitation by mechanisms not involving I_NaP or I_CAN (e.g., Koizumi and Smith, 2008; Peña and Ramirez, 2004).

4.4 Burst-Terminating Mechanisms and “Group Pacemaker” Hypothesis

The burst-terminating mechanism which is critical for bursting in the largest part of the bursting regions determined in the present model (Fig. 6) is based on a strong accumulation of [Na⁺]_in followed by activation of the Na⁺/K⁺ pump. Another[Na⁺]_in-dependent burst-terminating mechanism could be based on a Na⁺-activated potassium current (Krey et al., 2010; Wallen et al., 2007; Yuan et al., 2003), which was not considered in the present model. The plausibility of [Na⁺]_in-dependent burst termination in pre-BötC bursting in vitro, and specifically the plausibility of the Na⁺/K⁺ pump-based mechanism, has been indirectly supported by recent experimental studies (Krey et al., 2010) and requires further investigation. According to our model, the [Na⁺]_in accumulation can be provided by several cellular mechanisms, such as those involving I_NaP and I_CAN, or network interactions, which if they are strong enough (defined by Nw̄) could allow [Na⁺]_in accumulation via neuronal depolarization and fast sodium currents (I_Na), sufficient to activate the Na⁺/K⁺ pump-dependent burst-terminating mechanism. Correspondingly, our simulations have demonstrated a large region in the (g_tonic, N w) parameter space where bursting can occur even if I_NaP=I_CAN=0 (Fig. 6D,E). Interestingly, this emergent, network interactions-dependent bursting (that cannot be generated by single neurons) may reflect a so-called group-pacemaker mechanism (Rekling and Feldman, 1998). In this case, such a group-pacemaker bursting mechanism would have burst initiation provided by recurrent excitation via excitatory synaptic network interactions and burst termination provided by a Na⁺/K⁺ pump-dependent burst-terminating mechanism in each neuron. Moreover, generation of such group-pacemaker bursting does not need I_CAN, nor does it require any additional neuronal/network properties such as the depolarization block and associated transient depression of network synaptic interactions suggested by Rubin et al. (2009).

4.5 Model Limitations and Modeling Predictions

As with any other models, our model has a number of limitations which could affect our conclusions. Specifically, we only considered networks with all-to-all excitatory interactions and have not simulated physiologically more realistic networks with sparser connections between the neurons. We have only considered single-compartment models of individual neurons, although a consideration of two- and multicompartment neuronal models with ionic channels and other cellular properties distributed over neuronal compartments could potentially provide other single neuron and network behaviors not available with the single-compartment representation.

One of the predictions of our model is that the rhythm-generating mechanism operating in the pre-BötC excitatory network is state dependent. It may depend on the general level of neuronal excitation in the network (provided by external excitatory drive) and strength of synaptic interactions within the network. Hence, the critical involvement of a particular cellular mechanism in the population bursting may depend on the particular conditions, for example, those defining the average neuronal excitation in the network. Specifically, blocking I_NaP could effectively abolish the population bursting generated at a lower neuronal excitation in the network, whereas at a higher neuronal excitation, the cessation of the population rhythm would require suppression of both I_NaP and I_CAN, and even after that, according to our model prediction, the population bursting can be recovered by a subsequent further increase of neuronal excitation in the network (see Fig. 6E).

We also note that many of our results are based on the assumption that free sodium ions ([Na⁺]_in) are accumulated during cellular activity (i.e., during bursts) and activate a [Na⁺]_in-dependent burst-terminating mechanism operating in each cell independently of the source of [Na⁺]_in accumulation. We also suggest that this [Na⁺]_in-dependent burst-terminating mechanism is connected with the activation of the Na⁺/K⁺ pump. Moreover, at a high level of excitatory synaptic interactions in the network, bursting can occur without I_NaP and I_CAN (see Fig. 6D,E). However, such bursting, which is based entirely on excitatory neural interactions and the Na⁺/K⁺ pump-dependent burst termination, can occur only at a sufficiently high strength of synaptic interactions (as defined by Nw̄) and thus may not occur in networks with sparse or weak interconnections (low Nw̄). Note that a similar model and concept can, in principle, be developed with another [Na⁺]_in-activated burst-terminating mechanism based on a [Na⁺]_in-activated potassium current, which could perform a function similar to that of the Na⁺/K⁺ pump in the current model. However, despite some indirect support (Krey et al., 2010), these [Na⁺]_in-activated mechanisms remain highly hypothetical and are considered as model predictions requiring more thorough experimental investigations and testing.

In summary, we suggest that our analysis represents an important step forward in understanding the integration at the network level of a number of currently proposed cellular and network properties for the generation of Na⁺ and Ca²⁺-dependent rhythms in the pre-BötC, and possibly in other brainstem or spinal networks.