Abstract
It has been shown that, for women aged 50 years or older, the discriminatory accuracy of the Breast Cancer Risk Prediction Tool (BCRAT) can be modestly improved by the inclusion of information on common single nucleotide polymorphisms (SNPs) that are associated with increased breast cancer risk. We aimed to determine whether a similar improvement is seen for earlier onset disease. We used the Australian Breast Cancer Family Registry to study a population-based sample of 962 cases aged 35 to 59 years and 463 controls frequency matched for age and for whom genotyping data was available.
Overall, the inclusion of data on seven SNPs improved the area under the receiver operating characteristic curve (AUC) from 0.58 (95% confidence interval [CI]=0.55–0.61) for BCRAT alone to 0.61 (95% CI=0.58–0.64) for BCRAT and SNP data combined (p<0.001). For women aged 35 to 39 years at interview, the corresponding improvement in AUC was from 0.61 (95% CI=0.56–0.66) to 0.65 (95% CI=0.60–0.70; p=0.03), while for women aged 40 to 49 years at diagnosis, the AUC improved from 0.61 (95% CI=0.55–0.66) to 0.63 (95% CI=0.57–0.69; p=0.04). Using previously used classifications of low, intermediate and high risk, 2.1% of cases and none of the controls aged 35 to 39 years, and 10.9% of cases and 4.0% of controls aged 40 to 49 years were classified into a higher risk group.
Including information on seven SNPs associated with breast cancer risk improves the discriminatory accuracy of BCRAT for women aged 35 to 39 years and 40 to 49 years. Given the low absolute risk for women in these age groups, only a small proportion are reclassified into a higher category for predicted 5-year risk of breast cancer.
Keywords: Breast cancer, risk prediction, single nucleotide polymorphism, Breast Cancer Risk Assessment Tool
Introduction
In a clinical setting, breast cancer risk prediction models are used to estimate a woman’s risk of breast cancer, and some models also estimate the probability that she carries a mutation in BRCA1 or BRCA2. This information can be used to help her make decisions on screening or prevention that are tailored to her circumstances. On a population basis, identification of women at differing risk of breast cancer allows resources for screening and prevention programs to be better targeted and be more cost-effective. A number of breast cancer risk prediction models have been developed, all of which use age and family history of breast cancer as predictors. The different models vary in their use of other risk factors as predictors, and can include some or all of: family history of other cancers; known mutation status for BRCA1 and BRCA2; and measured environmental and lifestyle factors [1].
The National Cancer Institute’s Breast Cancer Risk Assessment Tool (BCRAT), originally published as the as the Gail model [2] and later modified [3], has become a popular clinical tool for estimating the five-year risk of invasive breast cancer for unaffected women aged 35 years or older. BCRAT was developed using logistic regression analysis of a large case-control study of white women from the United States. It uses established breast cancer risk factors (current age, number of affected first-degree relatives, age at menarche, age at first live birth, number of biopsies and presence of atypical hyperplasia) to estimate risk, but it does not take into account any mutations in breast cancer susceptibility genes. BCRAT has been validated using large population-based studies; it has been shown to be well calibrated to assess risk for groups of women, but it discriminates less well for individual risk assessment, especially for high-risk populations [1].
Because of the clinical usefulness of accurate individual breast cancer risk predictions, there has been interest in whether BCRAT can be improved by including information on other risk factors. For example, the inclusion of information on mammographic density, a heritable risk factor for breast cancer, resulted in a modest improvement in the discriminatory accuracy of BCRAT [4,5].
More recently, attention has turned to whether BCRAT is improved by including information on common single nucleotide polymorphisms (SNPs) that have been found to be associated with risk of breast cancer. Previous modelling and empirical research has reported a modest improvement in the discriminatory accuracy of BCRAT, as measured by the area under the receiver operating characteristic curve (AUC) [6–8], as well as improvement in the classification of women into high-risk groups [7,9,10].
It is not known whether combining SNP data with BCRAT affects the performance of the risk predictions for all women. Previous research has been limited to women aged 50 years and older [7,8], or has been limited in the scope of its analyses to assessment of changes in the AUC [10]. In this study, we investigate the effect of combining data from seven established breast cancer SNPs to the risk predictions from BCRAT for Australian women aged 35 to 59 years, in terms of calibration, discriminatory accuracy and risk group reclassification.
Methods
Australian Breast Cancer Family Registry
We studied cases and controls recruited to the Australian Breast Cancer Family Registry (ABCFR), which includes a population-based case-control-family study that has been described in detail previously [11–14]. Briefly, between 1992 and 1998, the ABCFR used the state population-based cancer registries in New South Wales and Victoria to recruit women who had incident diagnoses of histologically-confirmed first primary invasive breast cancer. Recruitment was limited to women living in metropolitan Sydney or Melbourne and included all women aged less than 40 years at diagnosis and a random sample of women aged 40 to 59 years at diagnosis. Controls were randomly selected from the electoral roll (for which registration is compulsory for all adult Australian citizens) and were from the same geographic regions and had the same age distribution as the cases.
A total of 1578 cases and 1021 controls were recruited to the ABCFR. All participants completed an interviewer-administered risk factor questionnaire and family history questionnaire that asked for details of any cancer diagnosis for themselves and for their first-degree and second-degree relatives. Participants were also asked to provide a small blood sample.
Approval for the study was obtained from the Human Research Ethics Committees of the University of Melbourne and the Cancer Councils of Victoria and New South Wales. All participants provided written informed consent before participation in the study.
SNP selection and genotyping
The seven SNPs used in this study were those included in the study by Mealiffe et al. [7]. These SNPs had been chosen because they had statistically significant associations with breast cancer that had been first identified by genome-wide association studies and independently confirmed by large case-control studies [15–17].
All cases and controls who had donated a blood sample were genotyped for the seven SNPs with the TaqMan assay (Applied Biosystems) using a 384 well format on a LightCycler480, and data were interpreted using LightCycler480 1.5.0 software (Roche Diagnostics, Castle Hill, Australia). Quality control was conducted as described in Easton et al. [15] and included a 2% replicate sample genotyping with >98% concordance and Sanger sequence confirmation of representative samples of each genotype.
Calculation of risk scores
We used BCRAT [2,3] to estimate the five-year absolute risk of invasive breast cancer for all cases aged 35 years or older at diagnosis and for all controls aged 35 years or older at interview. The BCRAT risk score was based on age, ethnicity, age at menarche, age at birth of first child and number of first-degree relatives with breast cancer. No information on the number of biopsies or presence of atypical hyperplasia was available and these variables were therefore coded as unknown for all participants. We obtained the BCRAT C# source code from http://www.cancer.gov/bcrisktool/ and extended it to facilitate automatic batch processing.1
Using the approach described in Mealiffe et al. [7] based on the assumption of independence of additive risks on the log OR scale, we calculated SNP risk score using previously published odds ratios (ORs) and risk-allele frequencies [15–17], summarised in Table 1 of Mealiffe et al. [7]. For each SNP, the unscaled population average risk was calculated as μ = (1 − p)2 + 2p(1 − p)OR + p2OR2, where p is the allele frequency of the high-risk allele, B, and OR is the previously published OR for the B allele versus the A allele. We then calculated adjusted risk values (with a population average risk equal to 1) as 1/μ, OR/μ and OR2/μ for the genotypes AA, AB and BB. The SNP risk score was calculated by multiplying the adjusted risk values for each of the seven SNPs. As in Mealiffe et al. [7], the combined risk score was calculated by multiplying the SNP risk score and the BCRAT risk score, under the assumption of independence.
Statistical Methods
We used logistic regression to estimate ORs and 95% confidence intervals (CIs) for the associations with breast cancer risk for: the individual variables used in the calculation of the BCRAT score; the individual SNP genotypes; and the logarithms of the BCRAT risk score, SNP risk score and combined risk score. For each of the seven SNPs, we calculated risk-allele frequencies and p-values under Hardy–Weinberg equilibrium for both cases and controls.
The performance of a risk prediction model is measured by its ability to accurately estimate population risk and individual risk. For populations, the calibration of a model is measured by comparing the overall numbers of observed and expected events [1,18]. For individual risk, the discriminatory accuracy of a model (the balance between sensitivity and specificity) is measured by the AUC [1,18], with an AUC of between 0.7 and 0.8 considered to be good discriminatory accuracy [1].
For the BCRAT risk score, SNP risk score and combined risk score, we used the Hosmer–Lemeshow goodness-of-fit test to assess the calibration by comparing the observed and expected numbers of cases and controls within groups defined by deciles of risk. We used Pearson correlation to test the independence of the BCRAT risk score and the SNP risk score. To assess the discriminatory accuracy, we used receiver operating characteristic curves and calculated the AUC for the BCRAT risk score, the SNP risk score and the combined risk score. We used bootstrap resampling to calculate confidence intervals for the AUC and confidence intervals and p-values for differences in AUC.
As in Mealiffe et al. [7], we used reclassification tables to quantify differences in classification of the BCRAT risk score and the combined risk score into groups defined as: low (<1.5%), intermediate (≥1.5% and <2.0%), and high (≥2.0%). Net reclassification improvement (NRI) was calculated as the sum of: the proportion of cases moving to a higher risk category and the proportion of controls moving to a lower risk category minus the proportion of cases moving to a lower risk category and the proportion of controls moving to a higher risk category. To test the hypothesis that NRI=0, we used an asymptotic Z test.
Statistical analyses were performed overall (using all case-control data), and stratified by age group (35 to 39 years, 40 to 49 years and 50 to 59 years), based on age at diagnosis for cases and age at interview for controls. All statistical tests were two-sided and p-values <0.05 were considered nominally statistically significant. All statistical analyses were conducted using Stata Release 12 [19].
Results
A total of 962 cases and 463 controls were eligible for inclusion in the present study because they were aged 35 years or older (at diagnosis for cases and at interview for controls) and had genotyping results for at least four of the seven SNPs being studied. For cases and controls, the distributions of the SNP genotypes and the questionnaire variables used in the calculation of the BCRAT risk score are shown in Table 1. For cases, the mean age at diagnosis was 45.9 years (standard deviation=7.5), and for controls, the mean age at interview was 44.2 years (standard deviation=7.4). Table 2 shows, for the high-risk allele of each of the SNPs, the allele frequency and p-value for Hardy–Weinberg equilibrium for cases and controls as well as the OR, 95% CI and p-value for breast cancer risk, overall and stratified by age group.
Table 1.
Distribution of questionnaire variables and SNP genotypes for cases and controls
| Case (N=962) | Control (N=463) | |||
|---|---|---|---|---|
| N | (%) | N | (%) | |
| Age* (years) | ||||
| 35 to 39 | 333 | (34.6) | 182 | (39.3) |
| 40 to 49 | 322 | (33.5) | 151 | (32.6) |
| 50 to 59 | 307 | (31.9) | 130 | (28.1) |
|
| ||||
| Number of first-degree relatives with breast cancer | ||||
| 0 | 830 | (86.3) | 427 | (92.2) |
| ≥1 | 132 | (13.7) | 36 | (7.8) |
|
| ||||
| Age at menarche (years) | ||||
| <12 | 181 | (18.8) | 86 | (18.6) |
| 12 | 205 | (21.3) | 110 | (23.8) |
| 13 | 281 | (29.2) | 125 | (27.0) |
| ≥14 | 293 | (30.5) | 140 | (30.2) |
| Missing | 2 | (0.2) | 2 | (0.4) |
|
| ||||
| Age at birth of first child (years) | ||||
| <20 | 91 | (9.5) | 46 | (9.9) |
| 20 to 24 | 259 | (26.9) | 128 | (27.6) |
| 25 to 29 | 278 | (28.9) | 132 | (28.5) |
| ≥30 | 155 | (16.1) | 90 | (19.4) |
| No term pregnancy | 179 | (18.6) | 67 | (14.5) |
|
| ||||
| Ethnicity | ||||
| White | 882 | (91.7) | 383 | (82.7) |
| Other | 68 | (7.1) | 37 | (8.0) |
| Missing | 12 | (1.2) | 43 | (9.3) |
|
| ||||
| Estrogen receptor | ||||
| Negative | 151 | (15.7) | ||
| Positive | 298 | (31.0) | ||
| Missing | 513 | (53.3) | ||
|
| ||||
| Progesterone receptor | ||||
| Negative | 143 | (14.9) | ||
| Positive | 306 | (31.8) | ||
| Missing | 513 | (53.3) | ||
|
| ||||
| rs2981582 (FGFR2) | ||||
| CC | 305 | (31.7) | 141 | (30.5) |
| CT | 461 | (47.9) | 247 | (53.4) |
| TT | 186 | (19.3) | 67 | (14.5) |
| Missing | 10 | (1.0) | 8 | (1.7) |
|
| ||||
| rs3803662 (TOX3) | ||||
| CC | 437 | (45.4) | 246 | (53.1) |
| CT | 408 | (42.4) | 177 | (38.2) |
| TT | 109 | (11.3) | 37 | (8.0) |
| Missing | 8 | (0.8) | 3 | (0.7) |
|
| ||||
| rs889312 (MAP3K1) | ||||
| AA | 432 | (44.9) | 227 | (49.0) |
| AC | 404 | (42.0) | 186 | (40.2) |
| CC | 113 | (11.8) | 44 | (9.5) |
| Missing | 13 | (1.4) | 6 | (1.3) |
|
| ||||
| rs13387042 (2q35) | ||||
| GG | 237 | (24.6) | 131 | (28.3) |
| GA | 456 | (47.4) | 210 | (45.4) |
| AA | 263 | (27.3) | 121 | (26.1) |
| Missing | 6 | (0.6) | 1 | (0.2) |
|
| ||||
| rs13281615 (8q24) | ||||
| AA | 295 | (30.7) | 163 | (35.2) |
| AG | 432 | (44.9) | 209 | (45.1) |
| GG | 210 | (21.8) | 66 | (14.3) |
| Missing | 25 | (2.6) | 25 | (5.4) |
|
| ||||
| rs4415084 (FGF10) | ||||
| CC | 263 | (27.3) | 158 | (24.1) |
| CT | 437 | (45.4) | 196 | (42.3) |
| TT | 178 | (18.5) | 73 | (15.8) |
| Missing | 84 | (8.7) | 36 | (7.8) |
|
| ||||
| rs3817198 (LSP1) | ||||
| TT | 413 | (42.9) | 215 | (46.4) |
| TC | 419 | (43.6) | 191 | (41.3) |
| CC | 116 | (12.1) | 52 | (11.2) |
| Missing | 14 | (1.5) | 5 | (1.1) |
Age at diagnosis for cases, age at interview for controls
Table 2.
Risk-allele frequencies, p-values for Hardy–Weinberg equilibrium and associations with breast cancer for each SNP, overall and stratified by age group
| SNP | Case | Control | OR | (95% CI) | p | ||
|---|---|---|---|---|---|---|---|
| Freq. | PHWE | Freq. | PHWE | ||||
| All* | |||||||
| rs2981582 (FGFR2) | 0.44 | 0.6 | 0.42 | 0.01 | 1.09 | (0.93–1.28) | 0.3 |
| rs3803662 (TOX3) | 0.33 | 0.4 | 0.27 | 0.5 | 1.31 | (1.10–1.55) | 0.002 |
| rs889312 (MAP3K1) | 0.33 | 0.2 | 0.30 | 0.5 | 1.15 | (0.97–1.36) | 0.1 |
| rs13387042 (2q35) | 0.51 | 0.2 | 0.49 | 0.05 | 1.09 | (0.94–1.27) | 0.3 |
| rs13281615 (8q24) | 0.45 | 0.03 | 0.39 | 0.9 | 1.29 | (1.10–1.51) | 0.002 |
| rs4415084 (FGF10) | 0.45 | 0.9 | 0.40 | 0.4 | 1.24 | (1.05–1.46) | 0.01 |
| rs3817198 (LSP1) | 0.34 | 0.5 | 0.32 | 0.3 | 1.11 | (0.94–1.31) | 0.2 |
|
| |||||||
| Aged 35 to 39 years | |||||||
| rs2981582 (FGFR2) | 0.48 | 0.5 | 0.41 | 0.4 | 1.32 | (1.01–1.73) | 0.04 |
| rs3803662 (TOX3) | 0.35 | 0.3 | 0.31 | 0.7 | 1.18 | (0.90–1.55) | 0.2 |
| rs889312 (MAP3K1) | 0.32 | 0.9 | 0.33 | 0.2 | 0.95 | (0.72–1.25) | 0.7 |
| rs13387042 (2q35) | 0.53 | 0.08 | 0.43 | 1.0 | 1.43 | (1.11–1.84) | 0.005 |
| rs13281615 (8q24) | 0.44 | 0.05 | 0.37 | 0.2 | 1.32 | (1.01–1.72) | 0.04 |
| rs4415084 (FGF10) | 0.45 | 0.4 | 0.41 | 0.6 | 1.19 | (0.90–1.58) | 0.2 |
| rs3817198 (LSP1) | 0.35 | 0.7 | 0.37 | 0.3 | 0.93 | (0.72–1.22) | 0.6 |
|
| |||||||
| Aged 40 to 49 years | |||||||
| rs2981582 (FGFR2) | 0.43 | 0.3 | 0.42 | 0.2 | 1.01 | (0.77–1.33) | 0.9 |
| rs3803662 (TOX3) | 0.34 | 0.4 | 0.27 | 0.3 | 1.40 | (1.03–1.90) | 0.03 |
| rs889312 (MAP3K1) | 0.33 | 0.2 | 0.25 | 0.004 | 1.43 | (1.07–1.92) | 0.02 |
| rs13387042 (2q35) | 0.52 | 1.0 | 0.50 | 0.02 | 1.07 | (0.82–1.39) | 0.6 |
| rs13281615 (8q24) | 0.48 | 0.8 | 0.40 | 0.7 | 1.39 | (1.05–1.85) | 0.02 |
| rs4415084 (FGF10) | 0.46 | 1.0 | 0.41 | 0.2 | 1.24 | (0.93–1.65) | 0.2 |
| rs3817198 (LSP1) | 0.33 | 0.5 | 0.29 | 1.0 | 1.21 | (0.90–1.62) | 0.2 |
|
| |||||||
| Aged 50 to 59 years | |||||||
| rs2981582 (FGFR2) | 0.41 | 0.8 | 0.42 | 0.04 | 0.93 | (0.69–1.26) | 0.7 |
| rs3803662 (TOX3) | 0.30 | 0.1 | 0.23 | 0.6 | 1.40 | (1.01–1.94) | 0.04 |
| rs889312 (MAP3K1) | 0.34 | 0.5 | 0.31 | 0.8 | 1.14 | (0.84–1.56) | 0.4 |
| rs13387042 (2q35) | 0.50 | 0.5 | 0.56 | 0.52 | 0.79 | (0.59–1.05) | 0.1 |
| rs13281615 (8q24) | 0.44 | 0.05 | 0.40 | 0.5 | 1.16 | (0.87–1.54) | 0.3 |
| rs4415084 (FGF10) | 0.44 | 0.7 | 0.38 | 0.02 | 1.28 | (0.95–1.72) | 0.1 |
| rs3817198 (LSP1) | 0.34 | 0.5 | 0.29 | 0.9 | 1.27 | (0.93–1.73) | 0.1 |
ORs adjusted for age group
Freq. = frequency of high-risk allele
PHWE = p-value for Hardy–Weinberg equilibrium
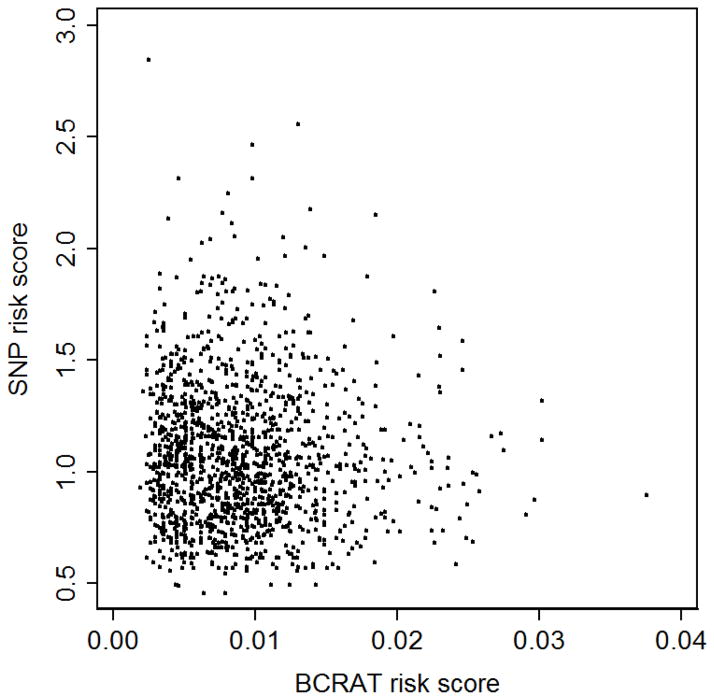
After log transformation, the three risk scores were associated with breast cancer overall, and for the subgroups of women aged 35 to 39 years and 40 to 49 years (both p<0.01; Table 3). For women aged 50 to 59 years, there was an association with breast cancer for the combined risk score (p=0.03), marginal evidence for an association for the BCRAT risk score (p=0.06), but no association for the SNP risk score (p=0.3). There was no correlation between the BCRAT risk score and the SNP risk score overall (R2= −0.04, p=0.1; Figure 1), or for the subgroups of women aged 35 to 39 years (R2= −0.02, p=0.1), aged 40 to 49 years (R2= −0.01, p=0.8) or aged 50 to 59 years (R2= −0.02, p=0.7).
Table 3.
Association between log-transformed risk scores and breast cancer, overall and stratified by age group
| OR | (95% CI) | p | χ2** | p | |
|---|---|---|---|---|---|
| All* | |||||
| Log (BCRAT risk score) | 2.74 | (1.93–3.89) | <0.001 | 3.34 | 0.9 |
| Log (SNP risk score) | 2.55 | (1.70–3.82) | <0.001 | 7.27 | 0.5 |
| Log (Combined risk score) | 2.74 | (2.09–3.60) | <0.001 | 6.25 | 0.6 |
|
| |||||
| Aged 35 to 39 years | |||||
| Log (BCRAT risk score) | 3.17 | (1.83–5.49) | <0.001 | 9.79 | 0.3 |
| Log (SNP risk score) | 3.50 | (1.78–6.86) | <0.001 | 12.89 | 0.1 |
| Log (Combined risk score) | 3.59 | (2.27–5.68) | <0.001 | 7.74 | 0.5 |
|
| |||||
| Aged 40 to 49 years | |||||
| Log (BCRAT risk score) | 3.47 | (1.80–6.71) | <0.001 | 7.78 | 0.5 |
| Log (SNP risk score) | 2.94 | (1.45–5.97) | 0.003 | 10.31 | 0.2 |
| Log (Combined risk score) | 3.30 | (2.00–5.43) | <0.001 | 14.81 | 0.06 |
|
| |||||
| Aged 50 to 59 years | |||||
| Log (BCRAT risk score) | 1.90 | (0.98–3.71) | 0.06 | 7.96 | 0.4 |
| Log (SNP risk score) | 1.51 | (0.74–3.10) | 0.3 | 3.80 | 0.9 |
| Log (Combined risk score) | 1.72 | (1.05–2.81) | 0.03 | 4.45 | 0.8 |
Adjusted for age group
Hosmer–Lemeshow χ2 goodness of fit test using 10 groups (8 df)
Fig. 1.
Scatterplot of the BCRAT risk score and the SNP risk score for all women
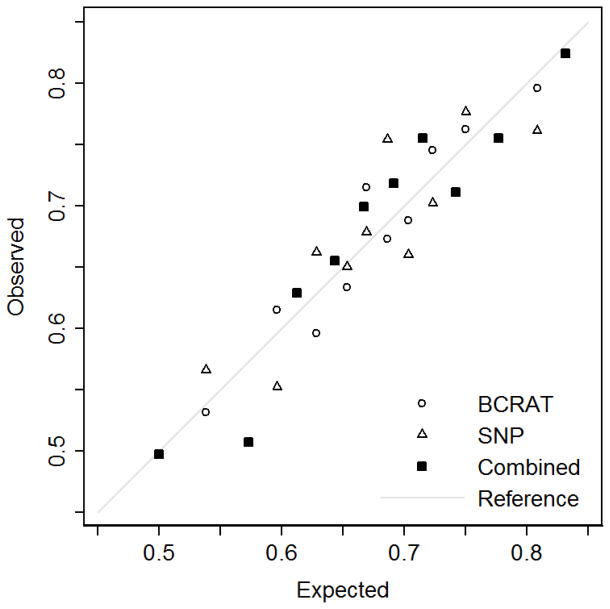
Table 3 shows that there was no evidence of poor calibration for the BCRAT risk score and the SNP risk score, overall and when stratified by age group (all p>0.1). For the combined risk score, there was marginal evidence of poor calibration for the subgroup aged 40 to 49 years (p=0.06), but not overall or for the other age groups (all p>0.5). Figure 2 shows the overall Hosmer–Lemeshow calibration plot of the proportions of observed and expected cases in groups defined by deciles.
Fig. 2.
Hosmer–Lemeshow calibration plot of the proportions of observed and expected cases for all women
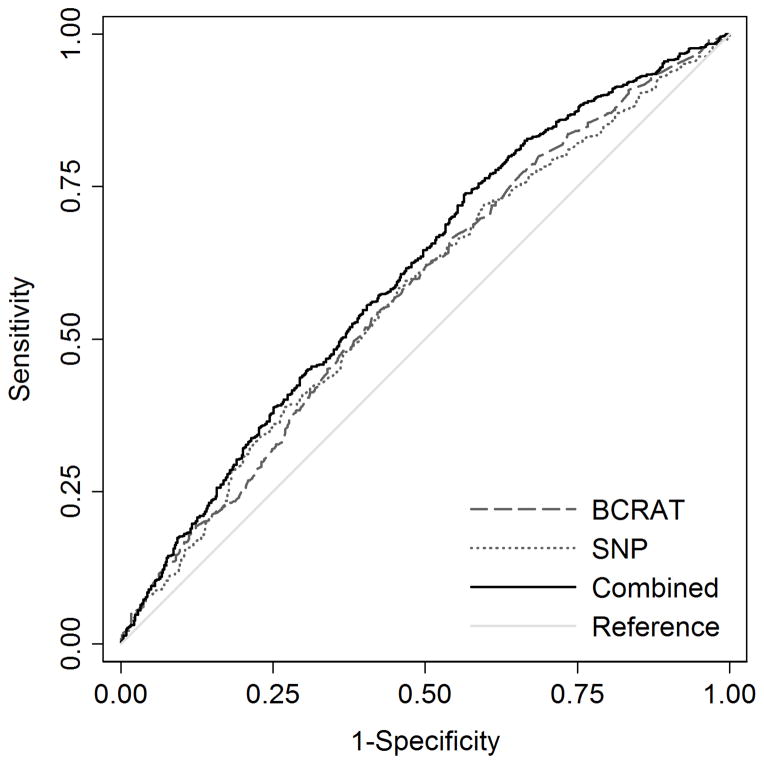
For all women, the ROC curves for the BCRAT risk score, the SNP risk score and the combined risk score are shown in Figure 1, and the corresponding AUCs and 95% CIs are shown in Table 4. The AUC of the combined risk score was greater than that of the BCRAT risk score (p<0.001). There was marginal evidence for a difference between the AUC for the combined risk score and the SNP risk score (p=0.06), but no difference between the AUC for the BCRAT risk score and the SNP risk score (p=1.0).
Table 4.
AUC and 95% CI for the BCRAT risk score, SNP risk score and combined risk score, overall and stratified by age group
| AUC | (95% CI) | |
|---|---|---|
| All | ||
| BCRAT risk score | 0.58 | (0.54–0.61) |
| SNP risk score | 0.57 | (0.54–0.61) |
| Combined risk score | 0.61 | (0.58–0.64) |
|
| ||
| Aged 35 to 39 years | ||
| BCRAT risk score | 0.60 | (0.55–0.65) |
| SNP risk score | 0.60 | (0.55–0.65) |
| Combined risk score | 0.65 | (0.60–0.70) |
|
| ||
| Aged 40 to 49 years | ||
| BCRAT risk score | 0.60 | (0.55–0.66) |
| SNP risk score | 0.58 | (0.53–0.64) |
| Combined risk score | 0.63 | (0.57–0.69) |
|
| ||
| Aged 50 to 59 years | ||
| BCRAT risk score | 0.54 | (0.48–0.60) |
| SNP risk score | 0.54 | (0.48–0.60) |
| Combined risk score | 0.56 | (0.51–0.62) |
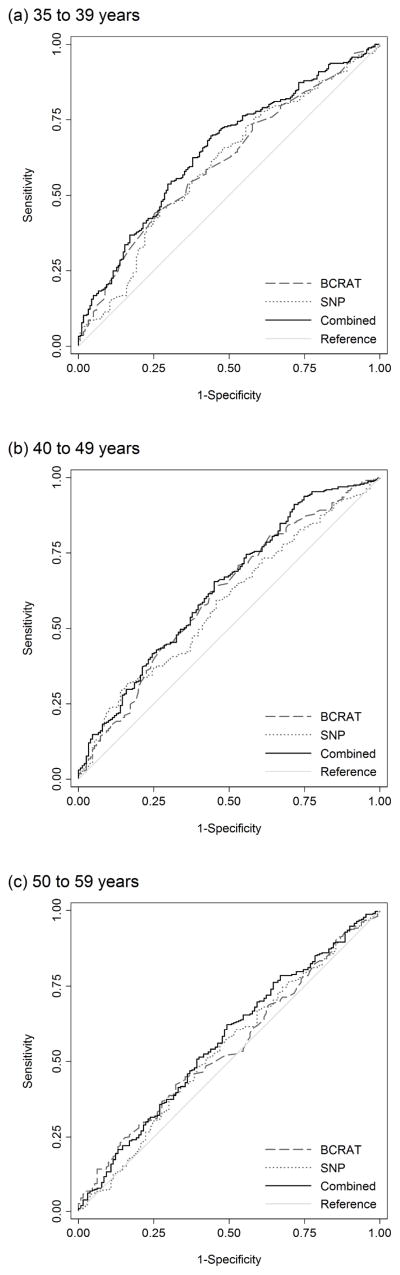
Figure 2 shows the ROC curves for the BCRAT risk score, the SNP risk score and the combined risk score for each of the subgroups of age at interview; the corresponding AUCs and 95% CIs are shown in Table 4. For the subgroup of women aged 35 to 39 years, the AUC for the combined risk score was greater than that of the BCRAT risk score (p=0.01). There was no difference in the AUCs for the combined risk score and the BCRAT risk score for women aged 40 to 49 years (p=0.2) or for women aged 50 to 59 years (p=0.3).
There were differences in the AUCs for the SNP risk score and combined risk score for women aged 35 to 39 years (p=0.03) and for women aged 40 to 49 years (p=0.04), but not for women aged 50 to 59 years (p=0.2). There were no differences in the AUCs for the SNP risk score and the BCRAT risk score for any of the age groups (35 to 39 years p=1.0; 40 to 49 years p=0.6; 50 to 59 years p=1.0).
Estrogen receptor (ER) and progesterone receptor (PR) status was available for 449 (46.7%) cases (298 ER+, 151 ER−, 306 PR+, 143 PR−). For the combined risk score, we found marginal evidence that the AUC for the ER+ subgroup (0.61, 95% CI=0.57–0.65) was higher than that of the ER− subgroup (0.55, 95% CI=0.49–0.59; p=0.07). For the BCRAT risk score and the SNP risk score, there were no differences in AUC by ER status (data not shown, both p>0.1). For PR status, there were no differences in the AUC for any of the three risk scores (data not shown, all p>0.2).
The BCRAT risk score and the combined risk score were both classified using categories defined as low risk (<1.5%), intermediate risk (≥1.5% and <2.0%) and high risk (≥2.0%) and are shown in Table 5. Using classifications based on the combined risk score, 103 (10.7%) cases and 28 (6.0%) controls were reclassified to a higher risk category, and 32 (3.3%) cases and 7 (1.5%) controls were reclassified to a lower risk category, than they had been based on classifications of the BCRAT risk score; the NRI, was 0.028 (p=0.5). Of women originally classified as intermediate risk on the BCRAT risk score, the NRI was 0.033 (p=0.5); 20 (28.6%) cases and 5 (23.8%) controls were reclassified into a higher risk category, while 21 (30.0%) cases and 6 (28.6%) controls were reclassified into a lower risk category using the combined risk score.
Table 5.
Classification of risk for the BCRAT risk score and the combined risk score, overall and stratified by age group
| Combined risk score | ||||||
|---|---|---|---|---|---|---|
| Cases
|
Controls
|
|||||
| BCRAT risk score | <1.5% | ≥1.5% and <2.0% | ≥2.0% | <1.5% | ≥1.5% and <2.0% | ≥2.0% |
| Overall | ||||||
| <1.5% | 769 | 66 | 17 | 411 | 18 | 5 |
| ≥1.5% and <2.0% | 21 | 29 | 20 | 6 | 10 | 5 |
| ≥2.0% | 2 | 9 | 29 | 0 | 1 | 7 |
|
| ||||||
| Aged 35 to 39 years | ||||||
| <1.5% | 323 | 7 | 1 | 182 | 0 | 0 |
| ≥1.5% and <2.0% | 1 | 1 | 0 | 0 | 0 | 0 |
| ≥2.0% | 0 | 0 | 0 | 0 | 0 | 0 |
|
| ||||||
| Aged 40 to 49 years | ||||||
| <1.5% | 267 | 22 | 4 | 139 | 4 | 1 |
| ≥1.5% and <2.0% | 7 | 12 | 9 | 4 | 2 | 1 |
| ≥2.0% | 0 | 0 | 1 | 0 | 0 | 0 |
|
| ||||||
| Aged 50 to 59 years | ||||||
| <1.5% | 179 | 37 | 12 | 90 | 14 | 4 |
| ≥1.5% and <2.0% | 13 | 16 | 11 | 2 | 8 | 4 |
| ≥2.0% | 2 | 9 | 28 | 0 | 1 | 7 |
For women aged 35 to 39 years, 97.3% of cases and 100% of controls were classified as low risk using both the combined risk score and the BCRAT risk score; 2.4% of cases were reclassified into a higher risk category using the combined risk score compared with the BCRAT risk score (NRI=0.021, p=0.4). For women aged 40 to 49 years, 82.9% of cases and 92.1% of controls were classified as low risk using both the combined risk score and the BCRAT risk score; 10.9% of cases and 4.0% of controls were reclassified into a higher risk category using the combined risk score compared with the BCRAT risk score (NRI=0.074, p=0.4). For women aged 50 to 59 years, 72.6% of cases and 80.8% of controls had the same classification using the BCRAT and combined risk scores; 19.5% of cases and 16.9% of controls were reclassified into a higher risk category, and 7.8% of cases and 2.3% of controls were reclassified into a lower risk category using the combined risk score compared with the BCRAT risk score (NRI= −0.029, p=0.5).
Discussion
We found that the log-transformed BCRAT risk score, SNP risk score and combined risk score were all associated with an increased risk of breast cancer, overall and when stratified by age group, except for the SNP risk score for women aged 50 to 59 years. The latter result is likely to be due to chance given that these SNPs have been shown to be associated with breast cancer by large case-control studies. For women aged 50 to 59 years, our estimated ORs were all within the CIs reported by Mealiffe et al. [7], but were higher for the BCRAT risk score, lower for the SNP risk score and similar for the combined risk score. The calculation of the combined risk score is based on the assumption that the BCRAT risk score and the SNP risk score are independent. We found no evidence of a correlation between the BCRAT risk score and the SNP risk score, overall or when stratified by age group.
The risk scores were all well calibrated, overall and when stratified by age group, with the possible exception of the combined risk score for women aged 40 to 49 years (p=0.06). For women aged 50 to 59 years, our results differed from those of Mealiffe et al. [7] who found that, while the SNP risk score was well calibrated, both the BCRAT risk score and the combined risk score were not.
We showed that, overall, the combined risk score provided a modest but statistically significant improvement in discriminatory accuracy over the BCRAT model, with an increase in the AUC from 0.58 to 0.61 (p<0.001). When stratified by age group, we found an improvement in discriminatory accuracy only for women aged 35 to 39 years, for whom the AUC increased from 0.61 to 0.65 (p=0.003). Mealiffe et al. [7] found an increase in the AUC from 0.56 to 0.59 using the combined risk score compared with the BCRAT risk score (p<0.001). In our study, for women aged 50 to 59 years, we found a similar AUC for the BCRAT risk score (0.55) but did not see an increase in the AUC using the combined risk score (0.56, p=0.4). Another study of women aged 50 years or more by Wacholder et al. [8] used data from 10 SNPs and reported that the AUC increased from 0.58 for the BCRAT risk score to 0.62 for the combined risk score (p<0.001). Using published data on relative risks and allele frequencies for seven SNPs, Gail [6] calculated that, for women aged over 50 years, combining SNP data with BCRAT risk scores would result in a modest improvement in the model’s discriminatory accuracy (increasing the AUC from 0.61 to 0.63).
Additional insight into the performance of risk prediction models can be obtained by looking at changes in classification of women into risk groups based on clinically important risk thresholds. We found little change in the classification of women aged 35 to 39 years and 40 to 49 years because the vast majority had a very low absolute risk of breast cancer that remained low using the combined risk score. For women aged 50 to 59 years, the group for which no improvement in discriminatory accuracy was seen, using the combined risk score resulted in changes to the risk group classifications (low, intermediate and high) for 27% of cases and 19% of controls. Using the same risk group thresholds, Mealiffe et al. [7] reported that 26% of cases and 14% of controls were reclassified into a higher risk group, and 14% of cases and 26% of controls were reclassified into a lower risk group using the combined risk score.
In the study by Wacholder et al. [8], the inclusion of data for 10 SNPs to BCRAT risk scores resulted in 20% of affected women being reclassified into lower, and 33% being reclassified into higher, risk groups defined by quintiles. Another study by Comen et al. [10] of reclassification improvement from combining SNP data with BCRAT risk predictions using unaffected women aged 25 to 85 years reported 20% being reclassified into lower, and 20% into higher, risk groups defined by quintiles. Further calculations by Gail [9] showed that, using a five-year breast cancer risk threshold of 2.0%, combining SNP data with BCRAT would result in 4.1% of unaffected women otherwise classified as low-risk being reclassified as high-risk, and 3.7% of unaffected women otherwise classified as high-risk being reclassified as low-risk.
In our study, two components of the BCRAT risk score, number of breast biopsies and atypical hyperplasia, were not available. While this may have resulted in underestimated AUCs for BCRAT and the combined risk score, our conclusions on the usefulness of combining SNP data with BRCAT assume that the associations between the SNP data and breast cancer risk are independent of the associations between BCRAT risk factors and breast cancer risk.
In summary, including information on seven SNPs associated with breast cancer risk improves the discriminatory accuracy of BCRAT for women aged 35 to 39 years and 40 to 49 years. Given the low absolute risk for women in these age groups, only a small proportion of are reclassified into a higher category for predicted 5-year risk of breast cancer. The results of this study may aid decisions on the clinical usefulness of combining SNP data with BCRAT, decisions that will also depend on local circumstances and resources.
Fig. 3.
Receiver operating characteristic curves for the BCRAT risk score (AUC=0.58, 95% CI=0.55–0.61), SNP risk score (AUC=0.58, 95% CI=0.54–0.61) and combined risk score (AUC=0.61, 95% CI=0.58–0.64)
Fig. 4.
Receiver operating characteristic curves for the BCRAT risk score, SNP risk score and combined risk score, for: (a) women aged 35 to 39 years (BCRAT AUC=0.60, 95% CI=0.55–0.65; SNP AUC=0.60, 95% CI=0.55–0.65; combined AUC=0.65, 95% CI=0.60–0.70), (b) 40 to 49 years (BCRAT AUC=0.61, 95% CI=0.55–0.66; SNP AUC=0.58, 95% CI=0.53–0.64; combined AUC=0.63, 95% CI=0.57–0.69) and (c) 50 to 59 years (BCRAT AUC=0.54, 95% CI=0.48–0.60; SNP AUC=0.54, 95% CI=0.48–0.60; combined AUC=0.56, 95% CI=0.51–0.62)
Acknowledgments
The ABCFR has been supported in Australia by the National Health and Medical Research Council, the New South Wales Cancer Council, the Victorian Health Promotion Foundation, the Victorian Breast Cancer Research Consortium, Cancer Australia and the National Breast Cancer Foundation. The ABCFR has also been supported by the National Cancer Institute, National Institutes of Health, USA under RFA CA-06-503 and through cooperative agreements with members of the Breast Cancer Family Registry: The University of Melbourne, Australia (U01 CA69638); Fox Chase Cancer Center, USA (U01 CA69631); Huntsman Cancer Institute, USA (U01 CA69446); Colombia University, USA (U01 CA69398); Cancer Prevention Institute of California, USA (U01 CA69417); and Cancer Care Ontario, Canada (U01 CA69467). The content of this article does not necessarily reflect the views or policies of the National Cancer Institute or any of the collaborating centres of the Breast Cancer Family Registry. The mention of trade names, commercial products or organisations does not imply endorsement by the US government or the Breast Cancer Family Registry.
KAP is supported by a National Breast Cancer Foundation Practitioner Fellowship.
Footnotes
The modified source code and executable file are available on request.
Conflict of interest
The authors declare that they have no conflict of interest.
References
- 1.Amir E, Freedman OC, Seruga B, Evans DG. Assessing women at high risk of breast cancer: a review of risk assessment models. J Natl Cancer Inst. 2010;102(10):680–691. doi: 10.1093/jnci/djq088. [DOI] [PubMed] [Google Scholar]
- 2.Gail MH, Brinton LA, Byar DP, Corle DK, Green SB, Schairer C, Mulvihill JJ. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst. 1989;81(24):1879–1886. doi: 10.1093/jnci/81.24.1879. [DOI] [PubMed] [Google Scholar]
- 3.Costantino JP, Gail MH, Pee D, Anderson S, Redmond CK, Benichou J, Wieand HS. Validation studies for models projecting the risk of invasive and total breast cancer incidence. J Natl Cancer Inst. 1999;91(18):1541–1548. doi: 10.1093/jnci/91.18.1541. [DOI] [PubMed] [Google Scholar]
- 4.Barlow WE, White E, Ballard-Barbash R, Vacek PM, Titus-Ernstoff L, Carney PA, Tice JA, Buist DS, Geller BM, Rosenberg R, Yankaskas BC, Kerlikowske K. Prospective breast cancer risk prediction model for women undergoing screening mammography. J Natl Cancer Inst. 2006;98(17):1204–1214. doi: 10.1093/jnci/djj331. [DOI] [PubMed] [Google Scholar]
- 5.Chen J, Pee D, Ayyagari R, Graubard B, Schairer C, Byrne C, Benichou J, Gail MH. Projecting absolute invasive breast cancer risk in white women with a model that includes mammographic density. J Natl Cancer Inst. 2006;98(17):1215–1226. doi: 10.1093/jnci/djj332. [DOI] [PubMed] [Google Scholar]
- 6.Gail MH. Discriminatory accuracy from single-nucleotide polymorphisms in models to predict breast cancer risk. J Natl Cancer Inst. 2008;100(14):1037–1041. doi: 10.1093/jnci/djn180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mealiffe ME, Stokowski RP, Rhees BK, Prentice RL, Pettinger M, Hinds DA. Assessment of clinical validity of a breast cancer risk model combining genetic and clinical information. J Natl Cancer Inst. 2010;102(21):1618–1627. doi: 10.1093/jnci/djq388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wacholder S, Hartge P, Prentice R, Garcia-Closas M, Feigelson HS, Diver WR, Thun MJ, Cox DG, Hankinson SE, Kraft P, Rosner B, Berg CD, Brinton LA, Lissowska J, Sherman ME, Chlebowski R, Kooperberg C, Jackson RD, Buckman DW, Hui P, Pfeiffer R, Jacobs KB, Thomas GD, Hoover RN, Gail MH, Chanock SJ, Hunter DJ. Performance of common genetic variants in breast-cancer risk models. N Engl J Med. 2010;362(11):986–993. doi: 10.1056/NEJMoa0907727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gail MH. Value of adding single-nucleotide polymorphism genotypes to a breast cancer risk model. J Natl Cancer Inst. 2009;101(13):959–963. doi: 10.1093/jnci/djp130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Comen E, Balistreri L, Gonen M, Dutra-Clarke A, Fazio M, Vijai J, Stadler Z, Kauff N, Kirchhoff T, Hudis C, Offit K, Robson M. Discriminatory accuracy and potential clinical utility of genomic profiling for breast cancer risk in BRCA-negative women. Breast Cancer Res Treat. 2011;127(2):479–487. doi: 10.1007/s10549-010-1215-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dite GS, Jenkins MA, Southey MC, Hocking JS, Giles GG, McCredie MR, Venter DJ, Hopper JL. Familial risks, early-onset breast cancer, and BRCA1 and BRCA2 germline mutations. J Natl Cancer Inst. 2003;95(6):448–457. doi: 10.1093/jnci/95.6.448. [DOI] [PubMed] [Google Scholar]
- 12.Hopper JL, Chenevix-Trench G, Jolley DJ, Dite GS, Jenkins MA, Venter DJ, McCredie MR, Giles GG. Design and analysis issues in a population-based, case-control-family study of the genetic epidemiology of breast cancer and the Co-operative Family Registry for Breast Cancer Studies (CFRBCS) J Natl Cancer Inst Monogr. 1999;(26):95–100. doi: 10.1093/oxfordjournals.jncimonographs.a024232. [DOI] [PubMed] [Google Scholar]
- 13.Hopper JL, Giles GG, McCredie MRE, Boyle P. Background, rationale and protocol for a case-control-family study of breast cancer. Breast. 1994;3(2):79–86. [Google Scholar]
- 14.McCredie MR, Dite GS, Giles GG, Hopper JL. Breast cancer in Australian women under the age of 40. Cancer Causes Control. 1998;9(2):189–198. doi: 10.1023/a:1008886328352. [DOI] [PubMed] [Google Scholar]
- 15.Easton DF, Pooley KA, Dunning AM, Pharoah PD, Thompson D, Ballinger DG, Struewing JP, Morrison J, Field H, Luben R, Wareham N, Ahmed S, Healey CS, Bowman R, Meyer KB, Haiman CA, Kolonel LK, Henderson BE, Le Marchand L, Brennan P, Sangrajrang S, Gaborieau V, Odefrey F, Shen CY, Wu PE, Wang HC, Eccles D, Evans DG, Peto J, Fletcher O, Johnson N, Seal S, Stratton MR, Rahman N, Chenevix-Trench G, Bojesen SE, Nordestgaard BG, Axelsson CK, Garcia-Closas M, Brinton L, Chanock S, Lissowska J, Peplonska B, Nevanlinna H, Fagerholm R, Eerola H, Kang D, Yoo KY, Noh DY, Ahn SH, Hunter DJ, Hankinson SE, Cox DG, Hall P, Wedren S, Liu J, Low YL, Bogdanova N, Schurmann P, Dork T, Tollenaar RA, Jacobi CE, Devilee P, Klijn JG, Sigurdson AJ, Doody MM, Alexander BH, Zhang J, Cox A, Brock IW, MacPherson G, Reed MW, Couch FJ, Goode EL, Olson JE, Meijers-Heijboer H, van den Ouweland A, Uitterlinden A, Rivadeneira F, Milne RL, Ribas G, Gonzalez-Neira A, Benitez J, Hopper JL, McCredie M, Southey M, Giles GG, Schroen C, Justenhoven C, Brauch H, Hamann U, Ko YD, Spurdle AB, Beesley J, Chen X, Mannermaa A, Kosma VM, Kataja V, Hartikainen J, Day NE, Cox DR, Ponder BA. Genome-wide association study identifies novel breast cancer susceptibility loci. Nature. 2007;447(7148):1087–1093. doi: 10.1038/nature05887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stacey SN, Manolescu A, Sulem P, Rafnar T, Gudmundsson J, Gudjonsson SA, Masson G, Jakobsdottir M, Thorlacius S, Helgason A, Aben KK, Strobbe LJ, Albers-Akkers MT, Swinkels DW, Henderson BE, Kolonel LN, Le Marchand L, Millastre E, Andres R, Godino J, Garcia-Prats MD, Polo E, Tres A, Mouy M, Saemundsdottir J, Backman VM, Gudmundsson L, Kristjansson K, Bergthorsson JT, Kostic J, Frigge ML, Geller F, Gudbjartsson D, Sigurdsson H, Jonsdottir T, Hrafnkelsson J, Johannsson J, Sveinsson T, Myrdal G, Grimsson HN, Jonsson T, von Holst S, Werelius B, Margolin S, Lindblom A, Mayordomo JI, Haiman CA, Kiemeney LA, Johannsson OT, Gulcher JR, Thorsteinsdottir U, Kong A, Stefansson K. Common variants on chromosomes 2q35 and 16q12 confer susceptibility to estrogen receptor-positive breast cancer. Nat Genet. 2007;39(7):865–869. doi: 10.1038/ng2064. [DOI] [PubMed] [Google Scholar]
- 17.Stacey SN, Manolescu A, Sulem P, Thorlacius S, Gudjonsson SA, Jonsson GF, Jakobsdottir M, Bergthorsson JT, Gudmundsson J, Aben KK, Strobbe LJ, Swinkels DW, van Engelenburg KC, Henderson BE, Kolonel LN, Le Marchand L, Millastre E, Andres R, Saez B, Lambea J, Godino J, Polo E, Tres A, Picelli S, Rantala J, Margolin S, Jonsson T, Sigurdsson H, Jonsdottir T, Hrafnkelsson J, Johannsson J, Sveinsson T, Myrdal G, Grimsson HN, Sveinsdottir SG, Alexiusdottir K, Saemundsdottir J, Sigurdsson A, Kostic J, Gudmundsson L, Kristjansson K, Masson G, Fackenthal JD, Adebamowo C, Ogundiran T, Olopade OI, Haiman CA, Lindblom A, Mayordomo JI, Kiemeney LA, Gulcher JR, Rafnar T, Thorsteinsdottir U, Johannsson OT, Kong A, Stefansson K. Common variants on chromosome 5p12 confer susceptibility to estrogen receptor-positive breast cancer. Nat Genet. 2008;40(6):703–706. doi: 10.1038/ng.131. [DOI] [PubMed] [Google Scholar]
- 18.Gail MH, Mai PL. Comparing breast cancer risk assessment models. J Natl Cancer Inst. 2010;102(10):665–668. doi: 10.1093/jnci/djq141. [DOI] [PubMed] [Google Scholar]
- 19.StataCorp. Stata Statistical Software: Release 12. StataCorp LP; College Station, TX: 2011. [Google Scholar]