Erratum to: Journal of Biological Physics 37 (1) 2011 79-90
DOI 10.1007/s10867-010-9200-x
The author regrets that the sign in (8) and some terms in (11) of the paper cited above were missing. Corrections to these errors are given as follows:
As a coarse-grained continuum model, DNA can be regarded an elastic thin rod. The central axis of rod is a spatial curve R(s, t): R2 →R3 parameterized by arc length s and time t. At a point P on the curve R(s, t), the Frenet frame P-NBT and a local orthonormal basis P-xyz are simultaneously set. In P-NBT, the positive direction of the principal normal PN points toward the concave side of the curve R(s, t); whereas in P-xyz, the x-axis and y-axis are the two principal inertia axes of the cross section through the point P. The angle between the principal normal PN and x-axis (or the binormal PB and y-axis) is called the twisting angle, denoted by χ. On the interfacial surface between the rod and solution, the Young-Laplace equation reads
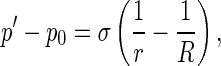 |
R1 |
where R and r are two principal curvature radii in which r is the radius of the rod cross-section, p0 is a constant pressure applied on the interfacial surface by the solution and p′ is the pressure on the interfacial surface by the rod. In (R1), we have reckoned a principal curvature radius as positive if it is drawn into the interior of the rod.
In terms of the action and reaction law, the pressure p applied on the rod by the interfacial surface is equal to p′ in magnitude, but they are opposite in direction. So in coordinates P-xyz, p can be decomposed into
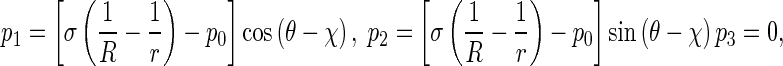 |
R2 |
where 𝜃 is the angle between PQ and PN. It has been proven that [1] thatR can be written as
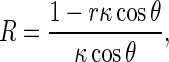 |
R3 |
where κis the curvature of the rod axis. Substituting (R3) into (R2) and integrating along the perimeter of the rod cross-section leads to
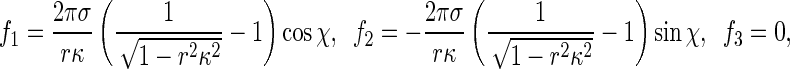 |
R4 |
which are the correct formulas characterizing the interfacial traction. Clearly, physics requires that −1 < rκ < 1. Compared with (11) in [1], 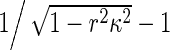 in (R4) can be regarded as a positive scaling factor. Therefore, using (R2), we can repeat the results in [1] and the conclusions in [1] are still available. A detailed investigation can refer to [2].
in (R4) can be regarded as a positive scaling factor. Therefore, using (R2), we can repeat the results in [1] and the conclusions in [1] are still available. A detailed investigation can refer to [2].
It should be stressed that, in a salt solution, geometrical configuration of a DNA chain is controlled by van der Waals force or electrostatic force between the DNA chain and the solution molecules. The interfacial traction is only a coarse-grained model characterizing these microscopic interactions. Since the interfacial traction is curvature-dependent, it is adequate to describe the shape of DNA in solution.
It is noted that the basic idea and main results presented in the paper are not affected by these missing terms [2].
Footnotes
The online version of the original article can be found at http://dx.doi.org/10.1007/s10867-010-9200-x.
References
- 1.Zaixing H. Modulating DNA configuration by interfacial traction: an elastic rod model to characterize DNA folding and unfolding. J. Biol. Phys. 2011;37:79–90. doi: 10.1007/s10867-010-9200-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ye X, Zaixing H, Shengnan W. An elastic rod model to evaluate effects of ionic concentration on equilibrium configuration of DNA in the salt solution. J. Biol. Phys. 2014;40:179–192. doi: 10.1007/s10867-014-9344-1. [DOI] [PMC free article] [PubMed] [Google Scholar]


