Sensor spacing affects the tissue impedance spectra of rabbit ventricular epicardium

Abstract

This study was designed to test the hypothesis that a complex composite impedance spectra develops when stimulation and recording of cardiac muscle with sufficiently fine spatial resolution in a four-electrode configuration is used. With traditional (millimeter scale) separations, the ratio between the recorded interstitial central potential difference and total supplied interstitial current is constant at all frequencies. This occurs because the fraction of supplied current that redistributes to the intracellular compartment depends on effective membrane resistance between electrodes, which is low, to a much greater extent than effective membrane capacitance. The spectra should therefore change with finer separations at which effective membrane resistance increases, as supplied current will remain primarily interstitial at lower frequencies and redistribute between compartments at higher frequencies. To test this hypothesis, we built arrays with sensors separated (d) by 804 μm, 452 μm, and 252 μm; positioned those arrays across myocyte axes on rabbit ventricular epicardium; and resolved spectra in terms of resistivity (ρ_t) and reactivity (χ_t) over the 10 Hz to 4,000 Hz range. With all separations, we measured comparable spectra with predictions from passive membrane simulations that used a three-dimensional structural framework in which intracellular, interstitial, and membrane properties were prescribed based on the limited data available from the literature. At the finest separation, we found mean ρ_t at 100 Hz and 4,000 Hz that lowered from 395 Ω-cm to 236 Ω-cm, respectively, with maximal mean χ_t of 160 Ω-cm. This experimental confirmation of spectra development in whole heart experiments is important because such development is central to achieve measurements of intracellular and interstitial passive electrical properties in cardiac electrophysiological experiments using only interstitial access.

the passive electrical properties of cardiac muscle control action potential propagation because the relative strength of intercellular coupling between adjacent myocytes influences the relationship between source charge generated during depolarization and downstream supply of current to resting cells that impose the electrical load. Although it is widely accepted that altered source-load interactions caused by gap junction remodeling and interstitial volume contraction promote arrhythmias by slowing conduction (7, 21, 24, 27), quantitative details regarding the intracellular and interstitial passive electrical properties are largely unavailable. This gap in understanding is especially pronounced on the cellular size scale. Values for the orthogonal intracellular (Rix,Riy,Riz) and interstitial (Rox,Roy,Roz) microimpedances remain unknown. Extensive quantitative species-, region-, and disease-dependent detail is available for membrane resistance (Rm), membrane capacitance (C_m), and the system of sarcolemmal currents that provide source charge because these parameters are readily identified with mature techniques applied in single cell studies (4, 7). Development of equally robust measurement strategies is necessary to achieve comparable detail for (Rox,Roy,Roz) and (Rix,Riy,Riz).

One possible approach that we have developed and tested using detailed computer modeling holds promise (19, 15, 16). That approach extends the four-electrode method used to measure material resistivity through delivery of supplied current via two outer stimulating electrodes and monitoring of the established potential field via two independent inner voltage-sensing electrodes. Our extension involves application of a robust framework for interpretation of the composite impedance (uCI) obtained from the ratio between the recorded interstitial potential difference (uPD) and the supplied current (I_stim), assuming a linear set of electrodes spaced center-to-center at 25 μm steps is available. Modeling suggests (Rox,Roy,Roz) measurement is possible using as few as three stimulating electrode combinations and low frequency because I_stim remains primarily interstitial on such a fine size scale. A structural framework that only accounts for interstitial flow paths alone is sufficient, with three unique measurements allowing resolution of the three orthogonal microimpedances. With (Rox,Roy,Roz) resolved, uCIs recorded during stimulation at intermediate and high frequencies allow (Rix,Riy,Riz) measurement. This occurs because membrane capacitance provides a pathway for I_stim redistribution between compartments. Integration of (Rix,Riy,Riz) into the structural framework for interpretation of a frequency spectra, defined in terms of its real (resistivity, ρ_t) and imaginary (reactivity, χ_t) components allows microimpedance measurement. The approach builds on theoretical analyses by Roth et al. (23), who predicted plateaus in the magnitude for the axial and radial conductivities in a skeletal muscle fiber associated with low and high temporal frequencies over a range of spatial frequencies consistent with relatively fine interelectrode separations. An attractive aspect of the theoretical approach is that intracellular access is not required, suggesting broad applicability for in vivo measurements.

We have successfully fabricated microelectrical-mechanical systems (MEMS) arrays that include electrodes patterned with sufficient spatial resolution to implement our method (18). However, the relatively high electrode-electrolyte impedances associated with the very small sensors necessary to achieve such fine separations have, to date, posed a practical challenge. With small electrodes, amplifier inputs for voltage sensing may not function as open circuits because each electrode-amplifier interconnection has the potential to establish a capacitive shunt to system ground that depends upon the electrode-electrolyte impedance (5, 10, 12, 25). Parasitic capacitance in the measurement system with our MEMS arrays influenced the uCI spectra in ways that made segmentation from the influence of the tissue on those spectra impractical. This issue is more managable when larger electrodes are used. Most investigators who have completed four-electrode measurements with whole heart preparations have used arrays with 250 μm to 1 mm diameter electrodes separated on a millimeter to centimeter size scale (29, 25, 26, 13, 1, 28, 17). Although arrangements of this type limit the influence of instrumentation, spectra do not develop with traditional separations because I_stim redistribution is equivalent at all frequencies.

We undertook the present study to establish the extent to which electrodes with sizes and separations between those used in traditional studies and available in our MEMS arrays allowed identification of predicted spectra in experiments with rabbit ventricular epicardium. To limit the influence of instrumentation, we relied heavily on active shielding shown previously to be effective in experiments using arrays with traditional electrode size and separation (17). With active shielding, supply of a replica of the measured signal to the outer conductor in a coaxial arrangement maintains a small voltage difference between the shield and measured signal that prevents formation of line capacitance on system interconnections (5, 12). Consistent with approaches to manage this issue in electrometer design, bounding coaxial connections with another conducting layer coupled to system ground for active triaxial shielding provides an additional potential benefit. Arrays were built here using a combination of hand assembly and printed circuit board (PCB) fabrication so that full triaxial shielding close to sensor tips was achieved for sensors ranging between 50 and 250 μm diameter. We then resolved spectra using different electrode separations with sensors primarily oriented across myocyte axes in experiments. Spectra compared favorably with computer simulations in which (Rox,Roy,Roz) and (Rix,Riy,Riz) assignments based on the limited macroscopic data available for passive electrical properties in this species were used. Most importantly, spectra in experiments with the finest electrode separations achieved suggested frequency dependent I_stim redistribution central to (Rox,Roy,Roz) and (Rix,Riy,Riz) measurement. This report therefore represents an important step toward removal of practical obstacles for improved description of passive intercellular electrical properties as a routine component of cardiac electrophysiological studies.

MATERIALS AND METHODS

The investigation conforms to the Guide for the Care and Use of Laboratory Animals, published by the National Institutes of Health. All animal study protocols were approved by the Institutional Animal Care and Use Committee at the University of Alabama Birmingham.

Stimulation and recording system.

All spectra were identified using the system documented in our recent report (17). Briefly, stimuli were delivered through an AC signal generation stage that supplied I_stim between two outer electrodes that oscillated 180° out of phase from one another. I_stim established a potential field sampled at two inner electrodes. Voltages at all electrodes were sensed with a head stage that eliminated DC offsets, established an active shield signal for each sensor, and generated a driven common signal supplied to the tissue bath. During stimulation, uPDs were archived to one of two channels with a personal computer-based data acquisition system at 100,000 samples/s using 16-bit samples in 1-s epochs. A separate signal (V_stim) proportional to I_stim was archived to the second channel, simultaneously. Each uPD and V_stim set of samples was then automatically approximated as a unit cosine wave with amplitude A and phase Ψ (A < Ψ) such that for a given frequency. uCI was expressed in terms of magnitude (uCI=A_uPD/A_Vstim) and phase (uCI=<(Ψ_Vstim −Ψ_uPD)). Stimulation over the 10 to 4,000 Hz range was performed in different acquisition intervals.

Individual sensors.

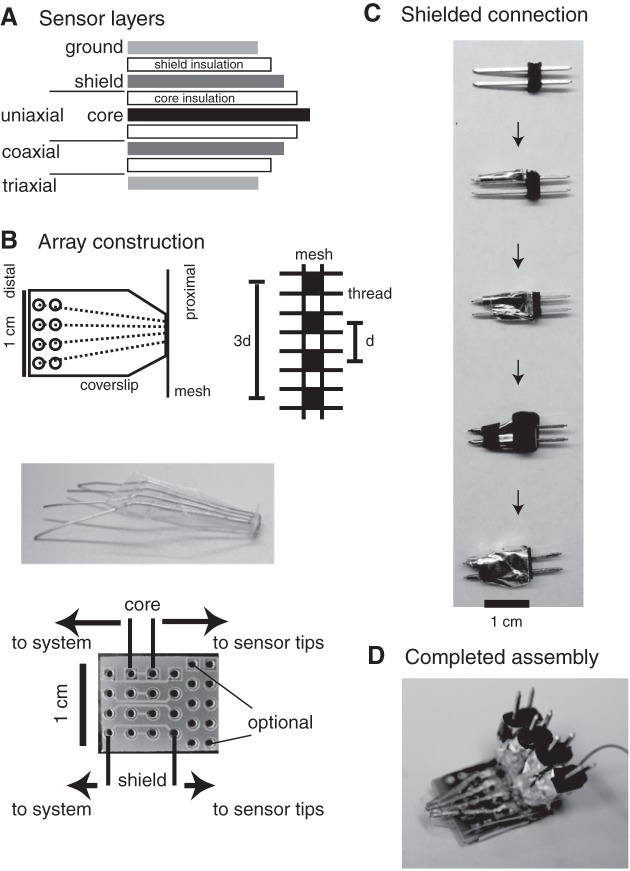
Sensors built with 250, 125, and 50 μm tips were assembled with an approach that involved wrapping layers around silver precision wires by hand that were subsequently placed into small PCBs. This procedure ensured layers shown schematically in Fig. 1A were carried as close to the sensor tip as practical. Initially, this allowed consideration of the extent to which different levels of shielding were beneficial for each sensor size. Each wire formed an electrode core that was insulated to create a uniaxial sensor that was optionally wrapped with a shield conductor and insulator to form a coaxial sensor, or was wrapped again in a ground layer to form a triaxial sensor. Uniaxial sensors were simply the precision wires. Coaxial sensors were built from wire routed through an ≈1.2-cm-long polytetrafluorethylene tubing section (Zeus, Orangeburg, SC) with 0.066 cm inner diameter or through polyimide tubing (Component Supply, Ontario, NY) with 0.032 cm inner diameter. The tubing section was wrapped in aluminum foil tape (Digi-Key Corporation, Thief River Falls, MN) and covered with nail polish, leaving ≈3 mm of shield conductor exposed at the distal end for connection to system electronics. Triaxial sensors were built by insulating the shield layer with polyimide (McMaster Carr, Princeton, NJ) and then thick foil (Berry Plastics Corporation, Franklin, KY) tapes.

Fig. 1.

Schematic diagrams of sensor layers (A) and array construction components (B) including plastic coverslips on which sensors were placed (B, top left), mesh through which sensors were routed (B, top right), photograph of sensors on coverslip (B, middle), and printed circuit boards to which sensors, shield connections, and interconnections to system electronics were located (bottom). C: triaxial connector pin assembly. D: completed coaxial array.

Array assembly.

Arrays were built using individual sensors positioned in four-electrode arrangements using a strategy that ensured electrode stability, accommodated different electrode sizes and separations, and limited mechanical degradation of arrays during interconnection with the system electronics. As shown in Fig. 1B (top left), that strategy involved routing the proximal end of each sensor through nylon mesh (Component Supply) and routing the distal end of each sensor through openings in a plastic coverslip onto which individual sensors were fixed using polyurethane. Sensors were routed through alternate openings in the mesh (Fig. 1B, top right). For 250 μm sensors, mesh with openings of 280 μm and thread diameters of 122 μm allowed center-to-center separations (d) of 804 μm. Mesh with smaller openings and thread diameters for arrays with 125 μm sensors allowed d = 452 μm. Even finer mesh allowed d = 252 μm separations with 50 μm sensors. The mesh and sensors were then glued to a precut plastic coverslip (Fig. 1B, middle). Holes on the distal end of the coverslip were positioned to register with solder through holes in a 1.5 × 1.2 cm² PCB (Fig. 1B, bottom). The distal core and shield wire of each sensor were routed through coverslip and PCB holes in the “to sensor” region, the coverslip was aligned with the PCB, a bead of polyurethane was fixed the coverslip to the top side of the PCB, and then all wires were soldered in place on the bottom side of the PCB. These steps limited movement of the fragile sensors during assembly and prevented mechanical connection to the system electronics from damaging arrays. Triaxial connection to the system electronics was established through individual male pin connectors modified as shown in Fig. 1C. Pins (Digi-Key Corporation) with center-to-center separations corresponding to the PCB separations between each core and shield hole on the “to system” rows were first wrapped in an ≈1 cm Teflon tube section (SPC Technology, Chicago, IL). That section was wrapped in foil tape, which extended around the plastic pin holder and attached to the shield pins. Heat shrink insulated the bottom of the pins at the tube end and the top of each connector. After insulation, additional foil tape was then wrapped around the connector to form a ground layer. These steps ensured full triaxial shielding to within ≈15 mm of all sensor tips. In arrays built with triaxial sensors, interconnection between the ground layer on each sensor and system ground was achieved by wrapping the array in additional foil tape. Full triaxial shielding close to sensor tips was achieved in these arrays. Sensors were chloridized before use to lower the electrode impedance from that of bare silver wire (11). Figure 1D shows one completed assembly.

Array calibration.

Individual arrays were then calibrated via analyses of spectra obtained from acquisition intervals during which the sensor tips were placed in a 0.15% sodium solution with resistivity of 345 Ω-cm loaded into our tissue bath, following van Oosterom et al. (29). Such calibration served four purposes. 1) The analytic predictions for uCI with a four-electrode arrangement including equally spaced sensors positioned inside an infinite isotropic volume conductor or on the surface of a semi-infinite volume conductor are ρ/4πd and ρ/2πd, respectively. Calibration allowed validation for individual arrays by ensuring uCIs fell in the range for a given electrode separation. 2) Because biological sources for capacitance were absent from calibration solution, changes in uCI with frequency indicated a potential increase in the electrode-electrolyte interface impedance of one or more sensors in an array. Calibration therefore allowed identification of candidate arrays with sensors to rechloridize before individual experiments. 3) Calibration allowed identification of a unique probe constant (Kp = 345 Ω-cm/uCI) for each array that we identified from mean uCI across all frequencies. This allowed expression of ρ_t and χ_t from heart experiments using ρ_t = Kp uCI cos(<uCI) χ_t = Kp uCI sin(<uCI) (Eq. 1), which was advantageous in practice because spectra were normalized for comparisons between different electrode separations with both terms having units of Ω-cm. 4) Use of Eq. 1 allowed identification of resistivity (ρ_ns) and reactivity (χ_ns) from acquisition intervals with arrays placed in the normal solution we used for heart perfusion. Comparisons between ρ_ns and ρ_t, and between χ_ns and χ_t provided additional measures of the extent to which sensor characteristics remained consistent between the start and end of a given experiment.

Rabbit heart experiments.

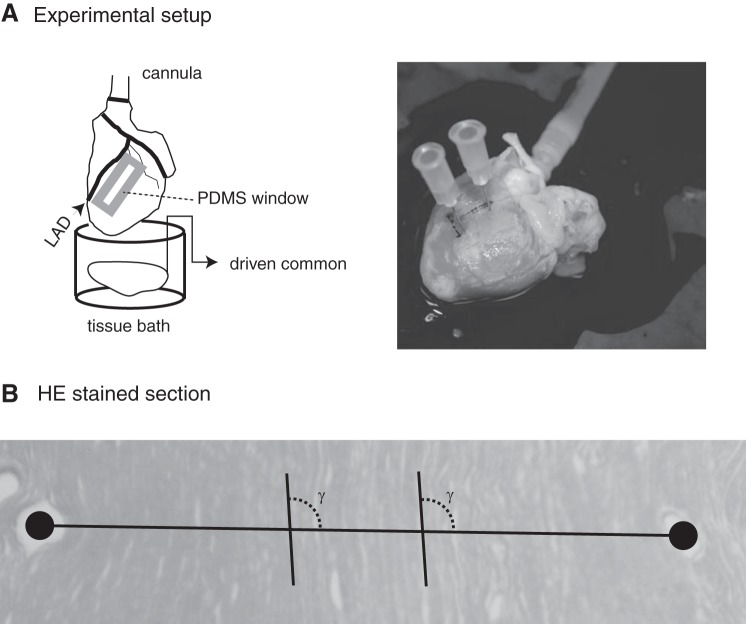
Experiments to resolve spectra were completed with 13 New Zealand white rabbits (3–5 kg) anesthetized with intramuscular ketamine (44 mg/kg) and xylazine (20 mg/kg), followed by intravenous heparin (2.0 ml) during isofluorane inhalation (0.3%). During each experiment, the heart was rapidly excised after a medial sternotomy and retrogradely perfused through the aorta with 3 to 4 l of recirculating, oxygenated (95% O₂-5% CO₂) normal solution containing (in g/l) 7.09 NaCl, 3.96 glucose, 0.4 MgCl₂, 0.34 KCl, 2.5 taurine, 0.65 creatine, 0.55 sodium pyruvate, 0.12 NaH₂PO₄, 2.4 NaHCO₃, and 0.27 CaCl₂. Figure 2A (left side) shows a schematic of the experimental arrangement. Temperature was maintained at 35°–37 ± 1° C, and pH was fixed at 7.3 to 7.4. Shortly after perfusion was established, a 1.25 × 2 cm² polydimethylsiloxane strip with 1 to 2 rectangular windows was carefully glued to the epicardium distal to the left anterior descending artery on the left ventricle. Epicardial muscle was visible in each window. Individual arrays were attached to the head stage of our measurement system, the head stage was moved so that the array was near an epicardial window, and a micromanipulator was used to hold the array tip against muscle in the window. Two to three successive acquisition intervals were then collected before a switch to a new array. Although this procedure was generally effective at maintaining contact between the electrodes and the preparations, all acquisition intervals were evaluated after the completion of the experiment to ensure ρ_t differed from ρ_ns. Acquisition intervals for which the lower bound on the 95% confidence interval for ρ_t was below the upper bound on the 95% confidence interval for ρ_ns were excluded from analyses.

Fig. 2.

A: schematic diagram of experimental setup (left) and photograph of 1 heart into which fiducials were placed at the end of an experiment. B: cropped hematoxylin and eosin (HE)-stained section with line between centroids of fiducials used to identify γ for orientation of electrodes relative to myocyte axes. PDMS, polydimethylsiloxane.

Statistical comparisons.

Populations of samples were first assembled based on frequency (10 to 4,000 Hz), electrode separation (804 μm, 452 μm, 252 μm), and media type (rabbit epicardium, normal solution, calibration solution) using all available arrays and experiment dates. Once assembled, individual samples from within each population were screened using the generalized extreme Studentized deviate ESD test (22) to remove outliers. This assumed a given population was a univariate data set that followed an approximately normal distribution. Every population was then described in terms of its mean, its standard deviation (SD) and its boundaries on the 95% confidence interval. This organization allowed comparisons between populations at different electrode separations to be used in unpaired t-tests to assess, for example, the impact of spacing on ρ_t. It also allowed more systematic comparisons across frequencies using one-way analysis of variance with Tukey-Kramer post hoc analyses to identify specific populations for a given electrode separation that differed from the other populations. A P ≤ 0.05 level of significance was used for all tests.

Myocyte orientation in the measurement region.

After each experiment, 23-gauge needles were inserted into epicardial tissue as close to the short axis of a window as possible (Fig. 2A, right side) to allow subsequent histologic characterization of the likely electrode orientation relative to myocyte axes in the measurement region. A ventricular tissue block including the polydimethylsiloxane window was dissected from the heart and stored in 10% formalin. After at least 4 days, the tissue was embedded in paraffin and sectioned 5 μm thick in a plane parallel to the epicardium. Sections were stained with hematoxylin and eosin. Individual slides were then imaged using a Nikon Coolpix 5000 camera (Nikon, Melville, NY) connected to an InfiniVar CFM-215 video microscope (Infinity Photo-Optical, Boulder, CO) using fiducial holes in the serial section to frame the image (Fig. 2B). A printout of each image was then generated, and a line was drawn through the fiducial centroids on the printout. The angle between this line and the myocyte axes (γ) was then measured at two to three locations between the fiducials using a protractor. Consistent with Fig. 2B, electrodes were primarily oriented across myocyte axes, as means ± SD for γ identified in all 13 experiments was 86° ± 22°.

Structural framework for spectra prediction.

To appreciate likely spectra resulting from stimulation and recording of heart tissue with different sensor spacings, we completed a set of simulations using the structural framework shown in Fig. 3. That framework included (40 × 20 × 15 = 12,000) individual building blocks in which (Rox,Roy,Roz), (Rix,Riy,Riz), and (R_m,C_m) were prescribed using macroscopic descriptions available from the literature. For the compartments, we defined R_c,s = (ρ_cα_c,s)/(f_c▵) with subscript c denoting intracellular (i) or interstitial (o) compartment, subscripts denoting direction (x,y,z), ρ compartment resistivity, f compartment volume fraction, ▵ the edge length for a building block and α an anisotropy ratio. We used ρ_i = 166 Ω-cm and ρ_o = 63 Ω-cm (6) and aligned myocyte axes with the x-direction, α_i,x, α_i,y, α_i,z of 1.0, 9.4, 9.4, respectively, (2) α_o,x, α_o,y, α_o,z of 1.0, 2.7, 2.7, respectively, (2), and f_i, f_o of 0.8 and 0.2, respectively (14). For the membrane, we defined Rm = (R_inV_cell)/▵ and C_m =(C_cell ▵³)/V_cell with input resistance R_in = 33.7 MΩ, cell capacitance C_cell = 72.5 pF and cell volume V_cell = 16,201 μm³ (4). Assigning (Rox,Roy,Roz), (Rix,Riy,Riz), and (R_m,C_m) for a given ▵ allowed numerical determination of transmembrane (Vm) and interstitial (φ_o) potentials at all building blocks using an approach that followed our earlier report (16). Because on-diagonal terms in the coefficient matrix included membrane reactance (Xm=j/ωC_m), which depended upon j = ✓−1 and angular frequency (ω), uCI and uCI were determined in each solution. Iterative solution was performed using MATLAB (MathWorks, Natick, MA) sparse matrix functions including the generalized minimum residual solver with incomplete Cholesky preconditioning to accelerate solutions. Source and sink building blocks were oriented across myocyte axes, and uPDs were acquired from the difference in φ_o between associated inner blocks separated by d = 2▵. Then, ρt and χt were identified using Eq. 1 and the expected probe constant for electrodes positioned on the boundary of a semi-infinite volume conductor (Kp = 2πd).

Fig. 3.

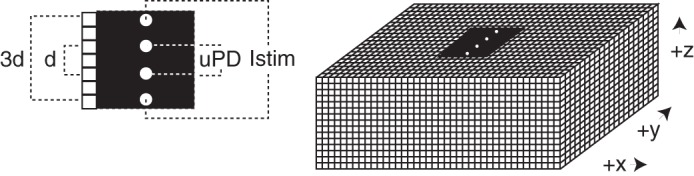
Schematic diagram of electrode separations (left) and 3-dimensional structural framework used for passive membrane simulations. Black region includes the surface location for the electrode array. The recorded interstitial central potential difference (uPD) was recorded from blocks separated by d = 2▵. The total supplied interstitial current (I_stim) was supplied from blocks separated by 3d = 6▵.

RESULTS

Model predictions.

Figure 4 shows modeled ρ_t and χ_t as functions of frequency for the three electrode separations achieved in array construction. With the use of d = 804 μm (Fig. 4A), the ρ_t range was fairly narrow at (287–265 = 22 Ω-cm) and maximum χ_t was only 7 Ω-cm, suggesting experimental identification of spectra development in the 10 Hz to 4,000 Hz range was impractical. In fact, experimental variability in different ρ_t and χ_t populations consistently exceeded these bounds. This spectra was therefore consistent with traditional separations at which supplied current equilibrates between compartments at all frequencies. With the use of d = 452 μm (Fig. 4B), the ρ_t range increased to 56 Ω-cm and maximum χ_t measured 27 Ω-cm, suggesting experimental identification of spectra development that was potentially practical, although challenging. This spectra was therefore consistent with a modest redistribution of supplied current between compartments. With the use of d = 252 μm (Fig. 4C), the ρ_t range increased further to 107 Ω-cm with distinct maxima and minima at low and high frequencies, respectively, whereas maximum χ_t measured 50 Ω-cm. This spectra was therefore consistent with a separation at which the low frequency response was established by supplied current that remained primarily interstitial, whereas the intermediate and high frequency responses were established by current that redistributed to the intracellular compartment by varying amounts that were frequency dependent.

Fig. 4.

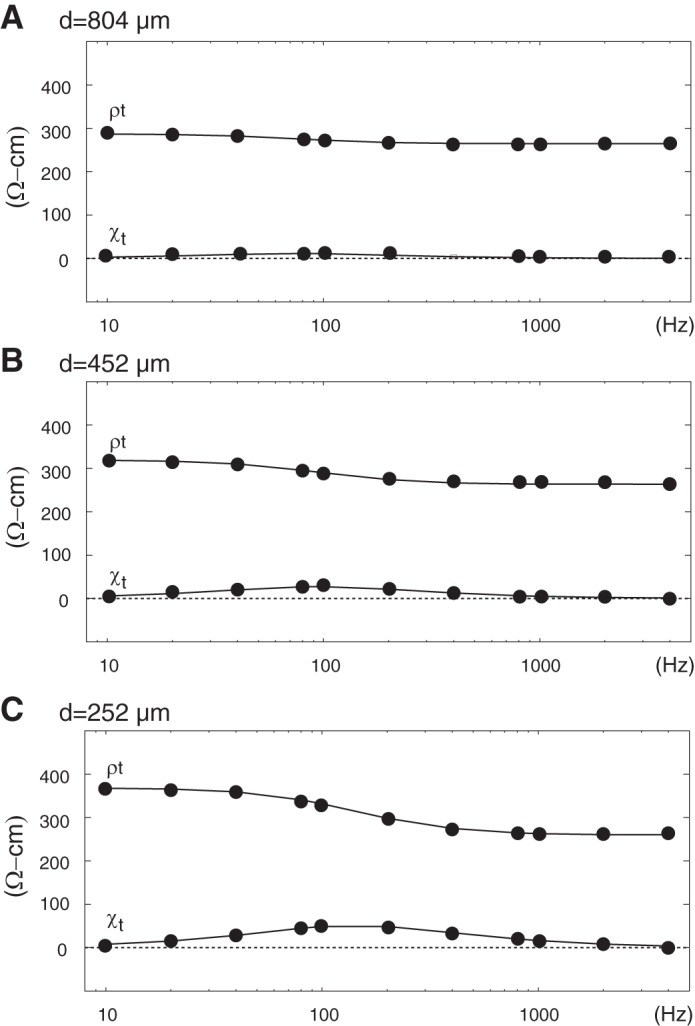
Predicted impedance spectra from passive membrane simulations with electrode separations (d) of 804 μm (A), 452 μm (B), and 252 μm (C).

Array calibration.

During initial calibration, we found limited impact of shielding to within 15 mm of individual sensor tips in arrays with wider electrode separations, since analysis of variance using uCI populations assembled by frequency showed no significant effect of frequency with d = 804 μm or d = 452 μm. We therefore used arrays built with uniaxial, coaxial, and triaxial sensors in rabbit experiments with these separations. This was not the case during calibration of arrays built from 50 μm sensors with d = 252 μm, however, since one-way analysis of variance including arrays with uniaxial sensors did show an effect of frequency. Repeating that analysis with uCI populations limited to arrays containing only coaxial or triaxial sensors eliminated significant differences. This observation led us to construct additional arrays with triaxial sensors for rabbit experiments in which we considered this separation. Arrays with uniaxial sensors were not used in these experiments. With d = 804 μm, we found pooled means ± SD for uCI of 0.67 ± 0.07 kΩ, which was within the range for predicted uCI for calibration solution of 0.34 to 0.68 kΩ. Pooled means ± SD for uCI of 1.13 ± 0.16 kΩ and 1.83 ± 0.42 kΩ with d = 452 μm and d = 252 μm, respectively, were also within predicted uCI ranges of 0.61 to 1.21 kΩ and 1.09 to 2.18 kΩ, respectively.

Recorded uPDs.

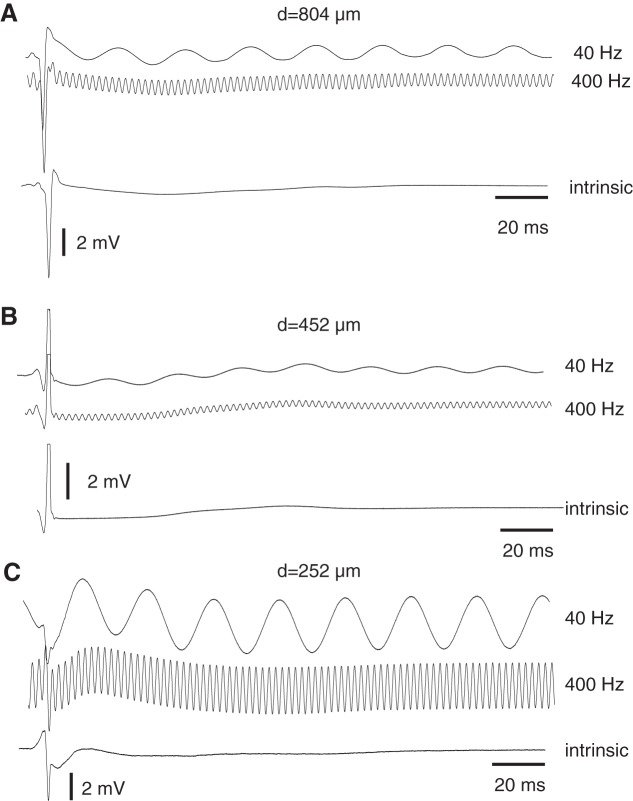
We completed two rabbit experiments with 15 different (5 uniaxial, 5 coaxial, 5 triaxial) arrays containing 250 μm sensors separated by 804 μm, two experiments with 15 different (5 uniaxial, 5 coaxial, 5 triaxial) arrays containing 125 μm sensors separated by 452 μm, and 9 experiments using 16 arrays (4 coaxial, 12 triaxial) containing 50 μm sensors separated by 252 μm. Figure 5 shows uPDs recorded from rabbit ventricle during selected acquisition intervals with arrays including each separation. Figure 5A shows waveforms during 40 Hz and 400 Hz stimulation aligned to the intrinsic uPD recorded during no stimulation from one acquisition interval with d = 804 μm. I_stim of ∼6 μA established sinusoidal components that made up the majority of each signal outside the narrow deflection associated with local depolarization of tissue near the electrodes. Figure 5B shows waveforms from an acquisition interval with d = 452 μm and a much lower I_stim of ∼300 nA. That I_stim reduced the sinusoidal components, although detection of uPD amplitude remained straightforward to achieve because local depolarization was completed rapidly. Figure 5C shows waveforms from an acquisition interval with d = 252 μm and I_stim of ∼1.5 μA. At this I_stim, sinusoidal components had comparable amplitudes with that of the local deflection associated with depolarization. Analogous uPDs were observed in all acquisition intervals analyzed.

Fig. 5.

uPDs from rabbit ventricle during 40 and 400 Hz aligned to intrinsic uPD recording using arrays with d = 804 μm (A), d = 452 μm (B), and d = 252 μm (C) separations.

Epicardial spectra.

Figure 6 shows mean ρ_t, χ_t, ρ_ns, and χ_ns with error bars demonstrating 95% confidence interval boundaries from populations assembled using different electrode separations and frequencies. As predicted for d = 804 μm (Fig. 6A), stimulation at different frequencies in the 10 Hz to 4,000 Hz range caused limited changes in any of these parameters. One-way analysis of variance identified no significant differences with frequency between any of the ρ_t populations. The range of mean ρ_t measured 21 Ω-cm, which was slightly larger than the range predicted by modeling with this electrode separation. Pooled means ± SD for ρ_t measured 189 ± 75 Ω-cm (N = 502). These findings were similar to those identified with ρ_ns, with the main difference being a much lower overall ρ_ns than ρ_t, as expected. Consistent with these observations, χ_t and χ_ns were both much smaller than their respective reactive components. Maximal mean χ_t at 32 Ω-cm did exceed that predicted by modeling, but was nevertheless well below pooled mean ρ_t. Collectively, these observations supported an interpretation of highly limited spectra development with the widest electrode separation tested. Findings with d = 452 μm (Fig. 6B) were also consistent with model predictions in a number of respects. For example, modeling predicted development of a larger ρ_t range than with the wider separation, and we found mean ρ_t varied 46 Ω-cm in our experiments with d = 452 μm. Differences between ρ_t populations across frequencies, however, were not significant. Pooled ρ_t measured 355 ± 202 Ω-cm (N = 693), which was significantly higher than pooled ρt with wider spacing. In addition, we found maximal mean χ_t of 94 Ω-cm. Although this exceeded modeling predictions, we nevertheless note that the resistive component was much larger than the reactive component, as expected. Collectively, these observations supported an interpretation of modest spectra development with this separation, consistent with the qualitative predictions from modeling. With d = 252 μm (Fig. 6C), one-way analysis of variance with post hoc analyses identified significant differences in the ρ_t populations at 2,000 Hz and 4,000 Hz from ρ_t populations at all other frequencies. Mean ρ_t at 2,000 Hz and 4,000 Hz measured 333 Ω-cm and 285 Ω-cm, respectively. By comparison, pooled ρ_t identified by combining all populations in the 10 Hz to 1,000 Hz range was 378 ± 274 Ω-cm (N = 1477). This pooled ρt was significantly higher than pooled ρt with both d = 452 μm and d = 804 μm. This occurred despite no analogous development with ρ_ns, suggesting the response was primarily related to placement of arrays on tissue as opposed to our use of small sensors. Spectra development contributed to a larger range for mean ρ_t at 164 Ω-cm than with the wider electrode separations. Development of χ_t at frequencies above 200 Hz was also apparent, with maximual mean χ_t measuring 160 Ω-cm. Collectively, these observations supported an interpretation that supplied current redistributed to the intracellular compartment to a greater extent with d = 252 μm than with wider electrode separations.

Fig. 6.

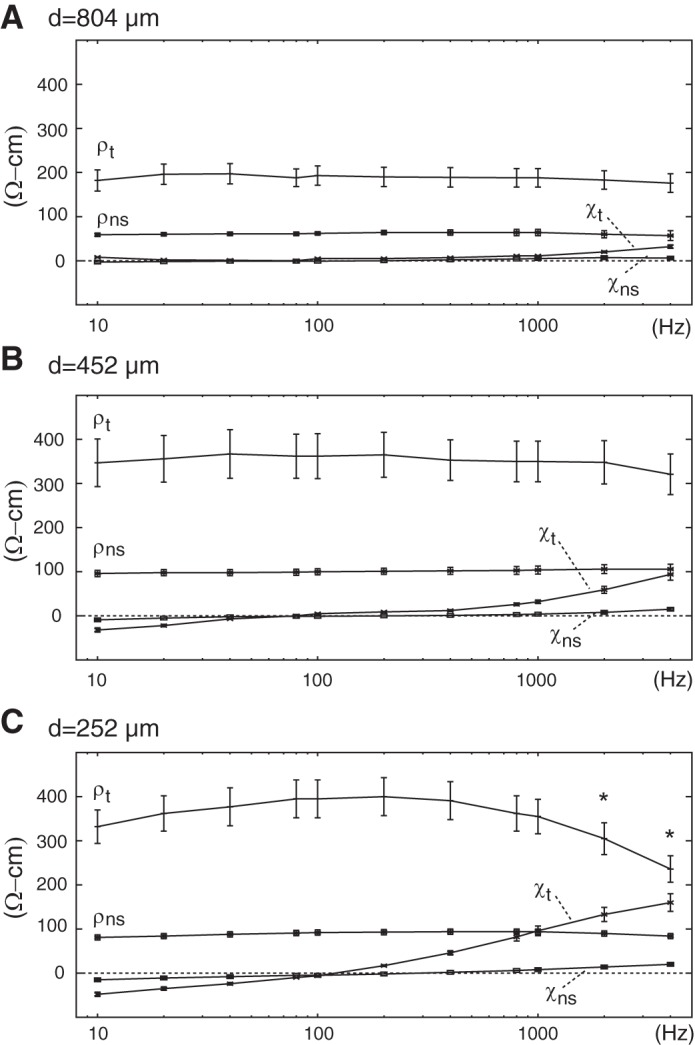
Impedance spectra from acquisition intervals with normal solution (ns) and rabbit epicardium (t) using electrode separations (d) of 804 μm (A), 452 μm (B), and 252 μm (C). Populations of samples for which statistically significant differences in ρ_t were identified are marked (*).

DISCUSSION

The main new finding that arose from the present study was our demonstration that 252 μm separation between 50 μm sensors provided sufficient spatial resolution to reveal impedance spectra development with electrodes oriented across myocyte axes in rabbit ventricular epicardium. With such fine separation, we found higher ρ_t and smaller χ_t at the lower frequencies considered and a reduction in ρt with development of χt as frequency increased. This response suggests interstitial current supplied in a four-electrode arrangement redistributed to the intracellular compartment via membrane capacitance at the higher frequencies while remaining primarily interstitial at the lower frequencies. Although a number of theoretical reports have predicted such redistribution with electrodes separated on a fine spatial scale, we present experimental confirmation in a whole heart preparation. This finding is important because resolution of such spectra provides an opportunity to segment interstitial from intracellular contributions to ρ_t, which to date has only been achieved effectively with preparations in which both interstitial and intracellular access is maintained (2, 6). Because continuous intracellular access is technically challenging in that fragile glass microlelectrodes and specialized tissue preparations are required, an ability to achieve segmentation using only interstitial access has the potential to improve quantitative descriptions for passive intercellular coupling in electrophysiologic studies with hearts.

Impact of array construction steps.

An important aspect of achieving this demonstration involved the array fabrication process that combined hand assembly with small PCBs to ensure electrode stability, accommodate different electrode sizes and separations, and limit mechanical degradation of arrays during interconnection with the system electronics. That process was central to integrating active shielding to within 15 mm of uniaxial, coaxial, and triaxial sensor tips, as well as shielding individual electrodes close to each tip in arrays with coaxial and triaxial sensors. Although the latter shielding provided marginal benefit in arrays built with 250 μm and 125 μm sensors, we found a statistically significant effect of frequency on uCI with arrays built from 50 μm uniaxial sensors during calibration that led us to only use arrays with coaxial or triaxial sensors in the associated rabbit experiments. We view our findings regarding the use of shielding as critical for the more challenging problem of using even smaller sensors to achieve separations on the 10 μm to 100 μm size scale. This suggests strategies for integration of active shielding into the fabrication process will be beneficial in MEMS array development.

Model predictions.

Our rationale for using the structural framework to predict ρ_t and χ_t for the specific electrode separations tested experimentally was based on the success of using that framework in an earlier study (16). In that report, we used 12.5 × 12.5 × 12.5 μm³ building blocks to complete time-dependent simulations in which a system of sarcolemmal currents specific to rabbit ventricular myocytes (20) represented active membrane. Adjusting frequency in different simulations allowed identification of spectra that developed in the 100 Hz to 10 kHz range when the electrodes were separated by 25 μm with that spectra being largely replicated in simulations with passive membrane properties used to approximate active membrane. The modeled spectra therefore shared features with Roth et al. (23), who considered spatial and temporal frequency dependence of axial and radial conductivities (inverse of resistivities) in a model of skeletal muscle. Those investigators identified a band of spatial frequencies over which two plateaus in magnitude developed. The plateau that developed at lower temporal frequencies was associated with spatial frequencies at which electrode separations were finer than the tissue space constant. The plateau that developed at higher temporal frequencies was associated with spatial frequencies at which electrode separations were wider than the tissue space constant. Intermediate between plateaus, magnitudes changed with temporal frequencies in ways that are consistent with the passive membrane simulations completed here using nominal values for (Rox,Roy,Roz), (Rix,Riy,Riz), and (R_m,C_m). In the present study, modeling predicted both the ρ_t range and maximal χ_t would in increase as electrodes were brought closer together for the specific separations used experimentally. Although these qualitative aspects of the predicted impedance spectra were confirmed experimentally, we do recognize development of χ_t with d = 252 μm was most pronounced at frequencies above 800 Hz, whereas predicted development was closer to 200 Hz. These quantitative differences suggest specific literature-based parameters used to derive (Rox,Roy,Roz), (Rix,Riy,Riz), and (R_m,C_m) were potentially dissimilar from the underlying parameters in our specific heart preparations.

Total tissue resistivities.

Although we measured significant differences between pooled ρ_t populations with all three sensor spacing studied experimentally, we note mean values for those populations were consistent with previous investigations in which traditional separations have been used. In a traditional four-electrode experiment, cardiac muscle is incorrectly assumed to be a uniform, isotropic monodomain structure whose material property can be expressed independent of geometry using ρ_t. These assumptions regarding structure must be considered with care, since complexities associated with the arrangement of the constitutive membrane and interstitial and intracellular elements and with the electrode orientation and position relative to those elements will all influence ρ_t. This is one reason that ρ_t measurements are often used in heart studies to provide qualitative descriptions of changes in intercellular coupling. For example, Owens et al. (13) used changes from control ρ_t to identify the onset of gap junction uncoupling in their studies of ischemia development in blood-perfused rabbit hearts, which in turn allowed comparison of that onset with other parameters that provided insight into the intricate transition to phase Ib ischemia. For our measurements in which electrodes were primarily oriented across epicardial fibers, we found mean ρ_t at 189 Ω-cm, 355 Ω-cm, and 378 Ω-cm with 804 μm, 452 μm, and 252 μm electrode separations, respectively. These ρ_t compare favorably with mean ρ_t of 184 Ω-cm and 191 Ω-cm reported along and across rabbit epicardial fibers, respectively, by Baynham and Knisley (1); 212 Ω-cm to 313 Ω-cm identified along and across canine epicardial fibers, respectively, by Steendijk et al. (26); and 410 Ω-cm identified in canine intramural experiments by van Oosterom et al. (29). All of these investigations used electrodes separated on a millimeter to centimeter size scale. Recognizing the potential impact of structural complexities on ρ_t measurements, the consistency we observed suggests use of this parameter as an index for composite material properties will remain valuable as one component of the transition to finer separations like those we envision in MEMS arrays.

Frequency dependence of impedance spectra.

Although this report includes experimental confirmation of spectra development resulting from the use of electrode separations 1 to 2 orders of magnitude finer than in previous investigations with whole heart preparations, we recognize that Gielen et al. (3) made similar measurements in skeletal muscle preparations. Those investigators used arrays with sensors separated by 500 μm and identified spectra over the 3 Hz to 1 MHz with electrodes oriented along (L) and across (T) fibers. Magnitude changes along fiber were observed above 100 Hz, whereas changes across fibers were observed between 1 kHz and 10 kHz for specific frequencies and electrode orientations developed over these frequency ranges. Spectra development with the two separate electrode orientations allowed estimation of unique resistivities for the interstitial and intracellular compartments at ρ_o,L = 351 Ω-cm, ρ_o,T = 746 Ω-cm, ρ_i,L = 224 Ω-cm, and ρi,T =187 Ω-cm. Similarly, Le Guyader et al. (8) used 25 μm electrodes at d = 158 μm in superfused canine papillary muscle experiments and found spectra development above 100 Hz. In a subsequent study (9), those investigators interpreted spectra resolved with d = 350 μm in this same preparation using a three-dimensional bidomain model based on a Fast Fourier Transform approach and identified ρ_o,L = 770 Ω-cm, ρ_o,T = 786 Ω-cm, ρ_i,L = 1,667 Ω-cm, and ρ_i,T = 2,571 Ω-cm. These parameters differ quantitatively from passive electrical properties we used in our simulations to predict likely impedance spectra for the electrode separations used in our rabbit heart experiments. Consistent with our intended microimpedance measurement approach, however, analyses of impedance spectra revealed through fine separation between stimulation and recording electrodes in a four-electrode arrangement was necessary to provide sufficient independent measurements for the estimation of directional compartment resistivities.

Limitations.

It is important to recognize certain limitations in assessing our findings. First, we did not attempt to measure (Rox,Roy,Roz) and (Rix,Riy,Riz) because the focus here was on resolution of the four-electrode impedance spectra necessary for implementation of our proposed microimpedance measurement technique. Although we anticipate integration of the additional stimulating electrodes necessary for that implementation will be practical to achieve in going forward, the lack of the additional independent combinations to achieve (Rox,Roy,Roz) measurement prevented subsequent refinement for (Rix,Riy,Riz) identification. Second, we cannot exclude the possibility that the electrode-electrolyte impedance had some influence on the resolved spectra with the smallest sensors tested. Although our confirmation of relatively small χ_ns as compared with χ_t, ρ_t, and ρ_ns suggests the response with d = 252 μm was primarily related to placement of arrays on tissue as opposed to the use of small sensors, an alternate design in which calibration and experimental recording from tissue and normal solution was completed using 50 μm sensors, and different electrode separations would be necessary to exclude this possibility. Third, the modeling predicted a transition from high to low ρ_t with χ_t development in the 40 Hz to 1,000 Hz range that included constant ρ_t and negligible χ_t at frequencies above 1,000 Hz. Analogous changes we found experimentally were in the 200 Hz to 4,000 Hz range, and since 4,000 Hz was the upper bound we used for stimulation all features of the transition predicted by modeling were not identified. That upper bound was effectively set by our measurement approach because uPD and I_stim were recorded at 100,000 samples/s during data acquisition. We were therefore unable to identify constant ρ_t and negligible χ_t at high frequency, suggesting an alternate design in which analog identification of uCI and uCI was performed would have practical advantages for more flexible spectra resolution.

Implications for (Rox,Roy,Roz) and (Rix,Riy,Riz) measurements.

The results we describe represent an important step toward routine monitoring of intercellular coupling strength in a way that will allow more complete interpretations of the relative intracellular and interstitial contributions to that coupling. Although (Rox,Roy,Roz) and (Rix,Riy,Riz) measurements were not completed in the present study, demonstration that 1) active shielding was effective in limiting the influence of instrumentation on the impedance spectra with 50 μm sensors at 252 μm separations, 2) spectra identified in rabbit experiments were qualitatively similar to model predictions assuming the structural framework we anticipate using for microimpedance measurements, and 3) ρ_t identified with finer separations than have ever been used in whole heart experiments were comparable to those from a range of previous investigations, all represent necessary steps toward implementation that can be used to quantify disease-, region-, tissue- and species-dependent uncoupling on a cellular size scale. Our goal for implementation remains the use of MEMS arrays whose formal fabrication will ensure precision in electrode sizes and locations, with spectra resolved using the overall measurement approach shown to be effective here.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Award HL-092049 and National Science Foundation Award CBET-0756078.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).