Localization bias and spatial resolution of adaptive and non-adaptive spatial filters for MEG source reconstruction

Abstract

This paper discusses the location bias and the spatial resolution in the reconstruction of a single dipole source by various spatial filtering techniques used for neuromagnetic imaging. We first analyze the location bias for several representative adaptive and non-adaptive spatial filters using their resolution kernels. This analysis theoretically validates previously reported empirical findings that standardized low-resolution electromagnetic tomography (sLORETA) has no location bias. We also find that the minimum-variance spatial filter does exhibit bias in the reconstructed location of a single source, but that this bias is eliminated by using the normalized lead field. We then focus on the comparison of sLORETA and the lead-field normalized minimum-variance spatial filter, and analyze the effect of noise on source location bias. We find that the signal-to-noise ratio (SNR) in the measurements determines whether the sLORETA reconstruction has source location bias, while the lead-field normalized minimum-variance spatial filter has no location bias even in the presence of noise. Finally, we compare the spatial resolution for sLORETA and the minimum-variance filter, and show that the minimum-variance filter attains much higher resolution than sLORETA does. The results of these analyses are validated by numerical experiments as well as by reconstructions based on two sets of evoked magnetic responses.

Introduction

Among the various technologies for noninvasive neural measurement, the major advantage of magnetoencephalography (MEG) is its ability to provide fine temporal resolution, in the order of milliseconds (Hämäläinen et al., 1993). In neuromagnetic imaging, the signals recorded by MEG sensors are resolved into functional maps of dynamic brain activity, while retaining this high temporal precision. Many studies have addressed the question of how this reconstruction can be done efficiently (Baillet et al., 2001).

One prominent class of techniques, known as adaptive spatial filtering, was originally developed in the field of array signal processing (van Veen and Buckley, 1988). A well-known example of this class, the minimum-variance spatial filter, has been successfully applied to MEG/EEG source reconstruction problems (Robinson and Vrba, 1999; Sekihara and Scholz, 1996; Sekihara et al., 2001, 2002a; van Veen et al., 1997). Another popular class of source reconstruction methods is that of minimum-norm-based tomographic reconstruction. This class includes the original minimum-norm method (Hämäläinen and Ilmoniemi, 1984), the weight-normalized minimum-norm method (Dale et al., 2000), and a recently proposed method called standardized low-resolution electromagnetic tomography (sLORETA) (Pascual-Marqui, 2002). This paper formulates these minimum-norm-based methods as non-adaptive spatial filters, and compares them with the adaptive minimum-variance spatial filter on a unified basis.

We first compare several representative (either adaptive or non-adaptive) spatial filters with respect to the bias they introduce in the reconstructed location of a single source in the absence of noise. It is shown that under these conditions sLORETA has no location bias. This fact has been found previously in computer simulations (Pascual-Marqui, 2002), and our analysis validates these empirical findings. We also show that the minimum-variance spatial filter does lead to biased source reconstructions, but that this bias can be eliminated by using the normalized lead field. We then focus on the bias-free two methods, sLORETA and the lead-field normalized minimum-variance filter, and analyze how they perform with noisy measurements. We find that, depending on the signal-to-noise ratio (SNR), the sLORETA reconstruction may have some source-location bias. The lead-field normalized minimum-variance filter, however, has no location bias even in the presence of noise. Finally, we compare the spatial resolution of the two methods and show that the minimum-variance filter generally attains much higher spatial resolution than sLORETA does.

Following a brief introduction of several representative non-adaptive and adaptive spatial filter formulations, we analyze their source-location biases in Bias for the estimated source location and Effects of noise on the location bias. Spatial resolution presents the spatial resolution comparison for sLORETA and the minimum-variance filter. Numerical experiments presents a series of numerical experiments that validate the arguments in Theory. In Comparison using evoked MEG data, we compare sLORETA and the minimum-variance filter by applying them to somatosensory-and auditory-evoked MEG data.

Theory

Spatial filter formulation

Definitions

We define the magnetic field measured by the mth detector coil at time t as b_m (t), and a column vector b(t) = [b₁ (t), b₂ (t), …, b_M (t)]^T as a set of measured data where M is the total number of sensor coils and superscript T indicates the matrix transpose. The covariance matrix of the measurement is denoted R_b, that is, R_b = 〈b(t)b^T(t)〉 where 〈·〉 indicates the ensemble average. (This matrix is actually equal to the second-order moment matrix but is customarily called the covariance matrix.) The spatial location is represented by a three-dimensional vector r:r = (x, y, z). The source moment magnitude at r and time t is denoted as s(r, t). The orientation of a source at r is defined as a three-dimensional vector η(r) = [η_x (r), η_y (r), η_z (r)]^T whose ζ component (where ζ equals x, y, or z) is equal to the cosine of the angle between the direction of the source moment and the ζ direction.

We define ${\mathit{l}}_m^{\zeta }(\mathit{r})$ as the output of the mth sensor; the output is induced by the unit-magnitude source located at r and directed in the ζ direction. The column vector l_ζ (r) is defined as ${\mathit{l}}_{\zeta }(\mathit{r})={[l_1^{\zeta }(\mathit{r}),l_2^{\zeta }(\mathit{r}),\dots ,l_M^{\zeta }(\mathit{r})]}^T$. The lead field matrix, which represents the sensitivity of the whole sensor array at r, is defined as L(r) = [l_x(r), l_y(r),lz (r)]. The lead-field vector in the source-moment direction is defined as l(r) where l(r) = L (r) η(r). Using the superposition law, the relationship between b(t) and s(r, t) is expressed as

$$\mathit{b}(t)=\int \mathrm{L}(\mathit{r})\mathit{\eta }(\mathit{r})s(\mathit{r},t)d\mathit{r}+\mathit{n}(t)=\int \mathit{l}(\mathit{r})s(\mathit{r},t)d\mathit{r}+\mathit{n}(t).$$ (1)

Here, n (t) is the additive noise. The spatial filter uses a simple linear operation for estimating the magnitude of source activities, such that

$$\widehat{s}(\mathit{r},t)={\mathit{w}}^T(\mathit{r})\mathit{b}(t),$$ (2)

where ŝ (r, t) is the estimate of the source magnitude, and a column vector w (r) is a set of the spatial-filter weights, which characterizes each spatial filter.

Adaptive and non-adaptive spatial filters

There are two types of spatial filters. One is a non-adaptive spatial filter in which the filter weights are independent from the measurements. The L₂-norm based tomographic reconstruction methods can in principle be interpreted as non-adaptive spatial filters. The most basic and well-known non-adaptive spatial filter is the minimum-norm spatial filter (Hämäläinen and Ilmoniemi, 1984). Its weight vector is given by

$$\mathit{w}(\mathit{r})={\mathbf{G}}^{-1}\mathit{l}(\mathit{r}).$$ (3)

The matrix G, often referred to as the gram matrix, is defined such that

$$\mathbf{G}=\int [\mathbf{L}(\mathit{r}){\mathbf{L}}^T(\mathit{r})]d\mathit{r}.$$ (4)

One variant of the minimum-norm filter is the weight-normalized minimum-norm filter (Dale et al., 2000) whose weights are given by

$$\mathit{w}(\mathit{r})=\frac{{\mathbf{G}}^{-1}\mathit{l}(\mathit{r})}{\sqrt{{\mathit{l}}^T(\mathit{r}){\mathbf{G}}^{-2}\mathit{l}(\mathit{r})}}.$$ (5)

Another variant of the minimum-norm filter, called sLORETA, has been recently proposed (Pascual-Marqui, 2002). The weight vector for sLORETA is

$$\mathit{w}(\mathit{r})=\frac{{\mathbf{G}}^{-1}\mathit{l}(\mathit{r})}{\sqrt{{\mathit{l}}^T(\mathit{r}){\mathbf{G}}^{-1}\mathit{l}(\mathit{r})}}.$$ (6)

The derivations of the above-mentioned filter weights are presented in Appendix B. It should be pointed out that because the gram matrix G is close to a singular matrix for a typical neuromagnetic measurement geometry, the regularization may be applied when calculating G⁻¹. That is, (G + γI)⁻¹ is calculated instead of calculating G⁻¹. The choice of regularization parameter γ has been the subject of many investigations (Hansen, 1998). The value of the regularization parameter is typically set to the average variance of the sensor noise.

An adaptive spatial filter uses weights that depend on the measurements. The best-known adaptive spatial filter is the minimum-variance spatial filter (Robinson and Vrba, 1999; van Veen et al., 1997); its weight vector is expressed as

$$\mathit{w}(\mathit{r})=\frac{{\mathbf{R}}_b^{-1}\mathit{l}(\mathit{r})}{[{\mathit{l}}^T(\mathit{r}){\mathbf{R}}_b^{-1}\mathit{l}(\mathit{r})]}.$$ (7)

In Eqs. (3)–(7), the lead field vector l(r), which is the lead field in the source-moment direction η(r), is used for deriving the filter weights. Here, since η(r) is generally unknown, the optimum direction η_opt(r), which gives the maximum filter output, can be used instead of the unknown η(r). That is, l(r) can be obtained using l(r) = L(r)η_opt(r) (Sekihara and Scholz, 1996).

Resolution kernel

To compare various spatial filter formulations, we need a tool to characterize how appropriately the weights have been chosen. The resolution kernel (Backus and Gilbert, 1968; de Peralta Menendez et al., 1997) can play this role. We introduce the resolution kernel, derived by combining Eqs. (1) and (2),

$$\widehat{s}(\mathit{r})=\int {\mathit{w}}^T(\mathit{r})\mathit{l}(\mathit{r}\prime )s(\mathit{r}\prime )d\mathit{r}\prime =\int ℛ(\mathit{r},\mathit{r}\prime )s(\mathit{r}\prime )d\mathit{r}\prime ,$$ (8)

where

$$ℛ(\mathit{r},\mathit{r}\prime )={\mathit{w}}^T(\mathit{r})\mathit{l}(\mathit{r}\prime ).$$ (9)

Here, the explicit notation of time t is omitted. This ℛ(r, r′) is called the resolution kernel. It expresses the relationship between the original and reconstructed source distributions. When a single source with a unit magnitude exists at r₁, we can substitute s(r) = δ (r − r₁) into Eq. (8), and write the reconstructed results as ŝ(r) = ℛ(r, r₁). Thus, the resolution kernel directly gives the spatial reconstruction that results from a single point source in the absence of noise.

Defining f as f = l(r₁), and substituting Eq. (3) into Eq. (9), the resolution kernel for the minimum-norm spatial filter is given by

$$ℛ(\mathit{r},{\mathit{r}}_1)={\mathit{l}}^T{\mathbf{G}}^{-1}\mathit{f},$$ (10)

where the explicit notation of r is omitted from l(r). Using Eq. (5), the resolution kernel of the weight-normalized minimum-norm spatial filter is

$$ℛ(\mathit{r},{\mathit{r}}_1)=\frac{{\mathit{l}}^T{\mathbf{G}}^{-1}\mathit{f}}{\sqrt{{\mathit{l}}^T{\mathbf{G}}^{-2}\mathit{l}}}.$$ (11)

The resolution kernel for sLORETA is given by

$$ℛ(\mathit{r},{\mathit{r}}_1)=\frac{{\mathit{l}}^T{\mathbf{G}}^{-1}\mathit{f}}{\sqrt{{\mathit{l}}^T{\mathbf{G}}^{-1}\mathit{l}}}=\sqrt{{\mathit{f}}^T{\mathbf{G}}^{-1}\mathit{f}}\text{cos}(\mathit{l},\mathit{f}|{\mathbf{G}}^{-1}),$$ (12)

where the generalized cosine is defined according to Eq. (41). Using Eq. (7), the resolution kernel for minimum-variance filter is expressed as

$$ℛ(\mathit{r},{\mathit{r}}_1)=\frac{{\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{f}}{{\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{l}}.$$ (13)

An important property for the resolution kernel is to have its maximum at the source location. If this is not the case, the reconstructed source distribution will contain systematic biases and may thus be totally different from the true source distribution. In the following subsection, we check the resolution kernels for each of the spatial filters described in Spatial filter formulation, to see whether the corresponding filter avoids spatial bias.

Bias for the estimated source location

The bias for the estimated source location is evaluated by checking whether the resolution kernel has its maximum at the source location r₁, that is, whether the condition below holds for any r (r ≠ r₁) in the reconstruction region

$$ℛ({\mathit{r}}_1,{\mathit{r}}_1)>ℛ(\mathit{r},{\mathit{r}}_1).$$ (14)

For the minimum-norm filter, this condition is expressed as

$${\mathit{f}}^T{\mathbf{G}}^{-1}\mathit{f}>{\mathit{l}}^T{\mathbf{G}}^{-1}\mathit{f}.$$ (15)

Because the norm of l becomes very large in a region close to the sensors, the above inequality obviously does not hold. Actually, it is well known that in the minimum-norm filter, the source reconstruction is severely biased toward the sensor array (Jeffs et al., 1987). Because of this fact, when applying the minimum-norm filter, the normalized lead field vector l˜ = l/∥l∥ is often used. The condition for no location bias in this case is

$${\tilde{\mathit{f}}}^T{\tilde{\mathbf{G}}}^{-1}\mathit{f}>{\tilde{\mathit{l}}}^T{\tilde{\mathbf{G}}}^{-1}\mathit{f}\text{or}{(\tilde{\mathit{f}}-\tilde{\mathit{l}})}^T{\tilde{\mathbf{G}}}^{-1}\mathit{f}>0$$ (16)

where f̃ = f / ∥f∥ and G̃ is the gram matrix obtained using G̃ = ∫[L (r) L^T (r)] / ∥ L (r)∥² d_r. There is no guarantee that the left-hand side of the second equation in Eq. (16) always has a positive value, because the signs may be different between a component of a vector f̃ – l̃ and the corresponding component of f. Therefore, it is clear that the minimum-norm method generally has a localization bias even with the normalized lead field—although it has no bias in some locations where Eq. (16) is coincidentally satisfied.

For the weight-normalized minimum-norm filter, the condition in Eq. (14) is expressed as

$$\frac{{\mathit{f}}^T{\mathbf{G}}^{-1}\mathit{f}}{\sqrt{{\mathit{f}}^T{\mathbf{G}}^{-2}\mathit{f}}}>\frac{{\mathit{l}}^T{\mathbf{G}}^{-1}\mathit{f}}{\sqrt{{\mathit{l}}^T{\mathbf{G}}^{-2}\mathit{l}}}.$$ (17)

It is not straightforward to see whether this inequality holds for any pair of l and f. However, we can numerically show that it does not generally hold, and we give, in Numerical experiments, a typical numerical example of biased source-reconstruction results obtained from this weight-normalized minimum-norm filter. For sLORETA, using Eq. (12), the condition in Eq. (14) is expressed as

$$\text{cos}(\mathit{l},\mathit{f}|{\mathbf{G}}^{-1})<1.$$ (18)

Since G⁻¹ is a positive definite matrix, this condition holds for any f and l (f ≠ l), as mentioned in Appendix A. It is empirically known that sLORETA has no location bias for a single source (Pascual-Marqui, 2002), and the analysis presented here validates this empirical observation.

For the minimum-variance spatial filter, the condition for having no location bias is

$$\frac{{\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{f}}{{\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{l}}<1.$$ (19)

Using Eqs. (39) and (40) in Appendix A, the above condition can be rewritten as

$$\frac{{\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{f}}{{\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{l}}=\frac{\Vert \mathit{f}\Vert }{\Vert \mathit{l}\Vert }\frac{\text{cos}(\mathit{l},\mathit{f})}{1+\alpha [1-{\text{cos}}^{\text{2}}(\mathit{l},\mathit{f})]}<1.$$ (20)

In the above equation, $\alpha =({\sigma }_1^2/{\sigma }_0^2){\Vert \mathit{f}\Vert }^2,\text{where}{\sigma }_1^2\text{and}{\sigma }_0^2$ are the power of source activity and noise power, as defined in Appendix A. This α is often referred to as the input power SNR. It can be seen that the inequality in Eq. (20) may not hold when ∥l∥ is small. This can happen in a region near the center of the sphere when the spherical homogeneous conductor model (Sarvas, 1987) is used to derive the lead field. As a result, severe artifacts appear near the center of the sphere. However, the use of the normalized lead field vector l̃ can avoid these artifacts, and the condition for no location bias in this case is expressed as

$$ℛ(\mathit{r},{\mathit{r}}_1)=\frac{{\tilde{\mathit{l}}}^T{\mathbf{R}}_b^{-1}\mathit{f}}{{\tilde{\mathit{l}}}^T{\mathbf{R}}_b^{-1}\tilde{\mathit{l}}}=\Vert \mathit{f}\Vert \frac{\text{cos}(\tilde{\mathit{l}},\mathit{f})}{1+\alpha [1-{\text{cos}}^2(\tilde{\mathit{l}},\mathit{f})]}<ℛ({\mathit{r}}_1,{\mathit{r}}_1)=\Vert \mathit{f}\Vert .$$ (21)

Since α has a positive value, it is clear that this inequality is always fulfilled for any f and l, and we can conclude that the minimum-variance spatial filter with the normalized lead field has no location bias.

Effects of noise on the location bias

In the preceding section, the location bias in the source reconstruction has been analyzed using the resolution kernel and such analysis should be valid when the SNR is high. However, when the SNR is low, the noise may cause bias in the estimated source location even though the resolution kernel has its maximum at the true source location. The output signal power at a location r is equal to ${\sigma }_1^2ℛ{(\mathit{r},{\mathit{r}}_1)}^2$, and the output noise power is equal to ${\sigma }_0^2{\Vert \mathit{w}(\mathit{r})\Vert }^2$. Therefore, the condition for no location bias is

$${\sigma }_1^2ℛ{({\mathit{r}}_1,{\mathit{r}}_1)}^2+{\sigma }_0^2{\Vert \mathit{w}({\mathit{r}}_1)\Vert }^2>{\sigma }_1^2ℛ{(\mathit{r},{\mathit{r}}_1)}^2+{\sigma }_0^2{\Vert \mathit{w}(\mathit{r})\Vert }^2.$$ (22)

This condition can be written as

$$\frac{ℛ{(\mathit{r},{\mathit{r}}_1)}^2}{ℛ{({\mathit{r}}_1,{\mathit{r}}_1)}^2}\frac{[1+\mathit{\Omega }(\mathit{r})/\alpha ]}{[1+\mathit{\Omega }({\mathit{r}}_1)/\alpha ]}<1,$$ (23)

where α is the input SNR and Ω(r) is given by

$$\mathit{\Omega }(\mathit{r})=\frac{{\Vert \mathit{f}\Vert }^2{\Vert \mathit{w}(\mathit{r})\Vert }^2}{ℛ{(\mathit{r},{\mathit{r}}_1)}^2}.$$ (24)

For sLORETA, using Eqs. (6), (12), and (24), Eq. (23) is rewritten as

$$\frac{1+\mathit{\Omega }(\mathit{r})/\alpha }{1+\mathit{\Omega }({\mathit{r}}_1)/\alpha }{\text{cos}}^{\text{2}}(\mathit{l},\mathit{f}|{\mathbf{G}}^{-1})<1.$$ (25)

It can be seen in Eq. (25) that when α is very large, this condition becomes identical to Eq. (18). However, in general, the value of α determines whether the condition in Eq. (25) is satisfied for any l and f. In our numerical experiments, we present examples of cases in which this condition is either fulfilled or not fulfilled.

For the lead-field normalized minimum-variance spatial filter, using the weight in Eq. (7) and the resolution kernel in Eq. (21), the condition for no location bias is

$$\frac{[1+\mathit{\Omega }(\mathit{r})/\alpha ]}{[1+\mathit{\Omega }({\mathit{r}}_1)/\alpha ]}\frac{{\text{cos}}^{\text{2}}(\tilde{\mathit{l}},\mathit{f})}{{[1+\alpha [1-{\text{cos}}^2(\tilde{\mathit{l}},\mathit{f})]]}^2}<1,$$ (26)

where Ω(r) in this case is given by

$$\mathit{\Omega }(\mathit{r})=\frac{{\Vert \mathit{f}\Vert }^2[{\tilde{\mathit{l}}}^T{\mathbf{R}}_b^{-2}\tilde{\mathit{l}}]}{{[{\tilde{\mathit{l}}}^T{\mathbf{R}}_b^{-1}\mathit{f}]}^2}.$$ (27)

Using Eqs. (37) and (38), the condition in Eq. (26) can be simplified to

$$\frac{1}{1+\alpha [1-{\text{cos}}^2(\tilde{\mathit{l}},\mathit{f})]}<1,$$ (28)

This relationship holds for any l̃ and f because α has a positive value, and this fact indicates that the lead-field normalized minimum-variance spatial filter has no location bias even when the SNR is low.

Spatial resolution

When the resolution kernel has its maximum at the source location, the reconstructed source distribution can be interpreted as the smoothed version of the true source distribution, and the main-lobe width of the resolution kernel can be a measure of the spatial resolution. To compare the main-lobe width of the kernel, the point-spread function, φ(r), is defined as the resolution kernel normalized by its peak value: φ (r) = ℛ(r,r₁)/ℛ(r₁,r₁). For sLORETA, φ(r) is expressed as

$$\varphi (\mathit{r})=\text{cos}(\mathit{l},\mathit{f}|{\mathbf{G}}^{-1}).$$ (29)

For the lead-field normalized minimum-variance spatial filter, it is expressed as

$$\varphi (\mathit{r})=\frac{\text{cos}(\tilde{\mathit{l}},\mathit{f})}{1+\alpha [1-{\text{cos}}^2(\tilde{\mathit{l}},\mathit{f})]}=\frac{\text{cos}(\mathit{l},\mathit{f})}{1+\alpha [1-{\text{cos}}^2(\mathit{l},\mathit{f})]}.$$ (30)

The above equation shows that the spread function strongly depends on the input SNR α. This dependency has been reported previously (Cox, 1973; Gross et al., 2003). The major difference between the sLORETA point-spread function and that of the minimum-variance filter is the denominator in Eq. (30). Because a usually has a value greater than the number of sensors¹ M, the denominator causes a rapid decay of the point spread function. Consequently, the spatial resolution of the minimum-variance filter is usually much higher than that of sLORETA. In Numerical experiments, numerical examples of the point-spread functions are presented to demonstrate the high spatial resolution of the minimum-variance filter.

Numerical experiments

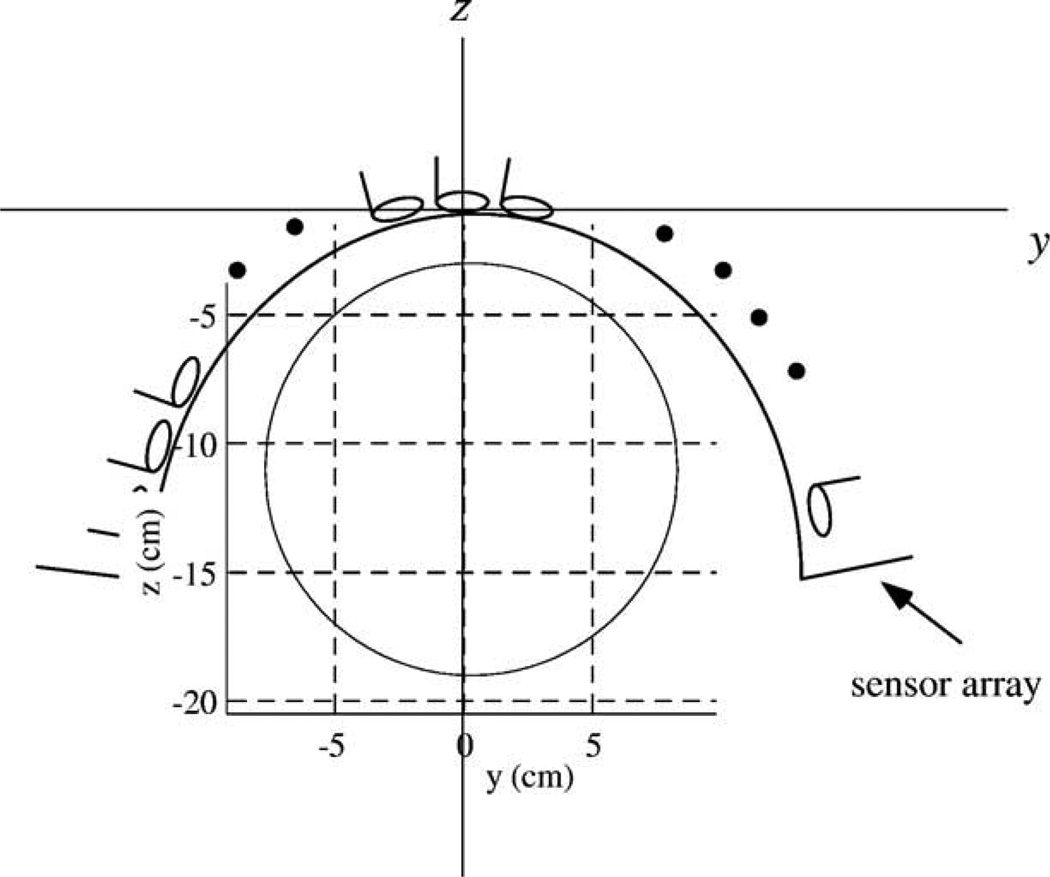
We used the coil configuration of the Magnes 2500™ neuro-magnetometer (4D Neuroimaging, San Diego) where 148 sensors are arranged on a helmet-shaped surface. As shown in Fig. 1, the coordinate origin was chosen as the center of the sensor array. The z direction is defined as the direction perpendicular to the plane of the coil located at this center. The x direction is defined as that from the posterior to the anterior, and the y direction is defined as that from the left to the right hemisphere. The values of (x, y, z) are expressed in centimeters.

Fig. 1.

The coordinate system used in the numerical experiments. The coordinate origin was set at the center of the sensor coil located at the center of the array. The plane at x = 0 cm is shown. The circle indicates the boundary of the sphere used for the forward calculations. The center of the sphere was set to (0, 0, −12).

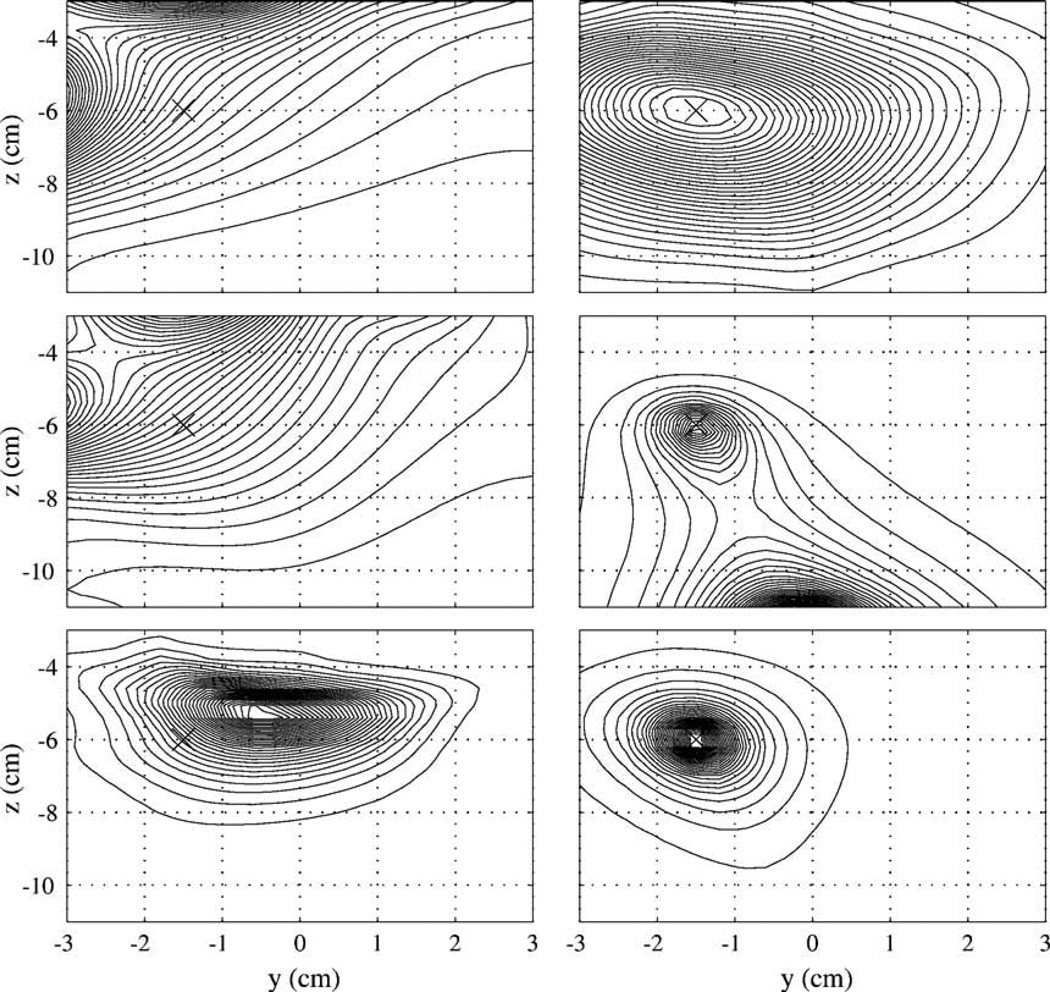
We first compare the location biases for the spatial filters described in Spatial filter formulation. To plot the resolution kernel, we assume that a point source exists at r₁ = (0, −1.5, −6). The power of the resolution kernel ℛ²(r, r₁) was plotted on the plane, x = 0. The results are shown in Fig. 2. Here, the contour plots on the left show, from top to bottom, respectively, the results of the minimum-norm filter, the minimum-norm filter with the normalized lead field, and the weight-normalized minimum-norm filter. The plots on the right show, from top to bottom, respectively, sLORETA, the minimum-variance filter, and the lead-field normalized minimum-variance filter. When deriving the weight vectors for these non-adaptive spatial filters, the gram matrix G was obtained by numerically integrating Eq. (4) over the volume defined as −5 ≤ x ≤ 5, −5 ≤ y ≤ 5, and −3 ≤ z ≤ 11, and the Tikhonov regularization was used for inverting G with the regularization constant set to 10⁻⁶ λ_max, where λ_max is the maximum eigenvalue of G. When deriving the minimum-variance results, the covariance matrix R_b was obtained using Eq. (36) with α = M where M is the total number of sensors and is equal to 148 in this computer simulation. Throughout these numerical experiments, the noise is assumed to be white Gaussian, and uncorrelated between sensor channels.

Fig. 2.

The plot of the square of the resolution kernel ℛ(r, r₁)² on the plane x = 0. The point source is located at (0, −1.5, −6) cm. The contour plots in the left-hand side from top to bottom, respectively, show the results of the minimum-norm filter, the lead-field normalized minimum-norm filter, and the weight-normalized minimum-norm filter. The plots in the right-hand side from the top to the bottom, respectively, show the results of sLORETA, the minimum-variance filter, and the lead-field normalized minimum-variance filter. The cross mark × indicates the source location. Each contour map is normalized by its maximum value and contains the same number of contour lines.

The resolution kernel for the minimum-norm filter, either with or without the lead-field normalization, shows a severe location bias toward the sensors, as mentioned in Bias for the estimated source location. The resolution kernel for the weight-normalized minimum-norm spatial filter has its maximum at a wrong location although the bias is not as large as that of the original minimum-norm method. The results clearly indicate that the relationship in Eq. (17) does not generally hold. The resolution kernel of sLORETA has its maximum at the source location. The resolution kernel for the minimum-variance spatial filter without the lead field normalization has two peaks: one at the source location and the other at the sphere origin, which is located at (0, 0, −12). The peak intensity at the sphere origin is much higher than that at the source location. The resolution kernel for the minimum-variance filter with the lead field normalization has its maximum at the source location. These results validate the arguments in Bias for the estimated source location.

We next tested the validity of the arguments regarding the effects of noise on the location bias. Assuming that a point source exists at (0, −1.5, −6), the power output 〈ŝ (r)²〉 is calculated using 〈ŝ (r)²〉 = w^T (r) R_bw (r). Here, the three input SNRs were tested: α = 8M, α = 4M, and α = M where M = 148. (As mentioned in Spatial resolution, the definition of α is given by $\alpha =({\sigma }_1^2/{\sigma }_0^2){\Vert \mathit{f}\Vert }^2$. We may use a different definition of the input SNR ζ that is closer to the definition conventionally used in MEG measurements, such that $\zeta =\sqrt{({\sigma }_1^2{\Vert \mathit{f}\Vert }^2/M)/{\sigma }_0^2}$. Namely, in this definition, ζ is equal to the square root of the field power average across sensor channels divided by the average noise power. Then, ζ is equal to 1, 2, and $2\sqrt{2}$ when α = M, α = 4M, and α = 8M, respectively).

The reconstructed results of this point source obtained from sLORETA are shown in Fig. 3a. The results from the lead-field normalized minimum-variance filter are shown in Fig. 3b. In Fig. 3, the contour maps from top to bottom, respectively, show the results for α = 8M, α = 4M, and α = M. These results show that sLORETA can detect the source at the correct location for the two cases of higher SNRs. It, however, cannot detect the source when α = M, that is, when the input SNR is the lowest among the three cases. The results here validate the conclusion that the SNR determines whether sLORETA reconstruction has the bias for the estimated source location. The results of the minimum-variance spatial filter show that, for all three SNR cases, it can detect the source at the correct location.

Fig. 3.

The results of the experiments regarding the effects of noise on location bias. (a) Results of point-source reconstruction from sLORETA and (b) those from the lead-field normalized minimum-variance filter. The point source is located at (0, −1.5, −6) cm. The contour plots from top to bottom, respectively, show the results for the input SNR α equal to 8M, 4M, and M. The cross mark × indicates the source location. Each contour map is normalized by its maximum value and contains the same number of contour lines.

The spatial resolution is next compared between sLORETA and the minimum-variance spatial filter. The point-spread functions φ(r) are plotted with respect to |r₁ – r| where r₁ = (0, 0, −6). The plot of the point-spread function with respect to the y (horizontal) direction is shown in Fig. 4. In this figure, the three solid lines indicate the spread-function of the minimum-variance filter for the cases of α = 8M, α = 4M, and α = M. The broken line indicates the kernel shape of sLORETA. These plots indicate that the spatial resolution of the minimum-variance filter is much higher than that of sLORETA. In the next section, sLORETA and the minimum-variance spatial filter are applied to two sets of evoked recordings to further demonstrate the difference in the spatial resolution between these two kinds of spatial filters.

Fig. 4.

The plot of the point-spread function (the normalized resolution kernel) in the horizontal (y) direction. The three solid lines indicate the spread-function of the minimum-variance filter for the cases of α = 8M, α = 4M, and α = M. The broken line indicates the point-spread function of sLORETA. The point source was assumed to exist at (0, 0, −6), and the abscissa expresses the distance from the source location in the y direction.

Comparison using evoked MEG data

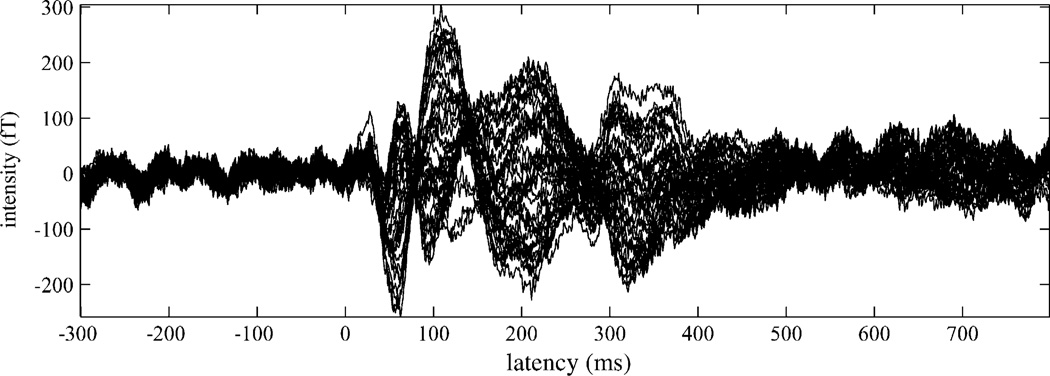
The somatosensory response was recorded using a 160-channel whole head sensor array (MEGVISION, Yokogawa Electric Corp, Tokyo, Japan) with an electric stimulus delivered to the right median nerve at the subject’s wrist with a 250-ms interstimulus interval. An epoch of 150 ms duration (50 ms pre- and 150 ms post-stimulus) was digitized at 10 kHz sampling frequency and a total of 10,000 epochs were averaged. The averaged somatosensory response is shown in Fig. 5 where the primary N20m peak is clearly identified.

Fig. 5.

The averaged somatosensory response obtained using a 160-channel whole head sensor array (MEGVISION, Yokogawa Electric Corp, Tokyo, Japan) with an electric stimulus. The stimulus was delivered to the right median nerve at the subject’s wrist with a 250-ms interstimulus interval. An epoch was digitized at 10 kHz sampling frequency and a total of 10,000 epochs were averaged. The recorded epochs were filtered with a bandpass filter of 3–300 Hz bandwidth.

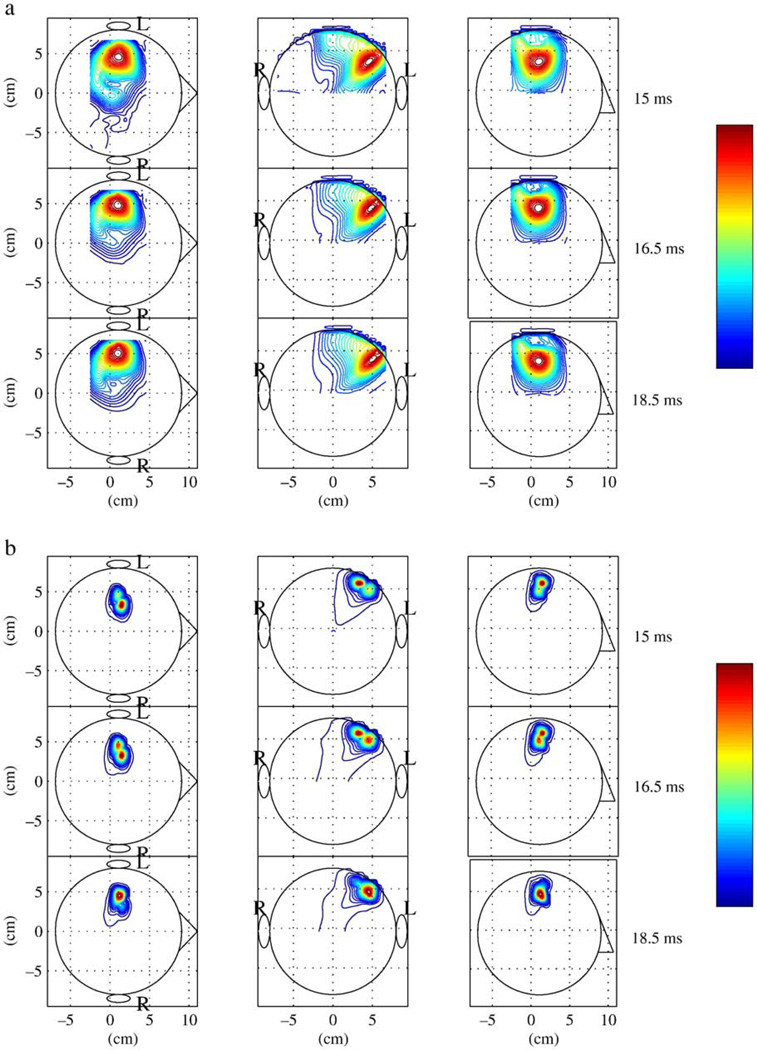
We first applied sLORETA to this somatosensory response. When calculating the filter weight in Eq. (6), the gram matrix was calculated by averaging L(r) L^T (r) over the whole brain region. We selected three time points, 15.5, 16.5, and 18.5 ms, near the vertex of the N20m peak. The reconstructed source-magnitude map at these time points obtained from sLORETA is shown in Fig. 6a. In this figure, the maximum intensity projection of the three-dimensional current density reconstruction ŝ (r, t)² onto the axial, coronal, and sagittal planes are shown in the right, middle, and left panels, respectively. Also, in this figure, the results in the upper, middle, and bottom rows, correspond respectively to the reconstruction at the latencies of 15, 16.5, and 18.5 ms. These results clearly indicate the activation of the left parietal region, probably near the primary somatosensory (SI) area. In these reconstruction results, however, there are no significant differences among the results at these three latencies.

Fig. 6.

(a) The reconstructed source-magnitude map at latencies of 15.5, 16.5, and 18.5 ms obtained using sLORETA. (b) The reconstructed source-magnitude map obtained using the lead-field normalized minimum-variance filter at the same latencies. The maximum intensity projections of the reconstructed three-dimensional current density onto the axial, coronal, and sagittal planes are shown in the right, middle and left panels, respectively. The letters L and R show the left and right hemisphere, respectively. The circles depicting a human head indicate the projections of the sphere used in the forward calculations. Each contour map is normalized by its maximum value, and contains the same number of contour lines. The color of the contour lines shows the relative intensity indicated by the color bar.

We next applied the minimum-variance spatial filter to this somatosensory response. In these experiments, the weight vector of the lead-field normalized minimum-variance filter is obtained and then the weight vector is projected onto the signal subspace of the measurement covariance matrix Rb. The resultant projected weight is used for the spatial filtering. This projection can avoid the SNR degradation caused by errors in the forward modeling or in estimating R_b from data samples (Sekihara et al., 2002). The sample covariance matrix was calculated using a time window between 12 and 96 ms. The reconstructed results at the same three latencies are shown in Fig. 6b. Compared to the results in Fig. 6a, the results in Fig. 6b exhibit much higher spatial resolution. Indeed, in Fig. 6b, two sources in the SI area can be resolved, and we can observe the lateral one becoming stronger while the medial source becomes weaker during the period between 15.5 and 18.5 ms². The comparison between Figs. 6(a) and (b) clearly demonstrates the high spatial resolution of the minimum-variance spatial filter.

The second data set consists of evoked magnetic responses recorded with simultaneously applied auditory and somatosensory stimuli using the 37-channel Magnes™ magnetometer (4D Neuroimaging, San Diego). In these measurements, we applied auditory and somatosensory stimuli with simultaneous onsets. The auditory stimulus was a 1000-Hz pure tone with a 200-ms duration; it was applied to the subject’s right ear. The somatosensory stimulus was a 30 ms-duration tactile pulse (17 psi) delivered to the distal segment of the right index finger. The data were acquired at a sampling frequency of 1 kHz for the prestimulus interval of 300 ms and the poststimulus interval of 800 ms and averaged for 256 epochs. The sensor array was placed on the left hemisphere and positioned to best record the M100 auditory response. The mean interstimulus interval was 2 s, randomly varied between 1.75 and 2.25 s. The measured magnetic responses are shown in Fig. 7.

Fig. 7.

The average evoked magnetic responses recorded with simultaneously applied auditory and somatosensory stimuli using the 37-channel Magnes™ magnetometer. The auditory stimulus was a 1000 Hz pure tone with a 200-ms duration; it was applied to the subject’s right ear. The somatosensory stimulus was a 30-ms duration tactile pulse (17 psi) delivered to the distal segment of the right index finger. The data was acquired at a sampling frequency of 1 kHz and averaged for 256 epochs. An on-line bandpass filter with a bandwidth from 1 to 400 Hz was used and no post-processing digital filter was applied.

The results of the source reconstruction from sLORETA and the minimum-variance spatial filter are, respectively, shown in Figs. 8a and b for the selected three time points of 60 ms, 120 ms, and 180 ms. In the minimum-variance filter reconstruction, the covariance matrix of the measurements, R_b, was calculated from the time window between 0 and 300 ms. The results for sLORETA in Fig. 8a cannot resolve the two sources in the primary somatosensory and the primary auditory cortices. However, the results from the lead-field normalized minimum-variance filter in Fig. 8b resolve these two sources. These results again demonstrate that the spatial resolution of the minimum-variance filter is much higher than that of sLORETA.

Fig. 8.

(a) The reconstructed source-magnitude map at latencies of 60, 120, and 180 ms obtained using sLORETA. (b) The reconstructed source-magnitude map obtained using the lead-field normalized minimum-variance filter at the same latencies. The maximum intensity projections of the three-dimensional current density reconstruction onto the axial, coronal, and sagittal planes are shown in the right, middle and left panels, respectively. The letters L and R show the left and right hemisphere, respectively. The circles depicting a human head indicate the projections of the sphere used in the forward calculations. Each contour map is normalized by its maximum value, and contains the same number of contour lines. The color of the contour lines shows the relative intensity indicated by the color bar.

Discussion and conclusion

The weight-normalized version of the minimum-variance filter has been used for MEG source reconstruction (Sekihara et al., 2001). The weight vector for this type of filter is given by

$$\mathit{w}(\mathit{r})=\frac{{\mathit{w}}_{MV}(\mathit{r})}{\Vert {\mathit{w}}_{MV}(\mathit{r})\Vert }=\frac{{\mathbf{R}}_b^{-1}\mathit{l}(\mathit{r})}{\sqrt{{\mathit{l}}^T(\mathit{r}){\mathbf{R}}_b^{-2}\mathit{l}(\mathit{r})}},$$ (31)

where w_MV(r) indicates the weight obtained from Eq. (7). The resolution kernel is then expressed as

$$ℛ(\mathit{r},{\mathit{r}}_1)=\frac{{\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{f}}{\sqrt{{\mathit{l}}^T{\mathbf{R}}_b^{-2}\mathit{l}}}.$$ (32)

Using Eqs. (37) and (38), the condition for the resolution kernel having maximum at the source location is given by

$$\frac{\text{cos}(\mathit{l},\mathit{f})}{\sqrt{1+\alpha (\alpha +2)(1-{\text{cos}}^2(\mathit{l},\mathit{f}))}}<1.$$ (33)

Because α is positive, the above condition obviously holds for any l and f. The condition for no location bias when noise exists is expressed as

$$\frac{1+\alpha (1-{\text{cos}}^2(\mathit{l},\mathit{f}))}{[1+\alpha (1-{\text{cos}}^2(\mathit{l},\mathit{f}))+\alpha (\alpha +1)(1-{\text{cos}}^2(\mathit{l},\mathit{f}))]}<1.$$ (34)

It is again clear that this condition holds for any l and f, and thus the weight-normalized minimum-variance filter does not have a location bias even when noise exists.

The comparison between Eqs. (5) and (31) shows the similarity between the weight-normalized minimum-norm and minimum-variance spatial filters. Actually, Eq. (5) is exactly the same as Eq. (31) if G is replaced with Rb. Assuming that the sensor noise is the spatially-uncorrelated Gaussian noise with the variance of ${\sigma }_0^2$, we have the relationship

$${\mathbf{R}}_b=\int \int [\mathbf{L}(\mathit{r}){\mathbf{L}}^T(\mathit{r}\prime )]\langle s(\mathit{r},t)s(\mathit{r}\prime ,t)\rangle d\mathit{r}d\mathit{r}\prime +{\sigma }_0^2\mathbf{I}.$$ (35)

Therefore, if 〈s(r, t) s(r′, t)〉 = σ²δ (r – r′), namely if the sources are the uniformly distributed incoherent sources, the above relationship reduces to ${\mathbf{R}}_b=\mathbf{G}+{\sigma }_0^2\mathbf{I}$, and the weight-normalized minimum-norm and minimum-variance filters are equal (Mosher et al., 2003). However, in general, these two spatial filters are very different and the weight-normalized minimum-variance filter can obtain unbiased estimates of the source locations, while the weight-normalized minimum-norm filter cannot, as we have shown here.

In summary, we have discussed the source location bias in the single-source reconstruction for several representative spatial filters and found that sLORETA and the lead-field normalized minimum-variance spatial filter do not have a source location bias. When measurement noise is taken into account, the SNR determines whether the results of the sLORETA reconstruction contains a bias in estimated source location. On the other hand, the lead-field normalized minimum-variance filter has no location bias even when noise exists. We compare the spatial resolution for sLORETA and the minimum-variance filter, and show that the minimum-variance filter provide much higher spatial resolution than sLORETA. The results of these arguments are validated by our numerical experiments as well as the experiments using evoked responses.

This paper compares adaptive and non-adaptive spatial filters with respect to source location bias and spatial resolution. As far as these performance measures are concerned, the results in this paper support the superiority of the adaptive filters over the non-adaptive filters. It should be mentioned that, however, to really determine the superiority of one over the other, a thorough investigation would be required, not only of these performance measures but also of other performance measures including robustness to various causes of error such as the existence of correlated sources, the effects of sample covariance, and the violation of the low-rank signal assumption. It should be noted that the results of our analysis in this paper regarding the performance of the adaptive filters indicate their asymptotic performance, which is obtained when the ideal covariance is used. The lead-field normalized minimum-variance filter may show some amount of the source bias when a sample covariance matrix is obtained from a limited number of time points. Also, it is well known that the reconstruction results from adaptive filters can be degraded when highly-correlated sources exist (Sekihara et al., 2002b), while non-adaptive filters are not influenced by source correlation. Therefore, investigations clarifying the complementarity of both types of spatial filters are needed, and such investigations are currently underway, with results to be published in the near future.

Appendix A

Mathematical preliminaries

This appendix provides mathematical preliminaries that help readers follow the discussion in Theory. Let us assume that a single source exists at r₁. Its moment magnitude is denoted s₁ (t) and its power is denoted ${\sigma }_1^2;{\sigma }_1^2=\langle s_1{(t)}^2\rangle$. The lead field vector at r₁ in the source direction is denoted f, namely, f = l(r₁). Then, the measured data b(t) is expressed as b(t) = s₁ (t) f + n(t) where n(t) is the additive noise. The noise is assumed to be white Gaussian noise uncorrelated among sensor channels. Thus, ${\sigma }_0^2\mathbf{I}=\langle \mathit{n}(t){\mathit{n}}^T(t)\rangle$, where ${\sigma }_0^2$ is the power of the noise. The measurement covariance matrix Rb is given by

$${\mathbf{R}}_b={\sigma }_0^2\mathbf{I}+{\sigma }_1^2\mathit{f}{\mathit{f}}^T.$$ (36)

Its inverse is expressed as

$${\mathbf{R}}_b^{-1}=\frac{1}{{\sigma }_0^2}(\mathbf{I}-\frac{\alpha }{1+\alpha }\frac{\mathit{f}{\mathit{f}}^T}{{\Vert \mathit{f}\Vert }^2}),$$ (37)

where $\alpha =({\sigma }_1^2/{\sigma }_0^2){\Vert \mathit{f}\Vert }^2$. For the dicussion in effects of noise on the location bias, the square inverse is derived as

$${\mathbf{R}}_b^{-2}=\frac{1}{{\sigma }_0^4}(\mathbf{I}-\frac{(2+\alpha )\alpha }{{(1+\alpha )}^2}\frac{\mathit{f}{\mathit{f}}^T}{{\Vert \mathit{f}\Vert }^2}).$$ (38)

Making use of the formula in Eq. (37), we have

$${\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{l}=\frac{1}{{\sigma }_0^2}({\Vert \mathit{l}\Vert }^2-\frac{\alpha }{1+\alpha }\frac{{({\mathit{l}}^T\mathit{f})}^2}{{\Vert \mathit{f}\Vert }^2})=\frac{{\Vert \mathit{l}\Vert }^2}{{\sigma }_0^2}(1-\frac{\alpha }{1+\alpha }{\text{cos}}^{\text{2}}(\mathit{l},\mathit{f})),$$ (39)

and

$${\mathit{l}}^T{\mathbf{R}}_b^{-1}\mathit{f}=\frac{1}{{\sigma }_0^2}({\mathit{l}}^T\mathit{f}-\frac{\alpha }{1+\alpha }\frac{({\mathit{l}}^T\mathit{f})({\mathit{f}}^T\mathit{f})}{{\Vert \mathit{f}\Vert }^2})=\frac{{\mathit{l}}^T\mathit{f}}{{\sigma }_0^2(1+\alpha )}.$$ (40)

Therefore, we can derive Eq. (20).

The definition of the generalized cosine between the two column vectors a₁ and a₂ with the metric C, where C is a positive definite matrix is

$${\text{cos}}^{\text{2}}({\mathit{a}}_1,{\mathit{a}}_2|\mathbf{C})=\frac{{({\mathit{a}}_1^T\mathbf{C}{\mathit{a}}_2)}^2}{({\mathit{a}}_1^T\mathbf{C}{\mathit{a}}_1)({\mathit{a}}_2^T\mathbf{C}{\mathit{a}}_2)},$$ (41)

or

$$\text{cos}({\mathit{a}}_1,{\mathit{a}}_2|\mathbf{C})=\frac{\left|{\mathit{a}}_1^T\mathbf{C}{\mathit{a}}_2\right|}{\sqrt{({\mathit{a}}_1^T\mathbf{C}{\mathit{a}}_1)({\mathit{a}}_2^T\mathbf{C}{\mathit{a}}_2)}}.$$ (42)

Here, the inequalities cos²(a₁, a₂|C) ≤ 1 and cos(a₁, a₂|C) ≤ 1 hold, because the Swartz inequality holds for any positive definite matrix C, that is,

$$({\mathit{a}}_1^T\mathbf{C}{\mathit{a}}_1)({\mathit{a}}_2^T\mathbf{C}{\mathit{a}}_2)\ge {({\mathit{a}}_1^T\mathbf{C}{\mathit{a}}_2)}^2.$$ (43)

When C is equal to the identity matrix I, the generalized cosine is simply written as cos²(a₁, a₂), which is equal to

$${\text{cos}}^2({\mathit{a}}_1,{\mathit{a}}_2)=\frac{{({\mathit{a}}_1^T{\mathit{a}}_2)}^2}{({\mathit{a}}_1^T{\mathit{a}}_1)({\mathit{a}}_2^T{\mathit{a}}_2)}.$$ (44)

Appendix B

Non-adaptive spatial filter formulations

This appendix shows how the non-adaptive spatial filter formulations described in Adaptive and non-adaptive spatial filters can be obtained from their well-known tomographic-reconstruction formulations. The tomographic-reconstruction formulations assume pixels, of which locations are denoted r₁, r₂, …, r_N where N is the total number of pixels. The composite lead field for all pixel locations are, then, defined as

$${\mathbf{L}}_N=[\mathbf{L}({\mathit{r}}_1),\mathbf{L}({\mathit{r}}_2),\dots ,\mathbf{L}({\mathit{r}}_N)].$$ (45)

Using L_N, the minimum-norm reconstruction method is expressed as

$$\left[\begin{array}{c}\widehat{\mathit{s}}({\mathit{r}}_1,t)\\ \widehat{\mathit{s}}({\mathit{r}}_2,t)\\ ⋮\\ \widehat{\mathit{s}}({\mathit{r}}_N,t)\end{array}\right]={\mathbf{L}}_N^T{({\mathbf{L}}_N{\mathbf{L}}_N^T)}^{-1}\mathit{b}(t)=\left[\begin{array}{c}{\mathbf{L}}^T({\mathit{r}}_1)\\ {\mathbf{L}}^T({\mathit{r}}_2)\\ ⋮\\ {\mathbf{L}}^T({\mathit{r}}_N)\end{array}\right]{({\mathbf{L}}_N{\mathbf{L}}_N^T)}^{-1}\mathit{b}(t),$$ (46)

where the vector ŝ(r_j, t) is the estimated three-dimensional source vector defined as

$$\widehat{\mathit{s}}({\mathit{r}}_j,t)={[{\widehat{s}}_x({\mathit{r}}_j,t),{\widehat{s}}_y({\mathit{r}}_j,t),{\widehat{s}}_z({\mathit{r}}_j,t)]}^T.$$

Therefore, from Eq. (46), we obtain

$$\widehat{\mathit{s}}({\mathit{r}}_j,t)={\mathbf{L}}^T({\mathit{r}}_j){({\mathbf{L}}_N{\mathbf{L}}_N^T)}^{-1}\mathit{b}(t).$$ (47)

In Eq. (47), the product ${\mathbf{L}}_N{\mathbf{L}}_N^T$ is equal to the gram matrix G, which is defined in Eq. (4), that is,

$${\mathbf{L}}_N{\mathbf{L}}_N^T=\sum _{j=1}^N\mathbf{L}({\mathit{r}}_j){\mathbf{L}}^T({\mathit{r}}_j)=\mathbf{G},$$ (48)

where errors caused due to the pixel discretization are neglected. Therefore, the three-dimensional current vector at r_j is obtained as

$$\widehat{\mathit{s}}({\mathit{r}}_j,t)={\mathbf{L}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{b}(t)={\mathbf{W}}^T({\mathit{r}}_j)\mathit{b}(t),$$ (49)

where the weight matrix W (r_j) is defined as W (r_j) = G⁻¹ L (r_j). The above equation is the vector spatial-filter formulation of the minimum-norm reconstruction method. To derive the scalar formulation, we assume that the orientation of each voxel is known and define the lead field in that voxel orientation as l(r_j). Then, the scalar spatial-filter formulation can also be derived as

$$\widehat{s}({\mathit{r}}_j,t)={\mathit{l}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{b}(t)={\mathit{w}}^T({\mathit{r}}_j)\mathit{b}(t),$$ (50)

where w(r_j) = G⁻¹ l (r_j) and the scalar ŝ (r_j, t) is the (signed) source magnitude. This weight vector is identical to that in Eq. (3).

Using the weight matrix for the minimum-norm filter W(r_j) defined above, the original form of the weight-normalized minimum-norm method proposed by Dale et al. (2000)³ is equal to

$$\widehat{\mathit{s}}({\mathit{r}}_j,t)=\frac{{\mathbf{W}}^T({\mathit{r}}_j)\mathit{b}(t)}{\sqrt{\mathit{t}\mathit{r}[{\mathbf{W}}^T({\mathit{r}}_j)\mathbf{W}({\mathit{r}}_j)]}}=\frac{{\mathbf{L}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{b}(t)}{\sqrt{\mathit{t}\mathit{r}[{\mathbf{L}}^T({\mathit{r}}_j){\mathbf{G}}^{-2}\mathbf{L}({\mathit{r}}_j)]}}.$$ (51)

Introducing the lead field in the voxel orientation l(r_j), the scalar formulation is derived as

$$\widehat{s}({\mathit{r}}_j,t)=\frac{{\mathit{l}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{b}(t)}{\sqrt{{\mathit{l}}^T({\mathit{r}}_j){\mathbf{G}}^{-2}\mathit{l}({\mathit{r}}_j)}}={\mathit{w}}^T({\mathit{r}}_j)\mathit{b}(t),$$ (52)

where $\mathit{w}({\mathit{r}}_j)={\mathbf{G}}^{-1}\mathit{l}({\mathit{r}}_j)/\sqrt{{\mathit{l}}^T({\mathit{r}}_j){\mathbf{G}}^{-2}\mathit{l}({\mathit{r}}_j)}$. This weight vector is identical to that in Eq. (5).

Finally, we derive the spatial-filter form of sLORETA. In this method, the minimum-norm reconstruction results are normalized by the square root of the resolution kernel. The resolution kernel of the vector minimum-norm filter in Eq. (49) is obtained as a 3 × 3 matrix W^T (r_j) L (r_j) = L^T (r_j) G⁻¹ L (r_j). Thus, the formulation equivalent to Eq. (20) in Pascual-Marqui (2002) is

$$\widehat{\mathit{s}}({\mathit{r}}_j,t)={[{\mathbf{L}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathbf{L}({\mathit{r}}_j)]}^{-1/2}{\mathbf{L}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{b}(t).$$ (53)

Substituting the lead field matrix L^T (r_j) with the lead field vector in the voxel orientation, l (r_j), in the above equation, the scalar version of sLORETA spatial filter is obtained as

$$\widehat{\mathit{s}}({\mathit{r}}_j,t)=\frac{{\mathit{l}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{b}(t)}{\sqrt{{\mathit{l}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{l}({\mathit{r}}_j)}}={\mathit{w}}^{\mathit{T}}({\mathit{r}}_j)\mathit{b}(t),$$ (54)

where $\mathit{w}({\mathit{r}}_j)={\mathbf{G}}^{-1}\mathit{l}({\mathit{r}}_j)/\sqrt{{\mathit{l}}^T({\mathit{r}}_j){\mathbf{G}}^{-1}\mathit{l}({\mathit{r}}_j)}$. This weight vector is identical to that in Eq. (6).