Overcoming Nonlinear Partial Volume Effects in Known-Component Reconstruction of Cochlear Implants

Abstract

Nonlinear partial volume (NLPV) effects can be significant for objects with large attenuation differences and fine detail structures near the spatial resolution limits of a tomographic system. This is particularly true for small metal devices like cochlear implants. While traditional model-based approaches might alleviate these artifacts through very fine sampling of the image volume and subsampling of rays to each detector element, such solutions can be extremely burdensome in terms of memory and computational requirements. The work presented in this paper leverages the model-based approach called “known-component reconstruction” (KCR) where prior knowledge of a surgical device is integrated into the estimation. In KCR, the parameterization of the object separates the volume into an unknown background anatomy and a known component with unknown registration. Thus, one can model projections of an implant at very high spatial resolution while limiting the spatial resolution of the anatomy - in effect, modeling NLPV effects where they are most significant. We present modifications of the KCR approach that can be used to largely eliminate NLPV artifacts, and demonstrate the efficacy of the modified technique (with improved image quality and accurate implant position estimates) for the cochlear implant imaging scenario.

INTRODUCTION

Accurate visualization of cochlear implants in post-operative imaging is critical for assessing intracochlear positioning, identifying possible trauma resulting from improper implant insertion, and predicting outcomes. [1] Furthermore, recent work has shown that position-dependant cochlear implant sound processing strategies lead to significant improvement in hearing outcomes. [2] Thus, accurate localization of electrodes relative to the auditory nerve, can facilitate better outcomes. While studies have shown efficacy in using both multi-slice CT [3] and flat-panel-based cone-beam CT (CBCT) [4], cochlear implant imaging remains difficult due to reconstruction artifacts, often making visualization of individual electrodes or the surrounding anatomy troublesome. Better visualization of the implant and surrounding anatomy would benefit postoperative assessment and help to facilitate minimally invasive procedures[5], potentially with intraoperative CBCT [6] for immediate correction of misplaced implants. Cochlear implants, typically composed of platinum or platinum-iridium alloys, have important features that are often near the spatial resolution limits of the scanner and are subject to a number of effects that make them particularly susceptible to metal artifacts (Figure 1). [7] Specific effects include: 1) beam-hardening due to high electron density; 2) photon starvation in low dose acquisitions; and 3) significant artifacts arising from nonlinear partial volume (NLPV) effects [8] (also known as exponential edge-gradient effects [9]).

Figure 1.

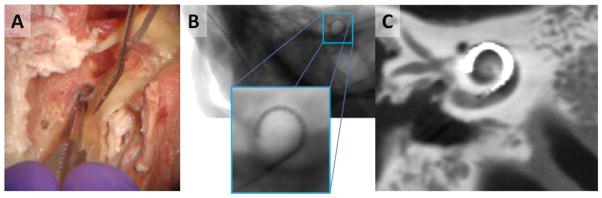
A) Surgical implantation of a cochlear implant is performed through a small opening in the cochlea. B) Projection image of a cochlear implant. While individual electrodes are near the spatial resolution limit, they are still apparent. C) In flat-panel CBCT, fine implant details and surrounding anatomy are difficult to visualize due to a number of artifacts including NLPV.

While there are various approaches to manage beam-hardening effects, and statistical methods have found application in the reduction of artifacts arising from photon starvation, eliminating NLPV effects can be more difficult. Although correction approaches [10] have been attempted, these have generally not been integrated into model-based and statistical reconstruction methods. Moreover, although one can potentially reduce NLPV effects through very fine sampling of the reconstruction volume and by casting multiple rays for each detector element, such an approach would have a high computational burden and memory requirements. Additionally, such fine sampling is likely to degrade the conditioning of the reconstruction and result in unfavorable noise levels.

We propose to leverage recent work in model-based reconstruction using known component reconstruction (KCR) [11–13] where the image volume is decomposed into an unknown background anatomy and a known component (e.g., the cochlear implant) that is unknown with respect to its position and deformation within the anatomy. This decomposition results in a new estimator that jointly reconstructs the background anatomy and provides the registration of the known device. This formulation of the reconstruction problem provides a unique opportunity to model NLPV effects, since the background anatomy and implant can be de-coupled, and projections through the known component can be modeled with much higher fidelity than would ordinarily be possible due to computational constraints and data limitations. In addition to reducing artifacts in the resulting image reconstruction, the KCR process yields a precise (sub-mm) solution of implant registration that could be taken as a measurement of implant position for purposes of electrode tuning. [2] Modifications of the KCR approach to handle NLPV effects are discussed in the following section.

METHODS

For simplicity, consider the monoenergetic KCR object model from [11] with a single known component written as

$$\mu ({\mu }_{\ast },\lambda )=\mathbf{D}\left\{\mathbf{W}(\lambda )s_I\right\}{\mu }_{\ast }+\mathbf{W}(\lambda ){\mu }_I.$$ (1)

Note that the single-component, monoenergetic form is easily extended to an arbitrary number of components and a polyenergetic model[14]. The attenuation volume is a function of the background anatomy (μ_*) and registration parameters (λ) associated with deformation and positioning of the implant model within the volume through the operator W(λ). The implant model provides a known structure and composition described by the attenuation volume (μ_I) and a support mask (s_I) which is largely binary (zero inside the implant and unity outside, with fractional values for voxels with mixed implant and anatomy). Because (1) allows for voxels to be comprised of both implant and anatomy, there is a unique opportunity to better model NLPV, as we will discuss below. For the cochlear implant imaging scenario, we have developed the implant model illustrated in Figure 2. This model can be discretized to arbitrarily fine voxels and has a deformable trajectory parameterized using B-splines and control points.

Figure 2.

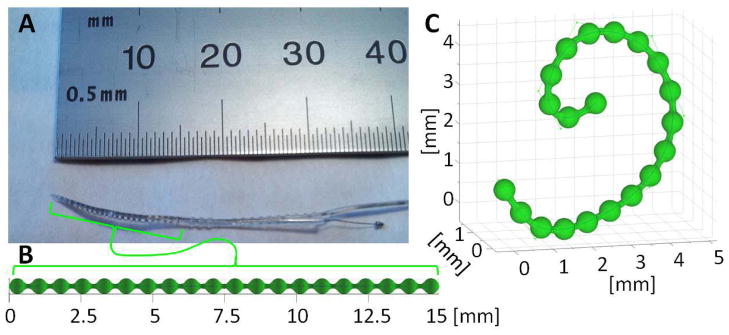
A) Photograph of the tip of a cochlear implant containing a series of platinum electrodes along a wire. B) An undeformed model of the metal components within a cochlear implant. C) The same model deformed using control points that define the trajectory of the center of the wire using B-splines. This model can be used within the KCR framework given a known composition to generate the implant mask (s_I), the implant attenuation (μ_I), and deformations thereof.

Using vector notation and a system matrix (A), projection data (y) would typically be modeled using Beer’s law as

$$\overline{y}=I_{0}exp\left[-\mathbf{A}\mu ({\mu }_{\ast },\lambda )\right]$$ (2)

where I₀ denotes scalar gain associated with exposure. However, this model does not approximate NLPV. A modified forward model that uses a system matrix (B) with fine sampling in both volume and projection domains is

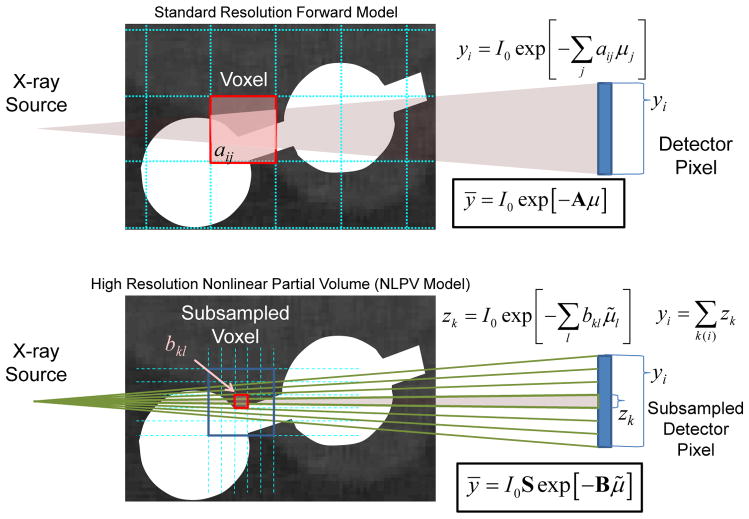
$$\overline{y}=I_0\mathbf{S}exp\left[-\mathbf{B}\mu ({\mu }_{\ast },\lambda )\right]$$ (3)

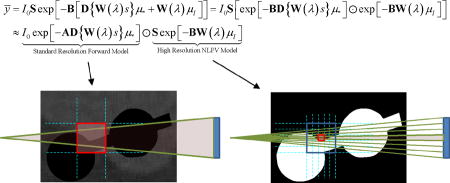
where the operator S aggregates fine detector subsamples up to the physical detector size. These models are illustrated in Figure 3. Ordinarily, adopting the fine sampling model in (3) comes with significant computational cost, and potentially increased noise due to small voxels. However, because KCR has the unique ability to separate implant and anatomy, we may circumvent the brute force supersampling approach by substituting the KCR object model of (1) into (3) and making the following approximation:

Figure 3.

Graphical illustration of a standard forward model (top) and a forward model that approximates NLPV effects (bottom). A small portion of inner ear anatomy is shown with two cochlear implant electrodes. Whereas a standard model relates the contribution (a_ij) of each voxel to each detector element (yi), a high-fidelity forward model breaks each voxel and each native detector element into smaller elements which are integrated at the detector to accommodate the distribution of x-rays within a single detector element. Computationally, the cost of the high-resolution model increases with the cube as voxel sizes are reduced and with the square as detector elements are subsampled.

(4)

In words, (4) represents the factoring of the forward model into the multiplication of projections of the background anatomy (μ_* term) and the implant (μ_I term). Because NLPV effects are less pronounced for coarse structures and smaller differences in attenuation value, we may approximate the μ_* portion of the forward model (patient anatomy, which is relatively homogeneous compared to the metal implant) with the usual, standard resolution forward model in (2), while employing a high resolution, high fidelity forward model for the μ_I portion (implant). The computational burden for computing high-resolution projections of μ_I is modest since the implant is compact in both the volume and in projections. Adopting the multiresolution forward model in (4) and following [14], one can construct a penalized-likelihood objective

$$\left\{{\widehat{\mu }}_{\ast },\widehat{\lambda }\right\}=argmax\mathit{L}({\mu }_{\ast },\lambda ;y)-\beta R({\mu }_{\ast })$$ (5)

with a log-likelihood term (L) and a regularization term (R). We solve this joint optimization problem using alternating maximizations using separable quadratic surrogates image updates [11] and Nelder-Mead registration updates.

RESULTS

To investigate the proposed methodology, we performed a simulation study comparing the proposed modified KCR approach with an ordinary penalized-likelihood method. A truth volume was derived from a high-resolution scan (150 μm voxels) of a temporal bone acquired using a flat-panel CBCT testbench. This volume was further upsampled to 50 μm and the B-spline based implant model was added (Figure 4). Projection data were generated using a flat-panel CBCT geometry (60 cm source-to-detector, 38 cm source-to-axis, 360 angles over 360°) with 0.48 mm detector pixels that were subsampled at 60 μm intervals and then aggregated to model NLPV. A relatively high exposure of 10⁵ photons per detector element was simulated and individual projection rays used a separable footprint [15] projection model.

Figure 4.

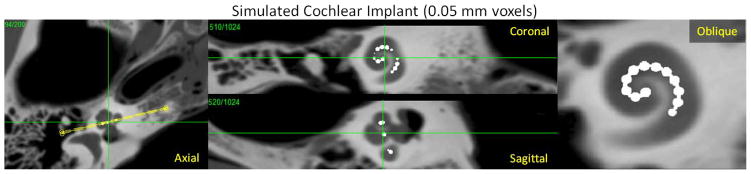
Simulated true volume based on high-resolution CBCT images of a temporal bone upsampled to 50 μm voxels and modified to include a simple cochlear implant model composed of a platinum wire and 20 spherical electrodes.

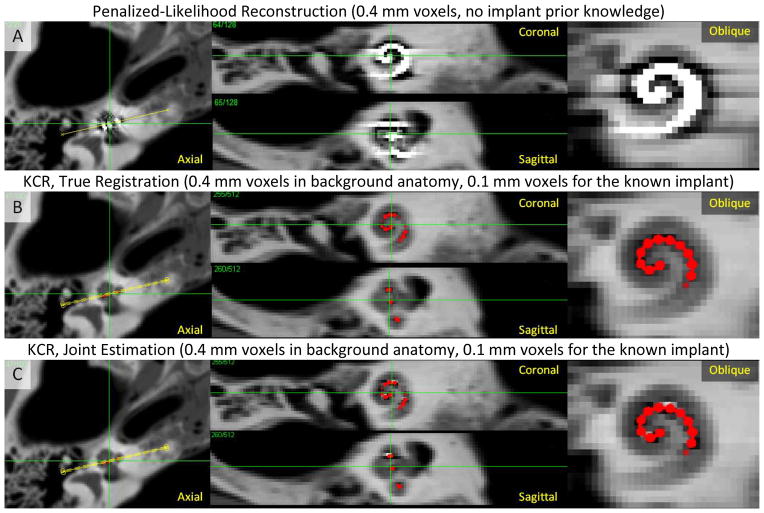
Figure 5 shows reconstructions demonstrating application of the KCR approach to cochlear imaging in a manner that mitigates NLPV effects. Figure 5A shows a conventional, quadratically penalized-likelihood reconstruction performed using 0.4 mm voxels and 200 iterations of OS-SPS, showing substantial NLPV artifacts including streaks, blooming, and systematic underestimation of attenuation immediately surrounding the implant - effectively obscuring the locations of individual electrodes. (Note that polyenergetic effects and x-ray scatter were not simulated and did not contribute to the observed artifacts). KCR computations used 0.4 mm voxels for the background anatomy, modeled the implant on a 0.1 mm grid, and modeled NLPV using detector pixels subsampled at 120 μm intervals (a mismatch from the 0.05 mm voxels and 60 μm intervals used for data generation). Two KCR cases were investigated: 1) 200 KCR iterations with knowledge of the true registration B-spline knot positions for the implant (Figure 5B); and 2) 500 KCR iterations with the full joint optimization - estimating both the image and the deformable registration using a mismatched B-spline model (Figure 5C). Both KCR images show a marked decrease in artifacts related to NLPV. Subtle artifacts are evident in the joint estimation due to errors in registration; however, the electrode positions are clear, and the surrounding anatomy is much better visualized with KCR than with traditional model-based reconstruction.

Figure 5.

KCR approach applied to imaging of a cochlear implant. A) Penalized-likelihood reconstruction at 0.4 mm voxels exhibits substantial artifacts due to inconsistencies arising from NLPV. B) KCR image (with implant position overlaid in red) computed using the variable resolution forward model to overcome NLPV effects (0.4 mm voxels and a 0.1 mm voxel implant model) with true registration parameters known. C) The KCR result using joint estimation of the image and the registration. Both KCR images show greatly reduced NLPV artifacts with subtle residual artifacts in the joint estimation due to registration errors.

One should recognize that KCR produces position estimates of the implant in addition to images. In these experiments we found the implant position estimation to be highly accurate. An illustration of the true and estimated implant position is shown in Figure 6. Note that the differing b-spline models between data generation and estimation are also illustrated, and while the estimation model is mismatched with generation, the b-spline trajectory is a close fit. The position estimate is very accurate with a maximum error between the two surfaces of about 50 μm - well below the size of individual electrodes and below both the anatomical background voxel size of 0.4 mm and the modeled implant voxel size of 100 μm. We believe that the residual registration errors are due, in part, to the relatively slow convergence of the Nelder-Mead registrations updates. Future studies will explore nature of these residual errors and other more sophisticated optimization strategies for registration.

Figure 6.

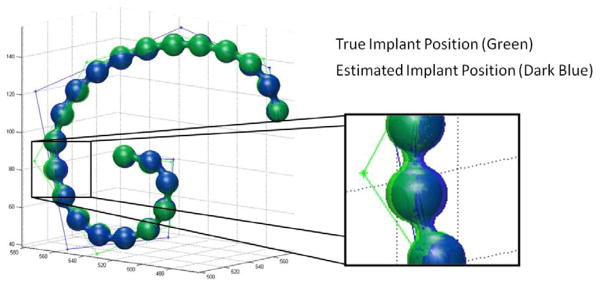
Illustration of the true and estimated cochlear implant positions. Surface renderings of the true and estimated implants are largely overlapping. A zoomed in version of the rendering shows a region of the implant where the position estimation error is largest; however, even in this region, the error is subvoxel (with a maximum error of about 50 μm) and much smaller than the diameter of the electrodes. One can also see the two sets of control points for the b-splines of the true and estimated implants. While mismatched in number of control points, the overall trajectory of the two splines are very close to each other.

CONCLUSION

This paper has introduced a novel model-based reconstruction approach that can mitigate NLPV artifacts. Based on the KCR approach, metallic devices (e.g., cochlear implants), which are particularly susceptible to NLPV effects, are modeled at very high resolution in both the image volume and in projections, capturing the most important part of NLPV. The remainder of the image volume (e.g., patient anatomy) is modeled at standard resolution which limits extra computation, and allows for specification of voxel size based on system resolution and noise (vs. the more strict NLPV requirements). We have demonstrated the efficacy of this approach in a cochlear imaging scenario and demonstrated near elimination of NLPV artifacts, which allows for visualization of individual electrodes on the implant, whereas traditional approaches are unable to resolve those features. Moreover, deformable registration estimates of the cochlear implant have sub-voxel accuracy providing additional information on the position of the implant within the cochlea. While this methodology is well-suited to the challenging task of cochlear implant localization and has great potential for impact in the tuning and assessment electrode positions; the technique is also general and can be adopted for NLPV artifact mitigation in other implant/known component scenarios as well.