Significance
The mechanism of movement of bacteria shows extensive diversity, and some bacteria glide on the substrate surface via an unknown process. Mycoplasma mobile is one of the fastest, exhibiting smooth gliding movement with a speed of 2.0–4.5 µm/s. By applying the modified in vitro ghost model of Mycoplasma mobile to high precision colocalization microscopy, steps of the regular size, ∼70 nm, were detected for the first time in bacteria, to our knowledge. The binding target of the gliding machinery, sialylated oligosaccharides, was expected to be randomly oriented on the surface and, thus, our results suggest that the machinery can drive the steps with a cycle of attachment and detachment even if there is no periodic structure on the substrate.
Keywords: bacteria tracking, gliding ghost, leg protein, pairwise distance function, F1-ATPase
Abstract
Among the bacteria that glide on substrate surfaces, Mycoplasma mobile is one of the fastest, exhibiting smooth movement with a speed of 2.0–4.5 μm⋅s−1 with a cycle of attachment to and detachment from sialylated oligosaccharides. To study the gliding mechanism at the molecular level, we applied an assay with a fluorescently labeled and membrane-permeabilized ghost model, and investigated the motility by high precision colocalization microscopy. Under conditions designed to reduce the number of motor interactions on a randomly oriented substrate, ghosts took unitary 70-nm steps in the direction of gliding. Although it remains possible that the stepping behavior is produced by multiple interactions, our data suggest that these steps are produced by a unitary gliding machine that need not move between sites arranged on a cytoskeletal lattice.
The fastest of the Mycoplasma species is Mycoplasma mobile (M. mobile); they glide with a speed of 2.0–4.5 μm⋅s−1 (1, 2). Under an optimal-growth condition, cultivated single M. mobile cells are flask-shaped (Fig. 1A) and glide smoothly across a substrate covered with surface-immobilized sialylated oligosaccharides (3) in the direction of protrusion at a constant speed (Movie S1). Genomic sequencing and analysis have revealed that the mechanism must differ from other forms of motor protein systems and bacterial motility, because M. mobile lacks genes encoding conventional motor proteins in eukaryotes, such as myosin, kinesin, and dynein, in addition to lacking other motility structures in bacteria, such as flagella and pili (4). So far, three proteins have been identified as a part of the gliding machinery (Fig. 1B, Bottom): Gli123 (5), Gli521 (6), and Gli349 (7). The machinery units localize around the cell neck, and their number has been estimated to be ∼450 (2, 5, 8). Gli349 extends out from the cell membrane and shows a rod structure, ∼100 nm in total, with two flexible hinges when isolated (9). Notably, the machinery is driven by hydrolysis of ATP to ADP and inorganic phosphate, caused by an unknown ATPase (10). Because of the large size and characteristic structure of Gli349, and a series of studies with mutants and inhibitory antibodies (2, 11), it has been hypothesized that Gli349 works as a “leg” by binding to and releasing from a substrate covered with randomly arranged sialylated oligosaccharides (2) consuming the chemical energy of ATP. In addition, the pivoting movement of an elongated cell suggests that there are units working not simultaneously but rather independently to propel the cell forward (12). To test this hypothesis and identify conformational changes of a key part of the gliding machinery, we here designed an assay to detect the movement of M. mobile by high precision colocalization microscopy. In the presence of an excess number of binding targets in the solution, which decreased the number of active legs, stepwise displacement was shown for the first time, to our knowledge, to occur in gliding bacteria.
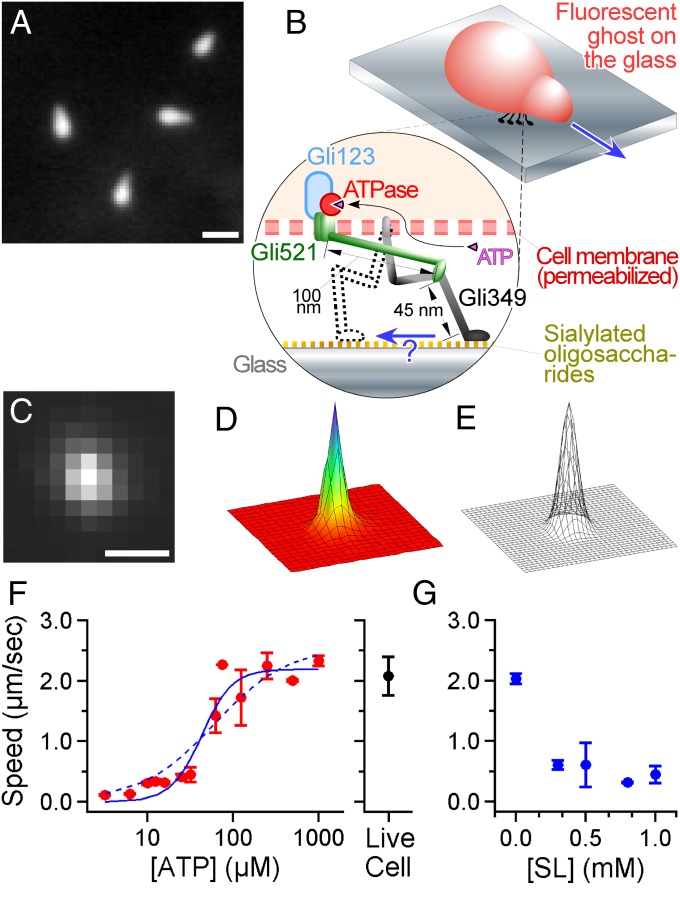
Fig. 1.
Nanometer-scale tracking of Mycoplasma gliding. (A) A dark-field image of M. mobile. The image was captured with center-stop optics to maintain the high numerical aperture of the objective, which enabled a high spatial resolution (35). (Scale bar: 1 μm.) (B, Upper) Illustration of the fluorescent ghost. The gliding machinery was distributed around the neck portion, but only the active machinery bound to the glass is shown for simplicity. (Bottom) A construction model of the gliding machinery comprising three proteins: Gli123, Gli521, and Gli349. See the review by Miyata (2) for more detail. (C) A fluorescent image of the labeled ghost was acquired with a time resolution of 2 ms. (Scale bar: 1 μm; pixel size: 240 nm.) (D) The intensity profile of C. The XY area is 5 × 5 μm. (E) Gaussian fitting to D. Nanometer-scale tracking is achieved by positioning the peak of the 2D Gaussian function fitting to the intensity profile of the ghost. (F, Left) The speed of gliding ghosts at different [ATP]s in the solution (n = 129). The cyan curve shows a fit with Michaelis–Menten kinetics; and Km are 2.6 µm⋅s−1 and 61 µM, respectively. The dotted cyan curve shows a fit with the kinetics including the Hill coefficient; , [ATP50] and n are 2.2 µm⋅s−1, 43 µM, and 2.4, respectively. (Right) The speed of living cells with no ATP in the solution (2.1 ± 0.1 µm⋅s−1; n = 22). (G) Effect of SL on the gliding velocity of the ghost at saturated [ATP]s, 0.3–1.0 mM (n = 50).
Results
Construction of an Assay for Tracking a Ghost with High Accuracy.
To track M. mobile with nanometer-scale precision, its cell surface was stained with a fluorescent probe, Cy3, and its position was localized by an EMCCD camera with a time resolution of 2 ms. Note that the shape of the cell is mostly symmetric and its size is less than 1 μm, which is close to the wavelength of visible light (Fig. 1 C and D). These two features made it possible to track the movements of the bacteria with nanometer-scale precision by fitting the intensity profile of a fluorescent cell with a 2D Gaussian function (Fig. 1E and Fig. S1), a technique (13) that has been successfully applied to submicron-scale plastic probes to detect the rotation of a single F1-ATPase, the smallest rotary molecular motor made of a single molecule (14, 15). Because motility at the cellular scale likely involves a large number of motors, isolating unitary conformational changes is essential for a complete understanding of the gliding mechanism. To dissect the movement, we used a permeabilized ghost model (10), in which the cell membrane was damaged with Triton X-100 and, thus, we could regulate the activity of ATPase by changing [ATP] (Fig. 1 B and F and Fig. S2). Finally, to reduce the number of functional gliding machinery units, sialylated oligosaccharides, which have been identified as the binding target of Gli349 (3, 16) and serve as a scaffold for M. mobile gliding, were added to the solution in the form of N-acetylneuraminyllactose (sialyllactose, SL). Notably, the gliding speed became slower with higher concentrations of SL (Fig. 1G), and the ghosts finally became unbound from the glass when [SL] was higher than 1.0 mM, presumably because the number of legs acting on the sialylated oligosaccharides on the glass was decreased as free SL was added to the solution. To optimize the conditions of the motility assay, 0.1% methylcellulose was also added to the solution to suppress the detachment of ghosts. Because the gliding speed did not alter much with or without methylcellulose (Fig. S3), we judged that the viscous drag against the gliding movement caused by a 0.1% concentration of methylcellulose was negligible.
Detection of Steps.
We recorded sequences of the gliding of ghosts under various [ATP]s at [SL] = 1.0 mM, and carefully observed their traces. Typically, the ghost glided with repetition of pauses and sudden displacements as shown in dense dots in Fig. 2A. This tendency was also confirmed at the high concentration of ATP (Fig. 2B), suggesting that the ghosts move not smoothly but rather intermittently under the condition where the number of acting legs was expected to be decreased. To check whether the displacements included a regular dispersion, we analyzed 937 ghosts at various ATP concentrations in the range of 6–1,330 μM. The period in which the ghost moved in a nearly straight line (e.g., the black portion in Fig. 2A) was further extracted. Although most runs showed creeping displacement and few intermittent pauses in the irregular manner, 196 ghosts showed more than two stepwise displacements. Among them, 134 records in 105 ghosts at [ATP] = 8–500 μM showed more than four clean steps. We also extracted 70 time courses in 60 ghosts that showed instantaneous stepping motion and could successfully be fitted with a step function by the step-finding algorithm as described in a later section.
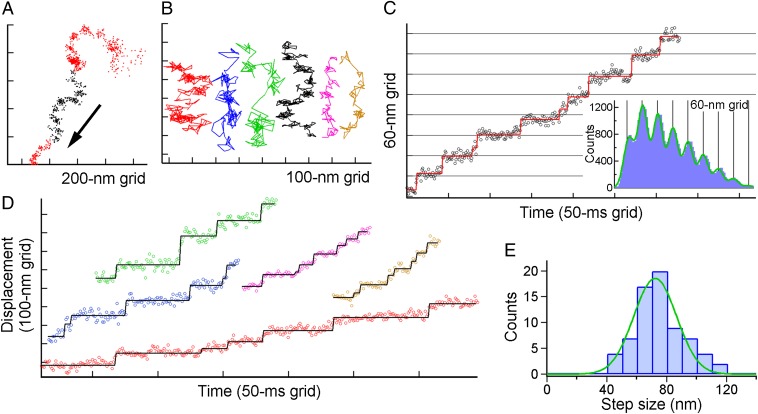
Fig. 2.
Steps of single ghosts of M. mobile driven by ATP. (A) A typical example of the XY trace of the single gliding ghost. Black points in the trace show the range in which we judge that the ghost moved in a nearly straight line and were subsequently analyzed with the pairwise distance function in C. (B) Examples of the trace at various concentrations of ATP. Red, blue, green, black, magenta, and orange represent [ATP] = 8, 16, 55, 90, 285, and 500 µM, respectively, and their colors coincide with those of the time course of the displacement in C and D. (C, Left) A typical example of the displacement along the gliding direction. Open circles are unfiltered data points, and rectangles in the displacement time course were the lines fitted with the step-finding algorithm. (Right) Histograms of the pairwise distance function (PDF) of the run. The green solid line is fitted to the sum of eight Gaussians. (D) Other examples of the displacement time course at various [ATP]s. (E) Histogram showing the distribution of step sizes estimated from the PDF analysis (n =70 runs in 60 ghosts; each run contains 4–9 steps) separated by 10-nm bins for clarity. The green solid curve shows the Gaussian distribution with 72 ± 14 nm.
An example of multiple steps is shown in Fig. 2C, Left. The unfiltered trajectory along the displacement direction showed clean steps with regular intervals, indicating that the movement driven by the gliding machinery of M. mobile may involve unitary steps. The existence of a step becomes apparent when the pairwise distance function (PDF) is applied to each run. As exemplified in Fig. 2C, Right, the intervals between pauses appeared as peaks of the PDF. The position of the peaks was precisely correlated with multiples of the size of a single step, suggesting that the gliding machinery repeats the stroke cycle for movement with high precision. The tendency was barely shown even in the absence of SL (Fig. S4); however, stepping was not instantaneous but gradual, possibly because the number of functional legs was still too large under this condition (Discussion). Displacements with regular steps were observed under a variety of [ATP]s (Fig. 2D), and particularly at a high [ATP], under which condition the dwells awaiting ATP binding were expected to be negligible from the estimation based on Fig. 1F. Fig. 2E shows a histogram of the step value determined from the PDF. The size of the step under these conditions was 72 ± 14 nm, assuming that the histogram comprises a single peak.
Characteristics of Dwell Time.
As reported for other molecular motors, the dwell time allows us to better understand the mechanism of motors at the molecular level in terms of chemo-mechanical coupling, i.e., the relationship between a chemical reaction (nucleotide binding and subsequent hydrolysis) and mechanical event (conformational change(s) of a motor). We applied a “step-finding algorithm” that was originally developed to analyze the position of tips of microtubules growing in a regular manner (17) to quantify the frequency and position of pauses. The fitting was performed to minimize the variation based on the algorithm (for details of the analysis, see Materials and Methods). As shown by the rectangles in Fig. 2 C and D, moments when stepping occurred were roughly estimated from the raw trajectory in each run. Histograms of the dwell time at various [ATP]s, 8–500 µM, were thus constructed from the fitting (Fig. 3A).
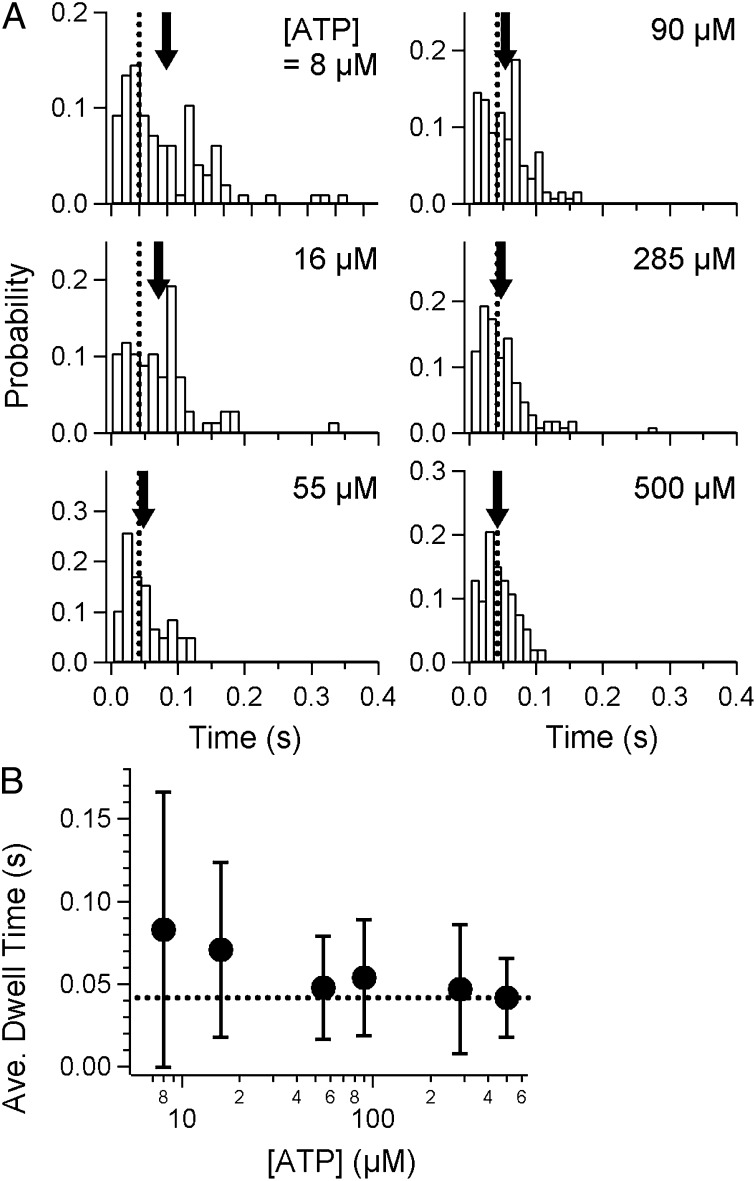
Fig. 3.
Dwell-time analysis of displacements. (A) Histograms of dwell times under various concentrations of ATP. Arrows indicate the average in each graph, and dashed lines indicate the average at 500 μM ATP. There was a slight, barely detectable increase at 8 and 16 μM, relative to that at 500 μM ATP, as shown by the gaps between the arrows and dashed lines. (B) Average of the dwell times (filled circles). The dashed line is the value at 500 μM ATP.
Note that, in our assay at this point, we were not able to determine the exact number of legs interacting with the surface, although steps of the regular size were successfully detected in each run. It may be possible that dwells with several or multiple motor units are incorporated in the histograms, which makes the interpretation of results quite complicated, as considered below in Discussion. The average of the dwell times at various [ATP]s is summarized in Fig. 3B. The maximum rate was estimated to be 24 s−1 at [ATP] = 500 µM, at which concentration the binding rate was expected to be almost saturated (Fig. 1F). A small increase in the dwell time was observed at the low [ATP]s of 8 and 16 μM, compared with that at 500 μM (arrows in Fig. 3A; P = 8.4 × 10−6 and 1.0 × 10−4, respectively, < 0.05 by Welch’s t test). Notably, the dwell time was merely doubled in the presence of SL at [ATP] ∼10 μM (Fig. 3B), whereas, in the absence of SL, the average gliding speed was ∼10 times lower compared with that at saturated [ATP] (Fig. 1F). This discrepancy may suggest that legs in the holding state could increase drag and, thus, reduce the speed of the movement driven by the leg in the power-stroke state only in the case that the number of legs was huge, while they immediately detached from the surface when they were fewer in number. This interpretation coincides with the observation of stepping without SL, in which the creeping displacement between steps was observed as shown in Fig. S4B, Inset.
Steps of Intact M. mobile.
To check whether the properties of steps in the ghost, especially their average size, were specific to the intact gliding machinery, we also analyzed the movement of M. mobile that was not treated with the detergent. Note that in this assay, we were not able to control the concentration of ATP inside the cell, and so we only reduced the number of legs by adding SL to the solution. As expected from the results of the ghost assay (Fig. 1G), the fraction of cells binding to the glass also depended on the concentration of SL in the solution (Fig. 4A). Gelatin was added to increase the solution viscosity, to make the fraction higher, and to maintain a sufficient number of cells on the surface for recording. The gliding speed decreased as SL was added to the solution (Fig. 4B), suggesting that the number of legs was successfully minimized. A single fluorescent particle was nonspecifically attached to the surface of the cell and was tracked with a nanometer-scale precision based on a technique for individual fluorescent probes (13) that has also been successfully applied to submicrometer-scale plastic probes to detect the rotation of a single F1-ATPase (15). As the speed decreased, the gliding showed intermittent pauses and, finally, stepwise movement appeared when 4–8 mM SL was added (Fig. 4C), although creeping was not eliminated during stepping. PDF analysis showed clear peaks being precisely correlated with multiples of the size of a single step (e.g., Fig. 4D). The size of step was estimated as 69 ± 11 nm (Fig. 4E; n = 35 runs in 23 cells), which was similar to the case of the ghost assay (P = 0.377 > 0.05 by Welch's t test). We conclude that the gliding machinery moves in unitary steps even when it operates under an intact condition where it is buried in the nontreated cell membrane, and the size of the step is ∼70 nm for both the ghosts and intact cells.
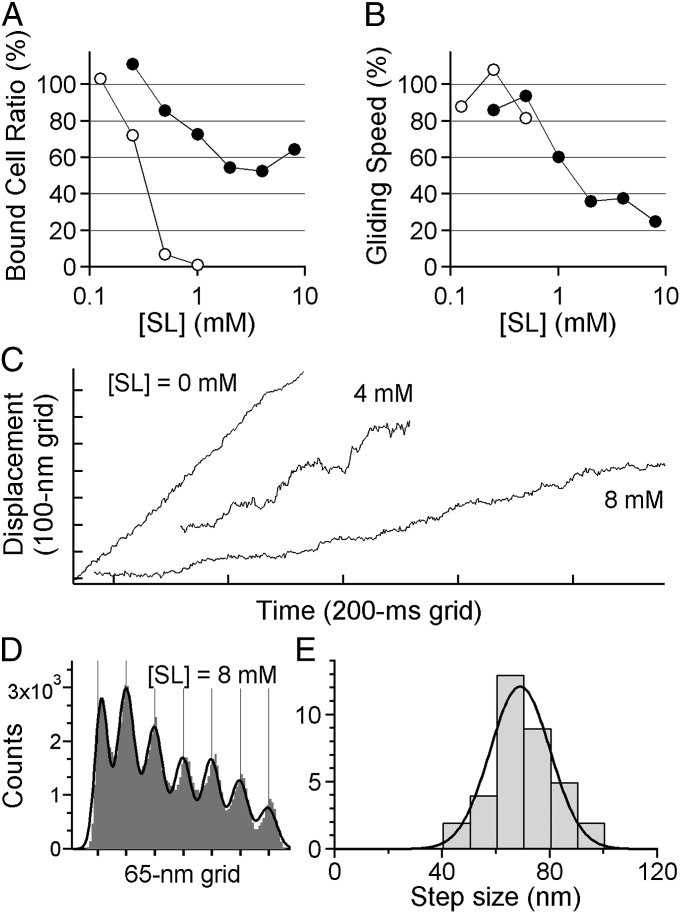
Fig. 4.
Steps of intact M. mobile without the detergent treatment. (A) Binding activity of intact M. mobile at various [SL]s. (B) Gliding speed. In A and B, filled and open circles show the data with or without, respectively, gelatin in the solution (n = 40); 100% means the number of cells bound to the glass surface at [SL] = 0 mM. (C) Gliding of intact M. mobile at various [SL]s. The displacement appeared smooth at 0 mM, whereas it became rather stepwise at 8 mM. (D) An example of histograms of the PDF analysis. The black line is fitted to the sum of seven Gaussians. (E) Histogram showing the distribution of step sizes of intact M. mobile from PDF analysis separated by 10 nm bins (n = 35 runs in 23 cells). The black curve shows the Gaussian distribution with 69 ± 11 nm.
Discussion
In this study, we established an assay in which the gliding motion of M. mobile was localized with nanometer-scale precision under an optical microscope. Cells were stained with a fluorescent probe and subsequently permeabilized on the glass to prepare the ghost model. Although the ghost showed frequent pauses and the histogram of PDF barely showed peaks of multiple numbers (Fig. S4), the steps were not clear because the stepping between pauses was not instantaneous but rather gradual (Fig. S4B, Inset). We further modified the motility assay system. The addition of free SL to the solution hindered the attachment of each leg to the sialylated oligosaccharides on the glass. Inversely, a high concentration of methylcellulose in the solution suppressed the detachment of M. mobile. By balancing these two conditions, stepwise displacement was finally achieved for the first time in gliding bacteria. Note that the concentration of SL approached that at which the ghost fully detaches from the surface. In fact, with the addition of SL, the average speed of ghosts decreased by about one-fourth (Fig. 1G). In the case that the duty ratio–the fraction of binding time over the single ATPase turnover–of the motor is low, it is generally considered that the average speed should decrease as the density of the motor decreases (18, 19). This model coincides with our observations.
Although the number of gliding machines involved in forward movement during the unitary step was not conclusively determined in our assay, we can infer a possible mechanism of the gliding machinery from the fact that the ghost showed clean and repetitive steps, as depicted in Fig. 2 C and D. One simple interpretation is that each 70-nm stepwise displacement corresponds to a single turnover in a single motor unit. In conventional linear motors such as myosin V, the size of a step is determined by the conformational change and additional Brownian search to land the next binding site on its track (20). However, the scenario including the track with a periodic structure is not the case for the gliding machinery of M. mobile, because its binding target is randomly oriented on the substrate surface. There might be unique and inherent characteristics that realize the huge but precise size of the steps. Probably, the specific conformational change in one of three (or more) machinery proteins directly determines the forward 70-nm movement of the ghost. Such conformational change itself could fluctuate largely and, thus, an additional mechanism would be needed to explain the occurrence of precise repetitive steps like those in Fig. 2. For example, it may be that the tip of the leg can bind to the target only when it makes a certain angle to the surface, as proposed for the mechanism of myosin (21, 22).
If the gliding machinery of M. mobile is a processive motor in the manner of kinesin-1 and myosin V, each of which has two functional domains in a single molecule and walks in a hand-over-hand manner by alternately using them (23, 24), then the dwell time between steps would be equal to the inverse of the rate of a rate-limiting chemical step of the single motor unit. In contrast, in the case that multiple active motors independently interact with the surface-immobilized sialylated oligosaccharides to move the ghost forward, the apparent dwell time would be expected to be shorter, because, in this case, one motor would stochastically induce the displacement before the rate-limiting chemical step in the other motor completed. With the above arguments in mind, we cannot evaluate the histograms in Fig. 3 without an assumption.
The increase in the dwell time was barely observed at low [ATP] (compare 8 and 16 µM), suggesting that the histograms may include a component that depends on [ATP]. Additionally, at high [ATP], the dwell time reached 42 ms, indicating the existence of a rate-limiting step, apart from ATP binding, on the order of 20 s−1 at most. The estimation of the average speed, (step size) × (rate) = (∼70 nm) × (∼20 s−1) = 1.4 μm⋅s−1, roughly coincides with the maximum speed of M. mobile. Additionally, if we assume that the number of legs is single, then kon of ATP and kcat of ATPase are estimated to be 15 × 10−6 s−1⋅M−1 and 15 s−1, respectively (Fig. S5, red curves), by the global fitting through histograms. Two chemical steps may be included at saturated [ATP] (Fig. S5, blue curve at 500 µM).
To address whether these estimations are proper, a reconstructed in vitro motile system, in which the number of gliding machineries is known to be one, is inevitable, as in cases of conventional motors such as myosin, kinesin, and dynein. The assay has not been established yet for the gliding machinery of M. mobile, because at least four proteins are needed and the legs are assumed to protrude from the membrane. In the future, some additional techniques, which incorporate protein arrangements in nanodiscs or liposomes, will be needed to reconstruct the unit as a whole active motor.
Because we cannot be certain about the number of active units when clean steps were detected in our present assay, one could argue that 70 nm is not the step size driven by the single assembly of the gliding machinery, but the sum of smaller steps driven by multiple motors. One possible scenario is that the clean 70-nm displacement is comprised of cooperative and sequential displacements of smaller steps. For example, repetitive small steps without an intermission longer than the time resolution of the observation system may appear as a large step, although strong cooperativity would be needed to explain the clear peaks in the histogram of PDF (Fig. 2C). Alternatively, the unbinding process of legs holding the ghost may directly determine the apparent size of each step. If the leg(s) that has just finished the conformational change still attaches to the ghost, it is probable that the leg subsequently works as a load when the other leg strokes and induces pauses at the halfway point of each step. This scenario would be similar to that reported for kinesin, in which the step sizes half those of a single motor were found as the result of force balance between two motors (25). To examine the above possibilities, again, a reconstructed in vitro motile system will be needed in the near future; in addition, it should be checked whether the motor in M. mobile can function as a processive motor.
From the structural point of view, what possible mechanisms can explain the regular step size of ∼70 nm? For the 8-nm step of kinesin and 36-nm step of myosin V, the sizes are determined by the repetitive structure of their substrate filaments, i.e., the microtubule and actin filaments, respectively. In contrast, M. mobile glides on a surface on which the binding target (16) is distributed randomly rather than being arranged in a regular manner. Additionally, because the leg protein, Gli349, is expected to be flexible rather than rigid (9), a simple stroke model like that of skeletal myosin (26), in which the lever part executes a stroke at a regular angle, is unlikely to explain the clear peaks of the PDF observed in Figs. 2C and 4D. Here, we propose a model in which stepwise movement is induced not by the tilting of the leg protein, but by the movement of the protein that connects the leg to ATPase. Gli521, which is assumed to work as a crank, is a rod-like structure with a size of 120 nm (27). The unidirectional movement and the large size of Gli521, in either the lateral, tilted, or rotating direction, could explain the step we observed. Because a protein similar to the catalytic subunit of F1-ATPase is located at the cytoskeleton-like structure that may arrange Gli123, Gli521, and Gli349 (28, 29), we hypothesize a model in which Gli521 converts a rotational motion of ATPase to a directed linear motion, much like a connecting rod between the wheels of a steam train. The movement of Gli521 may be effectively transmitted to Gli349 to make Gli349 pull against sialylated oligosaccharides on the glass. The broad distribution shown in Fig. 2E might be attributable to the variation of the binding configuration of Gli349 to the glass. In addition, to consistently maintain the regular steps, the detachment process of a leg is also important and could be regulated in terms of load dependence and directionality. This point, which is essential for elucidating the gliding mechanism in greater detail, will be addressed by measuring the unbinding force of a single leg of a ghost as in the case of myosin (30, 31), by using an optical trapping of the bead applied to the cell surface (32).
Materials and Methods
Preparation of the Fluorescent M. mobile.
A mutant strain of M. mobile, the P476R gli521 mutant, which binds to sialylated oligosaccharides more tightly than the wild-type strain (10, 11), was used in this study. Cells were cultured in Aluotto medium [2.1% (wt/vol) heart infusion broth, 0.56% yeast extract, 10% (vol/vol) horse serum, 0.025% thallium acetate, and 0.005% ampicillin] at 25 °C (33) until the absorbance at 600 nm reached 0.06–0.10. Cells in a culture with 1 mL of volume were collected by centrifugation at 12,000 × g for 4 min at 25 °C, resuspended in Aluotto medium, and subsequently incubated for 30 min before labeling. Cells were incubated in buffer A (75 mM sodium phosphate at pH 7.4 and 68.4 mM NaCl) containing 50 mM glucose and Cy3-NHS ester (GE Healthcare) for 2 h at room temperature and subsequently cleaned by two rounds of centrifugation after suspending with 500 and 200 µL of buffer A containing glucose.
Assay for Tracking the Gliding of Ghosts.
The flow chamber was comprised of two coverslips (No. 1, 0.12–0.17 mm thickness; Matsunami Glass) with different sizes (24 × 24 and 24 × 36 mm). Two pieces of double-sided tape, which were cut approximately 5 mm wide and 30 mm in length, were used as the spacers between coverslips (7). The resulting flow chamber had an internal volume of ∼7 µl. Aluotto medium was infused to the chamber and, thus, sialylated oligosaccharides included in the serum in the medium was nonspecifically bound to the glass surface. Fluorescent cells were infused into the chamber from one side and kept for 30 min. Unbound cells were removed with 20 µL of buffer B (buffer A containing 2 mM MgCl2, 1 mM DTT, and 1 mM EGTA). The solution in the chamber was replaced with 10 µL of buffer B containing 0.01% Triton X-100 (MP Biomedicals). Gliding cells were permeabilized with the surfactant and their movement was stopped and, thus, ghosts were prepared (10), typically within 1 min. The membrane permeabilization was judged by eye as the cytosol was ejected from the body and, thus, the density of the cells was reduced. At the moment when their density was reduced in the observation field, the solution was immediately replaced with 10 µL of buffer C [10 mM Tris⋅HCl at pH 7.5, 50 mM NaCl, 1 mM DTT, 1 mM EGTA, 2 mM MgCl2, and 0.5 mg/mL bovine-serum albumin (Sigma-Aldrich)] containing 1 mg⋅ml−1 DNase (Sigma-Aldrich). The chamber was subsequently washed with 10 µL of buffer C containing 0.1% methylcellulose (M0512, 4,000 cps at 2% solution; Sigma-Aldrich). Note that the drag force on the ghost from the viscosity of the surrounding fluid was calculated to be Fd = 2πηb/(ln(2b/a) – 0.5) × vglid = 0.008–0.07 pN and, thus, negligible (34), where the viscosity η is 1–5 cps for 0.1% methylcellulose solution; the half length of the ghost b is 0.5 µm; half of the size of the waist of the ghost a is 0.3 µm; and the gliding velocity vglid is 2–3 µm⋅s−1. The value of 5 cps was estimated from an extrapolation of the product information, and was used as the maximum viscosity of 0.1% methylcellulose solution, whereas 1 cps, equivalent to water, was used as the minimum viscosity in the case that M. mobile was too small to apply the macroscopic viscosity. Finally, to activate ghosts and observe their gliding, the solution was replaced with 30 µL of buffer C containing a desired amount of ATP (Sigma-Aldrich), 0.2 mg⋅mL−1 creatine kinase (Roche), 0.8 mg⋅mL−1 creatine phosphate (Roche), 1 mM N-acetylneuraminyllactose (SL; Sigma-Aldrich), and 0.1% methylcellulose. After the fluorescent image of the moving ghosts was captured, their phase-contrast image was also recorded to check whether each cell was successfully permeabilized and converted into a ghost; the density of ghosts was clearly lower than that of the living cells.
Gliding Assay of M. mobile with Fluorescent Beads.
After the infusion of unlabeled cells into the flow chamber, fluorescent beads of 100-nm diameter (Invitrogen) were infused. An individual bead could be nonspecifically attached to the cell membrane by chance, and the bead could be easily detected during its continuous movement on the glass surface when the flow chamber was observed under a fluorescence microscope.
Microscopy.
Fluorescent M. mobile was visualized under an inverted fluorescence microscope (Ti-E; Nikon Instruments) equipped with a 100× objective (Fluor 100 with Ph and 1.3 N.A.; Nikon Instruments), a filter set (TxRed-4040B; Semrock), an EMCCD camera (iXon+ DU860; Andor), a highly-stable customized stage (Chukousha), and an optical table (RS-2000; Newport). Projection of the image to the camera was made at 240 nm per pixel. Phase-contrast images of ghosts were also taken with another CCD camera (CS8420i; Toshiba TELI) to determine whether the cells were permeabilized by a surfactant. To acquire the image in Fig. 1A, a custom-made dark-field microscope (35) was used with a 100× objective (Plan Apo TIRF 1.4 N.A.; Olympus) and a CCD camera (CCD-300-RCX; Dage-MTI) under an inverted microscope (IX71; Olympus). In the gliding assay of M. mobile with a fluorescent bead, images were recorded by using a high-speed CCD camera system (HDR1600; Digimo).
Data Analyses.
Sequential images of the gliding of fluorescent ghosts were captured as 14-bit images with an EMCCD camera under 2-ms resolution and converted into a sequential TIF file without any compression. The position of single ghosts, (xc, yc), was determined by fitting each image with a 2D Gaussian including the cross-correlation term, cor, as , where I0 is the background intensity; A is a peak of the intensity of the ghost; and σx and σy are intensity variances along the x and y axis, respectively. For tracking of M. mobile, the parameters σx, σy, and cor were required to achieve a proper fitting, because single ghosts often appeared not as spherical but as ellipsoidal shapes. A was typically 800–2,000 under our capture conditions. In Fig. 1F, and were used as formulae for Michaelis–Menten kinetics and the kinetics including the Hill coefficient, respectively. To estimate the size of the unitary step, a PDF was independently adopted for each run showing stepwise displacement. A histogram with 5-nm bin width is shown in Fig. 2B and was fitted with the sum of the Gaussians with periodic intervals, Δ, as . Note that, in the case that stepwise displacements are always clean and pauses are stable, x0 should be 0 as indicated in the processive motor dynein (36). In contrast, creeping motions were observed to some extent in our measurement and, thus, we set the parameter x0 in the fitting. Back steps, i = –1 or less, were not included in the fitting, because they were not observed in our measurement.
Step-Finding Algorithm.
The step-finding algorithm was initially developed for quantitative detection of the growth and shrinkage of microtubule ends (17). The algorithm consists of three processes: (i) finding steps, (ii) evaluating the quality of the step fits, and (iii) finding the step distribution. (i) This process is the same as in the original method (17). Briefly, by fitting a single large step to the data based on a calculation of the χ2 statistics, the first step is determined. Next, the subsequent steps are found by fitting new steps to the dwells of the previous fitting, in the same way as for the first step. (ii) The second process was modified as follows: The quality of the fitting was based on evaluation of the variance of the displacement in each dwell, which was defined as . N is the number of steps. is a variance of the displacement in the i-th dwell. is a mean of the variances in each dwell. In addition, Q weighed by was used for the third process. In the case of under-fitting, the large values of and the weight (w) contribute to the low value of . In the case of overfitting, the values of are small but N is large, so that the summation of allows the value of to be low. (iii) The highest value basically represents the best fitting. In practical terms, a value of that was not the highest value (usually the second highest value) toward the overfitting, was often adopted as the best fitting, especially when some data had nonuniformity of fluctuation of the displacement.
Supplementary Material
Acknowledgments
We thank A. Upadhyaya for critical comments, M. P. Sheetz for comments on an earlier draft, and M. Kaya and A. Tatsuguchi for their technical advice and critical discussion. This study was supported in part by the Funding Program for Next Generation World-Leading Researchers Grant LR033 (to T.N.) from the Japan Society for the Promotion of Science, by Grant-in-Aid for Scientific Research on Innovative Areas “Harmonized Supramolecular Motility Machinery and Its Diversity (M.M. and T.N.) and “Fluctuation & Structure” (Grant 26103527 to T.N.), by Grant-in-Aid for Young Scientists (Grant 25893230 to D.N.) from the Ministry of Education, Culture, Sports, Science, and Technology of Japan, by the Asahi Glass Foundation (D.N.), by the Institute for Fermentation (D.N.), and by the Naito Foundation Natural Science Scholarship (D.N.).
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1310355111/-/DCSupplemental.
References
- 1.Rosengarten R, Kirchhoff H. Gliding motility of Mycoplasma sp. nov. strain 163K. J Bacteriol. 1987;169(5):1891–1898. doi: 10.1128/jb.169.5.1891-1898.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Miyata M. Unique centipede mechanism of Mycoplasma gliding. Annu Rev Microbiol. 2010;64:519–537. doi: 10.1146/annurev.micro.112408.134116. [DOI] [PubMed] [Google Scholar]
- 3.Nagai R, Miyata M. Gliding motility of Mycoplasma mobile can occur by repeated binding to N-acetylneuraminyllactose (sialyllactose) fixed on solid surfaces. J Bacteriol. 2006;188(18):6469–6475. doi: 10.1128/JB.00754-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jaffe JD, et al. The complete genome and proteome of Mycoplasma mobile. Genome Res. 2004;14(8):1447–1461. doi: 10.1101/gr.2674004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Uenoyama A, Miyata M. Identification of a 123-kilodalton protein (Gli123) involved in machinery for gliding motility of Mycoplasma mobile. J Bacteriol. 2005;187(16):5578–5584. doi: 10.1128/JB.187.16.5578-5584.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Seto S, Uenoyama A, Miyata M. Identification of a 521-kilodalton protein (Gli521) involved in force generation or force transmission for Mycoplasma mobile gliding. J Bacteriol. 2005;187(10):3502–3510. doi: 10.1128/JB.187.10.3502-3510.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Uenoyama A, Kusumoto A, Miyata M. Identification of a 349-kilodalton protein (Gli349) responsible for cytadherence and glass binding during gliding of Mycoplasma mobile. J Bacteriol. 2004;186(5):1537–1545. doi: 10.1128/JB.186.5.1537-1545.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Miyata M. Cell Motility “Molecular Mechanism of Mycoplasma Gliding -A Novel Cell Motility System”. New York: Springer; 2007. , pp 6, 137–175. [Google Scholar]
- 9.Adan-Kubo J, Uenoyama A, Arata T, Miyata M. Morphology of isolated Gli349, a leg protein responsible for Mycoplasma mobile gliding via glass binding, revealed by rotary shadowing electron microscopy. J Bacteriol. 2006;188(8):2821–2828. doi: 10.1128/JB.188.8.2821-2828.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Uenoyama A, Miyata M. Gliding ghosts of Mycoplasma mobile. Proc Natl Acad Sci USA. 2005;102(36):12754–12758. doi: 10.1073/pnas.0506114102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Uenoyama A, Seto S, Nakane D, Miyata M. Regions on Gli349 and Gli521 protein molecules directly involved in movements of Mycoplasma mobile gliding machinery, suggested by use of inhibitory antibodies and mutants. J Bacteriol. 2009;191(6):1982–1985. doi: 10.1128/JB.01012-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nakane D, Miyata M. Mycoplasma mobile cells elongated by detergent and their pivoting movements in gliding. J Bacteriol. 2012;194(1):122–130. doi: 10.1128/JB.05857-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thompson RE, Larson DR, Webb WW. Precise nanometer localization analysis for individual fluorescent probes. Biophys J. 2002;82(5):2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nishizaka T, et al. Chemomechanical coupling in F1-ATPase revealed by simultaneous observation of nucleotide kinetics and rotation. Nat Struct Mol Biol. 2004;11(2):142–148. doi: 10.1038/nsmb721. [DOI] [PubMed] [Google Scholar]
- 15.Sugawa M, Okada KA, Masaike T, Nishizaka T. A change in the radius of rotation of F1-ATPase indicates a tilting motion of the central shaft. Biophys J. 2011;101(9):2201–2206. doi: 10.1016/j.bpj.2011.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kasai T, et al. Role of binding in Mycoplasma mobile and Mycoplasma pneumoniae gliding analyzed through inhibition by synthesized sialylated compounds. J Bacteriol. 2013;195(3):429–435. doi: 10.1128/JB.01141-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kerssemakers JW, et al. Assembly dynamics of microtubules at molecular resolution. Nature. 2006;442(7103):709–712. doi: 10.1038/nature04928. [DOI] [PubMed] [Google Scholar]
- 18.Sakakibara H, Kojima H, Sakai Y, Katayama E, Oiwa K. Inner-arm dynein c of Chlamydomonas flagella is a single-headed processive motor. Nature. 1999;400(6744):586–590. doi: 10.1038/23066. [DOI] [PubMed] [Google Scholar]
- 19.Uyeda TQP, Warrick HM, Kron SJ, Spudich JA. Quantized velocities at low myosin densities in an in vitro motility assay. Nature. 1991;352(6333):307–311. doi: 10.1038/352307a0. [DOI] [PubMed] [Google Scholar]
- 20.Shiroguchi K, Kinosita K., Jr Myosin V walks by lever action and Brownian motion. Science. 2007;316(5828):1208–1212. doi: 10.1126/science.1140468. [DOI] [PubMed] [Google Scholar]
- 21.Ali MY, et al. Unconstrained steps of myosin VI appear longest among known molecular motors. Biophys J. 2004;86(6):3804–3810. doi: 10.1529/biophysj.103.037416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shiroguchi K, et al. Direct observation of the myosin Va recovery stroke that contributes to unidirectional stepping along actin. PLoS Biol. 2011;9(4):e1001031. doi: 10.1371/journal.pbio.1001031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yildiz A, Tomishige M, Vale RD, Selvin PR. Kinesin walks hand-over-hand. Science. 2004;303(5658):676–678. doi: 10.1126/science.1093753. [DOI] [PubMed] [Google Scholar]
- 24.Yildiz A, et al. Myosin V walks hand-over-hand: Single fluorophore imaging with 1.5-nm localization. Science. 2003;300(5628):2061–2065. doi: 10.1126/science.1084398. [DOI] [PubMed] [Google Scholar]
- 25.Leduc C, Ruhnow F, Howard J, Diez S. Detection of fractional steps in cargo movement by the collective operation of kinesin-1 motors. Proc Natl Acad Sci USA. 2007;104(26):10847–10852. doi: 10.1073/pnas.0701864104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ruff C, Furch M, Brenner B, Manstein DJ, Meyhöfer E. Single-molecule tracking of myosins with genetically engineered amplifier domains. Nat Struct Biol. 2001;8(3):226–229. doi: 10.1038/84962. [DOI] [PubMed] [Google Scholar]
- 27.Nonaka T, Adan-Kubo J, Miyata M. Triskelion structure of the Gli521 protein, involved in the gliding mechanism of Mycoplasma mobile. J Bacteriol. 2010;192(3):636–642. doi: 10.1128/JB.01143-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nakane D, Miyata M. Cytoskeletal “jellyfish” structure of Mycoplasma mobile. Proc Natl Acad Sci USA. 2007;104(49):19518–19523. doi: 10.1073/pnas.0704280104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tulum I, Yabe M, Uenoyama A, Miyata M. Localization of P42 and an F1-ATPase α-subunit homolog of the gliding machinery in Mycoplasma mobile revealed by newly developed gene manipulation and fluorescent protein tagging. J Bacteriol. 2014;196(10):1815–1824. doi: 10.1128/JB.01418-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nishizaka T, Miyata H, Yoshikawa H, Ishiwata S, Kinosita K., Jr Unbinding force of a single motor molecule of muscle measured using optical tweezers. Nature. 1995;377(6546):251–254. doi: 10.1038/377251a0. [DOI] [PubMed] [Google Scholar]
- 31.Nishizaka T, Seo R, Tadakuma H, Kinosita K, Jr, Ishiwata S. Characterization of single actomyosin rigor bonds: Load dependence of lifetime and mechanical properties. Biophys J. 2000;79(2):962–974. doi: 10.1016/S0006-3495(00)76350-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nishizaka T, Shi Q, Sheetz MP. Position-dependent linkages of fibronectin- integrin-cytoskeleton. Proc Natl Acad Sci USA. 2000;97(2):692–697. doi: 10.1073/pnas.97.2.692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Miyata M, et al. Gliding mutants of Mycoplasma mobile: Relationships between motility and cell morphology, cell adhesion and microcolony formation. Microbiology. 2000;146(Pt 6):1311–1320. doi: 10.1099/00221287-146-6-1311. [DOI] [PubMed] [Google Scholar]
- 34.Miyata M, Ryu WS, Berg HC. Force and velocity of Mycoplasma mobile gliding. J Bacteriol. 2002;184(7):1827–1831. doi: 10.1128/JB.184.7.1827-1831.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Masaike T, Koyama-Horibe F, Oiwa K, Yoshida M, Nishizaka T. Cooperative three-step motions in catalytic subunits of F1-ATPase correlate with 80° and 40° substep rotations. Nat Struct Mol Biol. 2008;15(12):1326–1333. doi: 10.1038/nsmb.1510. [DOI] [PubMed] [Google Scholar]
- 36.Mallik R, Carter BC, Lex SA, King SJ, Gross SP. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427(6975):649–652. doi: 10.1038/nature02293. [DOI] [PubMed] [Google Scholar]